Distributed Newton Methods for Strictly Convex Consensus Optimization Problems in Multi-Agent Networks

Abstract

Various distributed optimization methods have been developed for consensus optimization problems in multi-agent networks. Most of these methods only use gradient or subgradient information of the objective functions, which suffer from slow convergence rate. Recently, a distributed Newton method whose appeal stems from the use of second-order information and its fast convergence rate has been devised for the network utility maximization (NUM) problem. This paper contributes to this method by adjusting it to a special kind of consensus optimization problem in two different multi-agent networks. For networks with Hamilton path, the distributed Newton method is modified by exploiting a novel matrix splitting techniques. For general connected multi-agent networks, the algorithm is trimmed by combining the matrix splitting technique and the spanning tree for this consensus optimization problems. The convergence analyses show that both modified distributed Newton methods enable the nodes across the network to achieve a global optimal solution in a distributed manner. Finally, the distributed Newton method is applied to solve a problem which is motivated by the Kuramoto model of coupled nonlinear oscillators and the numerical results illustrate the performance of the proposed algorithm.

1. Introduction

A number of problems that arise in the context of wired and wireless networks can be posed as the minimization of a sum of functions, when each component function is available only to a specific agent [1]. Decentralized consensus optimization problems are an important class of these problems [2]. To solve these problems, distributed methods—which only require the agents to locally exchange information between each other—gain a growing interest with every passing day. Nedic and Ozdaglar [3,4] proposed distributed subgradient methods and provided convergence results and convergence rate estimates for this method. Some extensions [5,6] of this method were subsequently proposed. Ram et al. [5] adjusted a distributed subgradient method to address the problem of vertically and horizontally distributed regression in large peer-to-peer systems. Lobel and Ozdaglar [6] studied the consensus optimization problem over a time-varying network topolopy and proposed a distributed subgradient method that uses averaging algorithms for locally sharing information among the agents. Moreover, Ram et al. [1] proposed a distributed stochastic subgradient projection algorithm and explored the effects of stochastic subgradient errors on the convergence of the algorithm. These methods only used gradient or subgradient information of the objective functions, which suffered from slow convergence rate. Apart from these gradient or subgradient methods, Mota et al. [7] combined the centering alternating direction method of multiplier (ADMM) [8] and node-coloring technique and proposed a distributed ADMM (D-ADMM) algorithm for the consensus optimization problem. This method makes some improvements in convergence rate over distributed subgradient methods. Compared with conventional centralized methods, the distributed methods have faster computing efficiency and have been widely used in many fields, such as image processing [9,10], computer vision [11], intelligent power grids [12,13], machine learning [14,15], unrelated parallel machine scheduling problems [16], model predictive control (MPC) problems [17], and resource allocation problems in multi-agent communication networks [18,19].

These distributed algorithms mentioned above are all first-order methods, since they only use gradient or subgradient information of the objective function. To substitute for the distributed gradient method for solving the unconstrained minimization problem mentioned by Nedic and Ozdaglar [3], Mokhtari et al. [20] proposed a network Newton (NN)-K method based on the second-order information, where K is the number of Taylor series terms of the Newton step. NN-K can be implemented through the aggregation of information in K-hop neighborhoods in every iteration. Consequently, the communication between the adjacent nodes will increase exponentially with the augment of the number of iterations. To ensure the iterative results closer to the optimal value, a larger K should be selected and it is time-consuming—especially for large-scale networks.

Another second-order method—the distributed Newton method—was proposed by Wei et al. [21] to solve the network utility maximization (NUM) problem in a distributed manner. NUM can be formulated as a convex optimization problem with equality constraints by introducing some slack variables and the coefficient matrix of the equality constraints having full row rank. This distributed Newton-type second-order algorithm achieves superlinear convergence rate in terms of primal iterations, but it cannot solve consensus optimization problems in multi-agent networks. Tracing its root, the coefficient matrix of the constraint does not have full row rank, and predetermined routes cannot be given in the general optimization problem.

The distributed Newton method addressed in this study aims to solve the problem of minimizing a sum of strictly convex objective functions where the components of the objective are available at different nodes of a network. This paper adds to the growing body of knowledge regarding distributed second order methods. The contributions made by this paper are three-fold.

• Adjusting the distributed Newton algorithm for the NUM problem to a special kind of consensus optimization problem in multi-agent networks with a Hamilton path. To overcome the obstacle, computation of the dual step involves the global information of the Hessian matrix, and an iterative scheme based on a novel matrix splitting technique is devised. Further, the convergence of the distributed Newton algorithm is proved theoretically.
• A modified distributed Newton algorithm is proposed for consensus optimization problems in connected multi-agent networks. The coefficient matrix has full row rank by constructing a spanning tree of the connected network. Combined with the matrix splitting technique for NUM, the distributed Newton method for multi-agent convex optimization is proposed and a theory is presented to show the global convergence of the method.
• The effectiveness of the modified distributed Newton methods is demonstrated by a numerical experiment. The experiment is based on the Kuramoto model of coupled nonlinear oscillators. The proposed distributed Newton method can be applied to solve this model more efficiently compared with two first-order methods

The rest of the paper is organized as follows: Section 2 provides some necessary preliminaries. Section 3 formulates the general multi-agent strictly convex consensus optimization problem in connected networks. Section 4 presents a distributed inexact Newton method in networks with a Hamilton path. A solution algorithm to solve the problem in general connected networks is proposed in Section 5. Section 6 presents the simulation results to demonstrate convergence properties of the algorithms. Finally, conclusions and recommendations for future work are provided in Section 7.

2. Preliminaries

Consider a connected network with P nodes and E edges modeled by a undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, where $\mathcal{V}=\{1,2,\cdots ,P\}$ is the set of nodes and $\mathcal{E}\subset \mathcal{V}\times \mathcal{V}$ is the set of edges.

Referring to Wei et al. [21], the NUM problem can be written as follows:

$$\begin{array}{cc}\min \hfill & f\left(x\right)=f_1\left(x_1\right)+f_2\left(x_2\right)+\cdots +f_P\left(x_P\right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & Ax=c,\hfill \end{array}$$

(1)

where $f_i\left(x_i\right)$ is a strictly convex function, matrix A has full row rank, and c is a constant vector. This problem can be solved by an exact Newton method,

$$x^{k+1}=x^k+d^k▵x^k,$$

(2)

where $▵x^k$ is the Newton direction given as the solution of the following system of linear equations

$$\left[\begin{array}{cc}{\nabla }^{2}f\left(x^k\right)& A^{\prime }\\ A& 0\end{array}\right]\left[\begin{array}{c}▵x^k\\ {\omega }^k\end{array}\right]=-\left[\begin{array}{c}\nabla f\left(x^k\right)\\ 0\end{array}\right],$$

(3)

where $x^k$ is the primal vector, ${\omega }^k$ is the dual vector, $\nabla f\left(x^k\right)$ is the gradient vector, and ${\nabla }^{2}f\left(x^k\right)$ is the Hessian matrix. Moreover, ${\nabla }^{2}f\left(x^k\right)$ is abbreviated as $H_k$ for notational convenience.

Solving $▵x^k$ and ${\omega }^k$ in the preceding system yields

$$▵x^k=-H_k^{-1}(\nabla f\left(x^k\right)+A^{\prime }{\omega }^k),$$

(4)

$$\left(A{H}_k^{-1}{A}^{\prime }\right){\omega }^k=-A{H}_k^{-1}\nabla f\left(x^k\right).$$

(5)

Since $f\left(x\right)$ is a separable, strictly convex function, its Hessian matrix is a positive definite diagonal matrix, and hence Equation (4) can be easily computed by a distributed iterative scheme. Wei et al. [21] proposed a distributed Newton method for the NUM problem (1) by using a matrix splitting scheme to compute the dual vector ${\omega }^k$ in Equation (5) in a distributed manner. Let $C_k$ be a diagonal matrix, with diagonal entries

$${\left(C_k\right)}_{ll}={\left(A{H}_k^{-1}{A}^{\prime }\right)}_{ll},$$

(6)

Matrix $B_k$ is given by

$$B_k=A{H}_k^{-1}{A}^{\prime }-C_k.$$

(7)

Let matrix ${\overline{B}}_k$ be a diagonal matrix with diagonal entries

$${\left(\overline{B_k}\right)}_{ii}=\sum _{j=1}^L{\left(B_k\right)}_{ij}.$$

(8)

By splitting the matrix $A{H}_k^{-1}{A}^{\prime }$ as the sum of $C_k+{\overline{B}}_k$ and $B_k-{\overline{B}}_k$, the following theorem [21] can be obtained.

Theorem 1. 

For a given $k>0$, let $C_k$, $B_k$, ${\overline{B}}_k$ be the matrices defined in Equations (6)–(8). Let ${\omega }^0$ be an arbitrary initial vector. We can obtain the sequence $\left\{{\omega }^t\right\}$ by the following iteration

$${\omega }^{t+1}={(C_k+{\overline{B}}_k)}^{-1}({\overline{B}}_k-B_k){\omega }^t+{(C_k+{\overline{B}}_k)}^{-1}(-A{H}_k^{-1}\nabla f\left(x^k\right)).$$

(9)

Then, the spectral radius of the matrix ${(C_k+{\overline{B}}_k)}^{-1}({\overline{B}}_k-B_k)$ is strictly bounded above by 1 and the sequence $\left\{{\omega }^t\right\}$ converges to the solution of Equation (5) as $t\to \infty$.

Note that the predetermined routes and full row rank coefficient matrix are necessary when running the distributed Newton method for the NUM problem according to Reference [21]. Unfortunately, this property is usually not met in the general multi-agents consensus optimization problems.

3. Problem Formulation

For the multi-agents consensus optimization problems proposed in this paper, only agent p has access to its private cost function $f_p$ and can communicate with its neighbors using the network infrastructure. This situation can be illustrated in Figure 1; i.e., node 2 can communicate with its adjacent nodes 1, 3, 6, and 7. Node i has its own objective function $f_i$, and all nodes cooperate in minimizing the aggregate cost function $f\left(x\right)$

$$\begin{array}{cc}\underset{x}{\min }\hfill & f\left(x\right)=f_1\left(x\right)+f_2\left(x\right)+\cdots +f_P\left(x\right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & x\in R^n,\hfill \end{array}$$

(10)

where $x\in R^n$ is the global optimization variable. This problem is also known as the consensus optimization problem and its optimal solution is donated as $x^{*}$.

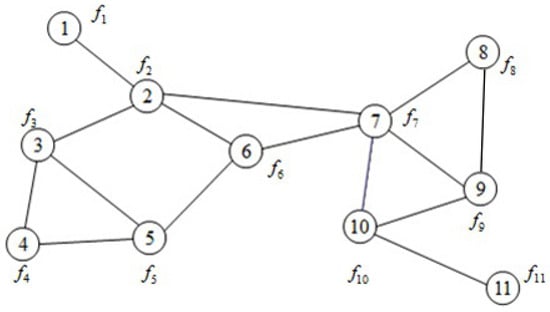
Figure 1. Network with $P=11$ nodes.

A common technique to decouple problem (10) is to assign copies of the global variable x to each node and then constrain all copies to be equal. Denoting the copy held by node p with $x_p\in R^n$, problem (10) is written equivalently as

$$\begin{array}{cc}\min \hfill & f_1\left(x_1\right)+f_2\left(x_2\right)+\cdots +f_P\left(x_P\right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & x_i=x_j,\{i,j\}\in \mathcal{E}.\hfill \end{array}$$

(11)

Problem (11) is no longer coupled by the common variable in all $f_p$, but instead by the new equations $x_i=x_j$, for all pairs of edges in the network $\{i,j\}\in \mathcal{E}$. These equations enforce all copies to be equal while the network is connected. Note that they can be written more compactly as $(B^T⨂I_n)x=0$, where $B\in R^{P\times E}$ is the node arc-incidence matrix of the graph, $I_n$ is the identity matrix in $R^n$, and ⨂ is the Kronecker product, $x=(x_1,x_2,\cdots ,x_P)\in {\left(R^n\right)}^P$ is the optimization variable. Each column of B is associated with an edge $(i,j)\in \mathcal{E}$ and has 1 and -1 in the ith and jth entry, respectively; the remaining entries are zeros. Problem (11) can be rewritten as

$$\begin{array}{cc}\min \hfill & f\left(x\right)={\sum }_{p=1}^{p=P}{f}_p\left(x_p\right)\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & Ax=0,\hfill \end{array}$$

(12)

where A is the coefficient matrix taking values $A=B^T⨂I_n$. In this paper we assume that the local costs $f_p$ are twice differentiable and strongly convex.

4. Distributed Newton Method For Multi-Agent Consensus Optimization Problems in Networks with a Hamilton Path

For some networks with particular topology structures (e.g., a Hamilton path), we can use special techniques to solve the proposed consensus optimization problem. In this section, a novel matrix splitting technique is devised for multi-agent consensus optimization problems in networks with a Hamilton path, which travels every node in the network just once. For simplicity, we renumber these nodes from 1 to $P(P=11)$ along this path as depicted in Figure 2. We know that every dual variable corresponds to one link, so ${\omega }_i$ ($i=1,2,\cdots ,P-1$) can be used to denote the dual variable ${\omega }_{i,i+1}$, which is stored in node i. In Figure 2, node 0 is the copy of node 1 and it is actually non-existent. We add the definition of ${\omega }_0=0$ and ${\omega }_P=0$ for the sake of analysis.

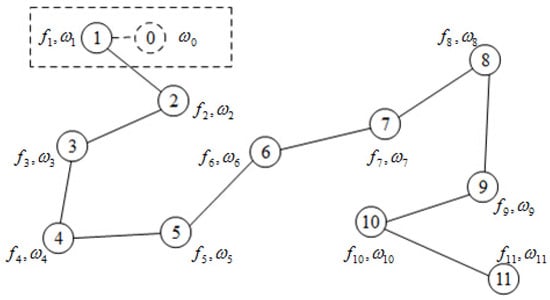
Figure 2. A Hamilton path of network with $P=11$ nodes.

From Figure 2, the coefficient matrix A in problem (12) is a dual-diagonal matrix given by

$$A=\left[\begin{array}{cccccccc}I\hfill & -I\hfill & 0\hfill & 0\hfill & & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & I\hfill & -I\hfill & 0\hfill & \cdots \hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & I\hfill & -I\hfill & & 0\hfill & 0\hfill & 0\hfill \\ & & ⋮\hfill & & \ddots \hfill & & ⋮\hfill & \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & \dots \hfill & I\hfill & -I\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & & 0\hfill & I\hfill & -I\hfill \end{array}\right],$$

(13)

where I is an identity matrix of dimension n.

Let $M_k$ be a diagonal matrix with diagonal entries

$${\left(M_k\right)}_{pp}={\left(A{H}_k^{-1}{A}^{\prime }\right)}_{pp}=Q_p^{-1}+Q_{p+1}^{-1},$$

(14)

where $Q_p={\left(H_k\right)}_{pp}=\frac{{\partial }^{2}f\left(x^k\right)}{\partial x_p^2}$ is the diagonal block of the Hessian matrix. Matrix $N_k$ is given by

$$N_k=A{H}_k^{-1}{A}^{\prime }-M_k,$$

(15)

By splitting matrix $A{H}_k^{-1}{A}^{\prime }$ as the sum of $M_k$ and $N_k$, a Jacobian iteration can be used to compute the dual vector ${\omega }^k$ in (5) in a distributed manner.

Theorem 2. 

For a given $k>0$, let $M_k$ and $N_k$ be the matrices defined in (14) and (15) and ${\omega }^0$ be an arbitrary initial vector. The sequence $\left\{{\omega }^t\right\}$ can be obtained by the iteration

$${\omega }^{t+1}=-M_k^{-1}{N}_k{\omega }^t-M_k^{-1}A{H}_k^{-1}\nabla f\left(x^k\right).$$

(16)

Then, the spectral radius of the matrix $M_k^{-1}{N}_k$ is strictly bounded above by 1 and the sequence $\left\{{\omega }^t\right\}$ converges to the solution of (5) as $t\to \infty$.

Proof of Theorem 2. 

The proof is described in Appendix A. ☐

There are many ways to split the matrix $A{H}_k^{-1}{A}^{\prime }$, Jacobian iteration is selected in our method due to two reasons. Firstly, considering the special structure of the matrices A and $H_k^{-1}$, the spectral radius of Jacobian matrix can be guaranteed strictly bounded above by 1 and thus the sequence $\left\{{\omega }^k\right\}$ converges as $k\to \infty$. Secondly, the matrix $M_k$ is diagonal, which guarantees that the dual variable is updated without global information.

Next, a distributed computation procedure to calculate the dual vector will be developed by rewriting the iteration (16).

Theorem 3.

The dual iteration (16) can be written as

$${\omega }_i^{t+1}={(Q_i^{-1}+Q_{i+1}^{-1})}^{-1}(Q_i^{-1}{\omega }_{i-1}^t+Q_{i+1}^{-1}{\omega }_{i+1}^t+a_i)i=1,2,\cdots ,P-1,$$

(17)

where $a_i=Q_{i+1}^{-1}{\nabla }_{i+1}f\left(x^k\right)-Q_i^{-1}{\nabla }_{i}f\left(x^k\right),{\omega }_0=0$ and ${\omega }_P=0$.

Proof of Theorem 3. 

The proof is described in Appendix B. ☐

From this theorem, each link variable ${\omega }_i$ is updated using its private result, $Q_i,{\nabla }_{i}f\left(x^k\right)$, and the information from its neighbors; i.e., ${\omega }_{i-1}^t,Q_{i+1}$, ${\nabla }_{i+1}f\left(x^k\right),{\omega }_{i+1}^t$. The adjacent nodes’ information is obtained directly through the information exchange. Therefore, the dual variable can be obtained in a distributed manner.

Once the dual variables are computed, the primal Newton direction can be obtained according to (4) as:

$$\left[\begin{array}{c}▵x_1^k\\ ▵x_2^k\\ ▵x_3^k\\ ⋮\\ ▵x_n^k\end{array}\right]=\left[\begin{array}{c}-Q_1^{-1}({\nabla }_{1}f\left(x^k\right)+{\omega }_1^k)\\ -Q_2^{-1}({\nabla }_{2}f\left(x^k\right)+{\omega }_2^k-{\omega }_1^k)\\ -Q_3^{-1}({\nabla }_{3}f\left(x^k\right)+{\omega }_3^k-{\omega }_2^k)\\ ⋮\\ -Q_n^{-1}({\nabla }_{n}f\left(x^k\right)-{\omega }_{n-1}^k)\end{array}\right].$$

(18)

From this equation system, the primal Newton direction is computed only using the local information $Q_i,{\nabla }_{i}f\left(x^k\right),{\omega }_i^k$, and ${\omega }_{i-1}^k$; hence, the calculation of Newton direction is decentralized.

For the consensus optimization problem (10), we convert it to a separable optimization problem with equality constraints (11) and introduce Equations (4) and (5) to solve it. However, the computation of the dual variable ${\omega }^k$ at a given primal solution $x^k$ cannot be implemented in a distributed manner, since the evaluation of the matrix inverse ${\left(A{H}_k^{-1}{A}^{\prime }\right)}^{-1}$ requires global information. We provide a decentralized computation of ${\omega }^k$ using Jacobian iteration. Then, the primal Newton direction is expressed in (18). Now we present the details of the algorithm.

Algorithm 1 is distributed and local. Node i receives $x_j^k$ from its neighbors and computes the values of $a_i,b_i$. Step 2 and Step 3 are dual iterations. Node i generates ${\omega }_i^{t+1}$ by using ${\omega }_{i-1}^t$ and ${\omega }_{i+1}^t$ from its neighbors and sends the estimates to them. We find that the values of $a_i,b_i$ are not changed at a given primal solution $x^k$. Hence, they are calculated only once before the iteration of dual variable. Lastly, Algorithm 1 computes the Newton direction $▵x_p^k$ and updates the primal variable $x_p^{k+1}$ based on the previous result $x_p^k$ and sends them to their neighbors. If some stopping criterion is met, the algorithm stops and produces the result within the desired accuracy.

Algorithm 1 is proposed based on networks with a Hamilton path. In the next section, a distributed inexact Newton algorithm is proposed for multi-agent consensus optimization problems in any connected network.

Algorithm 1. Distributed Inexact Newton Method in Networks with a Hamilton Path

Step 0: Initialization: Initialize primal variables $x^0$ and dual variables ${\omega }^0$, set the number of iterations $k=0$.

Step 1: For each node i,

If $i\ne P$, calculate $a_i$ and $b_i={(Q_i^{-1}+Q_{i+1}^{-1})}^{-1}$;

If $i=P$, continue.

End for.

Step 2: Set ${\omega }_0^t={\omega }_P^t={[0,0,\cdots ,0]}^{\prime }\in R^{n-1}$.

For each node i,

If $i=P$, continue; Otherwise, calculate

$${\omega }_i^{t+1}=b_i(Q_i^{-1}{\omega }_{i-1}^t+Q_{i+1}^{-1}{\omega }_{i+1}^t+a_i).$$

Send ${\omega }_i^{t+1}$ to ${\mathcal{N}}_i$.

End for.

Step 3: If some stopping criterion is met for ${\omega }^t$, continue; otherwise, set $t=t+1$ and go back to Step 2.

Step 4: For each node i

Calculate Newton direction $▵x_i^k$

Update the primal variable $x_i^{k+1}=x_i^k+▵x_i^k$ and send it to ${\mathcal{N}}_i$.

End for.

Step 5: If some stopping criterion is met, stop; otherwise, set $t=0,k=k+1$ and go back to Step 1.

5. Distributed Newton Method for Multi-agent Problems in General Connected Networks

This distributed Newton method is proposed for multi-agent consensus optimization problems in general connected networks. Before giving this method, a theorem is firstly introduced.

Theorem 4. 

In reference [22], each connected graph has at least one spanning tree.

Thus, we can find at least one spanning tree in a connected graph. Now we select an arbitrary node as the root of the tree. We call the nodes connecting to root the first-level nodes, and the nodes which connected to $i\mathrm{th}$-level nodes is called $(i+1)\mathrm{th}$-level nodes. All nodes are renumbered according to these levels. The dual variable ${\omega }_{i,j}$ corresponds to a link between node i and node j. In order to ensure that the coefficient matrix A has full row rank, we eliminate the links between nodes belonging to the same level. Without loss of generality, we choose node 6 to be the root of the tree, as shown in Figure 3. In order to facilitate the analysis, all nodes in Figure 3 are renumbered according to the rule of top-to-bottom and left-to-right as depicted in Figure 4. Figure 5 is the dual graph of the spanning tree. From this figure, we have the observation that the dual graph is no longer a tree and there are many circuits.

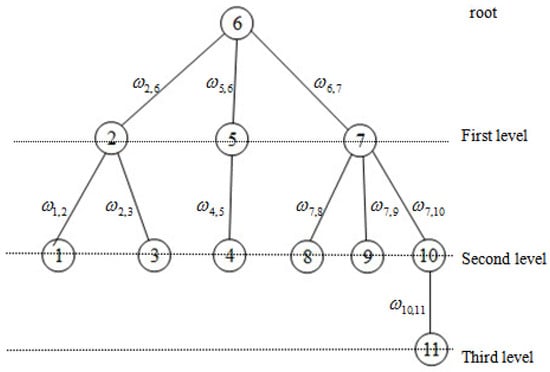
Figure 3. Spanning tree of network with 11 nodes in Figure 1.

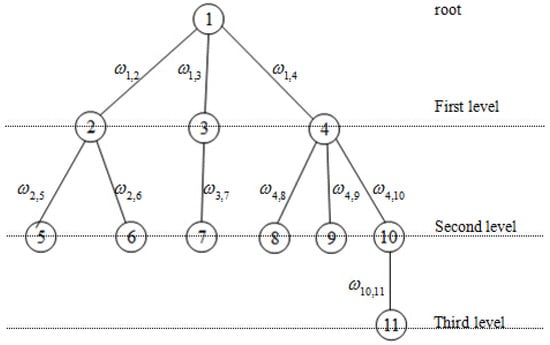
Figure 4. Spanning tree after renumbering.

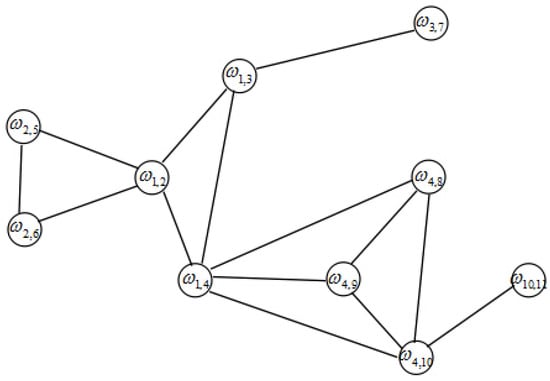
Figure 5. Dual graph for the network in Figure 3.

The coefficient matrix A of Figure 4 is a lower triangular matrix given by

$$A=\left[\begin{array}{cccccccc}I\hfill & -I\hfill & 0\hfill & 0\hfill & & 0\hfill & 0\hfill & 0\hfill \\ I\hfill & 0\hfill & -I\hfill & 0\hfill & \cdots \hfill & 0\hfill & 0\hfill & 0\hfill \\ I\hfill & 0\hfill & 0\hfill & -I\hfill & & 0\hfill & 0\hfill & 0\hfill \\ & & ⋮\hfill & & \ddots \hfill & & ⋮\hfill & \\ 0\hfill & 0\hfill & 0\hfill & I\hfill & \dots \hfill & 0\hfill & -I\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & & 0\hfill & I\hfill & -I\hfill \end{array}\right],$$

(19)

where $A_{l,l+1}=-I$ and $A_{l,i}=I$ if the link $\{l+1,i\}\in \mathcal{E}$.

Iteration Equation (9) in Theorem 1 can be used to compute the dual sequence $\left\{{\omega }^t\right\}$, since the matrix A has full row rank and the objective function is strictly convex. The matrix A in this problem has different forms with it in NUM, and therefore predetermined routes are not needed when we rewrite Equation (9).

Theorem 5. 

For each primal iteration k, the dual iteration (9) can be written as

$$\begin{array}{ccc}{\omega }_{i,j}^{t+1}\hfill & =\hfill & -a_{ij}[{\displaystyle \sum _{s\in {\mathcal{N}}_i/j}}sign(s,j)Q_i^{-1}{\omega }_{i,s}^t+{\displaystyle \sum _{s\in {\mathcal{N}}_j/i}}sign(s,i)Q_j^{-1}{\omega }_{j,s}^t-b_{ij}{\omega }_{i,j}^t+c_{ij}],\hfill \end{array}$$

(20)

where ${\mathcal{N}}_i/j$ is defined as the set of nodes connected to node i, excluding node j; sign $(r,s)=1$ if $r,s$ belongs to the same level and sign $(r,s)=-1$; otherwise, $a_{ij}={(D_i{Q}_i^{-1}+D_j{Q}_j^{-1})}^{-1}$, $b_{ij}=(D_i-1)Q_i^{-1}+(D_j-1)Q_j^{-1}$ and $c_{ij}=Q_i^{-1}{\nabla }_{i}f\left(x^k\right)-Q_j^{-1}{\nabla }_{j}f\left(x^k\right)$.

Proof of Theorem 5. 

The proof is described in Appendix C. ☐

From this theorem, each dual component ${\omega }_{i,j}^{t+1}$ is updated using its private result ${\omega }_{i,j}^t$ and the adjacent nodes’ information; i.e., ${\omega }_{i,p}^t,{\omega }_{j,p}^t,D_i$, $D_j$, $Q_i^{-1},Q_j^{-1},{\nabla }_{i}f\left(x^k\right),{\nabla }_{j}f\left(x^k\right)$. Therefore, the dual variable can be computed in a distributed manner. Next, we obtain the primal Newton direction in a distributed way.

Recall the definition of matrix A; i.e., $A_{li}=I$ and $A_{lj}=-I$ if $\{i,j\}\in \mathcal{E},i<j$, and $A_{lp}=0$ otherwise. Therefore, we have

$${\left(A^{\prime }{\omega }^k\right)}_l=\sum _{p\in {\mathcal{N}}_l,p>l}{\omega }_{l,p}-\sum _{p\in {\mathcal{N}}_l,p<l}{\omega }_{l,p}.$$

(21)

Thus, the Newton direction can be given by

$${(▵x^k)}_l=-Q_l^{-1}({\nabla }_{l}f\left(x^k\right)+\sum _{p\in {\mathcal{N}}_l,p>l}{\omega }_{l,p}-\sum _{p\in {\mathcal{N}}_l,p<l}{\omega }_{l,p}).$$

(22)

From this equation, the primal Newton direction is computed using only the local information $Q_l,{\nabla }_{l}f\left(x^k\right)$ and the dual information ${\omega }_{l,p}^k$ which is connected with node l. Hence, the calculation of Newton direction is decentralized.

For the consensus optimization problem (10), we have proposed a distributed inexact Newton method in the previous subsection. In order to get rid of the dependence on the network topology, we propose the following distributed Newton algorithm using a novel matrix splitting technique (Algorithm 2).

Algorithm 2. Distributed Inexact Newton Method for Arbitrary Connected Network

Step 0: Initialization: Initialize primal variables $x^0$ and dual variables ${\omega }^0$, set the number of iterations $k=0$.

Step 1: For each link $\{i,j\}\in \mathcal{E}$,

Calculate $a_{ij},b_{ij}$, and $c_{ij}$.

End for.

Step 2: For each link $\{i,j\}\in \mathcal{E}$,

Calculate ${\omega }_{i,j}^{t+1}$ by Equation (20) and send the result to nodes i and j.

End for.

Step 3: If some stopping criterion is met for ${\omega }^t$, continue; otherwise, set $t=t+1$ and go back to Step 2.

Step 4: For each node i,

Calculate Newton direction $▵x_i^k$ by Equation (22);

Update the primal variable $x_i^{k+1}=x_i^k+▵x_i^k$.

Send $x_i^{t+1}$ to ${\mathcal{N}}_i$.

End for.

Step 5: If some stopping criterion is met, stop; otherwise, set $t=0,k=k+1$, and go back to Step 1.

Algorithm 2 is also distributed and local. Step 2 and 3 are dual iterations. An immediate consequence of Theorem 6 is that the dual iteration is distributed. We find that the values of $a_{i,j},b_{i,j},c_{i,j}$ are not changed at a given primal solution $x^k$. Hence, they are calculated only once before the dual iteration. Lastly, Algorithm 2 computes the Newton direction $▵x_i^k$ and updates the primal variable $x_i^{k+1}$ based only on the previous result $x_i^k$ and the dual components of the nodes connected node i.

Algorithm 1 and Algorithm 2 are distributed, and they are second-order methods. We will demonstrate the effectiveness of the proposed distributed inexact Newton methods by applying them to the convex programming.

6. Numerical Experiments

In this section, we demonstrate the effectiveness of the proposed distributed Newton methods by applying them to solve a problem which is motivated by the Kuramoto model of coupled nonlinear oscillators [23]. This problem is selected in numerical experiments for two reasons. On one hand, the objective function of this problem is strict convex and separable, which are consistent with the requirement of the special consensus optimization problem. On the other hand, compared with least square problem, the Kuramoto model is more universal and representative. Our simulations were based on random network topology. The codes were written in MATLAB. All numerical experiments were run in MATLAB 7.10.0 on a laptop with Pentium(R) Dual-Core E5500 2.80GHz CPU and 2GB of RAM.

The problem can be reformulated on the form

$$\begin{array}{cc}\hfill \underset{x}{min}& {\sum }_{i=1}^{P}1-\sqrt{1-x_i^2}\\ \hfill s.t.& x_i=x_j,\forall i\ne j.\end{array}$$

The problem instances of this problem were generated in the following manner. The number of nodes was 100. We terminated all algorithms whenever reaching an absolute error $|x^k-x^{k-1}|={10}^{-4}$ or the iteration number exceeded ${10}^3$. In addition to the decentralized incremental algorithm, we also compared the proposed distributed Newton method with the distributed subgradient algorithm.

Figure 6 and Figure 7 show the convergence curves of the three methods under test with $P=100$. The curves shown in these figures are the corresponding absolute error and objective function value of the running average iterates of the three methods. The step size of the decentralized incremental algorithm is set to ${\alpha }_k=0.01$, and that of the distributed subgradient method is ${\alpha }_k=\frac{1}{k+1}$. From Figure 6, we observe that the proposed distributed Newton method and the distributed subgradient method exhibit comparable convergence behavior; both methods converge to a reasonable value within 10 iterations and outperform the decentralized incremental algorithm. For the decentralized incremental method, the convergence speed slows down when the iteration number becomes large. From Figure 7, we decrease the absolute value and see that the proposed Newton method performs better than the distributed subgradient algorithm. One should note that the distributed subgradient method is more computationally expensive than the proposed distributed Newton method, since in each iteration the former requires the computation of the projection of the iteration value.

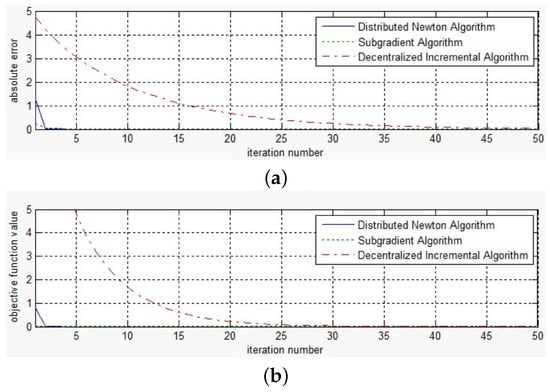
Figure 6. Absolute error along iterations for network with 100 nodes (1). (a) Absolute error; (b) Objective function value.

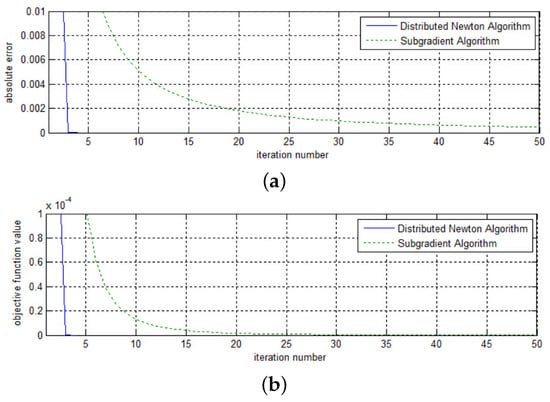
Figure 7. Absolute error along iterations for network with 100 nodes (2). (1). (a) Absolute error; (b) Objective function value.

7. Conclusions

This paper adjusted the distributed Newton methods for the NUM problem to solve the consensus optimization problem in different multi-agent networks. Firstly, a distributed inexact Newton method for consensus optimization problem in networks with a Hamilton path was devised. This method achieves the decomposition of a Hessian matrix by exploiting matrix splitting techniques. The convergence analysis of this method followed. Secondly, a distributed Newton algorithm for consensus optimization problems in general multi-agent networks was proposed by combining the matrix splitting technique for NUM and the spanning tree of the network. Meanwhile, the convergence analysis showed that the proposed algorithms enable the nodes across the network to achieve a global optimal solution in a distributed manner. Lastly, the proposed distributed inexact Newton method was applied to solving a problem which is motivated by the Kuramoto model of coupled nonlinear oscillators. The numerical experiment showed that the proposed algorithm converged with less iterations compared with the distributed projected subgradient method and the decentralized incremental approach. Moreover, the number of iterations of the proposed algorithm has a small change with the increase of the nodes’ number.

When constructing the spanning tree of an arbitrary connected network, the links between nodes belonging to the same level are eliminated in order to ensure that the coefficient matrix A has full row rank. In other words, a large number of network resources have not been effectively utilized. Consequently, the efficiency of the distributed inexact Newton algorithm can be further improved. In addition, the number of primal iterations is only considered in numerical experiments and compared with other two algorithms. We will take the number of dual iterations into consideration in future work.