Binocular 3D Object Recovery Using a Symmetry Prior
Abstract
:1. Introduction
2. Related Works
3. Proposed Algorithm
3.1. Notation
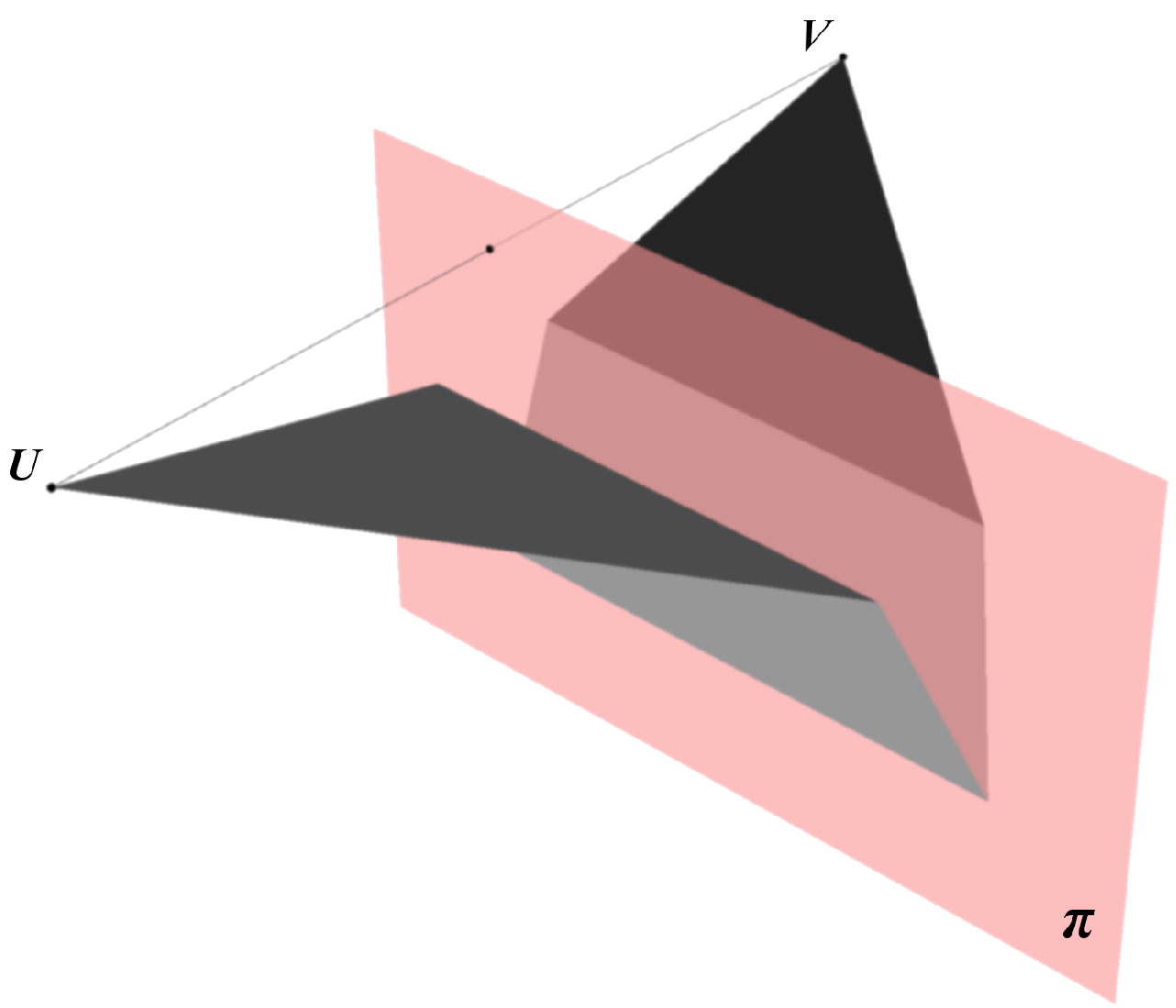
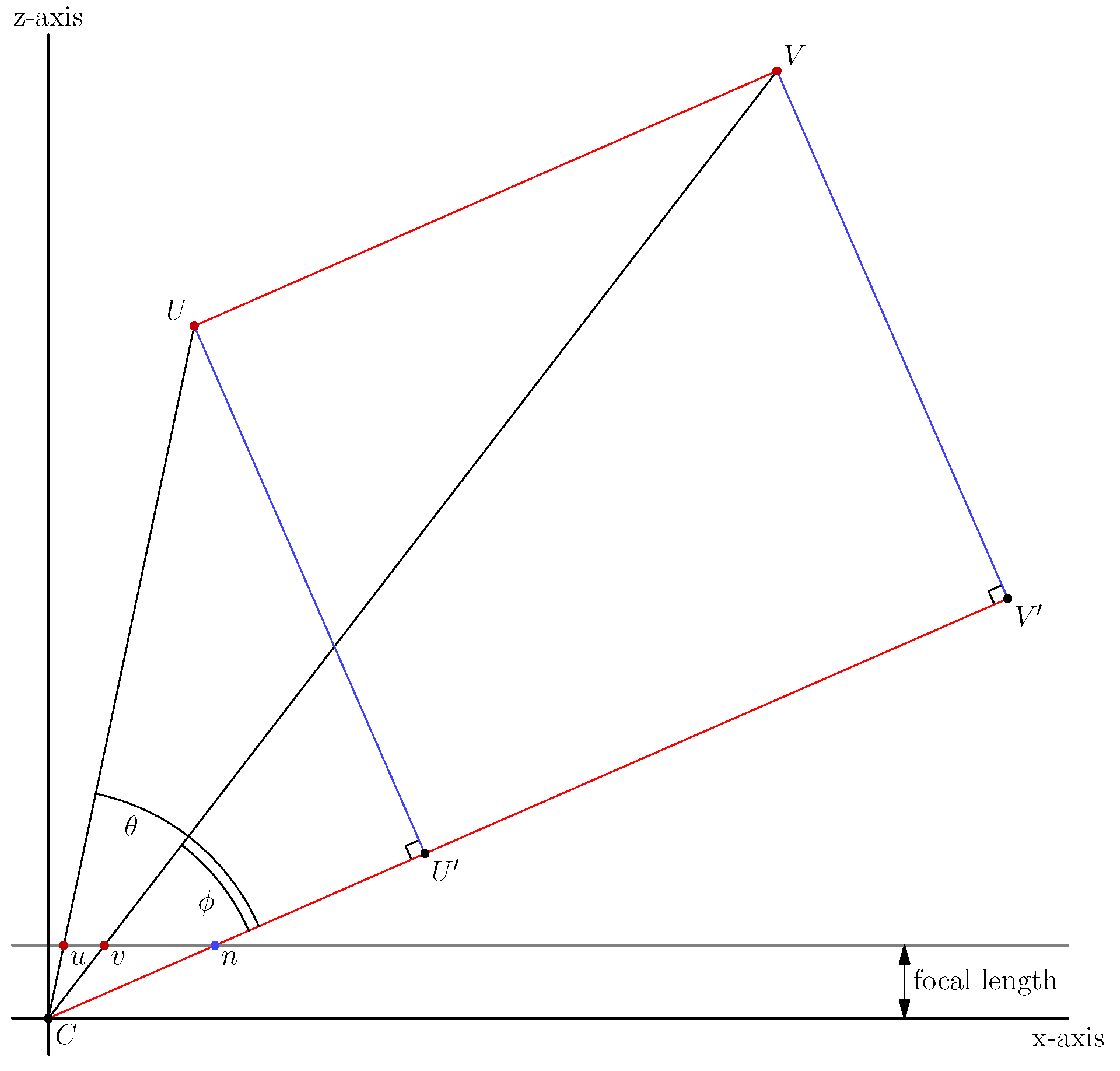
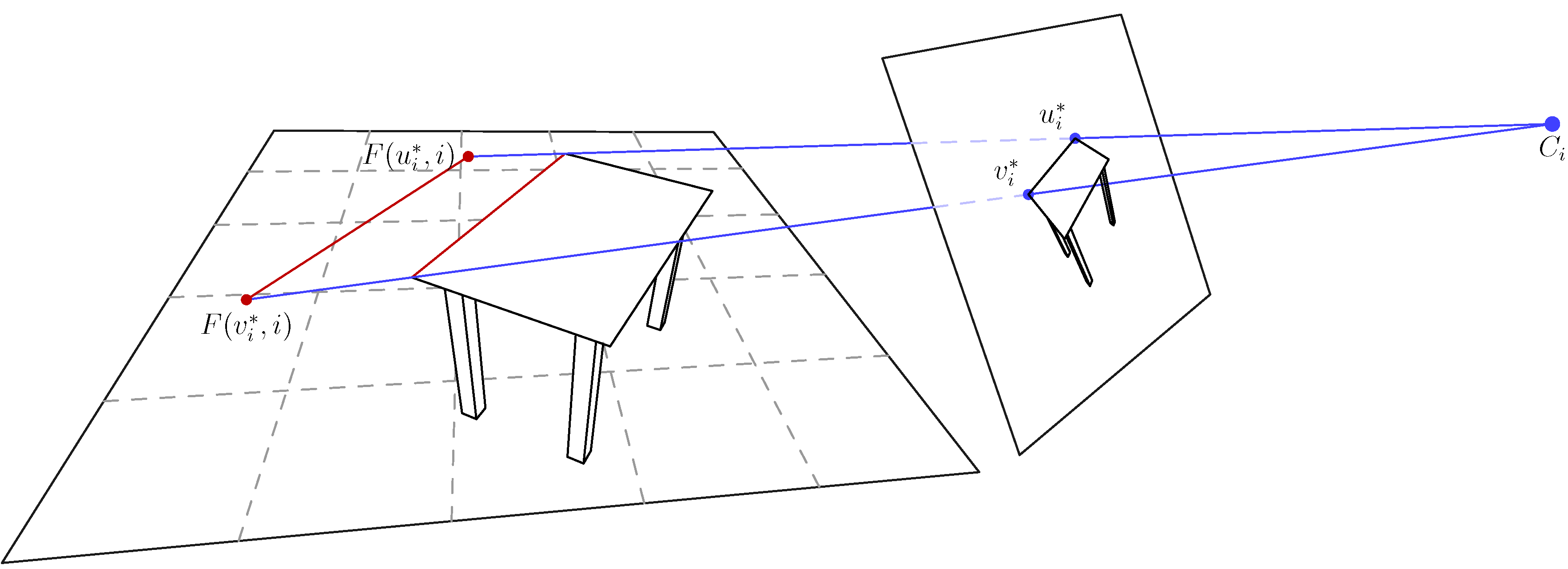
3.2. 3D Mirror Symmetry and Projective Geometry
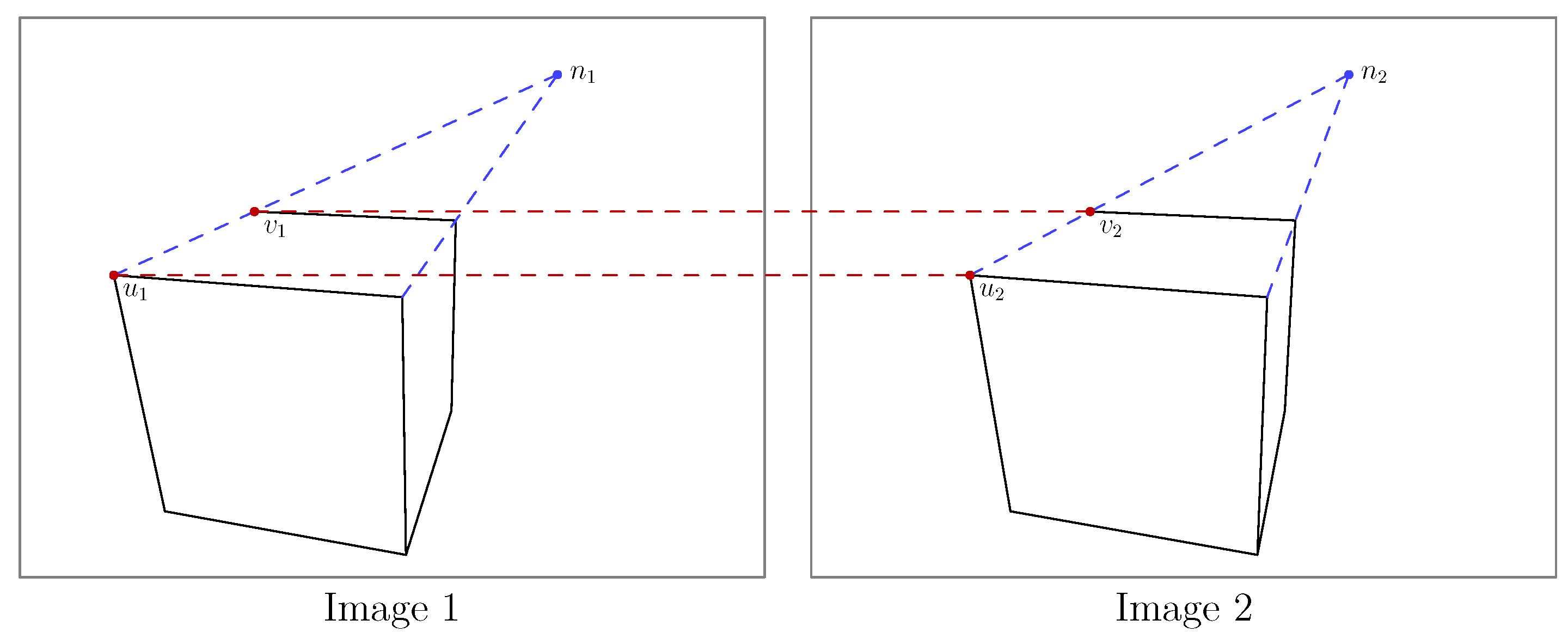
3.3. Solving the Symmetry Correspondence Problem with Two-View Geometry
3.4. Using a Floor Prior
3.5. Finding Symmetry Planes
3.6. Two Orthogonal Symmetry Planes
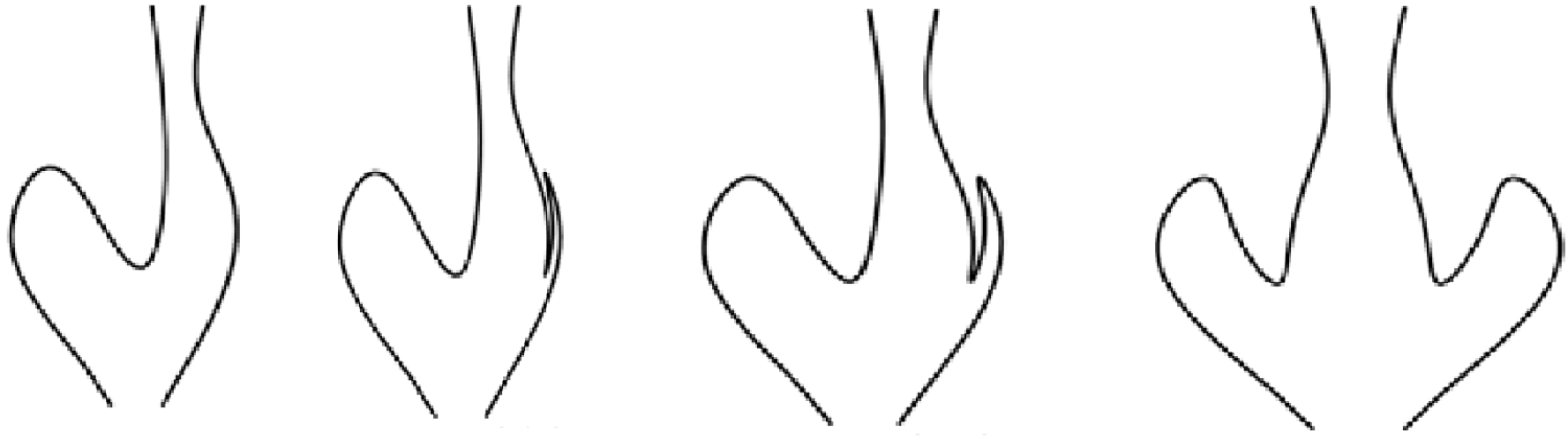
3.7. Recovering Objects with Short Curves
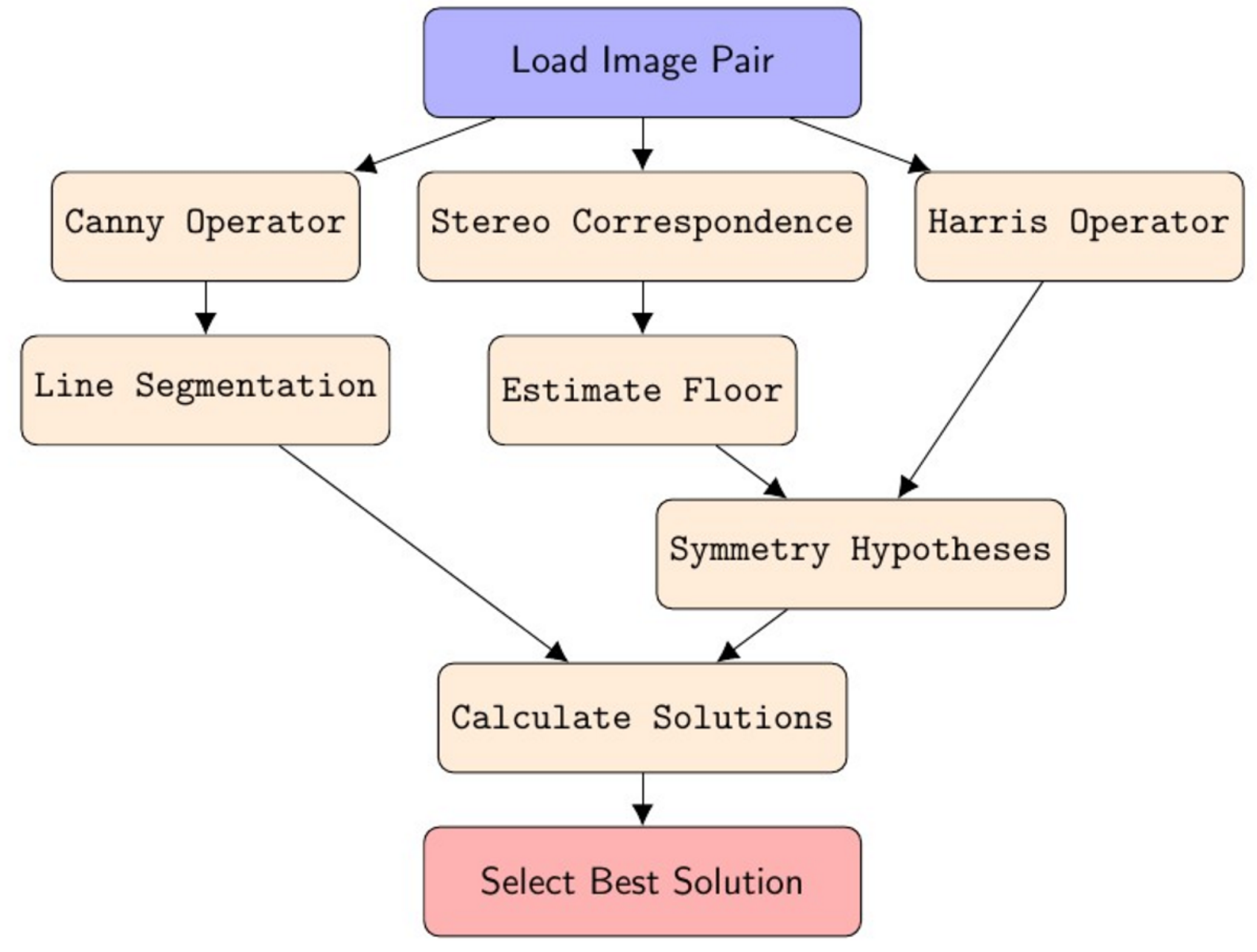
3.8. Overview of Algorithm
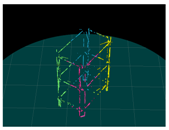
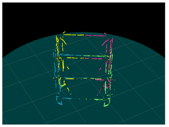
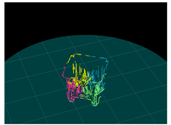
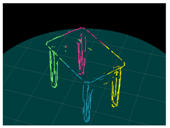
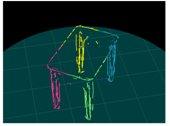
4. Results
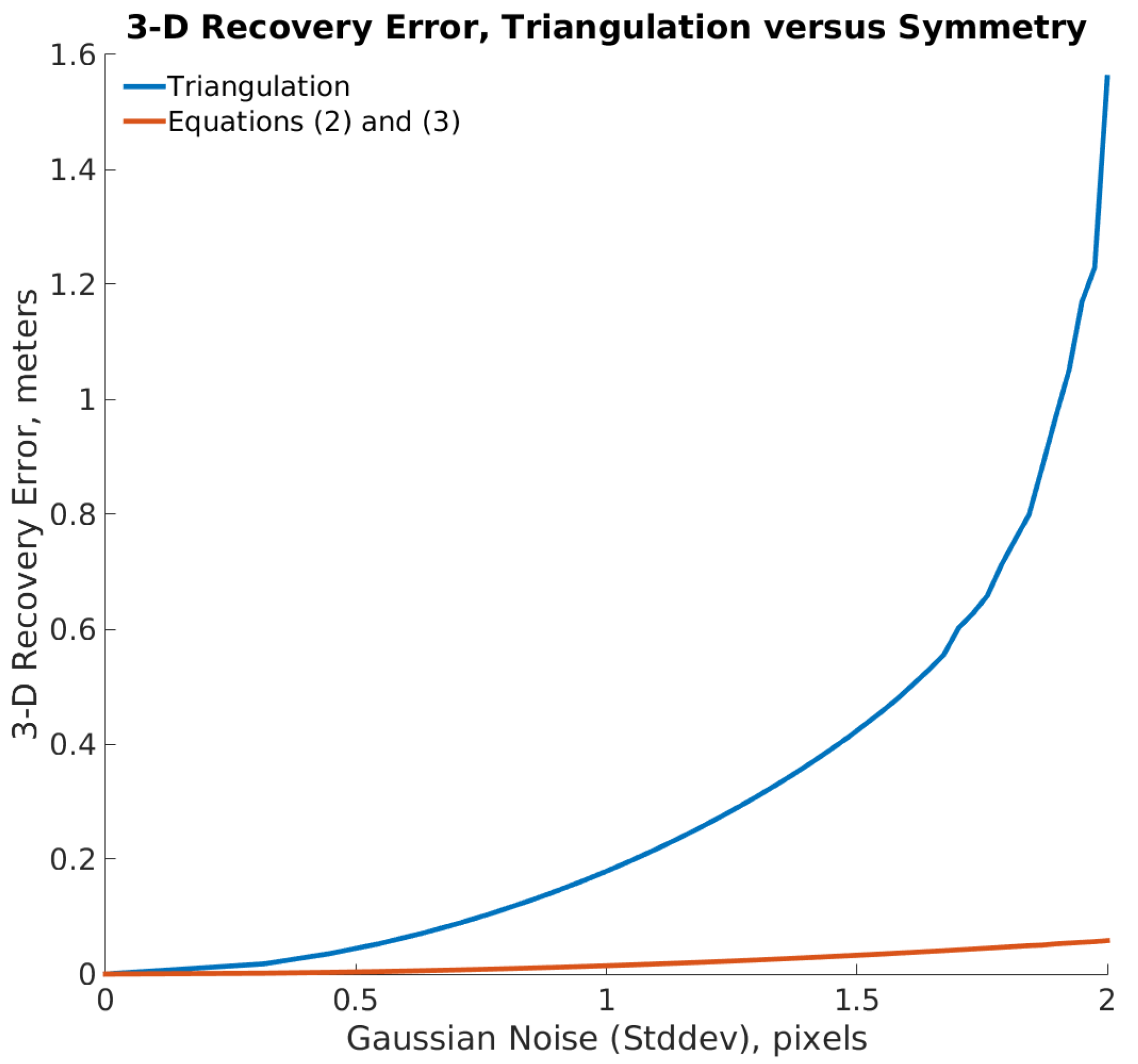
4.1. Simulation 1
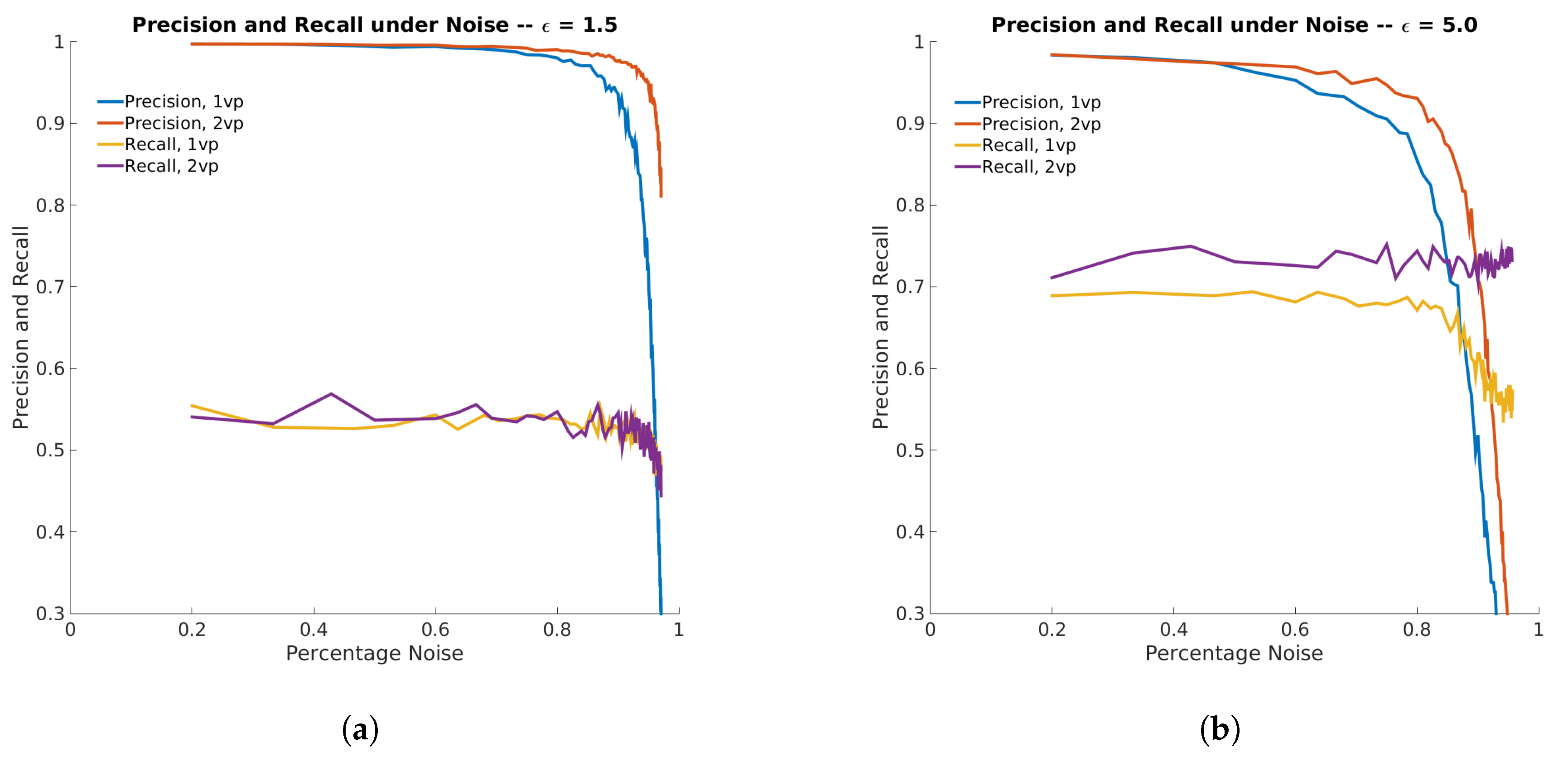
4.2. Simulation 2
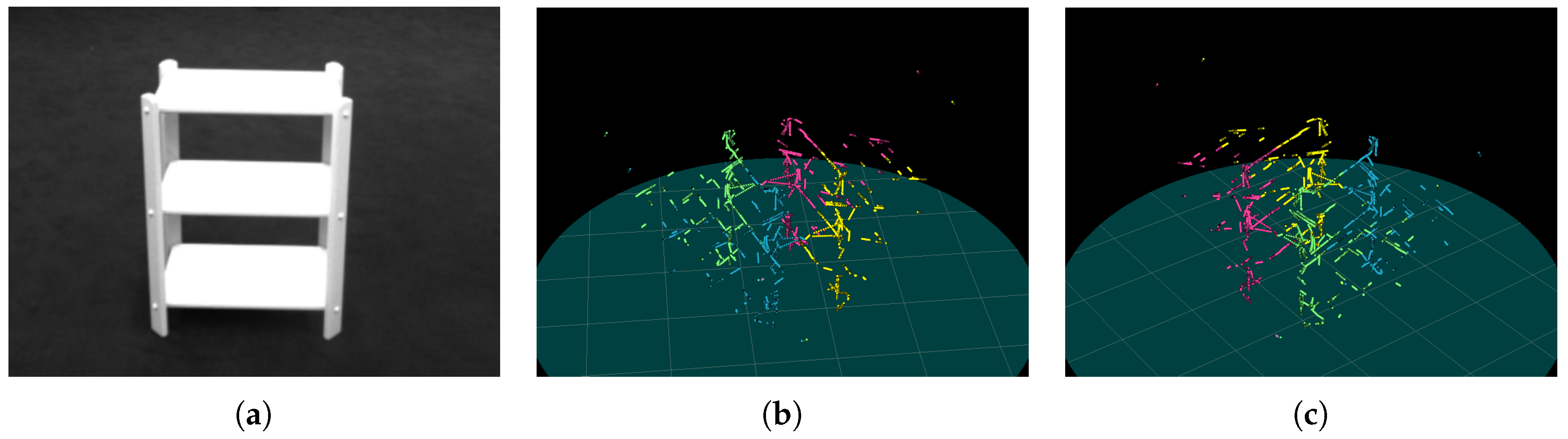
4.3. Experiment
4.3.1. Baseline for Comparison
4.3.2. Discussion
4.3.3. Comparison to Baseline
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Horn, B. Understanding image intensities. Artif. Intell. 1977, 8, 201–231. [Google Scholar] [CrossRef]
- Witkin, A. Recovering surface shape and orientation from texture. Artif. Intell. 1981, 17, 17–45. [Google Scholar] [CrossRef]
- Kanade, T. Recovery of the three-dimensional shape of an object from a single view. Artif. Intell. 1981, 17, 409–460. [Google Scholar] [CrossRef]
- Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; Henry Holt and Co., Inc.: New York, NY, USA, 1982. [Google Scholar]
- Hinton, G. Learning multiple layers of representation. Trends Cogn. Sci. 2007, 11, 428–434. [Google Scholar] [CrossRef] [PubMed]
- Dickinson, S. Challenge of image abstraction. In Object Categorization: Computer and Human Vision Perspectives; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Chalmers, A.; Reinhard, E.; Davis, T. Practical Parallel Rendering; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill-Posed Problems; Winston: Washington, DC, USA, 1977. [Google Scholar]
- Poggio, T.; Torre, V.; Koch, C. Computational vision and regularization theory. Nature 1985, 317, 314–319. [Google Scholar] [CrossRef] [PubMed]
- Pinker, S. How the Mind Works; W. W. Norton & Company: New York, NY, USA, 1997. [Google Scholar]
- Tsotsos, J.K. A Computational Perspective on Visual Attention; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Pizlo, Z.; Li, Y.; Sawada, T.; Steinman, R. Making a Machine That Sees Like Us; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Shepard, S.; Metzler, D. Mental rotation: Effects of dimensionality of objects and type of task. J. Exp. Psychol. Hum. Percept. Perform. 1988, 14, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Vetter, T.; Poggio, T.; Bülthoff, H. The importance of symmetry and virtual views in three-dimensional object recognition. Curr. Biol. 1994, 4, 18–23. [Google Scholar] [CrossRef]
- Sawada, T.; Li, Y.; Pizlo, Z. Shape Perception. In The Oxford Handbook of Computational and Mathematical Psychology; Oxford University Press: Oxford, UK, 2015; p. 255. [Google Scholar]
- Li, Y.; Sawada, T.; Shi, Y.; Steinman, R.; Pizlo, Z. Symmetry Is the sine qua non of Shape. In Shape Perception in Human and Computer Vision; Springer: London, UK, 2013; pp. 21–40. [Google Scholar]
- Li, Y.; Sawada, T.; Shi, Y.; Kwon, T.; Pizlo, Z. A Bayesian model of binocular perception of 3D mirror symmetrical polyhedra. J. Vis. 2011, 11, 11. [Google Scholar] [CrossRef] [PubMed]
- Palmer, E.; Michaux, A.; Pizlo, Z. Using virtual environments to evaluate assumptions of the human visual system. In Proceedings of the 2016 IEEE Virtual Reality (VR), Greenville, SC, USA, 19–23 March 2016; pp. 257–258. [Google Scholar]
- Marr, D.; Nishihara, H. Representation and Recognition of the Spatial Organization of Three-Dimensional Shapes. Proc. R. Soc. Lond. B Biol. Sci. 1978, 200, 269–294. [Google Scholar] [CrossRef] [PubMed]
- Binford, T. Visual perception by computer. In Proceedings of the IEEE Conference on Systems and Control, Miami, FL, USA, 15–17 December 1971; Volume 261, p. 262. [Google Scholar]
- Gordon, G. Shape from symmetry. In Proceedings of the Intelligent Robots and Computer Vision VIII: Algorithms and Techniques, Philadelphia, PA, USA, 1 March 1990; Volume 1192, pp. 297–308. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Rothwell, C.; Forsyth, D.; Zisserman, A.; Mundy, J. Extracting projective structure from single perspective views of 3D point sets. In Proceedings of the Fourth IEEE International Conference on Computer Vision, Berlin, Germany, 11–14 May 1993; pp. 573–582. [Google Scholar]
- Carlsson, S. European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 1998; pp. 249–263. [Google Scholar]
- Van Gool, L.; Moons, T.; Proesmans, M. Mirror and Point Symmetry under Perspective Skewing. In Proceedings of the Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1998; pp. 285–292. [Google Scholar]
- Hong, W.; Yang, A.; Huang, K.; Ma, Y. On symmetry and multiple-view geometry: Structure, pose, and calibration from a single image. Int. J. Comput. Vis. 2004, 60, 241–265. [Google Scholar] [CrossRef]
- Penne, R. Mirror symmetry in perspective. In International Conference on Advanced Concepts for Intelligent Vision Systems; Springer: Berlin/Heidelberg, German, 2005; pp. 634–642. [Google Scholar]
- Sawada, T.; Li, Y.; Pizlo, Z. Any pair of 2D curves is consistent with a 3D symmetric interpretation. Symmetry 2011, 3, 365–388. [Google Scholar] [CrossRef]
- Cham, T.; Cipolla, R. Symmetry detection through local skewed symmetries. Image Vis. Comput. 1995, 13, 439–450. [Google Scholar] [CrossRef]
- Cham, T.; Cipolla, R. Geometric saliency of curve correspondences and grouping of symmetric contours. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 1996; pp. 385–398. [Google Scholar]
- Cornelius, H.; Loy, G. Detecting bilateral symmetry in perspective. In Proceedings of the IEEE Computer Vision and Pattern Recognition Workshop, New York, NY, USA, 17–22 June 2006; p. 191. [Google Scholar]
- Cornelius, H.; Perd’och, M.; Matas, J.; Loy, G. Efficient symmetry detection using local affine frames. In Scandinavian Conference on Image Analysis; Springer: Berlin/Heidelberg, Germany, 2007; pp. 152–161. [Google Scholar]
- Shimshoni, I.; Moses, Y.; Lindenbaum, M. Shape reconstruction of 3D bilaterally symmetric surfaces. Int. J. Comput. Vis. 2000, 39, 97–110. [Google Scholar] [CrossRef]
- Köser, K.; Zach, C.; Pollefeys, M. Dense 3D reconstruction of symmetric scenes from a single image. In Joint Pattern Recognition Symposium; Springer: Berlin/Heidelberg, Germany, 2011; pp. 266–275. [Google Scholar]
- Wu, C.; Frahm, J.; Pollefeys, M. Repetition-based dense single-view reconstruction. In Proceedings of the IEEE Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 3113–3120. [Google Scholar]
- Yang, A.; Huang, K.; Rao, S.; Hong, W.; Ma, Y. Symmetry-based 3D reconstruction from perspective images. Comput. Vis. Image Underst. 2005, 99, 210–240. [Google Scholar] [CrossRef]
- Bokeloh, M.; Berner, A.; Wand, M.; Seidel, H.; Schilling, A. Symmetry detection using feature lines. Comput. Graph. Forum 2009, 28, 697–706. [Google Scholar] [CrossRef]
- Cordier, F.; Seo, H.; Park, J.; Noh, J. Sketching of mirror-symmetric shapes. IEEE Trans. Vis. Comput. Graph. 2011, 17, 1650–1662. [Google Scholar] [CrossRef] [PubMed]
- Cordier, F.; Seo, H.; Melkemi, M.; Sapidis, N. Inferring mirror symmetric 3D shapes from sketches. Comput.-Aided Des. 2013, 45, 301–311. [Google Scholar] [CrossRef]
- Öztireli, A.; Uyumaz, U.; Popa, T.; Sheffer, A.; Gross, M. 3D modeling with a symmetric sketch. In Proceedings of the Eighth Eurographics Symposium on Sketch-Based Interfaces and Modeling, Vancouver, BC, Canada, 5–7 August 2011; pp. 23–30. [Google Scholar]
- Sinha, S.; Ramnath, K.; Szeliski, R. Detecting and Reconstructing 3D Mirror Symmetric Objects. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2012; pp. 586–600. [Google Scholar]
- Gao, Y.; Yuille, A. Symmetric bon-rigid structure from motion for category-specific object structure estimation. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 408–424. [Google Scholar]
- Cohen, A.; Zach, C.; Sinha, S.; Pollefeys, M. Discovering and exploiting 3D symmetries in structure from motion. In Proceedings of the IEEE Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1514–1521. [Google Scholar]
- Michaux, A.; Jayadevan, V.; Delp, E.; Pizlo, Z. Figure-ground organization based on three-dimensional symmetry. J. Electron. Imaging 2016, 25, 061606. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Weinshall, D. Using bilateral symmetry to improve 3D reconstruction from image sequences. Comput. Vis. Image Underst. 1997, 67, 48–57. [Google Scholar] [CrossRef]
- Li, Y.; Sawada, T.; Latecki, L.; Steinman, R.; Pizlo, Z. A tutorial explaining a machine vision model that emulates human performance when it recovers natural 3D scenes from 2D images. J. Math. Psychol. 2012, 56, 217–231. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 6, 679–698. [Google Scholar] [CrossRef]
- Beckmann, N.; Kriegel, H.; Schneider, R.; Seeger, B. The R*-tree: An efficient and robust access method for points and rectangles. ACM Sigmod Rec. 1990, 19, 322–331. [Google Scholar] [CrossRef]
- Coughlan, J.; Yuille, A. Manhattan world: Orientation and outlier detection by bayesian inference. Neural Comput. 2003, 15, 1063–1088. [Google Scholar] [CrossRef] [PubMed]
- Bradski, G. The OpenCV Library. Available online: http://www.drdobbs.com/open-source/the-opencv-library/184404319 (accessed on 16 January 2017).
- Fischler, M.; Bolles, R. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Fourth Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Olsson, D.; Nelson, L. The Nelder–Mead simplex procedure for function minimization. Technometrics 1975, 17, 45–51. [Google Scholar] [CrossRef]
- François, A.; Medioni, G.; Waupotitsch, R. Reconstructing mirror symmetric scenes from a single view using 2-view stereo geometry. In Proceedings of the IEEE International Conference on Pattern Recognition, Quebec, QC, Canada, 11–15 August 2002; Volume 4, pp. 12–16. [Google Scholar]
- Fawcett, R.; Zisserman, A.; Brady, M. Extracting structure from an affine view of a 3D point set with one or two bilateral symmetries. Image Vis. Comput. 1994, 12, 615–622. [Google Scholar] [CrossRef]
- Mitsumoto, H.; Tamura, S.; Okazaki, K.; Kajimi, N.; Fukui, Y. 3D reconstruction using mirror images based on a plane symmetry recovering method. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 941–946. [Google Scholar] [CrossRef]
- Huynh, D. Affine reconstruction from monocular vision in the presence of a symmetry plane. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 1, pp. 476–482. [Google Scholar]
- Sawada, T.; Li, Y.; Pizlo, Z. Detecting 3D mirror symmetry in a 2D camera image for 3D shape recovery. Proc. IEEE 2014, 102, 1588–1606. [Google Scholar] [CrossRef]
- Li, B.; Peng, K.; Ying, X.; Zha, H. Simultaneous vanishing point detection and camera calibration from single images. In International Symposium on Visual Computing; Springer: Berlin/Heidelberg, Germany, 2010; pp. 151–160. [Google Scholar]
- Pirenne, M. Optics, Painting & Photography; JSTOR; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]


| Parameter | Reference | Value |
|---|---|---|
| RANSAC iterations for floor estimation | Section 3.4 | 500 iterations |
| RANSAC threshold for floor estimation | Section 3.4 | m |
| Harris block size | Section 3.5 | 3 |
| Harris k | Section 3.5 | 0.01 |
| Object point reprojection threshold | Equation (4) | pixels |
| Symmetry plane reprojection threshold | Equation (8) and Section 3.6 | pixels |
| Contour length | Section 3.7 | 15 pixels |
| Exemplar | # | Proposed Method | Michaux et al. [44] |
|---|---|---|---|
| Curved Stand | 8 | cm | cm |
| s | s | ||
| Short Stand | 7 | cm | cm |
| s | s | ||
| Bookshelf | 8 | cm | cm |
| s | s | ||
| Short Dense Stand | 5 | cm | cm |
| s | s | ||
| Mid Dense Stand | 6 | cm | cm |
| s | s | ||
| Tall Dense Stand | 7 | cm | cm |
| s | s | ||
| Short Table | 8 | cm | cm |
| s | s | ||
| Long Table | 7 | cm | cm |
| s | s | ||
| Rubbish Bin | 6 | cm | cm |
| s | s | ||
| Total/Average | 63 | cm | cm |
| s | s |
| Input (Left Image) | Input (Right Image) | 120-deg Rotation | 240-deg Rotation |
|---|---|---|---|
 |  | 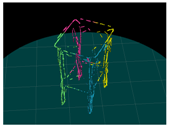 |  |
 |  | 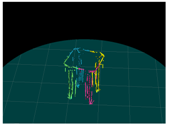 | 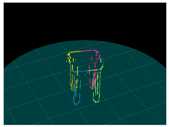 |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michaux, A.; Kumar, V.; Jayadevan, V.; Delp, E.; Pizlo, Z. Binocular 3D Object Recovery Using a Symmetry Prior. Symmetry 2017, 9, 64. https://doi.org/10.3390/sym9050064
Michaux A, Kumar V, Jayadevan V, Delp E, Pizlo Z. Binocular 3D Object Recovery Using a Symmetry Prior. Symmetry. 2017; 9(5):64. https://doi.org/10.3390/sym9050064
Chicago/Turabian StyleMichaux, Aaron, Vikrant Kumar, Vijai Jayadevan, Edward Delp, and Zygmunt Pizlo. 2017. "Binocular 3D Object Recovery Using a Symmetry Prior" Symmetry 9, no. 5: 64. https://doi.org/10.3390/sym9050064
APA StyleMichaux, A., Kumar, V., Jayadevan, V., Delp, E., & Pizlo, Z. (2017). Binocular 3D Object Recovery Using a Symmetry Prior. Symmetry, 9(5), 64. https://doi.org/10.3390/sym9050064






