Abstract
Roller bearings are the most widely used and easily damaged mechanical parts in rotating machinery. Their running state directly affects rotating machinery performance. Empirical mode decomposition (EMD) easily occurs illusive component and mode mixing problem. From the view of feature extraction, a new feature extraction method based on integrating ensemble empirical mode decomposition (EEMD), the correlation coefficient method, and Hilbert transform is proposed to extract fault features and identify fault states for motor bearings in this paper. In the proposed feature extraction method, the EEMD is used to decompose the vibration signal into a series of intrinsic mode functions (IMFs) with different frequency components. Then the correlation coefficient method is used to select the IMF components with the largest correlation coefficient, which are carried out with the Hilbert transform. The obtained corresponding envelope spectra are analyzed to extract the fault feature frequency and identify the fault state by comparing with the theoretical value. Finally, the fault signal transmission performance of vibration signals of the bearing inner ring and outer ring at the drive end and fan end are deeply studied. The experimental results show that the proposed feature extraction method can effectively eliminate the influence of the mode mixing and extract the fault feature frequency, and the energy of the vibration signal in the bearing outer ring at the fan end is lost during the transmission of the vibration signal. It is an effective method to extract the fault feature of the bearing from the noise with interference.
1. Introduction
Roller bearings are important components of rotating machinery. They are widely used in mechanical equipment. However, the bearing is one of the easily damaged mechanical parts in rotating machinery. Its running state directly affects the machinery performance. It was reported that bearing faults accommodate 45%–55% of motor failures [1,2]. Thus, the diagnosis of bearing faults plays a key role in the reliable operation of motors. Vibration analysis is one of the main methods in bearing monitoring and fault diagnosis. In general, when the bearing has broken down, the components induce impulses that can be detected in the acquired vibration signal. The fault vibration signals are non-stationary and nonlinear signals. Thus, the fault feature extraction of the bearing from nonlinear and non-stationary signals is a key step of fault diagnosis.
In recent years, a variety of fault diagnosis methods have been effectively exploited to detect motor bearing faults in order to keep machinery performing at the best state, avoiding abnormal event progression [3,4,5]. For fault diagnosis, vibration signal analysis is one of the most important methods. There exist various kinds of the vibration signal analysis methods, such as correlation analysis, time series analysis, fast Fourier transform, wavelet transform, empirical mode decomposition, blind signal separation, ensemble empirical mode decomposition, expert systems, fuzzy logic, neural networks, and so on. Ming et al. [6] proposed a novel fault diagnosis method based on orthogonal projection theory to extract the fault characteristic frequency for a roller bearing. Van Wyk et al. [7] proposed a powerful tool for bearing feature extraction and classification. Mohsen et al. [8] addressed the fault diagnosis of analog circuits based on a dictionary approach. Liu et al. [9] proposed a signal processing method/amplitude recovery method for the signal pre-processing. Rubini and Meneghetti [10] proposed the limits of the mentioned methodologies by showing their application to bearings affected by different pitting failures. Yu et al. [11] applied the empirical mode decomposition (EMD) method and Hilbert spectrum to diagnose faults of roller bearings. Li et al. [12] used the combination method of EMD and wavelet analysis for the detection of changes. Guo et al. [13] proposed the combination of median filter and EMD method to analyze the friction signal. Cheng et al. [14] proposed a frequency separation method based on EMD and the local Hilbert energy spectrum for gear fault diagnosis. Wu and Chung [15] proposed the hybrid method of EEMD and pure EMD to efficiently decompose the complicated vibration signals of rotating machinery. Lei and Zuo [16] proposed an improved Hilbert-huang transform (HHT) based on EEMD and sensitive IMFs to diagnose an early rub-impact fault of a heavy oil catalytic cracking machine. Jiang et al. [17] proposed an improved EEMD with multiwavelet packets for rotating machinery multi-fault diagnosis. Gong et al. [18] proposed a novel method based on EEMD to select time-frequency patterns for single-trial motor imagery EEG. Lei et al. [19] proposed a new adaptive EEMD method for fault diagnosis of rotating machinery. Ren et al. [20] proposed a new approach to measure the similarity. Shukla et al. [21] proposed a novel methodology to automatically classify the EEG of normal, inter-ictal and ictal subjects using EMD decomposition. Yang and Wu [22] proposed an EEMD and the marginal Hilbert spectrum analysis for evaluate the diagnostic effectiveness of gear deterioration. Vokelj et al. [23] proposed a novel multivariate and multiscale statistical process monitoring method in large slewing bearings. Özgür et al. [24] proposed the axial vibration of cracked nanorods with arbitrary boundary conditions by dividing the nanorod into two segments, and they were concerned with the free vibration of cantilever microbeams with an attached tip mass in a systematic manner [25,26]. Other feature extraction methods have been proposed in recent years [27,28,29,30,31,32,33,34,35,36,37,38].
In this study, a new feature extraction and diagnosis method based on the EEMD, optimal mode selection, and Hilbert transform is proposed. Firstly, the vibration signal is adaptively decomposed into a number of components by the EEMD method. Next, the correlation coefficients of each mode and original signal are calculated to select the IMF components with the largest correlation coefficient (i.e., optimal mode), which carried out the Hilbert transform. The transformed envelope spectrum is analyzed in order to extract the fault feature frequency and identify the fault state. Finally, the transmission characteristics of the vibration signal of the bearing inner ring and outer ring are analyzed and deeply studied, and the feature extraction method has been successfully applied to identify the inner ring and outer ring faults of a motor bearing.
2. Basic Method
2.1. EMD
The EMD [24] is an adaptive decomposition technique. The energy associated with various intrinsic time scales is directly extracted to generate a series of IMFs. This method can decompose non-linear and non-stationary data sequences to extract a series of amplitude modulated-frequency modulated (AM-FM) signal components. The EMD decomposes the original signal (S(x)) into a number of IMFs:
where rn(t) is residual error function, and represents average trend of signals. IMF components ,,,, contain different elements respectively from low to high frequency of signals.
2.2. EEMD
The EEMD method is an improvement of the EMD method, which solves the problem of mode mixing by adding Gaussian white noise. The decomposition process of the EEMD method is described as follows:
- Step 1:
- Gaussian white noise sequences are added to the target data.
- Step 2:
- The new target data is decomposed into a series of IMFs according to the EMD algorithm.
- Step 3:
- Different Gaussian white noise sequences with the same amplitude are added to the data for each time; repeat Step 1 and Step 2.
- Step 4:
- The mean value of the various IMF is taken as the final result, that is:
2.3. Hilbert Transform
The Hilbert transform is a kind of commonly used and effective signal demodulation method, which extracts the modulated signal from the signal and analyzes the change of the modulation signal. The Hilbert transform of one continuous time signal is equal to the output response of a linear system with the impulse response signal. The Hilbert transform of time signal x(t) is described as:
Then the analytical signal of x(t) is:
As can be determined from the signal features, the spectrum z(jΩ) of z(t) is equal to the zero spectrum in the negative frequency and double the spectrum in the positive frequency.
3. Experimental Environment and Theoretical Calculation
3.1. Experimental Environment
The experimental data of the roller bearing came from the Case Western Reserve University Bearing Data Center [39,40]. Bearing information of the drive end is shown in Table 1.

Table 1.
Bearing information (inches) of the drive end.
For the SKF 6205-2RS bearing in the experiment, the number of rolling elements () is nine, the rotating frequency () is 29.95 Hz at 1797 rpm, and the theoretical characteristic frequencies of faults are calculated. The results are shown in Table 2.

Table 2.
Fault characteristic frequency.
Two accelerometers are placed at the 3 o’clock, 6 o’clock, and 12 o’clock positions at the drive end and fan end of motor housing to collect vibration signals by using a 16-channel DAT. The vibration signal was sampled at 12,000 Hz and the duration of each vibration signal was 10 seconds. The fault diameters was 0.007 inches and the number of sampling points is 2048 in the experiment.
3.2. Theoretical Calculation of the Fault Characteristic Frequency of the Roller Bearing
The bearings have many types. Most of their structures are composed of an inner ring, outer ring, rolling elements, and cage train. The structure of the roller bearing is shown in Figure 1.
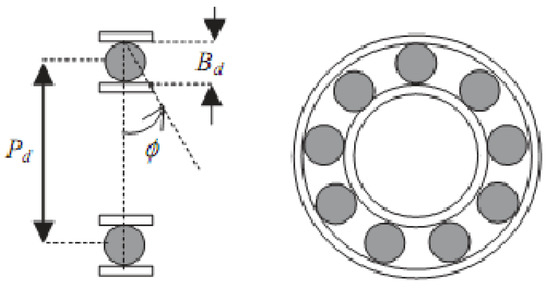
Figure 1.
Roller bearing.
where Bd is the roller element diameter, Pd is pitch diameter, and is angle (°) of the roller element.
The bearing speed, shape, and size are used to calculate the theoretical value of the fault characteristic frequency. The expressions are described as follows:
where , , and are the fault characteristic frequencies of the outer ring, inner ring, and roller element, respectively. is the rotating frequency (Hz), and is the number of rolling elements.
4. Fault Feature Extraction and Analysis
4.1. Fault Vibration Signal Decomposition
The fault vibration signals of the inner ring and the outer ring of the motor bearing are selected in the experiment. The EMD method is selected to compare with the EEMD method. The IMF components of the fault vibration signals are obtained by the EEMD and EMD methods. For the EEMD method, the added number of different white noise sequences is 500 and all deviations of different white noise sequences is 0.1. A set of fault vibration signals of the outer ring and the inner ring is decomposed into 11 IMF components and one residual component in Figure 2, Figure 3, Figure 4 and Figure 5.
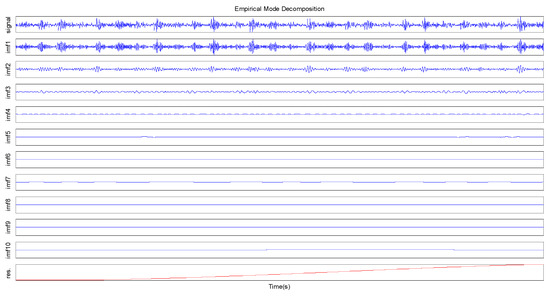
Figure 2.
The IMFs and residual components of the inner ring fault signal by the EMD method.
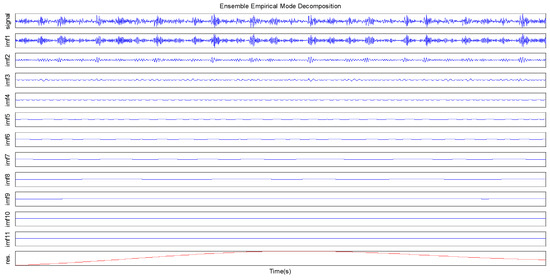
Figure 3.
The IMFs and residual components of the inner ring fault signal by the EEMD method.
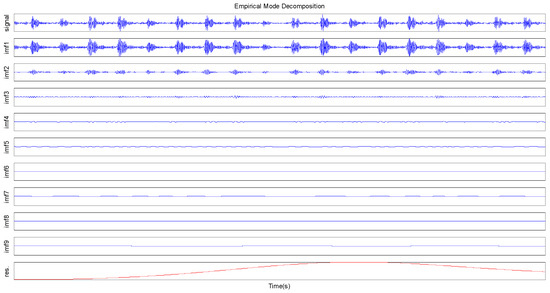
Figure 4.
The IMFs and residual components of the outer ring fault signal by the EMD method.
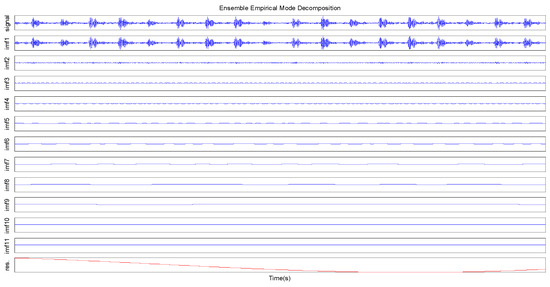
Figure 5.
The IMFs and residual components of the outer ring fault signal by the EEMD method.
As can be seen from Figure 2 and Figure 4, the IMF1 component in the EMD decomposition has the mixing phenomenon, and it includes a large number of signals with different scales. The IMF1 component includes a variety of frequencies, which can destroy the physical meaning of subsequent IMFs. Due to the existing mode mixing, it is not ideal to the test signal center frequency and extracted average amplitude. Compared with the EMD decomposition, the mixing phenomenon of each IMF component in the EEMD decomposition is improved in Figure 3 and Figure 5. The IMFs obtained by EEMD decomposition are a series of components from high frequency to low frequency. The multi-time scale periodic component of the original signal can be effectively described. Based on the above analysis, it can be seen that the EEMD method can better overcome the mode mining problem than the EMD method, and the EEMD method can more accurately obtain the time scale periodic characteristics of signals.
4.2. Selection of the Optimal Mode
Since the sample component of EEMD decomposition is larger, and the corresponding fault characteristics are embodied in the energy change in the specific frequency band, it is necessary to select the IMF with the most concentrated energy. This can accurately extract the effective fault information. According to the derivation of the literature, the correlation between the EEMD modes and the original signal is approximately equal to the self-correlation of each component. Inspired by the method [41], the correlation coefficient between each mode and original signal is used as the index to evaluate the reliability of mode components after EEMD.
where . and are the mode components and the original signal after EEMD, respectively. , , , and are the corresponding time domain mean and standard deviation, and E is a mathematical expectation. reflects the correlation between the mode components and original signal in the time domain. If the value of is larger, it shows that the component is more related to the original signal. That is to say, the self-correlation is larger. Thus, the mode with the maximum correlation is selected as the optimal mode of the EEMD, and it is regarded as the analysis sample for fault classification and identification.
4.3. Fault Feature Analysis Based on the Hilbert Transform
Due to the bearing installation error in the actual application, and the rolling element is not purely rolling, the fault characteristic frequency is not always exactly equal to the theoretical value. It is only necessary to find the approximate value of the characteristic frequency in the spectrum. Thus, the Hilbert transform is used to describe the envelope of the amplitude modulation or phase modulation. The results are shown in Figure 6 and Figure 7.
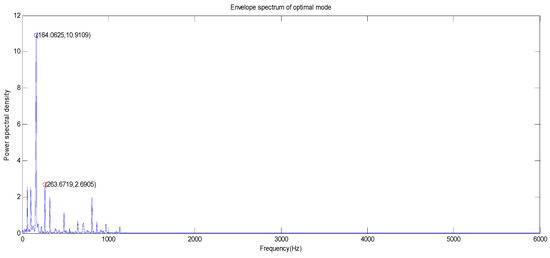
Figure 6.
The envelope spectrum of optimal mode of the inner ring fault signal.
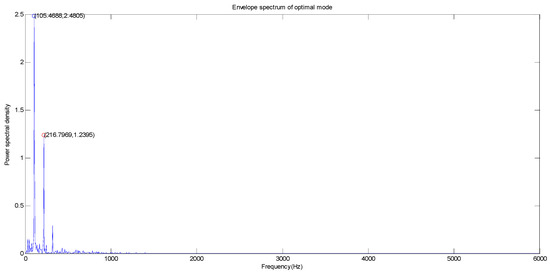
Figure 7.
The envelope spectrum of optimal mode of the outer ring fault signal.
As can be seen from Figure 6 and Figure 7 and Table 3, the largest amplitude peaks of the fault characteristic frequency of the vibration signal of the inner ring and the outer ring appear at frequencies of 164.06 Hz and 105.47 Hz, respectively. It can be seen that the largest amplitude peak of the fault characteristic frequency of the vibration signal of the inner ring (164.06 Hz) is close to the theoretical value (162.19 Hz), and the largest amplitude peak of the fault characteristic frequency of the vibration signal of the outer ring (105.47 Hz) is close to the theoretical value (107.29 Hz) in the envelope spectrum. The error values for the inner ring and the outer ring are 1.15% and 1.70%, respectively. Thus, they indicate that there is inner ring damage and outer ring damage in the motor bearing.

Table 3.
Statistics and analysis of results.
There are two improved particle swarm optimization (PSO) algorithms, which are the improved PSO (LWSPSO) algorithm by linearly changing of the learning factor and decreasing function of inertia weight, and the improved PSO (AWAPSO) algorithm by the arctangent change of the learning factor, decreasing function of inertia weight, and adaptive mutation strategy. In order to verify the effectiveness of the LWSPSO and AWAPSO algorithms, two improved PSO and PSO algorithms are used to optimize the support vector machine (SVM) here. The best fitness value and the average fitness value by using three algorithms are shown in Figure 1, Figure 2 and Figure 3 for the given dataset.
5. Transmission Analysis of the Vibration Signal
When the bearing fault occurs, two accelerometers are respectively placed at the 12 o’clock position at the drive end and fan end of motor housing to collect vibration signals in order to deeply study the fault signal transmission performance.
5.1. Transmission Analysis of the Fault Vibration Signal for the Inner Ring
When the bearing fault occurs in the inner ring, the optimal mode envelope spectra of the vibration signal at the drive end and fan end are shown in Figure 8 and Figure 9, respectively.
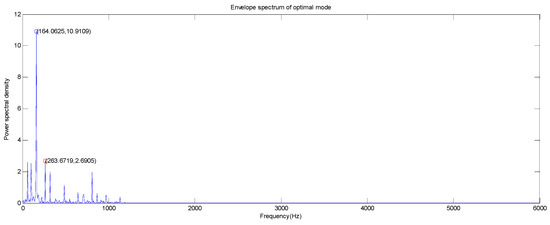
Figure 8.
The optimal mode envelope spectrum of the inner ring at the drive end.
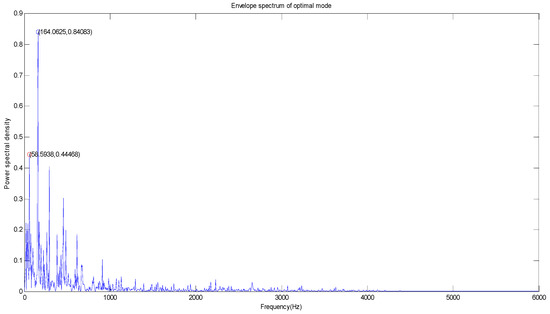
Figure 9.
The optimal mode envelope spectrum of the inner ring at the fan end.
As can be seen from Figure 8 and Figure 9, the largest amplitude peak of the fault characteristic frequency of the vibration signal of the inner ring at the drive end and fan end all appear at 164.06 Hz. The power spectral densities of the bearing inner ring at the drive end and the fan end are 10.9109 W/Hz and 0.8408 W/Hz, respectively. For the second large amplitude peak point, the second large amplitude peaks of the fault characteristic frequency of the vibration signal of the inner ring at the drive end and fan end are 263.67 Hz and 58.59 Hz, respectively. The power spectral densities of the bearing inner ring at the drive end and fan end second large amplitude peak are 2.6905 Hz and 0.4447 Hz, respectively. By comparing and analyzing the obtained results, the second large amplitude peak of the fault characteristic frequency of the vibration signal of the inner ring at the drive end (58.59 Hz) is close to the rotating frequency, and the power spectral density of the bearing inner ring at the drive end is much larger than the power spectral density of the bearing inner ring at the fan end. The compared and analyzed result indicates that the energy of the vibration signal of the bearing inner ring on the fan end is lost during the transmission of the vibration signal from the inner ring to the fan end of motor.
5.2. Transmission Analysis of the Fault Vibration Signal for the Outer Ring
When the bearing fault occurs in the outer ring, the optimal mode envelope spectrum of the collected vibration signal for the outer ring at the drive end and fan end are shown in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, respectively. Since the outer ring fault signal of the motor bearing is stationary, the outer ring fault position for the bearing load zone has direct effects on the vibration response of the motor bearing system. In order to analyze and quantify the effect, the experiments were conducted for the bearing outer ring fault at the 3 o’clock position, the 6 o’clock position (orthogonal to the load zone), and the 12 o’clock position at the drive end and fan end. The optimal mode envelope spectra of the collected vibration signal of the outer ring at the drive end and fan end at the 6 o’clock position are shown in Figure 10 and Figure 11, respectively. The optimal mode envelope spectra of the vibration signal of the outer ring at the drive end and fan end at the 3 o’clock position are shown in Figure 12 and Figure 13, respectively. The optimal mode envelope spectra of the collected vibration signal of the outer ring at the drive end and fan end at the 12 o’clock position are shown in Figure 14 and Figure 15, respectively.
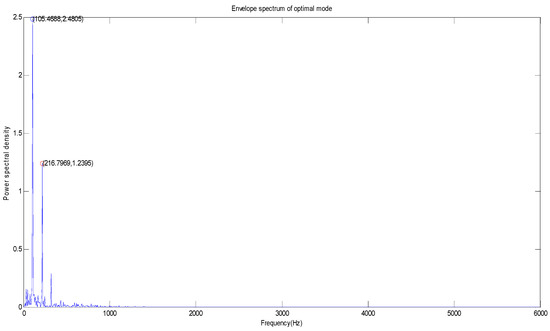
Figure 10.
The optimal mode envelope spectrum of the drive end of the outer ring at the 6 o’clock position.
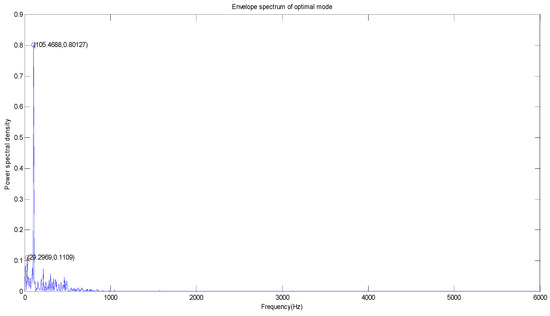
Figure 11.
The optimal mode envelope spectrum of the fan end of the outer ring at the 6 o’clock position.
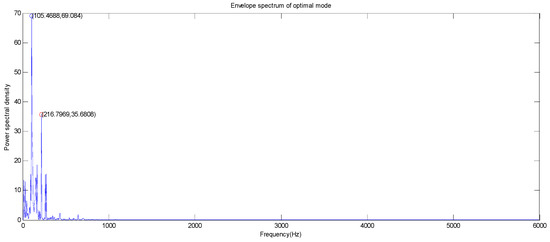
Figure 12.
The optimal mode envelope spectrum of the drive end of the outer ring at the 3 o’clock position.
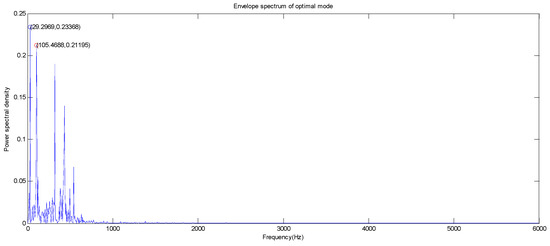
Figure 13.
The optimal mode envelope spectrum of the fan end of the outer ring at the 3 o’clock position.
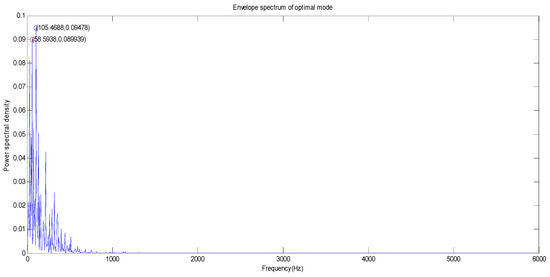
Figure 14.
The optimal mode envelope spectrum of the drive end of the outer ring at the 12 o’clock position.
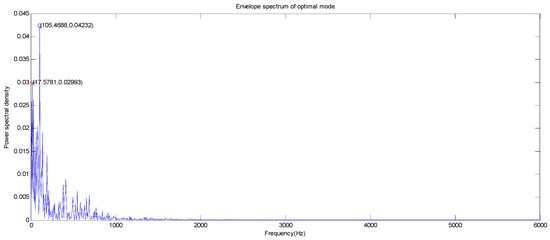
Figure 15.
The optimal mode envelope spectrum of the fan end of outer ring at the 12 o’clock position.
As can be seen from Figure 10 and Figure 11, the largest amplitude peaks of the fault characteristic frequency of the vibration signal of the outer ring at the drive end and fan end all appear at 105.47 Hz at the 6 o’clock position. The power spectral densities of the outer ring at the drive end and fan end are 2.4805 W/Hz and 0.8013 W/Hz, respectively. For the second large amplitude peak point, the second large amplitude peaks of the fault characteristic frequency of the vibration signal of the outer ring at the drive end and fan end appear at 216.80 Hz and 29.30 Hz, respectively. The power spectral densities of the bearing inner ring at the drive end and fan end are 1.2395 W/Hz and 0.1109 W/Hz, respectively, and the second large amplitude peak of the fault characteristic frequency of the vibration signal of the outer ring at the drive end (29.30 Hz) is close to the rotating frequency.
As can be seen from Figure 12 and Figure 13, the largest amplitude peaks of the fault characteristic frequency of the vibration signal of the outer ring at the drive end and fan end appear at a frequency of 105.47 Hz and 29.30 Hz at the 3 o’clock position, respectively. The power spectral densities of outer ring at the drive end and fan end are 69.084 W/Hz and 0.2339 Hz, respectively. For the second large amplitude peak point, the second large amplitude peaks of the fault characteristic frequency of the vibration signal of the outer ring at the drive end and fan end are 216.80 Hz and 105.47 Hz, respectively. The power spectral densities of the bearing outer ring at the drive end and fan end are 35.6808 W/Hz and 0.2120 W/Hz, respectively.
As can be seen from Figure 14 and Figure 15, the largest amplitude peaks of the fault characteristic frequency of vibration signal of the outer ring at the drive end and fan end all appear at 105.47 Hz at the 12 o’clock position. The power spectral densities of the outer ring at the drive end and fan end are 0.0948 W/Hz and 0.0423 Hz, respectively. For the second large amplitude point, the second large amplitude peaks of the fault characteristic frequency of the vibration signal of the outer ring at the drive end and fan end are 58.59 Hz and 17.58 Hz, respectively. The power spectral densities of the bearing outer ring at the drive end and fan end are 0.0899 W/Hz and 0.0299 W/Hz, respectively.
As can be seen from Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, for the 6 o’clock position and 12 o’clock position, the largest amplitude peaks of the fault characteristic frequency of the vibration signal of the outer ring at the drive end and fan end all appear at 105.47 Hz. For the 3 o’clock position, the largest amplitude peaks of the fault characteristic frequency of the vibration signal of the outer ring at the drive end and fan end appear at 105.47 Hz and 29.30 Hz, respectively. The largest power spectral density of the outer ring at the drive end is 69.084 W/Hz at the 3 o’clock position, and the largest power spectral density of the outer ring at the fan end is 0.8013 W/Hz at the 6 o’clock position. By comparing and analyzing the obtained results, the power spectral density of the bearing outer ring at the drive end is much larger than the power spectral density of the bearing outer ring at the fan end, and the second large amplitude peaks of the fault characteristic frequency of the vibration signal of the outer ring also changed the expectation for the reduced maximum amplitude peak. Thus, the compared and analyzed results indicate that the energy of the vibration signal of the bearing outer ring at the fan end is lost during the transmission of the vibration signal from the outer ring to the fan end of motor. The effective diagnosis method for motor bearing is to ensure the safety and reliable operation of the motor. In order to improve the fault diagnosis accuracy of the motor bearing, a new fault diagnosis method based on empirical mode decomposition, fuzzy entropy, an improved particle swarm optimization algorithm, and a support vector machine is proposed in this paper. Firstly, the vibration signals of the motor bearing is decomposed by EMD in order to obtain several IMFs. Then, the fuzzy entropy is used to effectively extract the features of the vibration signal, which are regarded as the input vectors of the SVM model. The improved learning factor and inertia weight, and the adaptive mutation strategy are used to improve the PSO algorithm in order to improve the optimization ability of the PSO algorithm, which is used to optimize the parameters of the SVM model for improving the classification accuracy. A new fault diagnosis model for the motor bearing based on combining EMD, fuzzy entropy, an improved PSO algorithm, and the optimized SVM is constructed in this paper.
6. Conclusions
In order to effectively extract the fault feature from the vibration signal of the motor bearing and study the transmission performance of the fault vibration signal, a fault feature extraction method based on integrating the EEMD, the correlation coefficient method, and the Hilbert transform is proposed. The vibration signals of the bearing inner ring and outer ring at the drive end and fan end at the 3 o’clock position, 6 o’clock position, and 12 o’clock position are selected to test and verify the effectiveness of the proposed fault feature extraction method and study the transmission characteristics. The experiment results show that the proposed fault feature extraction method can effectively eliminate the influence of the mode mixing and extract the fault feature frequency. The found fault characteristic frequency is close to the theoretical fault characteristic frequency. It is an effective method to extract the fault feature of the bearing from the noise with interference. The vibration signals at the drive end and the fan end are analyzed and compared in detail in order to deeply study the transmission characteristics of the fault vibration signal of the bearing inner ring and outer ring. The compared and analyzed results indicate that the energy of the vibration signal of the bearing outer ring at the fan end is lost during the transmission of the vibration signal from the outer ring to the fan end of the motor.
Due to the complexity of the vibration signal of the motor bearing, it requires more effective signal analysis methods to deal with the vibration signal. Thus, the feature extraction method needs to be studied further. The fault diagnosis method will be deeply studied in our future work.
Acknowledgments
The authors would like to thank all of the reviewers for their constructive comments. This research was supported by the National Natural Science Foundation of China (51475065, 51605068, U1433124), the Open Project Program of State Key Laboratory of Mechanical Transmissions (Chongqing University) (SKLMT-KFKT-201513), the Natural Science Foundation of Liaoning Province (2015020013), the Open Project Program of Sichuan Provincial Key Lab of Process Equipment and Control (GK201613), and the Open Project Program of the Traction Power State Key Laboratory of Southwest Jiaotong University (TPL1705).
Author Contributions
Wu Deng conceived the research subject and contributed to feature extraction, Huimin Zhao contributed to signal analysis, Xinhua Yang contributed to transmission analysis, Chang Dong carried out the experiments. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Nandi, S.; Toliyat, H.A.; Li, X. Condition monitoring and fault diagnosis of electrical motors—A review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Wang, S.B.; Cai, G.G.; Zhu, Z.K.; Huang, W.G.; Zhang, X.W. Transient signal analysis based on Levenberg-Marquardt method for fault feature extraction of rotating machines. Mech. Syst. Signal Proc. 2015, 54–55, 16–40. [Google Scholar] [CrossRef]
- Bououden, S.; Chadli, M.; Karimi, H.R. An ant colony optimization-based fuzzy predictive control approach for nonlinear processes. Inf. Sci. 2015, 299, 143–158. [Google Scholar] [CrossRef]
- Pan, Z.Q.; Zhang, Y.; Kwong, S. Efficient motion and disparity estimation optimization for low complexity multiview video coding. IEEE Trans. Broadcast. 2015, 61, 166–176. [Google Scholar]
- Zhang, Y.H.; Sun, X.M.; Wang, B.W. Efficient algorithm for K-barrier coverage based on integer linear programming. China Commun. 2016, 13, 16–23. [Google Scholar] [CrossRef]
- Ming, A.B.; Qin, Z.Y.; Zhang, W.; Chu, F.L. Spectrum auto-correlation analysis and its application to fault diagnosis of rolling element bearings. Mech. Syst. Signal Proc. 2013, 41, 141–154. [Google Scholar] [CrossRef]
- Van Wyk, B.J.; van Wyk, M.A.; Qi, G. Difference Histograms: A new tool for time series analysis applied to bearing fault diagnosis. Pattern Recognit. Lett. 2009, 30, 595–599. [Google Scholar] [CrossRef]
- Mohsen, A.A.K.; Abu El-Yazeed, M.F. Selection of input stimulus for fault diagnosis of analog circuits using ARMA model. AEU Int. J. Electron. Commun. 2004, 58, 212–217. [Google Scholar] [CrossRef]
- Liu, Y.K.; Guo, L.W.; Wang, Q.X.; An, G.Q.; Guo, M.; Lian, H. Application to induction motor faults diagnosis of the amplitude recovery method combined with FFT. Mech. Syst. Signal Proc. 2010, 24, 2961–2971. [Google Scholar] [CrossRef]
- Rubini, R.; Meneghetti, U. Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearings. Mech. Syst. Signal Proc. 2001, 5, 287–302. [Google Scholar] [CrossRef]
- Yu, D.J.; Cheng, J.S.; Yang, Y. Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings. Mech. Syst. Signal Proc. 2005, 19, 259–270. [Google Scholar] [CrossRef]
- Li, H.L.; Deng, X.Y.; Dai, H.L. Structural damage detection using the combination method of EMD and wavelet analysis. Mech. Syst. Signal Proc. 2007, 21, 298–306. [Google Scholar] [CrossRef]
- Guo, K.J.; Zhang, X.G.; Li, H.G.; Meng, G. Application of EMD method to friction signal processing. Mech. Syst. Signal Proc. 2008, 22, 248–259. [Google Scholar] [CrossRef]
- Cheng, J.S.; Yu, D.J.; Tang, J.S.; Yang, Y. Application of frequency family separation method based upon EMD and local Hilbert energy spectrum method to gear fault diagnosis. Mech. Mach. Theory 2008, 43, 712–723. [Google Scholar] [CrossRef]
- Wu, T.Y.; Chung, Y.L. Misalignment diagnosis of rotating machinery through vibration analysis via the hybrid EEMD and EMD approach. Smart Mater. Struct. 2009, 18, 095004. [Google Scholar] [CrossRef]
- Lei, Y.G.; Zuo, M.J. Fault diagnosis of rotating machinery using an improved HHT based on EEMD and sensitive IMFs. Meas. Sci. Technol. 2009, 20, 125701. [Google Scholar] [CrossRef]
- Jiang, H.K.; Li, C.L.; Li, H.X. An improved EEMD with multiwavelet packet for rotating machinery multi-fault diagnosis. Mech. Syst. Signal Proc. 2013, 36, 225–239. [Google Scholar] [CrossRef]
- Gong, P.; Chen, M.Y.; Zhang, L. EEMD-based selection of time-frequency patterns for motor imagery EEG. J. Comput. Inf. Syst. 2013, 9, 9211–9218. [Google Scholar]
- Lei, Y.; Li, N.; Lin, J.; Wang, S. Fault diagnosis of rotating machinery based on an adaptive ensemble empirical mode decomposition. Sensors 2013, 13, 16950–16964. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Wang, Y.L.; Huang, M.Y.; Chang, Y.L.; Kao, H.M. Ensemble empirical mode decomposition parameters optimization for spectral distance measurement in hyperspectral remote sensing data. Remote Sens. 2014, 6, 2069–2083. [Google Scholar] [CrossRef]
- Shukla, S.; Mishra, S.; Singh, B. Power quality event classification under noisy conditions using EMD-based de-noising techniques. IEEE Trans. Ind. Inform. 2014, 10, 1044–1054. [Google Scholar] [CrossRef]
- Yang, C.Y.; Wu, T.Y. Diagnostics of gear deterioration using EEMD approach and PCA process. J. Int. Meas. Confed. 2015, 61, 75–87. [Google Scholar] [CrossRef]
- Vokelj, M.; Zupan, S.; Prebil, I. EEMD-based multiscale ICA method for slewing bearing fault detection and diagnosis. J. Sound Vib. 2016, 370, 394–423. [Google Scholar] [CrossRef]
- Özgür, Y.M.; Çerçevik, A.E. Axial vibration analysis of cracked nanorods with arbitrary boundary conditions. J. Vibroeng. 2015, 16, 2907–2921. [Google Scholar]
- Özgür, Y.M. Stability analysis of gradient elastic microbeams with arbitrary boundary conditions. J. Mech. Sci. Technol. 2015, 29, 3373–3380. [Google Scholar]
- Özgür, Y.M.; Süheyla, Y.K.; Çerçevik, A.E. A practical method for calculating eigenfrequencies of a cantilever microbeam with the attached tip mass. J. Vibroeng. 2016, 18, 3070–3077. [Google Scholar]
- Gu, B.; Sheng, V.S.; Tay, K.Y.; Romano, W.; Li, S. Incremental Support Vector Learning for Ordinal Regression. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1403–1416. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Sheng, V.S. A Robust Regularization Path Algorithm for ν-Support Vector Classification. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 1241–1248. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Jiang, J.M.; Zhao, B.P.; Ma, T.H. A self-adaptive artificial bee colony algorithm based on global best for global optimization. Soft Comput. 2017. [Google Scholar] [CrossRef]
- Gu, B.; Sun, X.M.; Sheng, V.S. Structural Minimax Probability Machine. IEEE Trans. Neural Netw. Learn. Syst. 2016, PP. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Sheng, V.S.; Wang, Z.J.; Ho, D.; Osman, S.; Li, S. Incremental learning for ν-Support Vector Regression. Neural Netw. 2015, 67, 140–150. [Google Scholar] [CrossRef] [PubMed]
- Chandra, N.H.; Sekhar, A.S. Fault detection in rotor bearing systems using time frequency techniques. Mech. Syst. Signal Proc. 2016, 72–73, 105–133. [Google Scholar] [CrossRef]
- Yuan, C.H.; Sun, X.M.; LV, R. Fingerprint liveness detection based on multi-scale LPQ and PCA. China Commun. 2016, 13, 60–65. [Google Scholar]
- Xia, Z.H.; Wang, X.H.; Sun, X.M.; Wang, B.W. Steganalysis of least significant bit matching using multi-order differences. Secur. Commun. Netw. 2014, 7, 283–1291. [Google Scholar] [CrossRef]
- Tian, Q.; Chen, S.C. Cross-heterogeneous-database age estimation through correlation representation Learning. Neurocomputing 2017, 238, 286–295. [Google Scholar] [CrossRef]
- Xia, Z.H.; Wang, X.H.; Sun, X.M.; Liu, Q.S.; Xiong, N.X. Steganalysis of LSB matching using differences between nonadjacent pixels. Multimed. Tools Appl. 2016, 75, 1947–1962. [Google Scholar] [CrossRef]
- Bououden, S.; Chadli, M.; Filali, S.; El Hajjaji, A. Fuzzy model based multivariable predictive control of a variable speed wind turbine: LMI approach. Renew. Energy 2012, 37, 434–439. [Google Scholar] [CrossRef]
- Pan, Z.Q.; Lei, J.J.; Zhang, Y.; Sun, X.M.; Kwong, S. Fast motion estimation based on content property for low-complexity H.265/HEVC encoder. IEEE Trans. Broadcast. 2016, 62, 675–684. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 9 January 2017).
- Cai, Y.P.; Li, A.H.; Wang, T.Y.; Liang, X.P. Engine vibration time-frequency analysis based on EMD-Wigner-Ville. J. Vib. Eng. 2010, 23, 430–437. [Google Scholar]
- Vahidi, B.; Ghaffarzadeh, N.; Hosseinian, S.H. A wavelet-based method to discriminate internal faults from inrush currents using correlation coefficient. Int. J. Electr. Power Energy Syst. 2010, 32, 788–793. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).