1. Introduction
Recently, simultaneous wireless information and power transfer (SWIPT) has gained great interest due to its capability to deal with the energy scarcity in energy-constrained wireless networks [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10]. In the seminal works [
1,
2], the fundamental trade-off between information and power transfer in different point-to-point wireless channels was studied. On the other hand, two practical receiver designs for SWIPT, namely power splitting (PS) and time switching (TS), were firstly presented in [
3,
4]. Specifically, the PS-based receiver spits the received radio-frequency signal into two streams of different power for harvesting energy and decoding information, whereas the TS-based receiver switches over time between those two operations. The SWIPT has been adopted later in more complicated communication scenarios, including the broadband wireless system [
5], the cellular network [
6], the interference channel [
7,
8], and the relay channel [
9,
10]. This paper focuses on the last scenario.
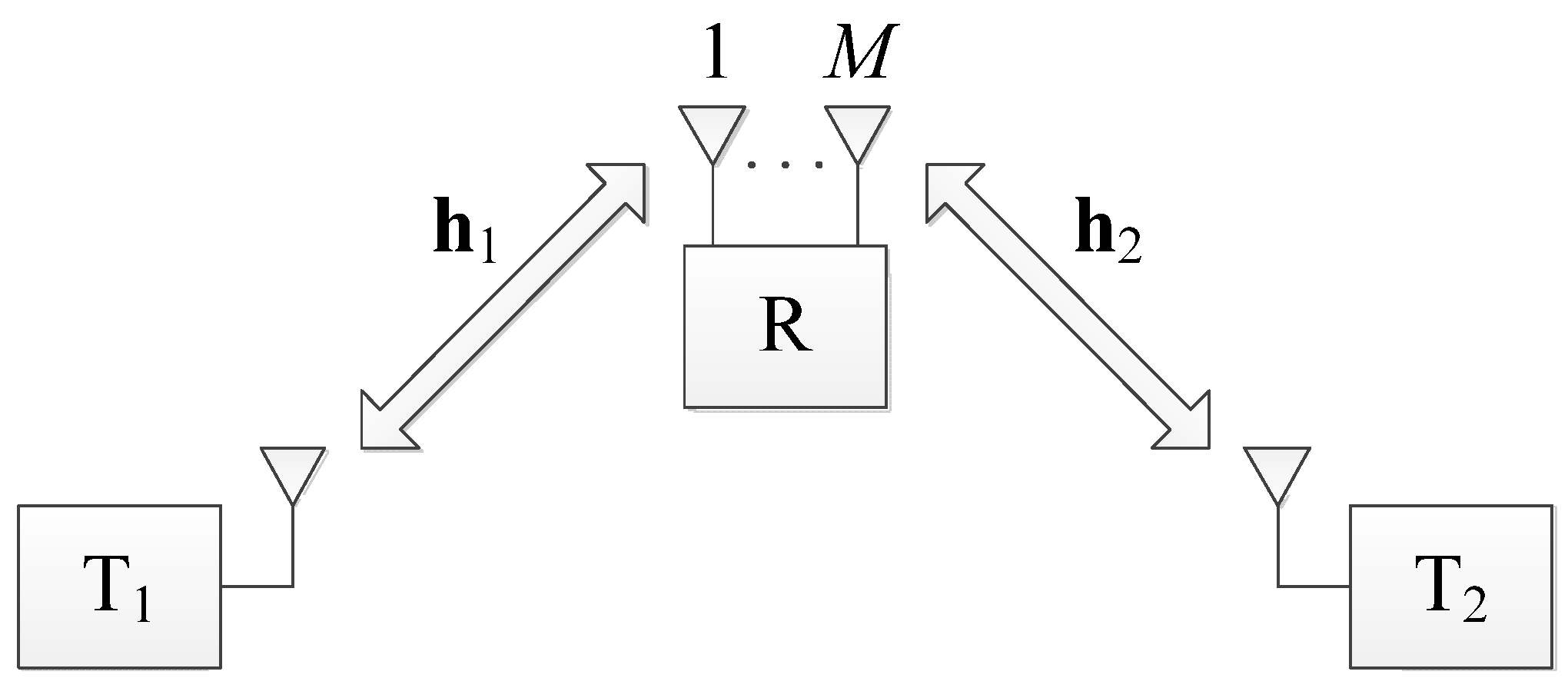
Many works in the literature (e.g., [
11,
12,
13,
14,
15]) have been devoted to two-way multi-antenna relaying (without SWIPT) as this approach can not only extend communication range but also improve spectral efficiency. In a basic two-way multi-antenna relay network (see
Figure 1), an intermediate relay node equipped with multiple antennas is used to assist two end nodes in exchanging their information. Nevertheless, application of SWIPT to this kind of network is still in its infancy [
16,
17,
18]. In [
16], the SWIPT-based beamforming design for a multi-antenna relay was considered to maximize the sum rate of its two-way relay network. In [
17], the authors presented a three-phase two-way relay network where an energy-constrained multi-antenna relay node harvests energy from a pair of single-antenna source nodes, and presented an optimal power allocation solution. In [
18], an optimal joint source and relay beamforming scheme for two-way multi-antenna relay networks with SWIPT was proposed based on the principle of singular value decomposition.
Depending on the nature and complexity of relays, relaying schemes can be classified into two main categories: non-regenerative relaying and regenerative relaying [
19]. Non-regenerative relaying generally implies that the relays only amplify their received signals before retransmitting them. Then, it is often referred to as amplify-and-forward (AF) relaying in the literature. Note that all existing works on two-way multi-antenna relaying with SWIPT (i.e., [
16,
17,
18]) are non-regenerative. On the other hand, regenerative relaying requires the relays to change the waveforms and/or the data contents by performing some processing in the digital domain. An example is the decode-and-forward (DF) relay, which receives the data from its immediate predecessor, decodes, re-encodes, and finally retransmits it. To the best of our knowledge, regenerative relaying has not yet been considered in the SWIPT-based two-way multi-antenna relay networks.
In this paper, we consider a two-way relay network in which two single-antenna end nodes communicate with each other through a multi-antenna relay node that is energy constrained. This relay node harvests energy from the two end nodes and use the harvested energy for forwarding their information. Based on two half-duplex relaying protocols, called power splitting-based relaying (PSR) and time switching-based relaying (TSR) [
9], for separate energy harvesting and information processing at the relay node, six multiple-antenna relaying schemes, namely PS-AF, PS-DF, PS-DF with space-time coding (PS-DF-STC), TS-AF, TS-DF, and TS-DF-STC, are designed for the considered network. In the DF-oriented design, network coding (NC) [
20] is applied to the end nodes’ information that is decoded at the relay node. Moreover, by having multiple antennas at the relay node, STC [
21] is used in the PS-DF-STC and TS-DF-STC schemes with the aim of achieving a better end-to-end decoding performance. Unlike the aforementioned works [
16,
17,
18], which are devoted to analyzing the relevant sum-rate performance, this paper will investigate the average bit error rates (BERs) of the proposed relaying schemes as a function of the number of relay antennas, power splitting ratio, and energy harvesting time.
The remainder of this paper is organized as follows.
Section 2 introduces the system model.
Section 3 and
Section 4 present the PS-based and TS-based multiple-antenna relaying schemes, respectively.
Section 5 compares the BER performance of these relaying schemes by simulations. Finally,
Section 6 concludes the paper.
Notation: Bold upper-case letters denote matrices and bold lower-case letters denote column vectors.
,
,
, and
denote the
-th element, transpose, conjugate transpose, and inverse of a matrix, respectively.
and
denote the modulation and demodulation functions, respectively.
,
, and
denote the absolute value, the expectation value, and the bit-wise exclusive OR operator, respectively.
,
,
, and
denote the Gaussian Q-function, complementary error function, ordinary Gamma function, Gauss hypergeometric function defined in (Equation (4.1), [
22]), (p. xxxvi, [
23]), (Equation (8.310.1), [
23]), and (Equation (9.100), [
23]), respectively. A circularly symmetric complex Gaussian random variable
with mean
and variance
is denoted as
. In the case of communication over a slow-fading channel, the average BER for binary phase shift keying (BPSK) modulation is defined by (Equation (5.1), [
22])
where
is the probability density function (PDF) of the instantaneous signal-to-noise ratio (SNR) of the received signal,
2. System Model
Consider a two-way relay network as shown in
Figure 1, where end nodes
and
, each of which is equipped with one antenna, exchange information through an energy-constrained intermediate relay node,
, possessing
antennas. This relay node will harvest energy from the two end nodes and use the harvested energy for forwarding their information. The relay node’s antennas are spatially spaced in such a way that the received/transmitted signals undergo statistically independent fading. Throughout this paper, perfect timing and synchronization among
,
, and
are assumed, and BPSK modulation is used at
and
. Let
(or
) denote the channel gain between the antenna of
(or
) and the
-th antenna of
, where
(or
) is due to the path loss with power path loss exponent
and distance
(or
) of the
link (or the
link), and
. We presume that all the channels are static over an interval of
, which denotes the total block time in which a certain block of information is exchanged between
and
(see
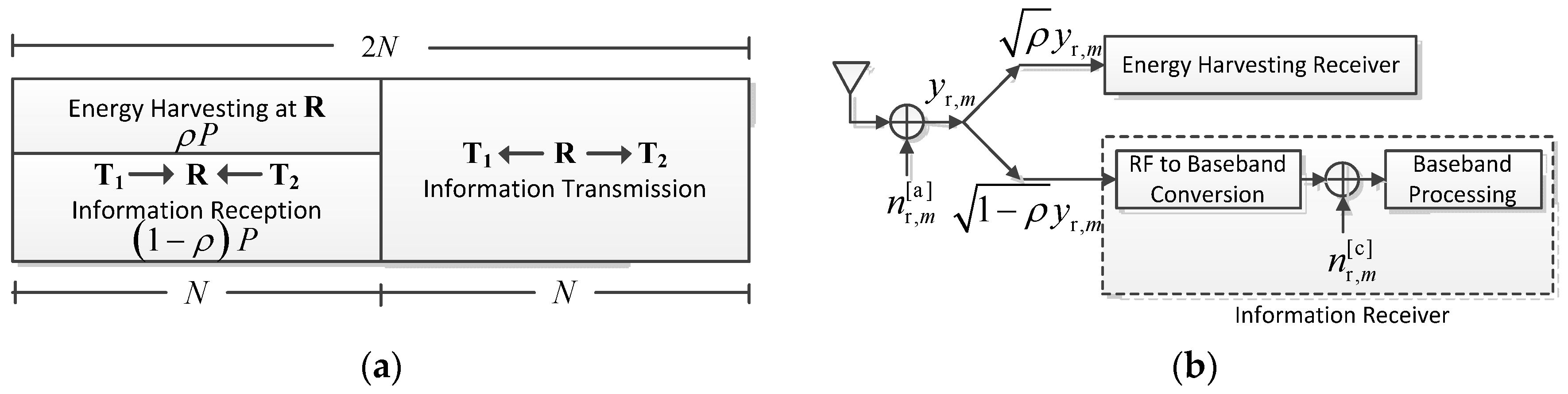
Figure 2a and
Figure 3a), and ignore the direct link between the end nodes owing to the larger distance compared with the
and
links [
16]. For analytical simplicity, we assume that the relay node is located halfway between the end nodes, and thus
. As mentioned in
Section 1, we consider two half-duplex relaying protocols for separate energy harvesting and information processing at the relay node, i.e., PSR and TSR.
3. PSR Protocol
Figure 2 illustrates the key parameters in the PSR protocol for energy harvesting and information processing at the relay node
and the block diagram of the corresponding receiver. In
Figure 2a, the first block time
is used for multiple access (MA) where the end nodes
and
transmit their signals simultaneously, and
is the total signal power. In the second block time
, the relay node processes this signal (according to the schemes that will be presented below) and broadcasts it. During the MA phase, the fraction of the received signal power
is used for energy harvesting, and the remaining received power
is used for information transmission, where
is the power splitting ratio. In other words, as shown in
Figure 2b, the portion of the received radio-frequency (RF) signal, denoted by
, is sent to the energy harvesting receiver and the remaining signal strength, denoted by
, drives the information receiver. In the following, we describe three multiple-antenna relaying schemes, which correspond to the PSR protocol.
3.1. PS-DF Scheme
In the MA phase, the received RF signal at the relay node can be modeled as:
where
and
are the transmitted power from
and
, respectively;
are the power ratios of
and
, respectively (i.e.,
);
and
are the normalized information signals from
and
, respectively (i.e.,
); and
is the additive white Gaussian noise (AWGN) at the
-th antenna of
. The energy harvesting receiver in
Figure 2b rectifies the RF signal
directly and gets the direct current to charge up the battery. Therefore, the harvested energy at the
-th antenna of the relay node during the MA phase is given by:
where
is the energy conversion efficiency (which depends on the rectification process and the energy harvesting circuitry [
9]). Meanwhile, the information receiver in
Figure 2b down-converts the RF signal
to baseband and processes the baseband signal, where
is the AWGN due to RF-band-to-baseband signal conversion. After down conversion, the sampled baseband signal vector at the relay node is given by:
Assuming that
,
,
,
, and
are known at the relay node and applying zero-forcing (ZF) detection, estimates of
and
, denoted by
and
, respectively, are obtained as:
(For discussions of how the relay node can obtain
and
, interested readers are referred to [
24,
25]).
Let
denote the instantaneous SNR of
, where
. It is straightforward to show that:
Defining
and using (Equation (16), [
26]), the PDF of
can be expressed as:
From Equations (6) and (7), we have:
Hence, the corresponding average BER can be derived as follows:
where the second equality is obtained by using the fact that
and (Equation (8.359.3), [
23]), and the fourth equality is obtained by using (Equation (6.455.1), [
23]).
The relay node then performs NC of
and
at bit level to obtain the composite signal. Specifically, let
be the estimated information bit sequence corresponding to
, where
. The composite signal is given by
. As in [
9], we assume that the processing power required by the transmit/receive circuitry at the relay node is negligible as compared to the power used for transmitting the composite signal in the broadcast (BC) phase. From Equation (3), the latter power is given by:
and the sampled received (baseband) signal at the end node
in the BC phase can be expressed as:
where
and
are the AWGN due to the antenna and that due to RF-band-to-baseband signal conversion, respectively. Assuming that
is known at
, an estimate of
is obtained as:
(For realizing this assumption, interested readers may consult [
24,
25]).
Denoting by
the instantaneous SNR of
at
, it can be shown that:
Defining
and using (p. 48, [
27]) and (Equations (5)–(8), [
28]), the PDF of
can be expressed as:
From Equations (13) and (14), we have:
Following the same procedure as in (9), the average BER associated with
is obtained as:
At the end node
, the intended signal
can be finally recovered by performing bit-level network decoding of
with its own signal
, and the corresponding end-to-end BER can be obtained as:
where:
is the average BER of
.
3.2. PS-DF-STC Scheme
For the MA phase, the description of the signal transmissions from the end nodes
and
to the relay node
can be done as in the PS-DF scheme, i.e., Equations (2)–(4). The aforementioned ZF estimation and bit-level NC also follow. The corresponding average BER (i.e.,
where
) is therefore the same as Equation (9). However, instead of transmitting the same composite bit sequence
simultaneously via
antennas in the BC phase, the relay node performs space-time block coding [
21] for this sequence, as outlined in [
29]. Specifically, let
be the space-time block-coded composite bit matrix whose dimension is
, where
is the block length of the corresponding space-time block code. If
consecutive composite bits, i.e.,
, are transmitted with this matrix, then the code rate is
. In this paper, we concentrate on the space-time block-coded composite bit matrices with the full code rate, i.e.,
. Such matrices for two, three, and four antennas are shown in
Table 1.
As a result, the sampled received (baseband) signal at the end node
in the BC phase can be expressed as:
where
is exemplified in
Table 1, and
includes the antenna and signal-conversion AWGNs at the corresponding time instants. Following [
30] and assuming that
are known at
, an estimate of
can be obtained as
It is straightforward to show that the instantaneous SNR of
at
is:
Defining
and using (p. 48, [
27]) and (Section “Related distributions”, [
31]), the PDF of
can be expressed as:
From Equations (21) and (22), we have:
Following the same procedure as in (9), the average BER associated with
is obtained as:
At the end node , the intended signal can be finally recovered by performing bit-level network decoding of with its own signal , and the corresponding end-to-end BER is obtained using Equation (17).
3.3. PS-AF Scheme
For the MA phase, the description of the signal transmissions from the end nodes
and
to the relay node
can be done as in the PS-DF scheme, i.e., Equations (2)–(4). In the BC phase, the relay node amplifies and forwards the information signal as:
where
and the sampled received (baseband) signal at the end node
is given by:
where
and
are defined below Equation (11). Assuming that
,
,
,
, and
are known at
, an estimate of the intended signal
can be obtained as:
Let
denote the instantaneous SNR of
at
. It is straightforward to show that:
and the corresponding end-to-end BER,
, is the average BER associated with
. Unfortunately, it is difficult, if not impossible, to find the PDF of
. Therefore, the end-to-end BER has no closed-form expression and is obtained by means of simulations.
4. TSR Protocol
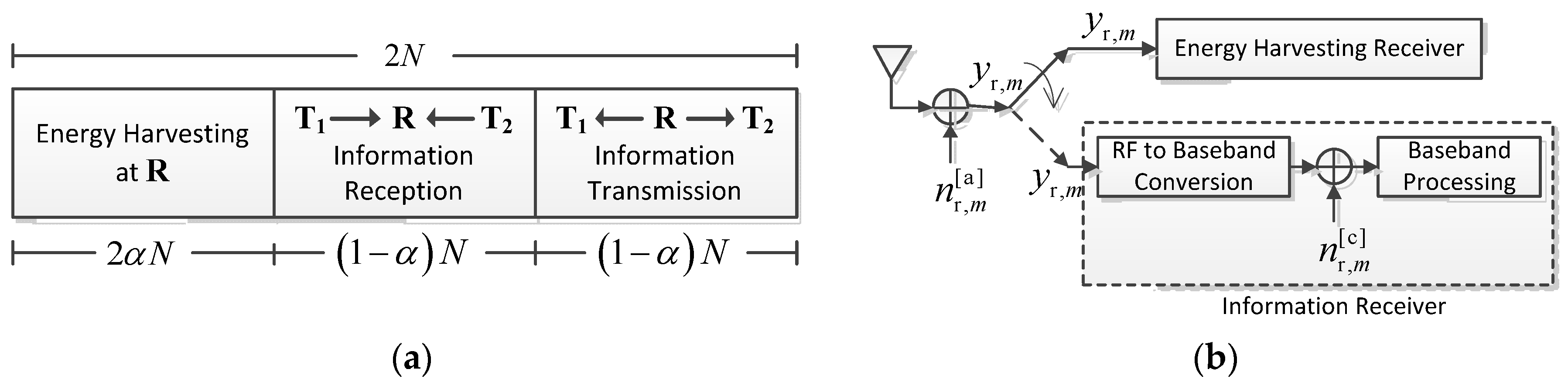
Figure 3 illustrates the key parameters in the TSR protocol for energy harvesting and information processing at the relay node
and the block diagram of the corresponding receiver. In
Figure 3a,
is the fraction of the total block time
in which the relay node harvests energy from the end nodes
and
, where
. The remaining block time
is used for information transmission, such that the first half of that is used for MA and the second half is used for BC. Assuming that the TSR protocol has the same energy constraint as the PSR protocol, the power of the total received signal at the relay node (during energy harvesting time and the MA phase) is
. In what follows, we describe three multiple-antenna relaying schemes, which correspond to the TSR protocol.
4.1. TS-DF Scheme
In the MA phase, the received RF signal at the relay node
is the same as Equation (2) except that
,
, and the harvested energy during the energy harvesting time is given by:
After RF-band-to-baseband signal conversion at the information receiver as shown in
Figure 3b, the sampled baseband signal vector is given by:
where
is the AWGN due to such conversion. Assuming that
,
,
, and
are known at the relay node and applying ZF detection, estimates of the information signals
and
, denoted by
and
. respectively, are obtained as:
It is straightforward to show that the instantaneous SNR of
is:
where
. From Equations (7) and (32), we have:
Following the same procedure as in Equation (9), the average BER associated with
is obtained as:
Then, the corresponding composite signal
is created and broadcasted in the same way as in the PS-DF case. In the BC phase, the sampled received (baseband) signal at the end node
is the same as Equation (11) except that:
Assuming that
are known at
, an estimate of
(i.e.,
) is obtained from Equation (12) together with Equation (35).
It can be shown that the instantaneous SNR of
at
is:
From Equations (14) and (36), we have:
Following the same procedure as in Equation (9), the average BER associated with
is obtained as:
At the end node , the intended signal can be finally recovered by performing bit-level network decoding of with its own signal , and the corresponding end-to-end BER is obtained using Equation (17).
4.2. TS-DF-STC Scheme
For the MA phase, the description of the signal transmissions from the end nodes and to the relay node can be done as in the TS-DF scheme, i.e., Equations (2), (29) and (30). The aforementioned ZF estimation and bit-level NC also follow. The corresponding average BER (i.e., where ) is therefore the same as Equation (34). During the BC phase, the relay node performs full-rate space-time block coding for the resultant composite bit sequence and the end nodes perform the corresponding sequence decoding and signal recovery, as in the PS-DF-STC case.
It is straightforward to show that the instantaneous SNR of an estimate of
at
is:
From Equations (22) and (39), we have:
Following the same procedure as in Equation (9), the average BER associated with
is obtained as:
The corresponding end-to-end BER is obtained using Equation (17).
4.3. TS-AF Scheme
For the MA phase, the description of the signal transmissions from the end nodes
and
to the relay node
can be done as in the TS-DF scheme. In the BC phase, the relay node amplifies and forwards the information signal as expressed in Equation (25), where:
and the sampled received (baseband) signal at the end node
is given by:
where
and
are defined below Equation (11). Assuming that
,
,
, and
are known at
, an estimate of the intended signal
can be obtained as:
Let
denote the instantaneous SNR of
at
. It is straightforward to show that:
and the corresponding end-to-end BER,
, is the average BER associated with
. Unfortunately, it is difficult, if not impossible, to find the PDF of
. Therefore, the end-to-end BER has no closed-form expression and is obtained by means of simulations.
5. Simulation Results
In this section, we evaluate the performance of the proposed multiple-antenna relaying schemes (i.e., PS-DF, PS-DF-STC, PS-AF, TS-DF, TS-DF-STC, and TS-AF) in terms of average BER of the end nodes and . Suppose that and are separated by a distance of m, and the relay is located halfway between them. Unless stated otherwise, we set the total signal power, W; the power ratios of and , ; the path loss exponent, ; the power energy conversion efficiency, ; the power splitting ratio in the PSR protocol, ; and the time fraction used for energy harvesting in the TSR protocol, .
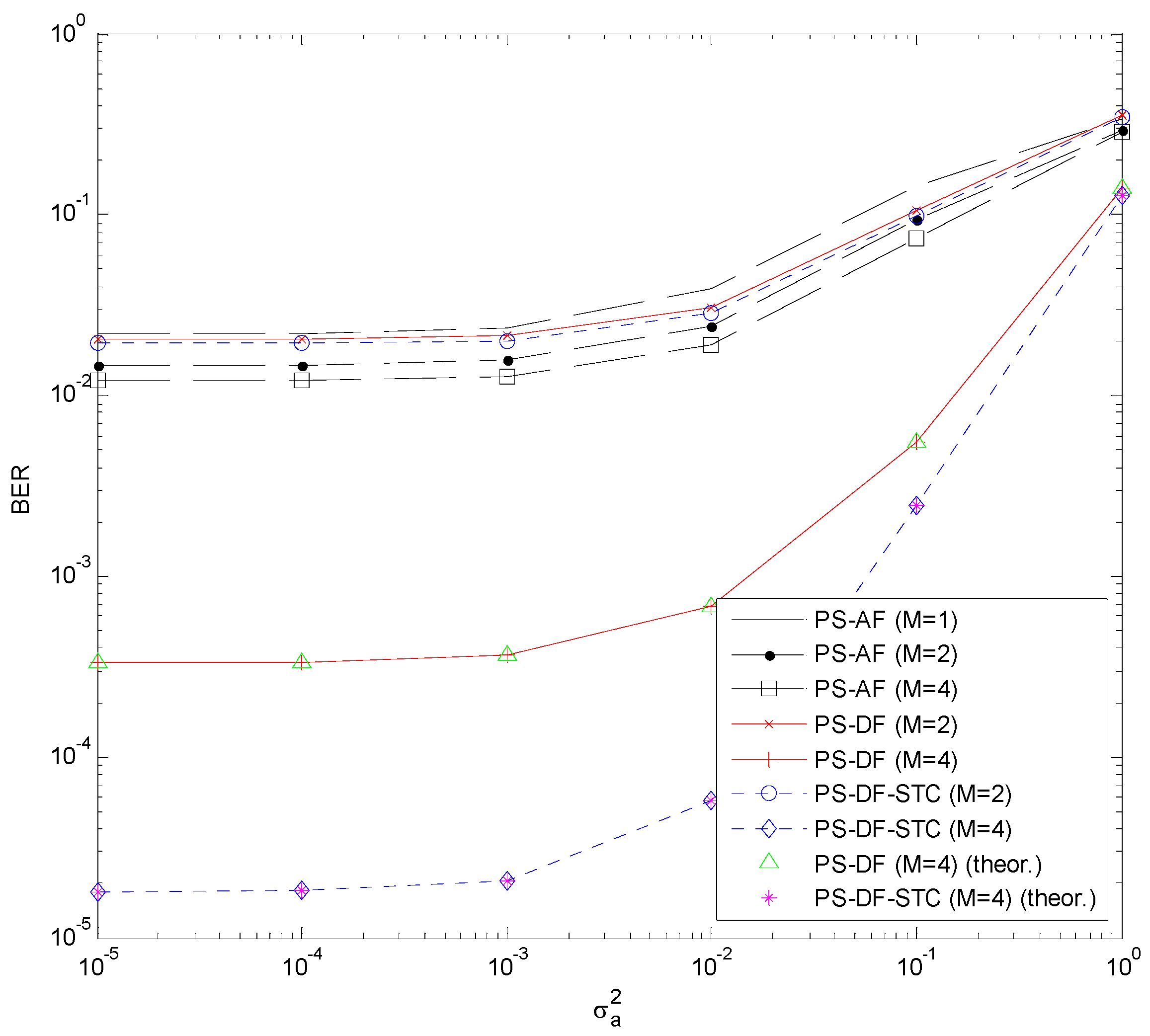
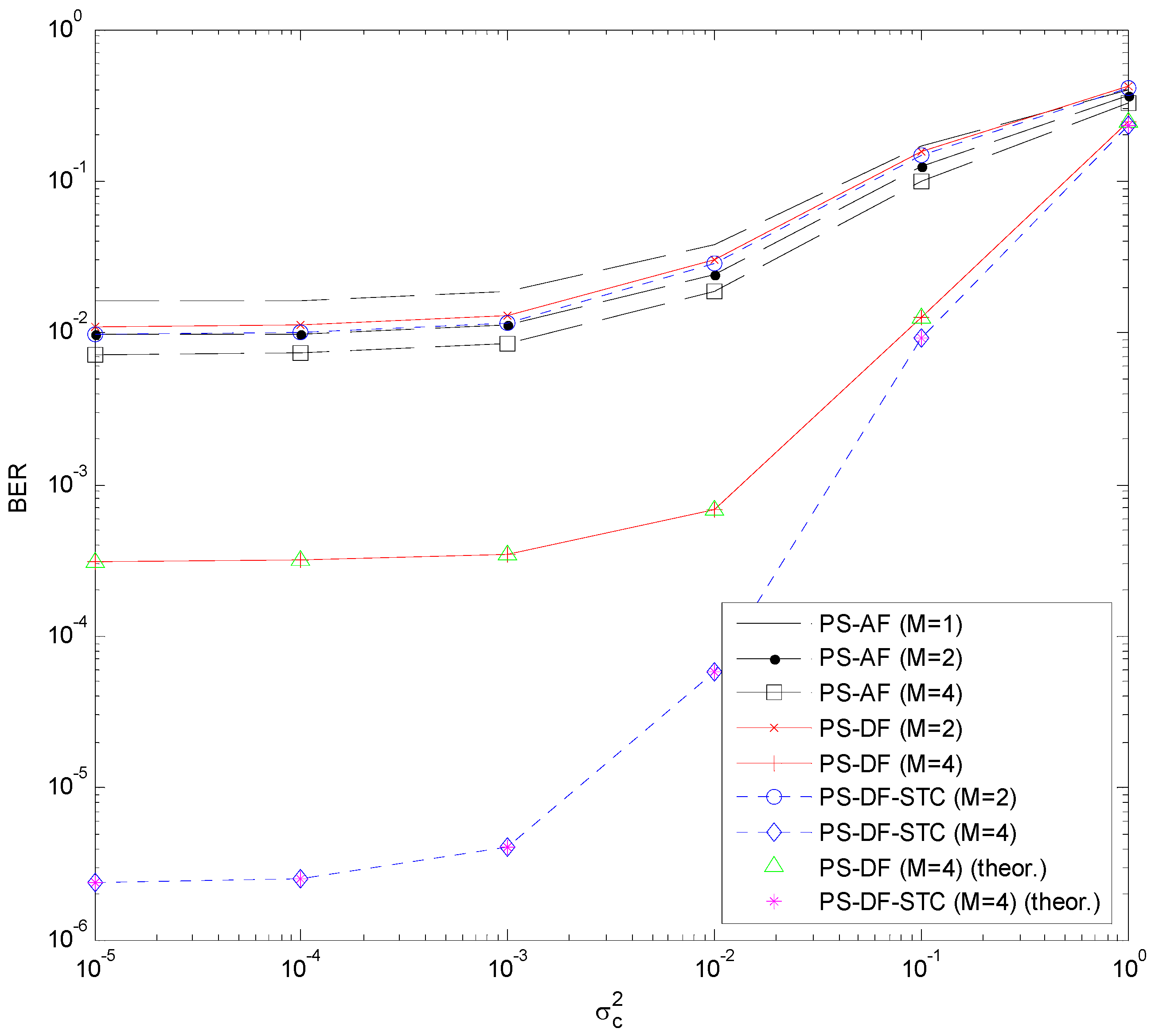
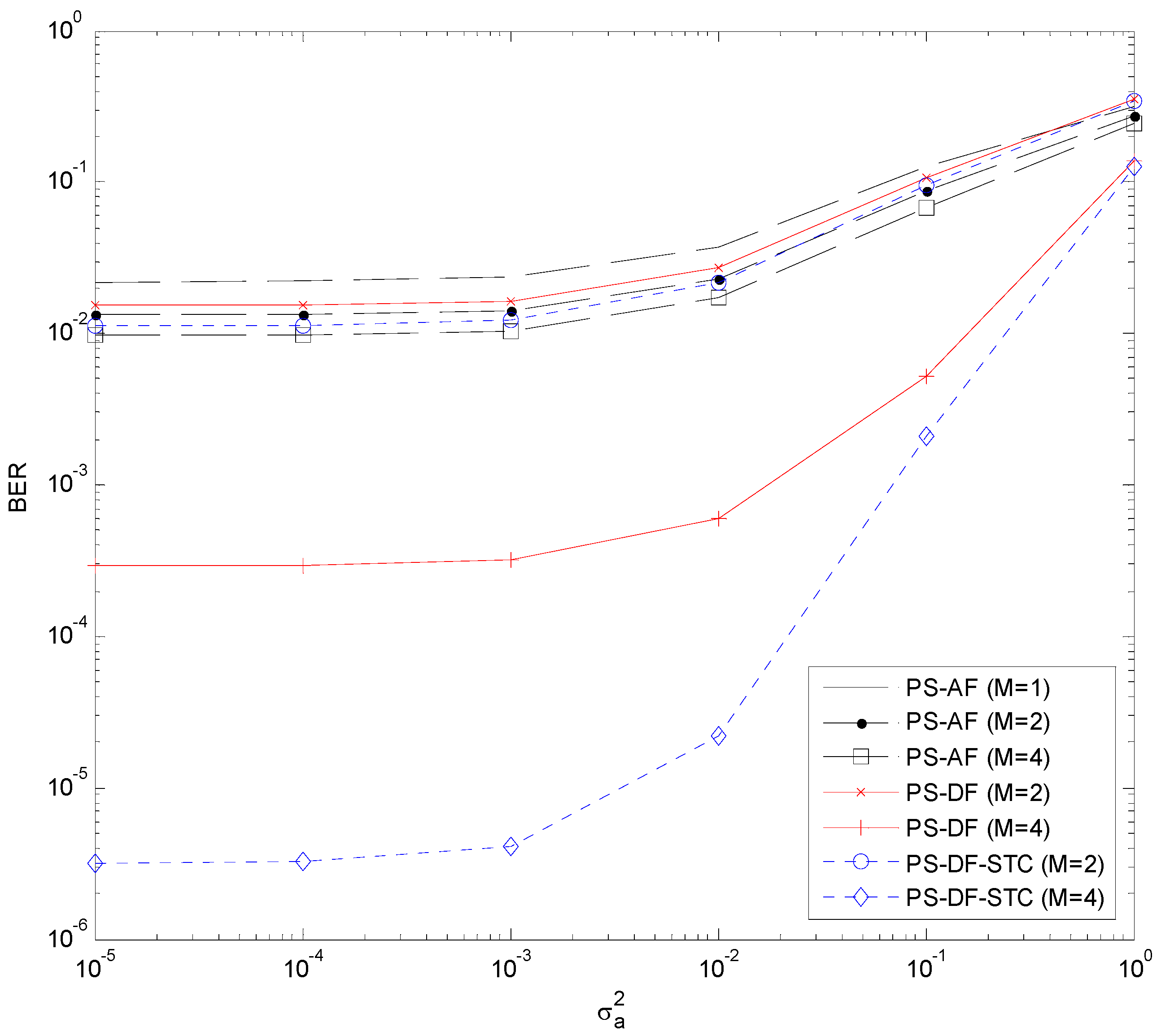
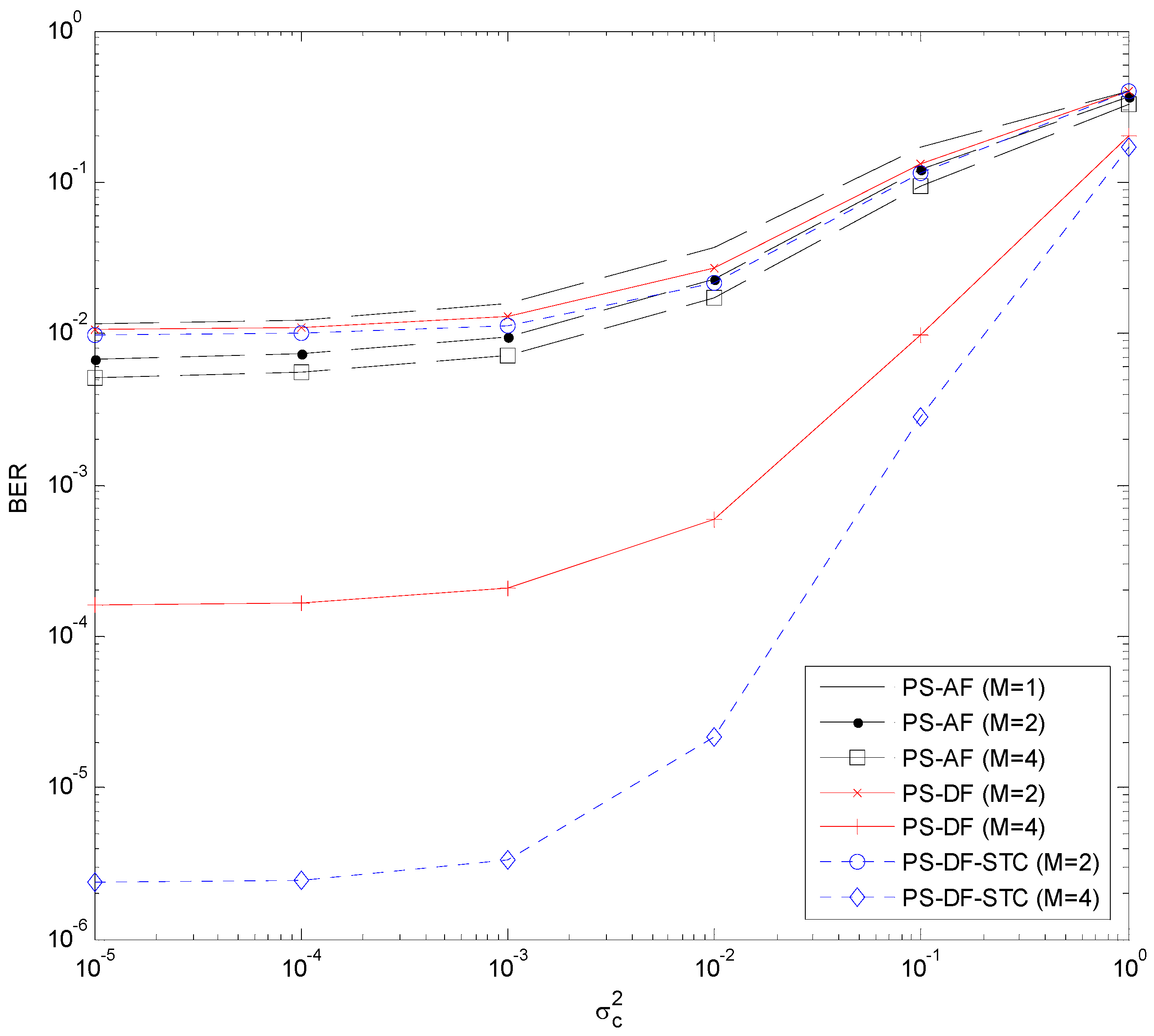
The simulated BERs of the PS-DF, PS-DF-STC, and PS-AF schemes are plotted versus antenna noise variance
for different numbers of relay antennas
(with fixed conversion noise variance
) in
Figure 4 and versus conversion noise variance
for different values of
(with fixed antenna noise variance
) in
Figure 5. The theoretical BER curves of the PS-DF scheme (computed with Equations (9), (16), and (17)) and the PS-DF-STC scheme (computed with Equations (9), (17), and (24)) are also included and labeled with “(theor.)”. We can see that the theoretical results perfectly match their simulation counterparts, which verifies the BER formulae derived in
Section 3.1 and
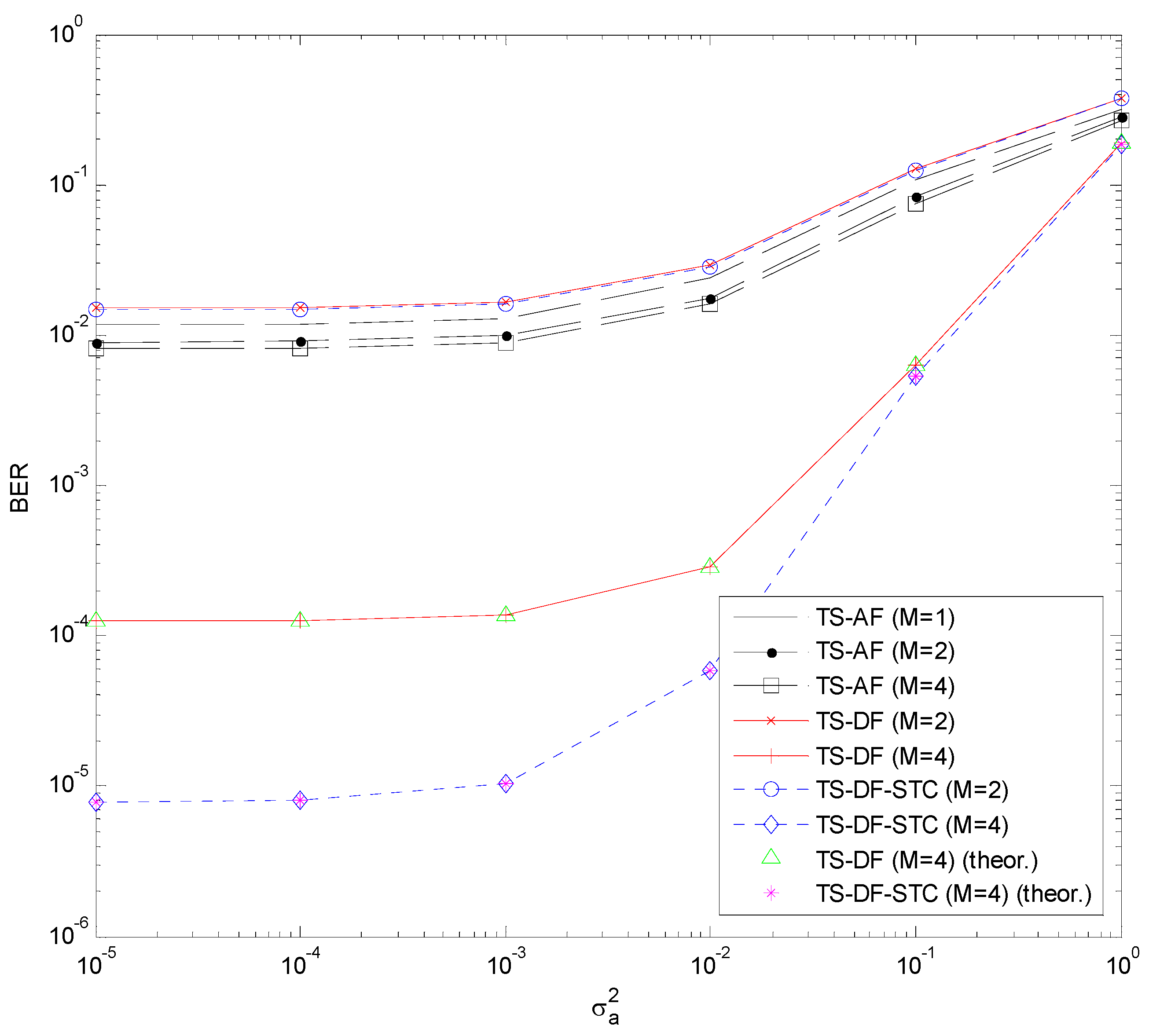
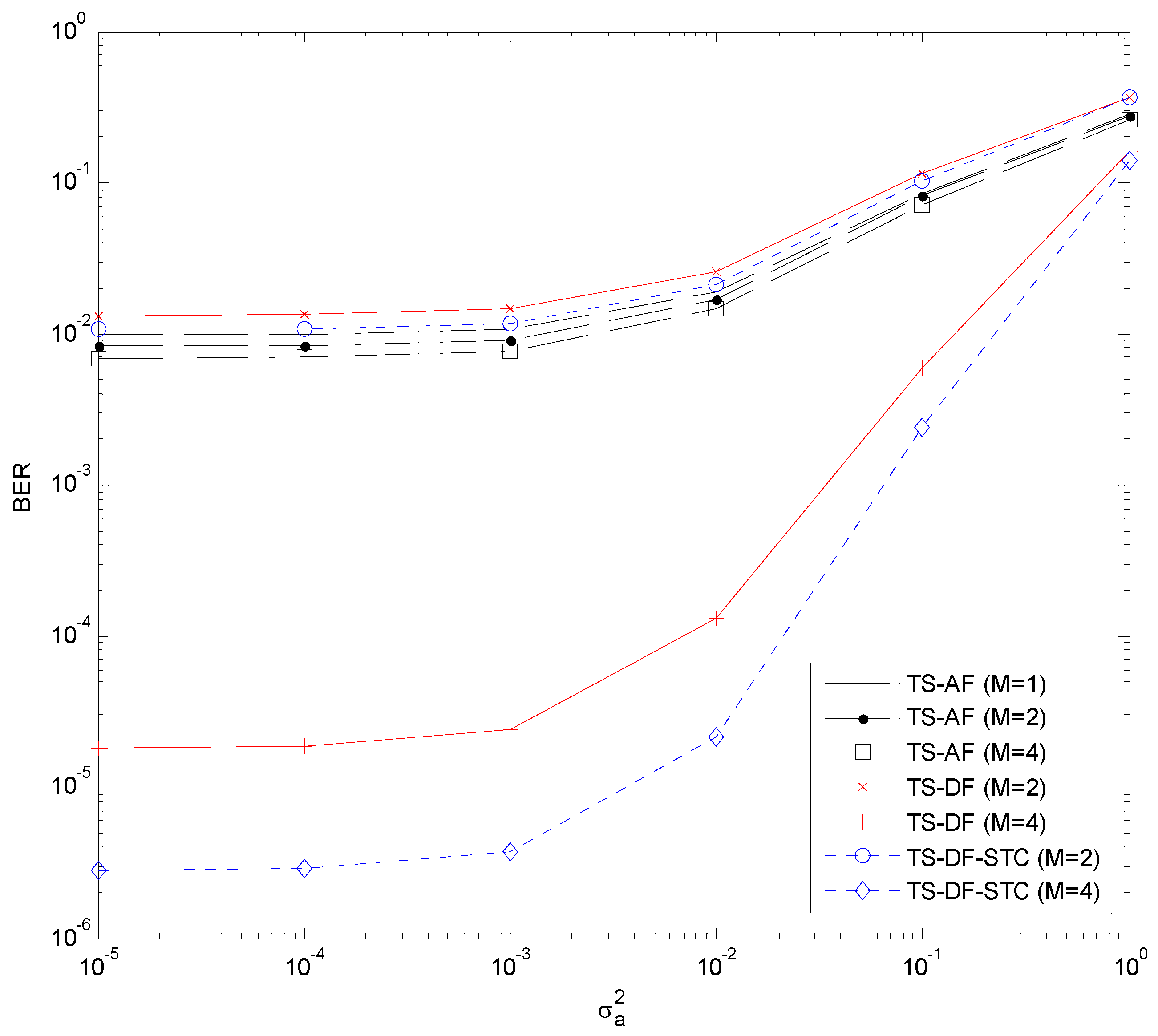
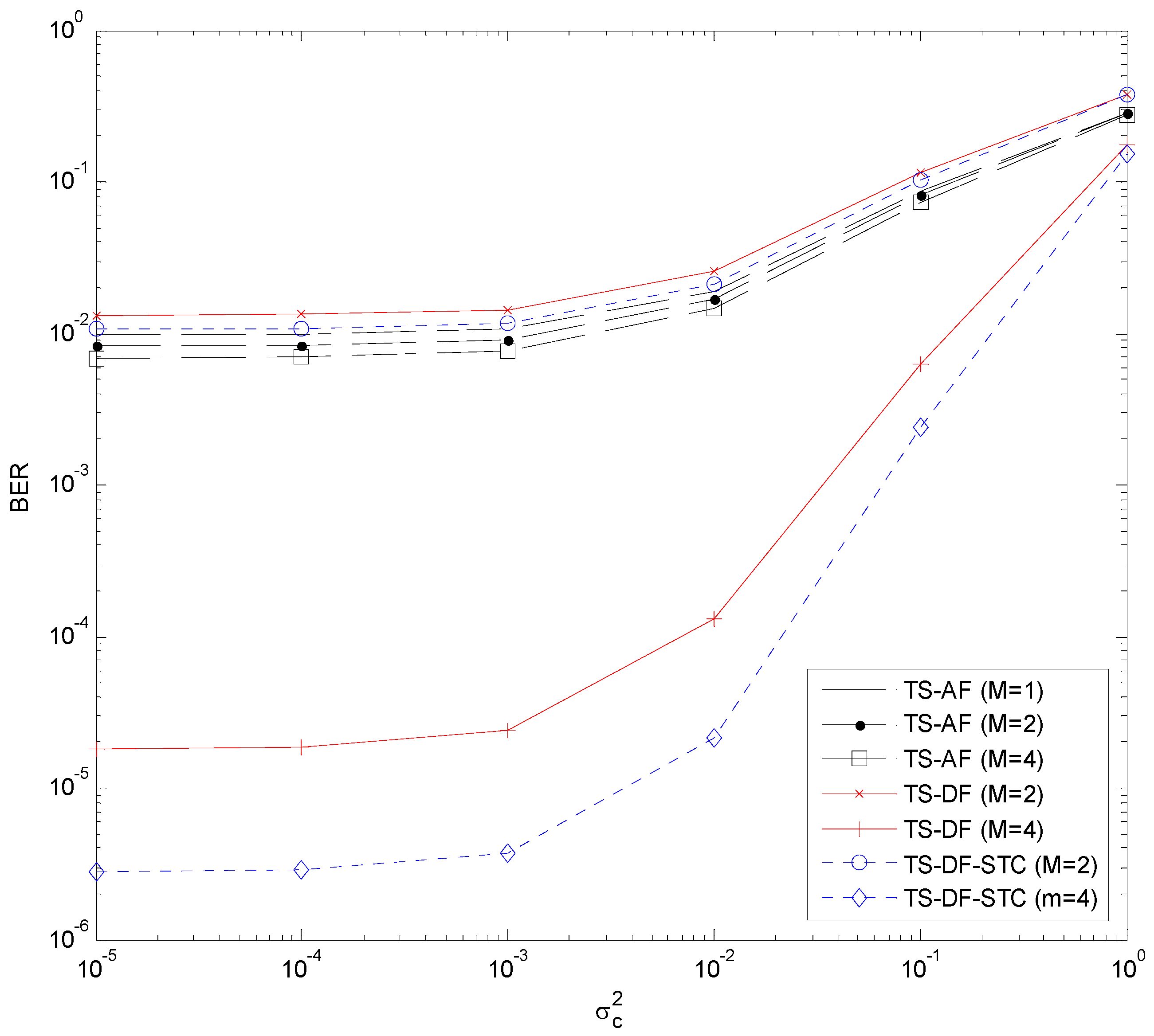
Section 3.2. Similarly, the results for the TS-DF, TS-DF-STC, and TS-AF cases are shown in
Figure 6 and
Figure 7. As seen, the theoretical BER results (computed with Equations (17), (34), and (38) for the TS-DF case, and with Equations (17), (34), and (41) for the TS-DF-STC case) agree well with the simulated ones, which validates the BER analysis in
Section 4.1 and
Section 4.2. It is clear that increasing the number of relay antennas generally improves the BER performance (the results at
are excluded to make the BER curves readable in all these figures). From
Figure 4 and
Figure 5, we can see that the BERs of the PS-DF, PS-DF-STC, and PS-AF schemes are comparable when
, and their difference becomes significant when
. In the latter case, the PS-DF-STC scheme performs best while the PS-AF scheme does worst. Similar performance trends can be observed in the TS-DF, TS-DF-STC, and TS-AF schemes, as illustrated in
Figure 6 and
Figure 7. Comparing
Figure 4 and
Figure 6 (or
Figure 5 and
Figure 7), one can find that, with the same number of relay antennas, the TS-DF and TS-AF schemes are generally superior to the PS-DF and PS-AF schemes, respectively.
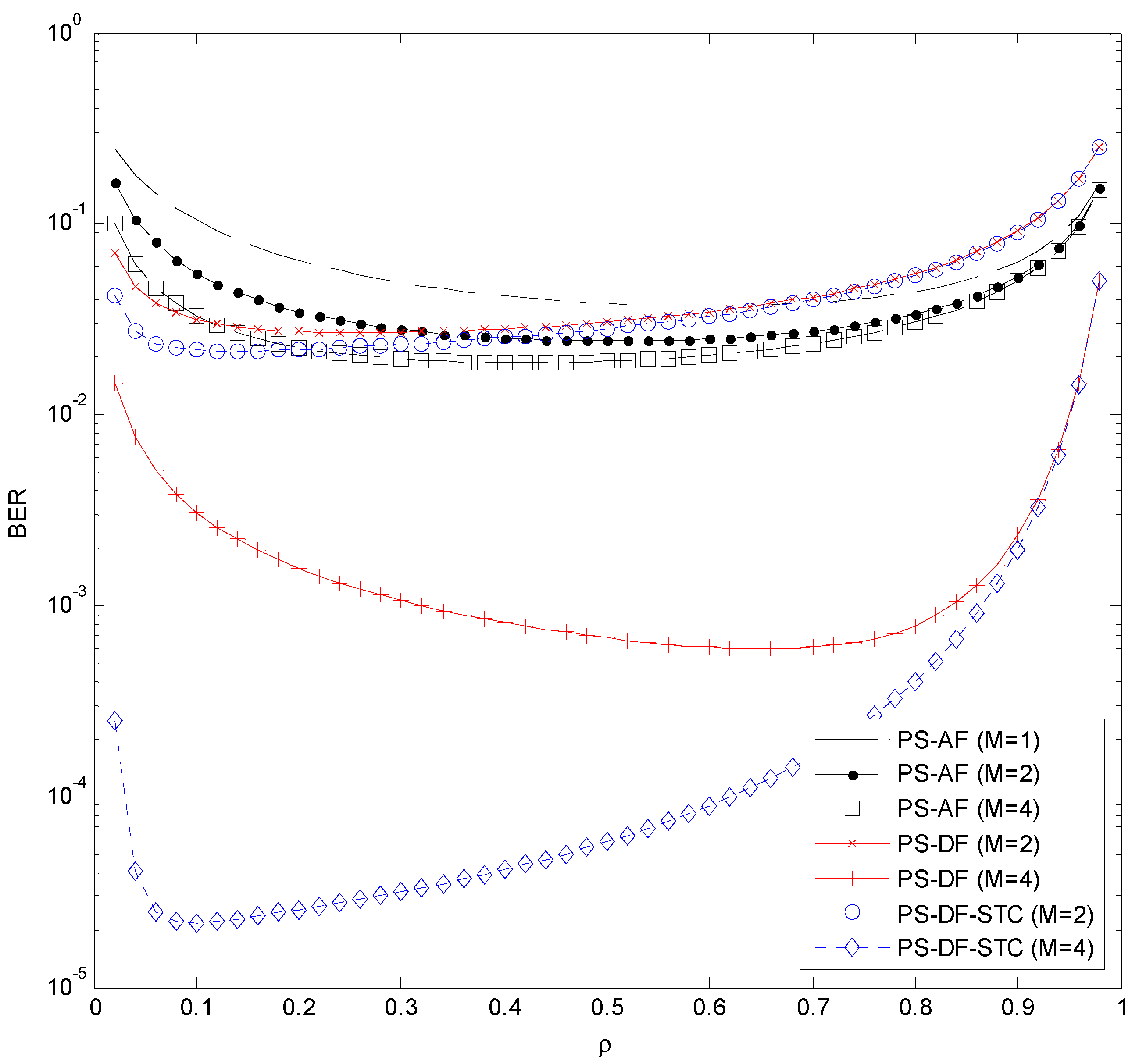
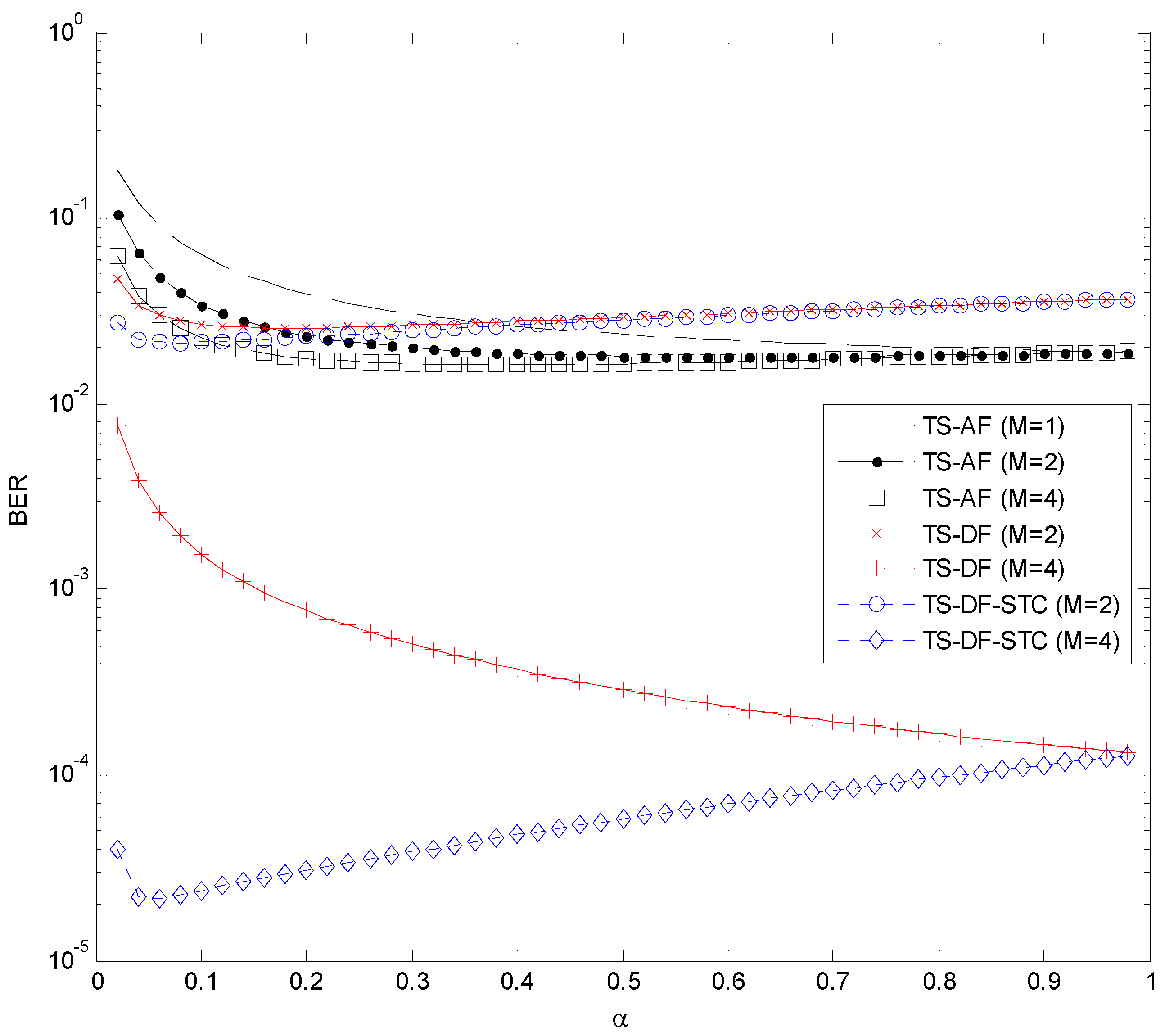
It would be interesting to study the effect of the power allocation parameters, i.e., power splitting ratio
and energy harvesting time
, on the BER performance. To this end, we show in
Figure 8 the BER as a function of
for the PS-DF, PS-DF-STC, and PS-AF schemes, and in
Figure 9 the BER as a function of
for the TS-DF, TS-DF-STC, and TS-AF schemes. From these two figures, we observe that, in general, equal power allocation, i.e.,
, is a good strategy for the PS-AF and TS-AF schemes. However, the optimal
and
which minimize the BERs of the PS-DF and TS-DF schemes, respectively, depend mainly on the number of relay antennas
. Specifically, these optimal
and
increase (toward
) as
increases. For example, the optimal
for the two-antenna PS-DF scheme is approximately 0.26 while that for the four-antenna PS-DF scheme is around 0.65 (See
Figure 8). In addition, the optimal
for the two-antenna PS-DF-STC scheme (or the optimal
for the two-antenna TS-DF-STC scheme) is nearly the same as that for the four-antenna PS-DF-STC scheme (or that for the four-antenna TS-DF-STC scheme). This result indicates that these optimal
and
are not sensitive to the value of
, unlike those for the PS-DF and TS-DF schemes, respectively.
To get a further insight into the impact of
and
, we plot the BER curves of the multiple-antenna relaying schemes with optimal power allocation (i.e., using the optimal
or
) in
Figure 10,
Figure 11,
Figure 12 and
Figure 13. Comparing these results to those in
Figure 4,
Figure 5,
Figure 6 and
Figure 7, we find that for all considered relaying schemes except TS-AF scheme, the performance gain of the optimal power allocation over the equal power allocation can become significant as
increases. Similar to the case of equal power allocation, the power optimization-based TS-DF and TS-AF schemes generally outperform their PS-DF and PS-AF counterparts, respectively.