1. Introduction
The frequency spectrum is treated as a valuable resource in the wireless communication field and is rendered inadequate for the increasing number of wireless services. In terms of the spectrum task report from the Federal Communication Commission (FCC), the usage of authorized spectrum alters according to geographic and temporal circumstances [
1]. Cognitive radio (CR) arises as a tempting solution to the spectrum congestion problem by enabling opportunistic access to underutilized licensed bands that are lightly occupied by a licensed user (LU). CR is characterized by the fact that it adapts to the actual environment by transforming its transmitting parameters, such as frequency, modulation, frame format, etc. [
2,
3]. A precondition of secondary access is the absence of interference for the primary system. Spectrum sensing thereby plays an essential role in cognitive radio networks (CRNs).
Among fundamental spectrum sensing techniques, energy detection is predominant due to its simple implementation, as well as low computational complexity [
4,
5]. However, spectrum sensing conducted by a single node is hindered by uncertainty originating from channel randomness, such as multipath fading and shadow effect [
6]. To combat these adverse impacts, collaborative spectrum sensing (CSS) schemes have been proposed to achieve spatial diversity in CRNs [
7,
8,
9]. In CSS, messages reported from different SUs are combined at the data fusion center (DFC); DFC subsequently makes a global decision on the absence/presence of the LU.
There exists abundant literature that has established the optimality of likelihood ratio test (LRT) concerning detection issues, such as [
10,
11,
12] and the references therein; yet, the computation complexity of LRT is quite high, and the closed form expressions of detection probability and false alarm probability cannot be derived. Quan et al. [
13] have put forward an optimal linear CSS method, which makes the final decision over a linear weighted combination of the local measurements. The computational complexity has been reduced, and the performance compared favorably with LRT-based optimal fusion rules, which can be achieved, as well; but the DFC requires specific report channels to acquire and update a priori information. In recent years, plenty of algorithms have been proposed owing to the unique advantages of the Dempster–Shafer (D-S) theory of evidence in terms of uncertainty representation [
14,
15,
16,
17,
18,
19]. In [
14], Dempster–Shafer theory is first applied in the data fusion of CSS. This method quantifies the channel condition between LU and SUs with credibility parameter and adopts D-S theory to fuse the local measurements with relevant credibility. Nhan and Insoo [
15] came up with an enhanced CSS scheme based on D-S theory and reliability source evaluation. It exploits the signal-to-noise ratios (SNRs) to assess the reliability degree for SUs. The reliability weight of SUs is then applied to adjust their observational information before making the global decision. However, it uses much bandwidth to transmit the sensing data with the number of SUs increasing.
Although the participation of multiple SUs in CSS contributes to the improvement of detection accuracy, the global decision making may be misguided when SUs intentionally or unintentionally send falsified sensing information to the DFC during cooperation. This sort of attack in CSS, called the spectrum sensing data falsification (SSDF) attack, has significantly degraded collaborative detection correctness. Hence, effective security mechanisms are fundamentally demanded in an opponent wireless environment. Han et al. [
16] propose an enhanced evidence theory-based CSS method to resist the SSDF attack. This scheme uses the similarity degree to evaluate the credibility of evidence and removes the evidence with low similarity degree from the combination. Facing the problem of faulty nodes in CRN, the CSS method in [
17] adopts a mutually supportive degree among different sensor nodes to support adapted decision. Another evidence theory-based secure CSS scheme is proposed in [
18], which employs robust statistics to calculate the distribution parameters of LU’s activity and estimates the SUs’ credibility with a simple counting technique. In addition, several detection approaches are adopted to counter distinct sorts of malicious SUs. In [
19], a trusted CSS method for mobile CRNs is proposed, which improves malicious SU detection utilizing both location reliability and D-S theory. Wang et al. [
20] take advantage of the “soft update” approach and evaluate the trustworthiness degree of SUs for enhancing the robustness of the CSS system.
However, these existing evidence theory-based CSS methods are not specifically suited for CRNs communications. This is basically because they are generally designed without considering challenges posed by the framework of resource-constrained nodes of CRNs; such as hardware limitations and low power budget. In addition, the majority of these CSS methods only consider SUs’ current difference, for instance the SNR difference or similarity degree diversity, to estimate the credibility of each SU. Although this current difference tends to reflect SUs’ reliability to some extent, it is unilateral and sometimes inexact, by virtue of the dynamic characteristic of wireless channels. Apart from real-time information, the statistical information about SUs’ historical sensing behavior reflecting their past credibility should also be taken into account in the evaluation of sensing credibility.
Therefore, in this paper, we propose a robust CSS scheme based on D-S evidence theory and credibility calculation. It is executed in four consecutive procedures, which are basic probability assignment (BPA), holistic credibility calculation, option and amelioration of BPA and evidence combination via the Dempster–Shafer rule, respectively. The major contributions of this paper can be summarized as follows:
A. Considering transmitted data rises with the increase of the number of nodes and the power restriction of SUs, we introduce projection approximation approach to half decrease the amount of required transmitted data from SUs to the DFC. This is achieved by adapting the D-S evidence theory to the binary hypothesis test of the cognitive radio context.
B. Instead of evaluating the SUs only with their current measurements, we propose to evaluate the credibility of each SU from both statistical reputation and the real-time difference. The proposed method can not only effectively distinguish malicious SUs from genuine ones based on their past sensing behaviors, but also hold the current sensing difference for SUs to realize superior real-time performance.
C. No prior knowledge such as the average SNR of each SU is demanded at DFC, which reduces the communication cost. Moreover, our proposed method is simple to implement. The reputation value maintenance can be conducted in an iterative manner, which requires no additional computational complexity or storage overhead.
The remainder of the paper is organized as follows. In
Section 2, we describe the system model with the energy detection and D-S theory; the attack models are introduced, as well. The robust Dempster–Shafer theory collaborative spectrum sensing method is proposed in
Section 3, which elaborates the holistic credibility calculation in detail. Simulations and conclusions are respectively presented in
Section 4 and
Section 5.
Section 4 presents numerical simulation results. Finally, the conclusions are drawn in
Section 5.
2. System Description
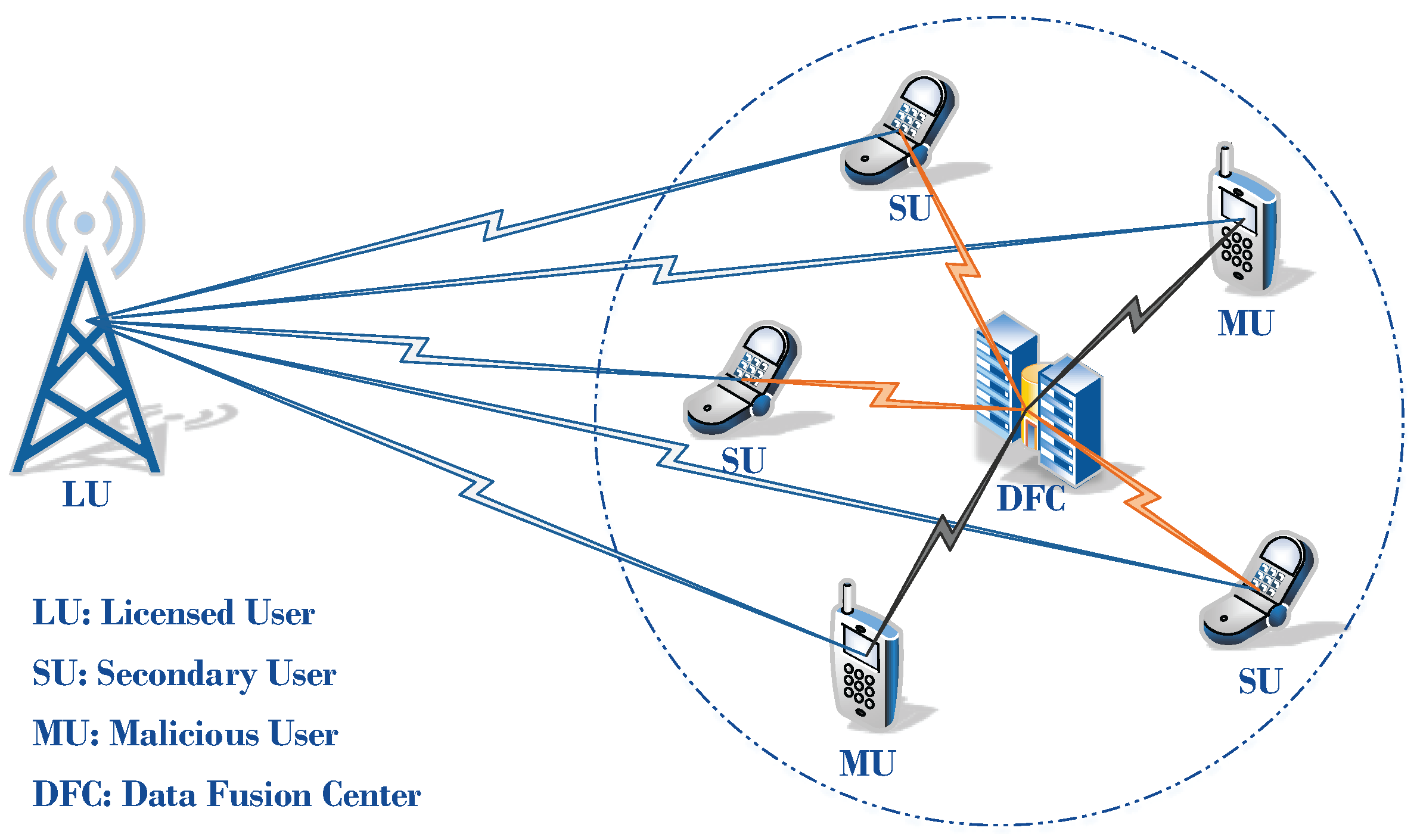
As a key technology for achieving opportunistic spectrum access, spectrum sensing aims to detect the presence of PUs accurately and quickly. In this article, we consider two processes for spectrum sensing, which the local spectrum sensing at each SU and the data fusion at the DFC. The CSS scenario in CRNs and two patterns of attack are described in this section.
2.1. Collaborative Spectrum Sensing
The network architecture we consider is a centralized network entity, such as a base-station in infrastructure-based networks, as showed in
Figure 1. Assume that the CR network consists of one licensed user base station, which may be active with probability
or idle with probability
in a sensing time slot,
n secondary users and one data fusion center. Firstly, the individual SU conducts local spectrum sensing independently, the process of which can be formulated as a binary hypothesis testing problem [
6]:
where
represents the signal transmitted by LU and
denotes the received signal at the
i-th SU. The signal
is distorted by the channel gain
, which is assumed to be constant during the sensing interval, and is further corrupted by the zero-mean additive white Gaussian noise (AWGN)
, i.e.,
. Hypothesis
indicates that the spectrum is currently occupied by PU, and hypothesis
indicates that spectrum is available for SUs; and
t represents time. Without loss of generality,
and
are assumed to be independent of each other.
Due to its applicability to a wide range of signals and mathematical amenity compared to other detectors, energy detection is adopted by each SU in the local spectrum sensing stage; the input signal energy is measured by the energy detector within a specific time interval. By applying a band-pass filter, the received energy at SU
can be expressed as [
4]:
where
is the
j-th sample of the received signal at SU
and
with
T and
W being detection time and channel bandwidth, respectively. Naturally,
is the time-bandwidth product. When
N is relatively large (e.g.,
),
can be approximated as a Gaussian random variable under both hypotheses and denoted as [
20]:
where
,
,
and
are the means and variances under hypotheses
and
, respectively.
Here, is the average signal-to-noise ratio (SNR) at SU. In the CSS scheme, SUs send their local measurements to DFC, which is in charge of further information processing. These measurements can either be the received energy or its function (like a one-bit hard decision or a double threshold decision), depending on the specific fusion rule utilized by DFC.
At the H-th sensing slot, the report of SU can be denoted as . Then, all of the reports received by DFC can be denoted as , and the DFC makes a final global decision about LU’s activity.
2.2. SSDF Attack Models
As illustrated in
Figure 1, certain compromised SUs exist among all SUs in CRNs. They report falsified results to DFC and expect DFC to make an incorrect global decision
under their misguidance. The means to tamper reports of malicious SUs can be multifold. This paper considers that malicious users (MUs) first distort their received energy accumulation and send the distorted energy to the DFC afterwards.
We investigate two SSDF attack models, the false alarm and miss detection (FAMD) attack and the false alarm (FA) attack, as presented in [
21]. Both can be described by three parameters, including the attack threshold (
η), the attack intensity factor (
ξ) and the attack probability (
). Specifically, these two attacks can be modeled as follows:
A. FAMD attack: For sensing slot H, the FAMD attacker launches an attack with probability . If it intends to attack during this round, it will compare with η. If the sensed energy exceeds the attack threshold η, it will report ; otherwise, the attacker reports . If the attacker chooses not to attack, it will just report . This attack model tends to increase the misdetection and false alarm probability, which results in both the inequitable utility of the available spectrum and more damaging disturbances to the LU.
B. FA attack: For sensing slot H, if sensed energy exceeds the attack threshold η, the attack will not be launched, and the energy will hold at . On the contrary, it will attack with probability by reporting . This attack model is inclined to cause false alarm probability increase and the available spectrum underutilization or the exclusive usage of it by FA attackers.
Under each of the two attack models, the distorted energy is utilized to produce local measurements, which are subsequently delivered to DFC. In this paper, the energy used by SU to create reports at the H-th sensing slot is expressed as , which is either the original for genuine SUs or the distorted for malicious SUs.
3. Faithworthy Collaborative Spectrum Sensing Based on Credibility and Evidence Theory for Cognitive Radio Networks
In this article, we propose a faithworthy CSS method based on credibility and evidence theory for CR networks. As first introduced by Dempster and later extended by Shafer, Dempster–Shafer (D-S) theory allows one to combine evidence from different sources and evaluate the credibility of the system state [
22], which is regarded as an effective approach for decision making, as well. Due to its capability of merging results reported by SUs under the effect of uncertainty, D-S theory is quite suitable for collaborative spectrum sensing in CRNs.
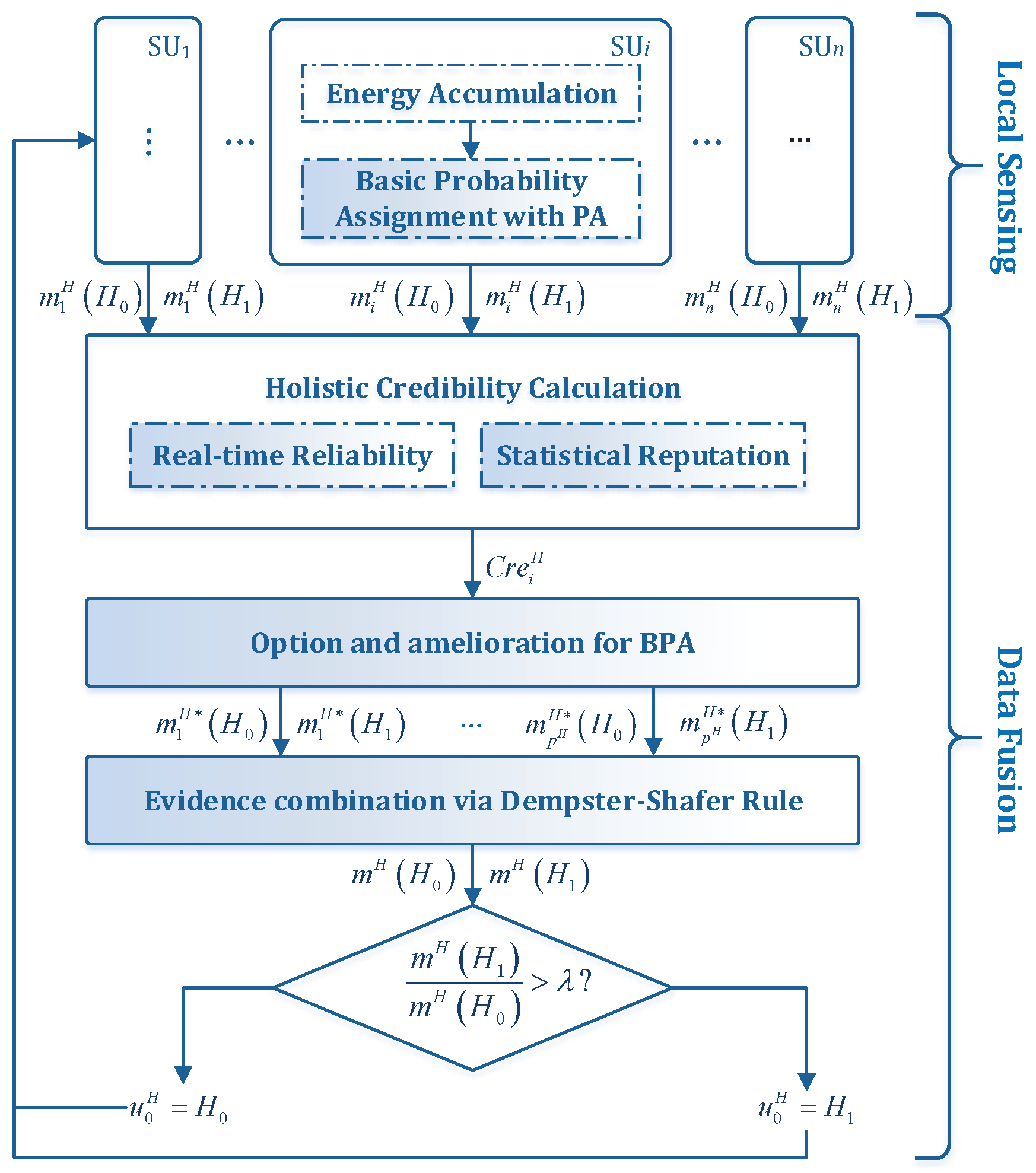
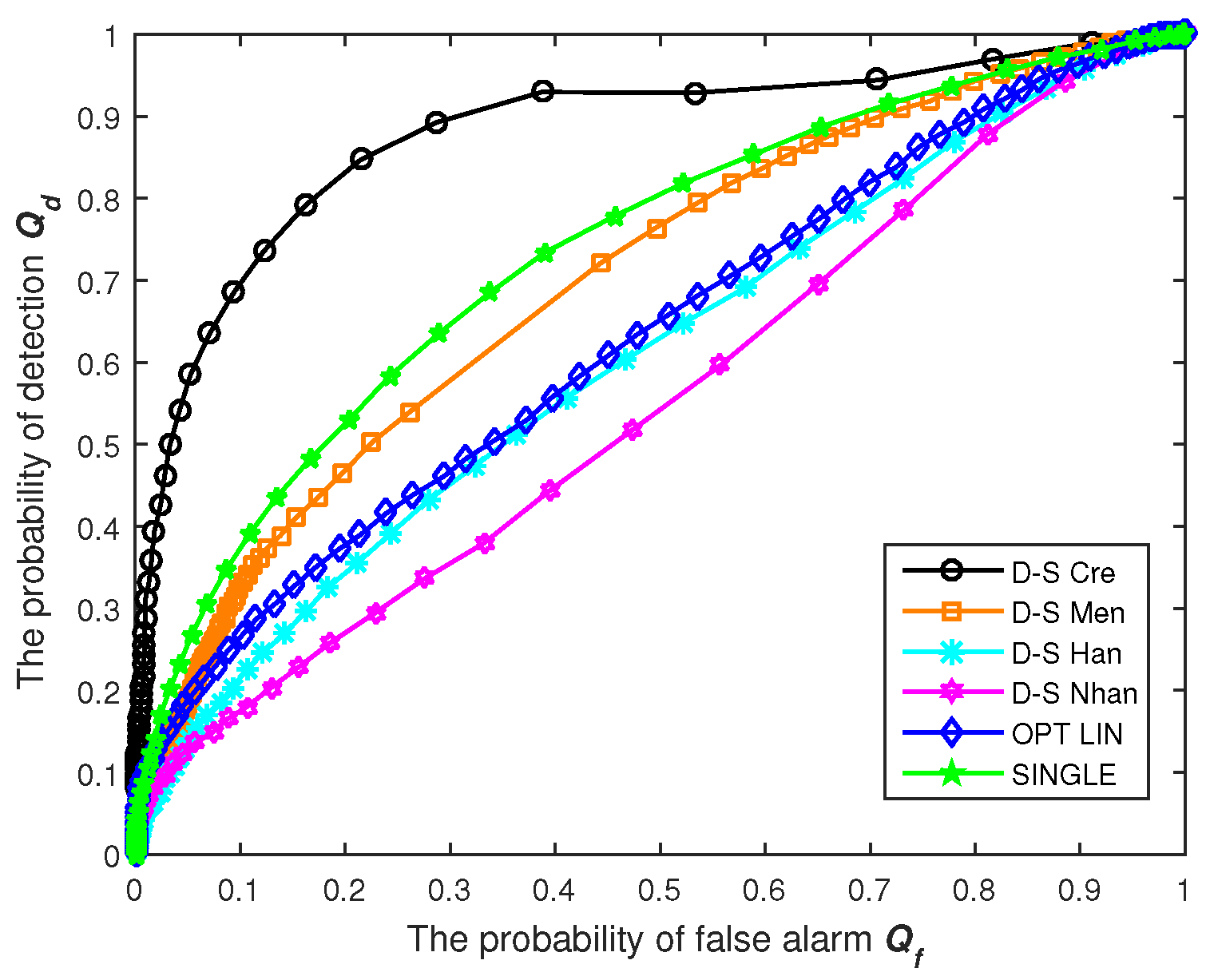
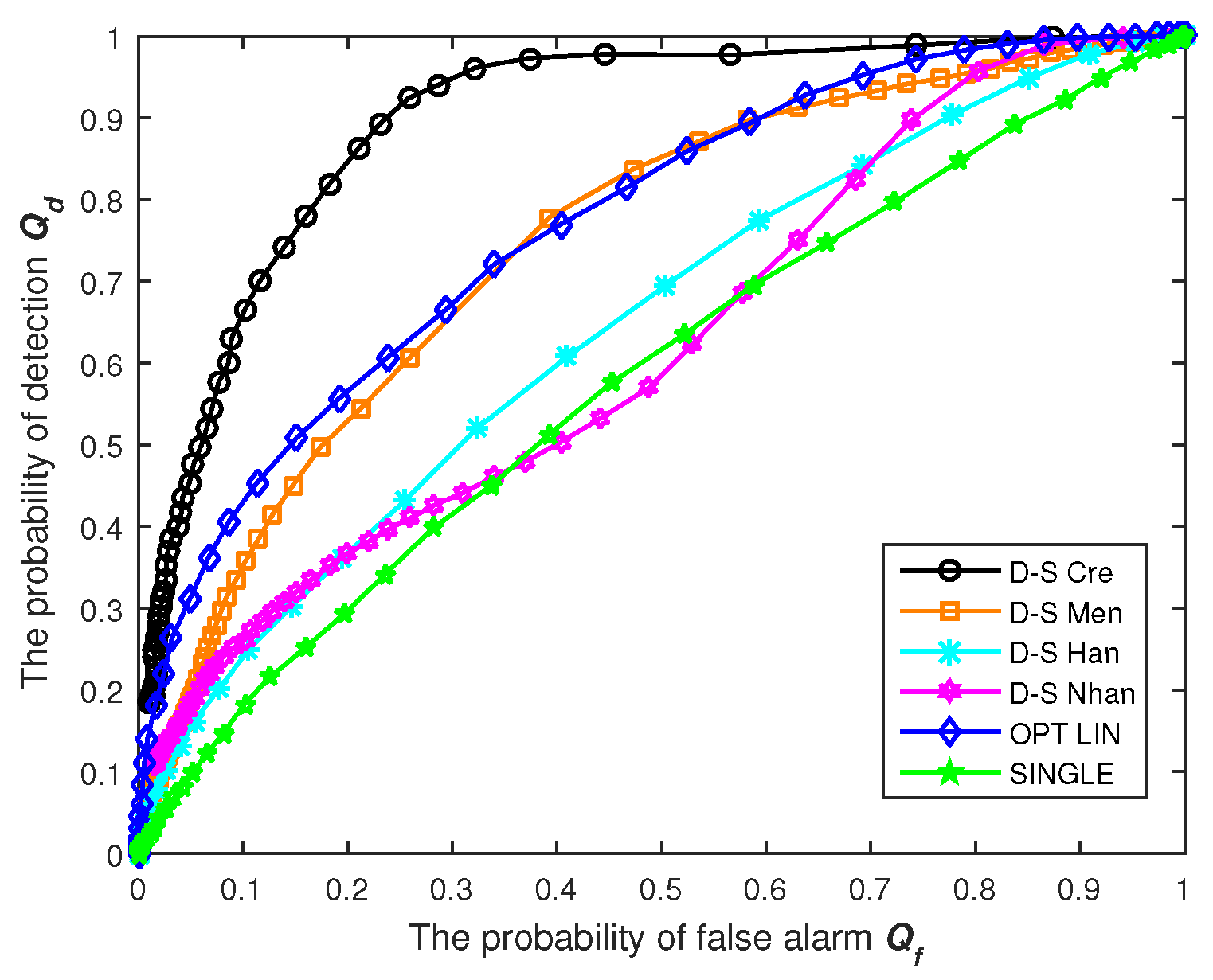
Figure 2 shows that the proposed faithworthy CSS method is executed in four consecutive procedures, which are basic probability assignment with the PA approach, holistic credibility calculation, option and amelioration for BPA and evidence combination via the Dempster–Shafer rule, respectively. We give the specific discussions in detail as follows.
3.1. Basic Probability Assignment with the PA Approach
Detecting LU’s state is a binary hypothesis testing problem in the context of spectrum sensing, and the recognition framework is
. Naturally,
is the set of all subsets of Ω, including the empty set ⌀. SUs act as the information source and provide a set of elementary evidences. For SU
, the evidence theory under the form of elementary masses assigns a belief mass to each element of the set
. These masses are defined as function
m, which maps the power set of Ω (i.e.,
) to the interval of
and satisfies the following conditions:
and
,
,
in the framework, and
is the cardinality of
[
19]. For
,
represents that one believes to pledge exactly to set
, when a certain piece of evidence is given [
23]. The set
satisfying
is called the focal set, and in the D-S theory of evidence, the plausibility and belief function are expressed as follows:
where
.
evaluates the minimum or definitive support for hypothesis
B, whereas
evaluates the maximum or possible support that could be put in hypothesis
B if more evidence became available. In the binary hypothesis test problem of CSS, in fact,
and
. Therefore, in the following discussion, BPA function
m is constantly utilized to denote the belief of hypotheses
and
.
After the process of energy accumulation, the BPA function for each sensing node SU
can be acquired according to the following equations [
19]:
where
; SUs then send the BPAs to DFC. That is to say, the report of SU
at the
H-th sensing slot is
.
Considering the power limitation of sensor nodes, the transmitting data from each SU to DFC need to be reduced. Under this circumstance, we propose to adjust BPA functions into modified BPA functions by utilizing a projection approximation (PA) technique.
On the basis of the fact that only hypotheses
and
are related to spectrum sensing, for the sake of ensuring that the modified BPA function is suitable for the D-S theory and has no impact on the performance of combination, we introduce the projection approximation approach to improve local BPA masses. At first, orthogonal decomposition is employed to project
onto the coordinate axes of hypotheses
and
, then the projection of
can be denoted as:
Afterwards, adding the original BPAs under two hypotheses to their projections on the corresponding coordinate axis and carrying out normalization, the modified BPA function
,
can thereby be obtained:
Due to , rendering , consequently, in accordance with the PA approach in (14) and (15), not only the transmitting data from SU to the DFC are half reduced, but also the bandwidth cost is deceased. This can be attributed to the fact that SU only requires transmitting , while other existing methods need to report both and . The PA approach enables one to almost half reduce the transmission data for n SUs. This means a great advantage if there exists a high number of SUs, especially when the transmitting and the receiving accounting for the most power consuming part of the SUs are obliged to be considered; this PA approach is capable of achieving a long operational life span of sensor battery. In addition, the situation of the limited spectrum resources is quite urgent in wireless communication; in this case, the PA method also possesses an extremely high benefit of bandwidth owing to the reduction in transmitting data.
3.2. Holistic Credibility Calculation
In order to remove or mitigate the harmful effect on the performance caused by the attack behaviors of MUs, the reports from distinct nodes are supposed to be treated with dissimilarity. In the proposed scheme, the credibility of each SU is evaluated by its holistic credibility, which contains two factors, i.e., the real-time reliability and the statistical reputation. Specifically, the real-time reliability of SU represents the credibility of BPAs from SU at the H-th sensing round, whilst the statistical reputation of SU represents the credibility of historical reports from SU. Through combining these two factors, both current and historical information about the credibility of each SU can be well exploited.
3.2.1. Real-Time Reliability
Since the local sensing results from the malicious SU will be distorted at some sensing slots, its evidence is not consistent with others’ all of the time. In other words, if the evidence of one SU is similar to other SUs, this SU acquires a higher supportive degree from other SUs. Otherwise, if single SU’s evidence is obviously different from others, it gets a less supportive degree from others. Then, it will be considered as untrustworthy and removed before fusing evidence at the DFC. Therefore, we can evaluate the real-time reliability of SU
based on its reports’ similarity with other SUs at each sensing round. Specifically, the similarity degree of reported BPAs between SU
and SU
can be represented by the following formulation [
16]:
Afterwards, the similarity degree matrix can be shown as:
The diagonal entries of the similarity degree matrix are all equal to one, and according to Equation (
14), the value of each similarity degree is less than or equal to one. Consequently, the similarity degree matrix evidently possesses a convergence property, which ensures the effectiveness and validity of the proposed sensing method under the harmful attack behavior launched by malicious SUs. Through adding up the general similarity degree of SU
with regard to other SUs, the support to the BPAs from SU
at the
H-th sensing slot is written as:
As a consequence, the real-time reliability of SU
can be acquired by normalizing the support and denoted as:
Nevertheless, CR networks have open and dynamic characteristics; there exist numerous possible factors that cause relatively low real-time reliability. Besides, the randomness of wireless channels (i.e., shadowing, fading effects and noise uncertainty) results in inaccurate BPA acquired by SUs at local sensing. Under the impact of all sorts of randomness, the performance of an honest SU can deteriorate severely at certain sensing slots. At that moment, its reported results have a great difference from others’ reports or even have high similarity with the reports from MUs. In addition, if the number of malicious SUs in the network increases, the malicious SUs will support mutually and falsify the evaluation of real-time reliability remarkably. Therefore, only with the assistance of real-time reliability, we can neither arrive at a conclusion that an SU is genuine or malicious precisely. To resolve this issue, we introduce a reputation mechanism into the proposed scheme.
3.2.2. Statistical Reputation
Although statistical reputation cannot evaluate SU’s credibility in a real-time manner, it is capable of obtaining the deduction concerning the historical reliability of SUs in line with their reported local results previously. Moreover, the statistical reputation is more stable due to its statistic characteristics; it is less likely to be affected by random interference. Therefore, statistical reputation and real-time reliability become mutually complementary; both factors should be jointly utilized to calculate the holistic credibility of cognitive users.
In most existing reputation-based CSS mechanisms [
24,
25,
26], the reputation values of SUs are computed by simple counting rules. If the transmitted result of one SU is consistent with the global result made by DFC, then the reputation of this node is increased by one; otherwise, reducing the reputation by one. Two main drawbacks exist in this method: Firstly, this way of reputation updating is based on the global decision made by DFC and updating via the strategy of “same increase and decrease”. When the correctness of the final decision cannot be guaranteed under the attack behavior of malicious SUs, the reference value of SU’s reputation acquired by this approach declines to some degree. Secondly, the computing mode of the counting rule only cares about the consistency between local reports and the global decision. However, the BPA forwarded by SUs are dissimilar at each sensing round, which contains different messages with regard to the operating state of the LU. The process mode “black or white” leads to unnecessary losses of useful information.
In order to overcome the above shortcomings, we consider the imperfection of the global decision made by DFC and utilize the BPA reported from SU and the BPA merged by DFC at the -th slot to update the statistical reputation of SU at the H-th slot. Specifically, for the sake of distinguishing with different situations when DFC makes final decisions, two parameters are defined: the self-evaluated faith and the center-evaluated faith f, respectively. The higher self-evaluated faith is, the more convinced that SU is of its reported BPA. Similarly, higher center-evaluated faith f means a higher degree of conviction that the DFC feels about its combined BPA. Both the self-evaluated faith and the center-evaluated faith f are calculated by the DFC.
At the
-th sensing round, the center-evaluated faith and the self-evaluated faith can be respectively expressed as:
where
and
represent the combined BPAs calculated by the DFC at the
-th slot (the computational formula is given in Section 3.4). Obviously,
and
. Hence, the statistical reputation of SU
can be calculated as follows:
where
represents the statistical reputation of SU
at the
-th sensing slot,
denotes the one-bit global decision made by the DFC,
denotes the suppositional local decision of SU
inferred by the DFC and
l is the decay factor. It is worth noting that there is no need for SU
to make a decision or transmit its local decision result (in order to reduce network overhead). The DFC can deduce the local judgment that will be made by SU
from its forwarded BPA (i.e., the reported BPA from SU
contains this information). The suppositional local decision of SU
inferred by the DFC can be denoted as:
where the decision threshold is determined by the DFC in terms of the different performance requirements of the spectrum sensing system.
The fundamental principle of the update mode of statistical reputation can be explained by Formula (24). In the first place, the variation tendency of statistical reputation depends on the one-bit global decision of DFC and the suppositional local decision . If is equal to , statistical reputation increases; otherwise, it decreases. This signifies that the cognitive user who makes the same decision result as DFC will obtain a higher statistical reputation. In the next place, the amplitude of variation of statistical reputation is decided by the center-evaluated faith and the self-evaluated faith jointly. If and are both close to one (here, SU and DFC are both convinced of their BPAs), the change size of statistical reputation is also close to one. If the DFC (or SU) lacks faith in its BPA, then (or ) will decrease, which leads to the changed size of diminishing correspondingly. Therefore, statistical reputation is capable of performing updating with a flexible increase/decrease and changeable size according to the transmitted BPAs from SUs and the combined BPA made by DFC in the last sensing round.
Furthermore, although the global decision made by DFC may have errors at some sensing round, it is still more reliable than the reported decision of a single node (due to diversity gain). In view of this fact, we introduce amendatory parameters α, β to adjust the relative position between DFC and a single node. Generally speaking, is set to ensure the center-evaluated faith plays an important role in the update of ; otherwise, the updating amplitude is basically decided by the self-evaluated faith of SU; hence, the changeable size of of each SU will become consistent basically, and the reputation assessment mechanism loses its function, as well. also reflects the difference in credibility degree between DFC and the single node. In practical application, parameters α and β can be adjusted by empirical data in the CSS system or be determined by experimental results when the number of malicious SUs and attack patterns are known.
The single SU may possess distinct sensing performance at different sensing rounds due to human factors or objective factors; the reference value of the reported results a long time ago is relatively low and cannot reasonably reflect the current performance of SU. Therefore, the decay factor l is introduced to make the quality of the results reported recently accounting for a larger proportion. l should not be set too small, otherwise the historical behavior information cannot be brought into sufficient usage; on the other hand, remaining sensitive to the potential behavior change of SUs requires that l should not be set too large, either.
Different SUs have different reported history; generally, only part of SUs’ statistical reputation values exceeds zero. We normalize the statistical reputations of these SUs, and
of SU
at the
H-th sensing slot can be denoted as:
In the initial stage,
. Apparently, manifold feasible modes can be utilized to combine the real-time reliability and statistical reputation effectively. Here, an easy and practicable mode is taken to acquire the holistic credibility by normalizing the sum of these two factors:
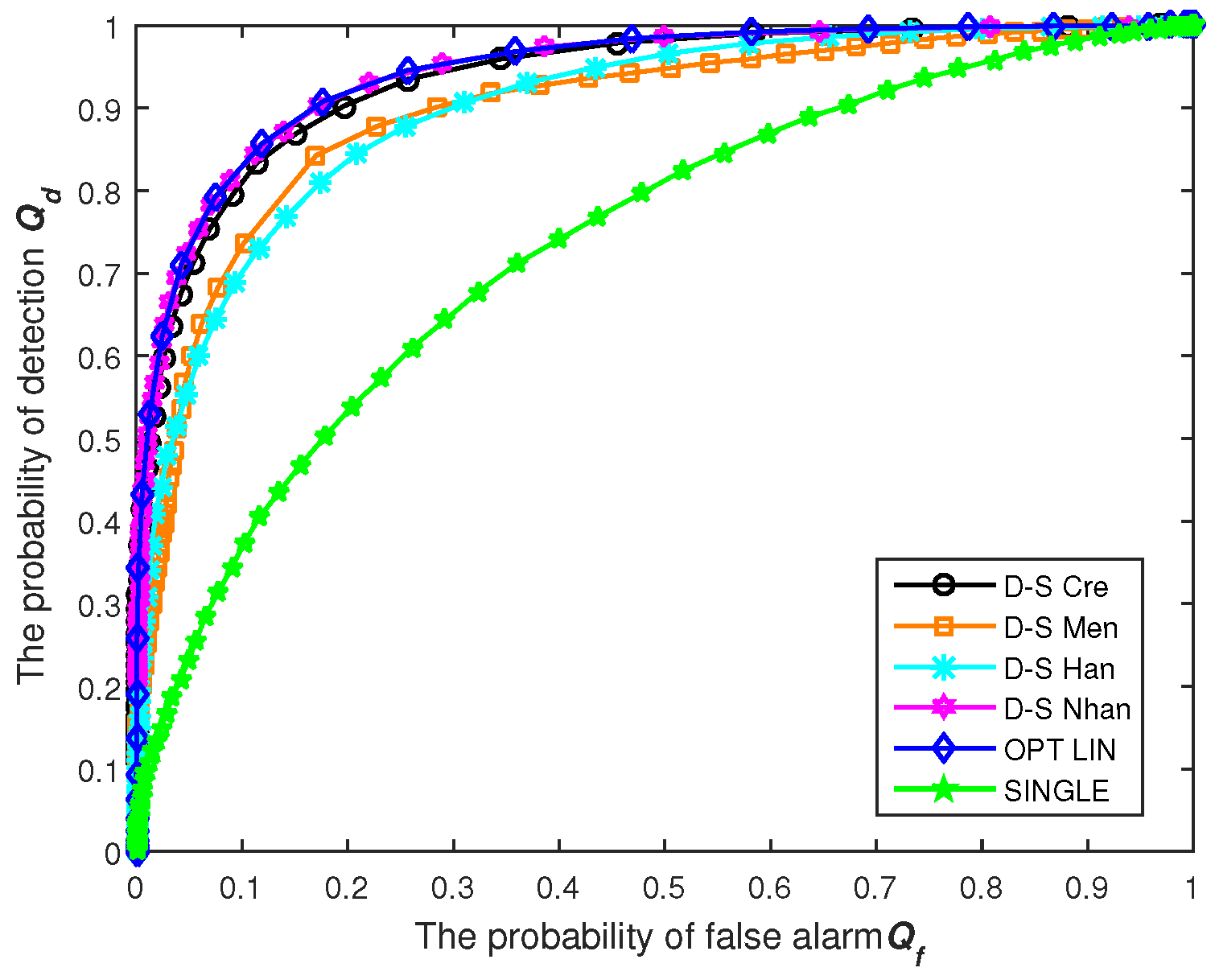
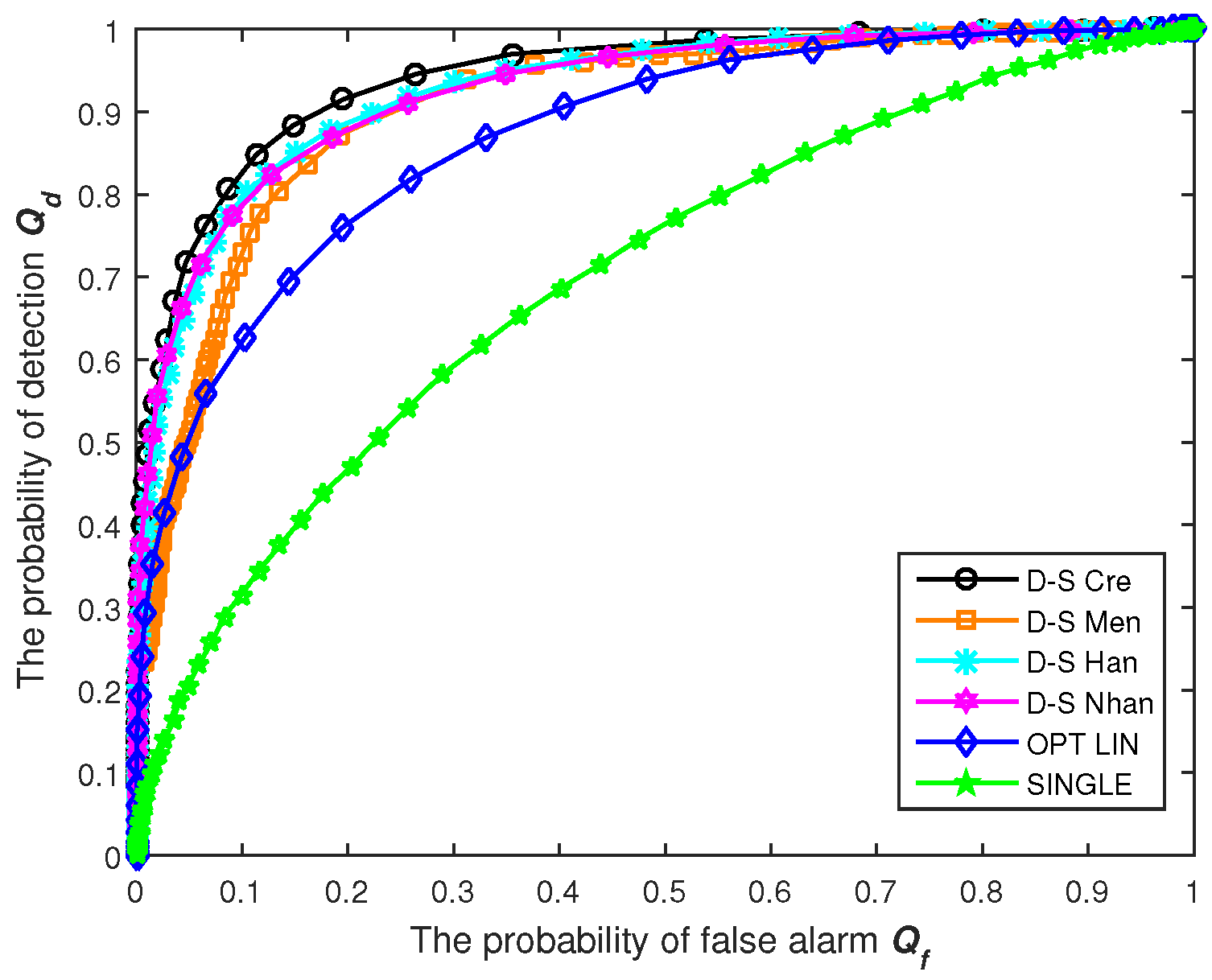
Consequently, the holistic credibility calculation can differentiate malicious SUs from genuine ones on account of their historical behaviors; besides, it can hold the current difference for SUs to realize better real-time performance, as well.
3.3. Option and Amelioration for BPA
In terms of the holistic credibility of SUs, the DFC is able to choose competent SUs to take part in the subsequent procedure of evidence combination. Concretely, we compare the holistic credibility
of SU
with a determined credibility threshold
ς. If
, then it will be treated as a malicious user and abandoned at time slot
H; conversely, if
exceeds threshold
ς, the BPAs of SU
will be ameliorated by the DFC with the homologous holistic credibility:
3.4. Evidence Combination via the Dempster–Shafer Rule
All of the adjusted BPAs are appropriately merged to obtain the combined BPAs in accordance with the D-S evidence theory [
22]:
where
and
represents the number of sensing nodes whose BPAs are opted and ameliorated to take part in the center data fusion at time round
H.
Finally, in accordance with the following decision rule, the combined BPAs
and
are utilized to make the final global decision. The DFC compares
with the decision threshold
λ. If
, the global decision
is
; if
, the global decision
is
.
λ is the same decision threshold as utilized in Equation (
25). Once the DFC make the global decision, the statistical reputation can be updated for the detection of the next round of collaborative spectrum sensing.