Game Algorithm for Resource Allocation Based on Intelligent Gradient in HetNet
Abstract
:1. Introduction
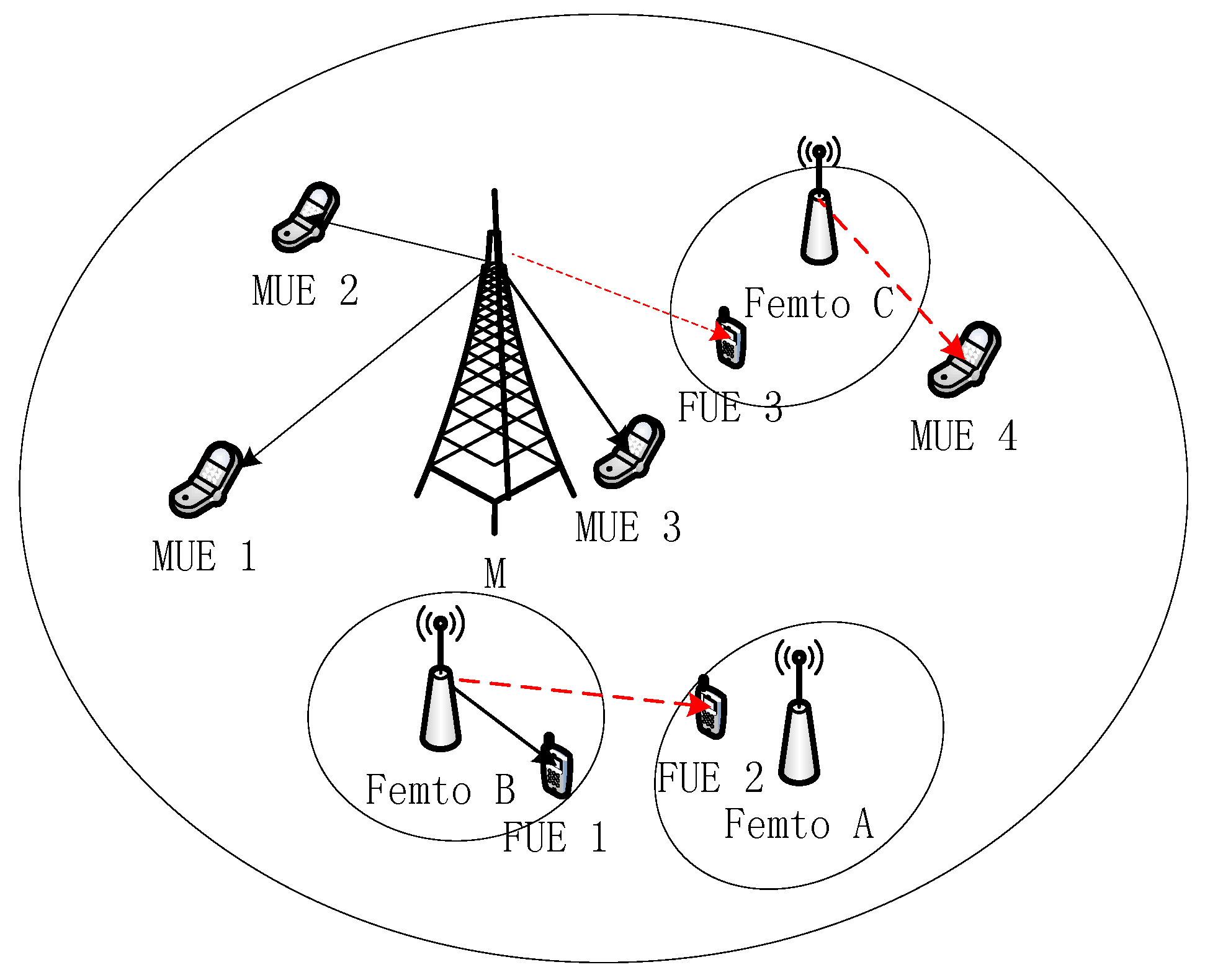
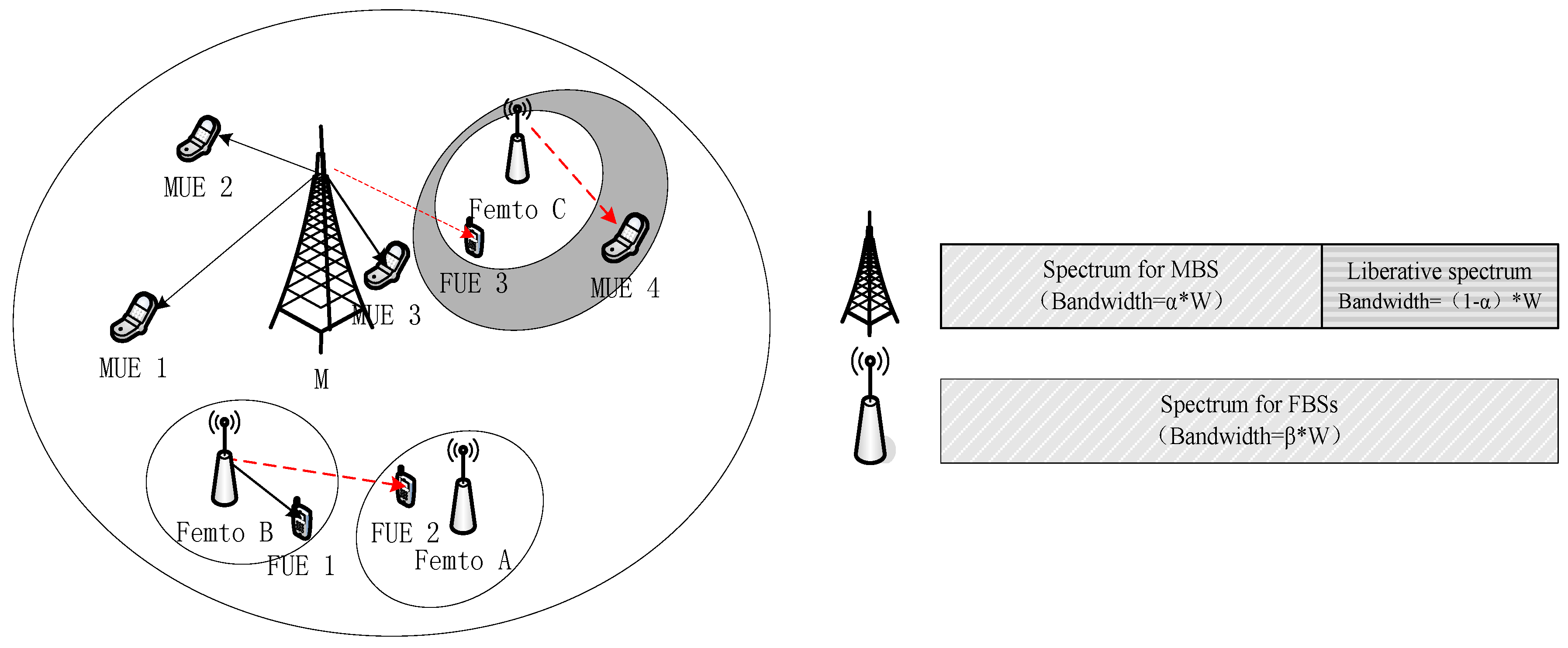
2. System Model
3. Stackelberg Game Model and Problem Statement
3.1. Common Algorithm
3.2. Utility Functions
3.3. Optimization Problems
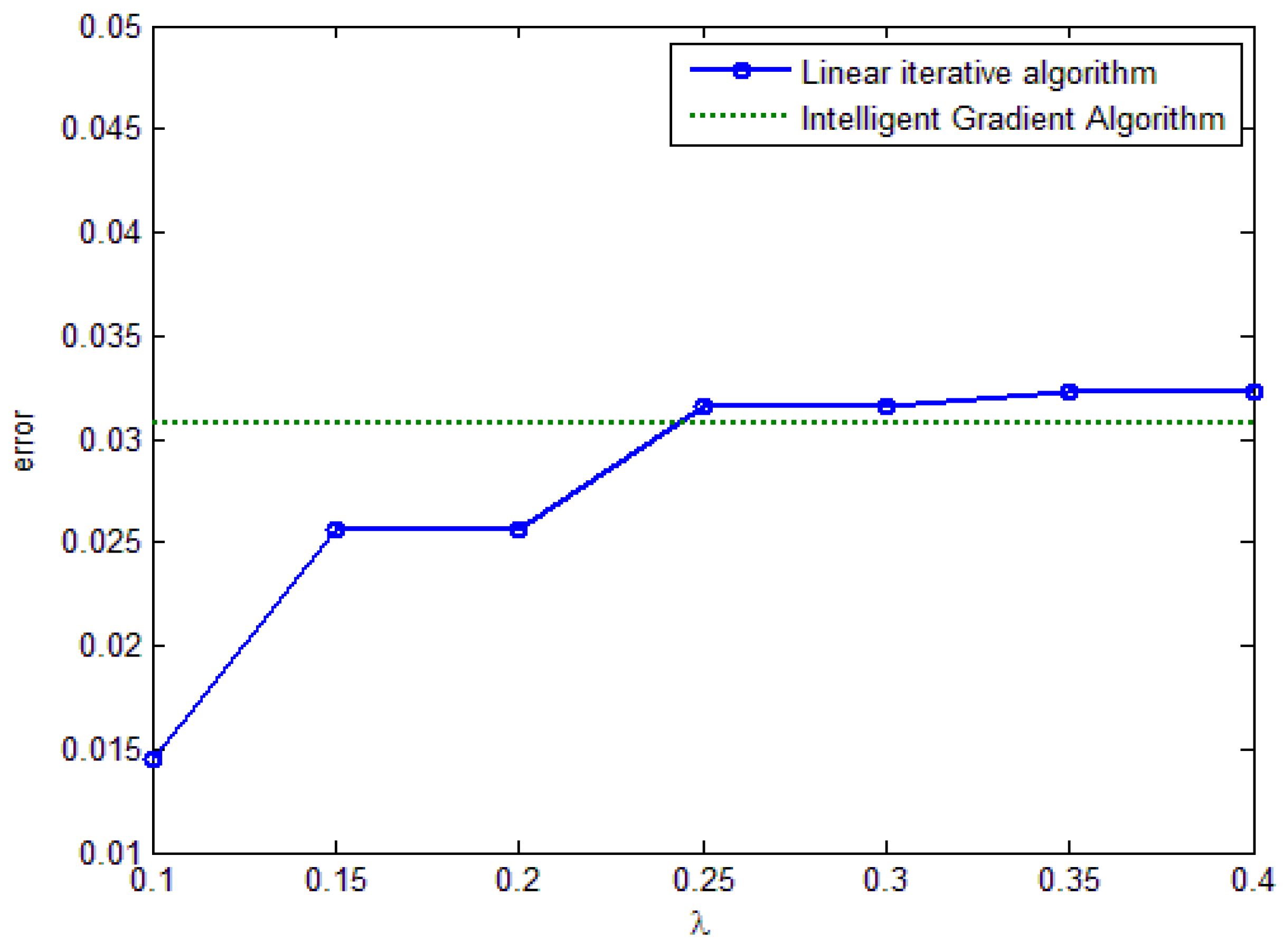
3.4. Intelligent Method Based on Gradient Algorithm
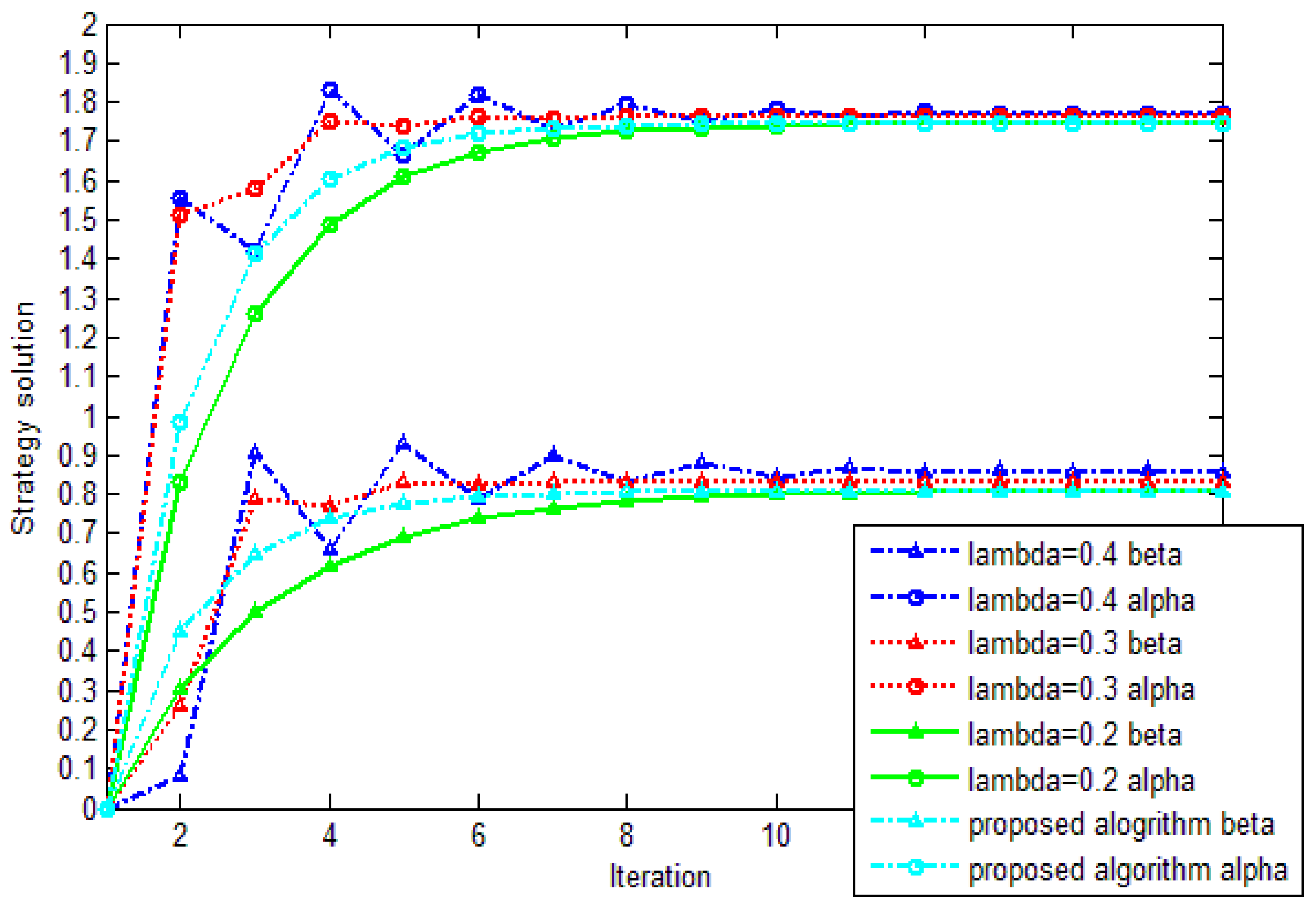
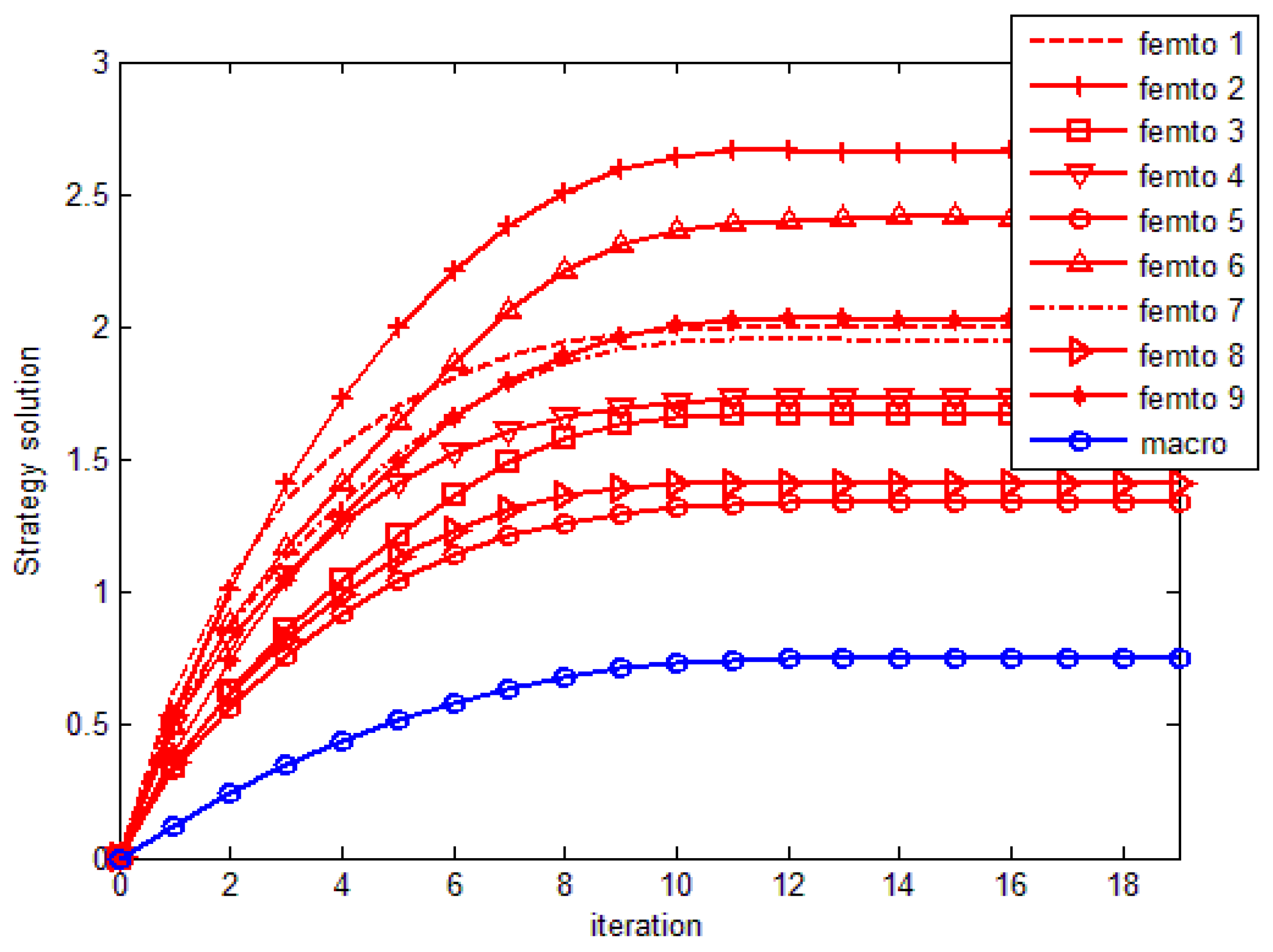
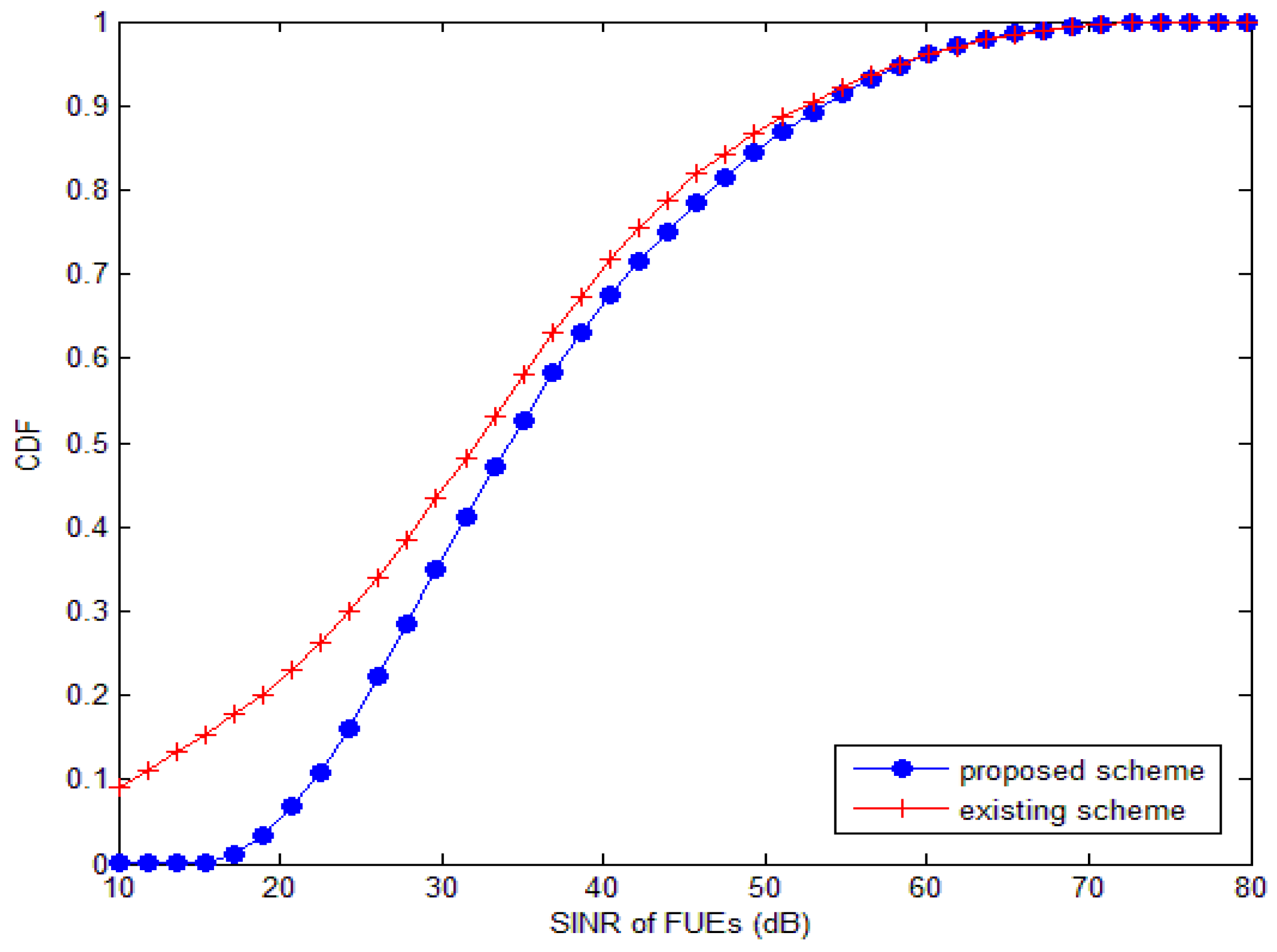
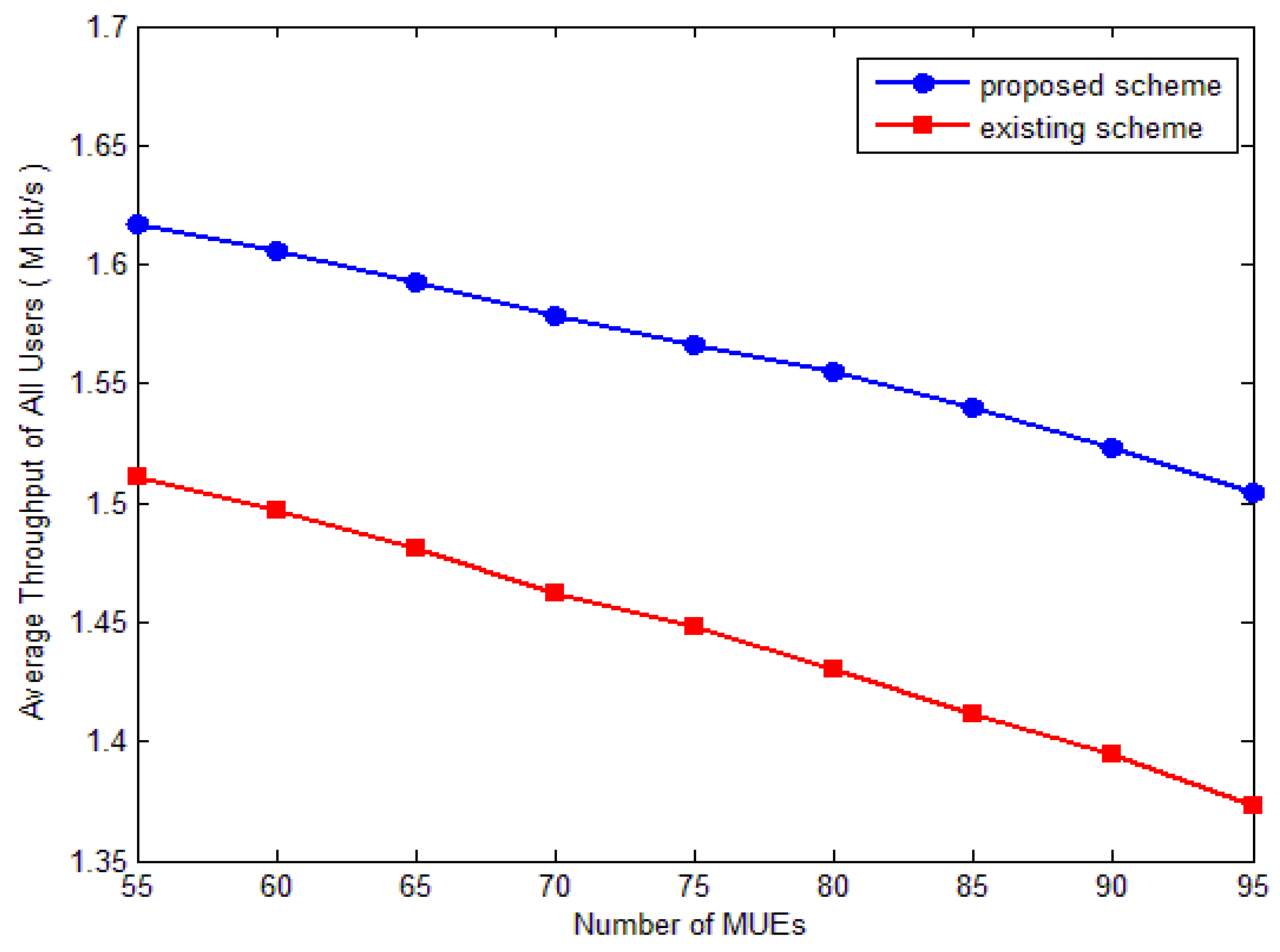
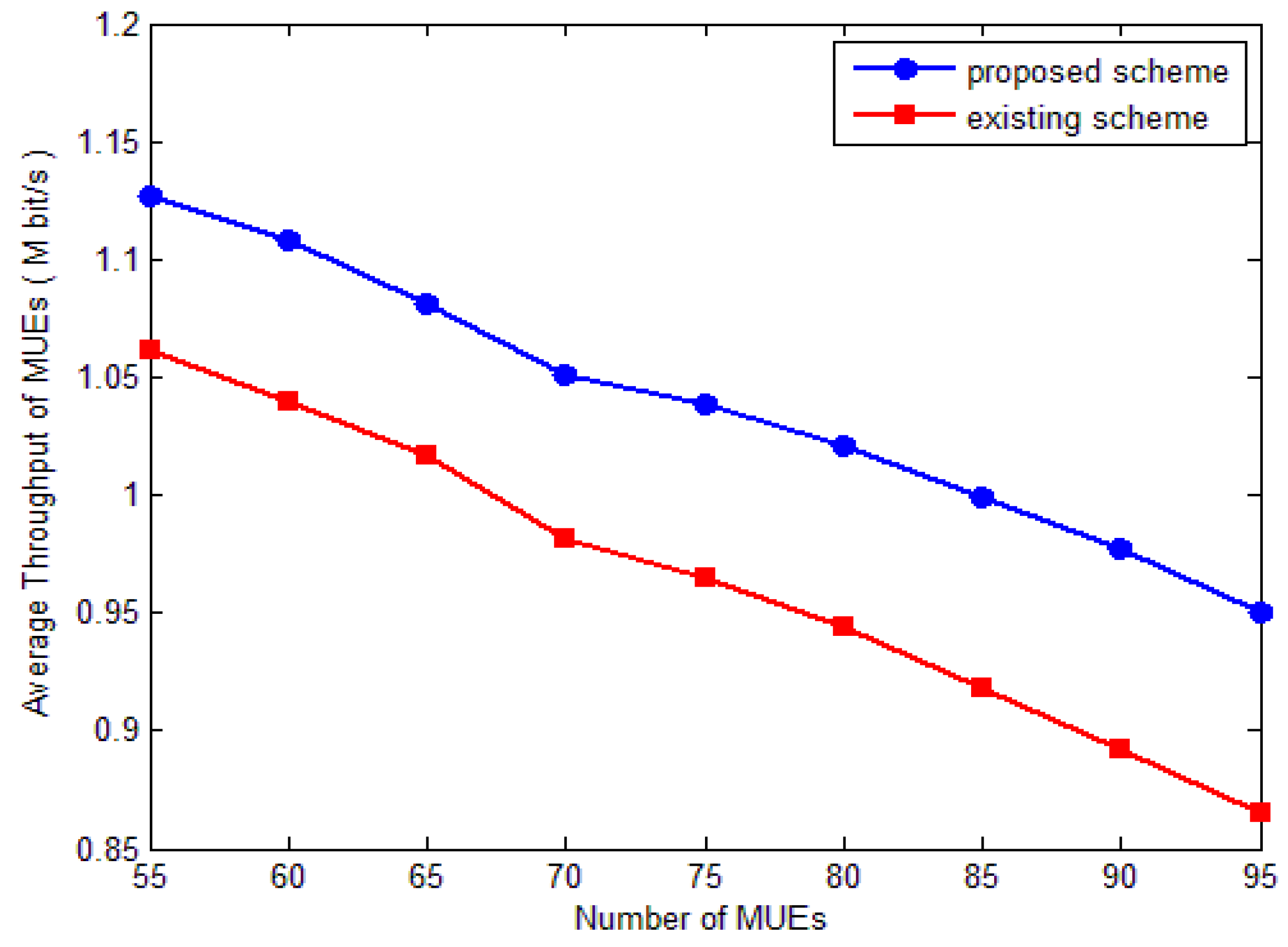
4. Simulation Results and Analyze
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chandrasekhar, V.; Andrews, J.G. Femtocell networks: A survey. IEEE Commun. Mag. 2008, 46, 59–67. [Google Scholar] [CrossRef]
- Elsawy, H.; Hossain, E. Stochastic geometry for modeling, analysis, and design of multi-tier and cognitive cellular wireless networks: A survey. IEEE Commun. Surv. Tutor. 2013, 15, 996–1019. [Google Scholar] [CrossRef]
- Dhillon, H.S.; Ganti, R.K. Modeling and analysis of K-Tier downlink heterogeneous cellular networks. IEEE J. Sel. Areas Commun. 2012, 30, 550–560. [Google Scholar] [CrossRef]
- Peng, M.; Wang, C. Recent advances in underlay heterogeneous networks: Interference control, resource allocation, and self-organization. IEEE Commun. Surv. Tutor. 2015, 17, 700–729. [Google Scholar] [CrossRef]
- Feng, D.; Jiang, C. A survey of energy-efficient wireless communications. IEEE Commun. Surv. Tutor. 2013, 15, 167–178. [Google Scholar] [CrossRef]
- Bu, S.; Yu, F.R. Interference-aware energy-efficient resource allocation for OFDMA-based heterogeneous networks with incomplete channel state information. IEEE Trans. Veh. Technol. 2015, 64, 6081–6085. [Google Scholar] [CrossRef]
- Pisarski, D.; Canudas, W.C. Nash game based distributed control design for balancing of traffic density over freeway networks. IEEE Trans. Control Netw. Syst. 2015, 1, 700–729. [Google Scholar] [CrossRef]
- Duan, L.; Huang, J.; Shou, B. Economics of femtocell service provision. IEEE Trans. Mob. Comput. 2013, 12, 2261–2273. [Google Scholar] [CrossRef]
- Chandrasekhar, V.; Andrews, J.G.; Shen, Z. Distributed power control in femtocell-underlay cellular networks. In Proceedings of the IEEE Conference on Global Telecommunications, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6.
- Yi, Y.; Zhang, J.; Zhang, Q. Spectrum leasing to femto service provider with hybrid access. In Proceedings of the IEEE Conference on Computer Communications (INFOCOM) 2012, Orlando, FL, USA, 25–30 March 2012; pp. 1215–1223.
- Kang, X.; Zhang, R.; Motani, M. Price-based resource allocation for spectrum-sharing femtocell networks: A stackelberg game approach. IEEE J. Sel. Areas Commun. 2012, 30, 538–549. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, J.; Zhang, Q. Utility-aware refunding framework for hybrid access femtocell network. IEEE Trans. Wirel. Commun. 2012, 11, 1688–1697. [Google Scholar] [CrossRef]
- Hamouda, S.; Zitoun, M.; Tabbane, S. Win–win relationship between macrocell and femtocells for spectrum sharing in LTE-A. IET Commun. 2014, 8, 1109–1116. [Google Scholar] [CrossRef]
- Hong, E.J.; Yun, S.Y.; Cho, D.H. Decentralized power control scheme in femtocell networks: A game theoretic approach. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009; pp. 415–419.
- Chandrasekhar, V.; Andrews, J.G. Spectrum allocation in tiered cellular networks. IEEE Trans. Commun. 2009, 57, 3059–3068. [Google Scholar] [CrossRef]
- Cheung, W.C.; Quek, T.Q.S.; Kountouris, M. Throughput optimization, spectrum allocation, and access control in two-tier femtocell networks. IEEE J. Sel. Areas Commun. 2012, 30, 561–574. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S. Resource allocation for cognitive radio-enabled femtocell networks with imperfect spectrum sensing and channel uncertainty. IEEE Trans. Veh. Technol. 2016, 65, 7719–7728. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, T.; Luo, K. Dynamic spectrum allocation for the downlink of OFDMA-based hybrid-access cognitive femtocell networks. IEEE Trans. Veh. Technol. 2016, 65, 1772–1781. [Google Scholar] [CrossRef]
- Yi, L.G.; Lu, Y.M. Two-tier interference elimination for femtocells based on cognitive radio centralized spectrum management. Ksii Trans. Internet Inf. Syst. 2014, 8, 1514–1531. [Google Scholar]
- Jacob, P.; James, A.; Madhukumar, A.S. Interference mitigation through reverse frequency allocation in multi-tier cellular network: A downlink perspective. Wirel. Netw. 2015, 21, 1613–1629. [Google Scholar] [CrossRef]
- Wang, W; Zhang, Q. Local cooperation architecture for self-healing femtocell networks. IEEE Trans. Wirel. Commun. 2014, 21, 42–49. [Google Scholar] [CrossRef]
- Dhillon, H.S.; Ganti, R.K.; Andrews, J.G. Load-aware modeling and analysis of heterogeneous cellular networks. IEEE Trans. Wirel. Commun. 2012, 12, 1666–1677. [Google Scholar] [CrossRef]
- Singh, S.; Dhillon, H.S.; Andrews, J.G. Offloading in heterogeneous networks: Modeling, analysis, and design insights. IEEE Trans. Wirel. Commun. 2013, 12, 2484–2497. [Google Scholar] [CrossRef]
- Boostanimehr, H.; Bhargava, V.K. Unified and distributed QoS-driven cell association algorithms in heterogeneous networks. IEEE Trans. Wirel. Commun. 2014, 14, 1650–1662. [Google Scholar] [CrossRef]
- Cho, S.; Wan, C. Coverage and load balancing in heterogeneous cellular networks with minimum cell separation. IEEE Trans. Mob. Comput. 2014, 13, 1955–1966. [Google Scholar] [CrossRef]
- Kim, S.Y.; Kwon, J.A.; Lee, J.W. Optimal subchannel and power allocation for multi-cell OFDMA systems. In Proceedings of the 2014 Sixth International Conference on Ubiquitous and Future Networks (ICUFN), Shanghai, China, 8–11 July 2014; pp. 231–232.
- Kim, W.; Kaleem, Z.; Chang, K.H. Power headroom report-based uplink power control in 3GPP LTE-A HetNet. EURASIP J. Wirel. Commun. Netw. 2015, 2015. [Google Scholar] [CrossRef]
- Tang, H.; Hong, P.; Xue, K.; Peng, J. Cluster-Based resource allocation for interference mitigation in LTE heterogeneous networks. In Proceedings of the 2012 IEEE Vehicular Technology Conference (VTC Fall), Quebec City, QC, Canada, 3–6 September 2012.
- Chen, W.; Yuan, L.; Tao, M. Stackelberg game for spectrum reuse in the two-tier LTE femtocell network. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 1888–1892.
- Kafeng, H.; Dan, L. Spectrum reuse scheme in two-tier HetNets: A Stackelberg game approach. In Proceedings of the IEEE International Conference on Computer and Communications, Chengdu, China, 10–11 October 2015; pp. 404–409.
- Rasmusen, E. Games and Information: An Introduction to Game Theory; Blackwell: Oxford, UK, 1994. [Google Scholar]
- Klusoň, J.; Nojiri, S.; Odintsov, S.D. New proposal for non-linear ghost-free massive $F(R)$ gravity: Cosmic acceleration and Hamiltonian analysis. Phys. Lett. B 2013, 726, 918–925. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Hydrostatic equilibrium and stellar structure in f(R), gravity. Phys. Rev. D 2010, 83, 064004. [Google Scholar]
| Parameters | Macrocell | Femtocell |
|---|---|---|
| System bandwidth | 20 MHz | 20 MHz |
| User density | 100/macro | 2–15/femto |
| Cell radius | 500 m | 15 m |
| Max transmit power of base stations | 43 dBm | 20 dBm |
| Fast fading | SCME | SCME |
| Noise level | −174 dBm/Hz | −174 dBm/Hz |
| 10 dB | 10 dB |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, F.; Dai, J.; Li, Y. Game Algorithm for Resource Allocation Based on Intelligent Gradient in HetNet. Symmetry 2017, 9, 34. https://doi.org/10.3390/sym9030034
Ye F, Dai J, Li Y. Game Algorithm for Resource Allocation Based on Intelligent Gradient in HetNet. Symmetry. 2017; 9(3):34. https://doi.org/10.3390/sym9030034
Chicago/Turabian StyleYe, Fang, Jing Dai, and Yibing Li. 2017. "Game Algorithm for Resource Allocation Based on Intelligent Gradient in HetNet" Symmetry 9, no. 3: 34. https://doi.org/10.3390/sym9030034
APA StyleYe, F., Dai, J., & Li, Y. (2017). Game Algorithm for Resource Allocation Based on Intelligent Gradient in HetNet. Symmetry, 9(3), 34. https://doi.org/10.3390/sym9030034






