New Applications of m-Polar Fuzzy Matroids

Abstract

Mathematical modelling is an important aspect in apprehending discrete and continuous physical systems. Multipolar uncertainty in data and information incorporates a significant role in various abstract and applied mathematical modelling and decision analysis. Graphical and algebraic models can be studied more precisely when multiple linguistic properties are dealt with, emphasizing the need for a multi-index, multi-object, multi-agent, multi-attribute and multi-polar mathematical approach. An m-polar fuzzy set is introduced to overcome the limitations entailed in single-valued and two-valued uncertainty. Our aim in this research study is to apply the powerful methodology of m-polar fuzzy sets to generalize the theory of matroids. We introduce the notion of m-polar fuzzy matroids and investigate certain properties of various types of m-polar fuzzy matroids. Moreover, we apply the notion of the m-polar fuzzy matroid to graph theory and linear algebra. We present m-polar fuzzy circuits, closures of m-polar fuzzy matroids and put special emphasis on m-polar fuzzy rank functions. Finally, we also describe certain applications of m-polar fuzzy matroids in decision support systems, ordering of machines and network analysis.

1. Introduction

Matroid theory had its foundations laid in 1935 after the work of Whitney [1]. This theory constitutes a useful approach for linking major ideas of linear algebra, graph theory, combinatorics and many other areas of Mathematics. Matroid theory has been a focus of active research during the last few decades.

Zadeh’s fuzzy set theory [2,3] handles real life data having non-statistical uncertainty and vagueness. Petković et al. [4] investigated the accuracy of an adaptive neuro-fuzzy computing technique in precipitation estimation. Various applications of fuzzy sets in the field of automotive and railway level crossings for safety improvements are studied in [5,6]. The fuzzy set plays a vital role to solve various multi-criteria decision making problems. Some applications of fuzzy theory in multi-criteria models are discussed in [7,8]. Zhang [9] extended fuzzy set theory to bipolar fuzzy sets and discusses the bipolar behaviour of objects. The idea which lies behind such a description is connected with the existence of “bipolar information”. For illustration, profit and loss, hostility and friendship, competition and cooperation, conflicted interests and common interests , unlikelihood and likelihood, feedback and feedforward, and so on, are generally two sides in coordination and decision making. Just like that, bipolar fuzzy set theory indeed has considerable impacts on many fields, including computer science, artificial intelligence, information science, decision science, cognitive science, economics, management science, neural science, medical science and social science. Recently, bipolar fuzzy set theory has been applied and studied speedily and increasingly. Thus, bipolar fuzzy sets not only have applications in mathematical theories but also in real-world problems [10,11,12].

In a number of real world problems, data come from m sources or agents $(m\ge 2)$, that is, multi-indexed information arises which cannot be mathematically expressed by means of the existing approaches of classical set theory, the crisp theory of graphs, fuzzy systems and bipolar fuzzy systems. The research presented in this paper is mainly developed to handle the lack of a mathematical approach towards multi-index, multipolar and multi-attribute data. Nowadays, analysts believe that the natural world is approaching the ideas of multipolarity. Multipolarity in data and information plays an important role in various domains of science and technology. In information technology, multipolar technology can be oppressed to operate large scale systems. In neurobiology, multipolar neurons in brain assemble a lot of information from other neurons. For instance, over a noisy channel, a communication channel may have a different network range, radio frequency, bandwidth and latency. In a food web, species may be of different types including strong, weak, vegetarian and non-vegetarian, and preys may be energetic, harmful and digestive. In a social network, the influence rate of different people may be different with respect to socialism, proactiveness, and trading relationship. A company may have different market power from others according to its product quality, annum profit, price control of its product, etc. These are multipolar information which are fuzzy in nature. To discuss such network models, we need mathematical and theoretical approaches which deal with multipolar information.

In view of this motivation, Chen et al. [13] extended bipolar fuzzy set theory and introduced the powerful idea of m-polar fuzzy sets. The membership value of an object, in an m-polar fuzzy set, belongs to ${[0,1]}^m$, which represents m different attributes of the object. Considering the idea of graphic structures, $m$-polar fuzzy sets can be used to describe the relationship among several individuals. In particular, m-polar fuzzy sets have found applications in the adaptation of accurate problems if it is necessary to make decisions and judgements with a number of agreements. For instance, the exact value of telecommunication safety of human beings is a point which lies in ${[0,1]}^m(m\approx 7\times {10}^9)$, since different people are monitored in different times. Some other applications include ordering and evaluation of alternatives and m-valued logic. m-polar fuzzy sets are shown to be useful to explore weighted games, cooperative games and multi-valued relations. In decision making issues, m-polar fuzzy sets are helpful for multi-criteria selection of objects in view of multipolar data. For example, m-polar fuzzy sets can be implemented when a country elects its political leaders, a company decides to manufacture an item or product, a group of friends wants to visit a country with multiple alternatives. In wireless communication, it can be used to discuss the conflicts and confusions of communication signals. Thus, m-polar fuzzy sets not only have applications in mathematical theories but also in real-world problems.

Akram and Younas [14] implemented the concept of m-polar fuzzy set into graph theory and discussed irregularity in m-polar fuzzy graphs. Several researchers have been applying this technique to explore various applications of m-polar fuzzy theory including grouping of objects [15], detecting human trafficking suspects [16], finding minimum number of locations [17] and decision support systems [18]. In 1988, Goetschel [19] studied the approach to the fuzzification of matroids and discussed the uncertain behaviour of matroids. The same authors [20] introduced the concept of bases of fuzzy matroids, fuzzy matroid structures and greedy algorithm in fuzzy matroids. Akram and Sarwar [15,21] have also discussed m-polar fuzzy hypergraphs, product formulae of distance for various types of m-polar fuzzy graphs and applications of m-polar fuzzy competition graphs in different domains. Akram and Waseem [22] constructed antipodal and self-median m-polar fuzzy graphs. Li et al. [23] considered different algebraic operations on m-polar fuzzy graphs. Hsueh [24] discussed independent axioms of matroids which preserve basic operational properties. Fuzzy matroids can be used to study the uncertain behaviour of objects but if the data have multipolar information to be dealt with, fuzzy matroids cannot give appropriate results. For this reason, we need the theory of m-polar fuzzy matroids to handle data and information with multiple uncertainties. In this research paper, we present the notion of m-polar fuzzy matroids and study various types of m-polar fuzzy matroids. We apply the concept of m-polar fuzzy matroids to graph theory, linear algebra and discuss their fundamental properties. We present the notion of closure of an m-polar fuzzy matroid and give special focus to the m-polar fuzzy rank function. We also describe certain applications of m-polar fuzzy matroids. We have used basic concepts and terminologies in this paper. For other notations, terminologies and applications not mentioned in the paper, the readers are referred to [22,25,26,27,28,29,30,31,32,33,34].

Throughout this research paper, we will use the notation “mF set” for an m-polar fuzzy set, denote the elements of an m-polar fuzzy set A as $(y,A(y\left)\right)$ and use $A^{*}$ as a crisp set and A as an m-polar fuzzy set.

2. Preliminaries

The term crisp matroid has various equivalent definitions. We use here the simplest definition of matroid.

Definition 1.

If Y is a non-empty universe and I is a subset of $P\left(Y\right)$, power set of Y, satisfying the following conditions,

1. 

$\mathit{If}{D}_1\in I\mathit{and}{D}_2\subset D_1\mathit{then},D_2\in I$,

2. 

$\mathit{If}{D}_1,D_2\in I\mathit{and}|D_1|<|D_2|\mathit{then}\mathit{there}\mathit{exists}{D}_3\in I\mathit{such}\mathit{that}{D}_1\subset D_3\subseteq D_1\cup D_2$.

The pair $M=(Y,I)$ is a matroid and I is known as the family of independent sets of M.

Definition 2.

([19]) If $M=(Y,I)$ is a matroid then the mapping $R:P\left(Y\right)\to \{0,1,2,\dots ,|Y\left|\right\}$ defined by

$$R\left(D\right)=max\left\{\right|F|:F\subseteq D,F\in I\}$$

is a rank function for M. If $D\in P\left(Y\right)$, R is known as rank of D.

Definition 3.

([19]) For any non-empty universe Y, a mapping $\mu :P\left(Y\right)\to [0,\infty )$ is called submodular if for each, $D,F\in P\left(Y\right)$,

$$\mu \left(D\right)+\mu \left(F\right)\ge \mu (D\cup F)+\mu (D\cap F).$$

Definition 4.

([2,3]) A fuzzy set $\mathsf{\tau }$ in a non-empty universe Y is a mapping $\mathsf{\tau }:Y\to [0,1]$. A fuzzy relation on Y is a fuzzy subset δ in $Y\times Y$. If $\mathsf{\tau }$ is a fuzzy set in Y and δ is a fuzzy relation on Y then we can say that δ is a fuzzy relation on $\mathsf{\tau }$ if $\delta (y,z)\le$ $min\left\{\mathsf{\tau }\right(y),\mathsf{\tau }(z\left)\right\}\mathrm{for}\mathrm{all}y,z\in Y$.

Definition 5.

([19]) If $\mathcal{F}\left(Y\right)$ is a power set of fuzzy subsets on Y and $\mathcal{I}\subseteq \mathcal{F}\left(X\right)$ which satisfy the following conditions,

1. 

If ${\mathsf{\tau }}_1\in \mathcal{I}$ and ${\mathsf{\tau }}_2\subset {\mathsf{\tau }}_1$ then, ${\mathsf{\tau }}_2\in \mathcal{I}$,

where, ${\mathsf{\tau }}_2\subset {\mathsf{\tau }}_1\Rightarrow {\mathsf{\tau }}_2\left(y\right)<{\mathsf{\tau }}_1\left(y\right)$, for every $y\in X$.

2. 

If ${\mathsf{\tau }}_1,{\mathsf{\tau }}_2\in \mathcal{I}$ and $|supp\left({\mathsf{\tau }}_1\right)|<|supp\left({\mathsf{\tau }}_2\right)|$ then there exists ${\mathsf{\tau }}_3\in \mathcal{I}$ such that

a. 

${\mathsf{\tau }}_1\subset {\mathsf{\tau }}_3\subseteq {\mathsf{\tau }}_1\cup {\mathsf{\tau }}_2$, for any $y\in X$, ${\mathsf{\tau }}_1\cup {\mathsf{\tau }}_2\left(y\right)=max\{{\mathsf{\tau }}_1\left(y\right),{\mathsf{\tau }}_2\left(y\right)\}$,

b. 

$m\left({\mathsf{\tau }}_3\right)\ge min\{m\left({\mathsf{\tau }}_1\right),m\left({\mathsf{\tau }}_2\right)\}$ where, $m\left(\nu \right)=min\left\{\nu \right(y):y\in supp(\nu \left)\right\}$.

The pair $\mathrm{M}=(X,\mathcal{I})$ is called a fuzzy matroid. $\mathcal{I}$ is known as the collection of independent fuzzy sets of $\mathrm{M}$.

Definition 6.

([13]) An mF set C on a non-empty set Y is a mapping $C=(P_1\circ C\left(z\right),P_2\circ C\left(z\right),\dots ,$ $P_m{\circ C\left(z\right)):Y\to [0,1]}^m$ where, the jth projection mapping is defined as $P_j\circ C:{[0,1]}^m\to [0,1]$.

Definition 7.

([22]) An mF relation $D=(P_1\circ D,P_2\circ D,\dots ,P_m\circ D)$ on C is a function $D:C\to C$ such that, $D\left(yz\right)\le inf\left\{C\right(y),C(z\left)\right\}$, for all $y,z\in Y$. That is, for all $y,z\in Y$ , $P_j\circ D\left(yz\right)\le inf\{P_j\circ C\left(y\right),P_j\circ C\left(z\right)\}$, for each $1\le j\le m$, where $P_j\circ C\left(z\right)$ and $P_j\circ D\left(yz\right)$ represent the jth membership values of the element z and the relation $yz.$

Definition 8.

([13,22]) An mF graph $G=(C,D)$ in a universe Y consists of two mappings $C:Y\to {[0,1]}^m$ and $D:Y\times Y\to {[0,1]}^m$ such that, $D\left(yz\right)\le inf\left\{C\right(y),C(z\left)\right\}$, for all $y,z\in Y$. That is, $P_j\circ D\left(yz\right)\le inf\{P_j\circ C\left(y\right),P_j\circ C\left(z\right)\}$, for each $1\le j\le m$. Note that $P_j\circ D\left(yz\right)=0$ for all $yz\in Y\times Y-E,1\le j\le m$ where, E is the set of edges having non-zero degree of membership. mF relation, D, is called symmetric if $P_j\circ D\left(yz\right)=P_j\circ D\left(zy\right)$ for all $y,z\in Y.$

3. Matroids Based on $\mathit{m}$F Sets

In this section, we define mF vector spaces, mF matroids and study their properties.

Definition 9.

An mF vector space over a field K is defined as a pair $\tilde{Y}=(Y,C_v)$ where, $C_v:Y\to {[0,1]}^m$ is a mapping and Y is a vector space over K such that for all $c,d\in F$ and $y,z\in Y$ $C_v(cy+dz)\ge inf\{C_v\left(y\right),C_v\left(z\right)\}$, i.e., for all $1\le i\le m$,

$$P_i\circ C_v(cy+dz)\ge inf\{P_i\circ C_v\left(y\right),P_i\circ C_v\left(z\right)\}.$$

Example 1.

Let Y be a vector space of $2\times 1$ column vectors over $\mathbb{R}$. Define a mapping $C_v:Y\to {[0,1]}^3$ such that for each $\mathit{z}={\left[\begin{array}{cc}x& y\end{array}\right]}^{\mathit{t}}$,

$$C_v\left(\mathit{z}\right)=\left\{\begin{array}{cc}(1,1,1),\hfill & \mathit{z}={\left[\begin{array}{cc}0& 0\end{array}\right]}^{\mathit{t}},\hfill \\ (1,\frac{1}{3},\frac{2}{3}),\hfill & \mathit{z}={\left[\begin{array}{cc}x& 0\end{array}\right]}^{\mathit{t}}\mathrm{or}r\mathit{z}={\left[\begin{array}{cc}0& y\end{array}\right]}^{\mathit{t}},\hfill \\ (1,1,1),\hfill & x\ne 0andy\ne 0.\hfill \end{array}\right.$$

It remains only to show that $\tilde{Y}=(Y,C_v)$ is a $3$-polar fuzzy vector space. For $\mathit{z}={\left[\begin{array}{cc}0& 0\end{array}\right]}^{\mathit{t}}$, the case is trivial. So the following cases are to be discussed.

Case 1.

Consider two column vectors $\mathit{z}={\left[\begin{array}{cc}x& y\end{array}\right]}^{\mathit{t}}$ and $\mathit{u}={\left[\begin{array}{cc}u& v\end{array}\right]}^{\mathit{t}}$ then, for any scalars c and d,

$$C_v(cz+d\mathit{u})=C_v\left(\left[\begin{array}{c}cx+du\\ cy+dv\end{array}\right]\right).$$

If either exactly one of c or d is zero or both are non-zero then, $cx+du\ne 0$ and $cy+dv\ne 0$ and so $C_v(c\mathit{z}+d\mathit{u})=(1,1,1)=inf\{C_v\left(\mathit{z}\right),C_v\left(\mathit{u}\right)\}.$ Also if $c=0$ and $d=0$ then , $C_v(c\mathit{z}+d\mathit{u})=(1,1,1).$

Case 2.

If $\mathit{z}={\left[\begin{array}{cc}x& 0\end{array}\right]}^{\mathit{t}}$ and $\mathit{u}={\left[\begin{array}{cc}0& v\end{array}\right]}^{\mathit{t}}$ then, $c\mathit{z}+d\mathit{u}={\left[\begin{array}{cc}cx& dv\end{array}\right]}^{\mathit{t}}$. If either both c and d are zero or both are non-zero then, $C_v(c\mathit{z}+d\mathit{u})=(1,1,1)>inf\{C_v\left(\mathit{z}\right),C_v\left(\mathit{u}\right)\}.$ If exactly one of c or d is zero then, $C_v(c\mathit{z}+d\mathit{u})=(1,\frac{1}{3},\frac{2}{3})=inf\{C_v\left(\mathit{z}\right),C_v\left(\mathit{u}\right)\}.$ Hence $\tilde{Y}$ is a 3-polar fuzzy vector space.

Definition 10.

Let $\tilde{Y}=(Y,C_v)$ be an mF vector space over K. A set of vectors ${\left\{{\mathit{x}}_k\right\}}_{k=1}^n$ is known as mF linearly independent in $\tilde{Y}$ if

1. 

${\left\{{\mathit{x}}_k\right\}}_{k=1}^n$ is linearly independent,

2. 

$C_v\left({\displaystyle \sum _{k=1}^n}{c}_k{\mathit{x}}_k\right)={\displaystyle \underset{k=1}{\overset{n}{\bigwedge }}}{C}_v\left(c_k{\mathit{x}}_k\right)$  for all ${\left\{c_k\right\}}_{k=1}^n\subset K$.

Definition 11.

A set of vectors $\mathcal{B}={\left\{{\mathit{x}}_k\right\}}_{k=1}^n$ is known to be an mF basis in $\tilde{Y}$ if $\mathcal{B}$ is a basis in Y and condition 2 of Definition 10 is satisfied.

Proposition 1.

If $\tilde{Y}=(Y,C_v)$ is an mF vector space then any set of vectors with distinct jth, for each $1\le j\le m$, degree of membership is linearly independent and mF linearly independent.

Proposition 2.

Let $\tilde{Y}=(Y,C_v)$ be an mF vector space then,

• $C_v\left(\mathbf{0}\right)={sup}_{\mathit{y}\in Y}{C}_v\left(\mathit{y}\right)$,
• $C_v\left(a\mathit{y}\right)=C_v\left(\mathit{y}\right)$ for all $a\in K\setminus \left\{0\right\}$ and $\mathit{y}\in Y$,
• If $C_v\left(\mathit{y}\right)\ne C_v\left(\mathit{z}\right)$ for some $\mathit{y},\mathit{z}\in Y$ then $C_v(\mathit{y}+\mathit{z})=C_v\left(\mathit{y}\right)\wedge C_v\left(\mathit{z}\right)$.

Remark 1.

If $\mathcal{B}$ is an mF basis of $\tilde{Y}$ then the membership value of every element of Y can be calculated from the membership values of basis elements, i.e., if $\mathit{u}={\sum }_{k=1}^n{c}_k{\mathit{u}}_k$ then,

$$C_v\left(\mathit{u}\right)=C_v\left({\displaystyle \sum _{k=1}^n}{c}_k{\mathit{u}}_k\right)={\displaystyle \underset{k=1}{\overset{n}{\bigwedge }}}{C}_v\left(c_k{\mathit{u}}_k\right)={\displaystyle \underset{k=1}{\overset{n}{\bigwedge }}}{C}_v\left({\mathit{u}}_k\right).$$

We now come to the main idea of this research paper called mF matroids.

Definition 12.

Let Y be a non-empty finite set of elements and $\mathcal{C}\subseteq \mathcal{P}\left(Y\right)$ be a family of mF subsets, $\mathcal{P}\left(Y\right)$ is an mF power set of Y, satisfying the following the conditions,

1. 

If ${\eta }_1\in \mathcal{C}$, ${\eta }_2\in \mathcal{P}\left(Y\right)$ and ${\eta }_2\subset {\eta }_1$ then, ${\eta }_2\in \mathcal{C}$,

where, ${\eta }_2\subset {\eta }_1\Rightarrow {\eta }_2\left(y\right)<{\eta }_1\left(y\right)$ for every $y\in Y$.

2. 

If ${\eta }_1,{\eta }_2\in \mathcal{C}$ and $|supp\left({\eta }_1\right)|<|supp\left({\eta }_2\right)|$ then there exists ${\eta }_3\in \mathcal{C}$ such that

a. ${\eta }_1\subset {\eta }_3\subseteq {\eta }_1\cup {\eta }_2$,

where for any $y\in Y,({\eta }_1\cup {\eta }_2)\left(y\right)=sup\{{\eta }_1\left(y\right),{\eta }_2\left(y\right)\}$,

b. $m\left({\eta }_3\right)\ge inf\{m\left({\eta }_1\right),m\left({\eta }_2\right)\}$,

$m\left({\eta }_i\right)=inf\left\{{\eta }_i\left(x\right)\right|x\in supp\left({\eta }_i\right)\}$, $i=1,2,3$.

Then the pair $\mathcal{M}\left(Y\right)=(Y,\mathcal{C})$ is called an mF matroid on Y, and $\mathcal{C}$ is a family of independent mF subsets of $\mathcal{M}\left(Y\right)$.

$\{\delta :\delta \in \mathcal{P}(Y),\delta \notin \mathcal{C}\}$ is the family of dependent mF subsets in $\mathcal{M}\left(Y\right)$. A minimal mF dependent set is called an $m$-polar fuzzy circuit. The family of all mF circuits is denoted by $C_r\left(\mathcal{M}\right)$. An mF circuit having n number of elements is called an mF $n$-circuit. An mF matroid can be uniquely determined from $C_r\left(\mathcal{M}\right)$ because the elements of $\mathcal{C}$ are those members of $\mathcal{P}\left(Y\right)$ that contain no member of $C_r\left(\mathcal{M}\right)$. Therefore, the members of $C_r\left(\mathcal{M}\right)$ can be characterized with the following properties:

• $Ø\notin C_r\left(\mathcal{M}\right)$,
• If ${\delta }_1$ and ${\delta }_2$ are distinct and ${\delta }_1\subseteq {\delta }_2$ then, $supp\left({\delta }_1\right)=supp\left({\delta }_2\right)$,
• If ${\delta }_1,{\delta }_2\in C_r\left(G\right)$ and for $A\in \mathcal{P}\left(Y\right)$, $A\left(e\right)=inf\{{\delta }_1\left(e\right),{\delta }_2\left(e\right)\}$, $e\in supp({\delta }_1\cap {\delta }_2)$ then there exists ${\delta }_3$ such that ${\delta }_3\subseteq {\delta }_1\cup {\delta }_2-\{(e,A\left(e\right)\}$.

Proposition 3.

If $\tilde{Y}=(Y,C_v)$ is an mF vector space of $p\times q$ column vectors over $\mathbb{R}$, and $\mathcal{C}$ is the family of linearly independent mF subsets ${\eta }_i$ in $\tilde{Y}$ then $(Y,\mathcal{C})$ is an mF matroid on Y.

Proposition 4.

If $\mathcal{M}=(Y,\mathcal{C})$ is an mF matroid and y is an element of Y such that $\mathcal{C}\cup \left\{\right(y,A\left(y\right)\left)\right\}$, $A\in \mathcal{P}\left(Y\right)$ is dependent. Then $\mathcal{M}\left(Y\right)$ has a unique mF circuit contained in $\mathcal{C}\cup \left\{\right(y,A\left(y\right)\left)\right\}$ and this mF circuit contains $\left\{\right(y,A\left(y\right)\left)\right\}$.

Definition 13.

Let Y be a non-empty universe. For any mF matroid, the mF rank function ${\mu }_r:\mathcal{P}\left(Y\right)\to {[0,\infty )}^m$ is defined as,

$${\mu }_r\left(\xi \right)=sup\left\{\right|\eta |:\eta \subseteq \xi \mathit{and}\eta \in \mathcal{C}\}$$

where, $\left|\eta \right|={\displaystyle \sum _{y\in Y}}\eta \left(y\right)$. Clearly the mF rank function of an mF matroid possesses the following properties:

1. 

If ${\eta }_1,{\eta }_2\in \mathcal{P}\left(Y\right)$ and ${\eta }_1\subseteq {\eta }_2$ then ${\mu }_r\left({\eta }_1\right)\le {\mu }_r\left({\eta }_2\right)$,

2. 

If $\eta \in \mathcal{P}\left(Y\right)$ then, ${\mu }_r\left(\eta \right)\le \left|\eta \right|$,

3. 

If $\eta \in \mathcal{C}$ then, ${\mu }_r\left(\eta \right)=\left|\eta \right|$.

We now describe the concept of mF matroids by various examples.

• A trivial example of an mF matroid is known as an mF uniform matroid which is defined as,

  $$\mathcal{C}=\{\eta \in \mathcal{P}(Y):|supp\left(\eta \right)|\le l\}.$$
  It is denoted by ${\mathcal{U}}_{l,n}=(Y,\mathcal{C})$ where, l is any positive integer and $\left|Y\right|=n$. The mF circuit of ${\mathcal{U}}_{l,n}$ contains those mF subsets $\delta$ such that $\left|supp\right(\delta \left)\right|=l+1$.
  Consider the example of a $2$-polar fuzzy uniform matroid $\mathcal{M}=(Y,\mathcal{C})$ where, $Y=\{e_1,e_2,e_3\}$ and $\mathcal{C}=\{\eta \in \mathcal{P}(Y):|supp\left(\eta \right)|\le 2\}$ such that for any $\eta \in \mathcal{P}\left(Y\right)$, $\eta \left(y\right)=\mathsf{\tau }\left(y\right)$, for all $y\in Y$ where,

  $$\mathsf{\tau }\left(y\right)=\left\{\begin{array}{cc}(0.2,0.3),\hfill & y=e_1\hfill \\ (0.4,0.5),\hfill & y=e_2\hfill \\ (0.1,0.3),\hfill & y=e_3\hfill \end{array}.\right.$$

  $$\begin{array}{}\mathcal{C}=& \{Ø,\left\{(e_1,0.2,0.3)\right\},\left\{(e_2,0.4,0.5)\right\},\left\{(e_3,0.1,0.3)\right\},\{(e_1,0.2,0.3),(e_2,0.4,0.5)\},\hfill \\ & \{(e_2,0.4,0.5),(e_3,0.1,0.3)\},\{(e_1,0.2,0.3),(e_3,0.1,0.3)\}\}.\hfill \end{array}$$
  The $2$-polar fuzzy circuit of $\mathcal{M}$ is $C_r\left(\mathcal{M}\right)=\{(e_1,0.2,0.3),(e_2,0.4,0.5),(e_3,0.1,0.3)\}.$ For $\eta =\{(e_2,0.4,0.5),(e_1,0.2,0.3)\}$, ${\mu }_r\left(\eta \right)=(0.6,0.8)$.
• mF linear matroid is derived from an mF matrix. Assume that Y represents the column labels of an mF matrix and ${\eta }_x$ denotes an mF submatrix having those columns labelled by Y. It is defined as,

  $$\mathcal{C}=\{{\eta }_x\in \mathcal{P}\left(Y\right):\mathrm{columns}\mathrm{of}{\eta }_x\mathrm{are}m\text{-polar fuzzy linearly independent}\}.$$
  For any ${\eta }_x\in \mathcal{P}\left(Y\right)$, $|{\eta }_x|={\displaystyle \sum _{k=1}^r}sup\{{\eta }_x\left(a_{k1}\right),{\eta }_x\left(a_{k2}\right),\dots ,{\eta }_x\left(a_{kc}\right)\}$, ${\eta }_x^{*}={\left[a_{ij}\right]}_{r\times c}$.
  Let $A=\{\mathbf{1},\mathbf{2},\mathbf{3},\mathbf{4}\}$ be a set of $3$-polar fuzzy $2\times 1$ vectors over $\mathbb{R}$ such that for any ${\eta }_x\in \mathcal{P}\left(Y\right)$, ${\eta }_x\left(y\right)=A\left(y\right)$ where,

  $$A=\left[\begin{array}{cccc}\mathbf{1}& \mathbf{2}& \mathbf{3}& \mathbf{4}\\ (0.1,0.2,0.3)& (0.3,0.4,0.5)& (0.5,0.6,0.7)& (0.7,0.8,0.9)\\ (0.2,0.3,0.4)& (0.4,0.5,0.6)& (0.6,0.7,0.8)& (0.8,0.9,1.0)\end{array}\right]$$

  .
  Take $\mathcal{C}=\{Ø,\{\mathbf{1}\},\{\mathbf{2}\},\{\mathbf{4}\},\{\mathbf{1},\mathbf{2}\},\{\mathbf{2},\mathbf{4}\left\}\right\}$ then, $\mathcal{M}\left(A\right)=(A,\mathcal{C})$ is a $3$-polar fuzzy matroid on A. The family of dependent $3$-polar fuzzy subsets of matroid $\mathcal{M}\left(A\right)$ is $\left\{\right\{\mathbf{3}\}$, $\{\mathbf{1},\mathbf{3}\}$, $\{\mathbf{1},\mathbf{4}\}$, $\{\mathbf{2},\mathbf{3}\}$, $\{\mathbf{3},\mathbf{4}\}\}\cup \{\mathit{\eta }:\mathit{\eta }\subseteq A,\left|supp\right(\mathit{\eta }\left)\right|\ge 3\}$. For $\mathit{\eta }=\{\mathbf{2},\mathbf{4}\}$, ${\mu }_r\left(\mathit{\eta }\right)=(1.5,1.7,1.9).$
• An mF partition matroid in which the universe Y is partitioned into mF sets ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_r$ such that

  $$\mathcal{C}=\{\eta \in \mathcal{P}\left(Y\right):|supp\left(\eta \right)\cap supp\left({\alpha }_i\right)|\le l_i,\mathrm{for}\mathrm{all}1\le i\le r\}$$

  for given positive integers $l_1,l_2,\dots ,l_r$. The circuit of an mF partition matroid is the family of those mF subsets $\delta$ such that $|supp\left(\delta \right)\cap supp\left({\alpha }_i\right)|=l_i+1.$
• The very important class of mF matroids are derived from mF graphs. The detail is discussed in Proposition 5. The mF matroid derived using this method is known as m-polar fuzzy cycle matroid, denoted by $\mathcal{M}\left(G\right)$. Clearly $\mathcal{C}$ is an independent set in G if and only if for each $\eta \in \mathcal{C}$, $supp\left(\eta \right)$ is not edge set of any cycle. Equivalently, the members of $\mathcal{M}\left(G\right)$ are mF graphs $\eta$ such that $supp\left(\eta \right)$ is a forest.
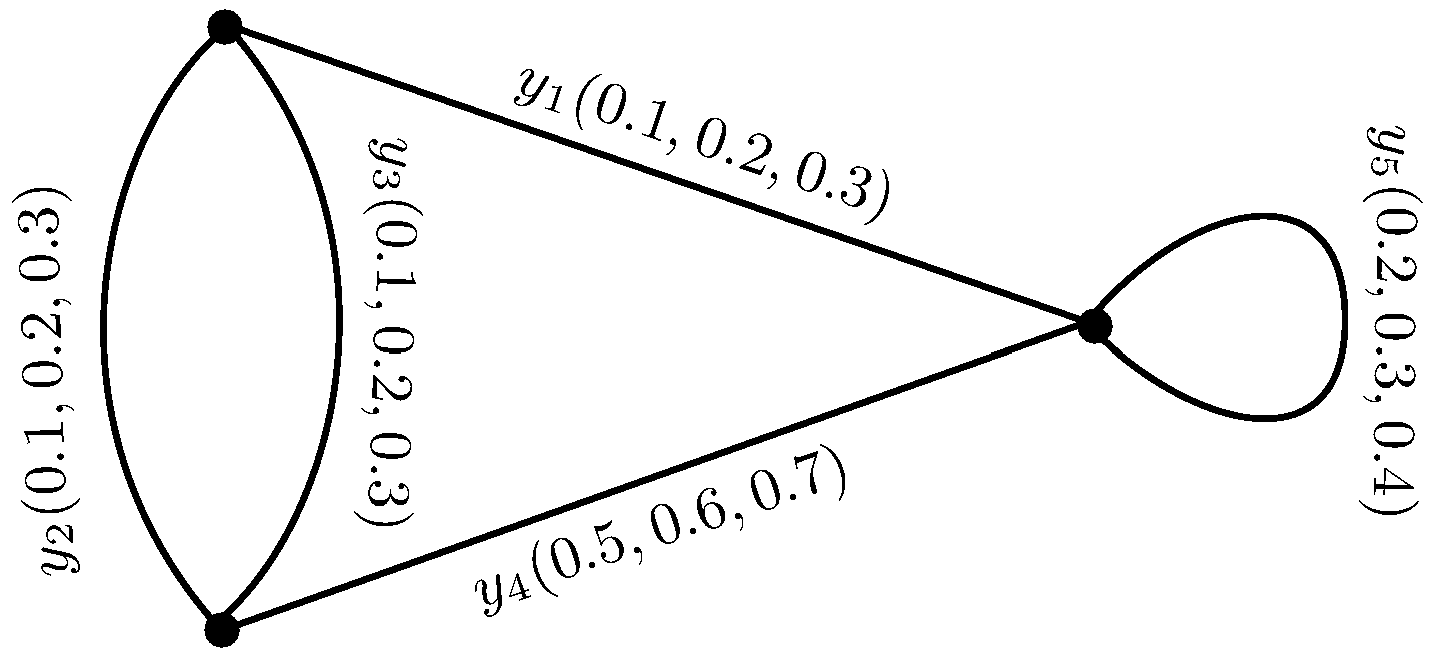
  Consider the example of an mF fuzzy cycle matroid $(Y,\mathcal{C})$ where, $Y=\{y_1,y_2,y_3,y_4,y_5\}$ and for any, $\eta \in \mathcal{C}$, $\mathit{\beta }\left(y\right)=D\left(y\right)$, $(C,D)$ is an mF multigraph on Y as shown in Figure 1.
  By Proposition 5, $C_r\left(G\right)=$ $\{\left\{(y_5,0.2,0.3,0,4)\right\}$, $\{(y_2,0.1,0.2,0.3)$, $(y_3,0.1,0.2,0.3)\}$, $\left\{\right(y_1,$ $0.1,$ $0.2,0.3)$, $(y_2,0.1,0.2,0.3)$, $(y_4,0.5,0.6,0.7)\}$, $\{(y_1,0.1,0.2,0.3)$, $(y_3,0.1,0.2,0.3)$, $(y_4,0.5,0.6,0.7)\left\}\right\}.$

  $$\begin{array}{cc}\hfill \mathcal{C}=& \{Ø,\left\{(y_1,0.1,0.2,0.3)\right\},\left\{(y_2,0.1,0.2,0.3)\right\},\left\{(y_3,0.1,0.2,0.3)\right\},\{(y_1,0.1,0.2,0.3),\hfill \\ & (y_2,0.1,0.2,0.3)\},\{(y_1,0.1,0.2,0.3),(y_4,0.5,0.6,0.7)\},\left\{(y_4,0.5,0.6,0.7)\right\},\{(y_2,0.1,0.2,0.3),\hfill \\ & (y_4,0.5,0.6,0.7)\},\{(y_1,0.1,0.2,0.3),(y_3,0.1,0.2,0.3)\},\{(y_3,0.1,0.2,0.3),(y_4,0.5,0.6,0.7)\}\}\hfill \end{array}$$
  For $\eta =\{(y_2,0.1,0.2,0.3),(y_4,0.5,0.6,0.7)\}$, ${\mu }_r\left(\eta \right)=(0.6,0.8,1.0)$.

Proposition 5.

For any mF graph $G=(C,D)$ on Y, if $C_r$ is the family of mF edge sets δ such that $supp\left(\delta \right)$ is the edge set of a cycle in $G^{*}$. Then $C_r$ is the family of mF circuits of an mF matroid on Y.

Proof. 

Clearly conditions 1 and 2 of Definition 12 hold. To prove condition 3, let ${\delta }_1$ and ${\delta }_2$ be mF edge sets of distinct cycles that have $yz$ as a common edge. Clearly, ${\delta }_3={\delta }_1\cup {\delta }_2-\left\{(yz,D\left(yz\right))\right\}$ is an mF edge set of a cycle and so condition 3 is satisfied. ☐

Example 2.

For any mF graph $G=(C,D)$ and $\mathbf{0}\le \mathit{t}\le \mathbf{1}$ define,

• $E_{\mathit{t}}=\{yz\in supp\left(D\right)|D\left(yz\right)\ge \mathit{t}\}$,
• $F_{\mathit{t}}=\left\{H\right|H\mathit{is}a\mathit{forest}\mathit{in}\mathit{the}\mathit{crisp}\mathit{graph}(Y,E_{\mathit{t}})\}$,
• ${\mathcal{C}}_{\mathit{t}}=\left\{E\left(F\right)\right|F\in F_{\mathit{t}}\}$, $E\left(F\right)$ is the edge set of F.
• Clearly $(E_{\mathit{t}},{\mathcal{C}}_{\mathit{t}})$ is a matroid for each $\mathbf{0}\le \mathit{t}\le \mathbf{1}$. Define $\mathcal{D}=\{\eta \in \mathcal{P}\left(Y\right)|{\eta }_{\mathit{t}}\in {\mathcal{C}}_{\mathit{t}},\mathbf{0}\le \mathit{t}\le \mathbf{1}\}$ then, $(Y,\mathcal{D})$ is an mF cycle matroid.

Theorem 1.

Let $\mathcal{M}=(Y,\mathcal{C})$ be an mF matroid and, for each $\mathbf{0}\le \mathit{t}\le \mathbf{1}$, define ${\mathcal{C}}_{\mathit{t}}=\left\{{\eta }_{\mathit{t}}\right|\eta \in \mathcal{C}\}$. Then $(Y,{\mathcal{C}}_{\mathit{t}})$ is a matroid on Y.

Proof. 

We prove conditions 1 and 2 of Definition 12. Assume that ${\eta }_{1\mathit{t}}\in {\mathcal{C}}_{\mathit{t}}$ and $\alpha \subseteq {\eta }_{1\mathit{t}}$. Define an mF set ${\eta }_2\in \mathcal{P}\left(Y\right)$ by

$${\eta }_2\left(y\right)=\left\{\begin{array}{cc}\mathit{t}& y\in \alpha ,\\ 0& \mathrm{otherwise}.\end{array}\right.$$

Clearly ${\eta }_2\subseteq {\eta }_1$, ${\eta }_2\in \mathcal{C}$ and ${\eta }_{2\mathit{t}}=\alpha$ therefore, $\alpha \in {\mathcal{C}}_{\mathit{t}}$. To prove condition 2, let ${\alpha }_1,{\alpha }_2\in {\mathcal{C}}_{\mathit{t}}$ and $|{\alpha }_1|<|{\alpha }_2|$. Then there exist ${\eta }_1$ and ${\eta }_2$ such that ${\eta }_{1\mathit{t}}={\alpha }_1$ and ${\eta }_{2\mathit{t}}={\alpha }_2$. Define ${\widehat{\eta }}_1$ and ${\widehat{\eta }}_2$ by

$${\widehat{\eta }}_1\left(y\right)=\left\{\begin{array}{cc}\mathit{t}\hfill & y\in {\eta }_1,\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.{\widehat{\eta }}_2\left(y\right)=\left\{\begin{array}{cc}\mathit{t}\hfill & y\in {\eta }_2,\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

It is clear that $supp\left({\widehat{\eta }}_1\right)<supp\left({\widehat{\eta }}_2\right)$. Since $\mathcal{M}$ is an mF matroid, there exists ${\eta }_3$ such that ${\widehat{\eta }}_1\subseteq {\eta }_3\subseteq {\widehat{\eta }}_1\cup {\widehat{\eta }}_2$. Since

$${\widehat{\eta }}_1\cup {\widehat{\eta }}_2\left(y\right)=\left\{\begin{array}{cc}\mathit{t}\hfill & y\in {\alpha }_1\cup {\alpha }_2,\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Therefore, there exists a set ${\alpha }_3$ such that

$${\eta }_3\left(y\right)=\left\{\begin{array}{cc}\mathit{t}\hfill & y\in {\alpha }_3,\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Also, ${\alpha }_1\subseteq {\alpha }_3\subseteq {\alpha }_1\cup {\alpha }_2$, ${\alpha }_3\in {\mathcal{C}}_{\mathit{t}}$. Hence ${\mathcal{M}}_{\mathit{t}}$ is a matroid on Y. ☐

Remark 2.

Let $\mathcal{M}=(Y,\mathcal{C})$ be an mF matroid and, for each $\mathbf{0}\le \mathit{t}\le \mathbf{1}$, ${\mathcal{M}}_{\mathit{t}}=(Y,{\mathcal{C}}_{\mathit{t}})$ be the matroid on a finite set Y as given in Theorem 1. As Y is finite therefore, there is a finite sequence $\mathbf{0}<{\mathit{t}}_1<{\mathit{t}}_2<\dots <{\mathit{t}}_n$ such that ${\mathcal{M}}_{{\mathit{t}}_i}=(Y,{\mathcal{C}}_{{\mathit{t}}_i})$ is a crisp matroid, for each $1\le i\le n$, and

1. 

${\mathit{t}}_0=\mathbf{0},{\mathit{t}}_n\le \mathbf{1}$,

2. 

${\mathcal{C}}_{\mathit{w}}\ne Ø$ if $\mathbf{0}<\mathit{w}\le {\mathit{t}}_n$ and ${\mathcal{C}}_{\mathit{w}}=Ø$ if $\mathit{w}>{\mathit{t}}_n$,

3. 

If ${\mathit{t}}_i<\mathit{w},\mathit{s}<{\mathit{t}}_{i+1}$ then, ${\mathcal{C}}_{\mathit{w}}={\mathcal{C}}_{\mathit{s}}$, $0\le i\le n-1$,

4. 

If ${\mathit{t}}_i<\mathit{w}<{\mathit{t}}_{i+1}<\mathit{s}<{\mathit{t}}_{i+2}$ then, ${\mathcal{C}}_{\mathit{w}}\supset {\mathcal{C}}_{\mathit{s}}$, $0\le i\le n-2$.

The sequence $\mathbf{0},{\mathit{t}}_1,{\mathit{t}}_2,\dots ,{\mathit{t}}_n$ is known as fundamental sequence of $\mathcal{M}$. Let ${\overline{\mathit{t}}}_i=\frac{1}{2}({\mathit{t}}_{i-1}+{\mathit{t}}_i)$ for $1\le i\le n$. The decreasing sequence of crisp matroids ${\mathcal{M}}_{{\mathit{t}}_1}\supset {\mathcal{M}}_{{\mathit{t}}_2}\supset \dots \supset {\mathcal{M}}_{{\mathit{t}}_n}$ is known as $\mathcal{M}$-indeced matroid sequence.

Theorem 2.

If Y is a finite set and $\mathbf{0}={\mathit{t}}_0<{\mathit{t}}_1<{\mathit{t}}_2<\dots <{\mathit{t}}_n\le \mathbf{1}$ is a finite sequence such that $(Y,{\mathcal{C}}_{{\mathit{t}}_1})$, $(Y,{\mathcal{C}}_{{\mathit{t}}_2})$, …, $(Y,{\mathcal{C}}_{{\mathit{t}}_n})$ is a sequence of crisp matroids. For each $m$-tuple $\mathit{t}$, where, ${\mathit{t}}_{i-1}<\mathit{t}\le {\mathit{t}}_i(1\le i\le n)$, assume that ${\mathcal{C}}_{\mathit{t}}={\mathcal{C}}_{{\mathit{t}}_i}$ and ${\mathcal{C}}_{\mathit{t}}=Ø$ if ${\mathit{t}}_n<\mathit{t}\le \mathbf{1}$.

Define ${\mathcal{C}}^{*}=\{\eta \in \mathcal{P}\left(Y\right)|{\eta }_{\mathit{t}}\in {\mathcal{C}}_{\mathit{t}},\mathbf{0}<\mathit{t}\le \mathbf{1}\}$ then $\mathcal{M}=(Y,{\mathcal{C}}^{*})$ is an mF matroid.

Proof. 

Let ${\eta }_1\in {\mathcal{C}}^{*}$, ${\eta }_2\in \mathcal{P}\left(Y\right)$, and ${\eta }_2\subseteq {\eta }_1$. Clearly ${\eta }_{1\mathit{t}}\in {\mathcal{C}}_{\mathit{t}}$, ${\eta }_{2\mathit{t}}\subseteq {\eta }_{1\mathit{t}}$, and since $(Y,{\mathcal{C}}_{\mathit{t}})$ is a crisp matroid therefore, ${\eta }_{2\mathit{t}}\in {\mathcal{C}}_{\mathit{t}}$, so ${\eta }_2\in {\mathcal{C}}^{*}$.

Assume that ${\eta }_1,{\eta }_2\in {\mathcal{C}}^{*}$ and $|supp\left({\eta }_2\right)|<|supp\left({\eta }_1\right)|$. Define

$$\mathit{\beta }=inf\{\underset{y\in supp\left({\eta }_1\right)}{inf}{\mathcal{C}}^{*}\left(y\right),\underset{y\in supp\left({\eta }_2\right)}{inf}{\mathcal{C}}^{*}\left(y\right)\}.$$

It is easy to see that $supp\left({\eta }_1\right),supp\left({\eta }_2\right)\in {\mathcal{C}}_{\mathit{\beta }}$. Since ${\mathcal{C}}_{\mathit{\beta }}$ is the family of independent sets of a crisp matroid therefore, there exists an independent set $A\in {\mathcal{C}}_{\mathit{\beta }}$ such that

$$supp\left({\eta }_2\right)\subset A\subseteq supp\left({\eta }_1\right)\cup supp\left({\eta }_2\right).$$

Let

$${\eta }_3\left(y\right)=\left\{\begin{array}{cc}{\eta }_2\left(y\right)\hfill & y\in supp\left({\eta }_2\right),\hfill \\ \mathit{\beta }\hfill & y\in A\setminus supp\left({\eta }_2\right),\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

The mF set ${\eta }_3$ satisfies condition 2 of Definition 12 and hence $(Y,{\mathcal{C}}^{*})$ is an mF matroid. ☐

Theorem 3.

Let $\mathcal{M}=(Y,\mathcal{C})$ be an mF matroid and for each $\mathbf{0}<\mathit{t}\le \mathbf{1}$, ${\mathcal{M}}_{\mathit{t}}=(Y,{\mathcal{C}}_{\mathit{t}})$ is a crisp matroid by Theorem 2. Let ${\mathcal{C}}^{*}=\{\eta \in \mathcal{P}\left(Y\right):{\eta }_{\mathit{t}}\in {\mathcal{C}}_{\mathit{t}},\mathbf{0}<\mathit{t}\le \mathbf{1}\}$. Then $\mathcal{C}={\mathcal{C}}^{*}$.

Proof. 

It is clear from the definition of ${\mathcal{C}}^{*}$ that $\mathcal{C}\subseteq {\mathcal{C}}^{*}$. To prove the converse part, we proceed on the following steps.

Suppose that $\{{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_p\}$ is the non-zero range of $\eta \in \mathcal{C}$ such that ${\mathit{\alpha }}_1>{\mathit{\alpha }}_2>\dots >{\mathit{\alpha }}_p>\mathbf{0}$. For each $1\le i\le p$, ${\eta }_{{\mathit{\alpha }}_i}\in {\mathcal{C}}_{{\mathit{\alpha }}_i}$ and ${\eta }_{{\mathit{\alpha }}_{i-1}}\subset {\eta }_{{\mathit{\alpha }}_i}$. Define ${\mathit{f}}_i\in \mathcal{P}\left(Y\right)$ by

$$f_i\left(y\right)=\left\{\begin{array}{cc}{\mathit{\alpha }}_i\hfill & \mathrm{if}y\in {\eta }_{{\mathit{\alpha }}_i},\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Since ${\eta }_{{\mathit{\alpha }}_i}\in {\mathcal{C}}_{{\mathit{\alpha }}_i}$ therefore, $f_i\in \mathcal{C}$ and ${\displaystyle \bigcup _{i=1}^q}{f}_i=\eta$. Assume that $supp\left(\eta \right)=\{y_1,y_2,\dots ,y_{n_p}\}$. We use the induction method to show that $\eta \in \mathcal{C}$. Since $f_1\in \mathcal{C}$ therefore, it remains to show that if ${\displaystyle \bigcup _{i=1}^{l-1}}{f}_i\in \mathcal{C}$ then, ${\displaystyle \bigcup _{i=1}^l}{f}_i\in \mathcal{C}$, for each $l<p$. Define

$$g_1\left(y\right)=\left\{\begin{array}{cc}{\mathit{\alpha }}_l\hfill & \mathrm{if}y\in \{y_1,y_2,\dots ,y_{n_{l-1}},y_{n_{l-1}+1}\},\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Since for each $1\le i\le l-1$, ${\mathit{\alpha }}_i>{\mathit{\alpha }}_l$ therefore, $g_1\subseteq f_l$ which implies that $g_1\in \mathcal{C}$. Define $h_1\in \mathcal{P}\left(Y\right)$ by

$$h_1\left(y\right)=\left\{\begin{array}{cc}\eta \left(y_{n_{l-1}+1}\right)={\mathit{\alpha }}_l\hfill & \mathrm{if}y=y_{n_{l-1}+1},\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Since by induction method ${\displaystyle \bigcup _{i=1}^{l-1}}{f}_i\in \mathcal{C}$ and $supp({\displaystyle \bigcup _{i=1}^{l-1}}{f}_i)=\{y_1,y_2,\dots ,y_{n_{l-1}}\}$, $m({\displaystyle \bigcup _{i=1}^{l-1}}{f}_i)>{\mathit{\alpha }}_l$ therefore, condition 2(b) of Definition 12 implies that ${\displaystyle \bigcup _{i=1}^{l-1}}{f}_i\cup h_1\in \mathcal{C}$. If $n_{l-1}+1=n_l$ then, ${\displaystyle \bigcup _{i=1}^l}{f}_i\in \mathcal{C}$ and we are done. But if on the other hand, $n_{l-1}+1<n_l$ then define,

$$g_2\left(y\right)=\left\{\begin{array}{cc}{\mathit{\alpha }}_l\hfill & \mathrm{if}y\in \{y_1,y_2,\dots ,y_{n_{l-1}},y_{n_{l-1}+1},y_{n_{l-1}+2}\},\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Since for each $1\le i\le l-1$, ${\mathit{\alpha }}_i>{\mathit{\alpha }}_l$ therefore, $g_2\subseteq f_l$ which implies that $g_2\in \mathcal{C}$. Define $h_2\in \mathcal{P}\left(Y\right)$ by

$$h_2\left(y\right)=\left\{\begin{array}{cc}\eta \left(y_{n_{l-1}+2}\right)={\mathit{\alpha }}_l\hfill & \mathrm{if}y=y_{n_{l-1}+2},\hfill \\ \mathbf{0}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Since $supp({\displaystyle \bigcup _{i=1}^{l-1}}{f}_i\cup h_1)=\{y_1,y_2,\dots ,y_{n_{l-1}},y_{n_{l-1}+1}\}$, $m({\displaystyle \bigcup _{i=1}^{l-1}}{f}_i\cup h_1)>{\mathit{\alpha }}_l$ therefore, condition 2(b) of Definition 12 implies that ${\displaystyle \bigcup _{i=1}^{l-1}}{f}_i\cup h_1\cup h_2\in \mathcal{C}$. If $n_{l-1}+1=n_l$ then, ${\displaystyle \bigcup _{i=1}^l}{f}_i\in \mathcal{C}$ and we are done. If o $n_{l-1}+2<n_l$ then we continue the process and obtain an mF set ${\mathit{\beta }}_n={\displaystyle \bigcup _{i=1}^{l-1}}{f}_i\cup h_1\cup h_2\cup \dots \cup h_n$ such that ${\mathit{\beta }}_n={\displaystyle \bigcup _{i=1}^l}{f}_i$ which completes the induction procedure and the proof. ☐

The submodularity of an mF rank function ${\mu }_r$ is quiet difficult and it depends on Theorem 3 and the following definition.

Definition 14.

Let ${\mathit{t}}_0,{\mathit{t}}_1,\dots ,{\mathit{t}}_n$ be the fundamental sequence of an mF matroid. For any $m$-tuple $\mathit{t},\mathbf{0}<\mathit{t}\le \mathbf{1}$, define ${\overline{\mathcal{C}}}_{\mathit{t}}={\mathcal{C}}_{{\overline{\mathit{t}}}_i}$ where, ${\mathit{t}}_{i-1}<\mathit{t}\le {\mathit{t}}_i$ and ${\overline{\mathit{t}}}_i=\frac{1}{2}({\mathit{t}}_{i-1}+{\mathit{t}}_i)$. If $\mathit{t}>{\mathit{t}}_n take {\overline{\mathcal{C}}}_{\mathit{t}}={\mathcal{C}}_{\mathit{t}}$. Define

$$\overline{\mathcal{C}}=\{\eta \in \mathcal{P}\left(Y\right):{\eta }_{\mathit{t}}\in {\overline{\mathcal{C}}}_{\mathit{t}},\mathrm{for}\mathrm{each}\mathit{t},\mathbf{0}<\mathit{t}\le \mathbf{1}\}.$$

Then $\overline{\mathcal{M}}=(Y,\overline{\mathcal{C}})$ is known as closure of $\mathcal{M}=(Y,\mathcal{C})$.

Example 3.

We now explain the concept of closure by an example of a $3$-polar fuzzy uniform matroid $\mathcal{M}=(Y,\mathcal{C})$ where, $Y=\{y_1,y_2,y_3\}$ and $\mathcal{C}=\{\eta \in \mathcal{P}(Y):|supp\left(\eta \right)|\le 1\}$ such that for any $\eta \in \mathcal{P}\left(Y\right)$, $\eta \left(y\right)=\tau \left(y\right)$, for all $y\in Y$ where,

$$\mathsf{\tau }\left(y\right)=\left\{\begin{array}{cc}(0.1,0.2,0.3),\hfill & y=y_1\hfill \\ (0.2,0.3,0.4),\hfill & y=y_2\hfill \\ (0.3,0.4,0.5),\hfill & y=y_3\hfill \end{array}.\right.$$

$$\mathcal{C}=\left\{Ø,\left\{(y_1,0.1,0.2,0.3)\right\},\left\{(y_2,0.2,0.3,0.4)\right\},\left\{(y_3,0.3,0.4,0.5)\right\}\right\}.$$

The fundamental sequence of $\mathcal{M}$ is $\{{\mathit{t}}_0=\mathbf{0},{\mathit{t}}_1=(0.1,0.2,0.3),{\mathit{t}}_2=(0.2,0.3,0.4),{\mathit{t}}_3=(0.3,0.4,0.5)\}$. From routine calculations, ${\overline{\mathit{t}}}_1=(0.05,0.1,0.15)$, ${\overline{\mathit{t}}}_2=(0.15,0.25,0.35)$, ${\overline{\mathit{t}}}_3=(0.25,0.35,0.45)$. Since for any $\mathbf{0}<\mathit{t}\le \mathbf{1}$, ${\overline{\mathcal{C}}}_{\mathit{t}}={\mathcal{C}}_{{\overline{\mathit{t}}}_i}$, $1\le i\le 3$, therefore, ${\mathcal{C}}_{{\overline{\mathit{t}}}_1}={\mathcal{C}}_{{\mathit{t}}_1}$, ${\mathcal{C}}_{{\overline{\mathit{t}}}_2}=\{\left\{y_2\right\},\left\{y_3\right\}\}$, ${\mathcal{C}}_{{\overline{\mathit{t}}}_2}=\left\{\left\{y_3\right\}\right\}$. Hence the closure of $\mathcal{C}$ can be defined as,

$$\begin{array}{cc}\hfill \overline{\mathcal{C}}=& \{Ø,\left\{(y_1,0.1,0.2,0.3)\right\},\left\{(y_2,0.2,0.3,0.4)\right\},\left\{(y_3,0.3,0.4,0.5)\right\},\{(y_1,0.1,0.2,0.3),(y_2,0.2,0.3,0.4)\},\hfill \\ & \{(y_1,0.1,0.2,0.3),(y_3,0.3,0.4,0.5)\},\{(y_2,0.2,0.3,0.4),(y_3,0.3,0.4,0.5)\}\}.\hfill \end{array}$$

Theorem 4.

The closure $\overline{\mathcal{M}}=(Y,\overline{\mathcal{C}})$ of an mF matroid $\mathcal{M}=(Y,\mathcal{C})$ is also an mF matroid.

The proof of this theorem is a clear consequence of Theorem 1.

Definition 15.

An mF matroid with fundamental sequence ${\mathit{t}}_0,{\mathit{t}}_1,\dots ,{\mathit{t}}_n$ is known as a closed mF matroid if for each ${\mathit{t}}_{i-1}<\mathit{t}\le {\mathit{t}}_i$ , ${\mathcal{C}}_{\mathit{t}}={\mathcal{C}}_{{\mathit{t}}_i}$.

Remark 3.

Note that the closure of an mF matroid is closed and that it is the smallest closed mF matroid containing $\mathcal{M}$. Also the fundamental sequence of $\mathcal{M}$ and $\overline{\mathcal{M}}$ is same.

Lemma 1.

If ${\overline{\mu }}_r$ and ${\mu }_r$ are mF rank functions of $\overline{\mathcal{M}}=(Y,\overline{\mathcal{C}})$ and $\mathcal{M}=(Y,\mathcal{C})$, respectively then ${\overline{\mu }}_r={\mu }_r$.

Assume that $\mathcal{M}=(Y,\mathcal{C})$ is an mF matroid with fundamental sequence ${\mathit{t}}_0,{\mathit{t}}_1,\dots ,{\mathit{t}}_n$ and rank function ${\mu }_r$. To prove that ${\mu }_r$ is submodular, we now define a function ${\widehat{\mu }}_r:\mathcal{P}\left(Y\right)\to {[0,\infty )}^m$ which is also submodular.

For any $\eta \in \mathcal{P}\left(Y\right)$, let $\mathbf{0}<{\mathit{\alpha }}_1<{\mathit{\alpha }}_2<\dots <{\mathit{\alpha }}_p$ be the non-zero range of $\eta$ and ${\mathit{\beta }}_1<{\mathit{\beta }}_2<\dots <{\mathit{\beta }}_q$ be the common refinement of ${\mathit{t}}_i^{\prime }s$ and ${\mathit{\alpha }}_j^{\prime }s$ defined as,

$$\{{\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_q\}=\{{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_p\}\cup \{{\mathit{t}}_1,{\mathit{t}}_2,\dots ,{\mathit{t}}_n\}.$$

$R_i$ is the rank function of crisp matroid ${\mathcal{M}}_{{\mathit{t}}_i}=(Y,{\mathcal{C}}_{{\mathit{t}}_i})$, for all $1\le i\le n$. For each integer j, there is an integer i, $1\le i\le n$, such that ${\mathit{t}}_{i-1}\le {\mathit{\beta }}_{j-1}<{\mathit{\beta }}_j\le {\mathit{t}}_i$. Then $(i,j)$ is known as a correspondence pair. For each correspondence pair $(i,j)$, define

$${\gamma }_j\left(\eta \right)=\left\{\begin{array}{cc}({\mathit{\beta }}_j-{\mathit{\beta }}_{j-1})R_i\left({\eta }_{{\mathit{\beta }}_j}\right)\hfill & \mathrm{if}{\mathit{\beta }}_j\le {\mathit{t}}_n,\hfill \\ \mathbf{0}\hfill & \mathrm{if}{\mathit{\beta }}_j>{\mathit{t}}_n.\hfill \end{array}\right.$$

Since for each ${\mathit{\beta }}_{j-1}<\mathit{\beta }<{\mathit{\beta }}_j$, ${\eta }_{\mathit{\beta }}={\eta }_{{\mathit{\beta }}_j}$. Define a new function ${\widehat{\mu }}_r:\mathcal{P}\left(Y\right)\to {[0,\infty )}^m$ by

$${\widehat{\mu }}_r={\displaystyle \sum _{j=1}^q}{\gamma }_j\left(\eta \right).$$

(1)

Lemma 2.

Assume that $\mathbf{0}<{\mathsf{\rho }}_1<{\mathsf{\rho }}_2<\dots <{\mathsf{\rho }}_p$ and $\{{\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_q\}\subseteq \{{\mathsf{\rho }}_1,{\mathsf{\rho }}_2,\dots ,{\mathsf{\rho }}_p\}$. For each i, $1\le i\le n$, let $(i,j)$ be the correspondence pair if ${\mathit{t}}_{i-1}\le {\mathsf{\rho }}_{j-1}<{\mathsf{\rho }}_j\le {\mathit{t}}_i$. For each correspondence pair $(i,j)$, define ${\gamma }_j^{*}:\mathcal{P}\left(Y\right)\to {\mathbb{R}}^m$ by

$${\gamma }_j^{*}\left(\eta \right)=\left\{\begin{array}{cc}({\mathsf{\rho }}_j-{\mathsf{\rho }}_{j-1})R_i\left({\eta }_{{\mathsf{\rho }}_j}\right)\hfill & if{\mathsf{\rho }}_j\le {\mathit{t}}_n,\hfill \\ \mathbf{0}\hfill & if{\mathsf{\rho }}_j>{\mathit{t}}_n.\hfill \end{array}\right.$$

Then ${\displaystyle \sum _{j=1}^q}{\gamma }_j\left(\eta \right)={\displaystyle \sum _{j=1}^q}{\gamma }_j^{*}\left(\eta \right)$.

Theorem 5.

If ${\mathit{t}}_0,{\mathit{t}}_1,\dots ,{\mathit{t}}_n$ is the fundamental sequence of an mF matroid $\mathcal{M}=(Y,\mathcal{C})$ and ${\widehat{\mu }}_r$ is defined by (1) then, ${\widehat{\mu }}_r$ is submodular.

Proof. 

Let ${\eta }_1,{\eta }_2\in \mathcal{P}\left(Y\right)$ and $\{{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_s\}$, $\{{\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_r\}$ be the non-zero ranges of ${\eta }_1$ and ${\eta }_2$, respectively. Define

$$\{{\mathsf{\rho }}_1,{\mathsf{\rho }}_2,\dots ,{\mathsf{\rho }}_p\}=\{{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_s\}\cup \{{\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_r\}\cup \{{\mathit{t}}_0,{\mathit{t}}_1,\dots ,{\mathit{t}}_n\}.$$

Lemma 2 implies that ${\widehat{\mu }}_r={\displaystyle \sum _{j=1}^q}{\gamma }_j^{*}\left(\eta \right)$. Since ${\mathsf{\rho }}_j-{\mathsf{\rho }}_{j-1}>\mathbf{0}$, for each j therefore, by the submodularity of the crisp rank function $R_i$,

$$\begin{array}{cc}\hfill {\displaystyle \sum _{j=1}^p}({\mathsf{\rho }}_j-{\mathsf{\rho }}_{j-1})R_i\left({\eta }_{1{\mathit{t}}_j}\right)-{\displaystyle \sum _{j=1}^p}({\mathsf{\rho }}_j-{\mathsf{\rho }}_{j-1})R_i\left({\eta }_{2{\mathit{t}}_j}\right)& \ge {\displaystyle \sum _{j=1}^p}({\mathsf{\rho }}_j-{\mathsf{\rho }}_{j-1})R_i({\eta }_{1{\mathit{t}}_j}\cup {\eta }_{2{\mathit{t}}_j})\hfill \\ & +{\displaystyle \sum _{j=1}^p}({\mathsf{\rho }}_j-{\mathsf{\rho }}_{j-1})R_i({\eta }_{1{\mathit{t}}_j}\cap {\eta }_{2{\mathit{t}}_j}).\hfill \\ \hfill \Rightarrow {\widehat{\mu }}_r\left({\eta }_1\right)+{\widehat{\mu }}_r\left({\eta }_1\right)\ge {\widehat{\mu }}_r({\eta }_1\cup {\eta }_2)+{\widehat{\mu }}_r({\eta }_1\cap {\eta }_2).\end{array}$$

☐

Example 4.

Consider a $3$-polar fuzzy matroid given in Example 3. For $\eta =\left\{(y_2,0.2,0.3,0.4)\right\}$, the non-zero range of η is $\{{\mathit{\alpha }}_1=(0.2,0.3,0.4)\}$. Define

$$\{{\mathit{\beta }}_1,{\mathit{\beta }}_2,{\mathit{\beta }}_3\}=\{{\mathit{t}}_0,{\mathit{t}}_1,{\mathit{t}}_2,{\mathit{t}}_3\}\cup \left\{{\mathit{\alpha }}_1\right\}=\{{\mathit{\beta }}_1=(0.1,0.2,0.3),{\mathit{\beta }}_2=(0.2,0.3,0.4),{\mathit{\beta }}_3=(0.3,0.4,0.5)\}.$$

Since ${\mathit{t}}_1={\mathit{\beta }}_1<{\mathit{\beta }}_2={\mathit{t}}_2$ therefore, $(2,2)$ is correspondence pair. Similarly $(3,3)$ is also a correspondence pair. Now ${\gamma }_1\left(\eta \right)=\mathbf{0}$,

$${\gamma }_2\left(\eta \right)=({\mathit{\beta }}_2-{\mathit{\beta }}_1)R_2\left({\eta }_{{\mathit{\beta }}_2}\right)=(0.1,0.1,0.1),{\gamma }_3\left(\eta \right)=({\mathit{\beta }}_3-{\mathit{\beta }}_2)R_3\left({\eta }_{{\mathit{\beta }}_3}\right)=(0,0,0).$$

Thus ${\widehat{\mu }}_r\left(\eta \right)=(0.1,0.1,0.1)$.

Theorem 6.

For any mF matroid, ${\mu }_r\ge {\widehat{\mu }}_r$.

Proof. 

Since ${\mu }_r={\overline{\mu }}_r$ therefore, assume that $\mathcal{M}$ is a closed mF matroid and ${\mu }_r\left({\eta }_1\right)\ne \mathbf{0}$ for some ${\eta }_1\in \mathcal{P}\left(Y\right)$. Suppose that there exists ${\eta }_2\in \mathcal{C}$${\eta }_2\subseteq {\eta }_1$ such that ${\mu }_r\left({\eta }_1\right)=\left|{\eta }_2\right|.$ We will show that ${\widehat{\mu }}_r\left({\eta }_1\right)\le \left|{\eta }_2\right|.$

Take ${\mathit{t}}_0<{\mathit{t}}_1<\dots <{\mathit{t}}_n$ as the fundamental sequence of $\mathcal{M}$ and ${\mathit{\alpha }}_1<{\mathit{\alpha }}_2<\dots <{\mathit{\alpha }}_p$ as the non-zero range of ${\eta }_1$. Let ${\mathit{\beta }}_1<{\mathit{\beta }}_2<\dots <{\mathit{\beta }}_q$ be defined by

$$\{{\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_q\}=\{{\mathit{\alpha }}_1,{\mathit{\alpha }}_2,\dots ,{\mathit{\alpha }}_p\}\cup \{{\mathit{t}}_0,{\mathit{t}}_1,\dots ,{\mathit{t}}_n\}.$$

For each $\mathbf{0}<\mathit{\beta }\le \mathbf{1}$, define

$${\mathcal{C}}_{\mathit{\beta }}^{{\eta }_1}=\{C\in {\mathcal{C}}_{\mathit{\beta }}:C\subseteq {\eta }_{1\mathit{\beta }}\},{\mathit{\beta }}^{*}=sup\{\mathit{\beta }:{\mathcal{C}}_{\mathit{\beta }}^{{\eta }_1}\ne Ø\}.$$

Remark 2 implies that ${\mathit{\beta }}^{*}={\mathit{\beta }}_{i^{*}}$, for some ${\mathit{\beta }}_{i^{*}}\in {\left\{{\mathit{\beta }}_j\right\}}_{j=1}^q$. The following properties of ${\mathit{\beta }}_{i^{*}}$ always hold:

(i)

${\mathit{\beta }}_{i^{*}}\le {\mathit{t}}_n$, ${\widehat{\mu }}_r\left({\eta }_1\right)={\displaystyle \sum _{i=1}^{i^{*}}}{\gamma }_i\left({\eta }_1\right)$.

(ii)

For ${\eta }_2\in \mathcal{C},{\eta }_2\subseteq {\eta }_1$ we have, $\mathbf{0}<{\eta }_2\left(y\right)\le {\mathit{\beta }}_{i^{*}}$ for each $y\in supp\left({\eta }_2\right)$.

For each integer $i\le i^{*}$, let $|C_{{\mathit{\beta }}_i}|=R_j\left({\eta }_{{\mathit{\beta }}_i}\right)$ where, $A_{{\mathit{\beta }}_i}\in {\mathcal{C}}_{{\mathit{\beta }}_i}^{{\eta }_1}$, ${\mathit{t}}_{i-1}\le {\mathit{\beta }}_{j-1}<{\mathit{\beta }}_j\le {\mathit{t}}_i$ and $R_i$ is rank function of $M_{{\mathit{t}}_i}$. Clearly, $|C_{{\mathit{\beta }}_{i^{*}}}|<|C_{{\mathit{\beta }}_{i^{*}-1}}|<\dots <|C_{{\mathit{\beta }}_1}|$ and define a new sequence $D_{{\mathit{\beta }}_{i^{*}}}\subseteq D_{{\mathit{\beta }}_{i^{*}-1}}\subseteq \dots \subseteq D_{{\mathit{\beta }}_1}$ such that $D_{{\mathit{\beta }}_{i^{*}}}=C_{{\mathit{\beta }}_{i^{*}}}$ and

$$D_{{\mathit{\beta }}_{i^{*}-1}}=\left\{\begin{array}{cc}{D}_{{\mathit{\beta }}_{i^{*}}}\hfill & \mathrm{if}|D_{{\mathit{\beta }}_{i^{*}}}|=|C_{{\mathit{\beta }}_{i^{*}-1}}|,\hfill \\ C_{{\mathit{\beta }}_{i^{*}-1}}^{\prime }\hfill & \mathrm{if}|D_{{\mathit{\beta }}_{i^{*}}}|<|C_{{\mathit{\beta }}_{i^{*}-1}}|,\hfill \end{array}\right.$$

where, $|C_{{\mathit{\beta }}_{i^{*}-1}}^{\prime }|=|C_{{\mathit{\beta }}_{i^{*}-1}}|$ and $D_{{\mathit{\beta }}_{i^{*}}}\subseteq C_{{\mathit{\beta }}_{i^{*}-1}}^{\prime }$ which is by condition 2 of Definition 12. Proceeding in this way, we can find a sequence ${\left\{D_{{\mathit{\beta }}_{i^{*}}}\right\}}_{i=1}^{i^{*}}$ such that

(i)

$D_{{\mathit{\beta }}_i}$ is maximal in $(Y,{\mathcal{C}}_{{\mathit{\beta }}_i}^{{\eta }_1})$

(ii)

$|D_{{\mathit{\beta }}_i}|=R_j\left({\eta }_{{\mathit{\beta }}_i}\right)$ where, i and j are such that ${\mathit{t}}_{i-1}\le {\mathit{\beta }}_{j-1}<{\mathit{\beta }}_j\le {\mathit{t}}_i$.

For each positive integer i, $1\le i\le i^{*}$, define ${\eta }_{2i}$ as mF set such that $supp\left({\eta }_{2i}\right)=D_{{\mathit{\beta }}_i}$ with non-zero range $\left\{{\mathit{\beta }}_i\right\}$. Let ${\eta }_2={\displaystyle \bigcup _{i=1}^{i^{*}}}{\eta }_{2i}$. Since ${\eta }_2\subseteq {\eta }_1$ and ${\eta }_2\in {\mathcal{C}}^{*}$ therefore, by Theorem 3,

$${\mu }_r\left({\eta }_1\right)=|{\eta }_2|\ge {\displaystyle \sum _{i=1}^{i^{*}}}({\mathit{\beta }}_i-{\mathit{\beta }}_{i-1})\left|D_{{\mathit{\beta }}_i}\right|={\widehat{\mu }}_r\left({\eta }_1\right).$$

☐

4. Applications

mF matroids have interesting applications in graph theory, combinatorics and algebra. mF matroids are used to discuss the uncertain behaviour of objects if the data have multipolar information and have many applications in addition to Mathematics.

4.1. Decision Support Systems

mF matroids can be used in decision support systems to find the ordering of n tasks if each task constitutes m linguistic values. All tasks are available at 0 time and each task has a profit p associated with its m properties and a deadline d. The profit $p_j$ can be gained if each mF task j is completed at the deadline $d_j$. The problem is to find the mF ordering of tasks to maximize the total profit. mF matroids can also be used in the secret sharing problem to share parts of secret information among different participants such that we have multipolar information about each participant.

It doesn’t look like an mF matroid problem because the mF matroid problem asks to find an optimal mF subset, but this problem requires one to find an optimal schedule. However, this is an mF matroid problem. The profit, penalty and expense of any ordering can be determined by an mF subset of tasks that are on or before time. For an mF subset S of deadlines $\{d_1,d_2,\dots ,d_n\}$ corresponding to tasks $\mathit{t}=\{{\mathit{t}}_1,{\mathit{t}}_2,\dots ,{\mathit{t}}_n\}$, if there is a ordering such that every task in S is on or before time, and all tasks out of S are late. The procedure for the selection of tasks has net time complexity is O$\left(n{2}^n\right)$.

4.2. Ordering of Machines/Workers for Certain Tasks

An important application is to divide a set of workers into different groups to perform a specific task for which they are eligible. Consider the example of allocating a collection of tasks to a set of workers $W_1,W_2,\dots ,W_7$ who are eligible to perform that task. The problem is to assign a task to a group of workers to be fulfilled in required time, accuracy and cost. The 3-polar fuzzy set of workers is,

$$\begin{array}{cc}\hfill W^{\prime }=& \{(W_1,0.8,0.9,0.9),(W_2,0.7,0.9,0.7),(W_3,0.7,0.7,0.6),(W_4,0.7,0.9,0.8),(W_5,0.6,0.9,0.8),\hfill \\ & (W_6,0.6,0.8,0.75),(W_7,0.7,0.7,0.6)\}.\hfill \end{array}$$

The degree of membership of each worker shows the time taken by them, the accuracy of the output if they work on the task and cost of the worker for service. The problem is to determine a collection of workers for tasks $T_1$ and $T_2$ such that,

$$\begin{array}{cc}\hfill T_1& =\{(W_i,W^{\prime }\left(W_i\right))\mid P_1\circ W_i\le 0.7,P_2\circ W_i\ge 0.7,P_3\circ W_i\le 0.7\},\hfill \\ \hfill T_2& =\{(W_i,W^{\prime }\left(W_i\right))\mid P_1\circ W_i\le 0.8,P_2\circ W_i\ge 0.9,P_3\circ W_i\le 0.9\}.\hfill \end{array}$$

The 3-polar fuzzy set of workers for both the tasks are,

$$\begin{array}{cc}\hfill T_1& =\{(W_2,0.7,0.9,0.7),(W_3,0.7,0.7,0.6),(W_6,0.6,0.8,0.75),(W_7,0.7,0.7,0.6)\},\hfill \\ \hfill T_2& =\{(W_1,0.8,0.9,0.9),(W_3,0.7,0.7,0.6),(W_4,0.7,0.9,0.8)\}.\hfill \end{array}$$

The workers $W_2,W_3,W_6,W_7$ are preferable for task ${\mathit{t}}_1$ and $W_1,W_3,W_4$ are preferable for task ${\mathit{t}}_2$.

4.3. Network Analysis

mF models can be used in network analysis problems to determine the minimum number of connections for wireless communication. The procedure for the selection of minimum number of locations from a wireless connection is explained in the following steps.

• Input the n number of locations $L_1,L_2,\dots ,L_n$ of wireless communication network.
• Input the adjacency matrix $\xi ={\left[L_{ij}\right]}_{n^2}$ of membership values of edges among locations.
• From this adjacency matrix, arrange the membership values in increasing order.
• Select an edge having minimum membership value.
• Repeat Step 4 so that the selected edge does not create any circuit with previous selected edges.
• Stop the procedure if the connection between every pair of locations is set up.

Here we explain the use of mF matroids in network analysis. The 2-polar fuzzy graph in Figure 2 represents the wireless communication between five locations $L_1,L_2,L_3,L_4,L_5$.

The degree of membership of each edge shows the time taken and cost for sending a message from one location to the other. Each pair of vertices is connected by an edge. However, in general we do not need connections among all the vertices because the vertices linked indirectly will also have a message service between them, i.e., if there is a connection from $L_2$ to $L_3$ and $L_3$ to $L_4$, then we can send a message from $L_2$ to $L_4$, even if there is no edge between $L_2$ and $L_4$. The problem is to find a set of edges such that we are able to send message between every two vertices under the condition that time and cost is minimum. The procedure is as follows. Arrange the membership values of edges in increasing order as, $\left\{\right(0.5,0.28)$, $(0.6,0.33)$, $(0.6,0.37)$, $(0.7,0.41)$, $(0.7,0.44)$, $(0.7,0.46)$, $(0.7,0.48)$, $(0.8,0.5)$, $(0.8,0.51)$, $(0.8,0.53)\}$. At each step, select an edge having minimum membership value so that it does not create any circuit with previous selected edges. The $2$-polar fuzzy set of selected edges is,

$$\{(L_3{L}_4,0.5,0.28),(L_3{L}_5,0.6,0.33),(L_1{L}_5,0.6,0.37),(L_2{L}_4,0.7,0.41),(L_1{L}_4,0.7,0.46)\}.$$

The communication network with minimum number of locations and cost is shown in Figure 3.

Figure 3 shows that only five connections are needed to communicate among given locations in order to minimize the cost and improve the network communication.

5. Conclusions

In this research paper, we have applied the powerful technique of mF sets to extend the theory of vector spaces and matroids. The mF models give more accuracy, precision and compatibility to the system when more than one agreements are to be dealt with. We have mainly introduced the idea of the mF matroid, implemented this concept to graph theory, linear algebra and have studied various examples including the mF uniform matroid, mF linear matroid, mF partition matroid and mF cycle matroid. We have also presented the idea of mF circuit, closure of mF matroid and put special emphasis on mF rank function. The paper is concluded with some real life applications of mF matroids in decision support system, ordering of machines to perform specific tasks and detection of minimum number of locations in wireless network in order to motivate the idea presented in this research paper. We are extending our work to (1) decision support systems based on intuitionistic fuzzy soft circuits, (2) fuzzy rough soft circuits, (3) and neutrosophic soft circuits.