Analyzing Spatial Behavior of Backcountry Skiers in Mountain Protected Areas Combining GPS Tracking and Graph Theory
Abstract
:1. Introduction
2. Materials and Methods
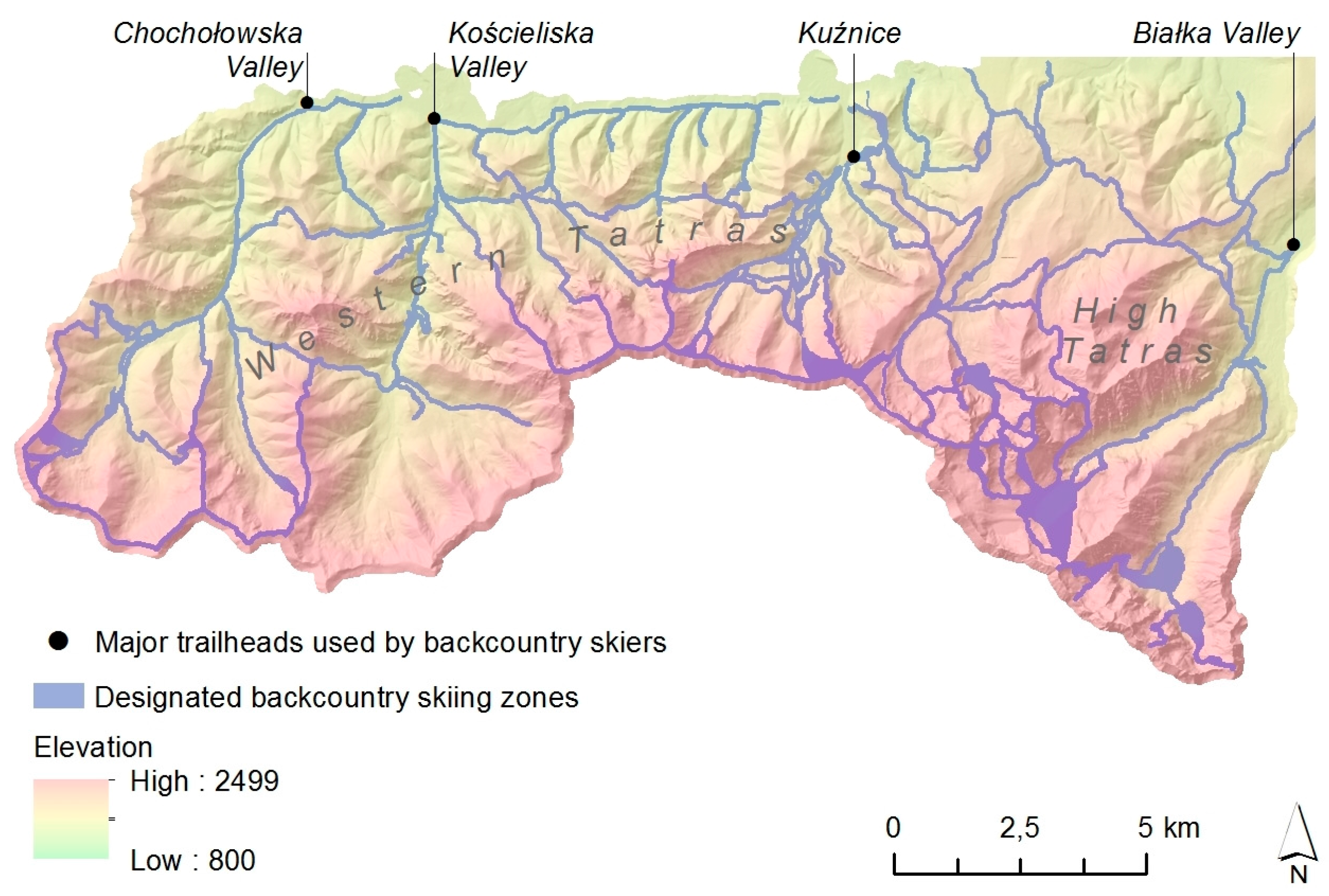
2.1. Study Area
2.2. Data
2.2.1. Inventory of Skiing Zones System
2.2.2. Mobility Data of Backcountry Skiers
2.3. Data Analysis
- GPS data pre-processing
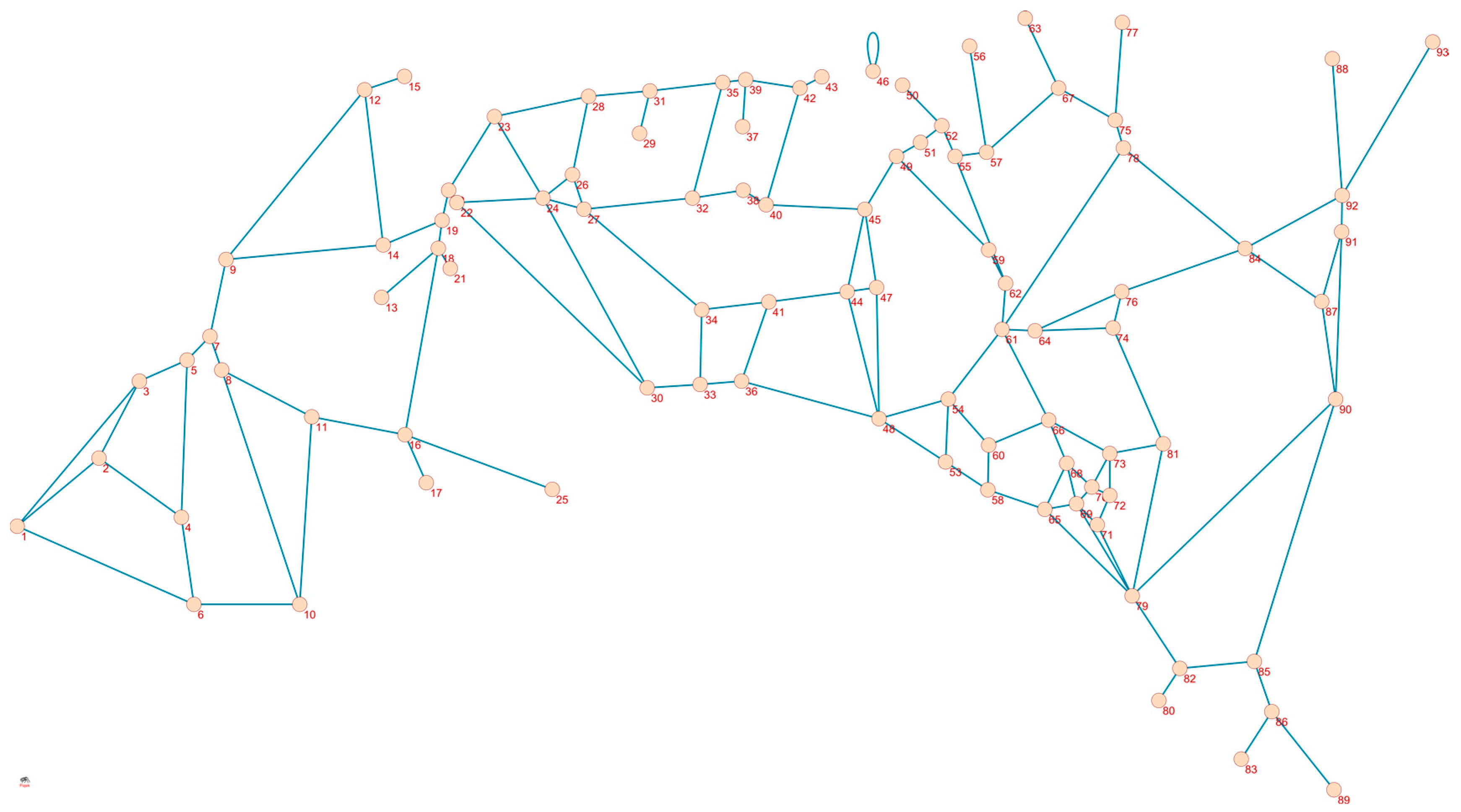
- Creation of the structural network (undirected graph)
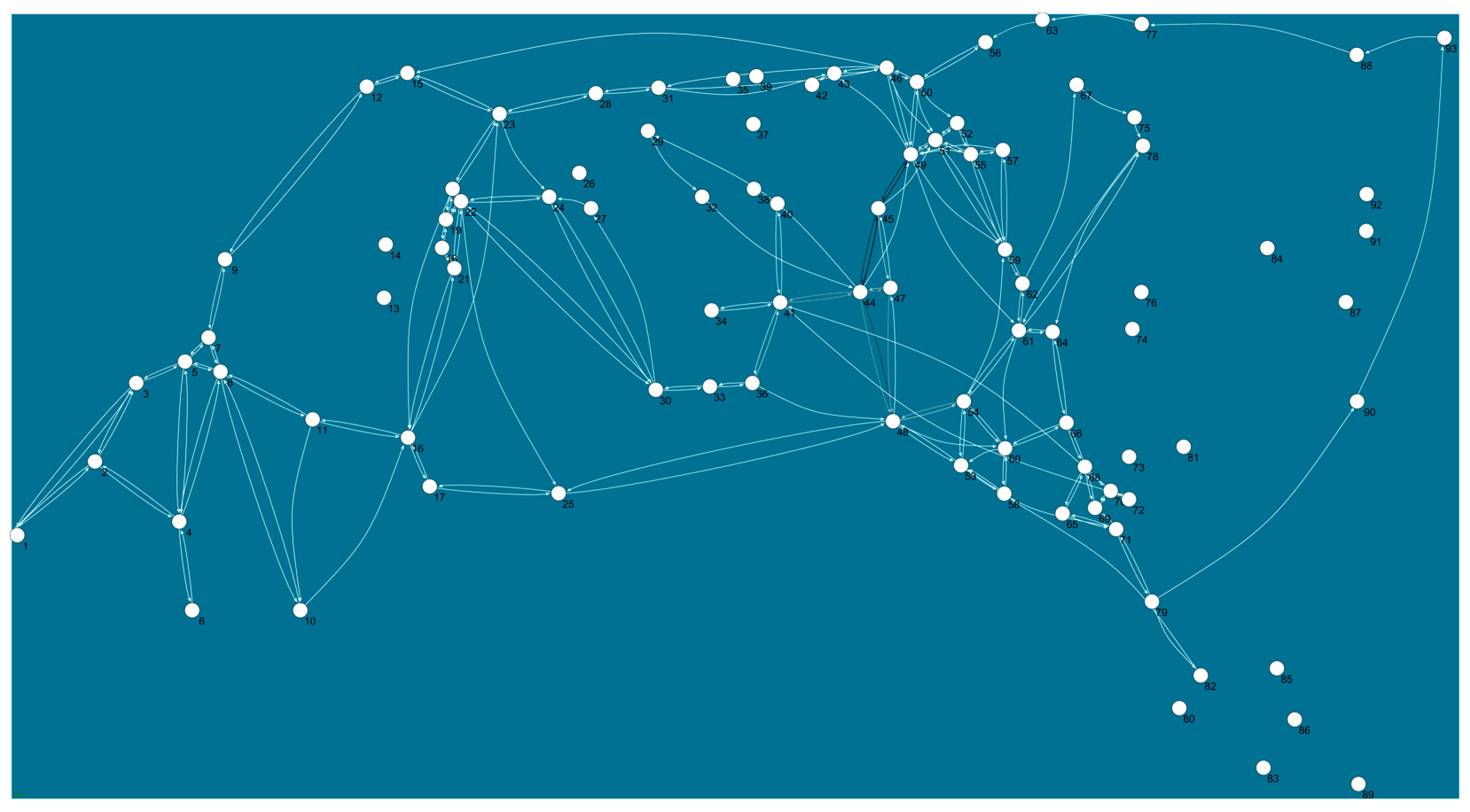
- Creation of the functional network (directed graph)
- Quantification of network connectivity indices
- Calculation of centrality measures of network nodes.
2.3.1. Pre-Processing of GPS Data
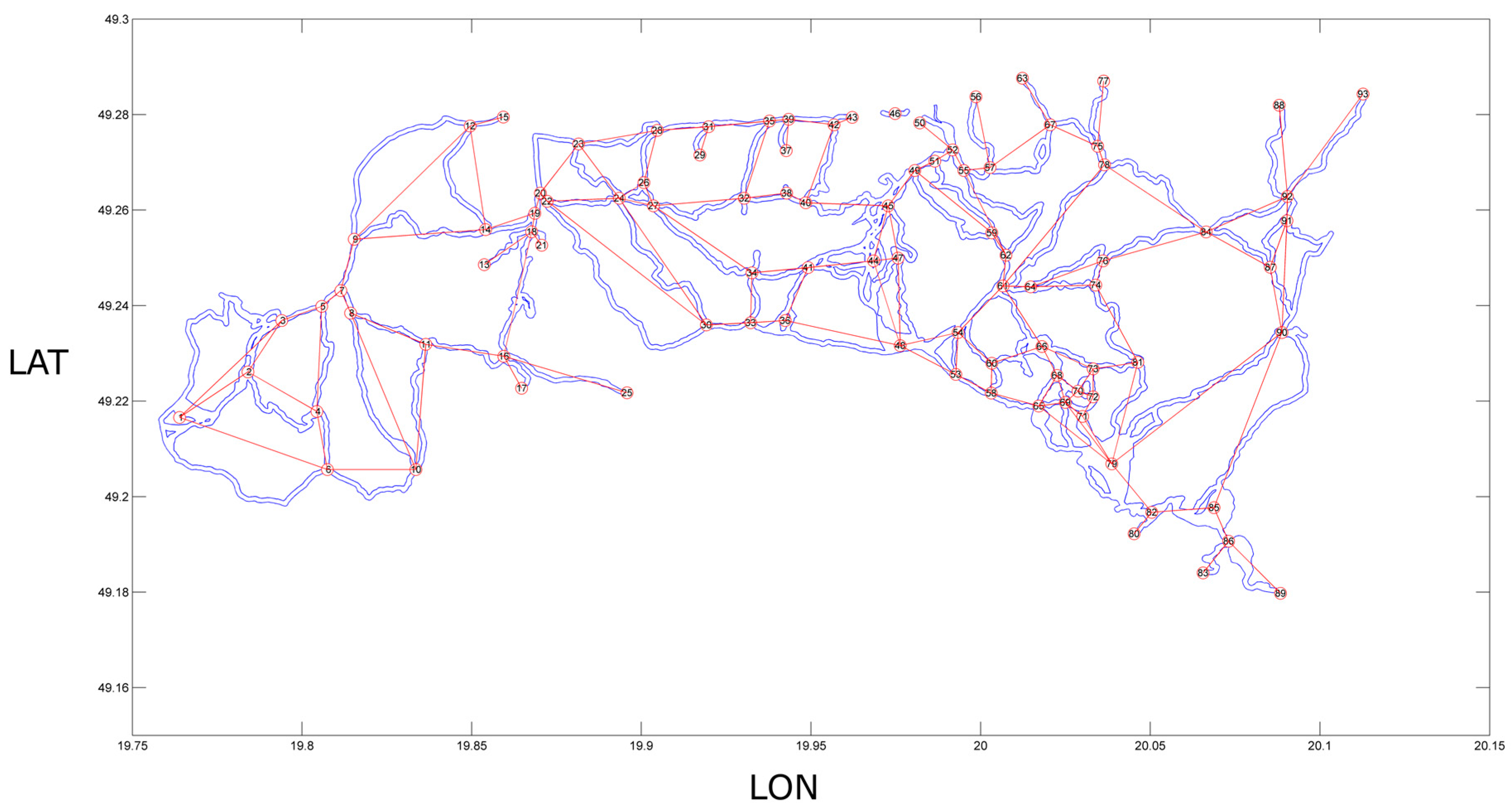
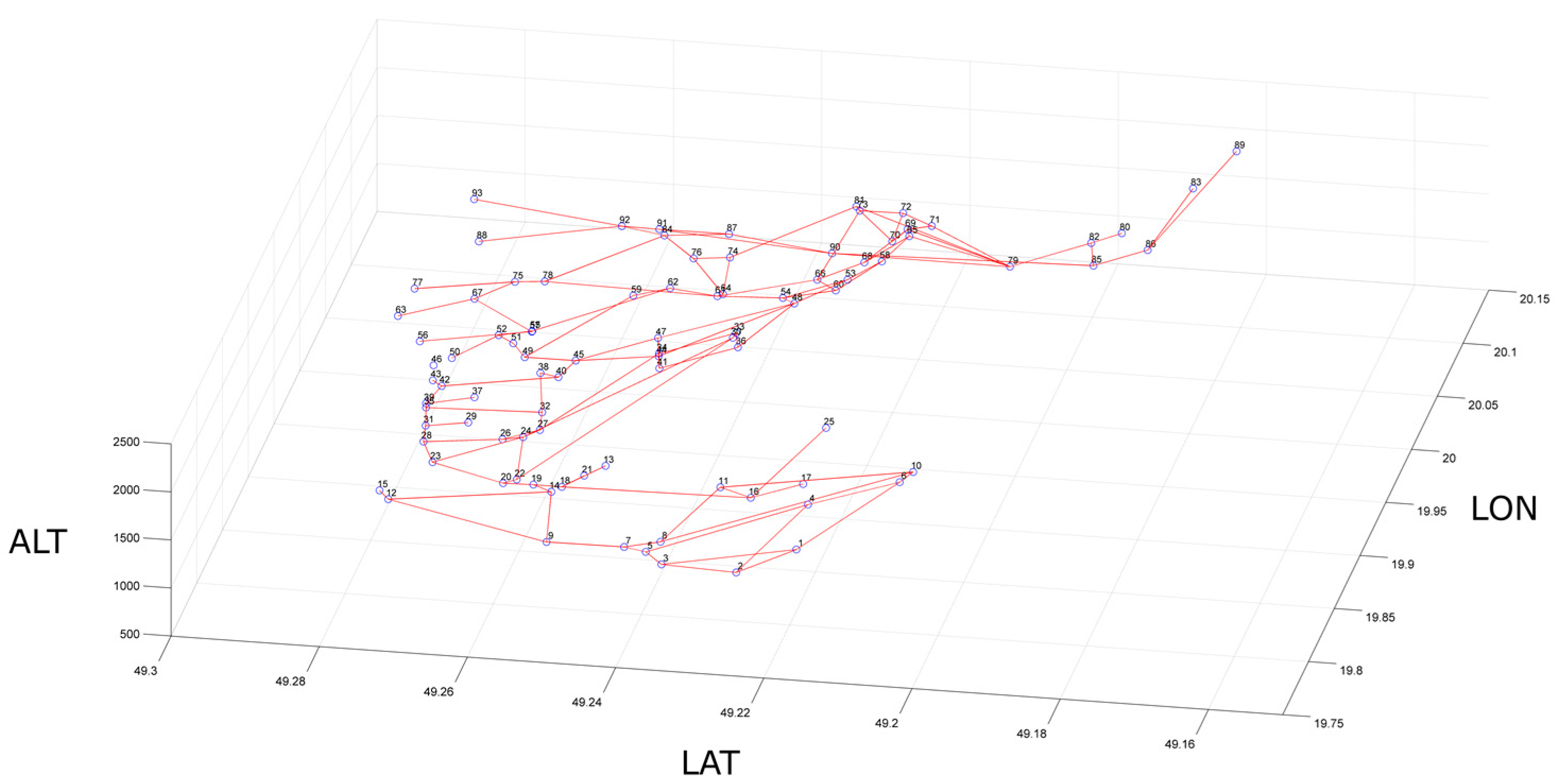
2.3.2. Creating the Structural Network
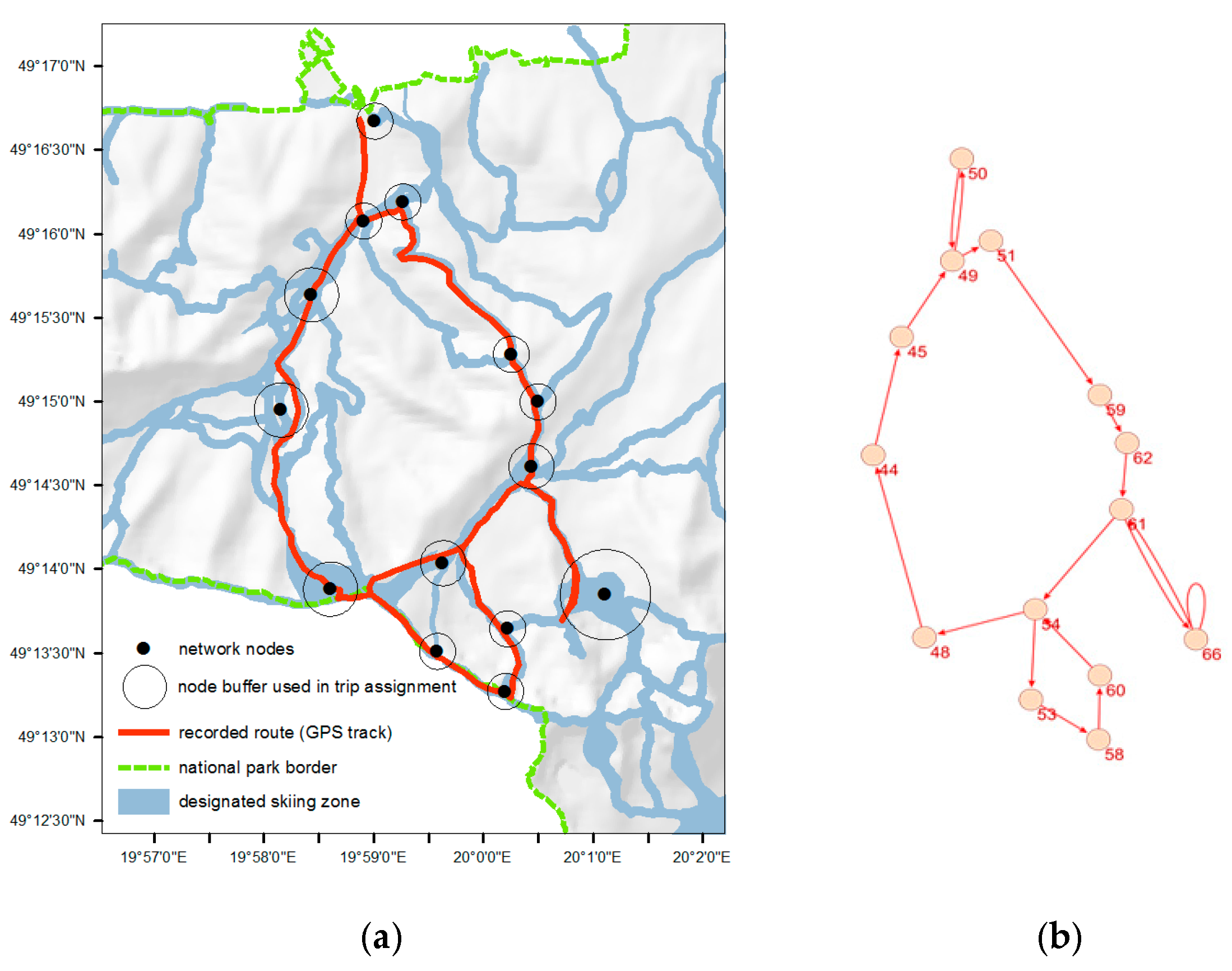
2.3.3. Creating the Functional Network
2.3.4. Calculating Network Connectivity Indices
- Kansky index where is the number of edges, is the number of vertices (the higher the value of , the more coherent the network);
- Kansky index , defining the ratio of the existing number of edges (e) to the maximum possible number of edges resulting from the number of vertices (v). The value ranges from 0 to 1, where the value of 1 indicates a completely connected network.
- Kansky index , where is a cyclomatic measure calculated as , where p is the number of isolated subgraphs. An value of 1 indicates a completely meshed network, and 0 indicates a very simple network.
2.3.5. Calculating Node Centrality Measures
3. Results
3.1. General Characteristics of the Structural and Functional Networks
3.2. Network Coherence (Connectivity Indices)
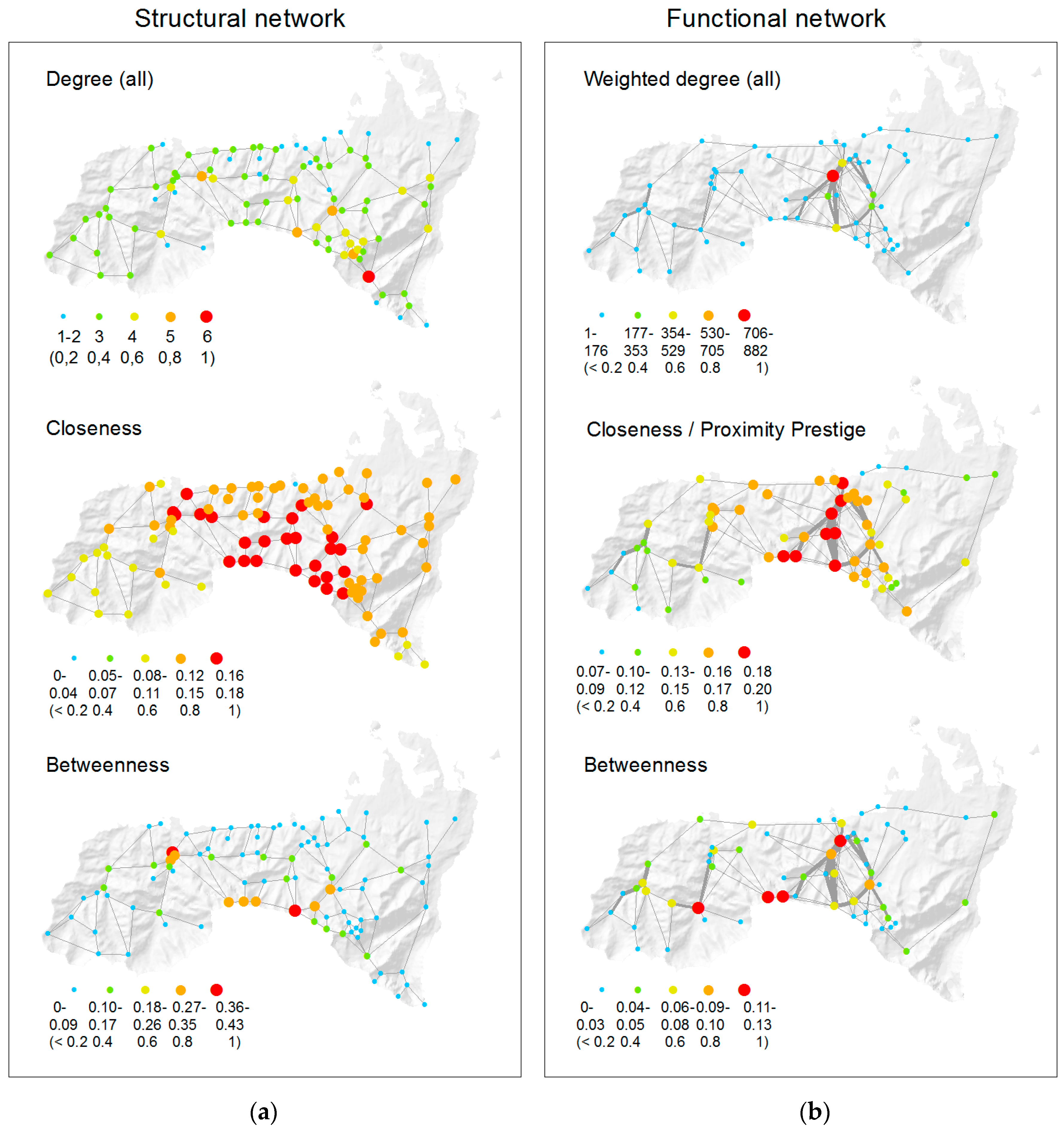
3.3. Relative Importance of Network Nodes (Centrality Measures)
4. Discussion and Conclusions
4.1. General Meaning of the Findings
4.2. Comparison of the Structural and Functional Networks in the Study Area
4.3. Limitations of the Proposed Methodology
4.4. Meaning of the Findings for Visitor Management in Protected Areas
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IUCN. Red List of Ecosystems. Available online: https://www.iucn.org/about/union/commissions/cem/cem_work/tg_red_list/ (accessed on 28 November 2017).
- Dudley, N. Guidelines for Applying Protected Area Management Categories; International Union for Conservation of Nature (IUCN): Gland, Switzerland, 2013. [Google Scholar]
- Newsome, D.; Moore, S.A.; Dowling, R.K. Natural Area Tourism: Ecology, Impacts and Management, 2nd ed.; Newsome, D., Moore, S.A., Dowling, R.K., Eds.; Channel View Publications: Bristol, UK; Tonawnda, NY, USA; North York, ON, Canada, 2012; ISBN 978-1-84541-381-1. [Google Scholar]
- Bell, S. Design for Outdoor Recreation; Taylor & Francis: Abingdon, UK, 2008; ISBN 978-1-134-10804-6. [Google Scholar]
- Cole, D.N.; Daniel, T.C. The science of visitor management in parks and protected areas: From verbal reports to simulation models. J. Nat. Conserv. 2003, 11, 269–277. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Pósfai, M. Network Science; Cambridge University Press: Cambridge, UK, 2016; ISBN 978-1-107-07626-6. [Google Scholar]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010; ISBN 978-0-19-920665-0. [Google Scholar]
- Scott, N.; Baggio, R.; Cooper, C. Network Analysis and Tourism: From Theory to Practice; Channel View Publications: Clevedon, UK; Buffalo, NY, USA, 2008; ISBN 978-1-84541-087-2. [Google Scholar]
- Baggio, R. Network science and tourism—The state of the art. Tour. Rev. 2017, 72, 120–131. [Google Scholar] [CrossRef]
- Rodrigue, J.-P.; Comtois, C.; Slack, B. The Geography of Transport Systems, 3rd ed.; Routledge: New York, NY, USA, 2013; ISBN 978-0-415-82254-1. [Google Scholar]
- Cessford, G.; Muhar, A. Monitoring options for visitor numbers in national parks and natural areas. J. Nat. Conserv. 2003, 11, 240–250. [Google Scholar] [CrossRef]
- D’Agata, R.; Gozzo, S.; Tomaselli, V. Network analysis approach to map tourism mobility. Qual. Quant. 2013, 47, 3167–3184. [Google Scholar] [CrossRef]
- Stimson, R. (Ed.) Handbook of Research Methods and Applications in Spatially Integrated Social Science; Edward Elgar Publishing: Cheltenham, UK, 2014; ISBN 978-0-85793-297-6. [Google Scholar]
- Arnberger, A.; Hinterberger, B. Visitor monitoring methods for managing public use pressures in the Danube Floodplains National Park, Austria. J. Nat. Conserv. 2003, 11, 260–267. [Google Scholar] [CrossRef]
- Shoval, N.; Isaacson, M. Tracking tourists in the digital age. Ann. Tour. Res. 2007, 34, 141–159. [Google Scholar] [CrossRef]
- Thimm, T.; Seepold, R. Past, present and future of tourist tracking. J. Tour. Future 2016, 2, 43–55. [Google Scholar] [CrossRef]
- Beeco, J.A.; Hallo, J.C.; Brownlee, M.T.J. GPS Visitor Tracking and Recreation Suitability Mapping: Tools for understanding and managing visitor use. Landsc. Urban Plan. 2014, 127, 136–145. [Google Scholar] [CrossRef]
- Meijles, E.W.; de Bakker, M.; Groote, P.D.; Barske, R. Analysing hiker movement patterns using GPS data: Implications for park management. Comput. Environ. Urban Syst. 2014, 47, 44–57. [Google Scholar] [CrossRef]
- D’Antonio, A.; Monz, C. The influence of visitor use levels on visitor spatial behavior in off-trail areas of dispersed recreation use. J. Environ. Manag. 2016, 170, 79–87. [Google Scholar] [CrossRef] [PubMed]
- Rupf, R.; Wyttenbach, M.; Köchli, D.; Hediger, M.; Lauber, S.; Ochsner, P.; Graf, R. Assessing the spatio-temporal pattern of winter sports activities to minimize disturbance in capercaillie habitats. J. Prot. Mt. Areas Res. 2011, 3, 23–32. [Google Scholar] [CrossRef]
- Orellana, D.; Wachowicz, M. Exploring patterns of movement suspension in pedestrian mobility. Geogr. Anal. 2011, 43, 241–260. [Google Scholar] [CrossRef] [PubMed]
- Beeco, J.A.; Brown, G. Integrating space, spatial tools, and spatial analysis into the human dimensions of parks and outdoor recreation. Appl. Geogr. 2013, 38, 76–85. [Google Scholar] [CrossRef]
- Taczanowska, K.; Muhar, A.; Brandenburg, C. Potential and limitations of GPS tracking for monitoring spatial and temporal aspects of visitor behaviour in recreational areas. In Proceedings of the Fourth International Conference on Monitoring and Management of Visitor Flows in Recreational and Protected Areas, Montecatini Terme, Italy, 14–19 October 2008; Raschi, A., Trampetti, S., Eds.; CNR-Ibimet: Firenze, Italy, 2008; pp. 451–456. [Google Scholar]
- TNP—Tatra National Park Tatra National Park. Available online: http://tpn.pl/poznaj (accessed on 1 November 2017 ).
- Bielański, M. Skitouring in Tatra National Park and Its Environmental Impacts. Ph.D. Thesis, University School of Physical Education, Cracow, Poland, 2013. [Google Scholar]
- TNP—Tatra National Park Decree Nr 3/2017 of the Tatra National Park Director from 23.02.2017 on Hiking, Bicycling and Skiing in the Area of the Tatra National Park. (Zarzadzenie nr 3/2017 Dyrektora Tatrzanskiego Parku Narodowego z dnia 23 lutego 2017 roku w sprawie ruchu pieszego, rowerowego oraz uprawiania narciarstwa na terenie Tatrzanskiego Parku Narodowego) 2017.
- Adamski, P.; Bielański, M. Analiza Danych Dotyczących Ruchu Wejściowego Narciarzy Skiturowych w Tatrzańskim Parku Narodowym, w Sezonach Zimowych 2013 Oraz 2013/2014 (Report); Tatra National Park: Zakopane, Poland, 2014; p. 23. [Google Scholar]
- MATLAB; Mathworks Inc.: Natick, MA, USA, 2012.
- Mrvar, A.; Batagelj, V. Analysis and visualization of large networks with program package Pajek. Complex Adapt. Syst. Model. 2016, 4, 6. [Google Scholar] [CrossRef]
- United States Geological Survey. United States Geological Survey SRTM Elevation Data 2017; United States Geological Survey: Reston, VA, USA.
- Batagelj, V.; Mrvar, A. Pajek—Analysis and Visualization of Large Networks. In Graph Drawing Software; Jünger, M., Ed.; Springer: Berlin, Germany, 2003; pp. 77–103. [Google Scholar]
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994; ISBN 978-1-139-78861-8. [Google Scholar]
- Taaffe, E.J.; Gauthier, H.L. Geography of Transportation; Prentice-Hall foundations of economic geography series; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973; ISBN 0133513955. [Google Scholar]
- Olliff, T.; Legg, K.; Kaeding, B. Effects of Winter Recreation on Wildlife of the Greater Yellowstone Area: A Literature Review and Assessment; Report to the Greater Yellowstone Coordinating Committee; National Park Service: Yellowstone National Park, WY, USA, 1999; p. 315.
- Andrienko, N.; Andrienko, G. Visual analytics of movement: An overview of methods, tools and procedures. Inf. Vis. 2013, 12, 3–24. [Google Scholar] [CrossRef]
- Andrienko, N.; Andrienko, G. V-Analytics. Available online: http://geoanalytics.net/V-Analytics/ (accessed on 9 December 2017).
- Burian, J.; Zajickova, L.; Popelka, S.; Rypka, M. Spatial Aspects of Movement of Olomuc and Ostrava Citizens. In SGEM2016 Conference Proceedings; 2016; Volume III, pp. 439–446. [Google Scholar]
- Fischer, M. GIS and Network Analysis. In Spatial Analysis and GeoComputation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 43–60. ISBN 978-3-540-35729-2. [Google Scholar]
- Taczanowska, K.; González, L.-M.; Garcia-Massó, X.; Muhar, A.; Brandenburg, C.; Toca-Herrera, J.-L. Evaluating the structure and use of hiking trails in recreational areas using a mixed GPS tracking and graph theory approach. Appl. Geogr. 2014, 55, 184–192. [Google Scholar] [CrossRef]
- Kolodziejczyk, K. Hiking Trails for Tourists in the “Chelmy” Landscape Park—Assessment of Their Route and Infrastructure Development. Pol. J. Sport Tour. 2011, 18, 324–329. [Google Scholar] [CrossRef]
- Styperek, J. Tourist hiking trails in Polish National Parks. Turyzm 2001, 11, 25–37. (In Polish) [Google Scholar]
- Li, W.; Ge, X.; Liu, C. Hiking trails and tourism impact assessment in protected area: Jiuzhaigou Biosphere Reserve, China. Environ. Monit. Assess. 2005, 108, 279–293. [Google Scholar] [CrossRef] [PubMed]
- Derezińska, M. Pochwala skialpinizmu, czyli o filozofii zacisnietych zebow. In Tatry; Tatra National Park: Zakopane, Poland, 2007; p. 30. (In Polish) [Google Scholar]
- Sejm of the Republic of Poland. Nature Conservation Act (Ustawa z dnia 16 Kwietnia 2004 r. o Ochronie Przyrody); Sejm of the Republic of Poland: Warsaw, Poland, 2004.
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Collins, J. Global Positioning System—Theory and Practice; Springer: New York, NY, USA, 2001; ISBN 978-3-7091-6199-9. [Google Scholar]
- Shoval, N. Tracking technologies and urban analysis. Cities 2008, 25, 21–28. [Google Scholar] [CrossRef]
- Korpilo, S.; Virtanen, T.; Lehvävirta, S. Smartphone GPS tracking—Inexpensive and efficient data collection on recreational movement. Landsc. Urban Plan. 2017, 157, 608–617. [Google Scholar] [CrossRef]
- Luke, D.A. A User’s Guide to Network Analysis in R, 1st ed.; Springer: New York, NY, USA, 2016; ISBN 978-3-319-23882-1. [Google Scholar]
- Fall, A.; Fortin, M.-J.; Manseau, M.; O’Brien, D. Spatial graphs: Principles and applications for habitat connectivity. Ecosystems 2007, 10, 448–461. [Google Scholar] [CrossRef]
- Sterl, P.; Eder, R.; Arnberger, A. Exploring factors in influencing the attitude of on-site ski mountaineers towards the ski touring management measures of the Gesäuse National Park. J. Prot. Mt. Areas Res. 2006, 2/1, 31–38. [Google Scholar] [CrossRef]
- Zeidenitz, C.; Mosier, H.J.; Hunziker, M. Outdoor recreation: From analysing motivations to furthering ecologically responsible behaviour. For. Snow Landsc. Res. 2007, 81, 175–190. [Google Scholar]
| Centrality Measure | Description | Mathematical Equation |
|---|---|---|
| Input degree | Number of edges entering to vertex i. | signal the position between node i and node j. |
| Output degree | Number of edges leaving vertex i. | |
| Degree (all) | Total number of edges connected to the vertex i. | |
| Closeness | Inverse sum of distances from a given vertex to all other vertices in the graph. | where is a topological distance between vertices |
| Betweenness | A number of times a vertex is crossed by shortest paths in the graph. | where is the number of geodesics connecting jk, and is the number that geodesics i is on. |
| Proximity prestige | Expresses the influence domain of a vertex by the average distance from all vertices in the influence domain. Pp value of 0 indicates that node i is unreachable; whereas Pp = 1 if all nodes are directly connected to node i. |
| Node Number | Degree | Closeness | Betweenness |
|---|---|---|---|
| 79 | 6 | 0.14 | 0.14 |
| 24 | 5 | 0.15 | 0.08 |
| 48 | 5 | 0.18 | 0.43 |
| 61 | 5 | 0.17 | 0.30 |
| 69 | 5 | 0.14 | 0.02 |
| 16 | 4 | 0.11 | 0.12 |
| 18 | 4 | 0.12 | 0.17 |
| 27 | 4 | 0.15 | 0.09 |
| 44 | 4 | 0.17 | 0.09 |
| 45 | 4 | 0.15 | 0.14 |
| Node Number | Weighted Input Degree | Weighted Output Degree | Weighted All Degree | Closeness | Betweenness | Proximity Prestige |
|---|---|---|---|---|---|---|
| 45 | 350 | 532 | 882 | 0.19 | 0.08 | 0.19 |
| 49 | 351 | 149 | 500 | 0.20 | 0.13 | 0.20 |
| 48 | 197 | 194 | 391 | 0.19 | 0.06 | 0.19 |
| 44 | 152 | 149 | 301 | 0.18 | 0.01 | 0.17 |
| 61 | 109 | 90 | 199 | 0.17 | 0.10 | 0.17 |
| 62 | 93 | 100 | 193 | 0.15 | 0.05 | 0.15 |
| 41 | 86 | 84 | 170 | 0.17 | 0.04 | 0.17 |
| 54 | 82 | 88 | 170 | 0.17 | 0.06 | 0.17 |
| 7 | 79 | 78 | 157 | 0.12 | 0.07 | 0.12 |
| 51 | 56 | 83 | 139 | 0.17 | 0.02 | 0.17 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taczanowska, K.; Bielański, M.; González, L.-M.; Garcia-Massó, X.; Toca-Herrera, J.L. Analyzing Spatial Behavior of Backcountry Skiers in Mountain Protected Areas Combining GPS Tracking and Graph Theory. Symmetry 2017, 9, 317. https://doi.org/10.3390/sym9120317
Taczanowska K, Bielański M, González L-M, Garcia-Massó X, Toca-Herrera JL. Analyzing Spatial Behavior of Backcountry Skiers in Mountain Protected Areas Combining GPS Tracking and Graph Theory. Symmetry. 2017; 9(12):317. https://doi.org/10.3390/sym9120317
Chicago/Turabian StyleTaczanowska, Karolina, Mikołaj Bielański, Luis-Millán González, Xavier Garcia-Massó, and José L. Toca-Herrera. 2017. "Analyzing Spatial Behavior of Backcountry Skiers in Mountain Protected Areas Combining GPS Tracking and Graph Theory" Symmetry 9, no. 12: 317. https://doi.org/10.3390/sym9120317
APA StyleTaczanowska, K., Bielański, M., González, L.-M., Garcia-Massó, X., & Toca-Herrera, J. L. (2017). Analyzing Spatial Behavior of Backcountry Skiers in Mountain Protected Areas Combining GPS Tracking and Graph Theory. Symmetry, 9(12), 317. https://doi.org/10.3390/sym9120317







