Reconstructing Damaged Complex Networks Based on Neural Networks
Abstract
:1. Introduction
2. Model
2.1. Small-World Network
2.2. Scale-Free Network
2.3. Network Damage Model
3. Reconstruction Method
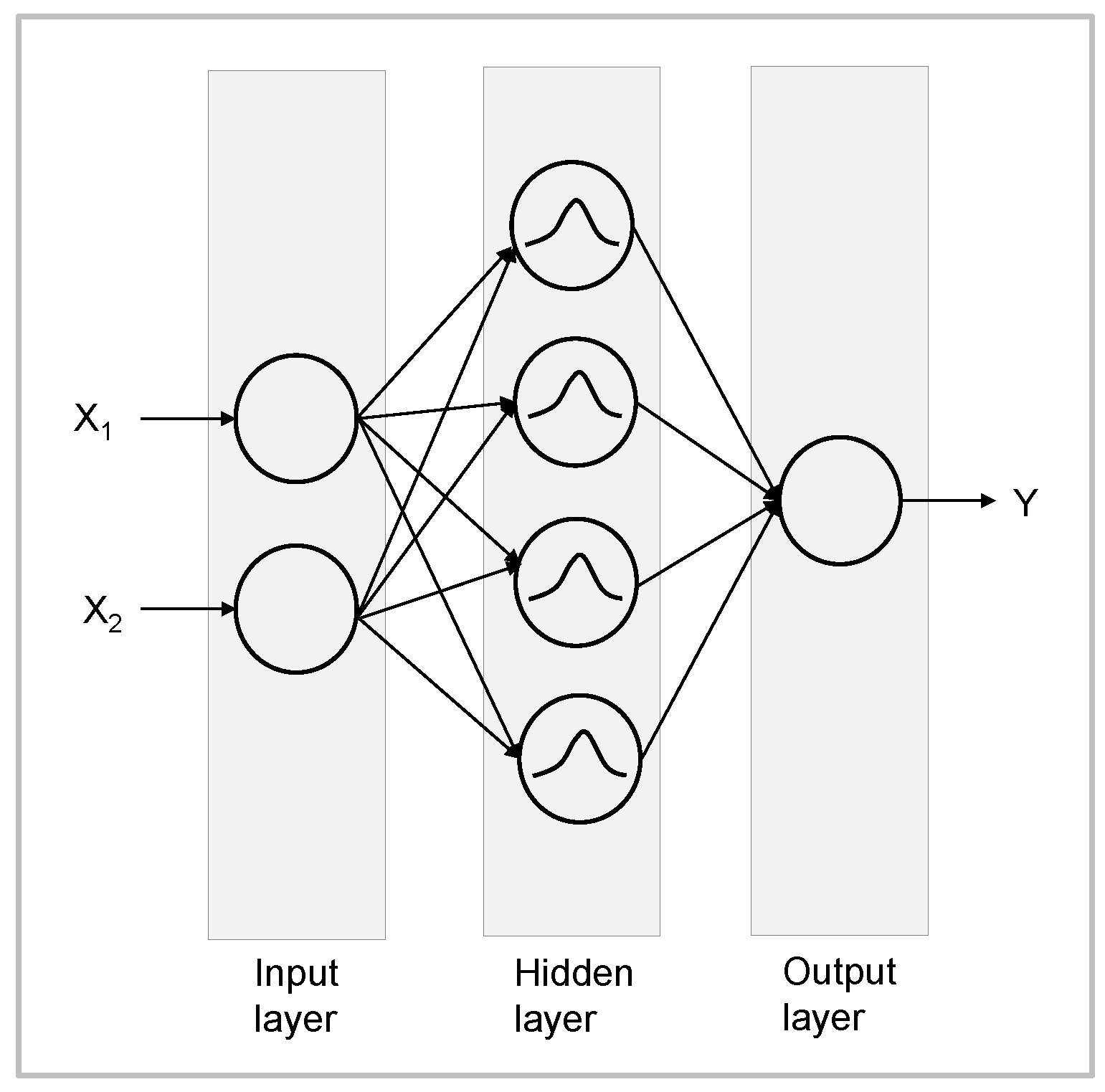
3.1. Neural Network Model
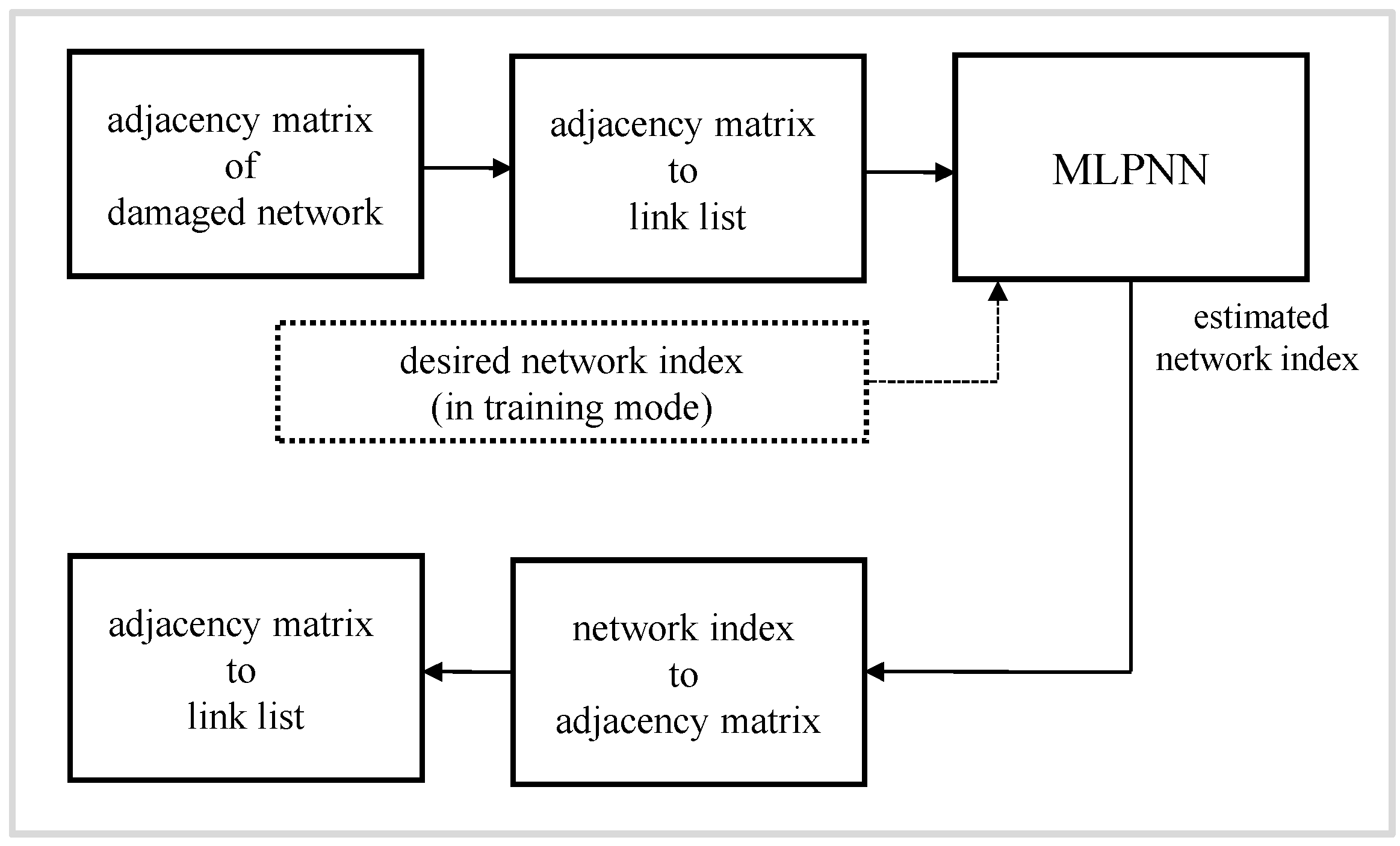
3.2. Neural Network Based Method
4. Performance Evaluations
4.1. Simulation Environment
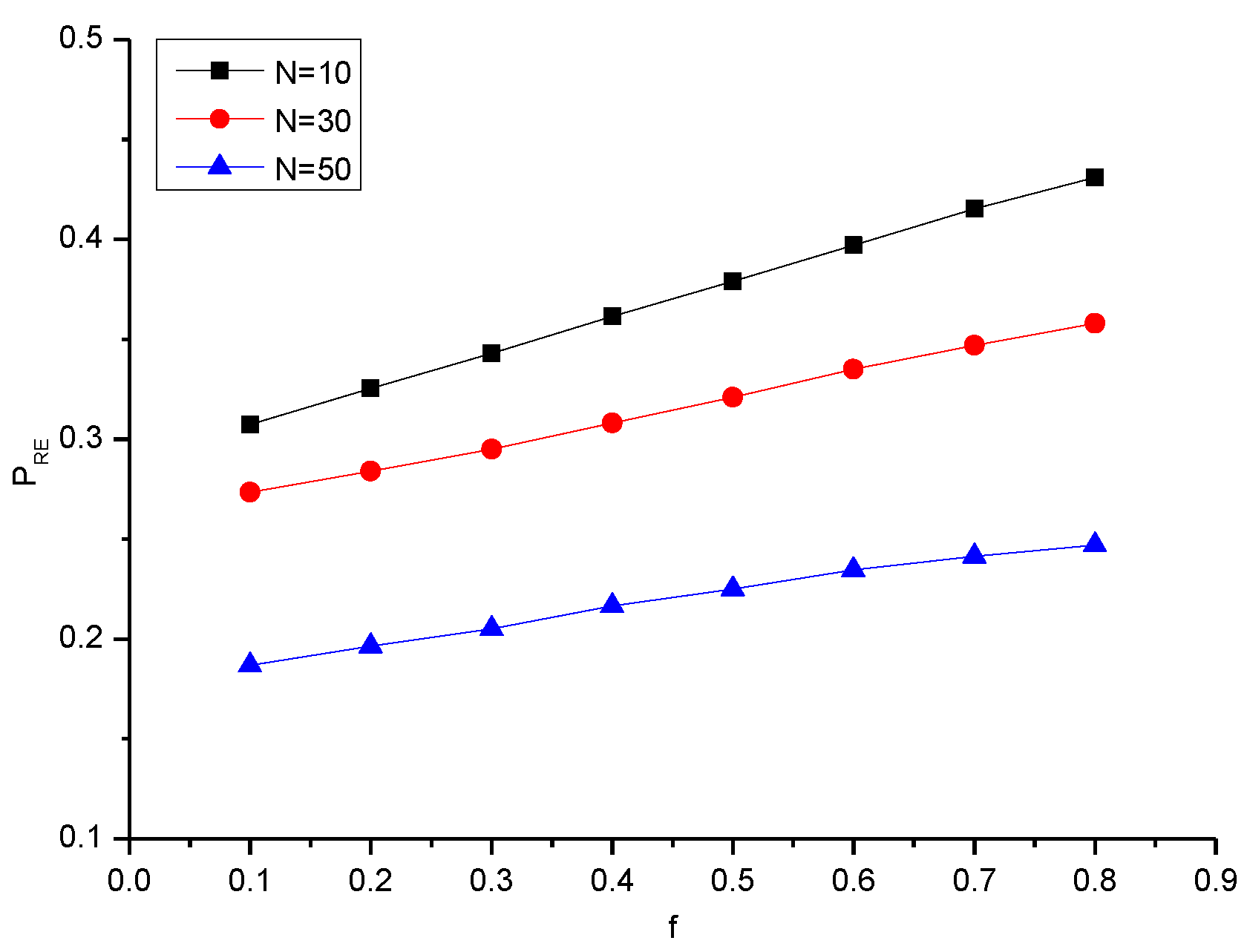
4.2. Small-World Network
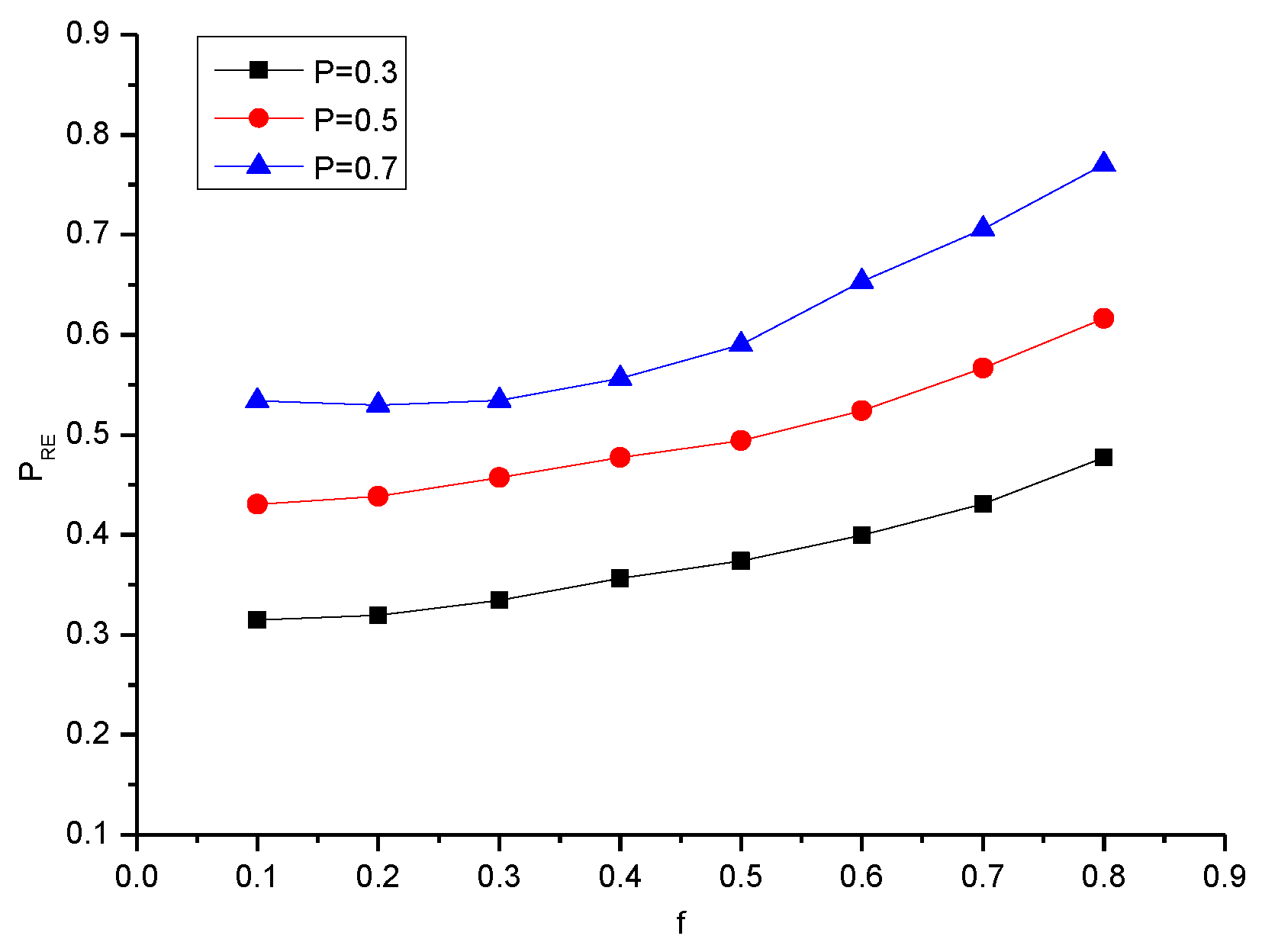
4.3. Scale-Free Network
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, X.F.; Chen, G. Complex networks: Small-world, scale-free and beyond. IEEE Circuits Syst. Mag. 2003, 3, 6–20. [Google Scholar] [CrossRef]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Sohn, I. Small-world and scale-free network models for IoT systems. Mob. Inf. Syst. 2017, 2017. [Google Scholar] [CrossRef]
- Barabási, A.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Albert, R.; Barabási, A. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Barabási, A.L. Scale-free networks: A decade and beyond. Science 2009, 325, 412–413. [Google Scholar] [CrossRef] [PubMed]
- Crucitti, P.; Latora, V.; Marchiori, M.; Rapisarda, A. Error and attack tolerance of complex networks. Phys. A Stat. Mech. Appl. 2004, 340, 388–394. [Google Scholar] [CrossRef]
- Tanizawa, T.; Paul, G.; Cohen, R.; Havlin, S.; Stanley, H.E. Optimization of network robustness to waves of targeted and random attacks. Phys. Rev. E 2005, 71, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.M.; Moreira, A.A.; Andrade, J.S.; Havlin, S.; Herrmann, H.J. Mitigation of malicious attacks on networks. Proc. Natl. Acad. Sci. USA 2011, 108, 3838–3841. [Google Scholar] [CrossRef] [PubMed]
- Ash, J.; Newth, D. Optimizing complex networks for resilience against cascading failure. Phys. A Stat. Mech. Appl. 2007, 380, 673–683. [Google Scholar] [CrossRef]
- Clauset, A.; Moore, C.; Newman, M.E.J. Hierarchical structure and the prediction of missing links in networks. Nature 2008, 453, 98–101. [Google Scholar] [CrossRef] [PubMed]
- Guimerà, R.; Sales-Pardo, M. Missing and spurious interactions and the reconstruction of complex networks. Proc. Natl. Acad. Sci. USA 2010, 106, 22073–22078. [Google Scholar] [CrossRef] [PubMed]
- Zeng, A. Inferring network topology via the propagation process. J. Stat. Mech. Theory Exp. 2013. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Macmillan: Basingstoke, UK, 1994. [Google Scholar]
- Zhang, M.; Diao, M.; Gao, L.; Liu, L. Neural networks for radar waveform recognition. Symmetry 2017, 9. [Google Scholar] [CrossRef]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.H.; Kung, S.Y.; Lin, L.J. Face recognition/detection by probabilistic decision-based neural network. IEEE Trans. Neural Netw. 1997, 8, 114–132. [Google Scholar] [PubMed]
- Fang, S.H.; Lin, T.N. Indoor location system based on discriminant-adaptive neural network in IEEE 802.11 environments. IEEE Trans. Neural Netw. 2008, 19, 1973–1978. [Google Scholar] [CrossRef] [PubMed]
- Sohn, I. Indoor localization based on multiple neural networks. J. Inst. Control Robot. Syst. 2015, 21, 378–384. [Google Scholar] [CrossRef]
- Sohn, I. A low complexity PAPR reduction scheme for OFDM systems via neural networks. IEEE Commun. Lett. 2014, 18, 225–228. [Google Scholar] [CrossRef]
- Sohn, I.; Kim, S.C. Neural network based simplified clipping and filtering technique for PAPR reduction of OFDM signals. IEEE Commun. Lett. 2015, 19, 1438–1441. [Google Scholar] [CrossRef]
- Watts, D.; Strogatz, S. Collective dynamics of ‘small-world’ network. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Kleinberg, J.M. Navigation in a small world. Nature 2000, 406, 845. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Models of the small world. J. Stat. Phys. 2000, 101, 819–841. [Google Scholar] [CrossRef]
- Holme, P.; Kim, B.J.; Yoon, C.N.; Han, S.K. Attack vulnerability of complex networks. Phys. Rev. E 2002, 65, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.; Picton, P. How to train a neural network: An introduction to the new computational paradigm. Complexity 1996, 1, 13–28. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]




| N/f | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|---|---|---|---|
| 10 | 0.307 | 0.325 | 0.343 | 0.361 | 0.379 | 0.397 | 0.415 | 0.431 |
| 30 | 0.273 | 0.284 | 0.295 | 0.308 | 0.321 | 0.335 | 0.347 | 0.358 |
| 50 | 0.186 | 0.196 | 0.205 | 0.216 | 0.225 | 0.234 | 0.241 | 0.246 |
| P/f | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.315 | 0.319 | 0.334 | 0.356 | 0.373 | 0.399 | 0.431 | 0.477 |
| 0.5 | 0.430 | 0.438 | 0.457 | 0.477 | 0.494 | 0.524 | 0.566 | 0.616 |
| 0.7 | 0.534 | 0.529 | 0.534 | 0.556 | 0.590 | 0.653 | 0.705 | 0.770 |
| M/f | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|---|---|---|---|
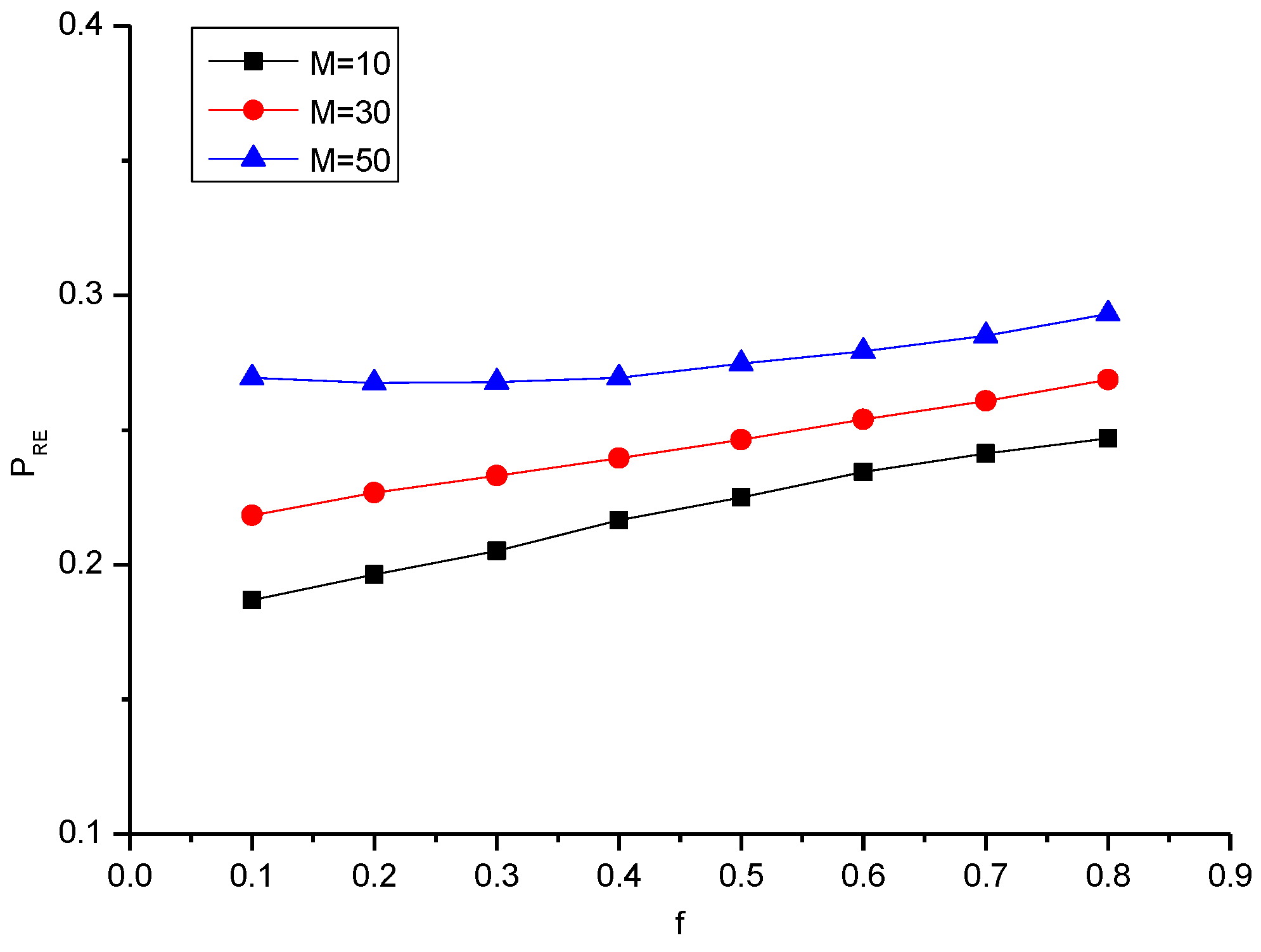
| 10 | 0.186 | 0.196 | 0.205 | 0.216 | 0.225 | 0.234 | 0.241 | 0.246 |
| 30 | 0.218 | 0.226 | 0.233 | 0.239 | 0.246 | 0.253 | 0.260 | 0.268 |
| 50 | 0.26 | 0.267 | 0.267 | 0.269 | 0.274 | 0.279 | 0.285 | 0.293 |
| N/f | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|---|---|---|---|
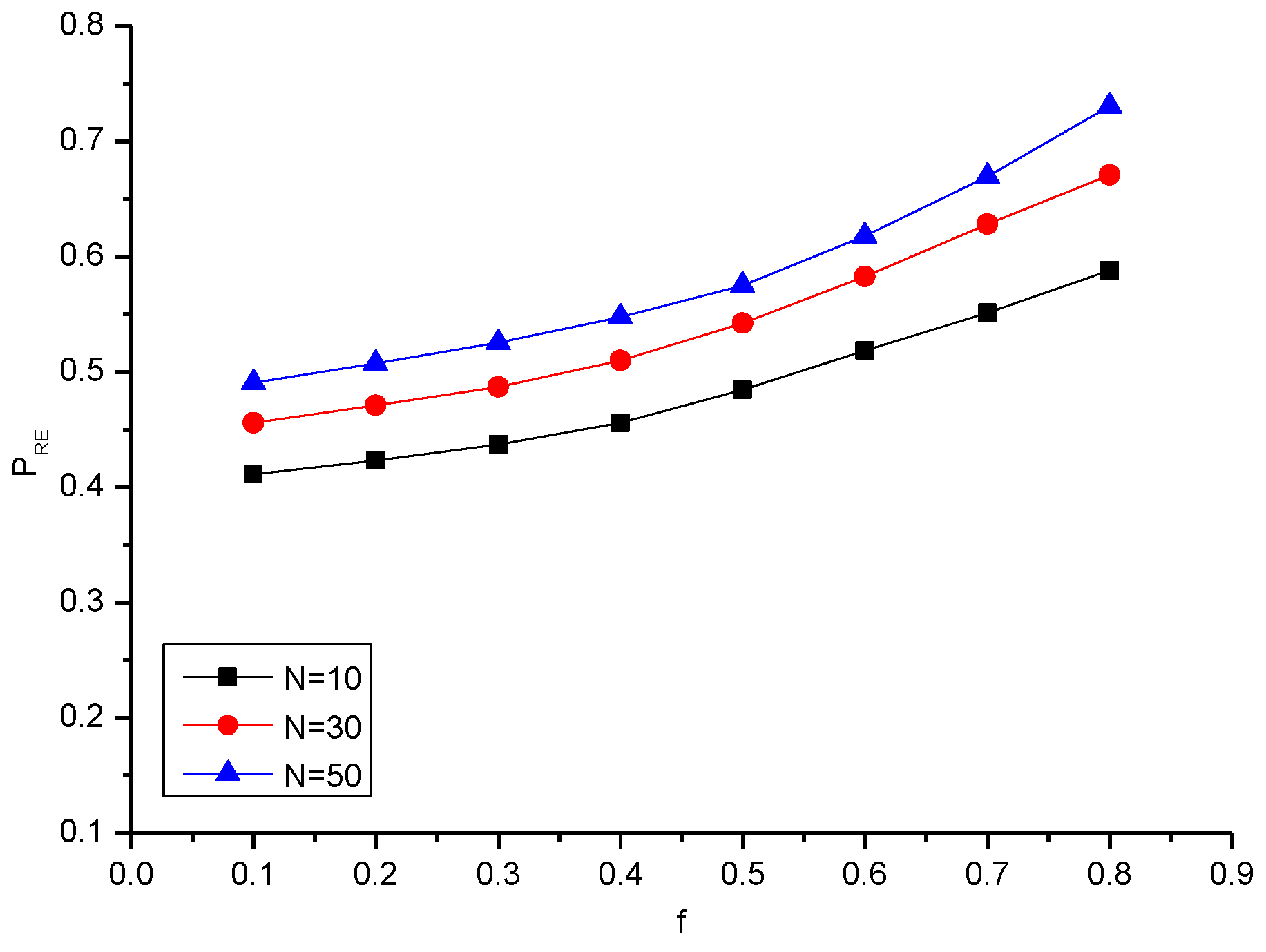
| 10 | 0.411 | 0.423 | 0.437 | 0.455 | 0.484 | 0.518 | 0.551 | 0.588 |
| 30 | 0.455 | 0.471 | 0.487 | 0.510 | 0.542 | 0.582 | 0.628 | 0.671 |
| 50 | 0.490 | 0.507 | 0.525 | 0.547 | 0.575 | 0.618 | 0.669 | 0.730 |
| M/f | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|---|---|---|---|
| 10 | 0.455 | 0.471 | 0.487 | 0.510 | 0.542 | 0.582 | 0.628 | 0.671 |
| 30 | 0.643 | 0.652 | 0.669 | 0.685 | 0.702 | 0.717 | 0.730 | 0.738 |
| 50 | 0.708 | 0.718 | 0.729 | 0.735 | 0.745 | 0.755 | 0.761 | 0.766 |
| mo/f | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|---|---|---|---|
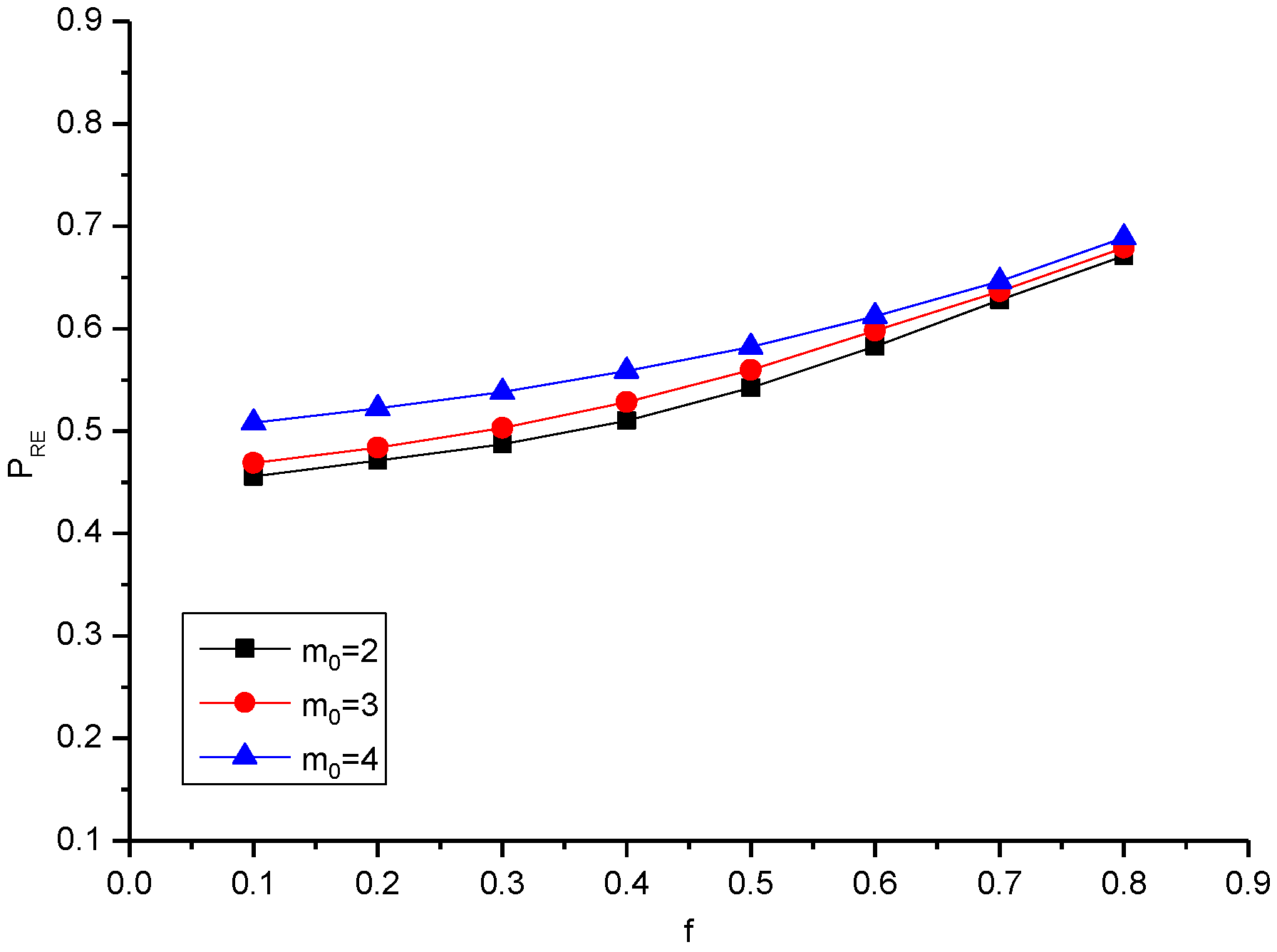
| 2 | 0.455 | 0.471 | 0.487 | 0.510 | 0.542 | 0.582 | 0.628 | 0.671 |
| 3 | 0.468 | 0.483 | 0.503 | 0.528 | 0.559 | 0.597 | 0.636 | 0.679 |
| 4 | 0.508 | 0.522 | 0.530 | 0.558 | 0.582 | 0.612 | 0.646 | 0.689 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.H.; Sohn, I. Reconstructing Damaged Complex Networks Based on Neural Networks. Symmetry 2017, 9, 310. https://doi.org/10.3390/sym9120310
Lee YH, Sohn I. Reconstructing Damaged Complex Networks Based on Neural Networks. Symmetry. 2017; 9(12):310. https://doi.org/10.3390/sym9120310
Chicago/Turabian StyleLee, Ye Hoon, and Insoo Sohn. 2017. "Reconstructing Damaged Complex Networks Based on Neural Networks" Symmetry 9, no. 12: 310. https://doi.org/10.3390/sym9120310
APA StyleLee, Y. H., & Sohn, I. (2017). Reconstructing Damaged Complex Networks Based on Neural Networks. Symmetry, 9(12), 310. https://doi.org/10.3390/sym9120310




