Chaotic Dynamical State Variables Selection Procedure Based Image Encryption Scheme
Abstract
1. Introduction
- Chaotic state variables are generated from four-dimensional chaotic systems; a minor alteration in the secret key will not only influence the diffusion stage, but also manipulate the permutation at the same time.
- In CDSVSP, the pixels of plain images are used to choose the state variable for encryption. Thus, different key streams will be generated for each individual plain image, even if the same secret keys are used. Therefore, by encrypting individual images, the attacker is unable to extract helpful information. This characteristic guarantees the security against the known-plaintext attacks.
- In the permutation stage, the added confusion procedure can also, to some extent, create a diffusion effect. As a result, the whole effect of diffusion is increased.
2. Selection Procedure
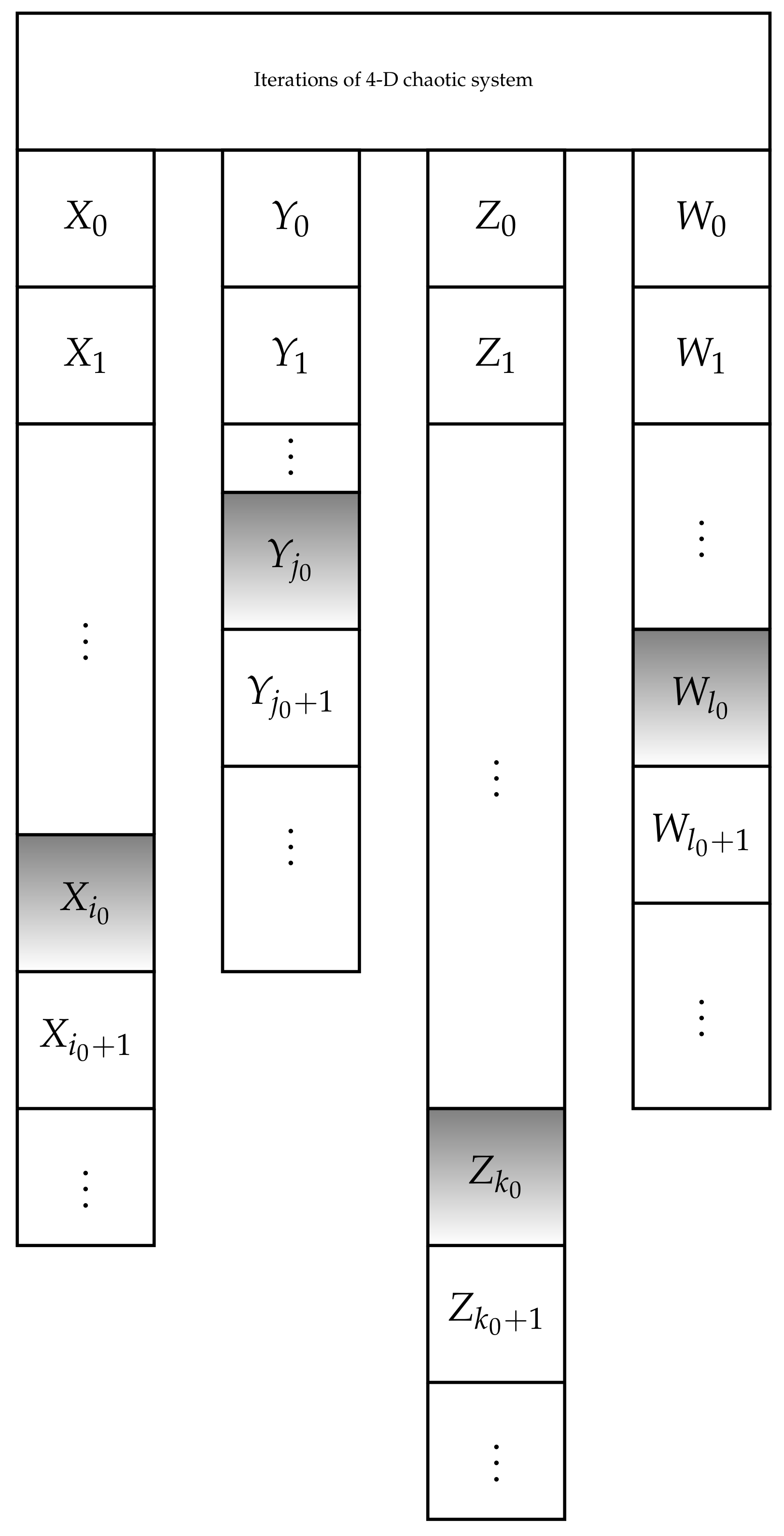
- Let where and are the states of X, Z and W in the i-th, j-th, k-th and l-th iteration, respectively. It should be noted that i, j, k and l do not need to be equal to each other.
- We define as the selected variable in that will be used to generate the key stream element for . The decision will be made by an indicator defined below:where is a tent map and both a and are parts of the secret keys.For the first pixel value, has to be set as a seed.
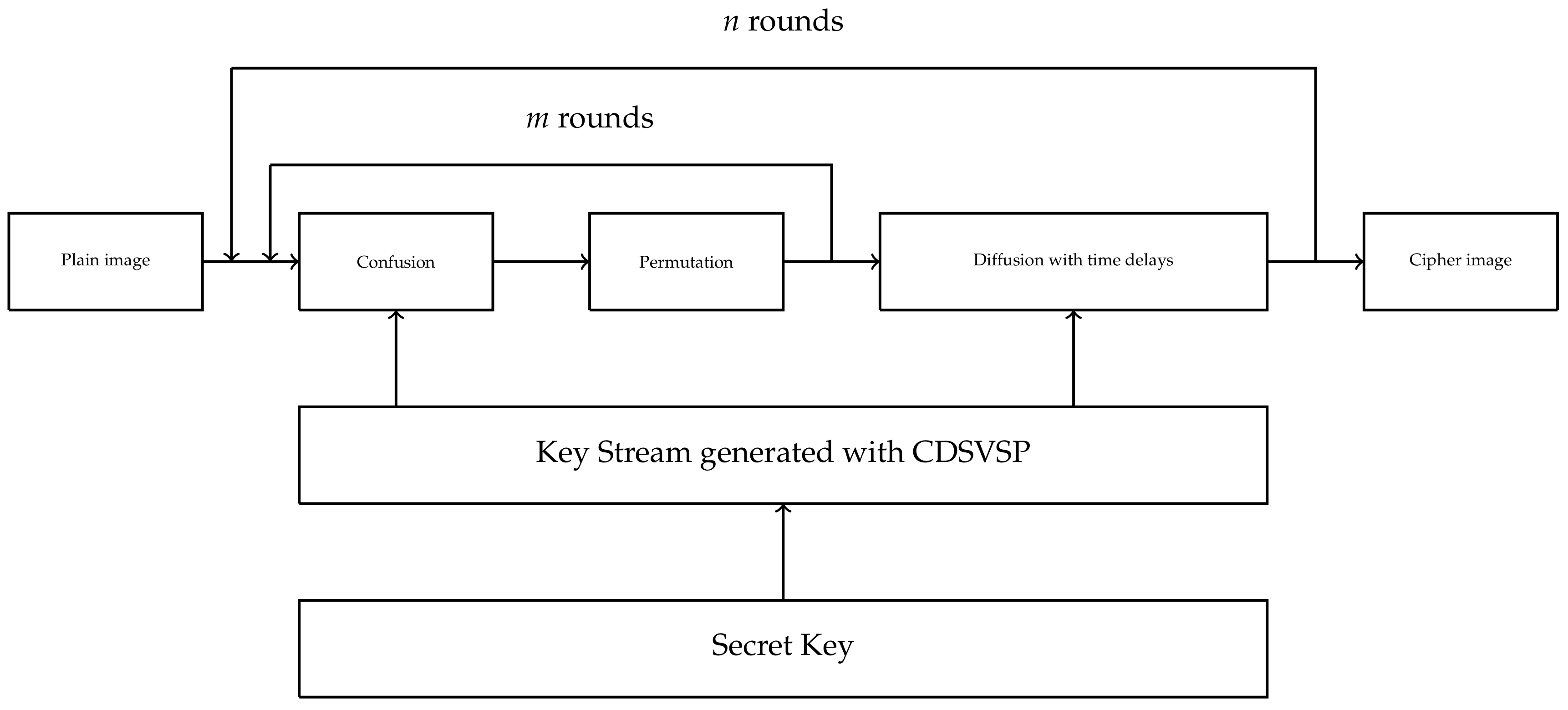
3. Proposed Image Encryption Scheme
3.1. Confusion Algorithm
3.2. Diffusion Algorithm
3.3. Proposed Algorithm for Image Encryption and Decryption
- Step 1:
- Iterate the Lü chaotic system (2) with for times continuously to avoid the harmful effect of the transitional procedure.
- Step 2:
- Obtain the current state variable by means of CDSVSP. An initial value is set as the secret key for the first pixel; iterate the Lü system (2) if needed.
- Step 3:
- Calculate the key stream for the current pixel with Equation (3).
- Step 4:
- The discretized tent map (1) is used to change the current pixel’s value.
- Step 5:
- Go back to Step 2 until the values of all pixels are changed.
- Step 6:
- Permute the pixels by using the discretized tent map (1) as described in the confusion algorithm.
- Step 7:
- Repeat Steps 1–6 m times.
- Step 8:
- Obtain the current state variable by means of CDSVSP applied on the currently processed pixel of the confused image. The initial value is set as the secret key for the first pixel.
- Step 9:
- Calculate the key stream for the current pixel with Equation (3).
- Step 10:
- Calculate the time-varying delays using the discretized tent map (1).
- Step 11:
- Mask the values of the currently processed pixel using Equation (4).
- Step 12:
- Go back to Step 8 until all pixels are encrypted.
- Step 13:
- Repeat all these steps n times to ensure the security requirements are met.
- Step 1:
- Iterate over the Lü chaotic system (2) with for times continuously to avoid the harmful effect of the transitional procedure.
- Step 2:
- Obtain the current state variable by means of CDSVSP. The initial value is known for the first pixel; iterate over the Lü chaotic system (2) if needed.
- Step 3:
- Calculate the key stream for current pixel by Equation (3).
- Step 4:
- Calculate the time-varying delays using the discretized tent map (1).
- Step 5:
- Unmask the values of the currently processed pixel by using Equation (5).
- Step 6:
- Go back to Step 2 until all pixels are undiffused.
- Step 7:
- Apply the reverse of permutation.
- Step 8:
- Obtain the current state variable by means of CDSVSP applied on the currently processed pixel of the image found after Step 7. The initial value is known for the first pixel.
- Step 9:
- Calculate the key stream for the current pixel by Equation (3).
- Step 10:
- Apply the inverse of the discretized tent map (6) to get the pixel value of the plain image.
- Step 11:
- Go back to Step 8 until all the pixels are unconfused.
- Step 12:
- Repeat Steps 7–11 m times.
- Step 13:
- Repeat all these steps n times to get the plain image.
4. Analysis and Simulation Results
4.1. Effectiveness Analysis
4.2. Efficiency Comparisons
4.3. Key Space Analysis
4.4. Key Sensitivity Analysis
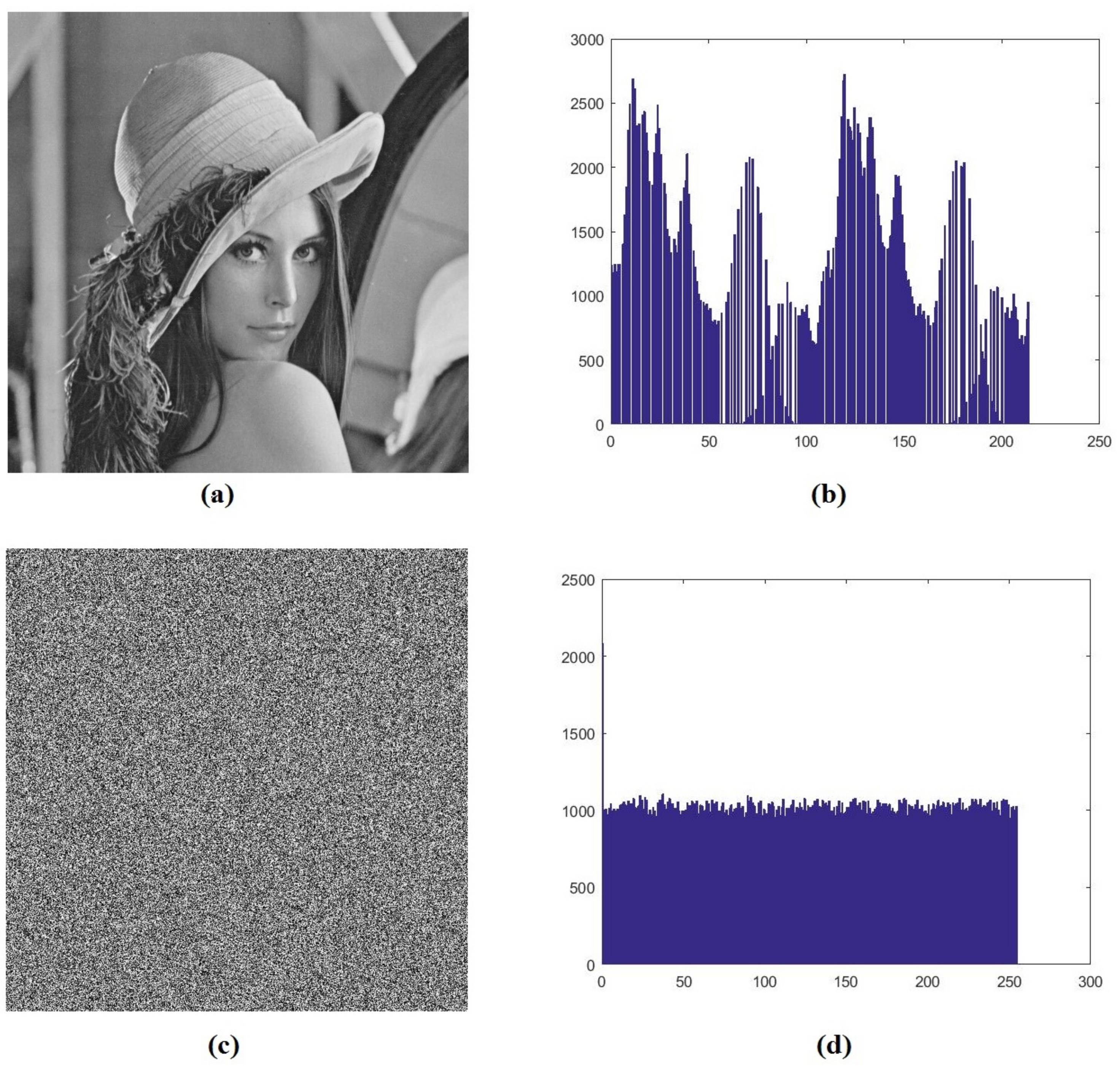
4.5. Histogram Analysis
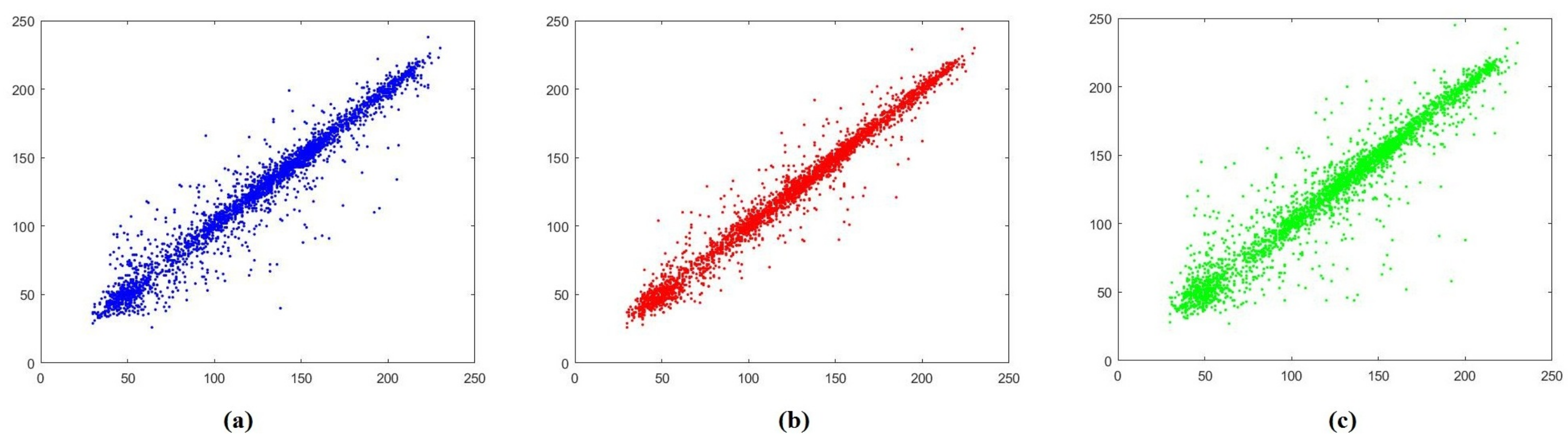
4.6. Correlation Analysis
4.7. Entropy Measure Analysis
5. Conclusions
- practical utilization of the proposed procedure and system;
- broader comparison of the obtained results with other approaches;
- searching for possibilities to increase the level of system security even further.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Cheddad, A.; Condell, J.; Curran, K.; McKevitt, P. A hashbased image encryption algorithm. Opt. Commun. 2010, 283, 879–893. [Google Scholar] [CrossRef]
- Tarmissi, K.; Hamza, A.B. Information-theoretic hashing of 3D objects using spectral graph theory. Expert Syst. Appl. 2009, 36, 9409–9414. [Google Scholar] [CrossRef]
- Zhou, Y.; Panetta, K.; Agaian, S.; Chen, C.L.P. Image encryption using p-Fibonacci transform and decomposition. Opt. Commun. 2012, 285, 594–608. [Google Scholar] [CrossRef]
- Bashir, Z.; Rashid, T.; Zafar, S. Hyperchaotic dynamical system based image encryption scheme with time-varying delays. Pac. Sci. Rev. A Nat. Sci. Eng. 2016. [Google Scholar] [CrossRef]
- Elsheh, E.; Hamza, A.B. Secret sharing approaches for 3D object encryption. Expert Syst. Appl. 2011, 38, 13906–13911. [Google Scholar] [CrossRef]
- Chen, G.; Mao, Y.; Chui, C.K. A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fractals 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Fu, C.; Lin, B.; Miao, Y.; Liu, X.; Chen, J. A novel chaos-based bit-level permutation scheme for digital image encryption. Opt. Commun. 2011, 284, 5415–5423. [Google Scholar] [CrossRef]
- García-Martínez, M.; Ontañón-Garcíab, L.J.; Campos-Cantóna, E.; Čelikovský, S. Hyperchaotic encryption based on multi-scroll piecewise linear systems. Appl. Math. Comput. 2015, 270, 413–424. [Google Scholar] [CrossRef]
- Lian, S.; Sun, J.; Wang, Z. A block cipher based on a suitable use of the chaotic standard map. Chaos Solitons Fractals 2005, 26, 117–129. [Google Scholar] [CrossRef]
- Mao, Y.; Chen, G.; Lian, S. A novel fast image encryption scheme based on 3D chaotic baker maps. Int. J. Bifurc. Chaos 2004, 14, 3613–3624. [Google Scholar] [CrossRef]
- Wong, K.; Kwok, B.; Law, W. A fast image encryption scheme based on chaotic standard map. Phys. Lett. A 2008, 372, 2645–2652. [Google Scholar] [CrossRef]
- Lang, J. Image encryption based on the reality-preserving multipleparameter fractional fourier transform. Opt. Commun. 2012, 285, 2584–2590. [Google Scholar] [CrossRef]
- Zhou, N.; Wang, Y.; Gong, L. Novel optical image encryption scheme based on fractional mellin transform. Opt. Commun. 2011, 284, 3234–3242. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X. Image encryption using dna complementary rule and chaotic maps. Appl. Soft Comput. 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
- Arroyo, D.; Li, S.; Amigo, J.; Alvarez, G.; Rhouma, R. Comment on image encryption with chaotically coupled chaotic maps. Phys. D Nonlinear Phenom. 2010, 239, 1002–1006. [Google Scholar] [CrossRef]
- Cokal, C.; Solak, E. Cryptanalysis of a chaos-based image encryption algorithm. Phys. Lett. A 2009, 373, 1357–1360. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Lo, K. Breaking a modified substitutiondiffusion image cipher based on chaotic standard and logistic maps. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 837–843. [Google Scholar] [CrossRef]
- Li, C.; Li, M.A.S.; Nunez, J.; Alvarez, G.C.G. On the security defects of an image encryption scheme. Image Vis. Comput. 2009, 27, 1371–1382. [Google Scholar] [CrossRef]
- Li, C.; Liu, Y.; Xie, T.; Chen, M. Breaking a novel image encryption scheme based on improved hyperchaotic sequences. Nonlinear Dyn. 2013, 73, 2083–2089. [Google Scholar] [CrossRef]
- Rhouma, R.; Solak, E.; Belghith, S. Cryptanalysis of a new substitutiondif-fusion based image cipher. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1887–1892. [Google Scholar] [CrossRef]
- Solak, E.; Cokal, C.; Yildiz, O.; Biyikoglu, T. Cryptanalysis of Fridrich’s chaotic image encryption. Int. J. Bifurc. Chaos 2010, 20, 1405–1413. [Google Scholar] [CrossRef]
- Wang, K.; Pei, W.; Zou, L.; Song, A.; He, Z. On the security of 3D cat map based symmetric image encryption scheme. Phys. Lett. A 2005, 343, 432–439. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Z.; Fang, J.A. Image encryption using chaotic coupled map lattices with time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2456–2468. [Google Scholar] [CrossRef]
- Hussain, I.; Shah, T.; Gondal, M.A. Application of S-box and chaotic map for image encryption. Math. Comput. Model. 2013, 57, 2576–2579. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, Z.; Fu, C.; Yu, H.; Zhang, L. A fast chaos-based image encryption scheme with a dynamic state variables selection mechanism. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 846–860. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystem. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Furht, B.; Kirovski, D. Multimedia Security Handbook; Ch. Chaos-Based Encryption for Digital Images and Videos; CRC Press: New York, NY, USA, 2004. [Google Scholar]
- Masuda, N.; Aihara, K. Cryptosystems with discretized chaotic maps. IEEE Trans. Circ. Syst. I 2002, 49, 28–40. [Google Scholar] [CrossRef]
- Chen, A.; Lu, J.; Yu, S. Generating hyperchaotic Lü attractor via state feedback control. Physica A 2006, 364, 103–110. [Google Scholar] [CrossRef]
- Stallings, W. Cryptography and Network Security: Principles and Practices; Pearson Education: London, UK, 2006. [Google Scholar]
- IEEE Computer Society. IEEE standard for binary floating-point arithmetic. ANSI/IEEE Std. 1985, 754–1985. [Google Scholar] [CrossRef]
- Öztürk, I.; Kiliç, R. Cycle lengths and correlation properties of finite precision chaotic maps. Int. J. Bifurc. Chaos 2014, 24, 1450107. [Google Scholar] [CrossRef]
- Li, S.; Chen, G.; Mou, X. On the dynamical degradation of digital piecewise linear chaotic maps. Int. J. Bifurc. Chaos 2005, 15, 3119–3151. [Google Scholar] [CrossRef]
- Wong, K.; Kwok, B.; Yuen, C. An efficient diffusion approach for chaos-based image encryption. Chaos Solitons Fractals 2009, 41, 2652–2663. [Google Scholar] [CrossRef]
- Fu, C.; Chen, J.J.; Zou, H.; Meng, W.H.; Zhan, Y. F.; Yu, Y.W. A chaos-based digital image encryption scheme with an improved diffusion strategy. Opt. Express 2012, 20, 2363–2378. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wong, K.; Liao, X.; Xiang, T.; Chen, G. A chaos-based image encryption algorithm with variable control parameters. Chaos Solitons Fractals 2009, 41, 1773–1783. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, K.; Yu, H.; Zhu, Z. An image encryption scheme using reverse 2-dimensional chaotic map and dependent diffusion. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 2066–2080. [Google Scholar] [CrossRef]
- Belazi, A.; El-Latif, A.A.A.; Diaconu, A.V.; Rhouma, R.; Belghith, S. Chaos-based partial image encryption scheme based on linear fractional and lifting wavelet transforms. Opt. Lasers Eng. 2017, 88, 37–50. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Chen, H. A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Opt. Lasers Eng. 2017, 90, 238–246. [Google Scholar] [CrossRef]
- Zhou, N.; Zhang, A.; Wu, J.; Pei, D.; Yang, Y. Novel hybrid image compression–encryption algorithm based on compressive sensing. Opt. Int. J. Light Electron Opt. 2014, 125, 5075–5080. [Google Scholar] [CrossRef]
- Shannon, C. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 18, 656–715. [Google Scholar] [CrossRef]

| Permutation Approaches | Rounds | NPCR | UACI |
|---|---|---|---|
| Proposed | 1 | ||
| Chen’s Results [26] | 1 | 15.87 | |
| Arnold cat map | 3 | 3.8147 × 10 | 1.4960 × 10 |
| Baker map | 3 | 3.8147 × 10 | 1.4960 × 10 |
| Standard map | 3 | 3.8147 × 10 | 1.4960 × 10 |
| Test Images | 1 Round | 1 Round | 2 Rounds | |||
|---|---|---|---|---|---|---|
| Permutation | Encryption | Overall | Encryption | Overall | Encryption | |
| NPCR | UACI | NPCR | UACI | NPCR | UACI | |
| Lena | 99.6094% | 32.8120% | 99.6136% | 33.4880% | 99.6002% | 33.4630% |
| Baboon | 99.6090% | 32.8388% | 99.6029% | 33.4859% | 99.6235% | 33.4671% |
| Peppers | 99.6132% | 33.2538% | 99.6185% | 33.4838% | 99.6269% | 33.4050% |
| Bridge | 99.5766% | 33.5782% | 99.6082% | 33.5055% | 99.6159% | 33.5187% |
| Boat | 99.5953% | 32.6331% | 99.6052% | 33.5188% | 99.6128% | 33.4390% |
| NPCR (%) | UACI (%) | Average Encryption Rounds | Average Required Chaotic Variables | Average Required Quantization Operations | |
|---|---|---|---|---|---|
| Proposed | >99.6 | >33.4 | 1 | 1.002 | 2 |
| Ref. [26] | >99.6 | >33.4 | 1 | 1.004 | 2 |
| Ref. [36] | >99.6 | >33.4 | 1 | 4 | 2 |
| Ref. [11] | >99.6 | >33.4 | 3 | 9 | 3 |
| Ref. [37] | >99.6 | >33.4 | 2 | 7 | 2 |
| Ref. [38] | >99.6 | >33.4 | 2 | 6 | 2 |
| Figures | Encryption Keys | Differences Ratio | |||
|---|---|---|---|---|---|
| Lena 1 | 15 | 99.5903% | |||
| Lena 2 | 99.6025% | ||||
| Lena 3 | 15 | 99.6220% | |||
| Lena 4 | 15 | 99.6048% | |||
| Average | 99.6049% | ||||
| 3000 Pairs | 4000 Pairs | |||
|---|---|---|---|---|
| Direction | Plain Image | Cipher Image | Plain Image | Cipher Image |
| Horizontal | 0.97454 | −0.00932 | 0.919702 | 0.020973 |
| Vertical | 0.986736 | 0.010248 | 0.958690 | −0.004789 |
| Diagonal | 0.959988 | −0.005223 | 0.893104 | 0.032478 |
| 8000 Pairs | 10,000 Pairs | |||
| Direction | Plain Image | Cipher Image | Plain Image | Cipher Image |
| Horizontal | 0.9239702 | 0.0145748 | 0.919298 | −0.017349 |
| Vertical | 0.9540613 | −0.000374 | 0.954782 | 0.0054973 |
| Diagonal | 0.9004525 | -0.000569 | 0.892229 | 0.0125824 |
| Test Images | Plain Image | Cipher Image |
|---|---|---|
| Lena | 7.4455 | 7.9994 |
| Baboon | 7.3713 | 7.9992 |
| Peppers | 7.5800 | 7.9993 |
| Bridge | 5.7922 | 7.9993 |
| Boat | 7.1914 | 7.9992 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashir, Z.; Wątróbski, J.; Rashid, T.; Zafar, S.; Sałabun, W. Chaotic Dynamical State Variables Selection Procedure Based Image Encryption Scheme. Symmetry 2017, 9, 312. https://doi.org/10.3390/sym9120312
Bashir Z, Wątróbski J, Rashid T, Zafar S, Sałabun W. Chaotic Dynamical State Variables Selection Procedure Based Image Encryption Scheme. Symmetry. 2017; 9(12):312. https://doi.org/10.3390/sym9120312
Chicago/Turabian StyleBashir, Zia, Jarosław Wątróbski, Tabasam Rashid, Sohail Zafar, and Wojciech Sałabun. 2017. "Chaotic Dynamical State Variables Selection Procedure Based Image Encryption Scheme" Symmetry 9, no. 12: 312. https://doi.org/10.3390/sym9120312
APA StyleBashir, Z., Wątróbski, J., Rashid, T., Zafar, S., & Sałabun, W. (2017). Chaotic Dynamical State Variables Selection Procedure Based Image Encryption Scheme. Symmetry, 9(12), 312. https://doi.org/10.3390/sym9120312





