1. Introduction
In 1926, the British physicist L. H. Thomas (1903–1992) resolved a discrepancy between observed line splittings of atomic spectra in an external magnetic field (Zeeman effect) and theoretical calculations at that time (see e.g., ref. [
1]). Thomas’s analysis [
2,
3] explains the observed deviations in terms of a special relativistic [
4] effect. He recognized that a sequence of two non-collinear pure Lorentz transformations (boosts) cannot be expressed as one single boost. Rather, two non-collinear boosts correspond to a pure Lorentz transformation combined with a spatial rotation. This spatial rotation is known as Wigner rotation or Thomas–Wigner rotation, the corresponding rotation angle is the Thomas–Wigner angle (see e.g., ref. [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21], and references therein).
The prevalent approach to discuss Thomas–Wigner rotations employs passive Lorentz transformations. An object is simultaneously observed from N inertial reference frames, denoted by . Frame is related to the next frame by a pure Lorentz transformation, where . Now, for given non-collinear boosts from frame to frame and then from to , there exists a unique third boost from to , such that is at rest with respect to both, frame and frame . It turns out, however, that the combined transformation , is not the identity transformation, but involves a spatial rotation.
In the present paper, following Jonsson [
22], an alternative route to visualize Thomas–Wigner rotations using active or “physical” boosts is attempted.
is accelerated starting from zero velocity in frame
, which is denoted by “laboratory frame” in the following. During its journey
performs several acceleration and/or deceleration manoeuvres and finally returns to its starting position. The visual impression of
moving through the series of acceleration phases and finally coming to rest in a rotated orientation (see
Section 5) hopefully outweigh the mathematical technicalities of the present approach.
The paper is sectioned as follows. First, the general approach is described and basic assumptions are introduced. The second section recalls uniform accelerations of Born-rigid objects. Sequences of uniform, non-collinear accelerations for a given vertex point within a planar grid of vertices and the trajectories of its neighbouring vertices are addressed in the following section. The last two sections present the visualization results and discuss their implications.
Appendix A examines the required number of boost steps, details of the computer algebraic calculations performed in this study are given in
Appendix B, details on how to access the corresponding computer source code are provided in section “
Supplementary Materials”.
For simplicity length units of light-seconds, abbreviated “ls” (roughly 300,000 km) are used with the speed of light taken to be unity.
2. Method
We consider the trajectory of a square-shaped grid
consisting of
M vertices.
is assumed to be Born-rigid, i.e., the distance between any two grid points, as observed in the momentarily comoving inertial frame (MCIF) (see e.g., ref. [
23], chapter 7) remains constant [
24]. The grid’s central point
R, which serves as the reference point, is uniformly accelerated for a given proper time period
. In order to obtain a closed trajectory several of these sections with constant proper acceleration, but different boost directions are joined together.
In
R’s MCIF, the directions and magnitudes of the vertices’ proper accelerations
(
) change discontinuously at the switchover from one boost section to the next. In the MCIF, the vectors
change simultaneously; in other frames, such as the laboratory frame, the change is asynchronous and
, despite its Born-rigidity, appears distorted and twisted (see
Section 5). On the other hand,
’s Born-rigidity implies that it is sufficient to calculate
R’s trajectory, the motion of the reference point
R uniquely determines the trajectories of the remaining
vertices [
25,
26]. We note that the spacetime separations between individual switchover events, linking boost steps
k and
, are spacelike. Thus, these switchover events are causally disconnected and each vertex has to be “programmed” in advance to perform the required acceleration changes [
27].
In the following, and denote the magnitude of the proper acceleration of ’s reference point R and the boost duration in terms of R’s proper time, respectively. To simplify the calculations, we impose the following four conditions on all N boosts:
- 〈1〉
The grid is Born-rigid.
- 〈2〉
At the beginning and after completion of the boost, is at rest in frame and R returns to its starting position.
- 〈3〉
R’s proper acceleration and the boost’s proper duration are the same in all N sections.
- 〈4〉
All boost directions and therefore all trajectories lie within the -plane.
Let the unit vector
denote the direction of the first boost in frame
. This first boost lasts for a proper time
, as measured by
R’s clock, when
R attains the final speed
with respect to frame
. Frame
is then defined as
R’s MCIF at this instant of time. The corresponding Lorentz matrix transforming a four-vector from frame
to frame
is
Here,
is the
unit matrix, the superscript
T denotes transposition, the Lorentz factor is
and, in turn,
. Similarly, frame
is
R’s MCIF at the end of the second boost, etc. In general, the Lorentz transformation from frame
to frame
is given by Equation (
1), with
replaced by
, the direction of the
boost in frame
.
Assumption 〈3〉 implies that the angles between consecutive boosts (“boost angles”)
are the only unknowns, since proper acceleration
and boost duration
are given parameters. In the following the “half-angle” parametrization,
is used; it allows us to write expressions involving
as polynomials in
T.
We will find that, first, no solutions exist if the number of boosts
N is four or less (see
Appendix A), second, for
, the solution is unique and, third, the boost angles
depend solely on the selected value of
. Changing
and/or
only affects the spatial and temporal scale of
R’s trajectory (see below).
The derivation of is simplified by noting that the constraints 〈2〉, 〈3〉 and 〈4〉 imply time reversal invariance. This means that R’s trajectory from destination to start, followed backward in time, is a valid solution as well and therefore for . Thus, for , the number of unknowns reduces from four to two, with and .
3. Uniform Acceleration of a Born-Rigid Object
In the laboratory frame, we consider the uniform acceleration of the reference point
R, initially at rest, and assume that the acceleration phase lasts for the proper time period
. During
, the reference point moves from location
to location
with unit vector
denoting the boost direction (see e.g., refs. [
14,
19,
28,
29,
30,
31]). The coordinate time duration
corresponding to the proper time duration
is
and
R attains the final speed
Let
G be an arbitrary vertex point of
at location
and
the projection of the distance vector from
R to
G onto the boost direction
. The vertices
G and
R start to accelerate simultaneously. Since
is Born-rigid (assumption 〈1〉) and analogous to Equations (
6)–(
8), we obtain for
G’s trajectory
At the end of the first boost phase, all grid points move at the same speed with respect to the laboratory frame; however, in the laboratory frame, the boost phase does not end simultaneously for all vertices. Simultaneity is only observed in
R’s MCIF. With
and Equation (
10), it follows that
’s Born-rigidity implies that the spatial distance between
G and
R at the end of the boost phase in
R’s MCIF is the same as their distance at the beginning of the boost phase. A brief calculation leads to
which simplifies to
and, with Equation (
11),
provided
. Equation (
13) expresses the well-known fact that the proper accelerations aboard a Born-rigid grid may differ from one vertex to the next. More specifically, at a location trailing the reference point
R, the acceleration exceeds
, vertex points leading
R accelerate less than
. (In relativistic space travel, the passengers in the bow of the spaceship suffer lower acceleration forces than those seated in the stern. This amenity of a more comfortable acceleration, however, is counterbalanced by faster ageing of the space travellers (Equation (
14)). These considerations, of course, assume Born-rigidly constructed space vehicles.)
The position-dependent acceleration is well known from the Dewan–Beran–Bell spaceship paradox [
32,
33] and ([
34], chapter 9). Two spaceships, connected by a Born-rigid wire, accelerate along the direction separating the two. According to Equation (
13), the trailing ship has to accelerate faster than the leading one. Conversely, if both accelerated at the same rate in the laboratory frame, Born-rigidity could not be maintained and the wire connecting the two ships would eventually break. This well-known, but admittedly counterintuitive fact is not a paradox in the true sense of the word and discussed extensively in the literature (see e.g., refs. [
35,
36,
37,
38,
39,
40]).
Equations (
13) and (
14) also imply that
and
, as the distance between a (trailing) vertex
G and the reference point
R approaches the critical value
Clearly, a Born-rigid object cannot extend beyond this boundary, which is referred to as “frame boundary” in the following.
Section 6.2 will discuss its consequences.
Finally, we note that Equation (
14) implies that a set of initially synchronized clocks mounted on a Born-rigid grid will in general fall out of synchronization once the grid is accelerated [
31]. Thus, the switchover events, which occur simultaneous in
R’s MCIF, are not simultaneous with respect to the time displayed by the vertex clocks. As already mentioned, the acceleration changes have to be “programmed” into each vertex in advance, since the switchover events are causally not connected and lie outside of each others’ lightcones [
41].
4. Sequence of Five Uniform Accelerations
The previous section discussed
R’s trajectory during the first acceleration phase (Equation (
10)). Now, we connect several of these segments to form a closed trajectory for
R. Let
denote
R’s start event as observed in frame
and
,
, etc. Correspondingly, denote the “switchover” events between 1st and 2st boost, 2nd and 3rd boost, etc., respectively. In the following, bracketed superscripts indicate the reference frame. Frame
, i.e.,
, is the laboratory frame, frame
is pulled back to frame
by the Lorentz transformation
(Equation (
1)). Generally, frame
is pulled back to frame
using the transformation matrix
.
It can be shown (see
Appendix A) that at least five boosts are needed to satisfy the four assumptions 〈1〉–〈4〉 listed in
Section 2. As illustrated in
Figure 1 for a sequence of
boosts the reference point starts to accelerate at event A and returns at event F via events B, C, D and E. The corresponding four-position
and four-velocity
are
and
respectively. Here, the four-vector
describes
R’s worldline from A to B (Equations (
6) and (
7));
,
,
and
are defined correspondingly. Assumption 〈2〉 implies that
and
To simplify the expressions in Equations (
16) and (
17), time reversal symmetry is invoked. It implies that the set of boost vectors
constitutes a valid solution, provided
is one and satisfies assumptions 〈1〉–〈4〉. Thereby, the number of unknowns is reduced from four to two, the angle between the boost vectors
and
, and the angle between
and
Figure 1 illustrates the sequence of the five boosts in the laboratory frame
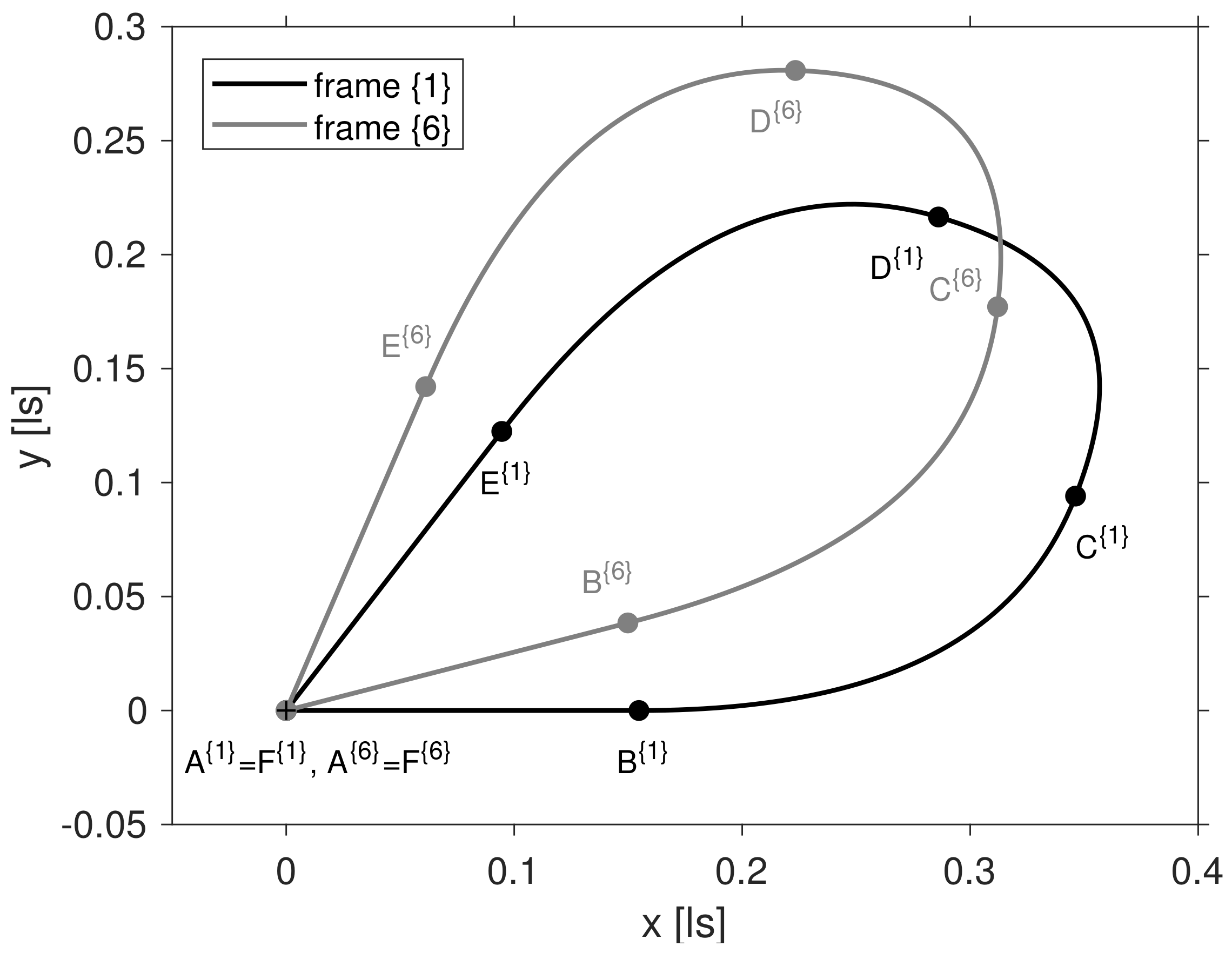
. Since the start and final velocities are zero,
R’s motion between A and B and, likewise, between E and F is rectilinear. In contrast, the trajectory connecting B and E (via C and D) appears curved in frame
; as discussed and illustrated below, the curved paths are in fact straight lines in the corresponding boost frame (
Figure 2).
From Equations (
17) and (
20) follows
with the two unknowns
and
(for details, see
Appendix B). Equation (
22) has two solutions:
provided
Assumption 〈2〉 implies that the spatial component of the event
vanishes, i.e.,
Since all motions are restricted to the
-plane, it suffices to consider the
x- and
y-components of Equation (
25). The
y-component leads to a product of the following two expressions:
and
(see
Appendix B). The solutions of equating expression (
27) to zero are disregarded since, for
, it yields:
which has no real-valued solution for
.
It turns out (see
Appendix B) that the
x-component of Equation (
25) results in an expression containing two factors as well, one of which is identical to the expression (
26). Thus, the roots of the polynomial (
26) solve Equation (
25).
The degree of the polynomial (
26) in terms of
is four; its roots are classified according to the value of the discriminant
(see e.g., ref. [
42]) which for expression (
26) evaluates to:
For non-trivial boost
, the discriminant is negative and the roots of the quartic polynomial consist of two pairs of real and complex conjugate numbers. The real-valued solutions are:
and
with
The solution from Equation (
31) turns out to be negative and thus does not produce a real-valued solution for
. The remaining two roots of the polynomial (
26)
correspond to replacing
by
in Equations (
30) and (
31); they are complex-valued and therefore disregarded as well. The second unknown,
, follows from Equation (
23) by choosing the positive square root
and using
(see Equation (
22)). For a given Lorentz factor
, the angles between the boost directions
and
are
and, with
and
, the orientation of the five boost directions
for
within the
-plane are obtained.
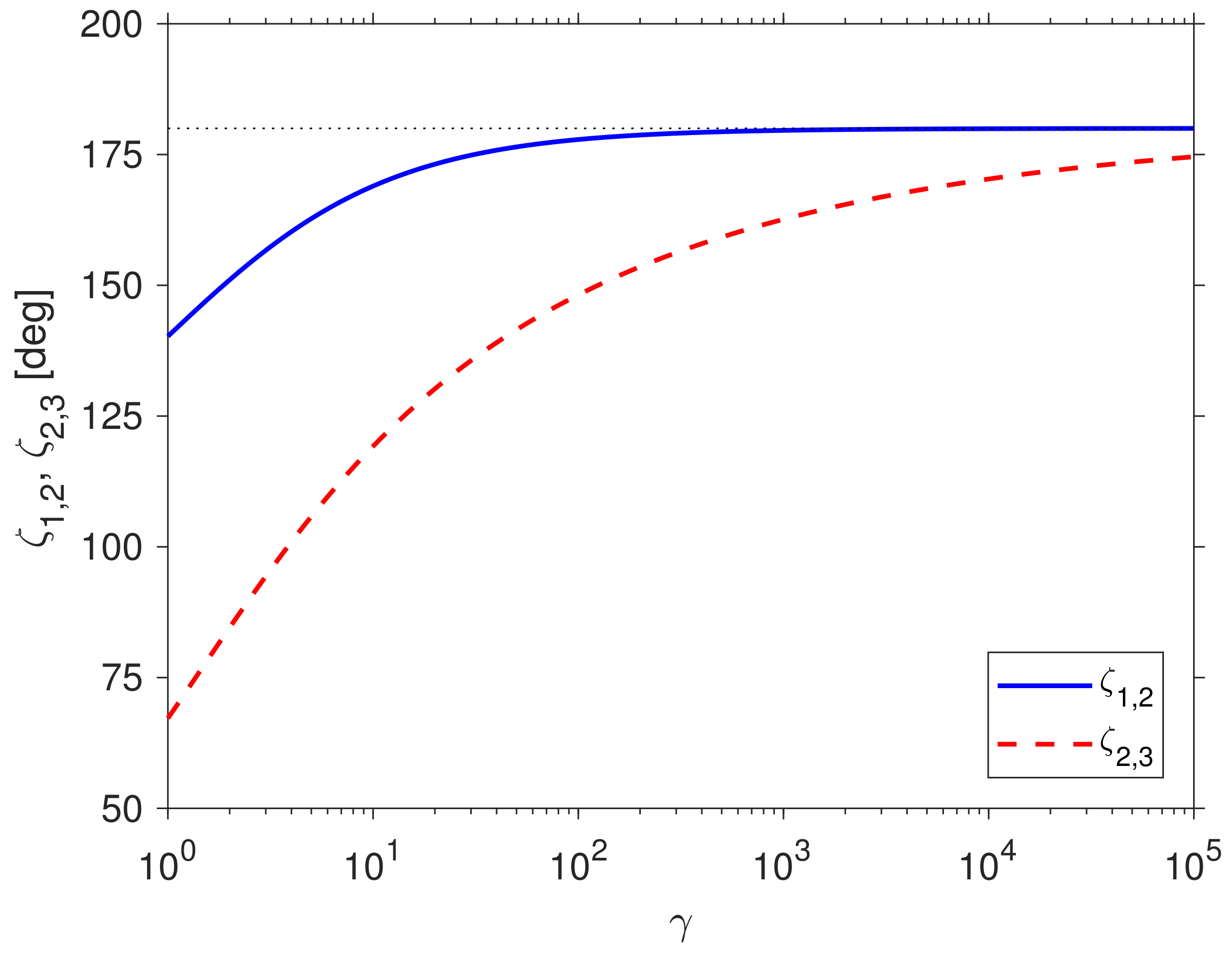
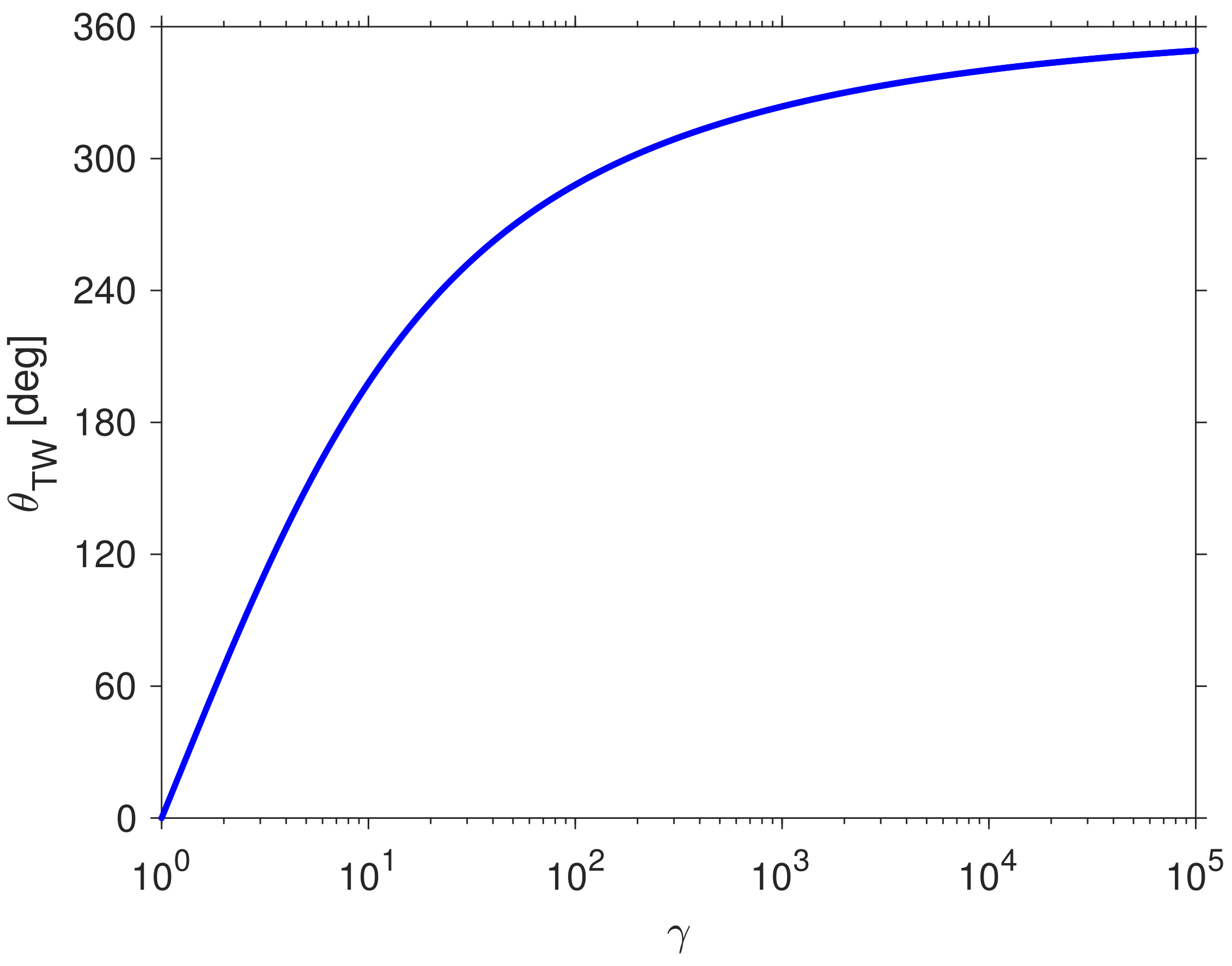
Figure 3 shows numerical values of the boost angles
and
as a function of
. The angles increase from
and
at
to
as
.
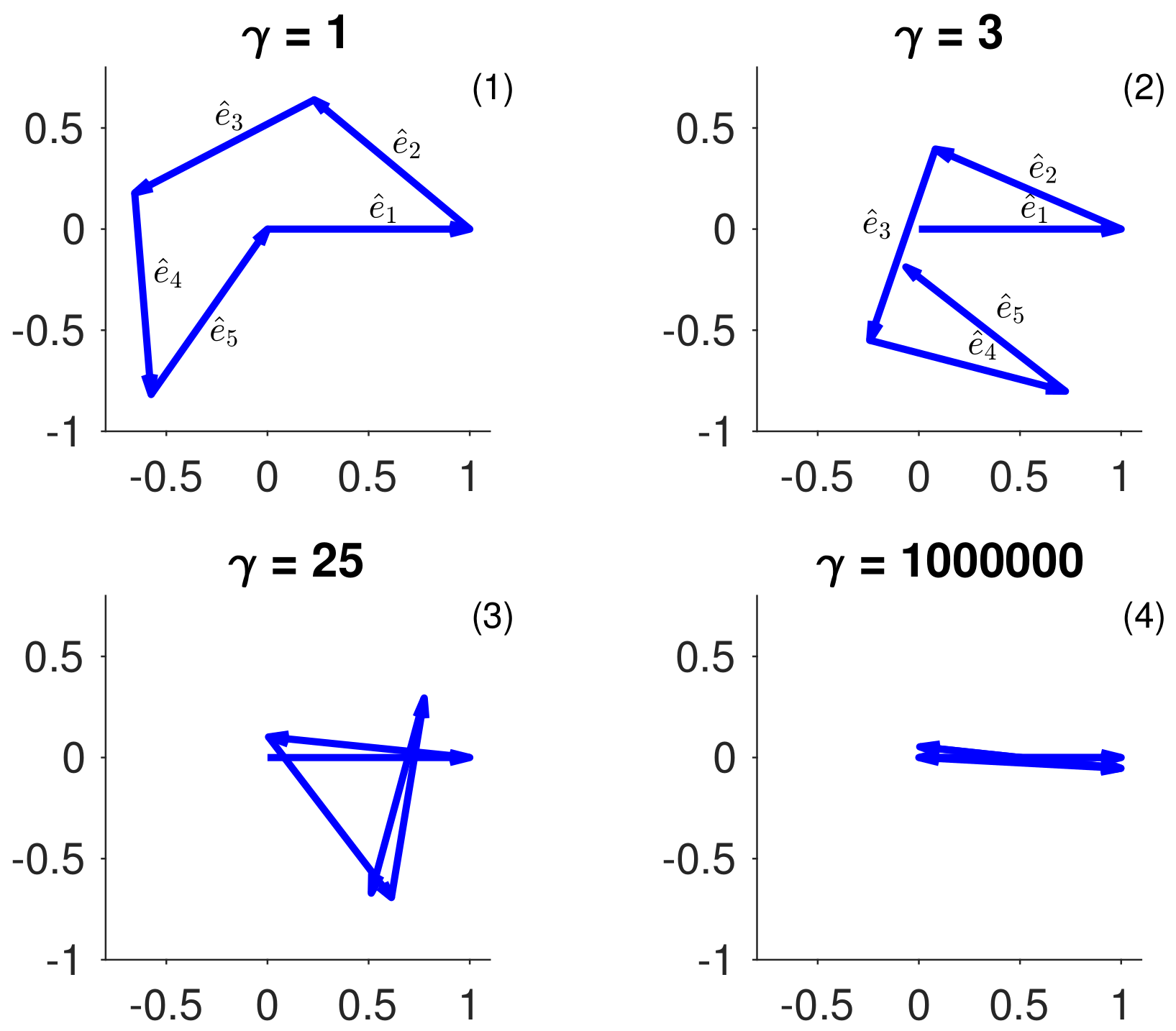
Figure 4 depicts the orientation of the five boost directions for several values of
. Here, the first boost vector
is taken to point along the
x-axis. We note that the panels in
Figure 4 do not represent a specific reference frame; rather, each vector
is plotted with respect to frame
(
). The four panels show the changes in boost directions for increasing values of
. Interestingly, the asymptotic limits
and
imply that in the relativistic limit
the trajectory of
R essentially reduces to one-dimensional motions along the
x-axis. At the same time, the Thomas–Wigner rotation angle increases to
as
(see the discussion in
Section 6 below).
Since the accelerated object is Born-rigid, the trajectories of all grid vertices
G are uniquely determined once the trajectory of the reference point
R is known [
25,
26,
41]. Following the discussion in
Section 3, the position and coordinate time of an arbitrary vertex
G, in the frame comoving with
R at the beginning of the corresponding acceleration phase, follows from Equation (
10). The resulting trajectories are discussed in the next section.
5. Visualization
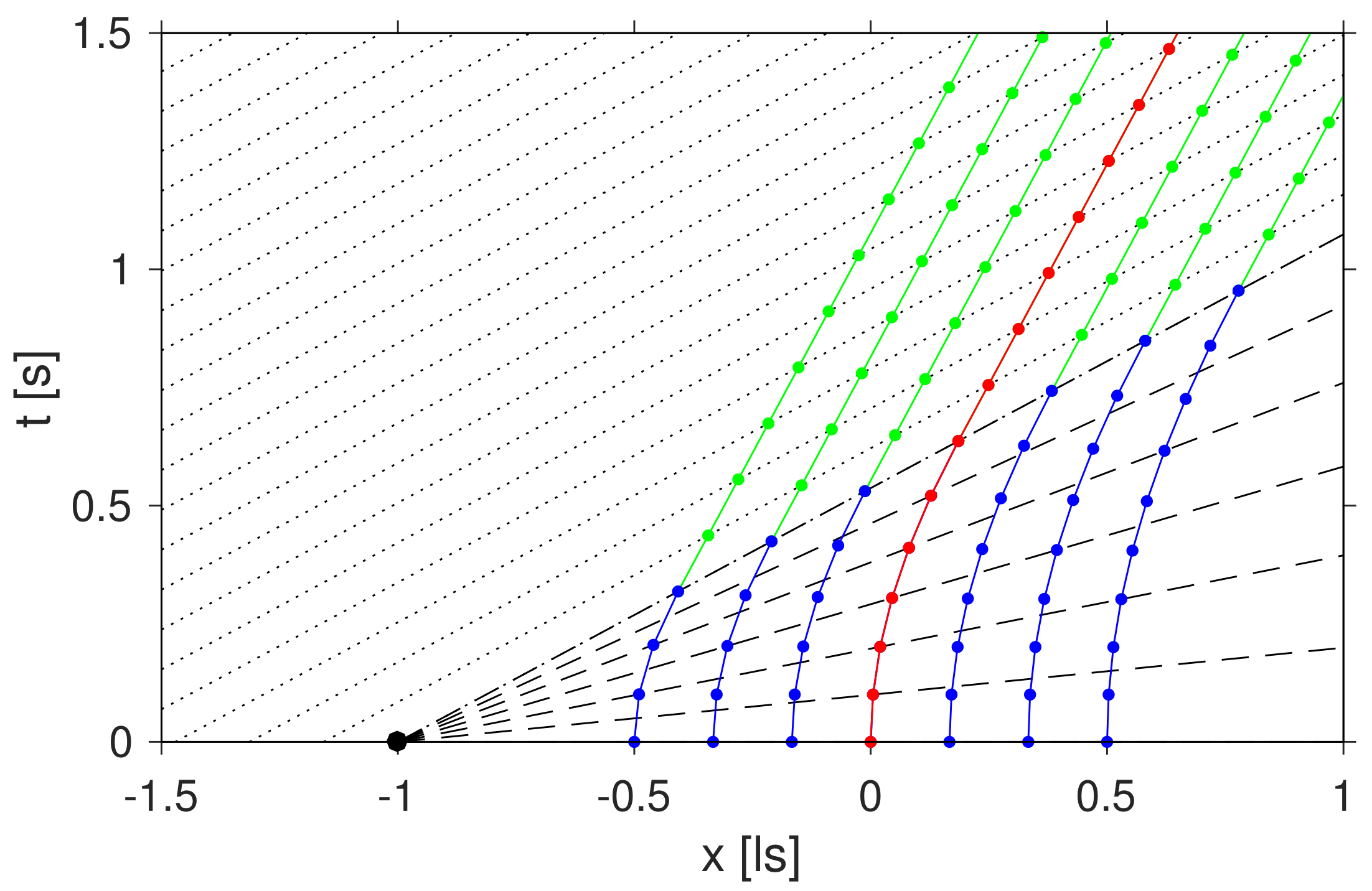
The trajectory of the reference point
R in the laboratory frame for a boost speed
, corresponding to
, is displayed in
Figure 1 (black solid line). The same trajectory as it appears to an observer in frame
is marked in grey. The two frames are stationary with respect to each other, but rotated by a Thomas–Wigner angle of about
. In addition, dots mark the locations of the four switchover events B, C, D and E in the two frames. As required by assumption 〈2〉, the starting and final positions, corresponding to the events A and F, coincide.
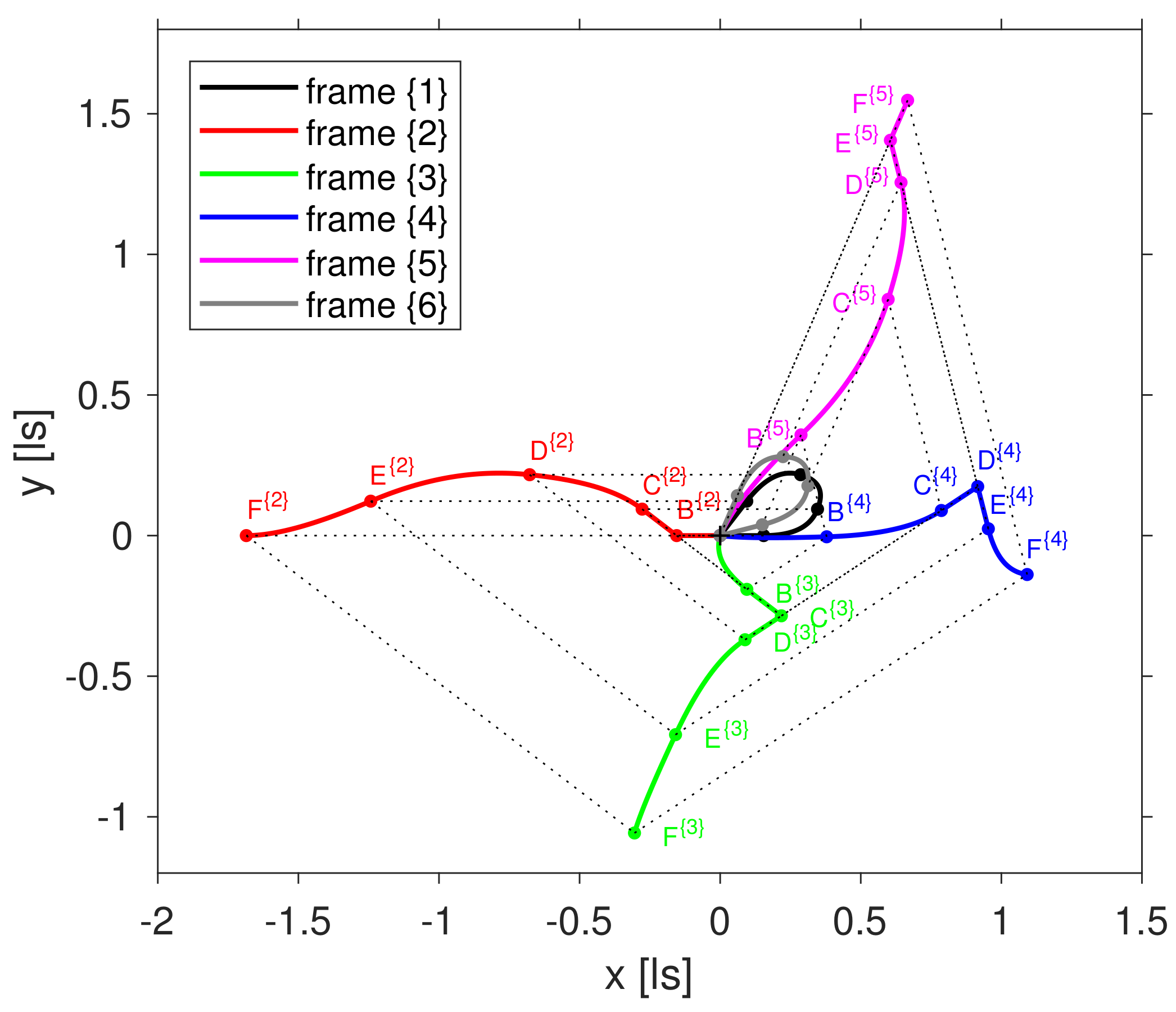
Figure 2 shows the same trajectories as
Figure 1. In addition,
R’s trajectories as recorded by observers in the frames
are plotted as well (solid coloured lines). Corresponding switchover events are connected by dashed lines. At
,
,
and
(and, of course, at the start event
and destination event
) the reference point
R slows down and/or accelerates from zero velocity producing a kink in the trajectory. In all other cases, the tangent vectors of the trajectories, i.e., the velocities are continuous at the switchover points.
With Equations (
30) and (
34), all necessary ingredients to visualize the relativistic motion of a Born-rigid object are available. In
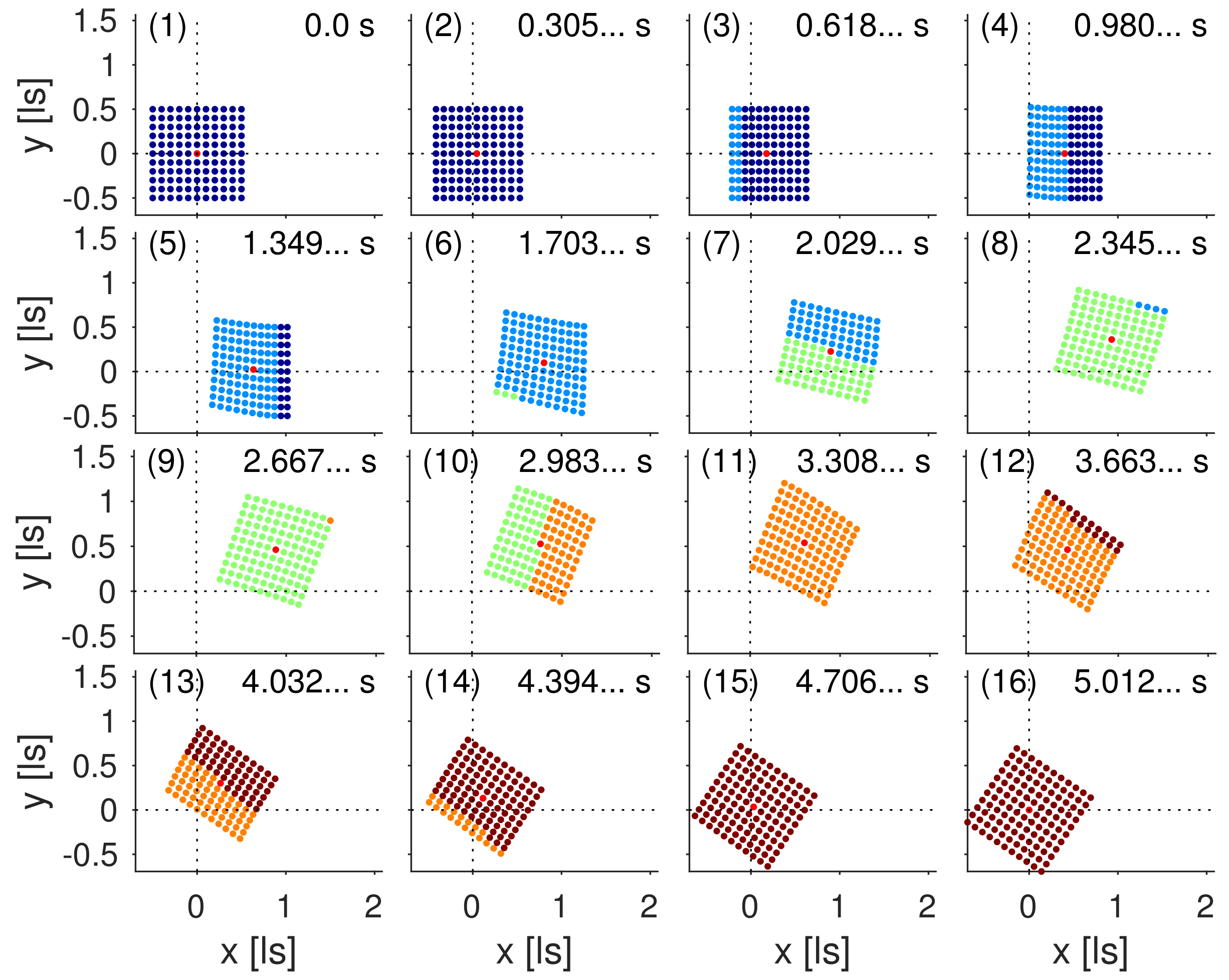
Figure 5, the object is modelled as a square-shaped grid of
points, arranged around the reference point
R. The object uniformly accelerates in the
-plane changing the boost direction four times by the angles
(as measured in frame
),
(frame
),
(frame
) and finally
(frame
). The vertices’ colour code indicates the corresponding boost section. The 16 panels depict the grid positions in the laboratory frame
for specific values of coordinate time displayed in the top right.
To improve the visual impression, the magnitude of the Thomas–Wigner rotation in
Figure 5 is enlarged by increasing the boost speed from
, used in
Figure 1 and
Figure 2, to
corresponding to
. Despite its appearance, the grid
is Born-rigid, and, in
R’s MCIF, the grid maintains its original square shape. In the laboratory frame, however,
appears compressed, when it starts to accelerate or decelerate and sheared, when one part of
has not yet finished boost
k, but the remaining part of
already has transitioned to the next boost section
. This feature is clearly evident from panels 4, 7, 10 or 13 in
Figure 5 with the occurrence of two colours indicating two boost sections taking effect at the same epoch of coordinate laboratory time. We note, however, that the switchover events occur simultaneously for all grid points in
R’s MCIF. The non-uniform colouring illustrate the non-simultaneity of the switchovers in the laboratory frame and thereby the relationship between Thomas–Wigner rotations and the non-existence of absolute simultaneity. A video animation is available online, details on how to access it are given in section “
Supplementary Materials”.
7. Conclusions
It is well known that pure Lorentz transformations do not form a group in the mathematical sense, since the composition of two transformations in general is not a pure Lorentz transformation again, but involves the Thomas–Wigner spatial rotation. The rotation is visualized by uniformly accelerating a Born-rigid object, consisting of a finite number of vertices, such that the object’s reference point returns to its starting location. It turns out that at least five boosts are necessary, provided, first, the (proper time) duration and the magnitude of the proper acceleration is the same within each boost and, second, the object’s motion is restricted to the -plane. Analytic expressions are derived for the angles between adjacent boost directions.
The visualization illustrates the relationship between Thomas–Wigner rotations and the relativity of simultaneity. The transition from one boost section to the next occurs synchronously in the MCIF of the object’s reference point. In the laboratory frame, however, the trailing vertices perform the transition to the next boost phase, which in general involves a direction change, earlier than the leading vertices. Thus, in this frame, the accelerated object not only contracts and expands along its direction of propagation, but also exhibits a shearing motion during the switchover phases. The simulations illustrate clearly that the aggregation of these shearing contributions finally adds up to the Thomas–Wigner rotation.
Accelerated motions induce frame boundaries, which no part of a physical, Born-rigid object may overstep. Thus, the object’s size is limited to a finite volume or area (if its motion is restricted to two spatial dimension) and Thomas–Wigner rotations by construction observe the special relativistic speed limit.