Aging Detection of Electrical Point Machines Based on Support Vector Data Description
Abstract
:1. Introduction
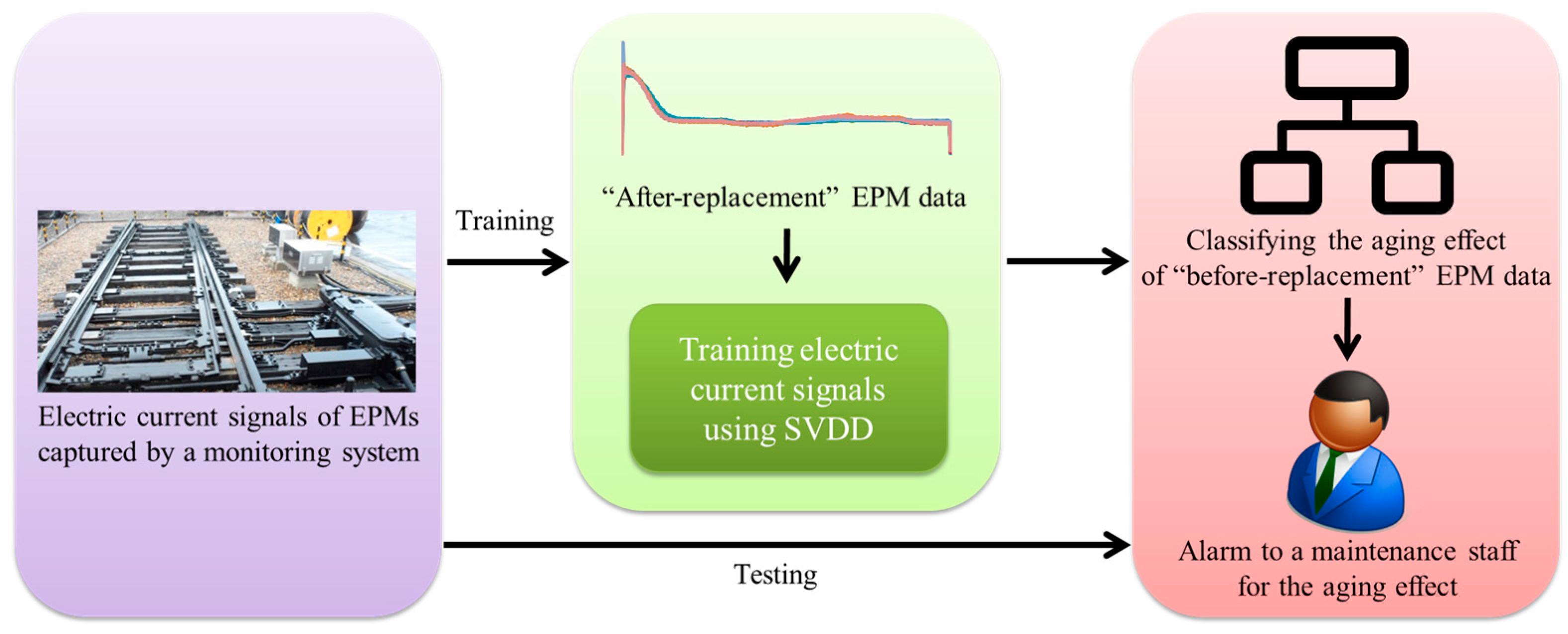
2. Method for Diagnosis of Aging in EPMs
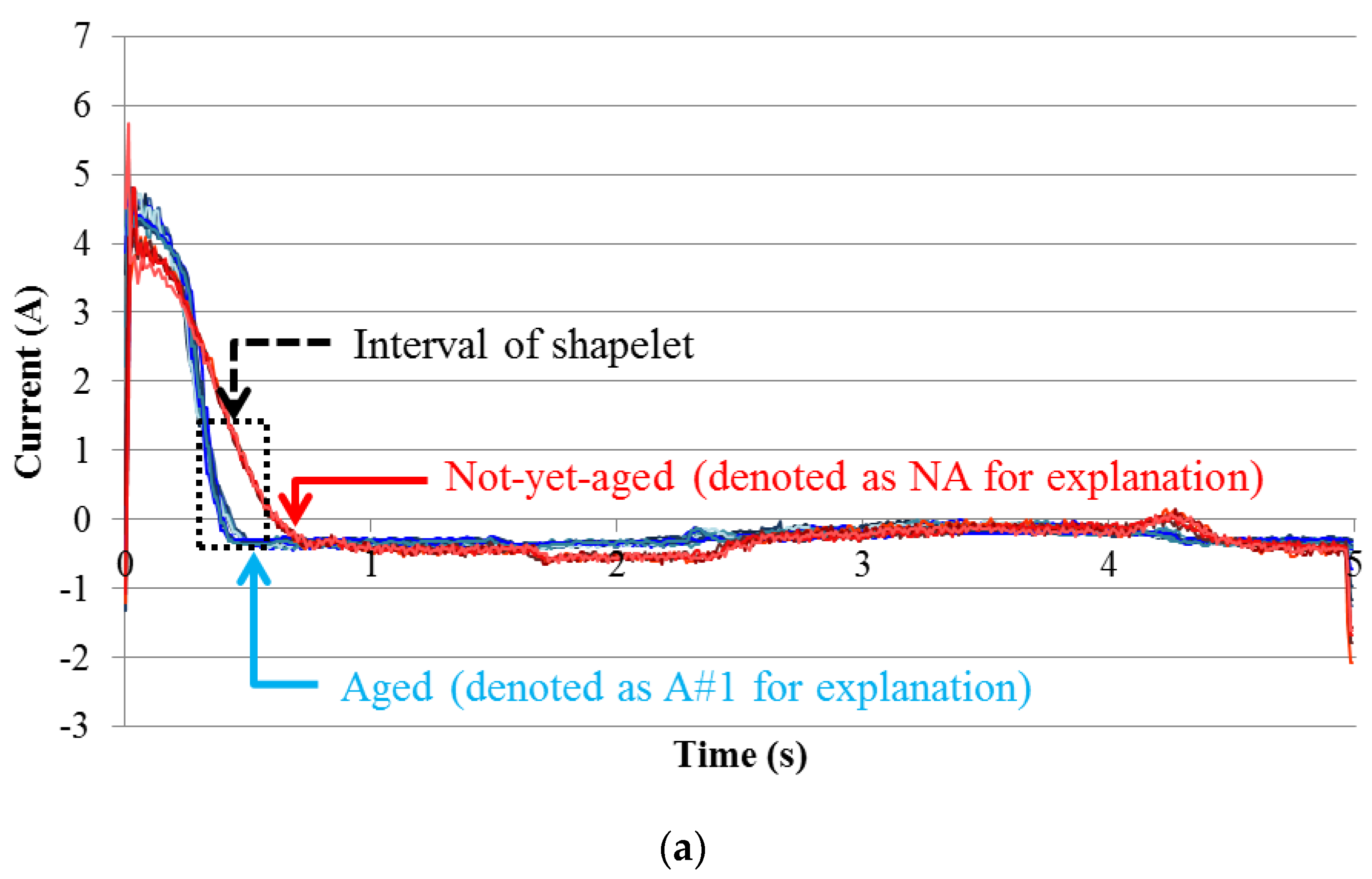
2.1. Data Preprocessing
2.2. SVDD for Detecting the Aging Effect of EPMs
3. Experimental Results
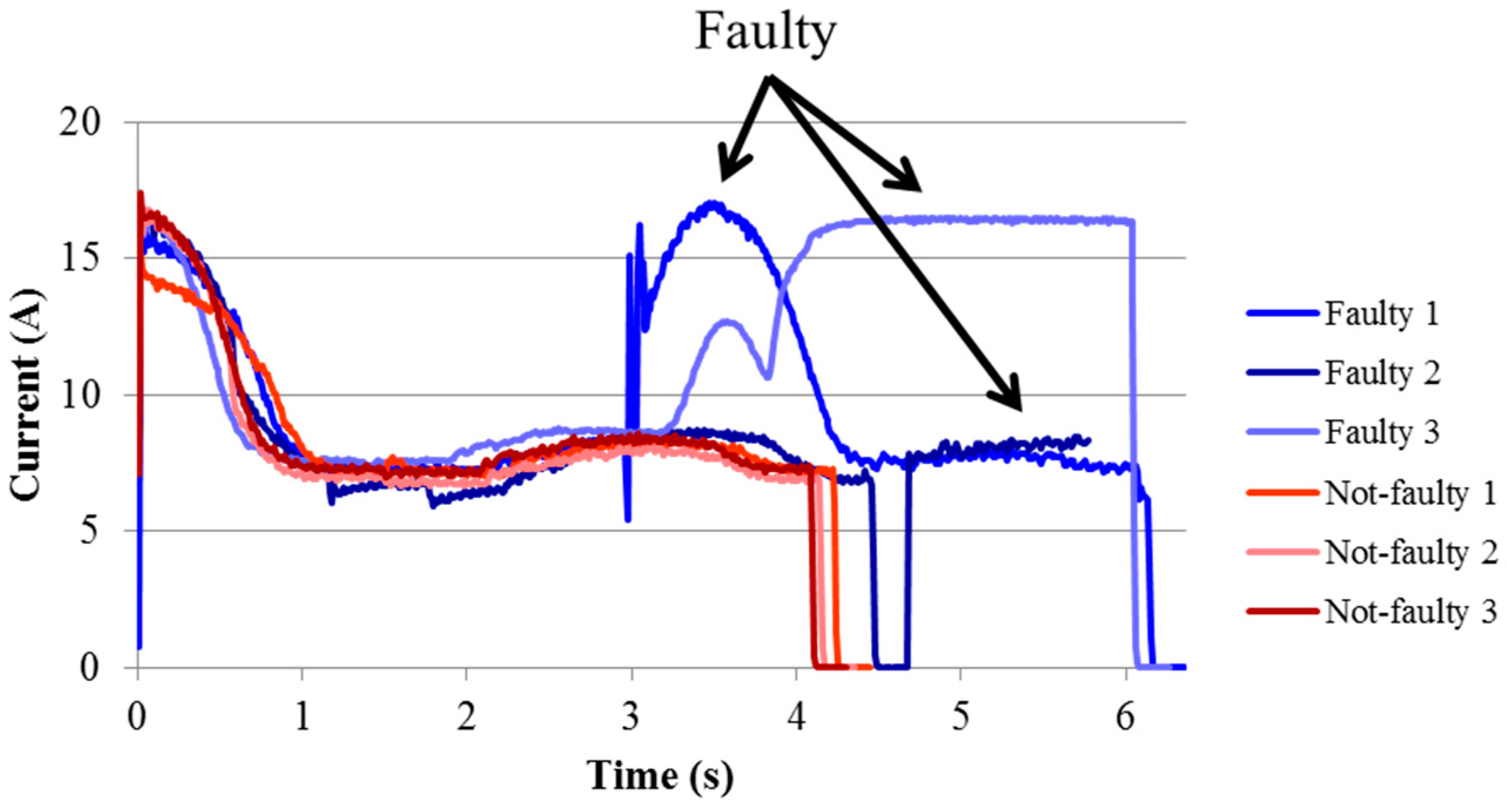
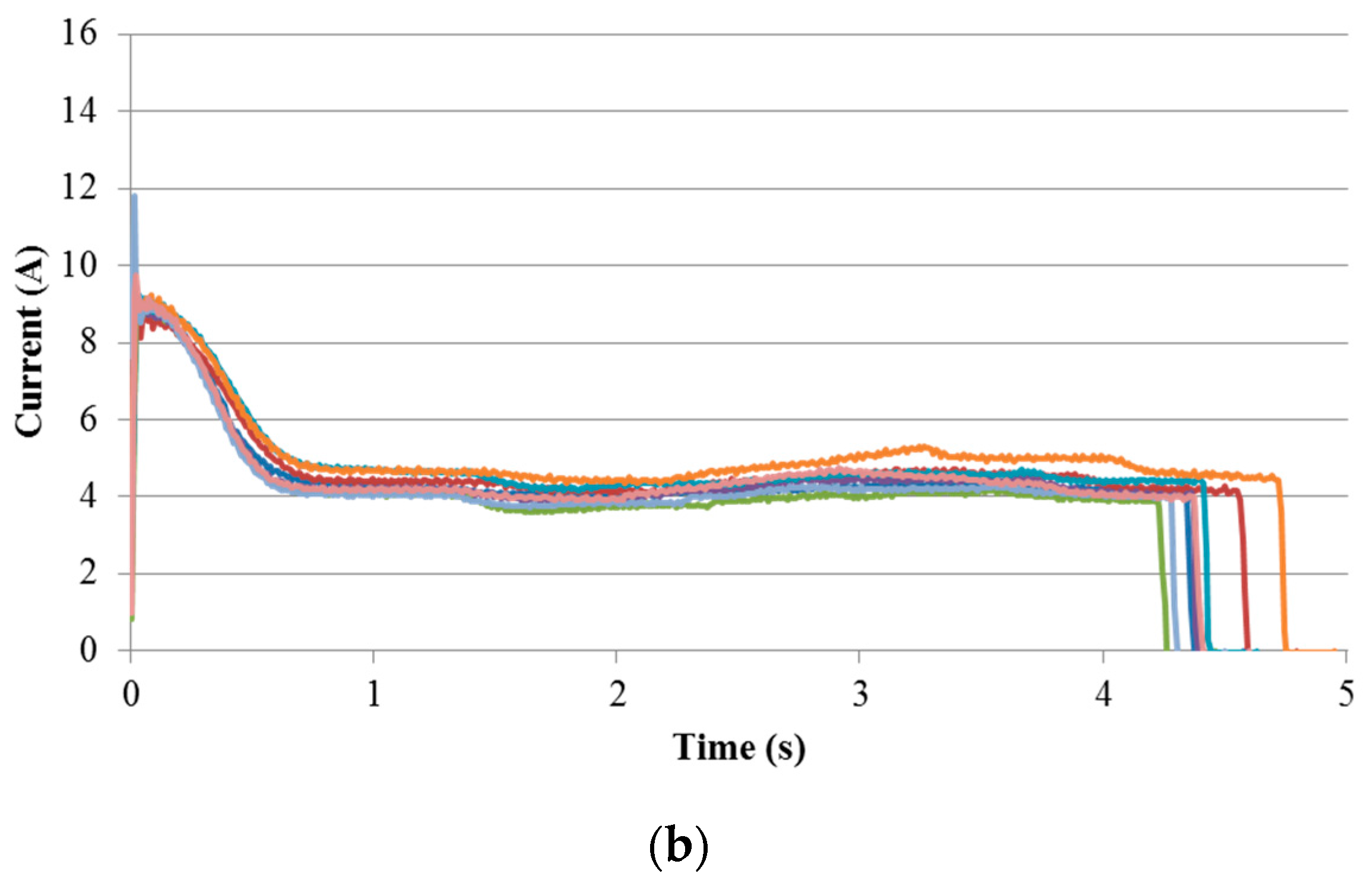
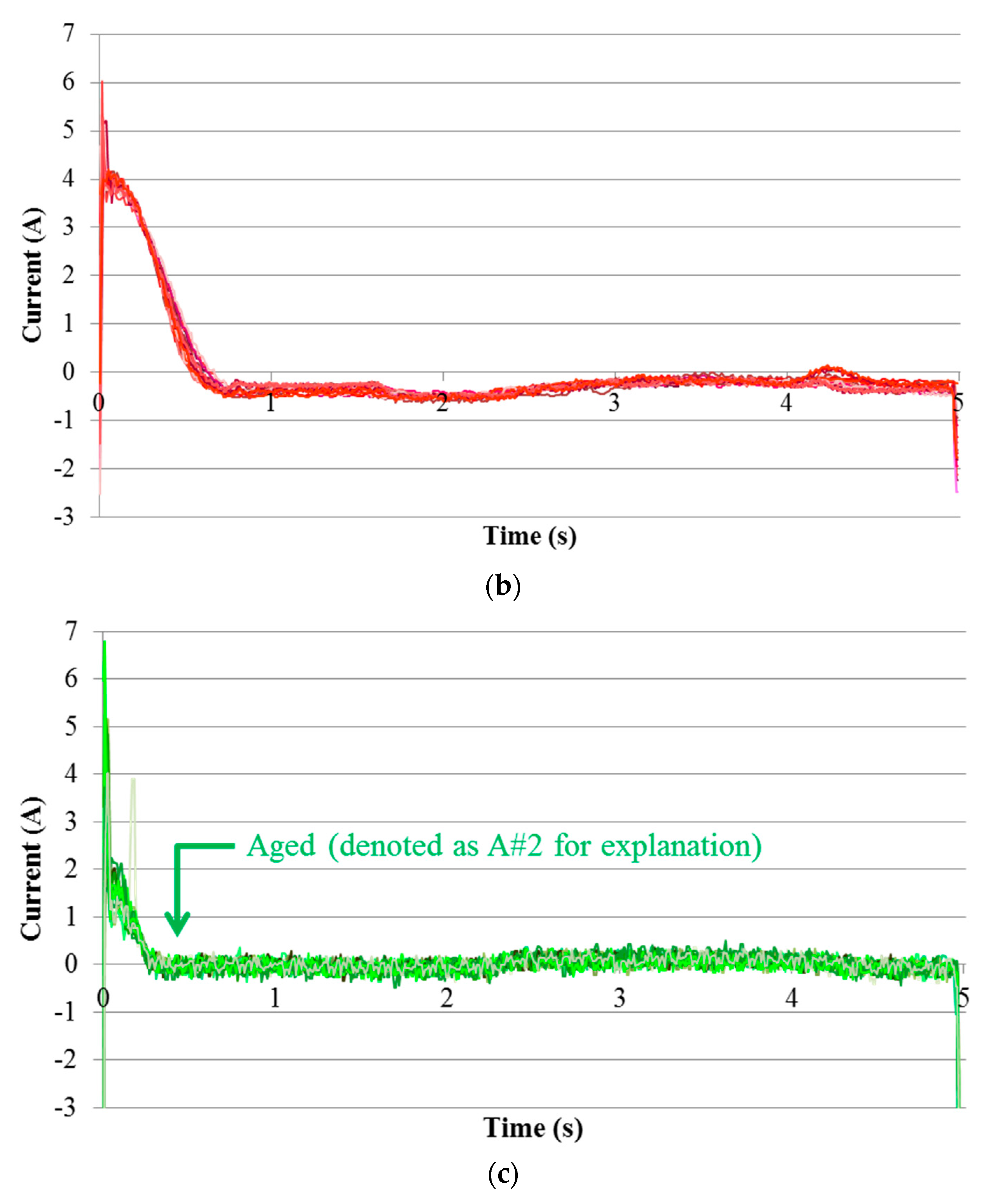
3.1. In-Field Current Signals
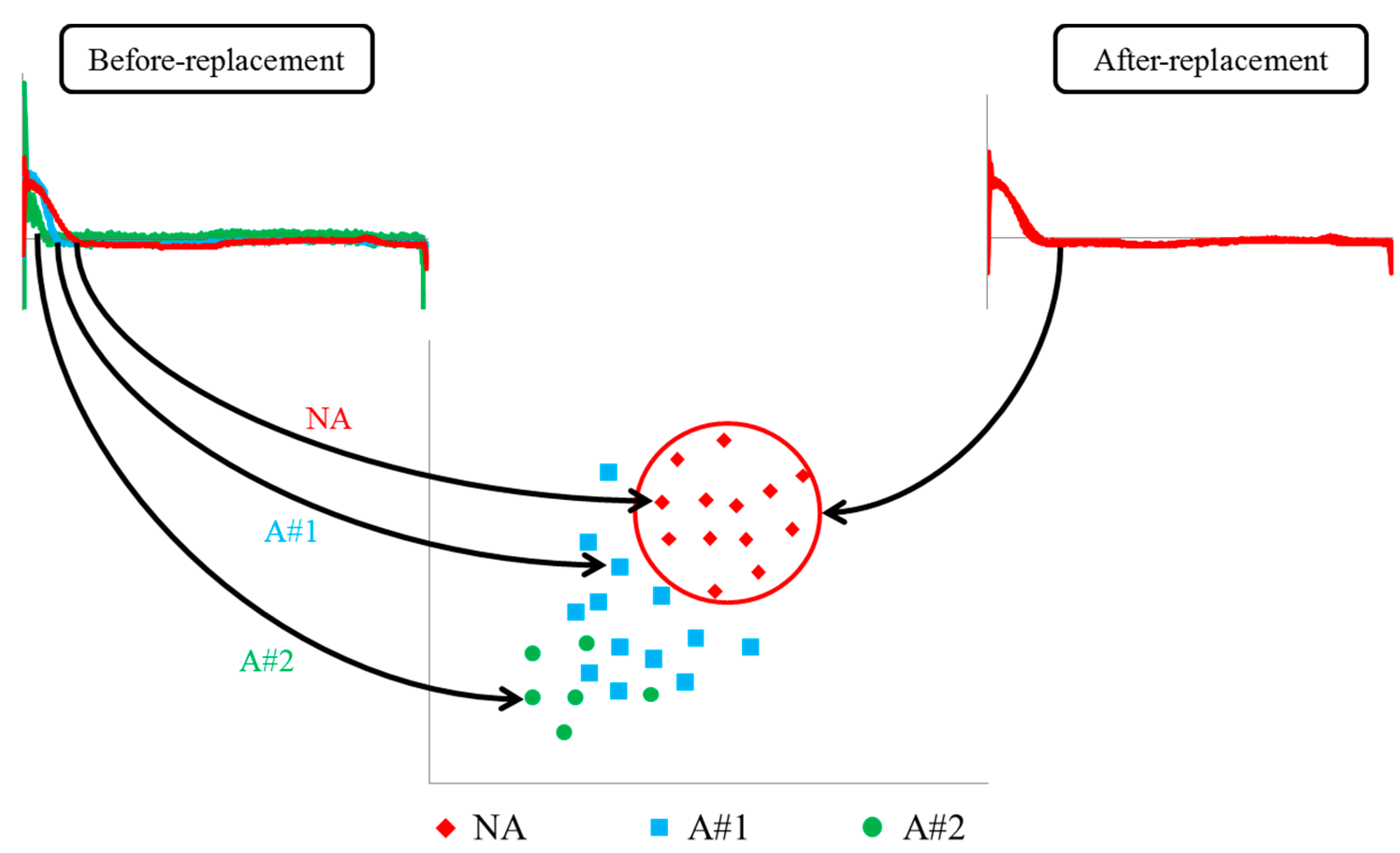
3.2. Results and Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yin, S.; Ding, X.; Zhou, D. Diagnosis and Prognosis for Complicated Industrial Systems-Part 1. IEEE Trans. Ind. Electron. 2016, 63, 2501–2505. [Google Scholar] [CrossRef]
- Fang, X.; Gebraeel, N.Z.; Paynabar, K. Scalable Prognostic Models for Large-scale Condition Monitoring Applications. IISE Trans. 2017, 49, 698–710. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Yang, X.; Dong, C. A Fault Feature Extraction Method for Motor Bearing and Transmission Analysis. Symmetry 2017, 9, 60. [Google Scholar] [CrossRef]
- Dalvand, F.; Dalvand, S.; Sharafi, F.; Pecht, M. Current Noise Cancellation for Bearing Fault Diagnosis Using Time-Shifting. IEEE Trans. Ind. Electron. 2017, 64, 8138–8147. [Google Scholar] [CrossRef]
- Jin, W.; Shi, Z.; Siegel, D.; Dersin, P.; Douziech, C.; Pugnaloni, M.; Cascia, P.; Lee, J. Development and Evaluation of Health Monitoring Techniques for Railway Point Machines. In Proceedings of the IEEE Conference on Prognostics and Health Management, Austin, TX, USA, 22–25 June 2015. [Google Scholar]
- Zhou, H.; Shi, T.; Liao, G.; Xuan, J.; Duan, J.; Su, L.; He, Z.; Lai, W. Weighted Kernel Entropy Component Analysis for Fault Diagnosis of Rolling Bearings. Sensors 2017, 17, 625. [Google Scholar] [CrossRef] [PubMed]
- Gilchrist, A. Introducing Industry 4.0; Apress: New York, NY, USA, 2016; pp. 195–215. [Google Scholar]
- Thurston, D.F. Broken Rail Detection: Practical Application of New Technology or Risk Mitigation Approaches. IEEE Veh. Technol. Mag. 2014, 9, 80–85. [Google Scholar] [CrossRef]
- Boldolamiri, N.; Sani, M.; Mirabadi, A. Time-Domain Stator Current Condition Monitoring: Analyzing Point Failures Detection by Kolmogorov-Smirnov (K-S) Test. Int. J. Electr. Comput. Energ. Electron. Commun. Eng. 2012, 6, 587–592. [Google Scholar]
- Zarembski, A.; Palese, J. Managing Risk on the Railway Infrastructure. In Proceedings of the 7th World Congress on Railway Research, Montreal, QC, Canada, 4–8 June 2006. [Google Scholar]
- Asada, T.; Roberts, C.; Koseki, C. An Algorithm for Improved Performance of Railway Condition Monitoring Equipment: Alternating-Current Point Machine Case Study. Transp. Res. Part C Emerg. Technol. 2013, 30, 81–92. [Google Scholar] [CrossRef]
- Lee, J.; Choi, H.; Park, D.; Chung, Y.; Kim, H.-Y.; Yoon, S. Fault Detection and Diagnosis of Railway Point Machines by Sound Analysis. Sensors 2016, 16, 549. [Google Scholar] [CrossRef] [PubMed]
- Vileiniskis, M. Fault Detection and Diagnosis Methods for Engineering Systems. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2015. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Kim, H.; Sa, J.; Chung, Y.; Park, D.; Yoon, S. Fault Diagnosis of Railway Point Machines using Dynamic Time Warping. Electron. Lett. 2016, 52, 818–819. [Google Scholar] [CrossRef]
- Rakthanmanon, T.; Keogh, E. Fast Shapelets: A Scalable Algorithm for Discovering Time Series Shapelets. In Proceedings of the SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; pp. 668–676. [Google Scholar]
- Sa, J.; Choi, Y.; Chung, Y.; Kim, H.-Y.; Park, D.; Yoon, S. Replacement Condition Detection of Railway Point Machines Using an Electric Current Sensor. Sensors 2017, 17, 263. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D. Rolling Bearing Fault Diagnostic Method based on VMD-AR Model and Random Forest Classifier. Shock Vib. 2016, 2016, 11. [Google Scholar] [CrossRef]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal Classifier for Imbalanced Data using Matthews Correlation Coefficient Metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef] [PubMed]
- He, M.; He, D. Deep Learning Based Approach for Bearing Fault Diagnosis. IEEE Trans. Ind. Appl. 2017, 53, 3057–3065. [Google Scholar] [CrossRef]
- Fuan, W.; Hongkai, J.; Haidong, S.; Wenjing, D.; Shuaipeng, W. An Adaptive Deep Convolutional Neural Network for Rolling Bearing Fault Diagnosis. Meas. Sci. Technol. 2017, 28, 18. [Google Scholar] [CrossRef]

| Station | Name of EPM | Operating Period | Total Movements | Aging Status |
|---|---|---|---|---|
| A | 22B | 2002.09–2014.12 | 4654 | Aging |
| 23A | 2002.05–2014.12 | 2059 | Aging | |
| 23B | 2002.05–2014.12 | 1284 | Aging | |
| 24A | 2002.09–2014.12 | 8968 | Aging | |
| 24B | 2002.09–2014.12 | 2596 | Aging | |
| 25 | 2002.05–2014.11 | 2981 | Aging | |
| 26B | 2002.05–2014.11 | 9388 | Aging | |
| 27B | 2002.09–2014.11 | 5367 | Aging | |
| 28 | 2002.09–2014.11 | 33,272 | Aging | |
| 52B | 2002.11–2014.11 | 3193 | Aging | |
| 54A | 2002.10–2014.11 | 8624 | Aging | |
| 54B | 2002.10–2014.11 | 8260 | Aging | |
| 57B | 2002.10–2014.11 | 13,674 | Aging | |
| 58 | 2002.10–2014.11 | 22,953 | Aging | |
| B | 21A | 2002.04–2014.12 | 4376 | Aging |
| 22A | 2002.04–2014.12 | 8245 | Aging | |
| 55 | 2000.12–2014.03 | 653 | Aging | |
| C | 22B | 2001.01–2014.05 | 107,927 | Aging |
| 23 | 2001.01–2014.05 | 70,022 | Aging | |
| 25B | 2002.01–2014.05 | 83,276 | Not aging | |
| 51A | 2002.01–2014.12 | 22,304 | Aging | |
| 54B | 2001.01–2014.12 | 12,875 | Aging | |
| 58A | 2001.01–2014.12 | 66,050 | Aging | |
| 59 | 2001.01–2014.12 | 77,214 | Aging | |
| D | 32 | 2004.04–2014.12 | 11,442 | Aging |
| E | 21B | 2000.12–2014.03 | 23,517 | Not aging |
| 22 | 1998.05–2014.03 | 113,811 | Aging | |
| 51A | 2002.04–2014.12 | 5778 | Not aging | |
| 52 | 2002.04–2014.12 | 391,141 | Not aging | |
| 55A | 2002.04–2014.12 | 52,906 | Not aging | |
| F | 51A | 2000.12–2014.03 | 6303 | Aging |
| 51B | 2001.12–2014.11 | 5209 | Aging | |
| 52 | 2000.12–2014.03 | 82,795 | Aging | |
| 53 | 2000.12–2014.11 | 12,195 | Aging | |
| G | 22 | 2000.01–2014.12 | 108,600 | Aging |
| 23A | 1997.01–2014.12 | 11,269 | Aging | |
| 23B | 1997.01–2014.12 | 11,282 | Aging | |
| 51A | 1997.01–2014.11 | 436 | Aging | |
| 53 | 1997.01–2014.12 | 62,658 | Aging |
| # of Repetitions | # of Folds | MCC | |||
|---|---|---|---|---|---|
| Proposed Method | Shapelet [16] | SVM [18] | Random Forest [19] | ||
| Repetition 1 | 1 | 0.94 | 0.86 | 0.89 | 0.88 |
| 2 | 0.93 | 0.87 | 0.86 | 0.90 | |
| 3 | 0.95 | 0.83 | 0.87 | 0.92 | |
| 4 | 0.94 | 0.85 | 0.87 | 0.96 | |
| 5 | 0.95 | 0.86 | 0.94 | 0.89 | |
| Repetition 2 | 1 | 0.94 | 0.86 | 0.91 | 0.91 |
| 2 | 0.96 | 0.77 | 0.96 | 0.87 | |
| 3 | 0.93 | 0.79 | 0.86 | 0.91 | |
| 4 | 0.94 | 0.84 | 0.88 | 0.71 | |
| 5 | 0.96 | 0.83 | 0.87 | 0.90 | |
| Repetition 3 | 1 | 0.95 | 0.81 | 0.97 | 0.91 |
| 2 | 0.90 | 0.83 | 0.85 | 0.95 | |
| 3 | 0.96 | 0.76 | 0.86 | 0.94 | |
| 4 | 0.97 | 0.84 | 0.91 | 0.92 | |
| 5 | 0.93 | 0.81 | 0.91 | 0.91 | |
| Repetition 4 | 1 | 0.94 | 0.92 | 0.98 | 0.91 |
| 2 | 0.93 | 0.85 | 0.85 | 0.89 | |
| 3 | 0.96 | 0.78 | 0.86 | 0.94 | |
| 4 | 0.95 | 0.84 | 0.92 | 0.86 | |
| 5 | 0.96 | 0.82 | 0.92 | 0.92 | |
| Repetition 5 | 1 | 0.89 | 0.81 | 0.88 | 0.93 |
| 2 | 0.96 | 0.91 | 0.85 | 0.95 | |
| 3 | 0.97 | 0.87 | 0.97 | 0.96 | |
| 4 | 0.95 | 0.81 | 0.98 | 0.88 | |
| 5 | 0.94 | 0.84 | 0.88 | 0.86 | |
| Average | – | 0.94 | 0.83 | 0.90 | 0.90 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sa, J.; Choi, Y.; Chung, Y.; Lee, J.; Park, D. Aging Detection of Electrical Point Machines Based on Support Vector Data Description. Symmetry 2017, 9, 290. https://doi.org/10.3390/sym9120290
Sa J, Choi Y, Chung Y, Lee J, Park D. Aging Detection of Electrical Point Machines Based on Support Vector Data Description. Symmetry. 2017; 9(12):290. https://doi.org/10.3390/sym9120290
Chicago/Turabian StyleSa, Jaewon, Younchang Choi, Yongwha Chung, Jonguk Lee, and Daihee Park. 2017. "Aging Detection of Electrical Point Machines Based on Support Vector Data Description" Symmetry 9, no. 12: 290. https://doi.org/10.3390/sym9120290
APA StyleSa, J., Choi, Y., Chung, Y., Lee, J., & Park, D. (2017). Aging Detection of Electrical Point Machines Based on Support Vector Data Description. Symmetry, 9(12), 290. https://doi.org/10.3390/sym9120290






