Analytical Treatment of Higher-Order Graphs: A Path Ordinal Method for Solving Graphs
Abstract
:1. Introduction
2. Materials and Methods
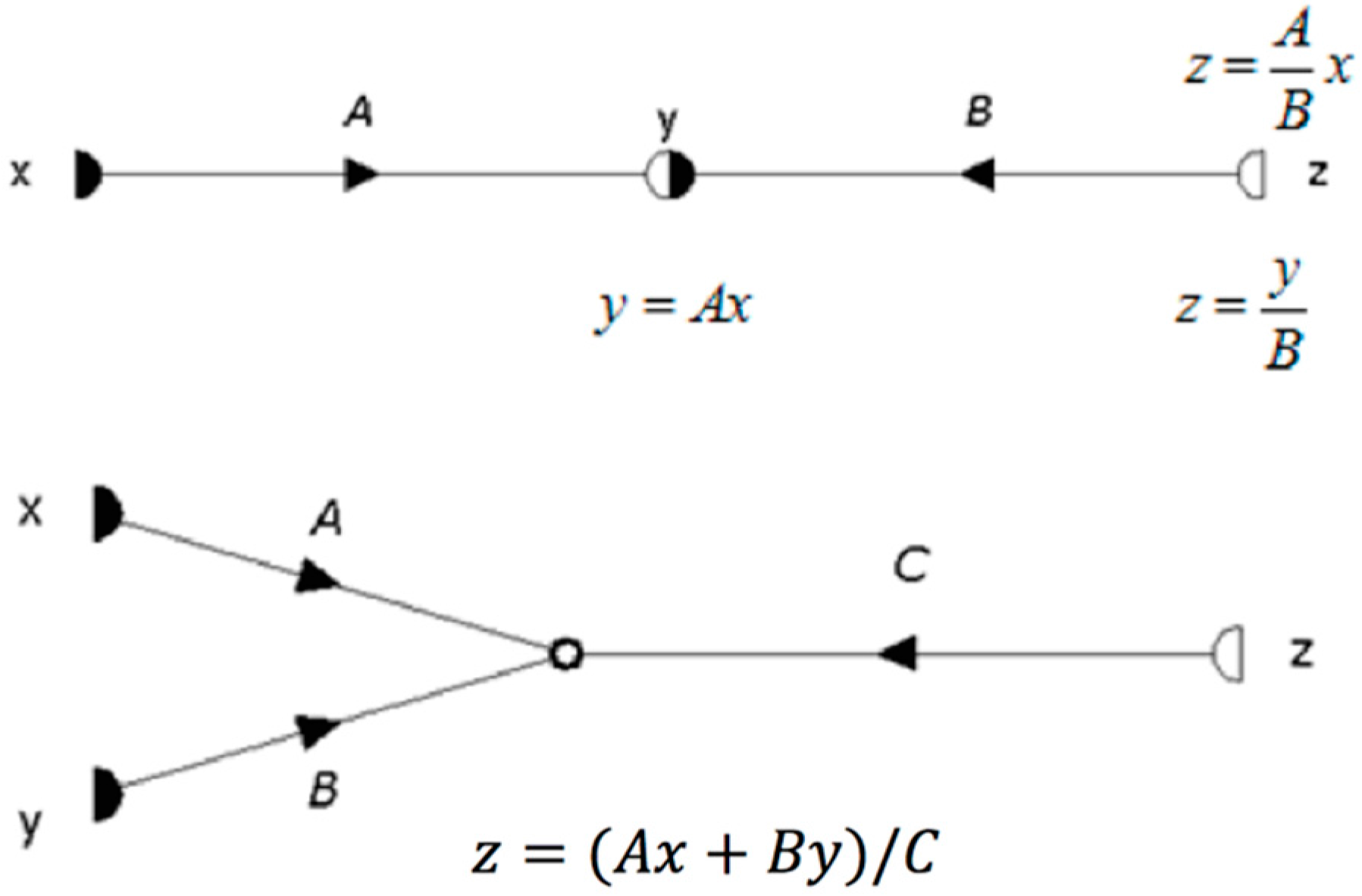
2.1. Flow Graphs
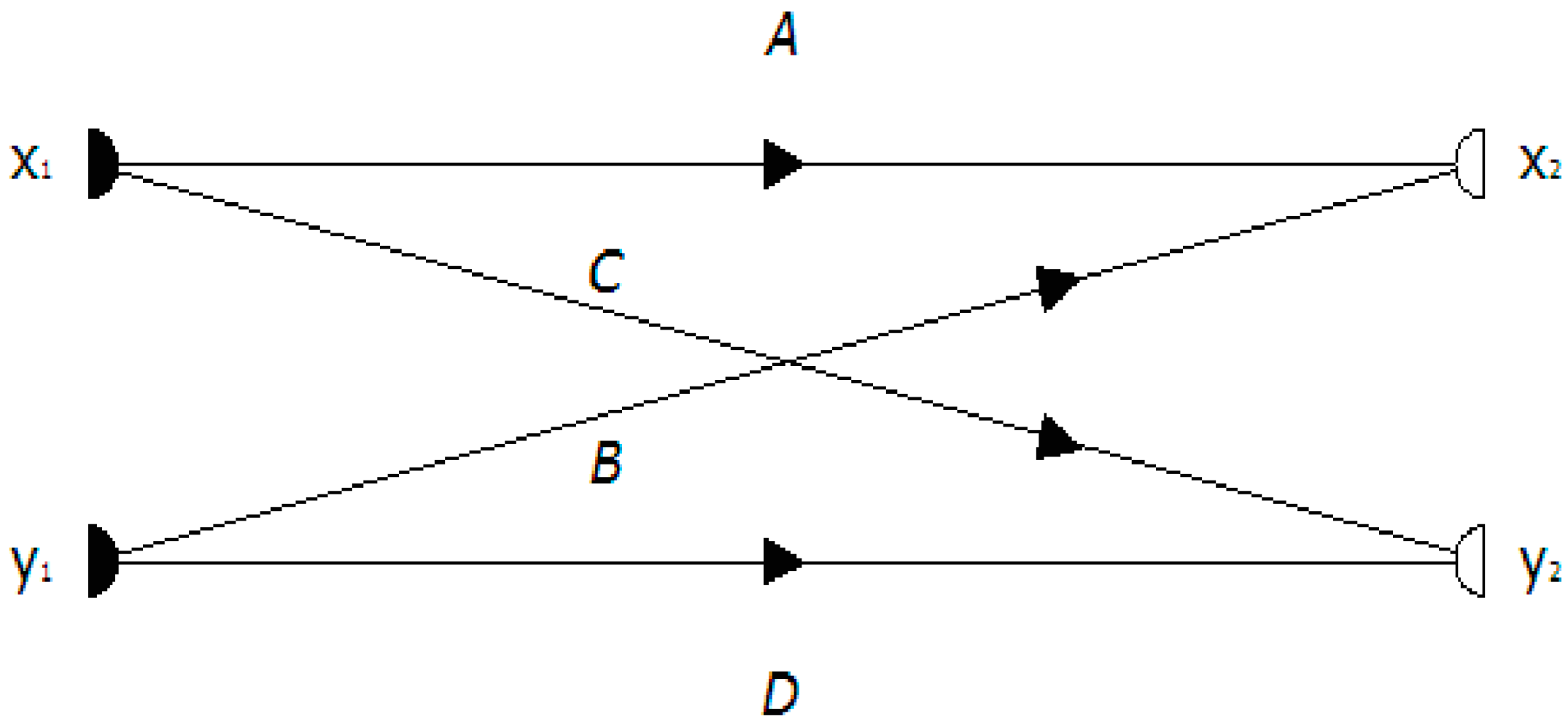
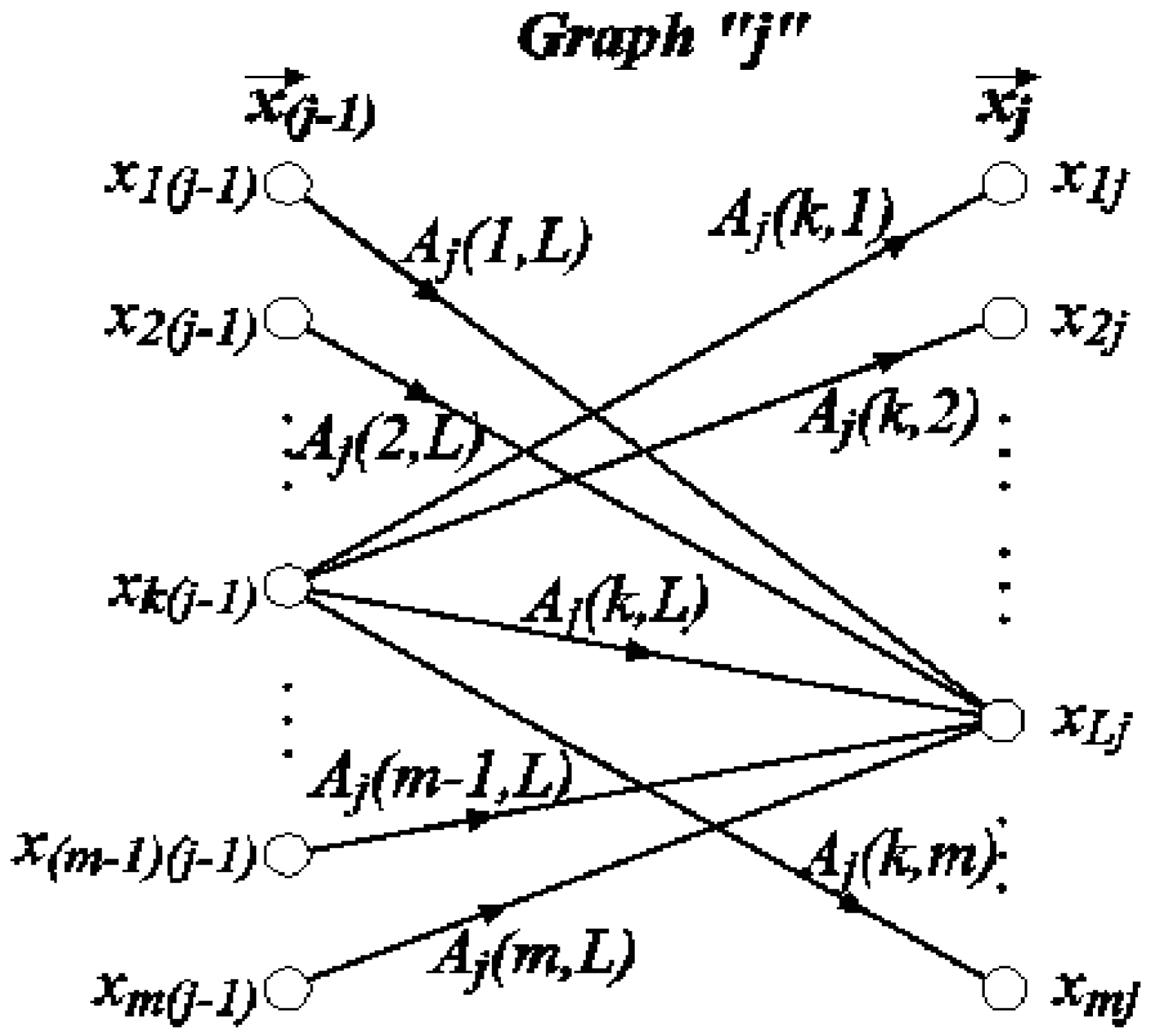
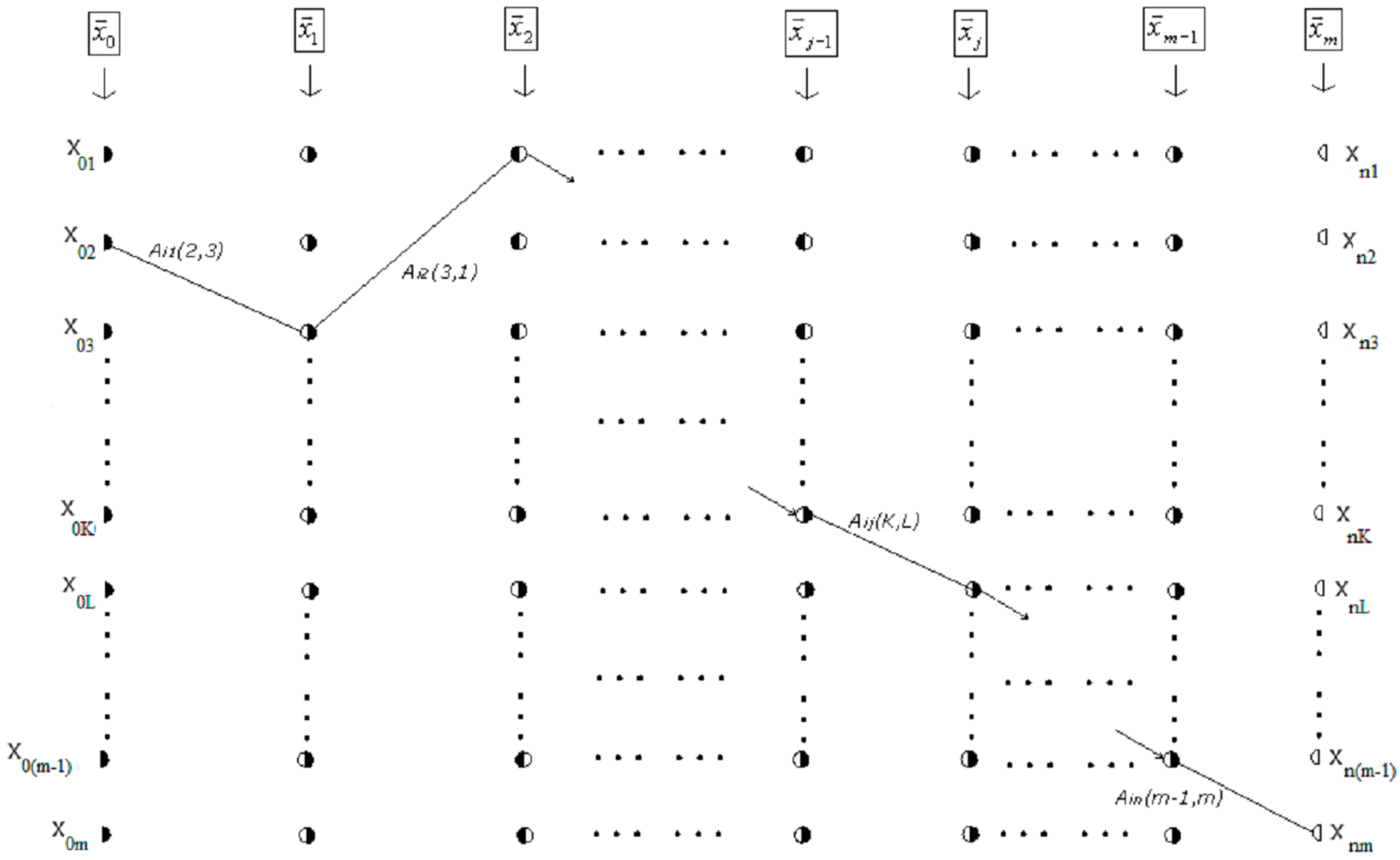
2.2. Graph Composition and Path Characterization
2.2.1. Ordinal of a Path and Path Value
2.2.2. Determination of the Characteristic Path Set
- I
- The path ordinal is subtracted by one.
- II
- Then, it is divided by m for n-times.
- III
- Finally, one is added to the remainders of the division, R1, C1, C2, …, Cn.
2.3. Examples and Concluding Remarks
2.3.1. The Contribution of and Input Parameter to an Output Parameter
| 12 − 1 = | 11 | 3 | 15 − 1 = | 14 | 3 | 18 − 1 = | 17 | 3 | |||||
| : | 3 | 3 | : | 4 | 3 | : | 5 | 3 | |||||
| : | : | 1 | : | : | 1 | : | : | 1 | |||||
| : | : | : | : | : | : | : | : | : | |||||
| 2 | 0 | 1 | 2 | 1 | 1 | 2 | 2 | 1 | |||||
| +1 | 3 | 1 | 2 | +1 | 3 | 2 | 2 | +1 | 3 | 3 | 2 |
2.3.2. The Total Solution
3. Results and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Euler, L. The Seven Bridges of Konigsberg. Comment. Acad. Sci. Imp. Petropolitanae 1741, 8, 128–140. [Google Scholar]
- Wang, S.; Zhao, D. Matrix Optics; Zhejiang University Press: Hangzhou, China, 2000. [Google Scholar]
- Feynman, R.P. Quantum Electrodynamics; Perseus: New York, NY, USA, 1998. [Google Scholar]
- Peskin, M.E.; Schroeder, D.V. Quantum Field Theory; Perseus: New York, NY, USA, 1995. [Google Scholar]
- Weissman, Y. Optical Network Theory; Artech: New York, NY, USA, 1992. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; North-Holland: Oxford, UK, 1976. [Google Scholar]
- Coates, C.L. Flow—Graph Solutions of Linear Algebric Equations. IRE Trans. Circuit Theory 1959, 6, 170–187. [Google Scholar] [CrossRef]
- Chen, W.-K. On Flow graph Solutions of Linear Algebric Equations. SIAM J. Appl. Math. 1967, 15, 136–142. [Google Scholar] [CrossRef]
- Kamal, H.; Bernabeu, E. High order graph formalism for multilayer structures. Opt. Int. J. Light Electron Opt. 2016, 127, 1384–1390. [Google Scholar] [CrossRef]


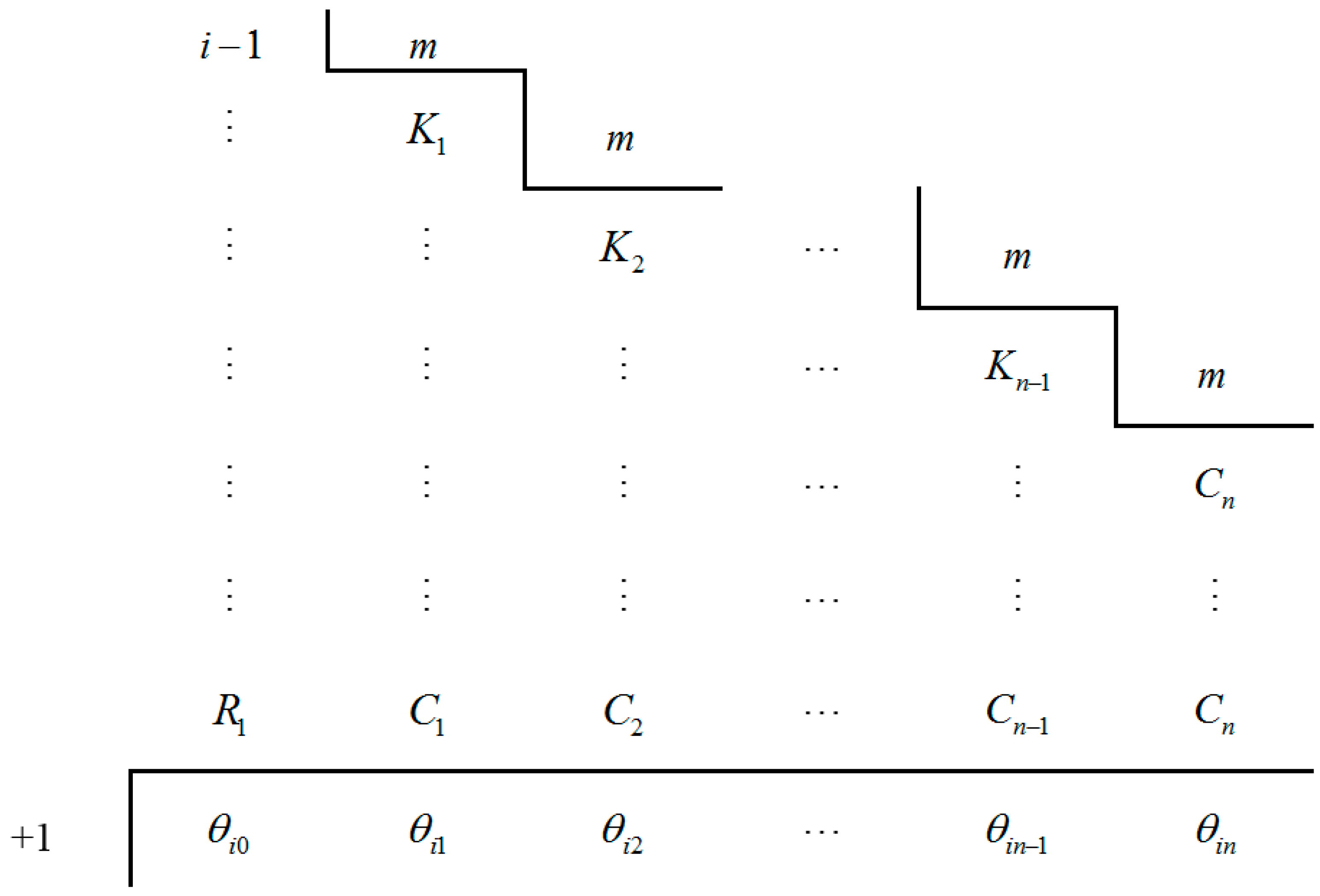
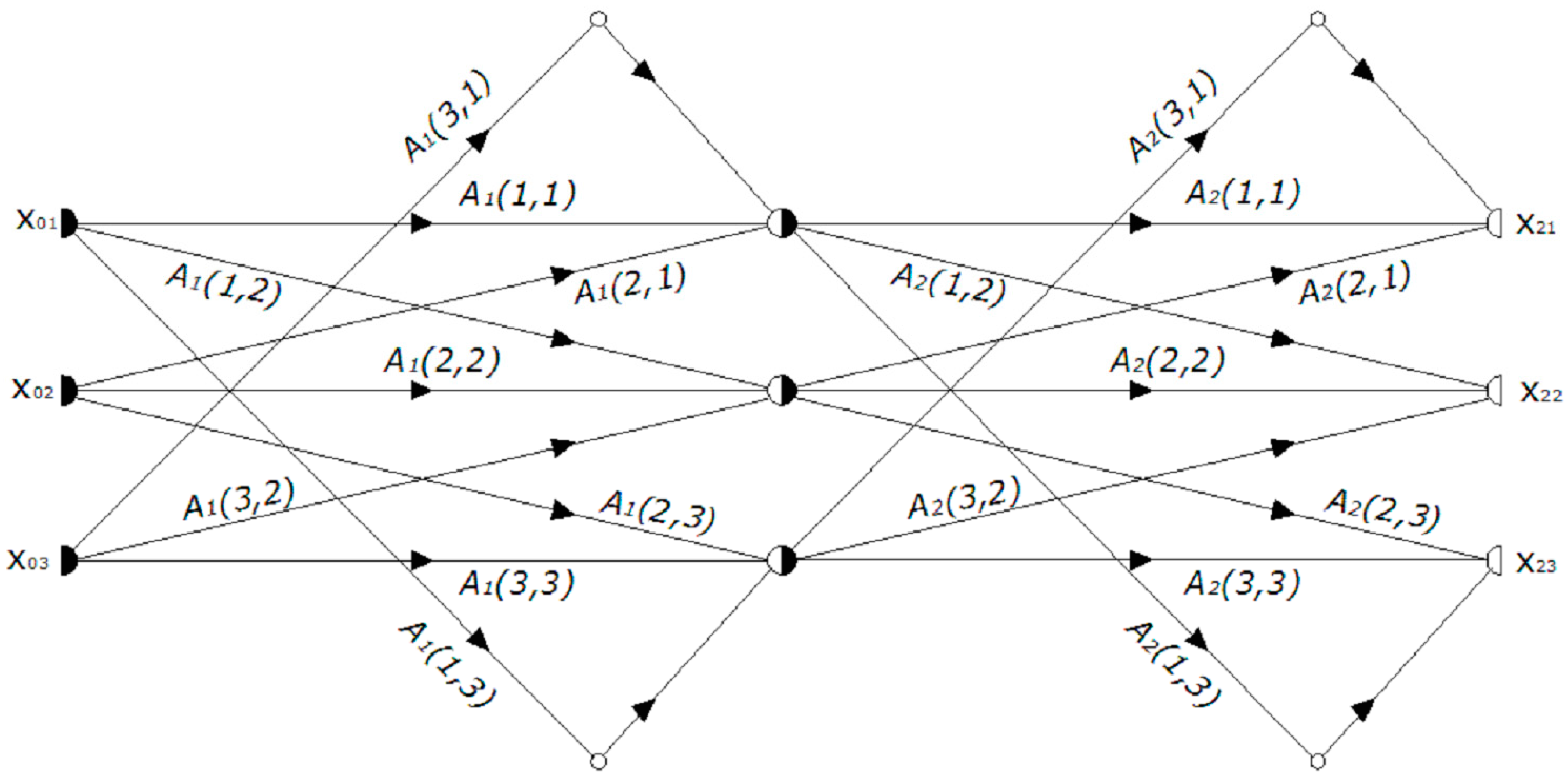

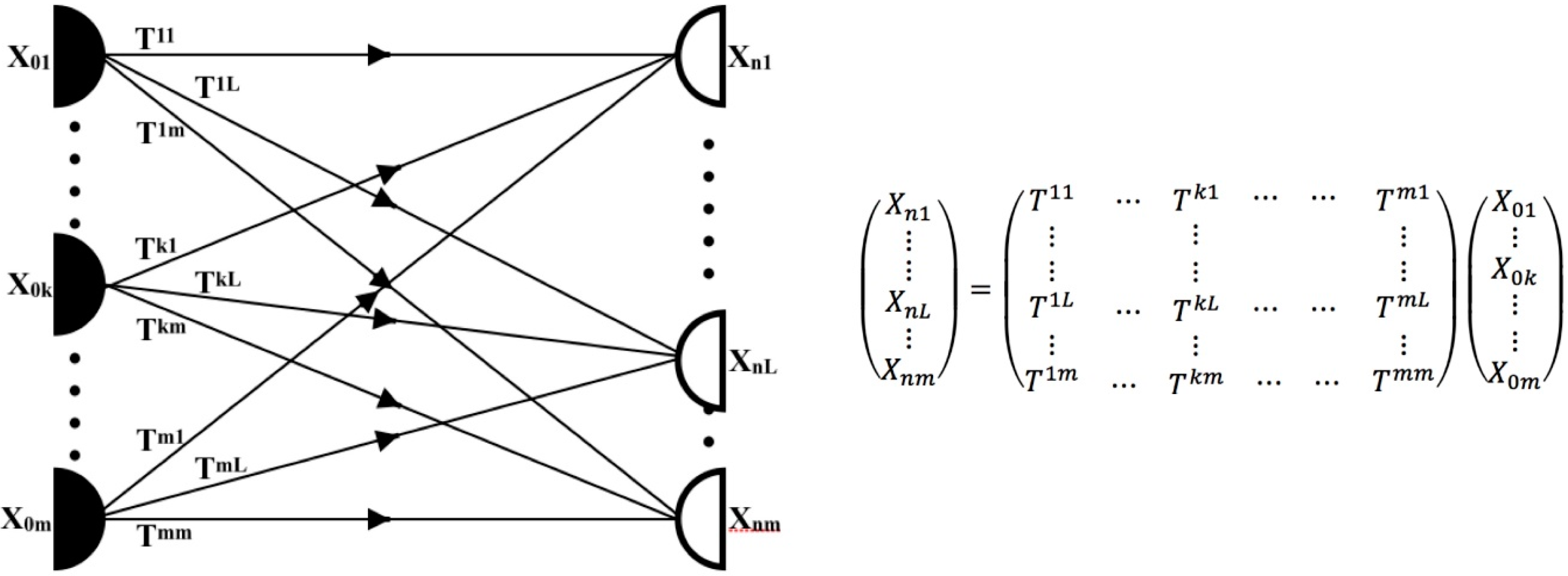
| i | θi0 | θi1 | θi2 | i | θi0 | θi1 | θi2 | i | θi0 | θi1 | θi2 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 10 | 1 | 1 | 2 | 19 | 1 | 1 | 3 | ||
| 2 | 2 | 1 | 1 | 11 | 2 | 1 | 2 | 20 | 2 | 1 | 3 | ||
| 3 | 3 | 1 | 1 | 12 | 3 | 1 | 2 | 21 | 3 | 1 | 3 | ||
| 4 | 1 | 2 | 1 | 13 | 1 | 2 | 2 | 22 | 1 | 2 | 3 | ||
| 5 | 2 | 2 | 1 | 14 | 2 | 2 | 2 | 23 | 2 | 2 | 3 | ||
| 6 | 3 | 2 | 1 | 15 | 3 | 2 | 2 | 24 | 3 | 2 | 3 | ||
| 7 | 1 | 3 | 1 | 16 | 1 | 3 | 2 | 25 | 1 | 3 | 3 | ||
| 8 | 2 | 3 | 1 | 17 | 2 | 3 | 2 | 26 | 2 | 3 | 3 | ||
| 9 | 3 | 3 | 1 | 18 | 3 | 3 | 2 | 27 | 3 | 3 | 3 |
| Pi | Path Value | Pi | Path Value | Pi | Path Value |
|---|---|---|---|---|---|
| P1 | A1(1,1)*A2(1,1) | P10 | A1(1,1)*A2(1,2) | P19 | A1(1,1)*A2(1,3) |
| P2 | A1(2,1)*A2(1,1) | P11 | A1(2,1)*A2(1,2) | P20 | A1(2,1)*A2(1,3) |
| P3 | A1(3,1)*A2(1,1) | P12 | A1(3,1)*A2(1,2) | P21 | A1(3,1)*A2(1,3) |
| P4 | A1(1,2)*A2(2,1) | P13 | A1(1,2)*A2(2,2) | P22 | A1(1,2)*A2(2,3) |
| P5 | A1(2,2)*A2(2,1) | P14 | A1(2,2)*A2(2,2) | P23 | A1(2,2)*A2(2,3) |
| P6 | A1(3,2)*A2(2,1) | P15 | A1(3,2)*A2(2,2) | P24 | A1(3,2)*A2(2,3) |
| P7 | A1(1,3)*A2(3,1) | P16 | A1(1,3)*A2(3,2) | P25 | A1(1,3)*A2(3,3) |
| P8 | A1(2,3)*A2(3,1) | P17 | A1(2,3)*A2(3,2) | P26 | A1(2,3)*A2(3,3) |
| P9 | A1(3,3)*A2(3,1) | P18 | A1(3,3)*A2(3,2) | P27 | A1(3,3)*A2(3,3) |
| T11 = P1 + P4 + P7 | T21 = P2 + P5 + P8 | T31 = P3 + P6 + P9 |
| T12 = P10 + P13 + P16 | T22 = P11 + P14 + P17 | T32 = P12 + P15 + P18 |
| T13 = P19 + P22 + P25 | T23 = P20 + P23 + P26 | T33 = P21 + P24 + P27 |
| Path Ordinal Pi | Path Set | Path Value |
|---|---|---|
| 1 | {1, 1…………...…..., 1} | P1 = A1(1,1)*………………An(1,1) |
| : | : | : |
| mn | {m, m…………….…, 1} | = A1(m,m)*………….An(m,1) |
| : | : | : |
| : | : | : |
| mn+1 | {m, m……………..., m} | = A1(m,m)*………...An(m,m) |
| … | … | |||
| : : | … | : : | … | : : |
| … | … | |||
| : : | … | : : | … | : : |
| … | … |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamal, H.; Larena, A.; Bernabeu, E. Analytical Treatment of Higher-Order Graphs: A Path Ordinal Method for Solving Graphs. Symmetry 2017, 9, 288. https://doi.org/10.3390/sym9110288
Kamal H, Larena A, Bernabeu E. Analytical Treatment of Higher-Order Graphs: A Path Ordinal Method for Solving Graphs. Symmetry. 2017; 9(11):288. https://doi.org/10.3390/sym9110288
Chicago/Turabian StyleKamal, Hala, Alicia Larena, and Eusebio Bernabeu. 2017. "Analytical Treatment of Higher-Order Graphs: A Path Ordinal Method for Solving Graphs" Symmetry 9, no. 11: 288. https://doi.org/10.3390/sym9110288
APA StyleKamal, H., Larena, A., & Bernabeu, E. (2017). Analytical Treatment of Higher-Order Graphs: A Path Ordinal Method for Solving Graphs. Symmetry, 9(11), 288. https://doi.org/10.3390/sym9110288





