Granular Structure of Type-2 Fuzzy Rough Sets over Two Universes

Abstract

Granular structure plays a very important role in the model construction, theoretical analysis and algorithm design of a granular computing method. The granular structures of classical rough sets and fuzzy rough sets have been proven to be clear. In classical rough set theory, equivalence classes are basic granules, and the lower and upper approximations of a set can be computed by those basic granules. In the theory of fuzzy rough set, granular fuzzy sets can be used to describe the lower and upper approximations of a fuzzy set. This paper discusses the granular structure of type-2 fuzzy rough sets over two universes. Definitions of type-2 fuzzy rough sets over two universes are given based on a wavy-slice representation of type-2 fuzzy sets. Two granular type-2 fuzzy sets are deduced and then proven to be basic granules of type-2 fuzzy rough sets over two universes. Then, the properties of lower and upper approximation operators and these two granular type-2 fuzzy sets are investigated. At last, several examples are given to show the applications of type-2 fuzzy rough sets over two universes.

1. Introduction

According to Chen et al., granular computing is a general computing theory for using granules such as classes, clusters, subsets, groups and intervals to build an efficient computational model for complex applications with huge amounts of data, information and knowledge [1].

Rough set theory [2], proposed by Pawlak in 1982, can be used to reveal and express knowledge hidden in information systems in the form of decision rules by the concepts of lower and upper approximations. Here, equivalence classes are used as the basic granules to express the lower and upper approximations. Taken in this sense, rough set theory is a granular computing method.

Traditional rough set theory only manipulated decision systems with symbolic attribute values, whereas in some real-world applications, the values of attributes could be both symbolic and real-valued. In 1990, Dubois and Prade [3] proposed the definition of fuzzy rough sets by combining fuzzy sets and rough sets, then many studies were carried out in the field of fuzzy rough sets [4,5,6,7,8,9,10,11,12,13,14]. In [15], fuzzy rough sets were applied to feature selection for the first time. Wu et al. studied the generalized fuzzy rough sets using both constructive and axiomatic approaches [16,17]. Mi and Zhang [18] introduced the definitions of generalized fuzzy lower and upper approximation operators determined by a residual implication and studied the composition of two approximation spaces. Yeung et al. [19] studied the lattice and topological structures of fuzzy rough sets. Chen et al. discussed the granular structure of fuzzy rough sets and developed a theory of granular computing based on fuzzy relations in [20]. They proposed the concept of granular fuzzy sets and investigated the properties of these sets using constructive and axiomatic approaches. The granular fuzzy sets were used to describe the lower and upper approximations of a fuzzy set within the framework of granular computing, and the structure of attribute reduction in terms of granular fuzzy sets was characterized.

Type-2 fuzzy rough set is a combination of rough sets and type-2 fuzzy sets. As an extension of fuzzy sets, type-2 fuzzy sets [21] are useful in circumstances where it is difficult to determine the exact membership functions of a fuzzy set because the membership degrees are fuzzy themselves. Type-2 fuzzy rough sets may solve problems with higher complexity, and there have been several literature works in this field [22,23,24]. In some practical applications, we often encounter situations involving more than one universe. For example, in medical diagnosis, a certain disease may simultaneously have several symptoms, whereas one symptom may be shared by different diseases. Zhang et al. [25] proposed a general study of interval-valued fuzzy rough sets on two universes of discourse. Sun et al. [26] defined the fuzzy compatible relation and presented the fuzzy rough set model on the different universes. Liu et al. proposed the graded rough set model on two distinct, but related universes in [27]. Ma et al. [28] presented the properties of the probabilistic rough set over two universes and discussed the uncertainty measure of the knowledge granularity and rough entropy for a probabilistic rough set over two universes. Sun et al. [29] considered a problem of emergency material demand prediction based on a fuzzy rough set model over two universes. Yang et al. proposed a fuzzy probabilistic rough set model on two universes and presented concepts of the inverse lower and upper approximation operators in [30]. However, type-2 fuzzy rough sets over two universes have not been discussed.

As generalizations of rough sets, type-2 fuzzy rough sets over one or two universes can be incorporated into the scope of granular computing if we can reveal their granular structures, and the granular structures will be beneficial to their application. In [24], we generalized the concepts of granular fuzzy sets in [20] to the frame of type-2 fuzzy sets and presented a definition of granular type-2 fuzzy sets without proof of its reasonability. Then, we discussed the granular structure of type-2 fuzzy rough sets over one universe based on these two granular type-2 fuzzy sets.

In this paper, the granular structure discussed in [24] will be generalized to the type-2 fuzzy rough sets over different universes based on novel granular type-2 fuzzy sets, which are deduced from the definition of type-2 fuzzy rough sets, and consequently, more reasonable than those given in [24]. The rest of this paper is organized as follows. Fundamental concepts and properties that will be used in this paper are reviewed in Section 2. Section 3 introduces the definition of a type-2 fuzzy rough set over two universes. In Section 4, the granular structure of type-2 fuzzy rough sets over two universes is discussed using granular type-2 fuzzy sets. Some illustrative examples are given in Section 5, and conclusions are presented in Section 6.

2. Preliminaries

2.1. Type-2 Fuzzy Sets

To facilitate the discussion, we introduce the basic definitions and properties of type-2 fuzzy sets in this section with reference to [31,32].

For a nonempty universe X, a type-2 fuzzy set $\tilde{A}$ on X can be characterized by a type-2 membership function ${\mu }_{\tilde{A}}(x,u)$, i.e.,

$$\tilde{A}=\{((x,u),{\mu }_{\tilde{A}}(x,u))|x\in X,u\in J_x\subseteq [0,1]\},$$

or

$$\tilde{A}={\int }_{x\in X}{\int }_{u\in J_x}{\mu }_{\tilde{A}}(x,u)/(x,u),J_x\subseteq [0,1],$$

where $0\le {\mu }_{\tilde{A}}(x,u)\le 1$ and $\int \int$ denotes union over all admissible x and u. $\tilde{F}(X)$ denotes the class of all type-2 fuzzy sets on the universe X.

For a given $x^{\prime }$, ${\mu }_{\tilde{A}}(x^{\prime },u)$ is a fuzzy set on $J_{x^{\prime }}$, which is called a vertical slice of ${\mu }_{\tilde{A}}(x,u)$ or a secondary membership function, and it can be denoted by ${\mu }_{\tilde{A}}(x^{\prime })$ or $f_{x^{\prime }}$. $J_{x^{\prime }}$ is called the primary membership of $x^{\prime }$. The amplitude of a secondary membership function is called a secondary grade. A vertical-slice representation of a type-2 fuzzy set is:

$$\tilde{A}={\int }_{x\in X}{\mu }_{\tilde{A}}(x)/x={\int }_{x\in X}[{\int }_{u\in J_x}{f}_x(u)/u]/x.$$

Mendel and John [32] presented a wavy-slice representation for discrete type-2 fuzzy sets (both X and $J_x$ are assumed to be discrete) in 2002. Suppose that X is discretized into N values, $x_1,\dots ,x_N,$ and that at each of these values, $J_{x_i}$ is discretized into $M_i$ values, i.e.,

$$\tilde{A}=[\sum _{k=1}^{M_1}{f}_{x_1}(u_1^{(k)})/u_1^{(k)}]/x_1+\dots +[\sum _{k=1}^{M_N}{f}_{x_N}(u_N^{(k)})/u_N^{(k)}]/x_N.$$

For a discrete type-2 fuzzy set $\tilde{A}$, take exactly one element from $J_{x_1}$, $J_{x_2},\dots$, $J_{x_N}$, namely $u_1^j$, $u_2^j,\dots$, $u_N^j$, each with its associated secondary grade, namely $f_{x_1}(u_1^j)$, $f_{x_2}(u_2^j),\dots$, $f_{x_N}(u_N^j)$, then we get a wavy-slice of $\tilde{A}$, i.e.,

$${\tilde{A}}_j=\sum _{i=1}^N[f_{x_i}(u_i^j)/u_i^j]/x_i,u_i^j\in J_{x_i}\subseteq [0,1],$$

which is called an embedded type-2 set. An embedded type-1 set $A_j$ is the union of all the primary memberships of set ${\tilde{A}}_j$, i.e.,

$$A_j=\sum _{i=1}^N{u}_i^j/x_i,u_i^j\in J_{x_i}\subseteq [0,1].$$

The total of ${\tilde{A}}_j$ is ${\prod }_{i=1}^N{M}_i$ and so is that of $A_j$.

The Representation Theorem [32] (the wavy-slice representation of a type-2 fuzzy set) proposed by Mendel and John indicates that a discrete type-2 fuzzy set $\tilde{A}$ can be represented as the union of its embedded type-2 sets, i.e.,

$$\tilde{A}=\sum _{j=1}^n{\tilde{A}}_j$$

where $n={\prod }_{i=1}^N{M}_i.$

Consider two discrete type-2 fuzzy sets $\tilde{A}$ and $\tilde{B}$, which are expressed by their embedded type-2 sets:

$$\tilde{A}=\sum _{j=1}^{n_A}{\tilde{A}}_j=\sum _{j=1}^{n_A}\sum _{i=1}^N\frac{f_{x_i}(u_i^j)/u_i^j}{x_i}$$

and:

$$\tilde{B}=\sum _{k=1}^{n_B}{\tilde{B}}_k=\sum _{k=1}^{n_B}\sum _{i=1}^N\frac{g_{x_i}(w_i^k)/w_i^k}{x_i},$$

the operations of union, intersection and complement are defined as follows:

$$\begin{array}{c}{\displaystyle \tilde{A}\bigcup \tilde{B}=}\hfill \\ \sum _{j=1}^{n_A}\sum _{k=1}^{n_B}\{[f_{x_1}(u_1^j)\wedge g_{x_1}(w_1^k)/u_1^j\vee w_1^k]/x_1+\dots +\hfill \\ [f_{x_N}(u_N^j)\wedge g_{x_N}(w_N^k)/u_N^j\vee w_N^k]/x_N\},\hfill \\ {\displaystyle \tilde{A}\bigcap \tilde{B}=}\hfill \\ \sum _{j=1}^{n_A}\sum _{k=1}^{n_B}\{[f_{x_1}(u_1^j)\wedge g_{x_1}(w_1^k)/u_1^j\wedge w_1^k]/x_1+\dots +\hfill \\ [f_{x_N}(u_N^j)\wedge g_{x_N}(w_N^k)/u_N^j\wedge w_N^k]/x_N\},\hfill \end{array}$$

$${(\tilde{A})}^c=\sum _{j=1}^{n_A}(\sum _{i=1}^N[f_{x_i}(u_i^j)/(1-u_i^j)]/x_i)=\sum _{i=1}^N(\sum _{j=1}^{M_i}[f_{x_i}(u_i^j)/(1-u_i^j)])/x_i.$$

The expressions for ${\mu }_{\tilde{A}\cup \tilde{B}}(x_i)$, ${\mu }_{\tilde{A}\cap \tilde{B}}(x_i)$ and ${\mu }_{{(\tilde{A})}^c}(x_i)$ can be obtained as:

$${\mu }_{\tilde{A}\cup \tilde{B}}(x_i)=\sum _{j=1}^{n_A}\sum _{k=1}^{n_B}{f}_{x_i}(u_i^j)\wedge g_{x_i}(w_i^k)/u_i^j\vee w_i^k\equiv {\mu }_{\tilde{A}}(x_i)\bigsqcup {\mu }_{\tilde{B}}(x_i),$$

$${\mu }_{\tilde{A}\cap \tilde{B}}(x_i)=\sum _{j=1}^{n_A}\sum _{k=1}^{n_B}{f}_{x_i}(u_i^j)\wedge g_{x_i}(w_i^k)/u_i^j\wedge w_i^k\equiv {\mu }_{\tilde{A}}(x_i)\sqcap {\mu }_{\tilde{B}}(x_i),$$

$${\mu }_{{(\tilde{A})}^c}(x_i)=\sum _{j=1}^{M_i}{f}_{x_i}(u_i^j)/(1-u_i^j)\equiv \neg {\mu }_{\tilde{A}}(x_i),$$

where ${\mu }_{\tilde{A}}(x_i)\bigsqcup {\mu }_{\tilde{B}}(x_i)$ and ${\mu }_{\tilde{A}}(x_i)\sqcap {\mu }_{\tilde{B}}(x_i)$ indicate the join and meet of the secondary membership functions ${\mu }_{\tilde{A}}(x)$ and ${\mu }_{\tilde{B}}(x_i)$, and $\neg {\mu }_{\tilde{A}}(x_i)$ indicates the negation of the secondary membership function ${\mu }_{\tilde{A}}(x_i)$.

Considering two discrete type-2 fuzzy sets $\tilde{A}$ and $\tilde{B}$, which have unique embedded type-2 sets, i.e.,

$$\tilde{A}=\sum _{i=1}^N\frac{f_{x_i}(u_i)/u_i}{x_i}\mathrm{and}\tilde{B}=\sum _{i=1}^N\frac{g_{x_i}(w_i)/w_i}{x_i},$$

then $\tilde{A}⪯\tilde{B}$ is defined as $u_i\le w_i$ and $f_{x_i}(u_i)\le g_{x_i}(w_i)(\forall i=1,\dots ,N).$

For a family of discrete type-2 fuzzy sets with unique embedded type-2 sets:

$${\tilde{A}}^{(\gamma )}=\sum _{i=1}^N\frac{f_{x_i}^{(\gamma )}(u_i^{(\gamma )})/u_i^{(\gamma )}}{x_i},\gamma \in \Gamma ,$$

where $\Gamma$ is a finite index set, the union of these type-2 fuzzy sets is:

$$\bigcup _{\gamma \in \Gamma }{\tilde{A}}^{(\gamma )}=\sum _{i=1}^N\frac{{\bigwedge }_{\gamma \in \Gamma }{f}_{x_i}^{(\gamma )}(u_i^{(\gamma )})/{\bigvee }_{\gamma \in \Gamma }{u}_i^{(\gamma )}}{x_i},$$

and the intersection of these type-2 fuzzy sets is:

$$\bigcap _{\gamma \in \Gamma }{\tilde{A}}^{(\gamma )}=\sum _{i=1}^N\frac{{\bigwedge }_{\gamma \in \Gamma }{f}_{x_i}^{(\gamma )}(u_i^{(\gamma )})/{\bigwedge }_{\gamma \in \Gamma }{u}_i^{(\gamma )}}{x_i}.$$

Obviously, ${\cup }_{\gamma \in \Gamma }{\tilde{A}}^{(\gamma )}⪯{\cup }_{\gamma \in \Gamma }{\tilde{B}}^{(\gamma )}$ and ${\cap }_{\gamma \in \Gamma }{\tilde{A}}^{(\gamma )}⪯{\cap }_{\gamma \in \Gamma }{\tilde{B}}^{(\gamma )}$ if ${\tilde{A}}^{(\gamma )}⪯{\tilde{B}}^{(\gamma )}(\forall \gamma \in \Gamma )$.

Let X and Y be two nonempty universes. A type-2 fuzzy relation from X to Y is a type-2 fuzzy set $\tilde{R}\in \tilde{F}(X\times Y)$. If $X=Y$, then $\tilde{R}$ is called a type-2 fuzzy relation on X.

A discrete type-2 fuzzy relation $\tilde{R}$ can be represented as the union of its embedded type-2 sets:

$$\tilde{R}=\sum _{l=1}^{n_R}{\tilde{R}}_e^l,$$

where $n_R\equiv {\prod }_{i=1}^n{\prod }_{j=1}^m{M}_{ij}$ ($M_{ij}=|J_{(x_i,y_j)}|$), and ${\tilde{R}}_e^l$ is the l-th embedded type-2 set of $\tilde{R}$.

2.2. Fuzzy Rough Sets

In 1982, Pawlak proposed the theory of rough set as a new mathematical tool for reasoning about data. For a finite and nonempty universe X, if $R\subseteq X\times X$ is an equivalence relation on X, i.e., R is reflexive, symmetric and transitive, the pair $(X,R)$ is called an approximation space. For any $x\in X$, ${[x]}_R=\{y\in X:(x,y)\in R\}$ is called the equivalence class containing x. The family of all equivalence classes defines a partition of the universe X. Two elements x and y are said to be indiscernible if they belong to the same equivalence class. Given an arbitrary set $A\subseteq X,$ it may be characterized by a pair of lower and upper approximations defined as:

$$\underline{R}A=\cup \{{[x]}_R:{[x]}_R\subseteq A\}=\{x\in X:{[x]}_R\subseteq A\},$$

$$\overline{R}A=\cup \{{[x]}_R:{[x]}_R\cap A\ne \varnothing \}=\{x\in X:{[x]}_R\cap A\ne \varnothing \}=\cup \{{[x]}_R:x\in A\}.$$

or:

$$\underline{R}A=\cap \{{({[x]}_R)}^c:x\in A^c\},\overline{R}A=\cap \{{({[x]}_R)}^c:A\subseteq {({[x]}_R)}^c\}.$$

That is to say, equivalence classes can be used as basic granules to approximate a set.

Let X be a nonempty universe and R be a fuzzy binary relation on X. The fuzzy rough set of a fuzzy set A is a pair $(\underline{R}(A),\overline{R}(A))$ such that for every $x\in X:$

$$\overline{R}(A)(x)\equiv \underset{y\in X}{sup}min\{R(x,y),{\mu }_A(y)\},$$

(1)

$$\underline{R}(A)(x)\equiv \underset{y\in X}{inf}max\{1-R(x,y),{\mu }_A(y)\}.$$

(2)

Chen et al. [20] discovered the granular structure of fuzzy rough sets and pointed out that fuzzy sets ${[x_{\lambda }]}_R^T$ and ${[x_{\lambda }]}_R^S$ were basic granules corresponding to the equivalence classes, which were defined as:

$${[x_{\lambda }]}_R^T(y)=T(R(x,y),\lambda ),{[x_{\lambda }]}_R^S(y)=S(N(R(x,y)),N(\lambda )),$$

where $x_{\lambda }$ is a fuzzy point, T is a triangular norm, S is a triangular conorm, N is a negator and T and S are dual with respect to N. For a T-fuzzy similarity relation R, the lower and upper approximations of a fuzzy set A can be expressed as the union or intersection of some basic fuzzy information granules:

$$\underline{R_{\vartheta }}A=\cup \{{[x_{\lambda }]}_R^T:{[x_{\lambda }]}_R^T\subseteq A\},\overline{R_T}A=\cup \{{[x_{A(x)}]}_R^T:x\in X\};$$

$$\underline{R_S}A=\cap \{{[x_{N(A(x))}]}_R^S:x\in X\},\overline{R_{\sigma }}A=\cap \{{[x_{\lambda }]}_R^S:A\subseteq {[x_{\lambda }]}_R^S\}.$$

3. Type-2 Fuzzy Rough Sets over Two Universes

Since type-2 fuzzy sets can be used to describe more uncertainties than type-1 fuzzy sets because the membership functions of type-2 fuzzy sets are themselves fuzzy, type-2 fuzzy rough sets can be used to solve problems with more uncertainties. In this section, we will extend the definition of type-2 fuzzy rough set proposed in [24], which was defined on one universe, to the circumstance of two different universes.

Definition 1.

Let X and Y be two nonempty finite universes and $\tilde{R}\in \tilde{F}(X\times Y)$ be a type-2 fuzzy relation from X to Y. The triple set $(X,Y,\tilde{R})$ is called a type-2 fuzzy approximation space over two different universes. For any type-2 fuzzy set $\tilde{B}\in \tilde{F}(Y)$, the lower approximation $\underline{\tilde{R}}(\tilde{B})$ and the upper approximation $\overline{\tilde{R}}(\tilde{B})$ of $\tilde{B}$ with respect to $(X,Y,\tilde{R})$ are two type-2 fuzzy sets in X, respectively. If $\tilde{R}$ and $\tilde{B}$ can be represented as $\tilde{R}={\sum }_{\gamma =1}^{n_R}{\tilde{R}}_{\gamma }and\tilde{B}={\sum }_{\beta =1}^{n_B}{\tilde{B}}_{\beta }$ by the representation theorem, we have:

$$\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })(x)=\frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\wedge }_{y\in Y}[(1-R_{\gamma }(x,y))\vee B_{\beta }(y)]},x\in X,$$

$$\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })(x)=\frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge B_{\beta }(y)]},x\in X,$$

where ${\tilde{R}}_{\gamma }$ and $R_{\gamma }$ are the embedded type-2 set and embedded type-1 set of $\tilde{R}$, respectively, and $R_{\gamma }^{*}(x,y)$ is the simplified notation of ${\tilde{R}}_{\gamma }((x,y),R_{\gamma }(x,y))$, whereas ${\tilde{B}}_{\beta }$ and $B_{\beta }$ are the embedded type-2 and embedded type-1 set of $\tilde{B}$, respectively, and $B_{\beta }^{*}(y)$ is the simplified notation of ${\tilde{B}}_{\beta }(y,B_{\beta }(y))$.

Consequently, $\underline{\tilde{R}}(\tilde{B})$ and $\overline{\tilde{R}}(\tilde{B})$ can be calculated by:

$$\underline{\tilde{R}}(\tilde{B})=\sum _{\gamma =1}^{n_R}\sum _{\beta =1}^{n_B}\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })$$

and

$$\overline{\tilde{R}}(\tilde{B})=\sum _{\gamma =1}^{n_R}\sum _{\beta =1}^{n_B}\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }).$$

The ordered pair $(\underline{\tilde{R}}(\tilde{B}),\overline{\tilde{R}}(\tilde{B}))$ is called a type-2 fuzzy rough set over two universes.

Note: If $\tilde{R}$ and $\tilde{B}$ degenerate to be interval type-2 fuzzy sets,

$$\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })(x)={\wedge }_{y\in Y}[(1-R_{\gamma }(x,y)\vee B_{\beta }(y))],$$

$$\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })(x)={\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge B_{\beta }(y)],$$

and:

$$\underline{\tilde{R}}(\tilde{B})=\sum _{\gamma =1}^{n_R}\sum _{\beta =1}^{n_B}\{\underset{y\in Y}{\bigwedge }[(1-R_{\gamma }(x,y)\vee B_{\beta }(y))]\}$$

$$\overline{\tilde{R}}(\tilde{B})=\sum _{\gamma =1}^{n_R}\sum _{\beta =1}^{n_B}\{\underset{y\in Y}{\bigvee }[R_{\gamma }(x,y)\wedge B_{\beta }(y)]\}.$$

If $\tilde{R}$ and $\tilde{B}$ degenerate to be type-1 fuzzy sets, then:

$$\underline{\tilde{R}}(\tilde{B})(x)={\wedge }_{y\in Y}[(1-R(x,y))\vee B(y)],$$

$$\overline{\tilde{R}}(\tilde{B})(x)={\vee }_{y\in Y}[R(x,y)\wedge B(y)],$$

which are in accordance with the definition of (type-1) fuzzy rough set over two universes given in [29].

Example 1.

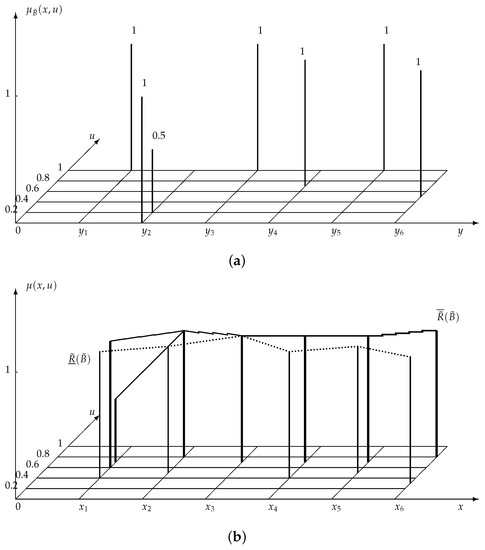
Let $X=\{x_1,\dots ,x_6\}$, $Y=\{y_1,\dots ,y_6\}$. Suppose $\tilde{R}$ is a type-2 fuzzy relation from X to Y, which can be defined as follows:

$$\tilde{R}(x_i,y_j)=\left(\begin{array}{cccccc}1/0.4& 1/0.6& 1/0.4& 0.5/0.7+1/0.6& 1/0.3& 1/0.2\\ 1/0.7& 1/0.3& 1/0.2& 1/0.5& 1/0.8& 1/0.6\\ 1/0.5& 1/0.2& 1/0.6& 1/0.3& 1/0.7& 1/0.1\\ 1/0.4& 1/0.6& 1/0.5& 1/0.7& 1/0.5& 1/0.3\\ 1/0.3& 1/0.5& 1/0.7& 1/0.3& 1/0.6& 1/0.8\\ 1/0.1& 1/0.7& 1/0.8& 1/0.6& 1/0.3& 1/0.2\end{array}\right).$$

Then, $\tilde{R}={\sum }_{\gamma =1}^2{\tilde{R}}_{\gamma }$, where ${\tilde{R}}_1$ and ${\tilde{R}}_2$ are embedded type-2 sets of $\tilde{R}$:

$${\tilde{R}}_1(x_i,y_j)=\left(\begin{array}{cccccc}1/0.4& 1/0.6& 1/0.4& 0.5/0.7& 1/0.3& 1/0.2\\ 1/0.7& 1/0.3& 1/0.2& 1/0.5& 1/0.8& 1/0.6\\ 1/0.5& 1/0.2& 1/0.6& 1/0.3& 1/0.7& 1/0.1\\ 1/0.4& 1/0.6& 1/0.5& 1/0.7& 1/0.5& 1/0.3\\ 1/0.3& 1/0.5& 1/0.7& 1/0.3& 1/0.6& 1/0.8\\ 1/0.1& 1/0.7& 1/0.8& 1/0.6& 1/0.3& 1/0.2\end{array}\right),$$

$${\tilde{R}}_2(x_i,y_j)=\left(\begin{array}{cccccc}1/0.4& 1/0.6& 1/0.4& 1/0.6& 1/0.3& 1/0.2\\ 1/0.7& 1/0.3& 1/0.2& 1/0.5& 1/0.8& 1/0.6\\ 1/0.5& 1/0.2& 1/0.6& 1/0.3& 1/0.7& 1/0.1\\ 1/0.4& 1/0.6& 1/0.5& 1/0.7& 1/0.5& 1/0.3\\ 1/0.3& 1/0.5& 1/0.7& 1/0.3& 1/0.6& 1/0.8\\ 1/0.1& 1/0.7& 1/0.8& 1/0.6& 1/0.3& 1/0.2\end{array}\right).$$

Considering a type-2 fuzzy set in Y (Figure 1a):

$$\tilde{B}=\frac{1/1}{y_1}+\frac{1/0+0.5/0.2}{y_2}+\frac{1/1}{y_3}+\frac{1/0.7}{y_4}+\frac{1/1}{y_5}+\frac{1/0.5}{y_6},$$

we have $\tilde{B}={\sum }_{\beta =1}^2{\tilde{B}}_{\beta }$, where:

$${\tilde{B}}_1=\frac{1/1}{y_1}+\frac{1/0}{y_2}+\frac{1/1}{y_3}+\frac{1/0.7}{y_4}+\frac{1/1}{y_5}+\frac{1/0.5}{y_6}$$

and

$${\tilde{B}}_2=\frac{1/1}{y_1}+\frac{0.5/0.2}{y_2}+\frac{1/1}{y_3}+\frac{1/0.7}{y_4}+\frac{1/1}{y_5}+\frac{1/0.5}{y_6}$$

are embedded type-2 sets of $\tilde{B},$ the lower approximation $\underline{\tilde{R}}(\tilde{B})$ and the upper approximation $\overline{\tilde{R}}(\tilde{B})$ of $\tilde{B}$ with respect to $(X,Y,\tilde{R})$ (Figure 1b) can be calculated as follows:

$$\underline{{\tilde{R}}_1}({\tilde{B}}_1)=\frac{0.5/0.4}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.4}{x_4}+\frac{1/0.5}{x_5}+\frac{1/0.3}{x_6},$$

$$\underline{{\tilde{R}}_1}({\tilde{B}}_2)=\frac{0.5/0.4}{x_1}+\frac{0.5/0.5}{x_2}+\frac{0.5/0.7}{x_3}+\frac{0.5/0.4}{x_4}+\frac{0.5/0.5}{x_5}+\frac{0.5/0.3}{x_6},$$

$$\underline{{\tilde{R}}_2}({\tilde{B}}_1)=\frac{1/0.4}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.4}{x_4}+\frac{1/0.5}{x_5}+\frac{1/0.3}{x_6},$$

$$\underline{{\tilde{R}}_2}({\tilde{B}}_2)=\frac{0.5/0.4}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.4}{x_4}+\frac{1/0.5}{x_5}+\frac{1/0.3}{x_6},$$

$$\underline{\tilde{R}}(\tilde{B})=\sum _{\gamma =1}^2\sum _{\beta =1}^2\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })=\frac{1/0.4}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.4}{x_4}+\frac{1/0.5}{x_5}+\frac{1/0.3}{x_6};$$

$$\overline{{\tilde{R}}_1}({\tilde{B}}_1)=\frac{0.5/0.7}{x_1}+\frac{1/0.8}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.7}{x_5}+\frac{1/0.8}{x_6},$$

$$\overline{{\tilde{R}}_1}({\tilde{B}}_2)=\frac{0.5/0.7}{x_1}+\frac{0.5/0.8}{x_2}+\frac{0.5/0.7}{x_3}+\frac{0.5/0.7}{x_4}+\frac{0.5/0.7}{x_5}+\frac{0.5/0.8}{x_6},$$

$$\overline{{\tilde{R}}_2}({\tilde{B}}_1)=\frac{1/0.6}{x_1}+\frac{1/0.8}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.7}{x_5}+\frac{1/0.8}{x_6},$$

$$\overline{{\tilde{R}}_2}({\tilde{B}}_2)=\frac{0.5/0.6}{x_1}+\frac{0.5/0.8}{x_2}+\frac{0.5/0.7}{x_3}+\frac{0.5/0.7}{x_4}+\frac{0.5/0.7}{x_5}+\frac{0.5/0.8}{x_6},$$

$$\overline{\tilde{R}}(\tilde{B})=\sum _{\gamma =1}^2\sum _{\beta =1}^2\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })=\frac{0.5/0.7+1/0.6}{x_1}+\frac{1/0.8}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.7}{x_5}+\frac{1/0.8}{x_6}.$$

Next, we will discuss the properties of the lower and upper approximation operators.

Lemma 1.

Let X and Y be two nonempty finite universes and $\tilde{R}$ be a type-2 fuzzy relation from X to Y. For any $\tilde{A},\tilde{B}\in \tilde{F}(Y)$, if ${\tilde{R}}_{\gamma },{\tilde{A}}_{\alpha },{\tilde{B}}_{\beta }$ are embedded type-2 sets of $\tilde{R},\tilde{A}$ and $\tilde{B}$ respectively, the following properties hold:

1. 

$\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }^c)={(\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }))}^c$;

2. 

$\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }^c)={(\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }))}^c$;

3. 

$\overline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha }\cup {\tilde{B}}_{\beta })=\overline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha })\cup \overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })$;

4. 

$\underline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha }\cap {\tilde{B}}_{\beta })=\underline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha })\cap \underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })$.

Proof. 

• For any $x\in X,$

  $$\begin{array}{ccc}\hfill {[\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })]}^c(x)& =& \neg (\frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge B_{\beta }(y)]})\hfill \\ & =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\wedge }_{y\in Y}[(1-R_{\gamma }(x,y))\vee B_{\beta }^c(y)]}\hfill \\ & =& \underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }^c)(x).\hfill \end{array}$$
• For any $x\in X,$

  $$\begin{array}{ccc}\hfill {[\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })]}^c(x)& =& \neg (\frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\wedge }_{y\in Y}[(1-R_{\gamma }(x,y))\vee B_{\beta }(y)]})\hfill \\ & =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge B_{\beta }^c(y)]}\hfill \\ & =& \overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }^c)(x).\hfill \end{array}$$
• For any $x\in X,$

  $$\begin{array}{ccc}\hfill \overline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha }\cup {\tilde{B}}_{\beta })(x)& =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge A_{\alpha }^{*}(y)\wedge B_{\beta }^{*}(y)]}{{\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge (A_{\alpha }(y)\vee B_{\beta }(y))]}\hfill \\ & =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge A_{\alpha }^{*}(y)]\wedge \{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]\}}{{\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge A_{\alpha }(y)]\vee \{{\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge B_{\beta }(y)]\}}\hfill \\ & =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge A_{\alpha }^{*}(y)]}{{\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge A_{\alpha }(y)]}\bigsqcup \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge B_{\beta }(y)]}\hfill \\ & =& \overline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha })(x)\bigsqcup \overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })(x).\hfill \end{array}$$
• For any $x\in X,$

  $$\begin{array}{c}\underline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha }\cap {\tilde{B}}_{\beta })(x)\hfill \\ & =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge A_{\alpha }^{*}(y)\wedge B_{\beta }^{*}(y)]}{{\wedge }_{y\in Y}[(1-R_{\gamma }(x,y))\vee ((A_{\alpha }(y)\wedge B_{\beta }(y))]}\hfill \\ & =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge A_{\alpha }^{*}(y)]\wedge \{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]\}}{{\wedge }_{y\in Y}[(1-R_{\gamma }(x,y))\vee A_{\alpha }(y)]\wedge \{{\wedge }_{y\in Y}[(1-R_{\gamma }(x,y))\vee B_{\beta }(y)]\}}\hfill \\ & =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge A_{\alpha }^{*}(y)]}{{\wedge }_{y\in Y}[(1-R_{\gamma }(x,y))\vee A_{\alpha }(y)]}\sqcap \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\wedge }_{y\in Y}[(1-R_{\gamma }(x,y))\vee B_{\beta }(y)]}\hfill \\ & =& \underline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha })(x)\sqcap \underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })(x).\hfill \end{array}$$

 ☐

Theorem 1.

Let X and Y be two nonempty finite universes and $\tilde{R}$ be a type-2 fuzzy relation from X to Y. For any $\tilde{A},\tilde{B}\in \tilde{F}(Y)$, the following properties hold:

1. 

$\underline{\tilde{R}}({\tilde{B}}^c)={(\overline{\tilde{R}}(\tilde{B}))}^c$;

2. 

$\overline{\tilde{R}}({\tilde{B}}^c)={(\underline{\tilde{R}}(\tilde{B}))}^c$;

3. 

$\overline{\tilde{R}}(\tilde{A}\cup \tilde{B})=\overline{\tilde{R}}(\tilde{A})\cup \overline{\tilde{R}}(\tilde{B})$;

4. 

$\underline{\tilde{R}}(\tilde{A}\cap \tilde{B})=\underline{\tilde{R}}(\tilde{A})\cap \underline{\tilde{R}}(\tilde{B})$.

Proof. 

1.

$\underline{\tilde{R}}({\tilde{B}}^c)={\sum }_{\gamma =1}^{n_R}{\sum }_{\beta =1}^{n_B}\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }^c)={\sum }_{\gamma =1}^{n_R}{\sum }_{\beta =1}^{n_B}{(\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }))}^c={(\overline{\tilde{R}}(\tilde{B}))}^c.$

2.

$\overline{\tilde{R}}({\tilde{B}}^c)={\sum }_{\gamma =1}^{n_R}{\sum }_{\beta =1}^{n_B}\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }^c)={\sum }_{\gamma =1}^{n_R}{\sum }_{\beta =1}^{n_B}{(\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta }))}^c={(\underline{\tilde{R}}(\tilde{B}))}^c.$

3.

$\begin{array}{ll}\overline{\tilde{R}}(\tilde{A}\cup \tilde{B})& ={\sum }_{\gamma =1}^{n_R}{\sum }_{\alpha =1}^{n_A}{\sum }_{\beta =1}^{n_B}\overline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha }\cup {\tilde{B}}_{\beta })\\ & ={\sum }_{\gamma =1}^{n_R}{\sum }_{\alpha =1}^{n_A}{\sum }_{\beta =1}^{n_B}[\overline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha })\cup \overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })]\\ & ={\sum }_{\gamma =1}^{n_R}{\sum }_{\alpha =1}^{n_A}\overline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha })\cup {\sum }_{\gamma =1}^{n_R}{\sum }_{\beta =1}^{n_B}\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })\\ & =\overline{\tilde{R}}(\tilde{A})\cup \overline{\tilde{R}}(\tilde{B}).\end{array}$

4.

$\begin{array}{ll}\underline{\tilde{R}}(\tilde{A}\cap \tilde{B})& ={\sum }_{\gamma =1}^{n_R}{\sum }_{\alpha =1}^{n_A}{\sum }_{\beta =1}^{n_B}\underline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha }\cap {\tilde{B}}_{\beta })\\ & ={\sum }_{\gamma =1}^{n_R}{\sum }_{\alpha =1}^{n_A}{\sum }_{\beta =1}^{n_B}[\underline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha })\cap \underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })]\\ & ={\sum }_{\gamma =1}^{n_R}{\sum }_{\alpha =1}^{n_A}\underline{{\tilde{R}}_{\gamma }}({\tilde{A}}_{\alpha })\cap {\sum }_{\gamma =1}^{n_R}{\sum }_{\beta =1}^{n_B}\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })\\ & =\underline{\tilde{R}}(\tilde{A})\cap \underline{\tilde{R}}(\tilde{B}).\end{array}$

 ☐

4. Granular Structure of Type-2 Fuzzy Rough Sets over Two Universes

The granular structures of classical rough sets and ordinary fuzzy rough sets are clear, and the lower and upper approximation sets can be represented by some basic granules. Here, we will discuss the basic granules in type-2 fuzzy rough sets over two universes, which can be used to calculate the lower and upper approximation sets of a type-2 fuzzy set.

In classical rough set theory, for a nonempty and finite universe X and an equivalent relation $R\subseteq X\times X$, the upper and lower approximation sets of $A\subseteq X$ can be defined as follows:

$$\overline{R}A=\cup \{{[x]}_R:x\in A\},$$

$$\underline{R}A=\cap \{{({[x]}_R)}^c:x\in A^c\}.$$

Take $A=\{y\}$ and $A=X-\{y\}={\{y\}}^c$ in the above two equations respectively, and we have:

$$\overline{R}(\{y\})=\cup \{{[x]}_R:x\in \{y\}\}={[y]}_R,$$

$$\underline{R}({\{y\}}^c)=\cap \{{({[x]}_R)}^c:x\in \{y\}\}={({[y]}_R)}^c.$$

Next, we will try to find the “equivalence classes” of a type-2 fuzzy point and its complement, both of which should be type-2 fuzzy sets.

Let Y be a nonempty universes. A type-2 fuzzy point in Y is a special type-2 fuzzy set defined as follows: for any $z\in Y$,

$$y_{\lambda }^{\mu }(z)=\left\{\begin{array}{cc}\mu /\lambda ,\hfill & \mathrm{if}z=y\hfill \\ 1/0,\hfill & \mathrm{if}z\ne y\hfill \end{array}\right.,$$

where $\lambda \in [0,1]$ and $\mu \in (0,1]$. The complement of $y_{\lambda }^{\mu }$, denoted by $\overline{y_{\lambda }^{\mu }}$, is also a type-2 fuzzy set on Y: for any $y\in Y$,

$$\overline{y_{\lambda }^{\mu }}(z)=\left\{\begin{array}{cc}\mu /1-\lambda ,\hfill & \mathrm{if}z=y\hfill \\ 1/1,\hfill & \mathrm{if}z\ne y\hfill \end{array}\right..$$

Definition 2.

Let X and Y be two nonempty finite universes. Suppose $\tilde{R}$ is a type-2 fuzzy relation from X to Y, ${\tilde{R}}_{\gamma }$ is an embedded type-2 set of $\tilde{R}$ and $R_{\gamma }$ is the corresponding embedded type-1 set. For a type-2 fuzzy point $y_{\lambda }^{\mu }\in \tilde{F}(Y)$, two granular type-2 fuzzy sets ${[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\wedge }$ and ${[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\vee }$ are defined as: for any $x\in X,$

$${[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\wedge }(x)=\overline{{\tilde{R}}_{\gamma }}(y_{\lambda }^{\mu })(x)=\frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge \mu }{R_{\gamma }(x,y)\wedge \lambda }$$

and

$${[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\vee }(x)=\underline{{\tilde{R}}_{\gamma }}(\overline{y_{\lambda }^{\mu }})(x)=\frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge \mu }{[1-R_{\gamma }(x,y)]\vee (1-\lambda )}.$$

Let $M_{{\tilde{R}}_{\gamma }}^{\wedge }=\{{[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\wedge }:y\in Y,\lambda \in [0,1],\mu \in (0,1]\}$, $M_{{\tilde{R}}_{\gamma }}^{\vee }=\{{[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\vee }:y\in Y,\lambda \in [0,1],\mu \in (0,1]\}.$

From the above definition, it is clear that ${({[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\wedge })}^c={[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\vee }$ and ${({[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\vee })}^c={[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\gamma }}^{\wedge }$.

Example 2.

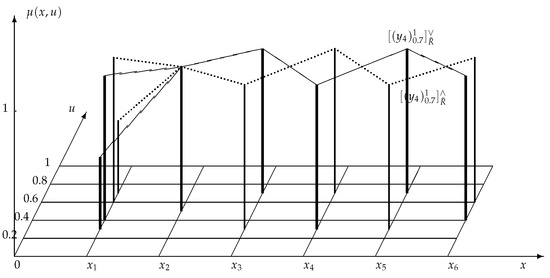
Consider the type-2 fuzzy relation $\tilde{R}$ given in the previous example. Take a type-2 fuzzy point ${(y_4)}_{0.7}^1,$ by

$${[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_{\gamma }}^{\wedge }(x_i)=\frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x_i,z)\wedge 1}{R_{\gamma }(x_i,y_4)\wedge 0.7},i=1,\dots ,6;\gamma =1,2,$$

we have

$${[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{0.5/0.7}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.3}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.3}{x_5}+\frac{1/0.6}{x_6},$$

$${[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_2}^{\wedge }=\frac{1/0.6}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.3}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.3}{x_5}+\frac{1/0.6}{x_6},$$

so:

$$\begin{array}{ccc}\hfill {[{(y_4)}_{0.7}^1]}_{\tilde{R}}^{\wedge }& =& \sum _{\gamma =1}^2{[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_{\gamma }}^{\wedge }\hfill \\ & =& \frac{0.5/0.7+1/0.6}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.3}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.3}{x_5}+\frac{1/0.6}{x_6}.\hfill \end{array}$$

By:

$${[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_{\gamma }}^{\vee }(x_i)=\frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x_i,z)\wedge 1}{[1-R_{\gamma }(x_i,y_4)]\vee (1-0.7)},i=1,\dots ,6;\gamma =1,2,$$

we have:

$${[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_1}^{\vee }=\frac{0.5/0.3}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.3}{x_4}+\frac{1/0.7}{x_5}+\frac{1/0.4}{x_6},$$

$${[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_2}^{\vee }=\frac{1/0.4}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.3}{x_4}+\frac{1/0.7}{x_5}+\frac{1/0.4}{x_6},$$

so:

$$\begin{array}{ccc}\hfill {[{(y_4)}_{0.7}^1]}_{\tilde{R}}^{\vee }& =& \sum _{\gamma =1}^2{[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_{\gamma }}^{\vee }\hfill \\ & =& \frac{0.5/0.3+1/0.4}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.3}{x_4}+\frac{1/0.7}{x_5}+\frac{1/0.4}{x_6}.\hfill \end{array}$$

${[{(y_4)}_{0.7}^1]}_{\tilde{R}}^{\wedge }$ and ${[{(y_4)}_{0.7}^1]}_{\tilde{R}}^{\vee }$ are depicted in Figure 2. Obviously, ${[{(y_4)}_{0.7}^1]}_{\tilde{R}}^{\wedge }$ is exactly the complement of ${[{(y_4)}_{0.7}^1]}_{\tilde{R}}^{\vee }$.

Theorem 2.

Let X and Y be two nonempty finite universes and $\tilde{R}$ be a type-2 fuzzy relation from X to Y. If ${\tilde{R}}_{\gamma }$ is an embedded type-2 set of $\tilde{R}$ and $R_{\gamma }$ is the corresponding embedded type-1 set, for $y\in Y,$${\lambda }_1,{\lambda }_2\in [0,1],$${\mu }_1,{\mu }_2\in (0,1],$ we have:

1. 

${[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\wedge }\cup {[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\wedge }={[y_{{\lambda }_1\vee {\lambda }_2}^{{\mu }_1\wedge {\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\wedge };$

2. 

${[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\wedge }\cap {[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\wedge }={[y_{{\lambda }_1\wedge {\lambda }_2}^{{\mu }_1\wedge {\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\wedge };$

3. 

${[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\vee }\cup {[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\vee }={[y_{{\lambda }_1\wedge {\lambda }_2}^{{\mu }_1\wedge {\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\vee };$

4. 

${[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\vee }\cap {[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\vee }={[y_{{\lambda }_1\vee {\lambda }_2}^{{\mu }_1\wedge {\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\vee }.$

Proof. 

• For any $x\in X$,

  $$\begin{array}{ccc}\hfill {[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\wedge }(x)\bigsqcup {[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\wedge }(x)& =& \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_1}{R_{\gamma }(x,y)\wedge {\lambda }_1}\bigsqcup \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_2}{R_{\gamma }(x,y)\wedge {\lambda }_2}\hfill \\ & =& \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_1\wedge {\mu }_2}{R_{\gamma }(x,y)\wedge ({\lambda }_1\vee {\lambda }_2)}={[y_{{\lambda }_1\vee {\lambda }_2}^{{\mu }_1\wedge {\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\wedge }(x).\hfill \end{array}$$
• For any $x\in X$,

  $$\begin{array}{ccc}\hfill {[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\wedge }(x)\sqcap {[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\wedge }(x)& =& \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_1}{R_{\gamma }(x,y)\wedge {\lambda }_1}\sqcap \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_2}{R_{\gamma }(x,y)\wedge {\lambda }_2}\hfill \\ & =& \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_1\wedge {\mu }_2}{R_{\gamma }(x,y)\wedge ({\lambda }_1\wedge {\lambda }_2)}={[y_{{\lambda }_1\wedge {\lambda }_2}^{{\mu }_1\wedge {\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\wedge }(x).\hfill \end{array}$$
• For any $x\in X$,

  $$\begin{array}{cc}& {[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\vee }(x)\bigsqcup {[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\vee }(x)\hfill \\ =& \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_1}{(1-R_{\gamma }(x,y))\vee (1-{\lambda }_1)}\bigsqcup \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_2}{(1-R_{\gamma }(x,y))\vee (1-{\lambda }_2)}\hfill \\ =& \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_1\wedge {\mu }_2}{(1-R_{\gamma }(x,y))\vee [1-({\lambda }_1\wedge {\lambda }_2)]}={[y_{{\lambda }_1\wedge {\lambda }_2}^{{\mu }_1\wedge {\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\vee }(x).\hfill \end{array}$$
• For any $x\in X$,

  $$\begin{array}{cc}& {[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\vee }(x)\sqcap {[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\vee }(x)\hfill \\ =& \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_1}{(1-R_{\gamma }(x,y))\vee (1-{\lambda }_1)}\sqcap \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_2}{(1-R_{\gamma }(x,y))\vee (1-{\lambda }_2)}\hfill \\ =& \frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge {\mu }_1\wedge {\mu }_2}{(1-R_{\gamma }(x,y))\vee [1-({\lambda }_1\vee {\lambda }_2)]}={[y_{{\lambda }_1\vee {\lambda }_2}^{{\mu }_1\wedge {\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\vee }(x).\hfill \end{array}$$

 ☐

Theorem 3.

Let X and Y be two nonempty finite universes. Suppose ${\tilde{R}}^{(1)}$ and ${\tilde{R}}^{(2)}$ are type-2 fuzzy relations from X to Y and ${\tilde{R}}_{\alpha }$ and ${\tilde{R}}_{\beta }$ are embedded type-2 sets of ${\tilde{R}}^{(1)}$ and ${\tilde{R}}^{(2)}$, respectively, then for $y\in Y,$$\lambda \in [0,1],$$\mu \in (0,1],$

1. 

${[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }\cap {\tilde{R}}_{\beta }}^{\wedge }={[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }}^{\wedge }\cap {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\beta }}^{\wedge };$

2. 

${[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }\cup {\tilde{R}}_{\beta }}^{\wedge }={[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }}^{\wedge }\cup {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\beta }}^{\wedge };$

3. 

${[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }\cap {\tilde{R}}_{\beta }}^{\vee }={[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }}^{\vee }\cup {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\beta }}^{\vee };$

4. 

${[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }\cup {\tilde{R}}_{\beta }}^{\vee }={[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }}^{\vee }\cap {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\beta }}^{\vee }.$

Proof. 

• For any $x\in X$,

  $$\begin{array}{ccc}\hfill {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }\cap {\tilde{R}}_{\beta }}^{\wedge }(x)& =& \frac{{\wedge }_{z\in Y}(R_{\alpha }^{*}(x,z)\wedge R_{\beta }^{*}(x,z))\wedge \mu }{R_{\alpha }(x,y)\wedge R_{\beta }(x,y)\wedge \lambda }\hfill \\ & =& \frac{[{\wedge }_{z\in Y}{R}_{\alpha }^{*}(x,z)\wedge \mu ]\wedge [{\wedge }_{z\in Y}{R}_{\beta }^{*}(x,z)\wedge \mu ]}{[R_{\alpha }(x,y)\wedge \lambda ]\wedge [R_{\beta }(x,y)\wedge \lambda ]}\hfill \\ & =& {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }}^{\wedge }(x)\sqcap {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\beta }}^{\wedge }(x).\hfill \end{array}$$
• For any $x\in X$,

  $$\begin{array}{ccc}\hfill {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }\cup {\tilde{R}}_{\beta }}^{\wedge }(x)& =& \frac{{\wedge }_{z\in Y}(R_{\alpha }^{*}(x,z)\wedge R_{\beta }^{*}(x,z))\wedge \mu }{[R_{\alpha }(x,y)\vee R_{\beta }(x,y)]\wedge \lambda }\hfill \\ & =& \frac{[{\wedge }_{z\in Y}{R}_{\alpha }^{*}(x,z)\wedge \mu ]\wedge [{\wedge }_{z\in Y}{R}_{\beta }^{*}(x,z)\wedge \mu ]}{[R_{\alpha }(x,y)\wedge \lambda ]\vee [R_{\beta }(x,y)\wedge \lambda ]}\hfill \\ & =& {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }}^{\wedge }(x)\bigsqcup {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\beta }}^{\wedge }(x).\hfill \end{array}$$
• For any $x\in X$,

  $$\begin{array}{ccc}\hfill {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }\cap {\tilde{R}}_{\beta }}^{\vee }(x)& =& \frac{{\wedge }_{z\in Y}(R_{\alpha }^{*}(x,z)\wedge R_{\beta }^{*}(x,z))\wedge \mu }{[1-R_{\alpha }(x,y)\wedge R_{\beta }(x,y)]\vee (1-\lambda )}\hfill \\ & =& \frac{[{\wedge }_{z\in Y}{R}_{\alpha }^{*}(x,z)\wedge \mu ]\wedge [{\wedge }_{z\in Y}{R}_{\beta }^{*}(x,z)\wedge \mu ]}{[(1-R_{\alpha }(x,y))\vee (1-\lambda )]\vee [(1-R_{\beta }(x,y))\vee (1-\lambda )]}\hfill \\ & =& {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }}^{\vee }(x)\bigsqcup {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\beta }}^{\vee }(x).\hfill \end{array}$$
• For any $x\in X$,

  $$\begin{array}{ccc}\hfill {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }\cup {\tilde{R}}_{\beta }}^{\vee }(x)& =& \frac{{\wedge }_{z\in Y}(R_{\alpha }^{*}(x,z)\wedge R_{\beta }^{*}(x,z))\wedge \mu }{[1-R_{\alpha }(x,y)\vee R_{\beta }(x,y)]\vee (1-\lambda )}\hfill \\ & =& \frac{[{\wedge }_{z\in Y}{R}_{\alpha }^{*}(x,z)\wedge \mu ]\wedge [{\wedge }_{z\in Y}{R}_{\beta }^{*}(x,z)\wedge \mu ]}{[(1-R_{\alpha }(x,y))\vee (1-\lambda )]\wedge [(1-R_{\beta }(x,y))\vee (1-\lambda )]}\hfill \\ & =& {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\alpha }}^{\vee }(x)\sqcap {[y_{\lambda }^{\mu }]}_{{\tilde{R}}_{\beta }}^{\vee }(x).\hfill \end{array}$$

 ☐

Lemma 2.

Let X and Y be two nonempty finite universes. Suppose $\tilde{R}$ is a type-2 fuzzy relation from X to Y, ${\tilde{R}}_{\gamma }$ is an embedded type-2 set of $\tilde{R}$ and $R_{\gamma }$ is the corresponding embedded type-1 set. For $y\in Y,$${\lambda }_1,{\lambda }_2\in [0,1],$${\mu }_1,{\mu }_2\in (0,1],$

1. 

If ${\lambda }_1\le {\lambda }_2,{\mu }_1\le {\mu }_2,$${[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\wedge }⪯{[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\wedge };$

2. 

If ${\lambda }_1\ge {\lambda }_2,{\mu }_1\le {\mu }_2,$${[y_{{\lambda }_1}^{{\mu }_1}]}_{{\tilde{R}}_{\gamma }}^{\vee }⪯{[y_{{\lambda }_2}^{{\mu }_2}]}_{{\tilde{R}}_{\gamma }}^{\vee }.$

Proof. 

Obviously. ☐

Theorem 4.

Let $\tilde{R}$ be a discrete type-2 fuzzy relation from X to Y, where X and Y are nonempty finite universes. For a discrete type-2 fuzzy set $\tilde{B}\in \tilde{F}(Y)$, if ${\tilde{R}}_{\gamma }$ and ${\tilde{B}}_{\beta }$ are embedded type-2 sets of $\tilde{R}$ and $\tilde{B}$ respectively, we have:

$$\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })={\cup }_{y\in Y}{[y_{B_{\beta }(y)}^{B_{\beta }^{*}(y)}]}_{{\tilde{R}}_{\gamma }}^{\wedge };$$

and:

$$\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })={\cap }_{y\in Y}{[y_{B_{\beta }^c(y)}^{B_{\beta }^{*}(y)}]}_{{\tilde{R}}_{\gamma }}^{\vee }.$$

Proof. 

For any $x\in X$,

$$\begin{array}{ccc}\hfill {\bigsqcup }_{y\in Y}{[y_{B_{\beta }(y)}^{B_{\beta }^{*}(y)}]}_{{\tilde{R}}_{\gamma }}^{\wedge }(x)& =& {\bigsqcup }_{y\in Y}\frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge B_{\beta }^{*}(y)}{R_{\gamma }(x,y)\wedge B_{\beta }(y)}\hfill \\ & =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\vee }_{y\in Y}[R_{\gamma }(x,y)\wedge B_{\beta }(y)]}=\overline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })(x).\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\sqcap }_{y\in Y}{[y_{B_{\beta }^c(y)}^{B_{\beta }^{*}(y)}]}_{{\tilde{R}}_{\gamma }}^{\vee }(x)& =& {\sqcap }_{y\in Y}\frac{{\wedge }_{z\in Y}{R}_{\gamma }^{*}(x,z)\wedge B_{\beta }^{*}(y)}{[1-R_{\gamma }(x,y)]\vee B_{\beta }(y)}\hfill \\ & =& \frac{{\wedge }_{y\in Y}[R_{\gamma }^{*}(x,y)\wedge B_{\beta }^{*}(y)]}{{\wedge }_{y\in Y}[(1-R_{\gamma }(x,y))\vee B_{\beta }(y)]}=\underline{{\tilde{R}}_{\gamma }}({\tilde{B}}_{\beta })(x).\hfill \end{array}$$

 ☐

We have mentioned in Section 2.2 that basic granules in the theory of the classic rough set are equivalence classes, and the lower and upper approximations of a crisp set can be computed by the basic granules or the complements of the basic granules. Similarly, in the theory of fuzzy rough set, Chen et al. [20] proved that ${[x_{\lambda }]}_R^T$ and ${[x_{\lambda }]}_R^S$, which are called basic granules of fuzzy rough sets, corresponded to the equivalence classes and the complements of equivalence classes, respectively, and the upper and lower approximations of a fuzzy set can be expressed as the union or intersection of basic granules. Taking $M_{{\tilde{R}}_{\gamma }}^{\wedge }$ and $M_{{\tilde{R}}_{\gamma }}^{\vee }$ as basic granule sets, the above theorem reveals that these basic granules can be used to compute the upper and lower approximations of a type-2 fuzzy set by the operators of union and intersection. Therefore, $M_{{\tilde{R}}_{\gamma }}^{\wedge }$ and $M_{{\tilde{R}}_{\gamma }}^{\vee }$ correspond to the equivalence classes and the complements of equivalence classes, respectively.

Example 3.

Similar to the previous example, we can calculate granular type-2 fuzzy sets of $y_{B_1(y)}^{{\tilde{B}}_1(y)}$ for any $y\in Y$:

$$\begin{array}{c}{[{(y_1)}_1^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{0.5/0.4}{x_1}+\frac{1/0.7}{x_2}+\frac{1/0.5}{x_3}+\frac{1/0.4}{x_4}+\frac{1/0.3}{x_5}+\frac{1/0.1}{x_6},\hfill \\ {[{(y_2)}_0^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{0.5/0}{x_1}+\frac{1/0}{x_2}+\frac{1/0}{x_3}+\frac{1/0}{x_4}+\frac{1/0}{x_5}+\frac{1/0}{x_6},\hfill \\ {[{(y_3)}_1^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{0.5/0.4}{x_1}+\frac{1/0.2}{x_2}+\frac{1/0.6}{x_3}+\frac{1/0.5}{x_4}+\frac{1/0.7}{x_5}+\frac{1/0.8}{x_6},\hfill \\ {[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{0.5/0.7}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.3}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.3}{x_5}+\frac{1/0.6}{x_6},\hfill \\ {[{(y_5)}_1^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{0.5/0.3}{x_1}+\frac{1/0.8}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.5}{x_4}+\frac{1/0.6}{x_5}+\frac{1/0.3}{x_6},\hfill \\ {[{(y_6)}_{0.5}^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{0.5/0.2}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.1}{x_3}+\frac{1/0.3}{x_4}+\frac{1/0.5}{x_5}+\frac{1/0.2}{x_6},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \overline{{\tilde{R}}_1}({\tilde{B}}_1)& =& \bigcup _{y\in Y}{[y_{B_1(y)}^{B_1^{*}(y)}]}_{{\tilde{R}}_1}^{\wedge }\hfill \\ & =& \frac{0.5/0.7}{x_1}+\frac{1/0.8}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.7}{x_5}+\frac{1/0.8}{x_6}.\hfill \end{array}$$

$$\begin{array}{c}{[{(y_1)}_0^1]}_{{\tilde{R}}_1}^{\vee }=\frac{0.5/1}{x_1}+\frac{1/1}{x_2}+\frac{1/1}{x_3}+\frac{1/1}{x_4}+\frac{1/1}{x_5}+\frac{1/1}{x_6},\hfill \\ {[{(y_2)}_{0.8}^{0.5}]}_{{\tilde{R}}_1}^{\vee }=\frac{0.5/0.4}{x_1}+\frac{0.5/0.7}{x_2}+\frac{0.5/0.8}{x_3}+\frac{0.5/0.4}{x_4}+\frac{0.5/0.5}{x_5}+\frac{0.5/0.3}{x_6},\hfill \\ {[{(y_3)}_0^1]}_{{\tilde{R}}_1}^{\vee }=\frac{0.5/1}{x_1}+\frac{1/1}{x_2}+\frac{1/1}{x_3}+\frac{1/1}{x_4}+\frac{1/1}{x_5}+\frac{1/1}{x_6},\hfill \\ {[{(y_4)}_{0.3}^1]}_{{\tilde{R}}_1}^{\vee }=\frac{0.5/0.7}{x_1}+\frac{1/0.7}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.7}{x_5}+\frac{1/0.7}{x_6},\hfill \\ {[{(y_5)}_0^1]}_{{\tilde{R}}_1}^{\vee }=\frac{0.5/1}{x_1}+\frac{1/1}{x_2}+\frac{1/1}{x_3}+\frac{1/1}{x_4}+\frac{1/1}{x_5}+\frac{1/1}{x_6},\hfill \\ {[{(y_6)}_{0.5}^1]}_{{\tilde{R}}_1}^{\vee }=\frac{0.5/0.8}{x_1}+\frac{1/0.5}{x_2}+\frac{1/0.9}{x_3}+\frac{1/0.7}{x_4}+\frac{1/0.5}{x_5}+\frac{1/0.8}{x_6},\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \underline{{\tilde{R}}_1}({\tilde{B}}_2)& =& \bigcap _{y\in Y}{[y_{B_2^c(y)}^{B_2^{*}(y)}]}_{{\tilde{R}}_1}^{\vee }\hfill \\ & =& \frac{0.5/0.4}{x_1}+\frac{0.5/0.5}{x_2}+\frac{0.5/0.7}{x_3}+\frac{0.5/0.4}{x_4}+\frac{0.5/0.5}{x_5}+\frac{0.5/0.3}{x_6}.\hfill \end{array}$$

5. Examples

Example 4.

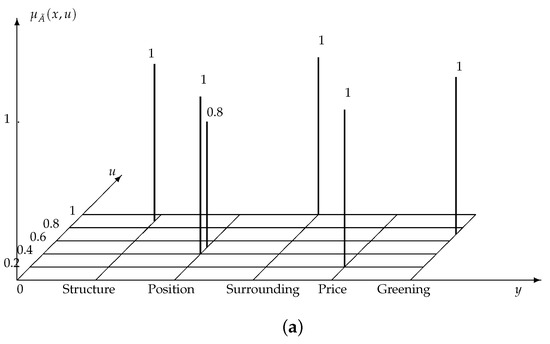
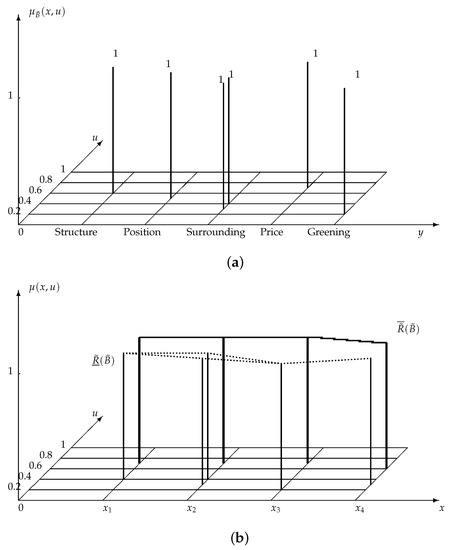
Suppose $X=\{x_1,x_2,x_3,x_4\}$ is a set of four different houses, all of which can be described by an attribute set $Y=\{y_1,y_2,y_3,y_4,y_5\},$ where $y_1$ stands for $Structure$, $y_2$ stands for $Position$, $y_3$ stands for $Surroundingfacilities$, $y_4$ stands for $Price$ and $y_5$ stands for $Greening$.

The correlation degree between X and Y (i.e., $\tilde{R}(x_i,y_j)$) is given in Table 1.

Suppose $\tilde{A}$ is a client who wants to purchase a house among the four alternative offers, and the demand of $\tilde{A}$ can be described by a type-2 fuzzy set (Figure 3a):

$$\tilde{A}=\frac{1/0.9}{y_1}+\frac{1/0.4+0.8/0.5}{y_2}+\frac{1/1}{y_3}+\frac{1/0.2}{y_4}+\frac{1/0.7}{y_5}.$$

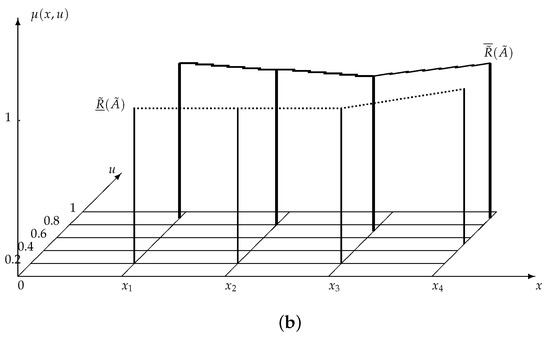
By the definitions of the lower and upper type-2 fuzzy rough approximation operators, we can calculate the lower and upper type-2 fuzzy rough approximations of $\tilde{A}$.

Since $\tilde{R}={\tilde{R}}_1+{\tilde{R}}_2$ and $\tilde{A}={\tilde{A}}_1+{\tilde{A}}_2$, where:

$${\tilde{R}}_1(x_i,y_j)=\left(\begin{array}{ccccc}1/1& 1/0.8& 1/0.3& 1/0.9& 1/0.6\\ 1/0.6& 1/0.3& 1/0.8& 1/1& 1/0.4\\ 1/0.4& 1/0.6& 1/0.5& 1/1& 1/0.8\\ 1/1& 1/0.5& 1/0.6& 1/0.3& 1/0.7\end{array}\right),$$

$${\tilde{R}}_2(x_i,y_j)=\left(\begin{array}{ccccc}1/1& 1/0.8& 0.5/0.4& 1/0.9& 1/0.6\\ 1/0.6& 1/0.3& 1/0.8& 1/1& 1/0.4\\ 1/0.4& 1/0.6& 1/0.5& 1/1& 1/0.8\\ 1/1& 1/0.5& 1/0.6& 1/0.3& 1/0.7\end{array}\right),$$

$${\tilde{A}}_1=\frac{1/0.9}{y_1}+\frac{1/0.4}{y_2}+\frac{1/1}{y_3}+\frac{1/0.2}{y_4}+\frac{1/0.7}{y_5},$$

$${\tilde{A}}_2=\frac{1/0.9}{y_1}+\frac{0.8/0.5}{y_2}+\frac{1/1}{y_3}+\frac{1/0.2}{y_4}+\frac{1/0.7}{y_5},$$

we have:

$$\underline{{\tilde{R}}_1}({\tilde{A}}_1)=\frac{1/0.2}{x_1}+\frac{1/0.2}{x_2}+\frac{1/0.2}{x_3}+\frac{1/0.5}{x_4},$$

$$\underline{{\tilde{R}}_1}({\tilde{A}}_2)=\frac{0.8/0.2}{x_1}+\frac{0.8/0.2}{x_2}+\frac{0.8/0.2}{x_3}+\frac{0.8/0.5}{x_4},$$

$$\underline{{\tilde{R}}_2}({\tilde{A}}_1)=\frac{0.5/0.2}{x_1}+\frac{1/0.2}{x_2}+\frac{1/0.2}{x_3}+\frac{1/0.5}{x_4},$$

and:

$$\underline{{\tilde{R}}_2}({\tilde{A}}_2)=\frac{0.5/0.2}{x_1}+\frac{0.8/0.2}{x_2}+\frac{0.8/0.2}{x_3}+\frac{0.8/0.5}{x_4}.$$

Thus,

$$\underline{\tilde{R}}(\tilde{A})=\frac{1/0.2}{x_1}+\frac{1/0.2}{x_2}+\frac{1/0.2}{x_3}+\frac{1/0.5}{x_4}.$$

From

$$\overline{{\tilde{R}}_1}({\tilde{A}}_1)=\frac{1/0.9}{x_1}+\frac{1/0.8}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.9}{x_4},$$

$$\overline{{\tilde{R}}_1}({\tilde{A}}_2)=\frac{0.8/0.9}{x_1}+\frac{0.8/0.8}{x_2}+\frac{0.8/0.7}{x_3}+\frac{0.8/0.9}{x_4},$$

$$\overline{{\tilde{R}}_2}({\tilde{A}}_1)=\frac{0.5/0.9}{x_1}+\frac{1/0.8}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.9}{x_4},$$

$$\overline{{\tilde{R}}_2}({\tilde{A}}_2)=\frac{0.5/0.9}{x_1}+\frac{0.8/0.8}{x_2}+\frac{0.8/0.7}{x_3}+\frac{0.8/0.9}{x_4},$$

we have:

$$\overline{\tilde{R}}(\tilde{A})=\frac{1/0.9}{x_1}+\frac{1/0.8}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.9}{x_4}.$$

Consequently (Figure 3b),

$$\underline{\tilde{R}}(\tilde{A})+\overline{\tilde{R}}(\tilde{A})=\frac{1/0.2+1/0.9}{x_1}+\frac{1/0.2+1/0.8}{x_2}+\frac{1/0.2+1/0.7}{x_3}+\frac{1/0.5+1/0.9}{x_4}.$$

Let:

$$T_1=\{i|\underset{x_i\in X}{max}\{C(\underline{\tilde{R}}(\tilde{A})(x_i))\}\},$$

$$T_2=\{j|\underset{x_j\in X}{max}\{C(\overline{\tilde{R}}(\tilde{A})(x_j))\}\},$$

$$T_3=\{k|\underset{x_k\in X}{max}\{C([\underline{\tilde{R}}(\tilde{A})+\overline{\tilde{R}}(\tilde{A})](x_k))\}\},$$

where $C(\underline{\tilde{R}}(\tilde{A})(x_i))$ is the centroid of $\underline{\tilde{R}}(\tilde{A})(x_i)$.

If $T_1\cap T_2\cap T_3\ne \varnothing$, then $x_i(i\in T_1\cap T_2\cap T_3)$ is the best choice of $\tilde{A}.$

If $T_1\cap T_2\cap T_3=\varnothing$, then consider $T_1\cap T_2$: if $T_1\cap T_2\ne \varnothing$, we have that $x_i(i\in T_1\cap T_2)$ is the best choice of $\tilde{A};$ if $T_1\cap T_2=\varnothing$, we take $x_i(i\in T_3)$ as the best choice of $\tilde{A}$ [29].

Since $T_1=\{4\}$, $T_2=\{1,4\}$, $T_3=\{4\}$, $x_4$ is the best house for $\tilde{A}$.

From the definition of $\tilde{A}$, it is clear that client $\tilde{A}$ pays most attention to $y_3$ and $y_1$, the surrounding facilities and the structure, and $y_4$, price, is the least important factor. $x_4$ is the best house both in surrounding facilities and structure.

Consider another client for house purchasing (Figure 4a):

$$\tilde{B}=\frac{1/0.6}{y_1}+\frac{1/0.5}{y_2}+\frac{1/0.3+1/0.4}{y_3}+\frac{1/0.7}{y_4}+\frac{1/0.2}{y_5}.$$

Take:

$${\tilde{B}}_1=\frac{1/0.6}{y_1}+\frac{1/0.5}{y_2}+\frac{1/0.3}{y_3}+\frac{1/0.7}{y_4}+\frac{1/0.2}{y_5}$$

and:

$${\tilde{B}}_2=\frac{1/0.6}{y_1}+\frac{1/0.5}{y_2}+\frac{1/0.4}{y_3}+\frac{1/0.7}{y_4}+\frac{1/0.2}{y_5},$$

Using the definition of granular type-2 fuzzy sets, we can compute the upper and lower approximations of $\tilde{B}$:

$$\overline{\tilde{R}}(\tilde{B})=\overline{{\tilde{R}}_1}({\tilde{B}}_1)+\overline{{\tilde{R}}_1}({\tilde{B}}_2)+\overline{{\tilde{R}}_2}({\tilde{B}}_1)+\overline{{\tilde{R}}_2}({\tilde{B}}_2),$$

$$\underline{\tilde{R}}(\tilde{B})=\underline{{\tilde{R}}_1}({\tilde{B}}_1)+\underline{{\tilde{R}}_1}({\tilde{B}}_2)+\underline{{\tilde{R}}_2}({\tilde{B}}_1)+\underline{{\tilde{R}}_2}({\tilde{B}}_2),$$

where:

$$\overline{{\tilde{R}}_1}({\tilde{B}}_1)={[{(y_1)}_{0.6}^1]}_{{\tilde{R}}_1}^{\wedge }\cup {[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_1}^{\wedge }\cup {[{(y_3)}_{0.3}^1]}_{{\tilde{R}}_1}^{\wedge }\cup {[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_1}^{\wedge }\cup {[{(y_5)}_{0.2}^1]}_{{\tilde{R}}_1}^{\wedge }$$

$$\overline{{\tilde{R}}_1}({\tilde{B}}_2)={[{(y_1)}_{0.6}^1]}_{{\tilde{R}}_1}^{\wedge }\cup {[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_1}^{\wedge }\cup {[{(y_3)}_{0.4}^1]}_{{\tilde{R}}_1}^{\wedge }\cup {[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_1}^{\wedge }\cup {[{(y_5)}_{0.2}^1]}_{{\tilde{R}}_1}^{\wedge }$$

$$\overline{{\tilde{R}}_2}({\tilde{B}}_1)={[{(y_1)}_{0.6}^1]}_{{\tilde{R}}_2}^{\wedge }\cup {[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_2}^{\wedge }\cup {[{(y_3)}_{0.3}^1]}_{{\tilde{R}}_2}^{\wedge }\cup {[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_2}^{\wedge }\cup {[{(y_5)}_{0.2}^1]}_{{\tilde{R}}_2}^{\wedge }$$

$$\overline{{\tilde{R}}_2}({\tilde{B}}_2)={[{(y_1)}_{0.6}^1]}_{{\tilde{R}}_2}^{\wedge }\cup {[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_2}^{\wedge }\cup {[{(y_3)}_{0.4}^1]}_{{\tilde{R}}_2}^{\wedge }\cup {[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_2}^{\wedge }\cup {[{(y_5)}_{0.2}^1]}_{{\tilde{R}}_2}^{\wedge }$$

$$\underline{{\tilde{R}}_1}({\tilde{B}}_1)={[{(y_1)}_{0.4}^1]}_{{\tilde{R}}_1}^{\vee }\cap {[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_1}^{\vee }\cap {[{(y_3)}_{0.7}^1]}_{{\tilde{R}}_1}^{\vee }\cap {[{(y_4)}_{0.3}^1]}_{{\tilde{R}}_1}^{\vee }\cap {[{(y_5)}_{0.8}^1]}_{{\tilde{R}}_1}^{\vee }$$

$$\underline{{\tilde{R}}_1}({\tilde{B}}_1)={[{(y_1)}_{0.4}^1]}_{{\tilde{R}}_1}^{\vee }\cap {[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_1}^{\vee }\cap {[{(y_3)}_{0.6}^1]}_{{\tilde{R}}_1}^{\vee }\cap {[{(y_4)}_{0.3}^1]}_{{\tilde{R}}_1}^{\vee }\cap {[{(y_5)}_{0.8}^1]}_{{\tilde{R}}_1}^{\vee }$$

$$\underline{{\tilde{R}}_2}({\tilde{B}}_1)={[{(y_1)}_{0.4}^1]}_{{\tilde{R}}_2}^{\vee }\cap {[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_2}^{\vee }\cap {[{(y_3)}_{0.7}^1]}_{{\tilde{R}}_2}^{\vee }\cap {[{(y_4)}_{0.3}^1]}_{{\tilde{R}}_2}^{\vee }\cap {[{(y_5)}_{0.8}^1]}_{{\tilde{R}}_2}^{\vee }$$

$$\underline{{\tilde{R}}_2}({\tilde{B}}_1)={[{(y_1)}_{0.4}^1]}_{{\tilde{R}}_2}^{\vee }\cap {[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_2}^{\vee }\cap {[{(y_3)}_{0.6}^1]}_{{\tilde{R}}_2}^{\vee }\cap {[{(y_4)}_{0.3}^1]}_{{\tilde{R}}_2}^{\vee }\cap {[{(y_5)}_{0.8}^1]}_{{\tilde{R}}_2}^{\vee }.$$

and:

$${[{(y_1)}_{0.6}^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{1/0.6}{x_1}+\frac{1/0.6}{x_2}+\frac{1/0.4}{x_3}+\frac{1/0.6}{x_4}$$

$${[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{1/0.5}{x_1}+\frac{1/0.3}{x_2}+\frac{1/0.5}{x_3}+\frac{1/0.5}{x_4}$$

$${[{(y_3)}_{0.3}^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{1/0.3}{x_1}+\frac{1/0.3}{x_2}+\frac{1/0.3}{x_3}+\frac{1/0.3}{x_4}$$

$${[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{1/0.7}{x_1}+\frac{1/0.7}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.3}{x_4}$$

$${[{(y_5)}_{0.2}^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{1/0.2}{x_1}+\frac{1/0.2}{x_2}+\frac{1/0.2}{x_3}+\frac{1/0.2}{x_4}$$

$${[{(y_3)}_{0.4}^1]}_{{\tilde{R}}_1}^{\wedge }=\frac{1/0.3}{x_1}+\frac{1/0.4}{x_2}+\frac{1/0.4}{x_3}+\frac{1/0.4}{x_4}$$

$${[{(y_1)}_{0.6}^1]}_{{\tilde{R}}_2}^{\wedge }=\frac{0.5/0.6}{x_1}+\frac{1/0.6}{x_2}+\frac{1/0.4}{x_3}+\frac{1/0.6}{x_4}$$

$${[{(y_2)}_{0.5}^1]}_{{\tilde{R}}_2}^{\wedge }=\frac{0.5/0.5}{x_1}+\frac{1/0.3}{x_2}+\frac{1/0.5}{x_3}+\frac{1/0.5}{x_4}$$

$${[{(y_3)}_{0.3}^1]}_{{\tilde{R}}_2}^{\wedge }=\frac{0.5/0.3}{x_1}+\frac{1/0.3}{x_2}+\frac{1/0.3}{x_3}+\frac{1/0.3}{x_4}$$

$${[{(y_4)}_{0.7}^1]}_{{\tilde{R}}_2}^{\wedge }=\frac{0.5/0.7}{x_1}+\frac{1/0.7}{x_2}+\frac{1/0.7}{x_3}+\frac{1/0.3}{x_4}$$

$${[{(y_5)}_{0.2}^1]}_{{\tilde{R}}_2}^{\wedge }=\frac{0.5/0.2}{x_1}+\frac{1/0.2}{x_2}+\frac{1/0.2}{x_3}+\frac{1/0.2}{x_4}$$

$${[{(y_3)}_{0.4}^1]}_{{\tilde{R}}_2}^{\wedge }=\frac{0.5/0.4}{x_1}+\frac{1/0.4}{x_2}+\frac{1/0.4}{x_3}+\frac{1/0.4}{x_4}$$

$${[{(y_1)}_{0.4}^1]}_{{\tilde{R}}_1}^{\vee }=\frac{1/0.6}{x_1}+\frac{1/0.6}{x_2}+\frac{}{}$$