A Recourse-Based Type-2 Fuzzy Programming Method for Water Pollution Control under Uncertainty
Abstract
1. Introduction
2. Methodology
- Step 1.
- Formulate the RTFP model.
- Step 2.
- Discrete probability distribution into several values with each corresponds to one probability.
- Step 3.
- Convert the output of T2FS into conventional fuzzy sets.
- Step 4.
- Conduct defuzzification of T2FS according to the critical value (CV)-based reduction method.
- Step 5.
- Run the RTFP model.
- Step 6.
- Obtain the optimal solutions of the objective function (), first-stage decision variable (), and second-stage decision variable ().
3. Case Study
- (1)
- COD discharge constraints:
- (2)
- Phosphorus discharge constraints:
- (3)
- Nitrogen discharge constraints:
- (4)
- Soil loss constraints:
- (5)
- Water supply balance constraint:
- (6)
- Product demand constraints:
- (7)
- Technical constraints:
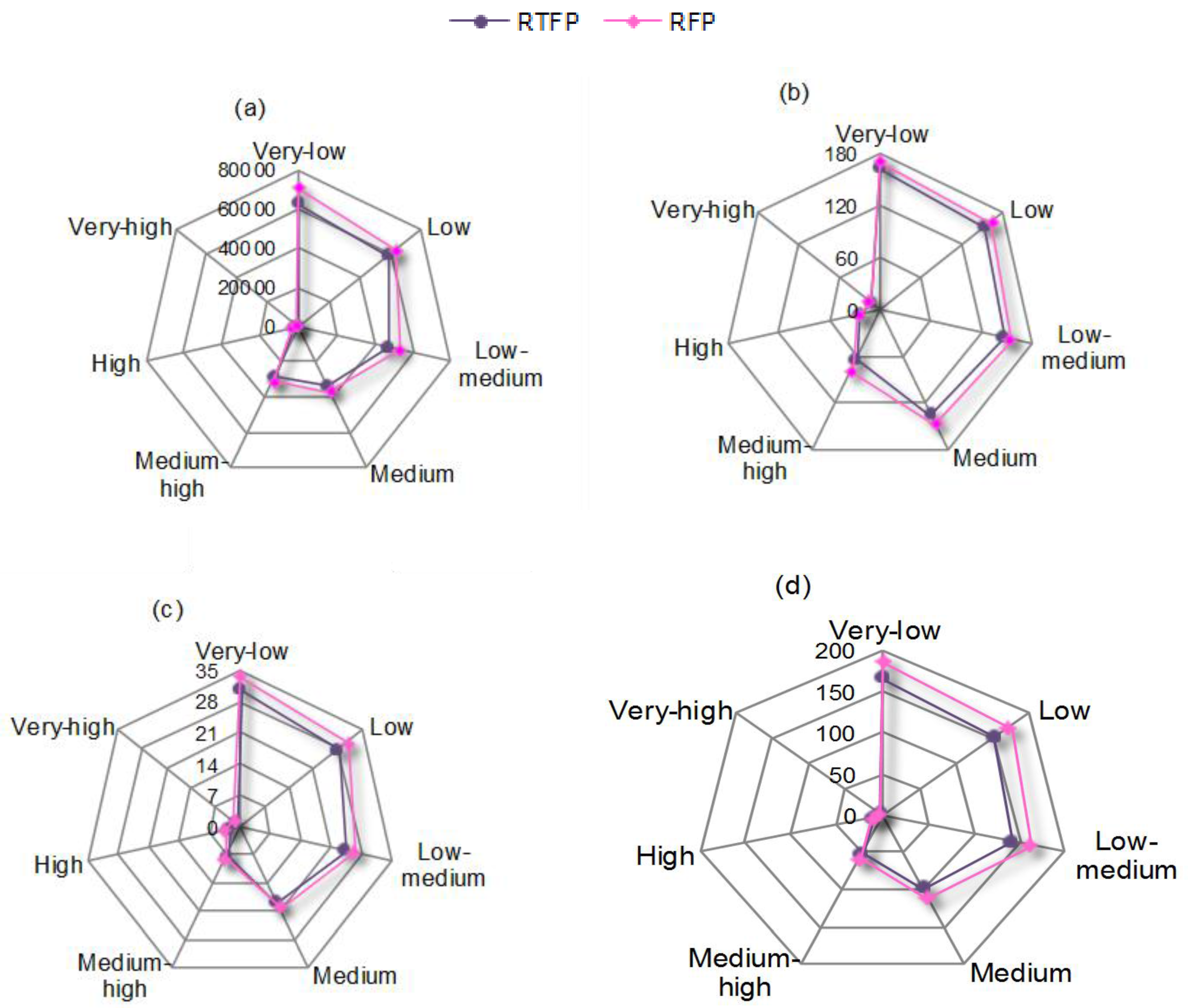
4. Results Analysis and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclatures
| i | index for economic activities; for agricultural activities, i = 1, 2, …, Ia; for fishery activities i = 1, 2, …, If (e.g., fish and prawn farming); for livestock husbandry activities i = 1, 2, …, Il; for industrial activities i = 1, 2, …, Ii (e.g., manufacturing, mining, architecture, transportation and others); for forestry activities i = 1, 2, …, Iw |
| j | index for zones; j = 1, 2, …, J |
| k | index for pollutants; k = 1, 2, …, K (e.g., COD discharge, TN loss, TP loss, and soil loss) |
| h | allowable pollutant discharge level; h = 1, 2, …, H |
| probability of occurrence allowable pollutant discharge level h (%) | |
| unit benefit from agricultural activity i in zone j (RMB¥/km2) | |
| land area target for agricultural activity i in zone j (km2) | |
| reduction of net benefit from agricultural activity i for excess discharge of pollutant k (RMB¥/kg when k = 2, 3; RMB¥/tonne when k = 4) | |
| discharge rate of pollutant k from agricultural activity i in zone j (kg/km2 when k = 2, 3; tonne /km2 when k = 4) | |
| decision variables representing amount by which the target of agricultural activity i discharge pollutant k exceeds standards in zone j when level is h (km2) | |
| unit benefit from fishery activity i in zone j (RMB¥/km2) | |
| land area target for fishery farming activity i in zone j (km2) | |
| reduction of net benefit from fishery activity i for excess discharge of pollutant k (RMB¥/kg) | |
| discharge rate of pollutant k from fishery activity i in zone j (kg/km2) | |
| decision variables representing amount by which target of fishery activity i discharge pollutant k exceeds standards in zone j when level is h (km2) | |
| unit benefit from livestock husbandry activity i in zone j (RMB¥/head) | |
| target for livestock husbandry activity i in zone j (head) | |
| reduction of net benefit from livestock husbandry activity i for excess discharge of pollutant (i.e., COD) (RMB¥/kg) | |
| discharge rate of pollutant (i.e., COD) from livestock husbandry activity i in zone j (kg/head) | |
| decision variables representing amount by which target of livestock husbandry activity i discharge pollutant (i.e., COD) exceeds standards in zone j when level is h (head) | |
| output target for industrial activity i in zone j (RMB¥) | |
| reduction of net benefit from industrial activity i for excess discharge of pollutant (i.e., COD) (RMB¥/kg) | |
| discharge rate of pollutant (i.e., COD) from industrial activity i in zone j (kg/RMB¥) | |
| decision variables representing amount by which target of industrial activity i discharge pollutant (i.e., COD) exceeds standards in zone j when level is h (RMB¥) | |
| unit benefit from forestry activity i in zone j (RMB¥/head) | |
| land area target for forestry activity i in zone j (unit) | |
| reduction of net benefit from forestry activity i for excess discharge of pollutant (i.e., soil loss) (RMB¥/tonne) | |
| discharge rate of pollutant (i.e., soil loss) from forestry activity i in zone j (tonne/km2) | |
| decision variables representing amount by which target of forestry activity i discharge pollutant (i.e., soil loss) exceeds standards in zone j when level is h (unit) | |
| COD discharge from fishery farming activity i in zone j (kg/km2) | |
| maximum allowable COD discharge for fishery farming activities in zone j with probability of occurrence under level h (kg) | |
| maximum allowable COD discharge for livestock husbandry activities in zone j with probability of occurrence under level h (kg) | |
| maximum allowable COD discharge for industrial activity i in zone j with probability of occurrence under level h (kg) | |
| maximum allowable COD discharge from economic activities with probability of occurrence under level h (kg) | |
| soil loss from agricultural activity i in zone j (tonne/km2) | |
| phosphorous content of soil corresponding to agricultural activity i in zone j (kg/tonne) | |
| runoff from agricultural activity i in zone j (kg/km2) | |
| dissolved phosphorous content of runoff corresponding to agricultural activity i in zone j (%) | |
| maximum allowable phosphorous loss from agricultural activities in zone j with probability of occurrence under level h (kg) | |
| dissolved phosphorous loss from fishery farming activity i in zone j (kg/km2) | |
| maximum allowable phosphorous loss from fishery farming activities in zone j with probability of occurrence under level h (kg) | |
| maximum allowable phosphorous loss from economic activities with probability of occurrence under level h (kg) | |
| nitrogen content of soil corresponding to agricultural activity i in zone j (kg/tonne) | |
| dissolved nitrogen content of runoff corresponding to agricultural activity i in zone j (%) | |
| maximum allowable nitrogen loss from agricultural activities in zone j with probability of occurrence under level h (kg) | |
| dissolved nitrogen loss from fishery activity i in zone j (kg/km2) | |
| maximum allowable nitrogen loss from fishery farming activities in zone j with probability of occurrence under level h (kg) | |
| maximum allowable soil loss from economic activities with probability of occurrence under level h (tonne) | |
| maximum allowable nitrogen loss from economic activities with probability of occurrence under level h (kg) | |
| maximum allowable soil loss from agricultural activities in zone j with probability of occurrence under level h (tonne) | |
| maximum allowable soil loss from forestry activities in zone j with probability of occurrence under level h (tonne) | |
| water demand for agricultural activity i (m3/km2) | |
| water demand for fishery activity i (m3/km2) | |
| water demand for livestock husbandry activity i (m3/head) | |
| water demand for industrial activity i (m3/RMB¥) | |
| water demand for forestry activity i (m3/km2) | |
| maximum allowable water resources supply amount in zone j (m3) | |
| minimum demand for agricultural activity i (km2) | |
| maximum demand for agricultural activity i (km2) | |
| minimum demand for fishery activity i (km2) | |
| maximum demand for fishery activity i (km2) | |
| minimum demand for livestock husbandry activity i (head) | |
| maximum demand for livestock husbandry activity i (head) | |
| minimum demand for industrial activity i (RMB¥) | |
| maximum demand for industrial activity i (RMB¥) |
References
- Pastori, M.; Udías, A.; Bouraoui, F.; Bidoglio, G. A multi-objective approach to evaluate the economic and environmental impacts of alternative water and nutrient management strategies in Africa. J. Environ. Inform. 2017, 29. [Google Scholar] [CrossRef]
- Steenbergen, R.D.J.M.; Gelder van, P.H.A.J.M.; Miraglia, S.; Vrouwenvelder, A.C.W.M. Safety, Reliability and Risk Analysis: Beyond the Horizon. In Proceedings of the 22nd Annual Conference on European Safety and Reliability (ESREL), Wroclaw, Poland, 14–18 September 2014; CRC Press-Taylor & Francis Group: Boca Raton, FL, USA, 2014; pp. 1115–1120. [Google Scholar]
- David, F.; Sandra, P. On the complementary nature of CGC-MS, CGC-FTIR, and CGC-AED for water pollution control. J. Sep. Sci. 2015, 14, 554–557. [Google Scholar] [CrossRef]
- Pietrucha-Urbanik, K.; Tchorzewska-Cieslak, B. Water Supply System Operation Regarding Consumer Safety Using Kohonen Neural Network; Steenbergen, R.D.J.M., van Gelder, P.H.A.J.M., Miraglia, S., Vrouwenvelder, A.C.W.M.T., Eds.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Li, Y.P.; Zhang, N.; Huang, G.H.; Liu, J. Coupling fuzzy-chance constrained program with minimax regret analysis for water quality management. Stoch. Environ. Res. Risk Assess. 2014, 28, 1769–1784. [Google Scholar] [CrossRef]
- Jorba, L.; Adillon, R. A generalization of trapezoidal fuzzy numbers based on modal interval theory. Symmetry 2017, 9, 198. [Google Scholar] [CrossRef]
- Hu, B.; Bi, L.Q.; Dai, S.S. The orthogonality between complex fuzzy sets and its application to signal detection. Symmetry 2017, 9, 175. [Google Scholar] [CrossRef]
- Dimitrov, V.; Driankov, D.; Petrov, A. Fuzzy equations and their applications to water pollution control. IFAC Proc. 1977, 10, 369–371. [Google Scholar] [CrossRef]
- Chang, N.B.; Chen, H.W.; Shaw, D.G. Water pollution control in river basin by interactive fuzzy interval multiobjective programming. J. Environ. Eng. 1997, 123, 1208–1216. [Google Scholar] [CrossRef]
- Karmakar, S.; Mujumdar, P.P. Grey fuzzy optimization model for water quality management of a river system. Adv. Water Resour. 2006, 29, 1088–1105. [Google Scholar] [CrossRef]
- Singh, A.P.; Ghosh, S.K.; Sharma, P. Water quality management of a stretch of river Yamuna: An interactive fuzzy multi-objective approach. Water Resour. Manag. 2007, 21, 515–532. [Google Scholar] [CrossRef]
- Sakawa, M. Interactive fuzzy goal programming for multiobjective nonlinear problems and its application to water quality management. Electron. Commun. Jpn. 2010, 68, 49–56. [Google Scholar] [CrossRef]
- Chmielowski, W.Z. Fuzzy Control in Environmental Engineering; Springer International Publishing: Basel, Switzerland, 2016. [Google Scholar]
- Forio, M.A.E.; Mouton, A.; Lock, K. Fuzzy modelling to identify key drivers of ecological water quality to support decision and policy making. Environ. Sci. Policy 2017, 68, 58–68. [Google Scholar] [CrossRef]
- Maeda, S.; Kuroda, H.; Yoshida, K. A GIS-aided two-phase grey fuzzy optimization model for nonpoint source pollution control in a small watershed. Paddy Water Environ. 2016, 1–14. [Google Scholar] [CrossRef]
- Liu, M.; Nie, G.; Hu, M. An interval-parameter fuzzy robust nonlinear programming model for water quality management. J. Water Resour. Prot. 2013, 5, 12–16. [Google Scholar] [CrossRef]
- Tavakoli, A.; Nikoo, M.R.; Kerachian, R. River water quality management considering agricultural return flows: application of a nonlinear two-stage stochastic fuzzy programming. Environ. Monit. Assess. 2015, 187, 158. [Google Scholar] [CrossRef] [PubMed]
- Ji, Y.; Huang, G.; Sun, W. Water quality management in a wetland system using an inexact left-hand-side chance-constrained fuzzy multi-objective approach. Stoch. Environ. Res. Risk Assess. 2016, 30, 621–633. [Google Scholar] [CrossRef]
- Wu, D.R.; Tan, W.W. Computationally Efficient Type-reduction Strategies for a Type-2 Fuzzy Logic Controller. In Proceedings of the 14th IEEE International Conference on Fuzzy System, Reno, NV, USA, 25–25 May 2005; pp. 353–358. [Google Scholar]
- Cervantes, L.; Castillo, O. Type-2 fuzzy logic aggregation of multiple fuzzy controllers for airplane flight control. Inf. Sci. 2015, 324, 247–256. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. A review on interval type-2 fuzzy logic applications in intelligent control. Inf. Sci. 2014, 279, 615–631. [Google Scholar] [CrossRef]
- Precup, R.E.; Angelov, P.; Costa, B.S.J.; Sayed-Mouchaweh, M. An overview on fault diagnosis and nature-inspired optimal control of industrial process applications. Comput. Ind. 2015, 74, 75–94. [Google Scholar] [CrossRef]
- Li, Y.P.; Huang, G.H.; Li, H.Z. A recourse-based interval fuzzy programming model for point-nonpoint source effluent trading under uncertainty. J. Am. Water Resour. Assoc. 2015, 50, 1191–1207. [Google Scholar] [CrossRef]
- Suo, C.; Li, Y.P.; Wang, C.X. A type-2 fuzzy chance-constrained programming method for planning Shanghai’s energy system. Int. J. Electr. Power Energy Syst. 2017, 90, 37–53. [Google Scholar] [CrossRef]
- Alcantud, J.C.R.; García-Sanz, M.D. Evaluations of infinite utility streams: Pareto Efficient and Egalitarian Axiomatics. Metroeconomica 2013, 64, 432–447. [Google Scholar] [CrossRef]
- Precup, R.E.; Sabau, M.C.; Petriu, E.M. Nature-inspired optimal tuning of input membership functions of Takagi-Sugeno-Kang fuzzy models for Anti-lock Braking Systems. Appl. Soft Comput. J. 2015, 27, 575–589. [Google Scholar] [CrossRef]
- Vrkalovic, S.; Teban, T.-A.; Borlea, I.-D. Stable Takagi-Sugeno fuzzy control designed by optimization. Int. J. Artif. Intell. 2017, 15, 17–29. [Google Scholar]
- Chen, Z.; Zhou, S.; Luo, J. A robust ant colony optimization for continuous functions. Expert Syst. Appl. 2017, 81, 309–320. [Google Scholar] [CrossRef]
- Tchórzewska-Cieślak, B.; Pietrucha-Urbanik, K.; Urbanik, M. Analysis of the gas network failure and failure prediction using the Monte Carlo simulation method. Eksploatacja i Niezawodnosc Maint. Reliab. 2016, 18, 254–259. [Google Scholar]
- Qin, R.; Liu, Y.K.; Liu, Z.Q. Methods of critical value reduction for type-2 fuzzy variables and their applications. J. Comput. Appl. Math. 2011, 235, 1454–1481. [Google Scholar] [CrossRef]
- Yongxin Bureau of Statistics Statistical Communiqué on the 2012 Economic and Social Development in Yongxin. Available online: http://old.yongxin.gov.cn/tjj/a/detail-7021.html (accessed on 28 October 2013).
- Huang, G.H.; Chen, B.; Qin, X.S.; Mance, E. An Integrated Decision Support System for Developing Rural Eco-Environmental Sustainability in the Mountain-River-Lake Region of Jiangxi Province, China; Final Report; United Nations Development Program: New York, NY, USA, 2006. [Google Scholar]
- Huang, G.H.; Qin, X.S.; Sun, W.; Nie, X.H.; Li, Y.P. An optimisation-based environmental decision support system for sustainable development in a rural area in China. Civ. Eng. Environ. Syst. 2009, 26, 65–83. [Google Scholar] [CrossRef]
- Statistics Bulletin of the National Economic and Social Development in Yongxin County. 2016. Available online: http://www.yongxin.gov.cn/doc/2017/04/25/52136.shtml (accessed on 25 April 2017).
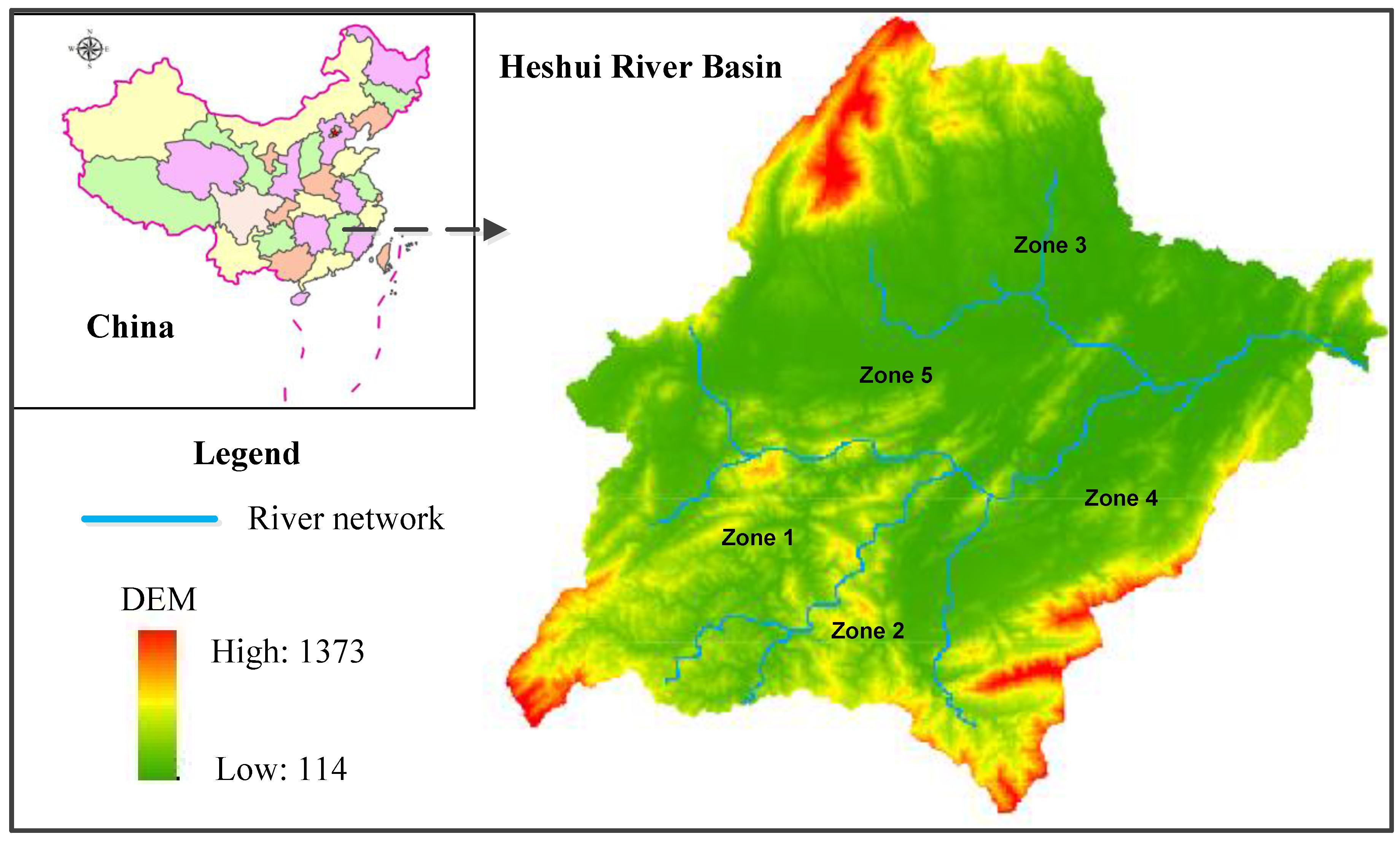
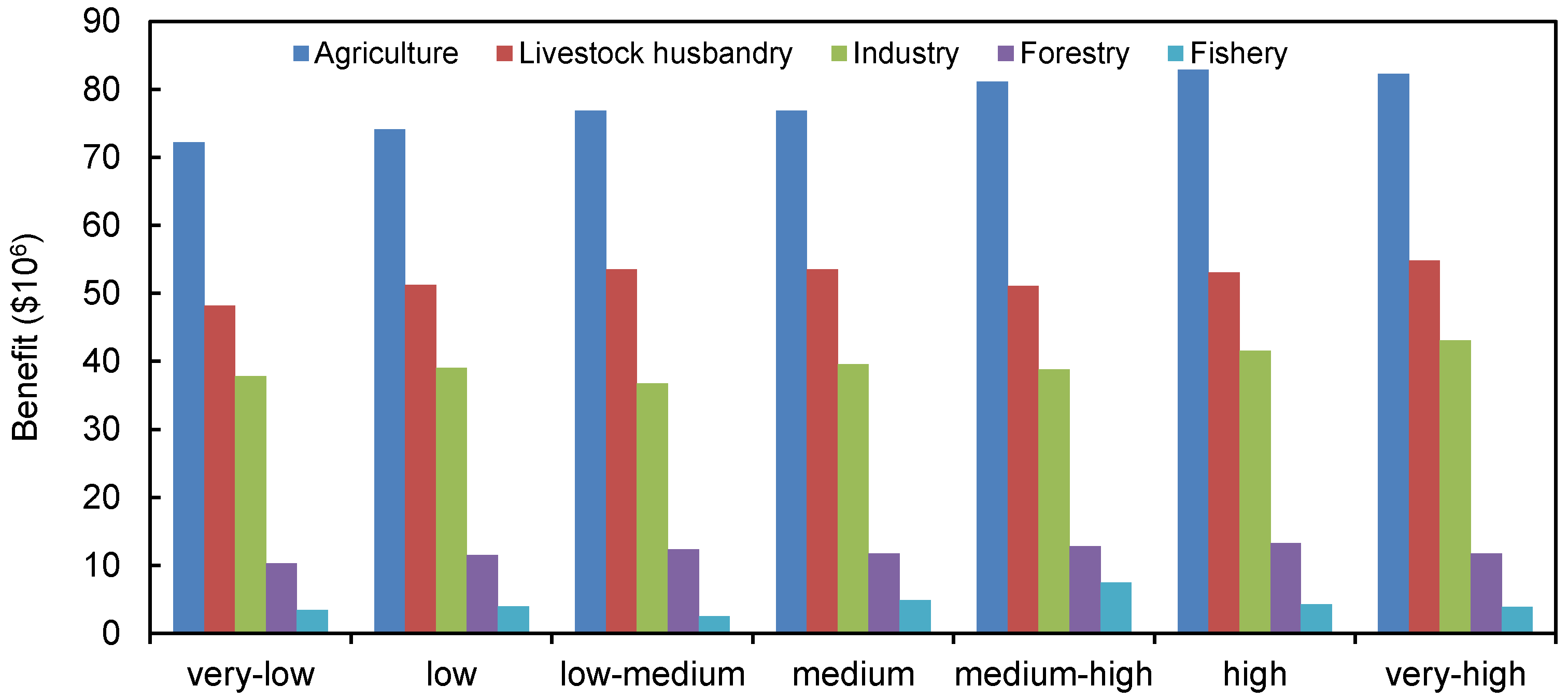
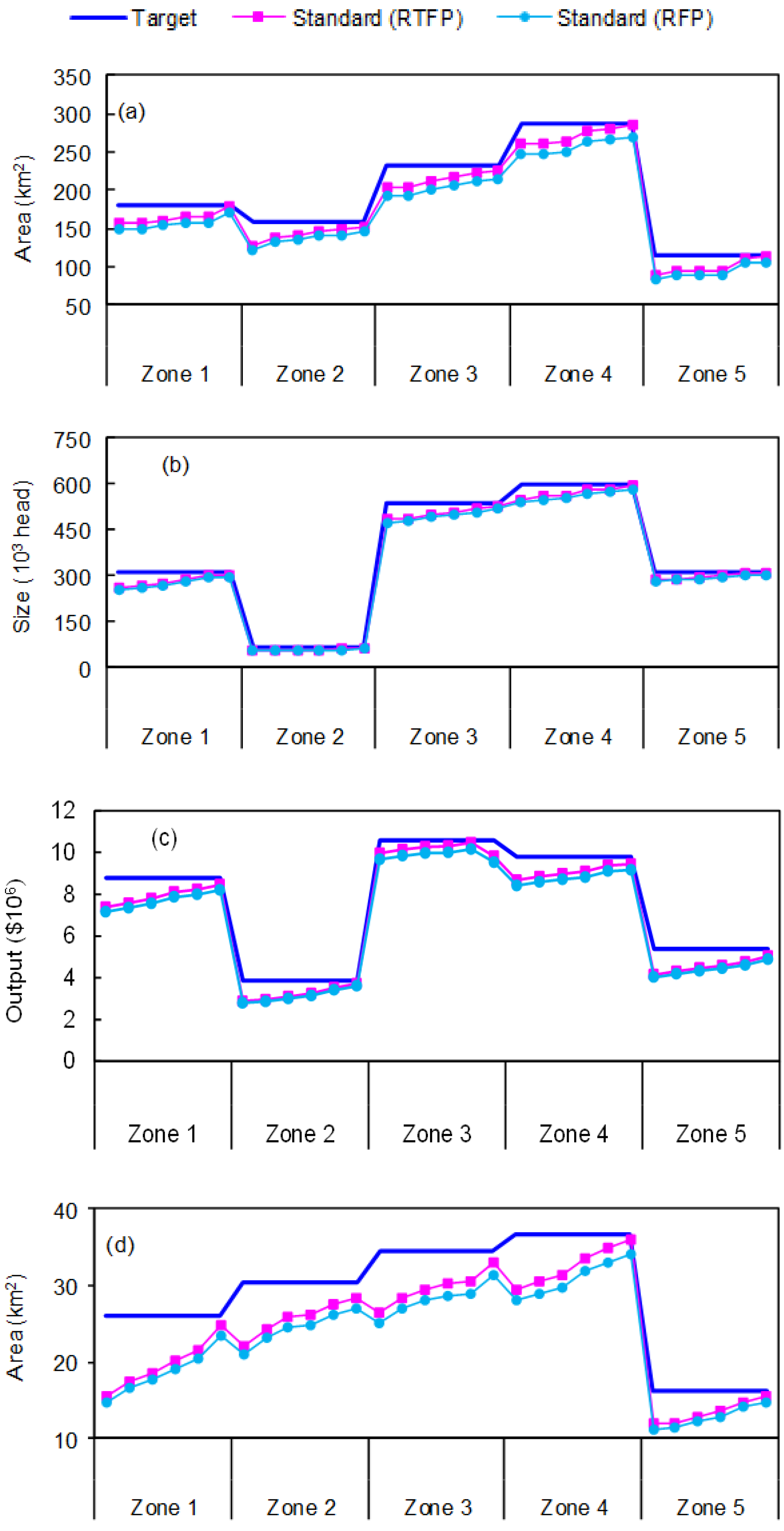
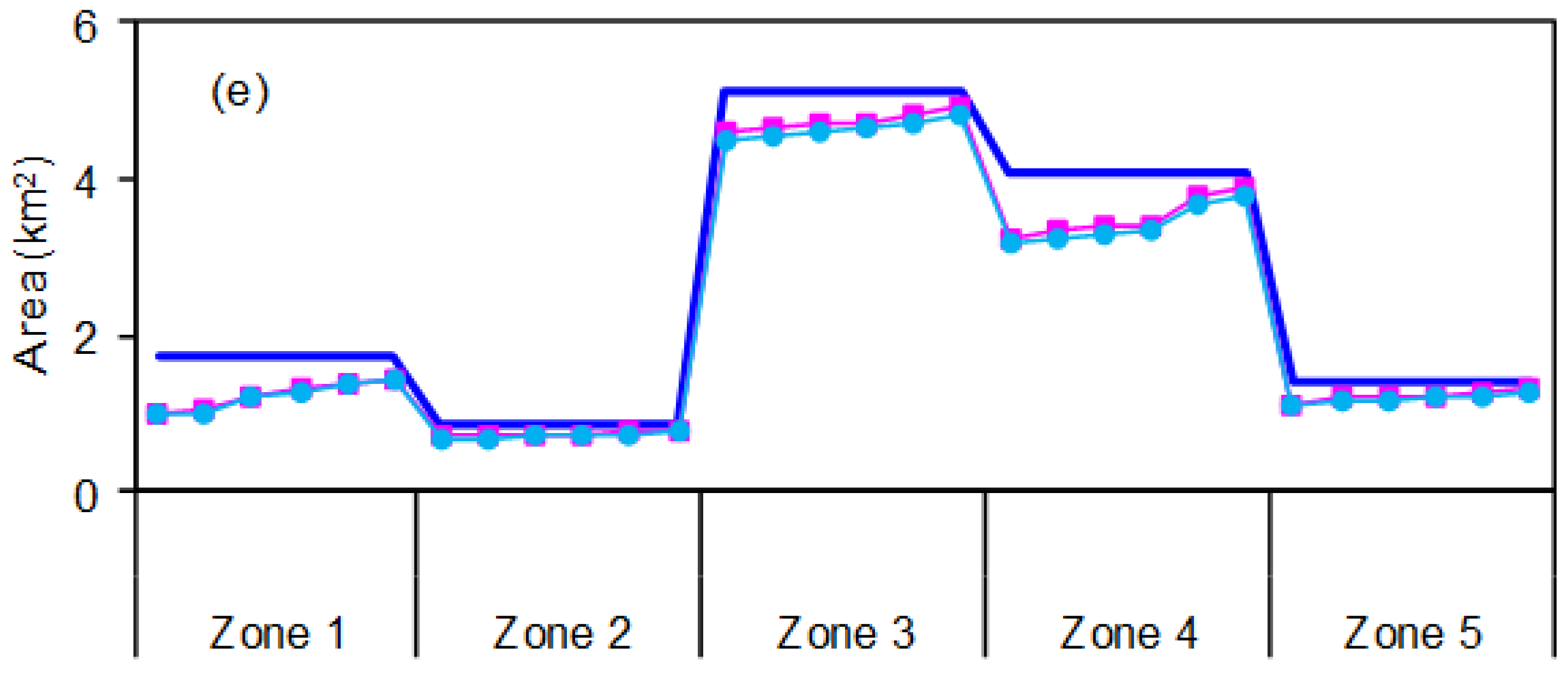
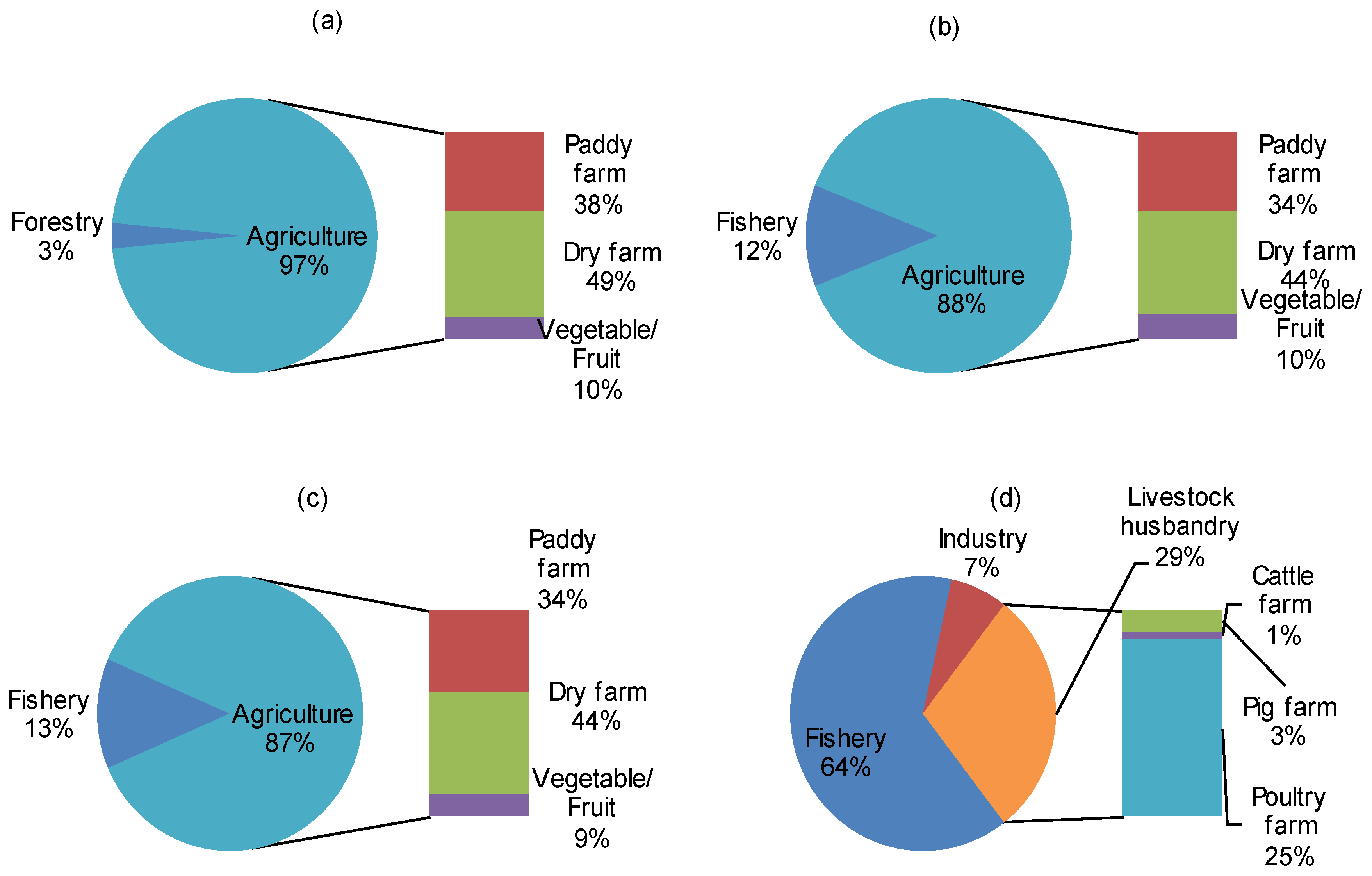
| Zone | Agriculture | ||
| Paddy Farm | Dry Farm | Fruit/Vegetable | |
| Unit Net Benefit (103 $/km2) | |||
| Zone 1 | (201.4, 272.6, 292.3; 0.2, 0.6) | (104.5, 148.4, 163.5; 0.2, 0.6) | (345.3, 457.4, 486.2; 0.2, 0.6) |
| Zone 2 | (174.2, 219.6, 269.6; 0.3, 0.5) | (96.9, 130.3, 140.9; 0.3, 0.5) | (152.9, 205.9, 215.1; 0.3, 0.5) |
| Zone 3 | (169.6, 231.7, 254.4; 0.4, 0.7) | (87.8, 112.1, 127.2; 0.4, 0.7) | (337.7, 472.6, 569.4; 0.4, 0.7) |
| Zone 4 | (187.8, 265.1, 290.8; 0.4, 0.7) | (92.4, 118.1, 124.2; 0.4, 0.7) | (254.5, 343.4, 384.7; 0.4, 0.7) |
| Zone 5 | (184.8, 245.4, 275.7; 0.5, 0.7) | (92.4, 122.7, 133.3; 0.5, 0.7) | (289.3, 390.8, 402.9; 0.5, 0.7) |
| Zone | Livestock Husbandry | ||
| Pig | Cattle | Poultry | |
| Unit Net Benefit ($/head) | |||
| Zone 1 | (152.5, 166.3, 170.1; 0.4, 0.7) | (785.4, 892.4, 998.4; 0.4, 0.7) | (5.3, 6.2, 7.1; 0.4, 0.7) |
| Zone 2 | (139.6, 151.2, 156.6; 0.5, 0.8) | (833.9, 933.6, 974.2; 0.5, 0.8) | (6.2, 6.8, 7.4; 0.5, 0.8) |
| Zone 3 | (139.6, 159.6, 161.2, 0.4, 0.7) | (732.9, 831.1, 868.1; 0.4, 0.7) | (4.7, 6.9, 7.1; 0.4, 0.7) |
| Zone 4 | (154.7, 172.2, 175.4; 0.3, 0.8) | (662.1, 734.9, 760.7; 0.3, 0.8) | (4.9, 6.7, 7.2; 0.3, 0.8) |
| Zone 5 | (158.5, 168.7, 185.2; 0.4, 0.8) | (904.8, 984.2, 999.2; 0.4, 0.8) | (6.2, 7.1, 7.8; 0.4, 0.8) |
| Pollutant | Level | Probability | Zone | ||||
|---|---|---|---|---|---|---|---|
| Zone 1 | Zone 2 | Zone 3 | Zone 4 | Zone 5 | |||
| COD (103 kg) | Very-low | 0.05 | 2453.5 | 496.4 | 3768.4 | 3284.2 | 2307.5 |
| Low | 0.10 | 2469.8 | 499.3 | 3780.8 | 3298.5 | 2213.3 | |
| Low-medium | 0.20 | 2498.3 | 500.3 | 3792.4 | 3390.7 | 2309.8 | |
| Medium | 0.30 | 2523.5 | 502.5 | 3897.9 | 3469.3 | 2468.3 | |
| Medium-high | 0.20 | 2760.7 | 515.6 | 4506.2 | 3607.8 | 2647.8 | |
| High | 0.10 | 2984.4 | 535.5 | 4512.5 | 3812.9 | 2851.2 | |
| Very-high | 0.05 | 3286.2 | 578.7 | 4714.7 | 4214.2 | 3154.9 | |
| TN (103 kg) | Very-low | 0.05 | 166.5 | 193.2 | 235.7 | 286.3 | 223.6 |
| Low | 0.10 | 216.4 | 297.3 | 307.3 | 369.4 | 374.3 | |
| Low-medium | 0.20 | 266.5 | 401.4 | 379.5 | 451.8 | 526.8 | |
| Medium | 0.30 | 324.3 | 506.7 | 458.8 | 561.2 | 679.2 | |
| Medium-high | 0.20 | 381.4 | 614.4 | 544.3 | 683.3 | 836.2 | |
| High | 0.10 | 457.2 | 747.5 | 653.9 | 815.5 | 994.1 | |
| Very-high | 0.05 | 545.5 | 883.9 | 756.3 | 935.8 | 1168.7 | |
| TP (103 kg) | Very-low | 0.05 | 24.2 | 31.1 | 35.6 | 43.2 | 39.9 |
| Low | 0.10 | 34.4 | 52.0 | 50.0 | 59.5 | 70.5 | |
| Low-medium | 0.20 | 44.5 | 73.5 | 64.5 | 76.6 | 101.7 | |
| Medium | 0.30 | 55.0 | 94.6 | 81.0 | 93.6 | 132.2 | |
| Medium-high | 0.20 | 65.1 | 118.1 | 100.2 | 113.9 | 165.4 | |
| High | 0.10 | 79.5 | 142.6 | 114.8 | 134.3 | 200.3 | |
| Very-high | 0.05 | 93.2 | 166.1 | 130.4 | 152.6 | 231.6 | |
| Soil loss (103 t) | Very-low | 0.05 | 97.3 | 92.5 | 133.4 | 168.5 | 61.7 |
| Low | 0.10 | 92.4 | 93.6 | 134.2 | 169.5 | 63.0 | |
| Low-medium | 0.20 | 99.6 | 94.7 | 135.3 | 170.7 | 64.2 | |
| Medium | 0.30 | 100.3 | 98.9 | 140.6 | 176.0 | 71.5 | |
| Medium-high | 0.20 | 118.0 | 133.1 | 155.7 | 186.1 | 82.7 | |
| High | 0.10 | 133.1 | 140.4 | 165.9 | 201.3 | 89.9 | |
| Very-high | 0.05 | 133.2 | 140.5 | 171.6 | 274.4 | 91.9 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, Y.; Huang, G.; Chen, L. A Recourse-Based Type-2 Fuzzy Programming Method for Water Pollution Control under Uncertainty. Symmetry 2017, 9, 265. https://doi.org/10.3390/sym9110265
Liu J, Li Y, Huang G, Chen L. A Recourse-Based Type-2 Fuzzy Programming Method for Water Pollution Control under Uncertainty. Symmetry. 2017; 9(11):265. https://doi.org/10.3390/sym9110265
Chicago/Turabian StyleLiu, Jing, Yongping Li, Guohe Huang, and Lianrong Chen. 2017. "A Recourse-Based Type-2 Fuzzy Programming Method for Water Pollution Control under Uncertainty" Symmetry 9, no. 11: 265. https://doi.org/10.3390/sym9110265
APA StyleLiu, J., Li, Y., Huang, G., & Chen, L. (2017). A Recourse-Based Type-2 Fuzzy Programming Method for Water Pollution Control under Uncertainty. Symmetry, 9(11), 265. https://doi.org/10.3390/sym9110265





