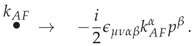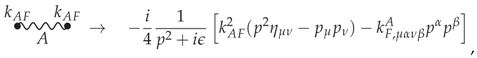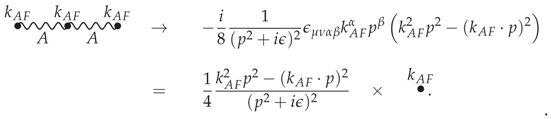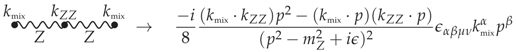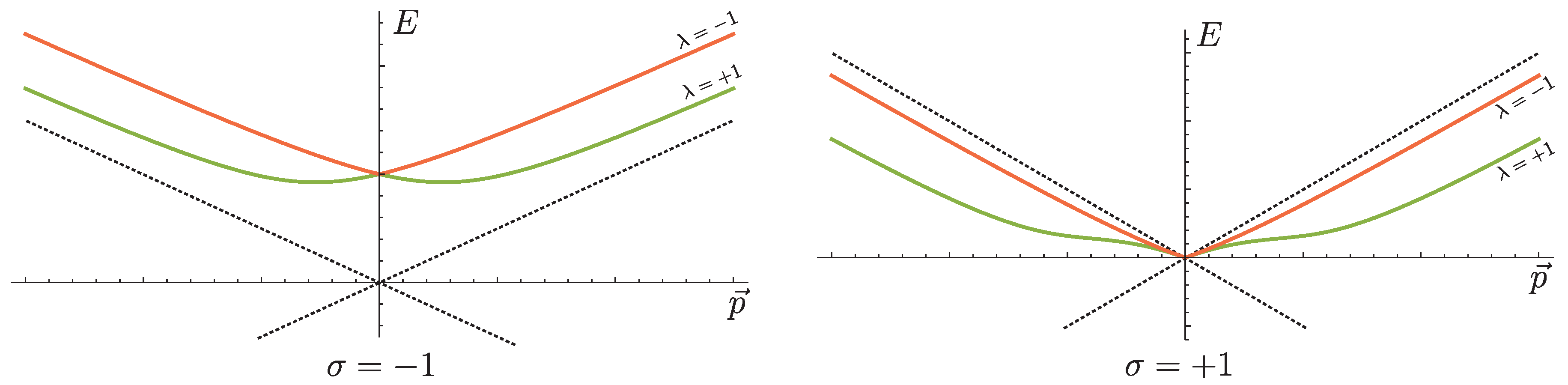1. Introduction
The main motivation to search for departures of relativity is that various candidate theories of gravity may allow for spontaneous Lorentz violation [
1,
2,
3,
4,
5,
6]. A framework that allows incorporation of Lorentz-violating effects into the Standard Model is the Standard-Model Extension (SME) [
7,
8], an effective field theory containing all Lorentz- and CPT-violating operators that are allowed by the remaining Standard-Model symmetries. The SME also contains all CPT-violating operators, since, in any local interacting quantum field theory, CPT violation implies Lorentz violation [
9]. While the SME, being an effective field theory, consists of terms of arbitrary mass dimension, we will consider in this work the superficially renormalizable part of the SME, called the minimal SME (mSME). When restricted to the electroweak part of the gauge sector, CPT and Lorentz violation is parametrized by two four-vector coefficients
and
, corresponding to the
and
gauge sectors, respectively. Each of them multiplies a CPT-violating Chern–Simons-like term of mass dimension three. The
term acts to modify the kinetic term of the
W-boson sector. For massive gauge bosons, it has been shown in [
10] that even in the presence of such a CPT-violating term, covariant quantization of the gauge field theory can be carried out consistently. In [
11], it was shown that the dispersion relation for
W bosons is modified in such a way as to allow for Cherenkov-like emission by high-energy fermions. This effect allows for the derivation of a bound on the
parameter by considering observational data on protons in ultra-high-energy cosmic rays.
For the
Z boson and the photon sectors, the situation is more complicated, due to the mixing that is provoked by electroweak symmetry breaking. As we will show in this paper, the
Z boson and the photon each receive CPT-violating contributions from both the
and
terms. To the lowest order, the effect on the photon sector is to provide a Chern–Simons term with a coefficient
that is a certain linear combination of
and
. The effect of such a term has been studied long ago in [
12], where an extremely strong bound on
was derived from astrophysical observations. (We refer to [
13] for an up-to-date list of experimental and observational bounds on SME parameters.)
However, as we will show in this work, it turns out that there are other, higher-order effects arising from the and terms that are provoked by the mixing between the photon and the Z-boson sectors. That is, even when one takes the extremely tight bound on at face value, the mixing with the Z sector provokes the appearance of other CPT-even and CPT-odd operators into the photon sector.
In this work, we will study in detail how this comes about. We will first use an intuitive perturbative argument to show how the mixing process arises at low energy for the photon sector. Then, we consider both the photon and Z-boson sectors together, and derive the polarization vectors and the dispersion relations. We study the latter in detail, showing how the Lorentz violation can give rise to negative-energy states. We also analyze the group velocity, and show it never exceeds c, assuring that causality is guaranteed. Finally, we discuss an application of the extended Hamiltonian formalism.
2. CPT and Lorentz Violation at Low Energy
The Lagrangian for the Standard-Model gauge fields
A and
Z, including the CPT-odd Lorentz-violating terms of the mSME, is given by
where
, and
with
and
. Because of the mixing term in Lagrangian (
1), the asymptotic fields are no longer
and
, but appropriate linear combinations of these fields and their derivatives. In the remainder of this paper, we will study the physical consequences of this.
As is well known, the photon parameter
is extremely strongly bound by astrophysical observations, by observing synchrotron radiation from radio galaxies (at
) [
12], as well as from from cosmic microwave background polarimetry studies (
) [
14]. In both cases, the listed bounds on the components of
are of the order of
GeV. In view of the above mixing, however, these bounds should presumably apply to the asymptotic states, rather than to the photon field
. That is, one should first diagonalize the kinetic Lagrangian in the full
A,
Z field space and then see which Lorentz-violating parameter applies to the massless propagating degrees of freedom.
Rather than performing such a full diagonalization, we will first do a perturbative analysis of the photon propagator. As a first step, we will only consider the
parameter. Up to the third order in
, the photon propagator can be expanded as
Truncating the external legs, the first-order diagram is represented by
For the truncated second-order diagram, one finds the CPT-even expression
where the Lorentz-violating tensor coefficient
has the symmetries of the Riemann tensor and can be interpreted as a contribution to the non-birefringent sector of the CPT-even Lorentz-violating tensor coefficient
. At the third order, we find
This represents a CPT-violating operator proportional to the first-order term (
6), with momentum-dependent proportionality factor. Altogether, up to third order in
, the corrections to the photon propagator yield
There is one problematic aspect, one notices in the expansion (
10): starting at quadratic order, the corrections diverge as
. This naturally happens because
amounts to the unperturbed photon mass-shell condition. For nonzero
the mass-shell condition will be modified, but, nevertheless, for very small
,
will be very close to zero on the mass shell. This means that it is unclear whether the successive terms in the expansion (
10) converge when the photon is taken on the mass shell.
For this reason, a better method is to simply work with the full
-modified photon propagator, for which an explicit and well-defined expression has been derived in [
10] (see Equation (
46) therein). It can be checked easily that an order-by-order expansion of expression (46) of [
10] yields, up to third order, the expression (
10).
Having incorporated fully the effect of the
term, we will now go ahead and include the last two CPT-odd terms of the Lagrangian (
1) parametrized by the Lorentz-violating parameters
and
. Representing the
-modified photon propagator by a double wavy line, the full modified photon propagator is given by the expansion
where the gray blob stands for the mixing terms
The first term, quadratic in
, represents the operator
with
This operator contributes to the non-birefringent sector of the
-even Lorentz-violating tensor coefficient
, analogously to Equation (
8). The third-order term
represents the lowest-order CPT-odd contribution to the full photon propagator due to the mixing with the
Z boson. The effect of the operator (
15) on the photon propagator is to modify the original
term by changing the vector
with
where, in the last equation, we used
as a very good approximation for the photon dispersion relation.
Clearly, the strong observational bounds referred to above apply to the components of
, not to
. Thus, it is in principle conceivable that the bound does not apply to (or is much weaker for)
, if somehow the effects of the two terms in (
17) in the relevant CPT-violating processes involved in the astrophysical observations were to (partially) cancel. In that case it might be conceivable that a strong bound on
might not imply an equally strong bound on
. Note, however, that the observational bounds on
have been established for at least two very different momentum scales, namely at radio frequencies as well as for CMB microwave frequencies. As the two terms in Equation (
17) have very different momentum structures, it is not possible that a fortuitous cancelation of their effects would occur for both sets of momenta. Thus, we conclude that the strong observational bounds apply for
as well as for the second term in (
17).
The higher-order terms in Equation (
12) can only be ignored at energies where
can be considered small (with
). This will be the case for most applications, notably at the energies that are used to determine bounds on
. However, when one wants to consider Cherenkov-like processes,
will have to be of order
and the higher-order terms cannot be neglected. For such high-energy processes, we cannot take the perturbative approach.
Since the bounds on
are obtained at comparatively low energies, we can use the fact that these bounds are so stringent to neglect
with respect to
. Therefore, from now on, we will consider the case where
, such that
. In that case, we can write Lagrangian
in Equation (
1) in terms of an eight-component “bi-four-vector”
, given by
The Lagrangian becomes:
where
,
, and
3. Polarization Vectors
Before treating the solutions of the equation of motion corresponding to (
19), let us review the simpler case of a single four-vector:
that was treated in detail in [
10]. In momentum space, the equation of motion of (
21) reads
where
are the eigenvectors of the equation-of-motion operator
. The index
runs over
, labeling the gauge mode, and three physical modes, respectively. It can be shown [
10] that the eigenvalues of
are given by the expressions
These observer-scalar functions of
and
define the dispersion relations for each of the polarization modes by fixing
. The corresponding eigenvectors
can be constructed explicitly [
10].
Let us now consider the equation of motion of Lagrangian
in momentum space, which can be written as:
where
, with
and
, are the eigenvectors of the equation-of-motion operator
. We will make the following ansatz for the eight-component polarization vectors:
Here,
and
are scalars that need to be determined. The four-vectors
are the eigenvectors of the equation-of-motion operator
introduced in Equation (
22). The fact that this ansatz works, hinges on the fact that there is only one Lorentz-violating four-vector in Equation (
22), i.e., on the fact that we put
to zero, allowing for the possibility that
would introduce a second independent Lorentz-violating four-vector, making the technical analysis much more complicated.
It turns out that the eigenvectors
correspond to eigenvalues
given by
with
. For “small” energies, we can expand the square roots of the final two expressions and obtain
From Equations (26) and (27), it is clear that the
modes are massless and the
modes are massive, at least in the limit of small Lorentz violation and low energies. We will therefore call the former mode the photon and the latter mode the
Z boson. The massless eigenvector corresponding to Equation (26c) corresponds to the longitudinal photon mode. We expect it to decouple upon applying a Becchi-Rouet-Stora-Tyutin quantization procedure, analogous to the one presented in [
10].
The explicit expressions for
and
are:
such that
and the eigenvectors
, when evaluated at the same four-momentum, obey
where
. A low-energy approximation for
and
reads
where the dots stand for terms of at least order
. Comparing to Equation (
18), we see that, in the limit of small Lorentz violation and low energy, the
(
mode corresponds to the conventional photon (
Z boson). In the mentioned limits, the modes thus also couple correctly to the conventional fermion currents.
4. Analysis of the Dispersion Relation
In this section, we analyse the dispersion relations for the different particle modes. In particular, we address the question of whether the Lorentz-violating dispersion relations have two roots for each mode. Moreover, we want to determine if any of the roots is degenerate.
The relevant Lorentz-violating dispersion relations can be written as
with
and
. First of all, we notice that
. Therefore, if the dispersion relation has two solutions (as we will show below), the usual redefinition of the negative-energy states will map them onto each other, i.e., particles and antiparticles have the same energy. Furthermore, since the square root (without
) on the right-hand side is always larger than or equal to
, the sign of
is determined by
, i.e.,
This shows that the photon mode always has spacelike (or lightlike) momenta, while the
Z-boson momentum is always timelike (see
Figure 1). This is to be contrasted with what happens when one does not consider the Lorentz-violating photon–
Z-boson mixing term, in which case both spacelike and timelike momenta are possible for the photon and the
Z-boson, as demonstrated in Ref. [
10]. Notice that the equality in Equation (
32) (for
) can only hold if
. This is only possible if
is spacelike/lightlike, or if
. Incidentally,
is always a solution of
, such that the photon dispersion relation always passes through this point in momentum space. Finally, it follows from Equation (
32) that the roots of
are different from those of
(for the same
), which answers part of the question about the degeneracy of the roots.
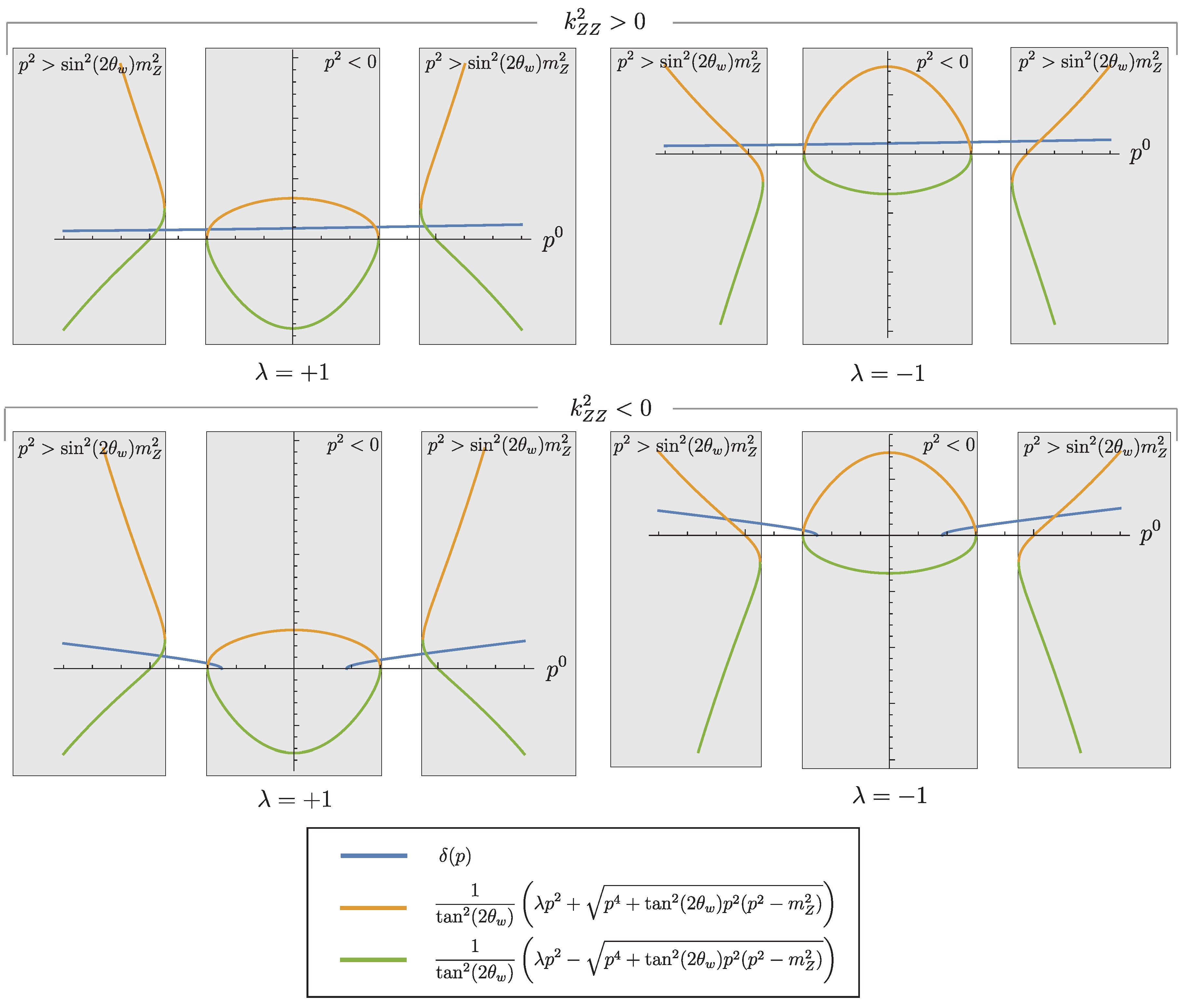
To further address the existence and degeneracy of the solutions of the dispersion relations, we solve Equation (
31) for
and obtain that to satisfy the dispersion relation, it must hold that
with
where the ± sign a priori has nothing to do with either
or
. Notice that Equation (
33) does not depend on
; however, using the constraint in Equation (
32), we can still select the appropriate roots, corresponding to
or to
. To clarify this, we have plotted
and
as a function of
in
Figure 2, for spacelike as well as timelike
and for
and
. It becomes clear that the intersections of the blue line (corresponding to
) with the yellow line (corresponding to
) that fall in the center gray patch (for which
), correspond to solutions of the dispersion relation with
, while the intersections in the leftmost and rightmost gray patches correspond to solutions of the dispersion relations with
.
To find the conditions under which the dispersion relations always have two real solutions each, we notice that the derivative of
with respect to
goes to
for
, while the derivative of
goes to
in that same limit (the sign in
corresponds to the sign in
, and not to the subscript of
). Furthermore, for spacelike
, the blue lines end on the horizontal
axis where
becomes imaginary. This means that, for spacelike
, the blue lines in the figures will always intersect both of the outer branches of the yellow or the green line in
Figure 2, unless the starting points of the blue branches lie in the left- and rightmost gray patches. However, it is easy to verify that
can only be imaginary if
is spacelike, showing that the starting points will, in fact, always lie in the middle gray patch. This then shows that—at least for spacelike
—the blue line intersects the yellow and green lines exactly four times for
and four times for
. These intersections correspond to the eight real roots of
for
for the case of spacelike
.
For timelike
, the situation is a little different. From the two top plots in
Figure 2, it is clear that the
dispersion relations always have two roots. They correspond to the intersections in the leftmost and rightmost gray patches in the figures. That these intersections always exist follows from considering the derivatives of
and
, as we did in the previous paragraph. The intersections in the middle gray patch (
), however, are not guaranteed to exist. It could happen that the blue line does not intersect the yellow line-piece in the middle patch if it lies entirely above this line-piece. In that case, the function
has complex roots. There exists, however, an observer-invariant condition to prevent the latter from happening. Following exactly the same procedure as we did in the appendix of Ref. [
10], one finds that there are always two non-degenerate, real roots, as long as
with
. In that case, we can always find a point where the blue line goes below the yellow line in the middle gray patch of
Figure 2, resulting in two intersections. This shows that the dispersion relations have two solutions each, also for timelike
.
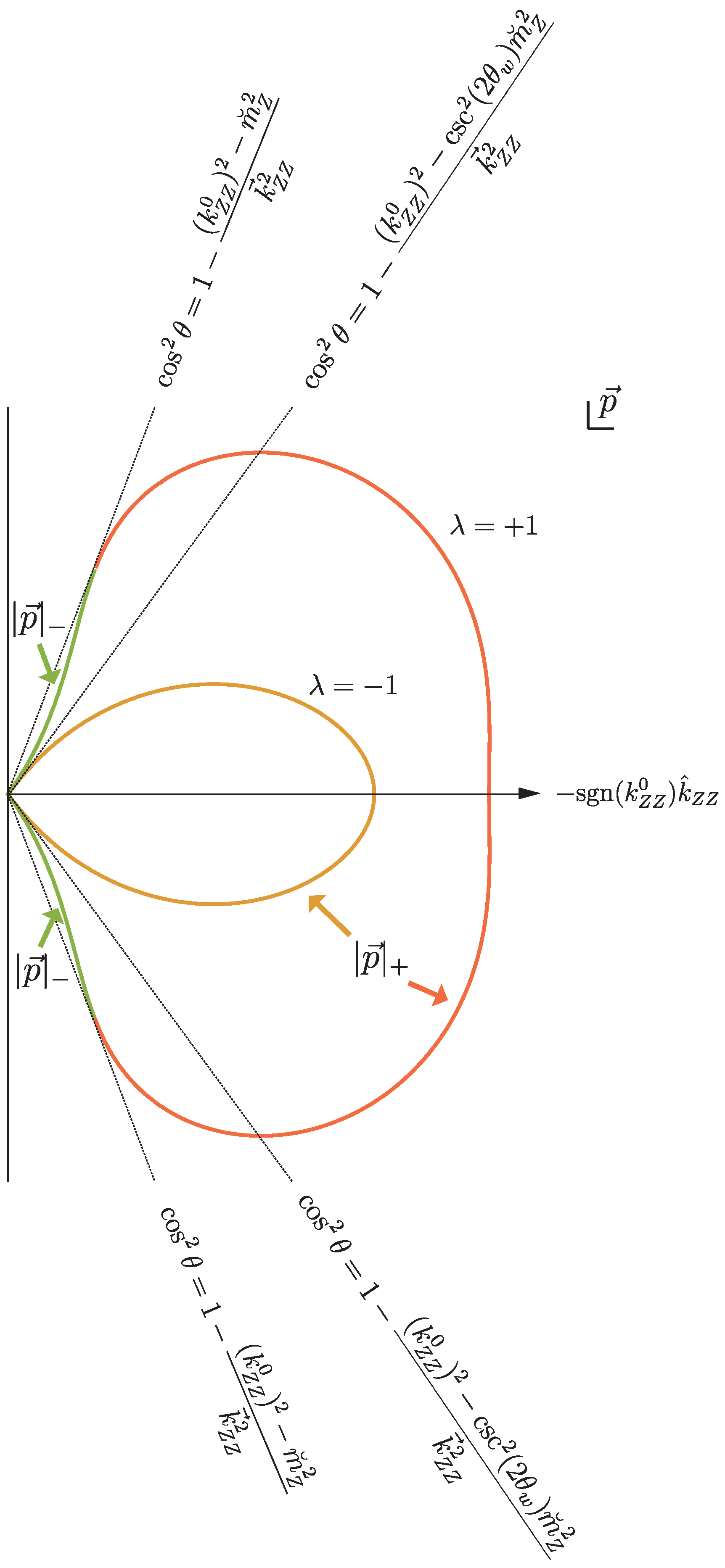
It is interesting to note that it might happen that the two intersections of the blue and yellow line lie on the same side of the line. In that case, the blue line lies above the yellow one at and the two roots have the same sign. If they both are on the left () side, the energy will be negative even after the usual redefinition of the negative-energy states, since one negative state will map onto another negative state in this case. We thus investigate under what conditions the blue line lies above the yellow line at .
At
, we get that
where
is the angle between
and
. Clearly,
is the situation we are looking for. We thus investigate
and see when this is negative. This function vanishes for
and for
(again, the ± sign is not related to the value of
or
). Moreover,
goes to
for
. Depending on the relative size of the two square roots in Equation (
38), these thus define a
-interval for which both roots of the dispersion relation have the same sign. The second square root is always imaginary if
Thus, if this inequality holds, there is no physical -interval for which , i.e., the roots are always real and have different signs. After redefining the roots, all energies are positive.
On the other hand, if
, then negative energies can occur. Provided this condition holds, the second square root in Equation (
38) is real if
where the second term on the right-hand side is always smaller than one, due to Equation (
35). The second square root in Equation (
38) is larger than the first square root if
Furthermore,
is a condition for the energy to be negative after redefinition. This can be seen by realizing that the minimum of
lies at
. This thus determines if the minimum, and therefore also the two roots (if they have the same sign), lie to the left or to the right of the
line. Together with this condition, Equations (
40) and (
41) both define a momentum cone around
. The cone defined by Equation (
41) is smaller than the one defined by Equation (
40). For the
mode, the direction of the photon momentum has to lie within the smaller cone, for the energy to be negative. The absolute momentum then has to obey
. This is depicted in
Figure 3.
For the
mode, the energy is negative for the same directions if
. However, for
, there is an extra set of angles for which the energy can be negative, outside the smaller cone, but inside the larger cone (see
Figure 3). For these directions, the energy is negative if
. Notice that this also means that there are observer frames, where only the
mode can have negative energies. In those frames, only the larger cone, defined by Equation (
40), exists.
We thus found that each of the four dispersion relations
for
always has two non-degenerate roots, as long as Equation (
35) holds. Moreover, roots corresponding to
can never coincide with roots for
(for the same
). The only degeneracy in the Lorentz-violating dispersion relations can thus come from roots for
being equal to roots for
(for the same value of
). Inspection of Equations (
31) and (
33) shows that this can only happen if
, which means that
. In addition, for
, one also needs
to solve the dispersion relation, which means that
must be lightlike, while, for
, one needs
. Such that the degenerate momenta are:
In all of these cases, the Lorentz-violating term in the Lagrangian vanishes, which also happened in Ref. [
10], where we showed that it did not result in serious problems for the quantization. We expect that this will also not happen in the current case.
7. Extended Hamiltonian Formalism
In order to elucidate the behavior of the particle states derived above, we consider the classical mechanical limit that can be obtained using an extended Hamiltonian formalism developed in [
15]. The procedure involves picking an appropriate eigenvalue of the off-shell dispersion relation as the extended Hamiltonian function. Hamilton’s equations can then be used to identify the appropriate classical wave packet velocity. A Legendre transformation then provides the appropriate Lagrangian corresponding to that particular eigenvalue of the dispersion relation. In the present context, the appropriate Hamiltonian functions are given by
where
e is a 1D metric (or einbein) on the world-line determined as a Lagrange-multiplier condition on the Lagrangian. The physical four-velocity can be defined in terms of the four-vector
in the previous section by using the four-velocity of the corresponding wave packets which are given by Hamilton’s equations as
The corresponding Lagrangians are found using a Legendre transformation and are given as
This expression demonstrates that, when is small, the solutions behave similarly to the conventional massive Z and massless photon expressions, while the mixing becomes significant when . In particular, the Lagrange densities of the states for become equal there, indicating a symmetric behavior between these polarizations of the photon and Z-boson states. The Lagrangian can be expressed in terms of and e by inverting the velocity-momentum relation. The expressions for involve complicated solutions to a fourth-order polynomial that can be formally written down, but they are of little obvious physical insight, so instead we work to second-order in k, which is a good approximation at low energies where the mixing between photon and Z-boson states is relatively small.
To second-order in
k, these expressions are
where
, yielding the approximate Lagrangian
Note that this expression reduces to the same form as the massive, CPT-violating Lagrangian in [
15] when
and
, with a slightly different condition. For the states
, the Lagrange multiplier condition
implies
When this value for
e is substituted into the Lagrangian, it becomes
This provides a new example for a corresponding Finsler space function of the bipartite form analyzed in Ref. [
16] when Wick-rotated to Euclidean space. Interestingly, for the
states, the condition
, so this Lagrangian formalism fails to describe these states in this approximation.
8. Discussion
When considering the full
electroweak sector of the Standard-Model Extension, imposing gauge invariance forces the Lorentz- and CPT-breaking parameters to appear diagonally in the gauge-invariant fields. Electroweak symmetry breaking will induce mixing between these initial parameters, which leads to physical effects that depend on the energy scale. High-precision photon experiments place stringent bounds on the CPT-violating photon coupling, despite being corrected by a momentum-dependent term in Equation (
17). Experiments performed at varying energies confirm that there can be no accidental cancellation of these contributions, so the bounds quoted on
in the literature are safe from induced interference effects of and CPT violation in the
Z-boson sector. By extending the polarization vectors found in [
10], we were able to solve for the exact dispersion relations of the full coupled system involving both the
Z boson and the photon for the case of nonzero
, while
is assumed to be zero. We find that, at low energies, two of the Lorentz-violating modes behave similarly to the massive
Z boson while the other two behave as massless photons. The photon states are always found to be spacelike, while the
Z-boson states are always timelike, which prevents Cherenkov-like
Z-boson emission, in contrast to what happens in the
W sector [
11]. The factor in Equation (
43) has been shown to be positive definite and can therefore be used as an phase-space normalization factor (as in Ref. [
10,
11]), while the group velocities are always causal. These facts are crucial to define the quantum theory consistently in nonconcordant frames where the energies can go negative as described in [
10] for the massive CPT-violating photon case. The extended Hamiltonian formalism has been used to provide classical mechanical Lagrangians for the particles involved. When working to second-order in
k, in the perturbative regime, we find that the Lagrangian for the massive modes leads to a bipartite form, while the massless modes lead to a trivial Lagrangian, as happens in the conventional photon case. The resulting nontrivial Lagrangian provides a new example of an physical model that can be described using bipartite Finsler geometry described in [
16]. The analysis done in this paper is complementary to the one in Ref. [
10] for the case of the photon with nonzero
. It would be interesting to consider the general case in which both
and
are nonzero, which should be a fully consistent model as well, but one we expect to be quite challenging to analyze. The results obtained in this work can be expected to be approximately valid for nonzero, small
, as long as the effects of the latter on the process or quantity under consideration are negligible compared to those of
. For instance, when considering birefringence effects on the photon at low energy this would mean that the first term on the right-hand side of Equation (
17) is taken to be negligigle with respect to the second one. Effects of nonzero
will be most pronounced at small four-momentum. For instance,
will no longer be a solution of the photon dispersion relation (see Equation (
32) and below).