A Method for Fuzzy Soft Sets in Decision-Making Based on an Ideal Solution

Abstract

In this paper, a decision model based on a fuzzy soft set and ideal solution approaches is proposed. This new decision-making method uses the divide-and-conquer algorithm, and it is different from the existing algorithm (the choice value based approach and the comparison score based approach). The ideal solution is generated according to each attribute (pros or cons of the attributes, with or without constraints) of the fuzzy soft sets. Finally, the weighted Hamming distance is used to compute all possible alternatives and get the final result. The core of the decision process is the design phase, the existing decision models based on soft sets mostly neglect the analysis of attributes and decision objectives. This algorithm emphasizes the correct expression of the purpose of the decision maker and the analysis of attributes, as well as the explicit decision function. Additionally, this paper shows the fact that the rank reversal phenomenon occurs in the comparison score algorithm, and an example is provided to illustrate the rank reversal phenomenon. Experiments indicate that the decision model proposed in this paper is efficient and will be useful for practical problems. In addition, as a general model, it can be extended to a wider range of fields, such as classifications, optimization problems, etc.

1. Introduction

The complicated problems in economics, engineering, environmental science and social science are full of imprecision and vagueness. For the various types of uncertainties presented in these problems, the methods in classical mathematics are not always successful. There are some mathematical tools for dealing with uncertainties. Some of them are probability theory, fuzzy set theory, rough set theory, and interval mathematics, but all these theories have their own difficulties. In 1999, Molodtsov [1] introduced the concept of soft sets, which can be considered as a new mathematical tool for dealing with uncertainties. It has proven useful in many fields such as decision-making, data analysis, forecasting and texture classification [2].

Research works on soft set theory and its applications in various fields are progressing rapidly, and many significant results have been achieved. Maji et al. [3] initiated the study of hybrid structures involving fuzzy sets and soft sets and introduced the notion of fuzzy soft set. Qin et al. [4] combine interval sets and soft sets. Zhang [5] studies interval soft sets. Shao and Qin [6] define fuzzy soft lattices and discuss their structure. Basu [7] introduce the structure and form of soft set theory. Li et al. [8] investigates roughness of fuzzy soft sets, introduced the concept of fuzzy soft rough sets. Bustince [9] proved that fuzzy sets are intuitionistic fuzzy sets. Torra et al. [10] extended this theory by introducing hesitant fuzzy sets. An extension of traditional fuzzy sets that permit the membership degree of an element to be a set of several possible values in $[0,1]$ and whose main purpose is to model the uncertainty produced by human doubt when eliciting information [11].

There is vast literature on fuzzy soft sets and their applications, including many successful generalizations. The comparison score and choice value are two different approaches applying soft set theory to decision-making problems. Maji et al. [3] pioneered soft set based decision-making and firstly proposed the choice value based approach. They established the criterion that an object could be selected if it maximizes the choice value of the problem. The comparison score based approach is proposed by Roy et al. [12] to dealing with the fuzzy soft set based decision-making problems. In this approach, they compare the membership values of two objects with respect to a common attribute to determine which one relatively possesses that attribute. Rodríguez et al. [13] overviewed on fuzzy modeling of complex linguistic preferences in decision-making and pointed out the different points of view used in each proposal to model these complex preferences. Kong et al. [14] revised this method, and their revision (the fuzzy choice value based method) has been proved as another method based on the maximum fuzzy choice value. Feng et al. [15] presented a novel approach to fuzzy soft set based decision-making problems by using level soft sets. They investigated the fuzzy soft set based decision-making problems more deeply, and their new method can be successfully applied to some decision-making problems.

The core of the decision process is the design phase. Firstly, the purpose of the decision maker should be expressed very clearly. Secondly, the data set should be analyzed accurately. Thirdly, choose the correct and efficient decision-making function. In general, the traditional decision-making algorithm (the score based method and the choice value based method) based on soft sets have some shortcomings. Firstly, the purpose of the decision maker is ignored, and it is generally assumed that the greater the value of each attribute, the better. Secondly, the analysis of the data set is ignored. In the fuzzy soft sets $(\tilde{F},A)$, all the attributes are treated uniformly, that is, all attributes are treated as good attributes. Sometimes, the value of the attribute is not the bigger the better, for example, expensive. Thirdly, there is ambiguity of the decision function such as comparison score algorithm because of reversal phenomenon occurred in this algorithm, which can lead to unacceptable choices in practice. It is unrealistic to use a fixed method to deal with the ever-changing problems. Therefore, based on the above factors, a decision model based on the ideal solution is proposed for the fuzzy soft set decision problem.

We will shortly describe the algorithm. In this study, we use the divide-and-conquer algorithm to design a decision-making model, and the model can dynamically adjust the ideal solution according to each attribute (positive attributes, negative attributes, and constraint attributes) of the fuzzy soft set. In addition, the weighted Hamming distance is used to compute all possible choices and get the final result. In other words, the $(\tilde{F},A)$ is a fuzzy soft set, according to the membership function of each attribute, and the ideal solution $u_{goal}$ can be generated. By measuring the similarity between object $u_x$ and $u_{goal}$, the object that is the most similar to $u_{goal}$ is the optimal choice. The algorithm emphasizes the correct expression of the purpose of the decision maker at the design stage and emphasizes the analysis of attributes, as well as the explicit decision function. This clear decision-making structure makes fuzzy soft sets more practical in decision-making.

The rest of this paper is organized as follows. Section 2 describes the basic concept of soft set theory. Section 3 gives an analysis of previous soft set-based decision-making algorithms and their limitations. Section 4 presents an alternative approach to the decision model by ‘ideal solution’ algorithm, and Section 5 shows the real-life applications of the proposed algorithm. Section 6 presents conclusions and future work.

2. Fuzzy Sets, Soft Sets and Fuzzy Soft Sets

In this section, we recall some fundamental notions of fuzzy sets, soft sets, and fuzzy soft sets, their relation to decision-making, and existing research.

2.1. Fuzzy Sets

In 1965, Zadeh [16] created a mathematical method of describing the fuzzy phenomenon in mathematics-fuzzy set theory.

Definition 1.

([16]) Let U be a set, called a universe. A fuzzy set μ on U is defined by a membership function $\mu :U\to [0,1]$. For any $x\in U$, the $\mu (x)$ represents the extent to which the x belongs to the fuzzy set μ.

The fuzzy sets $\mu (x)$ is denoted as follows:

$$\mu (x)=\{(x,\mu (x)),x\in U\}.$$

(1)

A fuzzy set can be discrete or continuous. For discrete fuzzy sets, $\mu (x)$ can be expressed as follows:

$$\mu (x)=\sum _{i=1}^n(\mu (x_i)/x_i).$$

(2)

n is the number of elements in U.

There are several forms of operations on fuzzy sets. According to maximum-minimal operator Zadeh proposed by [16], the intersection, union, and complement on fuzzy sets are defined as follows:

$$(\mu \cap \upsilon )(x)=\mu (x)\wedge \upsilon (x),$$

$$(\mu \cup \upsilon )(x)=\mu (x)\vee \upsilon (x),$$

$${\mu }^c(x)=1-\mu (x).$$

The decision-making theory plays a fundamental role in many scientific branches, such as AI (Artificial Intelligence), robots and big data. It is mainly developed in the setting of fuzzy decision theory. In 1965, fuzzy sets were proposed to confront the problems of linguistic or uncertain information. With the successful applications in the field of automatic control, fuzzy sets have been incorporated into fuzzy decision-making for dealing with decision-making problems. The idea of applying fuzzy sets in decision sciences comes from the seminal paper of Bellman and Zadeh. The application of the Bellman-Zadeh approach to decision-making in the fuzzy environment proposed in [17].

2.2. Soft Sets and Fuzzy Soft Sets

We review some fundamental notions of soft sets and fuzzy soft sets. Let U be the universe set and E be the set of all possible parameters under consideration with respect to U. Usually, parameters are attributes, characteristics, or properties of objects in U. $(U,E)$ will be called a soft space. Molodtsov defined the notion of a soft set in the following way:

Definition 2.

([1]) A pair $(F,A)$ is called a soft set over U, where $A\subseteq E$ and F is a mapping given by $F:A\to P(U)$.

In other words, a soft set over U is a parameterized family of subsets of U. A is called the parameter set of the soft set $(F,A)$. For $e\in A$, $F(e)$ may be considered as the set of e-approximate elements of $(F,A)$. For illustration, we consider the following example of soft set.

Example 1.

Suppose that there are six houses in the universe U given by $U=\{h_1,h_2,h_3,h_4,h_5,h_6\}$ and $E=\{e_1,e_2,e_3,e_4,e_5\}$ is the set of parameters. $e_1$, $e_2$, $e_3$, $e_4$ and $e_5$ stand for the parameters ‘expensive’, ‘beautiful’, ‘wooden’, ‘cheap’ and ‘in the green surroundings’, respectively.

In this case, to define a soft set means to point out expensive houses, beautiful houses, and so on. The soft set $(F,E)$ may describe the ‘attractiveness of the houses’ that Mr.X is going to buy. Suppose that $F(e_1)=\{h_2,h_4\}$, $F(e_2)=\{h_1,h_3\}$, $F(e_3)=\{h_3,h_4,h_5\}$, $F(e_4)=\{h_1,h_3,h_5\}$, $F(e_5)=\left\{h_1\right\}$. Then, the soft set $(F,E)$ is a parameterized family $\{F(e_i);1\le i\le 5\}$ of subsets of U and give us a collection of approximate descriptions of an object. $F(e_1)=\{h_2,h_4\}$ means ‘houses $h_2$ and $h_4$’ are ‘expensive’.

Maji et al. [18] introduced the concept of fuzzy soft sets by combining soft set and fuzzy set.

Definition 3.

([18]) Let $(U,E)$ be a soft space. A pair $(\tilde{F},A)$ is called a fuzzy soft set over U, where $A\subseteq E$ and $\tilde{F}$ is a mapping given by $\tilde{F}:A\to \tilde{F}(U)$, $\tilde{F}(U)$ is the set of all fuzzy subsets on U.

Let us denote ${\mu }_{\tilde{F}(e)}(x)$ the membership degree that object x holds attribute e where $x\in U$ and $e\in A$. Then, $\tilde{F}(e)$ can be written as $\tilde{F}(e)=\{<x,{\mu }_{\tilde{F}(e)}(x)>|x\in U\}$.

Definition 4.

([18]) Let $(\tilde{F},A)$ and $(\tilde{G},B)$ be a fuzzy soft set over a common universe U.

(1) 

$(\tilde{F},A)$ is said to be a fuzzy soft subset of $(\tilde{G},B)$, denoted by $(\tilde{F},A)\subseteq (\tilde{G},B)$, if $A\subseteq B$ and $\forall e\in A$, $\tilde{F}(e)\subseteq \tilde{G}(e)$.

(2) 

$(\tilde{F},A)$ is said to be a null fuzzy soft set, denoted by ${\varnothing }_A$, if $\tilde{F}(e)=\varnothing$ for any $e\in A$.

(3) 

$(\tilde{F},A)$ is said to be a absolute fuzzy soft set, denoted by $U_A$, if $\tilde{F}(e)=U$ for any $e\in A$.

Definition 5.

([19]) For any fuzzy soft set $(\tilde{F},E)$ over U, a pair $({\tilde{F}}^{-1},E)$ is called an induced fuzzy soft set over E of $(\tilde{F},E)$, where ${\tilde{F}}^{-1}(x)=\{e\in E,x\in \tilde{F}(e)\}$ for each $x\in U$.

Definition 6.

The quadruple $(U,A,F,V)$ is called an information system, where $U=\{x_1,\dots ,x_n\}$ is a universe containing all interested objects, $A=\{a_1,\dots ,a_n\}$ is a set of attributes, $V={\bigcup }_{i=1}^m{V}_i$ where $V_j$ is the value set of the attribute $a_j$, and $F=\{f_1,\dots ,f_m\}$ where $f_j:\bigcup \to V_j$.

Information systems can represent fuzzy sets, soft sets, and fuzzy soft sets. If $(F,A)$ is a soft set over the universe U, then $(F,A)$ is a Boolean-valued information system $S=(U,A,V_{\{0,1\}},f)$. As shown in

Table 1. Soft set $(F,A)$ represented as a boolean-valued information system.

U	${\mathit{e}}_1$	${\mathit{e}}_2$	${\mathit{e}}_3$	${\mathit{e}}_4$
$x_1$	0	0	0	0
$x_2$	0	1	0	1
$x_3$	0	1	1	1
$x_4$	1	0	0	0
$x_5$	1	0	1	0

.

A soft set is a simple information system in which the attributes only take two values 0 and 1, and partition-type soft sets and information systems are the same formal structures.

If $(\tilde{F},A)$ is a fuzzy soft set over the universe U, then $(\tilde{F},A)$ is a real-valued information system $S=(U,A,V_{[0,1]},f)$, as shown in

Table 2. Fuzzy soft set $(\tilde{F},A)$ represented as a real-valued information system.

U	${\mathit{e}}_1$	${\mathit{e}}_2$	${\mathit{e}}_3$	${\mathit{e}}_4$	${\mathit{e}}_5$	${\mathit{e}}_6$	${\mathit{e}}_7$
$x_1$	0.2	0.4	0.1	0.5	0.8	0.1	0.1
$x_2$	0.3	0.2	0.3	0.6	0.3	0.9	0.6
$x_3$	0.3	0.1	0.6	0.7	0.8	0.8	0.3
$x_4$	0.3	0.7	0.9	0.9	0.1	0.4	0.5
$x_5$	0.3	0.9	0.1	0.3	0.2	0.2	0.3
$x_6$	0.3	0.9	0.1	0.3	0.9	0.7	0.8
$x_7$	0.3	0.9	0.1	0.3	0.2	0.8	0.9
$x_8$	0.3	0.9	0.1	0.3	0.1	0.4	0.2

.

3. Fuzzy Soft Set Based Decision-Making and Their Limitations

The decision-making is a process of choosing among alternative courses of action for the purpose of attaining a goal or goals. The decision-making problems based on fuzzy soft sets actually is multi attributes decision-making problems. Two different approaches applying soft set theory to decision-making problems: the choice value based approach and the comparison score based approach. Maji et al. [3] proposed the choice value algorithm for the application of soft set theory in decision-making problems. Roy and Maji [12] proposed the comparison score based approach to solving fuzzy soft set based decision-making problems.

3.1. The Choice Value Algorithm (Algorithm 1)

Let $(F,A)$ be a soft set, $(F,A)$ can be expressed as a binary table. Let $h_{ij}$ be the entries in the table, and if $h_i\in F(e_i)$, then $h_{ij}=1$. Otherwise, $h_{ij}=0$. The choice value $c_i$ of an object $h_i$ is computed by $c_i={\sum }_j{h}_{ij}$, the object with the maximum choice value is selected as the optimal decision. The algorithm is as follows:

Algorithm 1 The choice value algorithm

1: Input the soft set $(F,A)$. 2: Compute the choice values $c_i$ for each object $h_i$, where $c_i={\sum }_j{h}_{ij}$. 3: The decision is $h_{i}if{c}_i=ma{x}_j{c}_j$. 4: If i has more than one value then any one of $h_i$ may be chosen.

For decision-making problems using soft sets, the choice value of an object precisely represents the number of ‘good’ attributes possessed by the object. Hence, it is reasonable to select the object with the maximum choice value as the optimal alternative.

Example 2.

From

Table 3. A soft set $(F,A)$ with choice values.

$\mathit{U}$	${\mathit{e}}_1$	${\mathit{e}}_2$	${\mathit{e}}_3$	${\mathit{e}}_4$	Choice Value
$h_1$	1	1	1	1	4
$h_2$	1	1	1	0	3
$h_3$	1	0	1	1	3
$h_4$	1	0	1	0	2
$h_5$	1	0	0	0	1
$h_6$	1	1	1	1	4

, it can be seen that Mr. X will select the house $h_1$ or $h_6$.

In real decision-making problems, the choice parameters are not entirely of the equal importance. To cope with such problems, we can impose different weights to different decision parameters. Additionally, it has been generalized to deal with the fuzzy soft set. In this case, the choice value will be computed by: $c_i={\sum }_{j}F(e_j)(h_i)$, where $F(e_j)(h_i)$ is the membership value of $h_i$ with respect to fuzzy set $F(e_j)$. Table 3 and

Table 4. A weighted soft set $(F,A)$ with choice values.

$\mathit{U}$	${\mathit{e}}_1,{\mathit{w}}_1=\frac{1}{2}$	${\mathit{e}}_2,{\mathit{w}}_2=\frac{1}{4}$	${\mathit{e}}_3,{\mathit{w}}_3=\frac{1}{8}$	${\mathit{e}}_4,{\mathit{w}}_4=\frac{1}{16}$	Choice Value
$h_1$	1	1	1	1	0.9375
$h_2$	1	1	1	0	0.8750
$h_3$	1	0	1	1	0.6875
$h_4$	1	0	1	0	0.6250
$h_5$	1	0	0	0	0.5000
$h_6$	1	1	1	1	0.9375

are examples of the soft sets and weighted soft sets with choice values, respectively.

Example 3.

From Table 4, it can be seen that Mr. X will select the house $h_1$ or $h_6$.

Remark 1.

The choice value algorithm is essentially a weighted sorting algorithm, the logic is rational and understandable and the computation processes are straightforward. Algorithm 1, which returns the maximum value in an array with size of n and it takes O(n) times. The time complexity of the algorithm is O(n).

However, there is a prerequisite for using this method, that is, all attributes are ‘good’ descriptions, and the greater the value, the better. However, in practice, attributes may be ‘good’, ‘bad’, and ‘constrained’, so this algorithm needs to be further improved according to the actual problem.

3.2. The Comparison Score Algorithm (Algorithm 2)

In the comparison score algorithm, rather than utilizing the concept of choice values designed for crisp soft sets, it compares the membership values of two objects concerning a common attribute to determine which one relatively possesses that attribute. The algorithm is as follows:

Algorithm 2 The comparison score algorithm

1: Input the fuzzy soft sets $(\tilde{F},A)$. 2: Construct the comparison-table of the fuzzy soft sets $(\tilde{F},A)$ and compute $r_i$ and $t_i$ for $o_i$, $\forall i$. 3: Compute the score of $o_i$, $\forall i$. 4: The decision is $S_k$ if, $S_k=ma{x}_i{S}_i$. 5: If k has more than one value then any one of $o_k$ may be chosen.

The comparison table of a fuzzy soft set $(\tilde{F},A)$ is a square table in which rows and columns are both labeled by the objects $o_1,o_2,\dots ,o_n$ of the universe. The entries $c_{ij}$ indicate the number of parameters for which the membership value of $o_i$ exceeds or equal to the membership value of $o_j$. The $c_{ij}$ is computed by

$$\begin{array}{c}\hfill c_{ij}=|\{e\in A;F(e)(o_i)\ge F(e)(o_j)\}|.\end{array}$$

(3)

The row-sum $r_i$ of object $o_i$ is computed by

$$\begin{array}{c}\hfill r_i=\sum _{j=1}^n{c}_{ij}.\end{array}$$

(4)

The column-sum $t_j$ of object $o_j$ is computed by

$$\begin{array}{c}\hfill t_i=\sum _{i=1}^n{c}_{ij}.\end{array}$$

(5)

The score $s_i$ of object $o_i$ is defined as

$$\begin{array}{c}\hfill s_i=r_i-t_i.\end{array}$$

(6)

The objects with the maximum score computed from the comparison table will be regarded as the optimal decision.

Example 4.

We consider fuzzy soft set $(\tilde{F},A)$ given in Table 2. The comparison table and the comparison score table of $(\tilde{F},A)$ are given in

Table 5. The comparison table of fuzzy soft set $(\tilde{F},A)$.

U	${\mathit{x}}_1$	${\mathit{x}}_2$	${\mathit{x}}_3$	${\mathit{x}}_4$	${\mathit{x}}_5$	${\mathit{x}}_6$	${\mathit{x}}_7$	${\mathit{x}}_8$
$x_1$	7	2	2	1	3	2	3	3
$x_2$	5	7	4	4	6	4	5	6
$x_3$	6	4	7	3	6	4	5	6
$x_4$	6	4	5	7	5	3	3	6
$x_5$	5	2	3	3	7	4	5	6
$x_6$	6	4	4	5	7	7	5	7
$x_7$	5	3	4	5	7	6	7	7
$x_8$	5	2	2	4	5	4	4	7

and

Table 6. The comparison score table of fuzzy soft set $(\tilde{F},A)$.

	Row-Sum $({\mathit{r}}_{\mathit{i}})$	Column- Sum $({\mathit{t}}_{\mathit{i}})$	Comparison Score $({\mathit{s}}_{\mathit{i}})$
$h_1$	23	45	−22
$h_2$	41	28	13
$h_3$	41	31	10
$h_4$	39	32	7
$h_5$	35	46	−11
$h_6$	45	34	11
$h_7$	44	37	7
$h_8$	33	48	−15

, respectively. From Table 6, it is seen that Mr. X will select the house $h_2$.

Remark 2.

The number of objects in the fuzzy soft set $(\tilde{F},A)$ is assumed to be n. For calculating each entry of the comparison table, the objects need to compare with each other, and the complexity of computing the comparison table is $O(n^2)$. The complexity of computing each score of each object is $O(2n)$, and the complexity of selecting the max value is $O(n)$. Thus, the complexity of Algorithm 2 is $O(n^2)$.

However, the comparison score algorithm presents certain limitations. Alcantud [20] shows that Algorithm 2 may result in a loss of information along the construction of a resultant fuzzy soft set from the multi-observer data. The main novelty in his proposal regarding Algorithm 2 is in the definition of the comparison matrix. Our concerns are as follows:

1.

Rank reversal occurs in the comparison score algorithm. In this phenomenon, the objects’ order of preference changes when an object is added to or removed from the decision problem. We will illustrate this phenomenon in Section 3.3.

2.

Add/delete an object, and the comparison matrix needs to be recalculated. This means that a new comparison table has to be recalculated when the attributes/objects need to be added/deleted, which indicates that plenty of recalculations should be involved to get a new solution set.

3.

Attribute importance is considered to be the equal importance, and then the option cannot be distinguished according to the importance of the attribute.

3.3. Rank Reversal in the Comparison Score Algorithm

In a decision-making problem, the rank reversal means a change in the rank ordering of the preferability of possible alternative decisions when the method of choosing changes or the set of other available alternatives changes. Such a phenomenon was first pointed out by Belton and Gear [21]. Some decision-making algorithms have been criticized for the possible rank reversal phenomenon caused by the addition or deletion of an alternative [21,22,23,24].

There are strong arguments on which a fuzzy soft sets based decision-making method is more reasonable than others. The purpose of this paper is not to contribute further to that debate, but to point out problems and analyze the causes, and prepare for further improvements. Here, an example is provided to illustrate the rank reversal phenomenon in the comparison score algorithm.

Example 5.

Let $(\tilde{F},A)$ be a fuzzy soft set; it can be expressed in Equation (7). By the comparison score algorithm, we can get comparison table (8) and comparison score (9):

$$\begin{array}{c}(\tilde{F},A)=\left[\begin{array}{cccccc}0.2& 0.3& 0.6& 0.3& 0.9& 0.6\\ 0.9& 0.1& 0.3& 0.9& 0.7& 0.8\\ 0.4& 0.1& 0.5& 0.8& 0.1& 0.1\end{array}\right],\hfill \end{array}$$

(7)

$$\begin{array}{c}ComparisonTable=\left[\begin{array}{ccc}6& 3& 4\\ 3& 6& 5\\ 2& 2& 6\end{array}\right],\hfill \end{array}$$

(8)

$$\begin{array}{c}ComparisonScore=\left[\begin{array}{ccc}13& 11& 2\\ 14& 11& 3\\ 10& 15& -5\end{array}\right].\hfill \end{array}$$

(9)

From the comparison score (9), it is seen that $h_2$ will be chosen, and we have a sorted sequence $h_2\succ h_1\succ h_3$.

Example 6.

 We add an object $h_4=(0.9,0.3,0.3,0.2,0.8,0.9)$ to $(\tilde{F},A)$, as Equation (10), and then we can get comparison table (11) and comparison score (12):

$$\begin{array}{c}(\tilde{F},A)=\left[\begin{array}{cccccc}0.2& 0.3& 0.6& 0.3& 0.9& 0.6\\ 0.9& 0.1& 0.3& 0.9& 0.7& 0.8\\ 0.4& 0.1& 0.5& 0.8& 0.1& 0.1\\ 0.9& 0.3& 0.3& 0.2& 0.8& 0.9\end{array}\right],\hfill \end{array}$$

(10)

$$\begin{array}{c}ComparisonTable=\left[\begin{array}{cccc}6& 3& 4& 4\\ 3& 6& 5& 3\\ 2& 2& 6& 2\\ 3& 5& 4& 6\end{array}\right],\hfill \end{array}$$

(11)

$$\begin{array}{c}ComparisonScore=\left[\begin{array}{ccc}17& 14& 3\\ 17& 16& 1\\ 12& 19& -7\\ 18& 15& 3\end{array}\right].\hfill \end{array}$$

(12)

From the comparison score (12), it is seen that $h_1$ and $h_4$ will be chosen, and we have a sorted sequence ($h_1=h_4)\succ h_2\succ h_3$.

Remark 3.

Examples 5 and 6 show that rank reversal phenomenon occurs in the comparison score algorithm; it caused by the addition or deletion of an object. As can be seen from Examples 5 and 6, the ranking between $h_1$ and $h_2$ is $h_2\succ h_1$ before $h_4$ is introduced, but becomes $h_1\succ h_2$ after $h_4$ is added, where the symbol ‘≻’ means ‘is superior to.’ The ranking is reversed after the addition of alternative $h_4$. Such a phenomenon is referred to as rank reversal, which may occur not only when a copy of an alternative is added, but also when a new alternative is added as well as when an existing alternative is removed. In some cases, this may lead to total rank reversal, where the order of preferences is entirely inverted. That is, that the alternative considered the best, with the inclusion or removal of an alternative, then becomes the worst. Such a phenomenon in many cases may not be acceptable, for example, the ranking of candidates in recruitment, choosing the best students according to their grades, and so on. In practice, we can construct special test problems to test the validity of the decision-making algorithm. If the solution shows some logical contradictions, then one might argue that there is a problem with the method that derives them.

In classical mathematics, the decision-making problems description is $(A,\Theta ,\Xi ,\kappa ,D)$ (Grabisch et al.) [25]. The A is the set of alternatives or possible actions. The $\Theta$ is a set of states of the environment in which decisions are taken. The $\Xi$ is a set of consequences resulting from the choice of a particular alternative. The $\kappa$ is a mapping $A\times \Theta \to \Xi$ specifying a consequence for each element of the environment. The space $A\times \Theta$ defines the solution space. The D is the decision function $D:\Theta \to R$ reflects the preference structure of the decision maker.

Definition 7.

([26]) The decision function D incorporates the goals of the decision maker. It induces a preference ordering on the set of consequences Ξ such that

$$\begin{array}{c}\hfill {\xi }_i\succ {\xi }_{j}iffD({\xi }_i)\succ D({\xi }_j),\end{array}$$

(13)

where ${\xi }_i,{\xi }_j\in \Xi$, and ≻ is the preference relation, i.e., consequence is preferred to consequence.

Let $(\tilde{F},A)$ be two fuzzy soft sets on the universe U. Suppose that $o_i$ and $o_j$ are objects in the universe U. In the fuzzy soft set $(\tilde{F},A)$, let D be the decision function, and $D(o_i)\succ D(o_j)$ . Add an object $o_k$ to $(\tilde{F},A)$, let $D^{{}^{\prime }}$ be the decision function, but $D^{{}^{\prime }}(o_j)\succ D^{{}^{\prime }}(o_i)$. This means $D\ne D^{{}^{\prime }}$, the decision function changed caused by the addition of an object.

From Examples 5 and 6, we can see $D(o_2)\succ D(o_1)$ in Example 5, but $D^{{}^{\prime }}(o_1)\succ D^{{}^{\prime }}(o_2)$ in Example 6. The instability of the selection result indicates that the ‘decision rule’ is ambiguous, that is, the decision function will be changed according to the addition/deletion of objects.

In practice, suppose k students $U=\{n_1,n_2,\dots ,n_k\}$ participated in a competition, by the comparison score algorithm, you can choose the desired candidate $n_x$ and $n_x\in U$. When a new student $n_{k+1}$ participation in the competition, $U^{{}^{\prime }}=U\cup \left\{n_{k+1}\right\}$, by the comparison score algorithm you can choose the desired candidate $n_y$, and $(n_y\in Uand{n}_y\ne n_x)$. This means the ranking of $n_x$ and $n_y$ is reversed when candidate $n_{k+1}$ participation in the competition. In real life, a decision maker’s preference ordering between two alternatives should remain unchanged if an additional alternative added or removed. Usually, if $n_x<n_{k+1},$ then $n_{k+1}$ will be chosen, else $n_x$ still be selected.

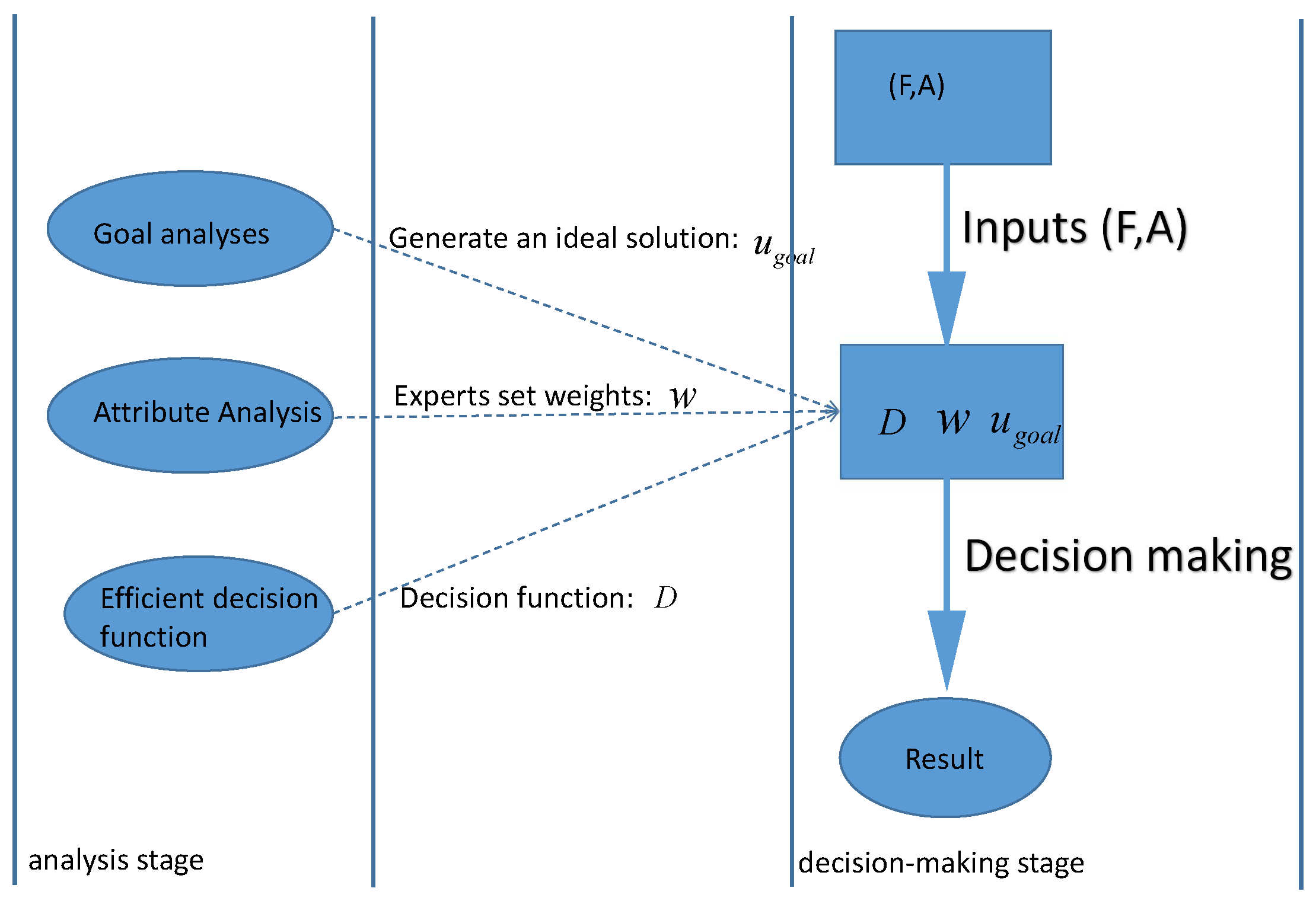
4. Improved Decision-Making Algorithm Based on Fuzzy Soft Set and Ideal Solution

Most of our real-life problems are imprecise in nature. The classical crisp mathematical tools are not capable of dealing with such problems. The fuzzy set theory has been used quite extensively to deal with such imprecisions. In general, the traditional decision-making algorithm based on soft sets have some shortcomings. All the attributes are treated uniformly, that is, all attributes are treated as ‘good’ attributes. Sometimes, the value of the attribute is not the bigger the better, for example, ‘expensive’. The purpose of the decision maker ignored, and it usually assumed that the bigger (the value of each attribute) the better. It is unrealistic to use a fixed method to deal with the ever-changing problems.

In order to overcome these shortcomings, this paper proposes improvement from the following aspects, as shown in Figure 1:

Firstly, the ideal solution is introduced in the design phase, that is, a very clear decision objective is formulated. We will illustrate this in Section 4.1.

Secondly, make clear the meaning of attributes. The attribute will be divided into ‘pros’ and ‘cons’ attributes. The ‘pros attribute’ is a ‘good’ description of the object, and the ‘cons attribute’ is a ‘bad’ description of the object. At the same time, whether attributes contain constraints is also taken into account. We will illustrate this in Section 4.2.

Finally, when an ideal solution is generated, the decision is made by comparing the similarity between the object and the ideal solution. We will illustrate this in Section 4.3.

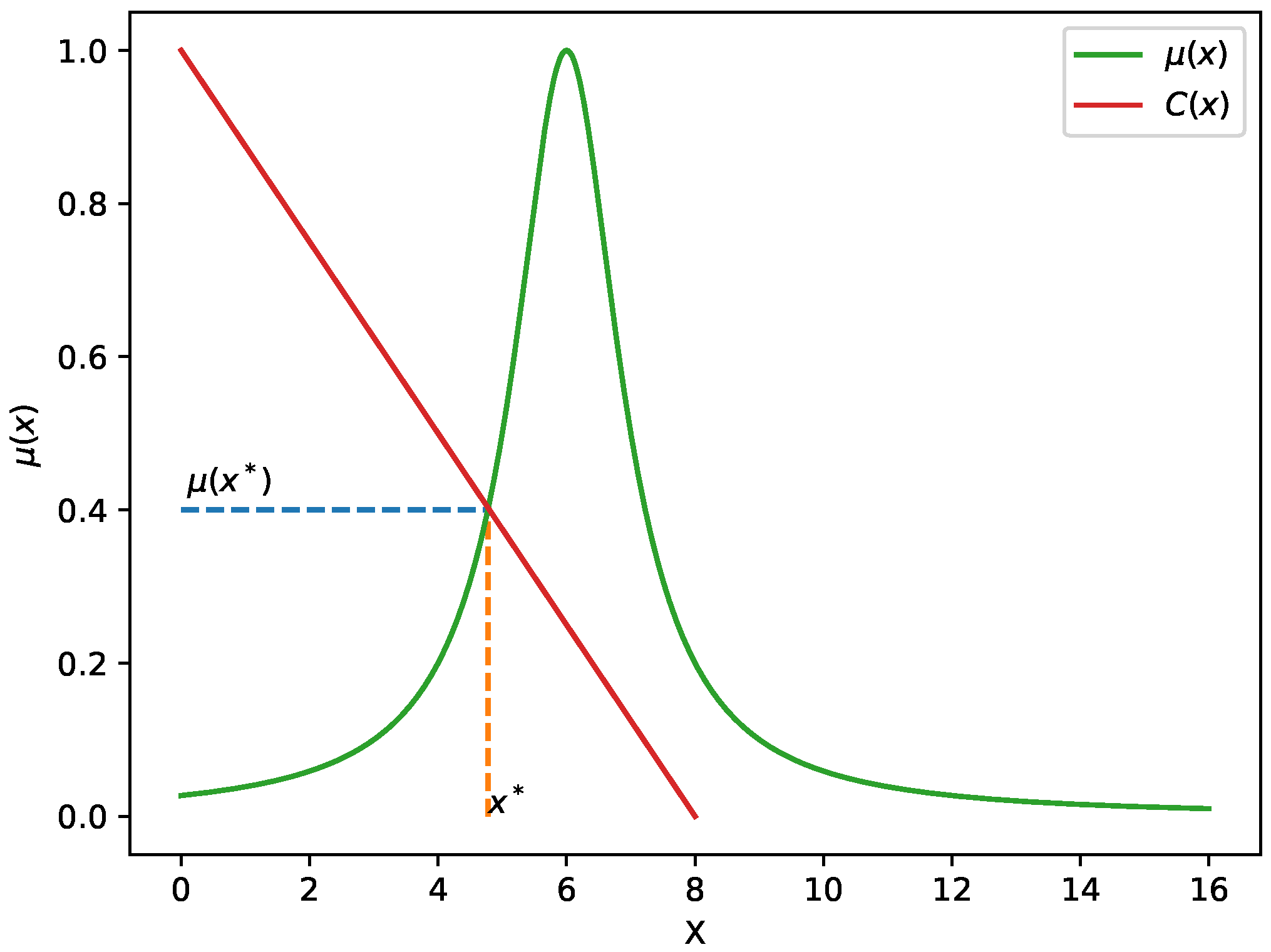
4.1. The Ideal Solution Method

Yoon and Hwang [27] developed the algorithm for order preference by similarity to the ideal solution in 1981. The ideal solution method aims to obtain the best compromise solution, which is the one that is the closest to the ideal solution, that is, it has the shortest distance from the ideal solution. Let $S=(S_1,S_2,\dots ,S_n)$, $S_i=(s_{i1},s_{il},\dots ,s_{im})$, $i=1,\dots ,n$ be a solution of a decision-making problem from the ith group member, m be the number of objectives $(m>1)$. Let $S_0=(s_{01},s_{0l},\dots ,s_{0m})$ be the ideal solution. The ideal solution method is formulated as follows:

$$\begin{array}{c}findp\hfill \\ s.t.d^{\ast }=d_p=min\{d_i;i=1,2,\dots ,n\}\hfill \\ =min\{\sum _{j=1}^m|s_{ij}^{{}^{\prime }}-s_{0j}|;i=1,2,\dots ,n\},\hfill \end{array}$$

(14)

where

$$\begin{array}{c}{s}_{ij}^{{}^{\prime }}=\left\{\begin{array}{c}\frac{s_{ij}}{{\tilde{s}}_j},if{\tilde{s}}_j\ne 0,\hfill \\ 0,if{\tilde{s}}_j=0,\hfill \end{array}\right.i=1,2,\dots ,n,j=1,2,\dots ,m,\hfill \\ {\tilde{s}}_j=max\{s_{ij};i=1,2,\dots ,n\},j=1,2,\dots ,m.\hfill \end{array}$$

(15)

When an ideal solution $S_0=(s_{01},s_{0l},\dots ,s_{0m})$ is generated, the algorithm starts to measure the distance of the ideal solution to the other candidates. A distance matrix D for each objective of solutions to the ideal solution is thus established:

$$\begin{array}{c}D=\left[\begin{array}{cccc}(d_{11})& (d_{12})& \dots & (d_{1m})\\ (d_{21})& (d_{22})& \dots & (d_{2m})\\ ⋮& ⋮& & ⋮\\ (d_{n1})& (d_{n2})& \dots & (d_{nm})\end{array}\right],\hfill \end{array}$$

(16)

where $d_{ij}=|s_{ij}^{\prime }-s_{0j}|,i=1,\dots ,n,j=1,\dots ,m$.

The distances from different objective values of each solution are obtained:

$$\begin{array}{c}\hfill d_i=\sum _{j=1}^m{d}_{ij},i=1,\dots ,n.\end{array}$$

(17)

The final solution that has the shortest distance is then found from

$$\begin{array}{c}findp\hfill \\ s.t.d^{\ast }=d_p=min\{d_i,i=1,2,\dots ,n\},1\le p\le n,\hfill \end{array}$$

(18)

where $d^{\ast }$ is the shortest total-distance between the solutions and the ideal solution, and the pth solution is the closest solution as the final compromise solution of this decision-making problem.

4.2. The Ideal Solution of Each Attribute

In practice, when we use a soft set to solve a problem, the attribute can be a ‘good’ description of an object or a ‘bad’ one. Likewise, attributes sometimes contain constraints, and sometimes do not contain constraints. In this situation, a choice value based approach and comparison score based approach are not useable. In other words, there are two prerequisites for the choice value based approach and the comparison score based approach, that is, on the universal U, all attributes are positive descriptions and are unconstrained. For each attribute, a bigger value indicates a better candidate. In reality, this is not always reasonable.

Bellman and Zadeh proposed [17] a fuzzy decision model in 1970, and discuss how to apply these concepts to the decision-making process under a fuzzy environment.

Definition 8.

([17]) The X represents all possible strategies, and the fuzzy objective $\tilde{G}$ is a fuzzy set on the X, the membership function ${\mu }_{\tilde{G}}:X\to [0,1]$. The objective function is the reaction of the decision-maker to a certain ambiguity of the target. The ${\mu }_{\tilde{G}}$ response strategy x achieves satisfaction with target $\tilde{G}$.

Definition 9.

([17]) Let $\tilde{G}$ and $\tilde{C}$ be fuzzy targets and fuzzy constraints in universal X, the fuzzy decision $\tilde{D}$ is also a fuzzy set of X, and it is defined as the intersection of $\tilde{G}$ and $\tilde{C}$, that is, $\tilde{D}=\tilde{G}\cap \tilde{C}$, the membership function is

$$\begin{array}{c}{\mu }_{\tilde{D}}(x)=min\{{\mu }_{\tilde{G}}(x),{\mu }_{\tilde{C}}(x)\}.\end{array}$$

In fuzzy decision-making, the membership function of ${\mu }_{\tilde{G}}(x)$ that achieves maximum value strategy is called maximizing strategy, and the membership function is

$$\begin{array}{c}\hfill {\mu }_{\tilde{D}}(x^{\ast })=ma{x}_{x\in X}min\{{\mu }_{\tilde{G}}(x),{\mu }_{\tilde{C}}(x)\}.\end{array}$$

For the attribute with constraints, we can use Bellman and Zadeh’s model to find the best solution. For the attribute without constraints, it is a maximum/minimum problem.

Let $U=\{u_1,u_2,\dots ,u_n\}$ and $(\tilde{F},A)$ be a fuzzy soft set of dimension k over U, $e_j\in A$. For attribute $e_j$, let ${\mu }_j$ be the membership function and $j\in \{1,2,\dots ,k\}$. $\tilde{F}(e_j)=\{{\mu }_j(u_1)/u_1,{\mu }_j(u_2)/u_2,\dots ,{\mu }_j(u_n)/u_n\}$. Let ${\Re }_{e_j}$ be the maximum target of attribute $e_j$, ${\Re }_{e_j}={\mu }_{j\tilde{D}}(x^{\ast })$.

Definition 10.

Let $(\tilde{F},A)$ be a fuzzy soft set, and ${\mu }_{j\tilde{G}}(x)$ is the membership function of attribute $e_j$. ${\mu }_{j\tilde{C}}(x)$ is the constraint function. The ideal solution of $e_j$ is formulated as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\Re }_{e_j}=ma{x}_{x\in X}min\{{\mu }_{j\tilde{G}}(x),{\mu }_{j\tilde{C}}(x)\},\hfill \\ s.t.x\in U,\hfill \end{array}\right.\end{array}$$

(19)

as shown in Figure 2.

Let $(\tilde{F},A)$ be a fuzzy soft set,${\mu }_{j\tilde{G}}(x)$ is the membership function of attribute $e_j$ and without constraints function.

Definition 11.

The attribute $e_j$ without constraints is a ‘good’ description, and the ideal solution is the maximum value of ${\mu }_j(x)$. The ideal solution of $e_j$ is formulated as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\Re }_{e_j}=max{\mu }_j(x),\hfill \\ s.t.x\in U,\hfill \end{array}\right.\end{array}$$

(20)

as shown in Figure 3a.

Definition 12.

The attribute $e_j$ without constraints is a ‘bad’ description, and the ideal solution is the minimum value of ${\mu }_j(x)$. The ideal solution of $e_j$ is formulated as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\Re }_{e_j}=min{\mu }_j(x),\hfill \\ s.t.x\in U,\hfill \end{array}\right.\end{array}$$

(21)

as shown in Figure 3b.

The ideal solution $u_{goal}$ of $(\tilde{F},A)$ is the combination of each attribute $u_{goal}=\{{\Re }_{e_1},{\Re }_{e_2},\dots ,{\Re }_{e_k}\}$.

4.3. The Decision Function—Hamming Distance

The decision function is used to determine the similarity between $u_x$ and $u_{goal}$ in the fuzzy soft set. Many algorithms can be used as efficient decision functions, especially when the fuzzy soft set $(\tilde{F},A)$ has many objects, such as fuzzy S-trees, signature trees, t-concept lattice, Artificial Bee Colony (ABC) algorithm [28,29,30,31], and so on. Here, we use the widely used Hamming distance.

The normalized Hamming distance is a useful technique for calculating the differences between two elements, two sets, etc [32]. For two sets A and B, it can be defined as follows.

Definition 13.

A normalized Hamming distance of dimension n is a mapping $d_H:R_n\times R_n\to R$ such that:

$$\begin{array}{c}\hfill d_H(A,B)=\frac{1}{n}(\sum _{i=1}^n|a_i-b_i|),\end{array}$$

where $a_i$ and $b_i$ are the ith arguments of the sets $A=\{a_1,a_2,\dots ,a_n\}$ and $B=\{b_1,b_2,\dots ,b_n\}$, respectively.

Let $(\tilde{F},A)$ be a fuzzy soft set over U. All attributes have the same degree of importance, $u_{goal}$ is the ideal solution, and $u_i$ is the object. The decision-making problem becomes the optimization problem:

$$\begin{array}{c}\left\{\begin{array}{c}min{d}_H(u_{goal},u_i),\hfill \\ s.t.u_i\in U,\hfill \end{array}\right.i=1,2,\dots ,n.\end{array}$$

(22)

Definition 14.

A weighted Hamming distance of dimension n is a mapping $d_{WH}:R_n\times R_n\to R$ that has an associated weighting vector W of dimension n such that the sum of the weights is 1 and $w_j\in [0,1]$. Then:

$$\begin{array}{c}\hfill d_{WH}(A,B)=(\sum _{i=1}^n{\omega }_i|a_i-b_i|),\end{array}$$

where $a_i$ and $b_i$ are the ith arguments of the sets $A=\{a_1,a_2,\dots ,a_n\}$ and $B=\{b_1,b_2,\dots ,b_n\}$, respectively.

Almost all methods of decision-making problems require information regarding the relative importance of each attribute. The relative importance is usually given by a set of weights that are normalized to sum to one. In the case of n attributes, a weight set is $\omega =({\omega }_1,{\omega }_2,\dots ,{\omega }_n)$ and ${\sum }_{j=1}^n{\omega }_j=1$. The weights can be assigned by the decision maker directly, or calculated using the eigenvector method or the weighted least square method. The IOWA operator was introduced by Yager and Filev [33].

Definition 15.

([33]) An IOWA operator of dimension n is a mapping $f:R^n\to R$ that has an associated weighting vector ω of dimension n such that the sum of the weights is 1 and $w_j\in [0,1]$. Then,

$$\begin{array}{c}\hfill f_{IOWA}(<u_1,a_1>,<u_2,a_2>,\dots ,<u_n,a_n>)=\sum _{j=1}^n{w}_j{b}_j,\end{array}$$

where $b_j$ is the $a_i$ value of the IOWA pair $u_i$ ,$a_i$ having the jth largest $u_i$, $u_i$ is the order inducing variable and $a_i$ is the argument variable.

Let $(\tilde{F},A)$ be a fuzzy soft set over U, all attributes have the same degree of importance, the attribute has a weight of $\omega$, $u_{goal}$ is the optimal target, and $u_i$ is the object. The decision-making problem becomes the optimization problem:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}min{d}_{WH}(u_{goal},u_i),\hfill \\ s.t.u_i\in U,\hfill \end{array}\right.i=1,2,\dots ,n.\end{array}$$

(23)

4.4. The Decision-Making Algorithm Based on Fuzzy Soft Sets and Ideal Solution

Let $U=\{u_1,u_2,\dots ,u_n\}$ and $(\tilde{F},A)$ be a fuzzy soft set with k attributes $A=\{e_1,e_2,\dots ,e_k\}$, as Equation (24):

$$\begin{array}{c}\hfill (\tilde{F},A)=\left[\begin{array}{cccc}(u_{11})& (u_{12})& \dots & (u_{1k})\\ (u_{21})& (u_{22})& \dots & (u_{2k})\\ ⋮& ⋮& & ⋮\\ (u_{n1})& (u_{n2})& \dots & (u_{nk})\end{array}\right].\end{array}$$

(24)

We can analyze each attribute $e_x$ independently, and the ideal solution ${\Re }_{e_x}$ of each attribute can be obtained. The analysis and processing are described in Section 4.2.

By combining the ideal solution of each attribute, we can get the ideal solution $u_{goal}$ of the fuzzy soft sets:

$$\begin{array}{c}\hfill u_{goal}=\{{\Re }_{e_1},{\Re }_{e_2},\dots ,{\Re }_{e_k}\}.\end{array}$$

The decision-making fuzzy soft set $(\widetilde{FD},A)$ can be expressed in matrix form as Equation (25):

$$\begin{array}{c}\hfill (\widetilde{FD},A)=\left[\begin{array}{cccc}({\Re }_{e_1})& ({\Re }_{e_2})& \dots & ({\Re }_{e_k})\\ (u_{11})& (u_{12})& \dots & (u_{1k})\\ (u_{21})& (u_{22})& \dots & (u_{2k})\\ ⋮& ⋮& & ⋮\\ (u_{n1})& (u_{n2})& \dots & (u_{nk})\end{array}\right].\end{array}$$

(25)

In the fuzzy soft set $(\tilde{F},A)$, we first establish the ideal solution and then find the object closest to the ideal solution through the choice algorithm, which is the result of selection. The decision-making algorithm based on fuzzy soft sets and ideal solution (Algorithm 3) is formulated as follows:

$$\begin{array}{c}findp,\hfill \\ s.t.d^{\ast }=d_p=min\{d_i;i=1,2,\dots ,n\},\hfill \end{array}$$

(26)

where $d_i=d_{H_i}(u_{goal},u_i);i=1,2,\dots ,n$ when using the normalized Hamming distance and $d_i=d_{W{H}_i}(u_{goal},u_i);i=1,2,\dots ,n$ when using the weighted Hamming distance, respectively.

The algorithm is as follows:

Algorithm 3 The decision-making algorithm based on fuzzy soft sets and ideal solution

1: Input the fuzzy soft set $(\tilde{F},A)$. 2: Sort the attributes $(e_1,e_2,\dots ,e_n)$ in descending order according to its weight, and set the IOWA operator $\omega$ according to the purpose of the decision maker. 3: Compute the optimization target $u_{goal}=\{{\Re }_1,{\Re }_2,\dots ,{\Re }_k\}$ according to membership function of each attribute. 4: Compute the Hamming distance $d_i(u_{goal},u_i),i=1,2,\dots ,n$. 5: The decision is $d_k$ if, $d_k=mi{n}_k{d}_i$. 6: If k has more than one value, then any one of $o_k$ may be chosen.

Remark 4.

If $u_{goal}=\{1,1,\dots ,1\}$ and $d_H(u_{goal},u_i)$ is used, it is a choice value decision-making model. If $u_{goal}=\{1,1,\dots ,1\}$ and $d_{WH}(u_{goal},u_i)$ is used, it is a weighted choice value decision-making model. It should be noted that $u_{goal}=\{1,1,\dots ,1\}$ is not always reasonable in practical problems.

As can be seen from

Table 7. Features of the fuzzy soft set based decision-making algorithms.

Algorithm	Time Complexity	Subjective Weights	Attribute Analysis	Decision Function
[3]	$O(N)$	Yes	No	Choice value
[12]	$O(N^2)$	No	No	Comparison matrix
[14]	$O(N)$	Yes	No	Fuzzy choice value
[15]	$O(N)$	Yes	No	Choice value of level soft set
[20]	$O(N^2)$	No	No	New relative comparison matrix
Algorithm 3	$O(N)$	Yes	Yes	Similarity measure & Substitutable

, the fuzzy soft sets and ideal solution based algorithm focuses on the modular structure, and it emphasizes the analysis of decision objectives, attributes analysis and the flexible decision function. In Algorithm 3, each object needs to compare with the ideal solution, and, to deal with n items, its algorithm complexity is $O(n)$.

5. Numerical Experiments

We provide numerical experiments in this section. We will use an example to illustrate Algorithm 3, see Section 5.1. In Section 5.2, we will use Hwang and Yoon [27]’s example to illustrate the algorithm proposed in this paper. As a comparison, the traditional method and the algorithm proposed in this paper are applied to this example. We’ve added Python programs and validation data to validate examples in this article easily [34].

5.1. Example of Fuzzy Soft Sets and Ideal Solution Based Decision-Making Algorithm

Let $U=\{u_1,u_2,\dots ,u_8\}$ and $(\tilde{F},A)$ be a fuzzy soft set with seven attributes. Then, we add the $u_{goal}$ to $(\tilde{F},A)$ and the decision fuzzy soft set as Equation (27).

Assuming that all attributes are ‘good’ description and without constraints. By Equation (20) , ${\mu }_{goal}=\{1,1,\dots ,1\}$:

$$\begin{array}{c}\hfill (\widetilde{FD},A)=\left[\begin{array}{cccccccc}& e_1& e_2& e_3& e_4& e_5& e_6& e_7\\ u_{goal}& 1& 1& 1& 1& 1& 1& 1\\ u_1& 0.2& 0.4& 0.1& 0.5& 0.8& 0.1& 0.1\\ u_2& 0.3& 0.2& 0.3& 0.6& 0.3& 0.9& 0.6\\ u_3& 0.3& 0.1& 0.6& 0.7& 0.8& 0.8& 0.3\\ u_4& 0.3& 0.7& 0.9& 0.9& 0.1& 0.4& 0.5\\ u_5& 0.3& 0.9& 0.1& 0.3& 0.2& 0.2& 0.3\\ u_6& 0.3& 0.9& 0.1& 0.3& 0.9& 0.7& 0.8\\ u_7& 0.3& 0.9& 0.1& 0.3& 0.2& 0.8& 0.9\\ u_8& 0.3& 0.9& 0.1& 0.3& 0.1& 0.4& 0.2\end{array}\right],\end{array}$$

(27)

$$\begin{array}{c}\hfill d_H(u_{goal},u_1)=\frac{4.8}{7},d_H(u_{goal},u_2)=\frac{3.8}{7},\\ \hfill d_H(u_{goal},u_3)=\frac{3.4}{7},d_H(u_{goal},u_4)=\frac{3.2}{7},\\ \hfill d_H(u_{goal},u_5)=\frac{4.7}{7},d_H(u_{goal},u_6)=\frac{3.0}{7},\\ \hfill d_H(u_{goal},u_7)=\frac{3.5}{7},d_H(u_{goal},u_8)=\frac{4.7}{7}.\end{array}$$

From the normalized Hamming distance, it is seen that $u_6$ will be chosen.

Letting $\omega =\{\frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\frac{1}{32},\frac{1}{64},0\}$,

$$\begin{array}{c}\hfill d_{WH}(u_{goal},u_1)=0.714,d_{WH}(u_{goal},u_2)=0.686,\\ \hfill d_{WH}(u_{goal},u_3)=0.653,d_{WH}(u_{goal},u_4)=0.481,\\ \hfill d_{WH}(u_{goal},u_5)=0.569,d_{WH}(u_{goal},u_6)=0.539,\\ \hfill d_{WH}(u_{goal},u_7)=0.559,d_{WH}(u_{goal},u_8)=0.569.\end{array}$$

From the weighted Hamming distance, it is seen that $u_4$ will be chosen.

5.2. Algorithm Comparison

A country decided to purchase a fleet of jet fighters from the U.S. The Pentagon officials offered the characteristic information of four models that may be sold to that country. The Air Force analyst team of that country agreed that six characteristics (attributes) should be considered. They are maximum speed ($X_1$) ferry range ($X_2$), maximum payload ($X_3$), purchasing cost ($X_4$), reliability ($X_5$), and maneuverability ($X_6$). The measurement units for the attributes are mach, miles, pounds, dollars (in millions), high-low scale, and high-low scale, respectively. The decision matrix for the fighter aircraft selection problem, then, is:

$$\begin{array}{c}\hfill D=\left[\begin{array}{ccccccc}& X_1& X_2& X_3& X_4& X_5& X_6\\ A_1& 2.0& 1500& 20000& 5.5& average& veryhigh\\ A_2& 2.5& 2700& 18000& 6.5& low& average\\ A_3& 1.8& 2000& 21000& 4.5& high& high\\ A_4& 2.2& 1800& 20000& 5.0& average& average\end{array}\right].\end{array}$$

(28)

5.2.1. The Traditional Decision-Making Method

Attribute ratings are usually normalized to eliminate computational problems caused by different measurement units in a decision matrix. Linear normalization is a simple procedure that divides the ratings of a certain attribute by its maximum value. The normalized value of $x_{ij}$ is given as

$$\begin{array}{c}\hfill r_{ij}=\frac{x_{ij}}{x_j^{\ast }}i=1,\dots ,m;j=1,\dots ,n,\end{array}$$

(29)

where $x_j^{\ast }$ is the maximum value of the jth attribute. Clearly, the attribute is more satisfactory as $r_{ij}$ approaches 1, $(0\le r_{ij}\le 1)$:

$$\begin{array}{c}\hfill D=\left[\begin{array}{ccccccc}& X_1& X_2& X_3& X_4& X_5& X_6\\ A_1& 0.8& 0.56& 0.95& 0.82& 0.71& 1.0\\ A_2& 1.0& 1.0& 0.86& 0.69& 0.43& 0.56\\ A_3& 0.72& 0.74& 1.0& 1.0& 1.0& 0.78\\ A_4& 0.88& 0.64& 0.95& 0.9& 0.71& 0.56\end{array}\right].\end{array}$$

(30)

The key idea of the weighting method is to transform the multiple objectives in the decision-making problem into weighted single objective functions, which are described as follows (Zadeh, 1963) [17]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}maxwf(x)={\sum }_{i=1}^k{\omega }_i{f}_i(x),\hfill \\ s.t.x\in X,\hfill \end{array}\right.\end{array}$$

where $\omega =\{{\omega }_1,{\omega }_2,\dots ,{\omega }_k\}$ is a vector of weighting coefficients assigned to the objective functions.

Let $(\tilde{F},A)=D$, and $e_j$ the jth attribute. Let ${\omega }_1={\omega }_2={\omega }_3={\omega }_4={\omega }_5={\omega }_6=\frac{1}{6}$.

The decision table is as shows in the following:

$$\begin{array}{c}\hfill \tilde{D}=\left[\begin{array}{ccccccc}& X_1& X_2& X_3& X_4& X_5& X_6\\ A_1& 0.8& 0.56& 0.95& 0.82& 0.71& 1.0\\ A_2& 1.0& 1.0& 0.86& 0.69& 0.43& 0.56\\ A_3& 0.72& 0.74& 1.0& 1.0& 1.0& 0.78\\ A_4& 0.88& 0.64& 0.95& 0.9& 0.71& 0.56\end{array}\right]Score=\left[\begin{array}{c}\omega f(x)\\ 0.8067\\ 0.7567\\ 0.8733\\ 0.7733\end{array}\right].\end{array}$$

(31)

From Equation (31), $A_3$ will be chosen.

Remark 5.

Let $(\tilde{F},A)=D$, and $e_j$ the jth attribute. By using linear normalization,

$$\begin{array}{c}{\mu }_{e_j}(x)=\frac{x}{x_j^{\ast }},j=1,\dots ,n,\hfill \end{array}$$

where $x_j^{\ast }$ is the maximum value of the jth attribute.

In other words, in the traditional decision-making mode, the membership function of the attribute is always established in the form of a linear function. This is not always accurate and feasible.

5.2.2. The Decision-Making Based on Fuzzy Soft Sets and Ideal Solution

In this subsection, we illustrate the decision process with the following examples. Suppose three groups of air force analyst team make the following goals:

Team 1:

“Spare no expense to buy a jet fighter, and the jet fighter that is the fastest, most stable and has the best maneuverability".

Team 2:

“Buy a jet fighter with a budget of 5 million, and a jet fighter that is stable and has the best maneuverability”.

Team 3:

“Spend the least money to buy the indicators of a relatively good jet fighter”.

Let $A=\{$$e_1=‘\mathrm{maximum}\mathrm{speed}’$, $e_2=‘\mathrm{ferry}\mathrm{range}’$, $e_3=‘\mathrm{maximum}\mathrm{payload}’$, $e_4=‘\mathrm{purchasing}$ cost’, $e_5=‘\mathrm{reliability}’$, $e_6=‘\mathrm{maneuverability}’$}. The attributes { $e_1=‘\mathrm{maximum}\mathrm{speed}’$, $e_2=‘\mathrm{ferry}\mathrm{range}’$, $e_3=‘\mathrm{maximum}\mathrm{payload}’$, $e_5=‘\mathrm{reliability}’$, $e_6=‘\mathrm{maneuverability}’$ } are ‘pros’ attributes, and they are all positive descriptions of jet fighters. For the attribute $\{e_4=‘\mathrm{purchasing}\cos \mathrm{t}’\}$, of course, the cheaper, the better.

For Team 1, the attribute $\{e_4=‘\mathrm{purchasing}\cos \mathrm{t}’\}$ is a factor that doesn’t need to be considered, no matter how expensive it is. The attribute $\{e_1=‘\mathrm{maximum}\mathrm{speed}’\}$ is the primary consideration, $\{e_5=‘\mathrm{reliability}’\}$ second, and finally consider $\{e_6=‘\mathrm{maneuverability}’\}$. Other factors are relatively unimportant. Therefore, the degree of importance is: $e_1>e_5>e_6>(e_2=e_3)>e_4$.

For Team 2, the attribute $\{e_4=‘\mathrm{purchasing}\cos \mathrm{t}’\}$ is the primary consideration. This is a user constraint, and, by Equation (19), we can get the ideal solution of $e_4$. The attributes $\{e_5=‘\mathrm{reliability}’\}$ and $\{e_6=‘\mathrm{maneuverability}’\}$ are relatively important attributes, and $e_5>e_6$ . Therefore, the degree of importance is: $e_4>e_5>e_6>(e_1=e_2=e_3)$.

For Team 3, the attribute $\{e_4=‘\mathrm{purchasing}\cos \mathrm{t}’\}$ is the primary consideration, and the cheaper the better. All other attributes are secondary attributes that are equally important, which is: $e_4>(e_1=e_2=e_3=e_5=e_6)$.

The attributes are normalized by a small number of samples, and a rigorous decision maker needs to analyze each indicator carefully. To determine its membership function through investigation and research (the definition of membership function is subjective, and the optimal membership function is not the problem discussed in this paper), we can obtain the optimal goal of our decision more accurately.

Suppose the membership function of each attribute is formulated as follows.

Let ${\mu }_1(x)$ be the membership function of fast jet fighters:

$$\begin{array}{c}\hfill {\mu }_1(x)=\left\{\begin{array}{c}1,x\ge 3.5,\hfill \\ \frac{1}{1+e^{-2.1\times (x-1.5)}},0.5<x<3.5,\hfill \\ 0,x\le 0.5.\hfill \end{array}\right.\end{array}$$

Let ${\mu }_2(x)$ be the membership function of ferry range:

$$\begin{array}{c}\hfill {\mu }_2(x)=\left\{\begin{array}{c}1,x\ge 3200,\hfill \\ \frac{1}{1+e^{-0.003\times (x-2000)}},1000<x<3200,\hfill \\ 0,x\le 1000.\hfill \end{array}\right.\end{array}$$

Let ${\mu }_3(x)$ be the membership function of maximum payload:

$$\begin{array}{c}\hfill {\mu }_3(x)=\left\{\begin{array}{c}1,x\ge \mathrm{32,000},\hfill \\ \frac{1}{e^{-0.0005\times (x-\mathrm{20,000})}},\mathrm{15,000}<x<\mathrm{32,000},\hfill \\ 0,x\le \mathrm{15,000}.\hfill \end{array}\right.\end{array}$$

Let ${\mu }_4(x)$ be the membership function of the expensive jet fighter:

$$\begin{array}{c}\hfill {\mu }_4(x)=\left\{\begin{array}{c}\frac{1}{1+e^{-(x-3)}},0<x,\hfill \\ 0,x\le 0.\hfill \end{array}\right.\end{array}$$

Let ${\mu }_5(x)$ be the membership function of reliability:

$$\begin{array}{c}\hfill {\mu }_5(x)=\left\{\begin{array}{c}\frac{1}{4},0\le x<0.25,\hfill \\ \frac{2}{4},0.25\le x<0.5,\hfill \\ \frac{3}{4},0.5\le x<0.75,\hfill \\ 1,0.75\le x\le 1.\hfill \end{array}\right.\end{array}$$

Let ${\mu }_6(x)$ be the membership function of maneuverability:

$$\begin{array}{c}\hfill {\mu }_6(x)=\left\{\begin{array}{c}\frac{1}{4},0\le x<0.25,\hfill \\ \frac{2}{4},0.25\le x<0.5,\hfill \\ \frac{3}{4},0.5\le x<0.75,\hfill \\ 1,0.75\le x\le 1.\hfill \end{array}\right.\end{array}$$

The decision table for the fighter aircraft selection can be changed to a fuzzy soft set, as Equation (32):

$$\begin{array}{c}\hfill (\tilde{F},A)=\left[\begin{array}{ccccccc}& e_1& e_2& e_3& e_4& e_5& e_6\\ A_1& 0.741& 0.182& 0.5& 0.924& 0.5& 1\\ A_2& 0.891& 0.891& 0.269& 0.971& 0& 0.5\\ A_3& 0.652& 0.5& 0.622& 0.818& 0.75& 0.75\\ A_4& 0.813& 0.354& 0.5& 0.881& 0.5& 0.5\end{array}\right].\end{array}$$

(32)

Example 7.

Team 1: Spare no expense to buy a jet fighter, and the jet fighter that is the fastest, most stable and has the best maneuverability.

Without user constraints, the weight of attributes is: $e_1>e_5>e_6>(e_2=e_3)>e_4$.

Let $\omega =\{{\omega }_1=\frac{1}{2},{\omega }_5=\frac{1}{4},{\omega }_6=\frac{1}{8},{\omega }_2=\frac{1}{16},{\omega }_3=\frac{1}{16},{\omega }_4=0\}$, ${\sum }_{i=1}^6{\omega }_i=1$.

${\Re }_1=1,{\Re }_2=1,{\Re }_3=1,{\Re }_4=0,{\Re }_5=1,{\Re }_6=1$, $u_{goal}=\{1,1,1,0,1,1\}$,

$$\begin{array}{c}\hfill (\widetilde{FD},A)=\left[\begin{array}{ccccccc}& e_1& e_2& e_3& e_4& e_5& e_6\\ A_{goal}& 1& 1& 1& 0& 1& 1\\ A_1& 0.741& 0.182& 0.5& 0.924& 0.5& 1\\ A_2& 0.891& 0.891& 0.269& 0.971& 0& 0.5\\ A_3& 0.652& 0.5& 0.622& 0.818& 0.75& 0.75\\ A_4& 0.813& 0.354& 0.5& 0.881& 0.5& 0.5\end{array}\right],\end{array}$$

(33)

$$\begin{array}{c}\hfill d_{WH}(A_{goal},A_1)=0.337,d_{WH}(A_{goal},A_2)=0.419,\\ \hfill d_{WH}(A_{goal},A_3)=0.323,d_{WH}(A_{goal},A_4)=0.353.\end{array}$$

From the weighted Hamming distance, it is seen that $A_3$ will be the choice because it is the closest object to $A_{goal}$. In addition, $d_{A_2}\succ d_{A_4}\succ d_{A_1}\succ d_{A_3}$.

Example 8.

Team 2: Buy a jet fighter with a budget of 5 million, and a jet fighter that is stable and has the best maneuverability.

The prices include user constraints: $x^{\ast }=5,then,{\Re }_4={\mu }_4(5)=0.881.$

The weight of attributes is: $e_4>(e_5=e_6)>(e_1=e_2=e_3)$.

Let $\omega =\{{\omega }_4=\frac{14}{60},{\omega }_5=\frac{11}{60},{\omega }_6=\frac{11}{60},{\omega }_1=\frac{8}{60},{\omega }_2=\frac{8}{60},{\omega }_3=\frac{8}{60}\}$, ${\sum }_{i=1}^6{\omega }_i=1$.

${\Re }_1=1,{\Re }_2=1,{\Re }_3=1,{\Re }_4=0.881,{\Re }_5=1,{\Re }_6=1$, $u_{goal}=\{1,1,1,0.881,1,1\}$.

$$\begin{array}{c}\hfill (\widetilde{FD},A)=\left[\begin{array}{ccccccc}& e_1& e_2& e_3& e_4& e_5& e_6\\ A_{goal}& 1& 1& 1& 0.881& 1& 1\\ A_1& 0.741& 0.182& 0.5& 0.924& 0.5& 1\\ A_2& 0.891& 0.891& 0.269& 0.971& 0& 0.5\\ A_3& 0.652& 0.5& 0.622& 0.818& 0.75& 0.75\\ A_4& 0.813& 0.354& 0.5& 0.881& 0.5& 0.5\end{array}\right],\end{array}$$

(34)

$$\begin{array}{c}\hfill d_{WH}(A_{goal},A_1)=0.312,d_{WH}(A_{goal},A_2)=0.423,\\ \hfill d_{WH}(A_{goal},A_3)=0.270,d_{WH}(A_{goal},A_4)=0.361.\end{array}$$

From the weighted Hamming distance, it is seen that $A_3$ will be the choice. In addition, $d_{A_2}\succ d_{A_4}\succ d_{A_1}\succ d_{A_3}$.

Example 9.

Team 3: Spend the least money to buy the indicators of a relatively good jet fighter”.

Without user constraints, the weight of attributes is: $e_4>(e_1=e_2=e_3=e_5=e_6)$.

Let $\omega =\{{\omega }_4=\frac{5}{15},{\omega }_5=\frac{2}{15},{\omega }_6=\frac{2}{15},{\omega }_2=\frac{2}{15},{\omega }_3=\frac{2}{15},{\omega }_1=\frac{2}{15}\}$, ${\sum }_{i=1}^6{\omega }_i=1$.

${\Re }_1=1,{\Re }_2=1,{\Re }_3=1,{\Re }_4=0,{\Re }_5=1,{\Re }_6=1$, $u_{goal}=\{1,1,1,0,1,1\}$.

$$\begin{array}{c}\hfill (\widetilde{FD},A)=\left[\begin{array}{ccccccc}& e_1& e_2& e_3& e_4& e_5& e_6\\ A_{goal}& 1& 1& 1& 0& 1& 1\\ A_1& 0.741& 0.182& 0.5& 0.924& 0.5& 1\\ A_2& 0.891& 0.891& 0.269& 0.971& 0& 0.5\\ A_3& 0.652& 0.5& 0.622& 0.818& 0.75& 0.75\\ A_4& 0.813& 0.354& 0.5& 0.881& 0.5& 0.5\end{array}\right]\end{array}$$

(35)

$$\begin{array}{c}\hfill d_{WH}(A_{goal},A_1)=0.585d_{WH}(A_{goal},A_2)=0.650\\ \hfill d_{WH}(A_{goal},A_3)=0.503d_{WH}(A_{goal},A_4)=0.605\end{array}$$

From the weighted Hamming distance, it is seen that $A_3$ will be the choice. In addition, $d_{A_2}\succ d_{A_4}\succ d_{A_1}\succ d_{A_3}$.

Remark 6.

The decision-making based on fuzzy soft sets and the ideal solution has some advantages. Firstly, the soft set model can be combined with other mathematical models. When it is combined with fuzzy decision-making, the soft set is a natural multi-attribute decision making model, which holds a wide range of application prospects in decision-making and analysis. Secondly, in the traditional ideal solution algorithm, it can be seen that the normalization process is the process of establishing the membership function $\mu (x)$. There are many commonly used normalization methods, i.e., Equation (29), but few of them can reflect the nature of the problem. The fuzzy soft set already contains the membership function $\mu (x)$, which can be used well. Thirdly, from the analysis of the attributes of the fuzzy soft sets, we can see that the attributes themselves are associated with each other. For example, ‘price’ and other attributes are related to each other, usually because of their high performance and therefore high pricing. Therefore, some attributes have less impact on the decision results because other attributes already contain information about that attribute.

6. Conclusions

The decision-making is a significant problem, and a good decision system will undoubtedly play a huge role in promoting economy, management, and society. However, it is hard for us to expect a single mathematical model to accomplish such a difficult task. There are mainly two different approaches applying soft set theory to decision-making problems. One is based on choice value, and the other is based on comparison score. This paper analyzes the existing problems of these two methods. The choice value algorithm is not always reasonable in practice because it lacks the analysis of attributes. At the same time, we point out that the comparison score algorithm has the phenomenon of rank reversal, which can be further analyzed and improved. This paper is dedicated to the analysis of these approaches and proposes a new decision-making algorithm. We focus on the application of fuzzy soft set and ideal solutions in decision-making problems. From the decision-making process, we have found that the core of the decision process is the design phase, which is to formulate a model for an identified decision problem. Therefore, this paper emphasizes the analysis of decision objectives, attributes analysis and explicit decision function. Based on these results, we can further probe the practical applications of soft set theory in decision-making problems. Thanks to this modular structure, we can design more efficient decision functions for this model. Moreover, how to avoid rank reversal of the comparison score algorithm is another promising research topic.