1. Introduction
For solving decision-making problems in a fuzzy environment, the overall utilities of a set of alternatives are represented by fuzzy sets or fuzzy numbers. A fundamental problem of a decision-making procedure involves ranking a set of fuzzy sets or fuzzy numbers. Ranking functions, reference sets and preference relations are three categories with which to rank a set of fuzzy numbers. For a detailed discussion, we refer the reader to surveys by Chen and Hwang [
1] and Wang and Kerre [
2,
3]. For ranking a set of fuzzy numbers, this paper concentrates on those fuzzy preference relations that are able to represent preference relations in linguistic or fuzzy terms and to make pairwise comparisons. To propose the fuzzy preference relation, Nakamura [
4] employed a fuzzy minimum operation followed by the Hamming distance. Kołodziejczyk [
5] considered the common part of two membership functions and used the fuzzy maximum and Hamming distance. Yuan [
6] compared the fuzzy subtraction of two fuzzy numbers with real number zero and indicated that the desirable properties of a fuzzy ranking method are the fuzzy preference presentation, rationality of fuzzy ordering, distinguishability and robustness. Li [
7] included the influence of levels of possibility of dominance. Lee [
8] presented a counterexample to Li’s method [
7] and proposed an additional comparable property. The methods of Wang et al. [
9] and Asady [
10] were based on deviation degree. Zhang et al. [
11] presented a fuzzy probabilistic preference relation. Zhu et al. [
12] proposed hesitant fuzzy preference relations. Wang [
13] adopted the relative preference degrees of the fuzzy numbers over average.
This paper evaluates and compares two fundamental fuzzy preference relations—one is proposed by Nakamura [
4] and the other by Kołodziejczyk [
5]. The intersection of two membership functions and the decomposition of two fuzzy numbers are main differences between these two preference relations. Since the desirable criteria cannot easily be represented in mathematical forms, their performance measures are often tested by using test examples and judged intuitively. To this end, we consider eight complex cases that represent all the possible cases the way two fuzzy numbers can overlap with each other. For Nakamura’s and Kołodziejczyk’s fuzzy preference relations, this paper analyzes and compares the ordering behaviors of the decomposition and intersection through a group of extensive cases.
The organization of this paper is as follows—
Section 2 briefly reviews the fuzzy sets and fuzzy preference relations and presents the eight test cases.
Section 3 analyzes Nakamura’s fuzzy preference relation and presents an algorithm.
Section 4 presents the behaviors of Kołodziejczyk’s fuzzy preference relation.
Section 5 analyzes the effect of the decomposition and intersection on fuzzy preference relations. Finally, some concluding remarks and suggestions for future research are presented.
2. Fuzzy Sets and Test Problems
We first review the basic notations of fuzzy sets and fuzzy preference relations. Consider a fuzzy set A defined by a universal set of real numbers by the membership function , where .
Definition 1. Let A be a fuzzy set. The support of A is the crisp set . A is called normal when . An -cut of A is a crisp set . A is convex if, and only if, each of its -cut is a convex set.
Definition 2. A normal and convex fuzzy set whose membership function is piecewise continuous is called a fuzzy number.
Definition 3. A triangular fuzzy number A, denoted , is a fuzzy number with membership function given by: where . The set of all triangular fuzzy numbers on is denoted by .
Definition 4. For a fuzzy number A, the upper boundary set of A and the lower boundary set of A are respectively defined as: and: Definition 5. The Hamming distance between two fuzzy numbers A and B is defined by:
Definition 6. Let A and B be two fuzzy numbers and be an operation on , such as +, ─, *, …. By extension principle, the extended operation on fuzzy numbers can be defined by: Definition 7. A fuzzy preference relation R is a fuzzy binary relation with membership function indicating the degree of preference of fuzzy number A over fuzzy number B.
R is reciprocal if, and only if, for all fuzzy numbers A and B.
R is transitive if, and only if, and implies for all fuzzy numbers A, B and C.
R is a fuzzy total ordering if, and only if, R is both reciprocal and transitive.
R is robust if, and only if, for any given fuzzy numbers and , there exists for which , for all fuzzy number and .
For simplicity, we denote for the degree of preference of fuzzy number B over fuzzy number A.
The evaluation criteria for the comparison of two fuzzy numbers cannot easily be represented in mathematical forms therefore it is often tested on a group of selected examples. The membership functions of two fuzzy numbers can be overlapping/nonovelapping, convex/nonconvex, and normal/non-normal. All the approaches proposed in the literature seem to suffer from some questionable examples, especially for the portion of overlap between two membership functions.
Let
and
be two triangular fuzzy numbers.
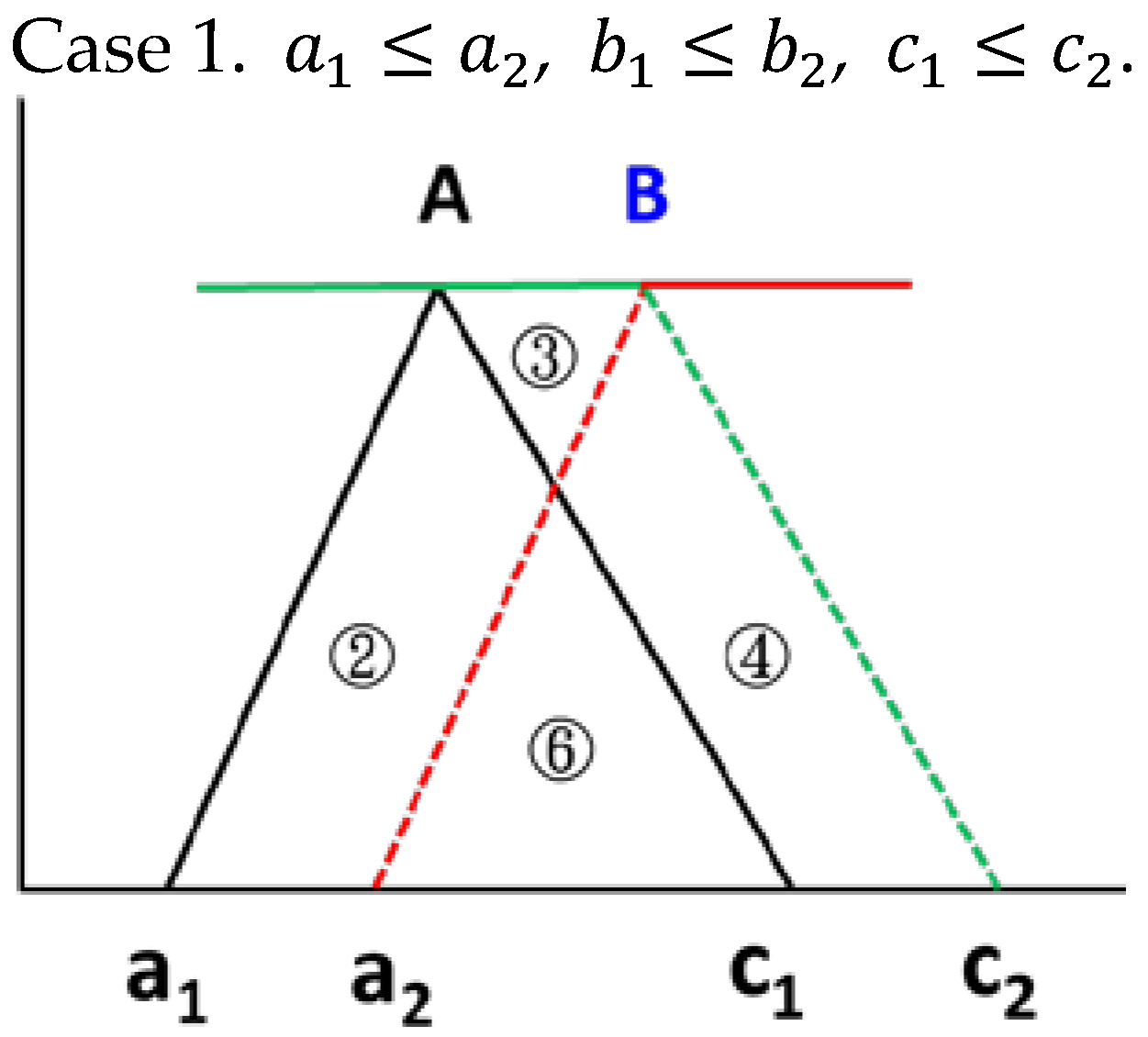
Figure 1 displays eight test cases of representing all the possible cases the way two fuzzy numbers
A and
B can overlap with each other.
Table 1 shows the area
of
i-th region in each case. More precisely, the eight extensive test cases are as follows:
- Case 1.
, ,
- Case 2.
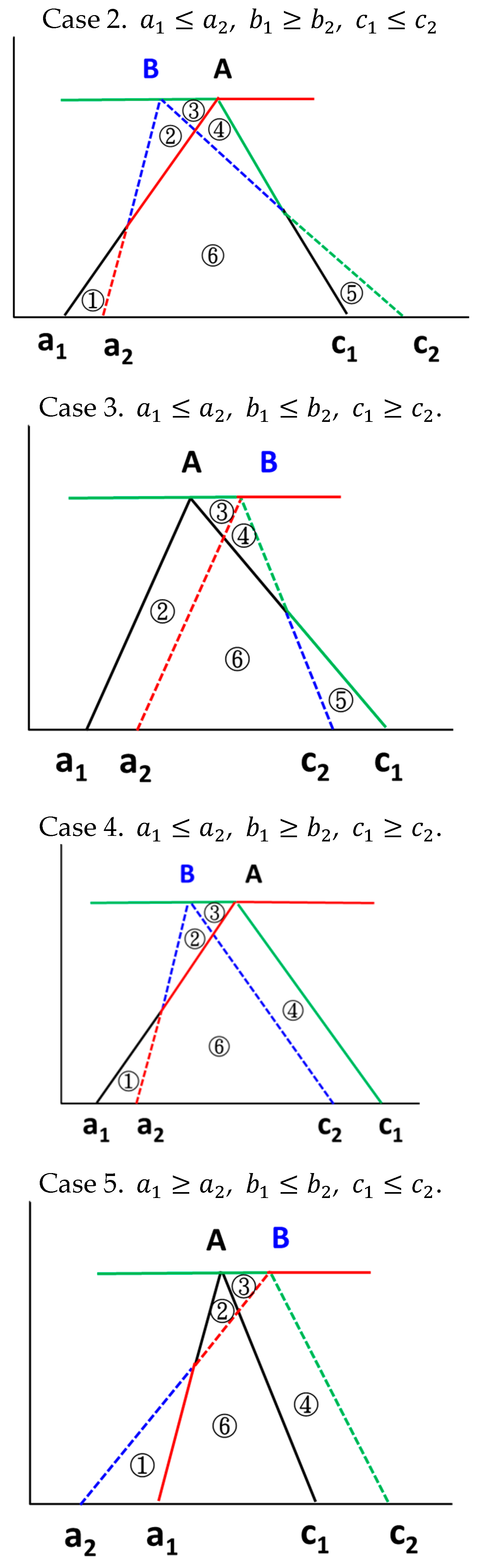
, ,
- Case 3.
, ,
- Case 4.
, ,
- Case 5.
, ,
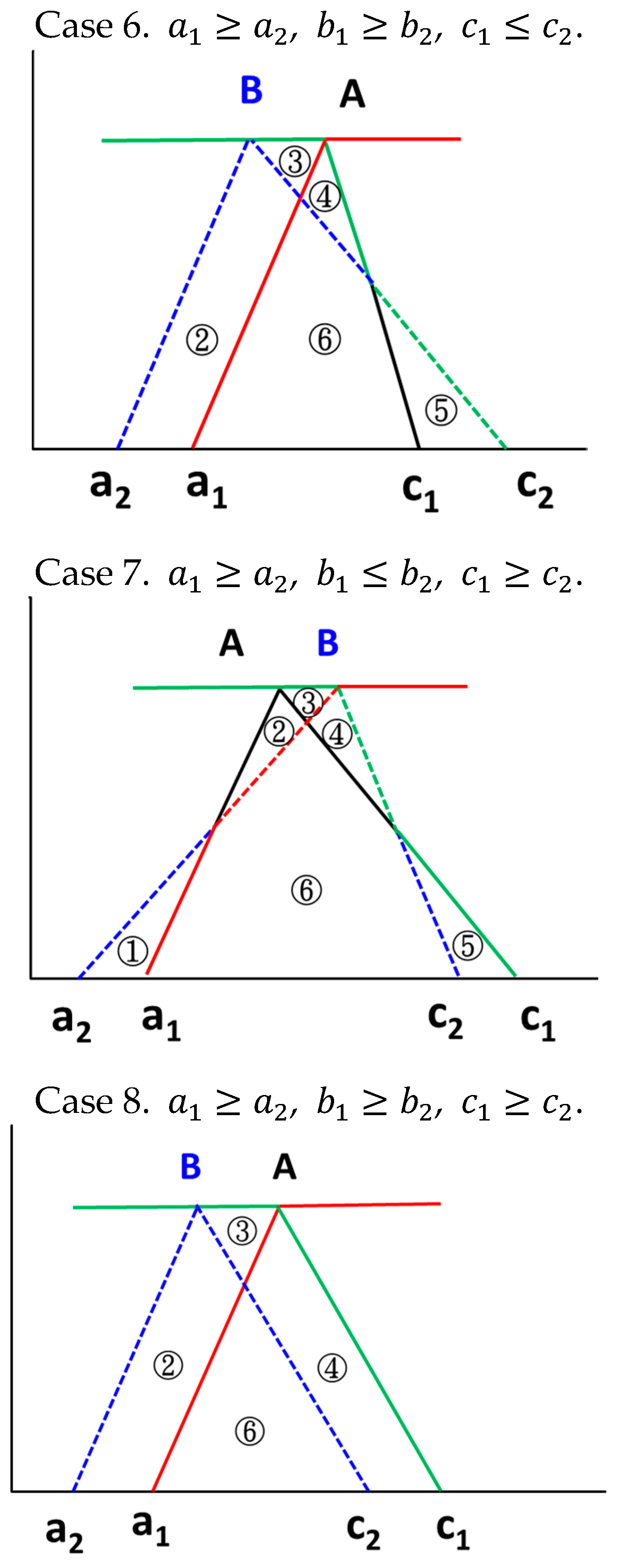
- Case 6.
, ,
- Case 7.
, ,
- Case 8.
, , .
3. Nakamura’s Fuzzy Preference Relation
Using fuzzy minimum, fuzzy maximum, and Hamming distance, Nakamura’s fuzzy preference relations [
4] are defined as follows:
Definition 8. For two fuzzy numbers A and B, Nakamura [
4]
defines and as fuzzy preference relations by the following membership functions:and:respectively. Yuan [
6]
showed that N is reciprocal and transitive, but not robust. Wang and Kerre [
3]
derived that: and: For two triangular fuzzy numbers
and
, then:
so:
Define:
then:
Let , and . The steps for implementing the Nakamura’s fuzzy preference relation are as in Algorithm 1:
| Algorithm 1. Nakamura’s fuzzy preference relation |
| If |
| If |
| If , then else . |
| else if , then else |
| . |
| else if |
| If , then else |
| . |
| else if , then else . |
Table 2 shows the values of
and
for each test case. The first observation of this table is that:
Secondly, comparing the values of with that of , we have that and . If , we obtain that , , , , and .
5. Two Comparative Studies of Decomposition and Intersection of Two Fuzzy Numbers
If the fuzzy number
A is less than the fuzzy number
B, then the Hamming distance between
A and
is large. Two representations are adopted. One is
. The other is
which decomposes
A into
and
. To analyze the effect of decomposition, we consider the following preference relations without decomposition:
and:
which are the counterparts of the Kołodziejczyk’s preference relations
and
. Therefore, the preference relations
and
consider the decomposition of fuzzy numbers, while
and
do not. The preference relations
and
consider the intersection of two membership functions, while
and
do not. For completeness,
Table 4 displays the values of
,
,
,
,
and
of each test case in terms of the values of
. The
considers both decomposition and intersection of two fuzzy numbers, while
do not. From
to
, two representations are:
and:
The first feature of
Table 4 is that the differences between
and
and between
and
are
. More precisely, the numerators and denominators of both
and
include
for cases 1, 3, 5 and 7, the denominators of both
and
include
for cases 2, 4, 6 and 8. Therefore,
represents the effect of the decomposition of fuzzy numbers. The differences between
and
and between
and
are
. More precisely, the numerators and denominators of both
and
include
and
, respectively. Therefore,
represents the effect of the intersection of two membership functions. After some computations, the characteristics of
,
,
and
are described as follows:
Theorem 1. Let .
- (1)
If , or , , then . If , or , , then .
- (2)
If , then . If , then .
- (3)
If , then . If , then .
- (4)
If , then . If , then .
- (5)
If , or , , then . If , or , , then .
For each test case of two triangular fuzzy numbers
and
, we analyze the behaviors of
,
,
and
by applying Theorem 1 as follows: Firstly, for
, we have:
for case 1. For cases 3, 5 and 7, we have the following results.
- (1)
From , we have that if , then ; if , then
- (2)
.
- (3)
From , it follows that if , then if , then .
- (4)
.
- (5)
If , then . If , then .
Therefore, for the cases 3, 5 and 7, if
, then:
and:
Secondly, for
, we have:
for case 8. For cases 2, 4 and 6, we have the following results.
- (1)
From , we obtain if , then ; if , then .
- (2)
.
- (3)
From , it follows thatif , then ; if , then .
- (4)
.
- (5)
If , then . If , then .
Therefore, for the cases 2, 4 and 6, if
, then:
and:
For the two triangular fuzzy numbers
and
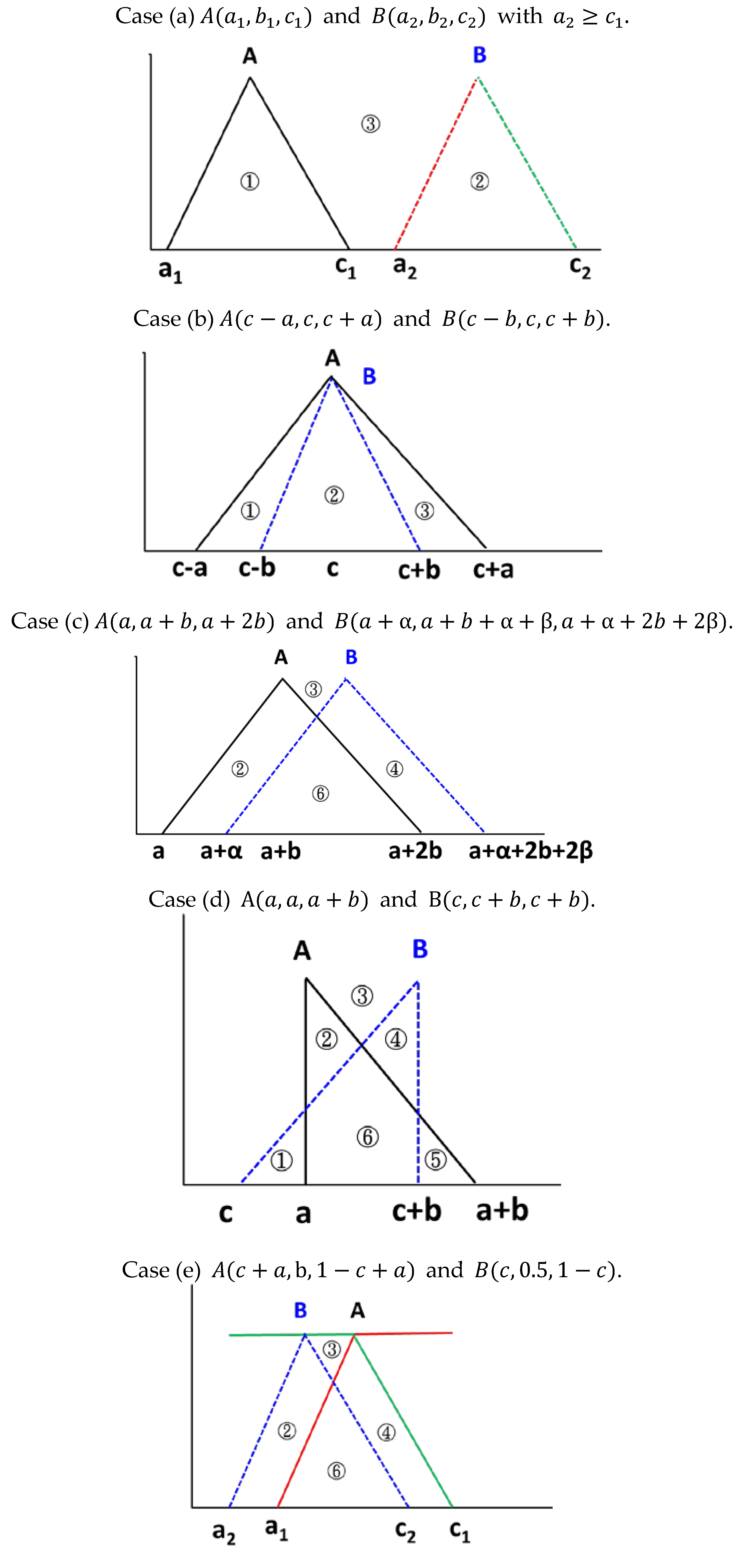
, the second comparative study is comprised of the five case studies shown in
Figure 2, which compares the fuzzy preference relations
,
,
and
.
Case (a) and with .
For this simple case, all the preference relations give the same degree of preference of B over A.
Case (b) and .
From the viewpoint of probability, the fuzzy numbers A and B have the same mean, but B has a smaller standard deviation. The results indicate that the differences between the decomposition and intersection of A and B cannot affect the degree of preference for B over A.
Case (c) and .
For this case, the fuzzy number
B is a right shift of
A. Therefore,
B should have a higher ranking than
A based on the intuition criterion. We obtain:
and:
All methods prefer B, but is indecisive. More precisely,
If , then , so
If , then , so
If , then , so .
Hence, a conflicting ranking order of exists in this case.
Case (d) and with .
This case is more complex for the partial overlap of
A and
B. The membership function of
B has the right peak,
B expands to the left of
A for the left membership function, and
A expands to the right of
B for the right membership function. We have:
and:
It follows that:
If , then and , so ;
If , then and , so ;
If , then and , so ;
If , then and , so ;
If , then and , so ;
If , then and , so .
Three special subcases are considered as follows:
- (1)
Subcase (d1) If , then and , therefore , so . However, , and .
- (2)
Subcase (d2) If , then and , therefore , , so . However, and .
- (3)
Subcase (d3) If and , then , , , , so .
Therefore, if , then , , and , so ; if , then , , and , so .
Case (e) and .
For this case, the membership function B is symmetric with respect to . The membership function of A is parallel translation of that of B except its peak. We have the following results:
- (1)
. If , then , so . For simplicity, the other two conditions are omitted.
- (2)
. If , then , so .
- (3)
and . If , then and , so .
Four special subcases are considered as follows:
- (1)
Subcase (e1) If , then , so . However, , and .
- (2)
Subcase (e2) If , then , , so . However, and .
- (3)
Subcase (e3) If and , then , , , , so .
- (4)
Subcase (e4) If , then , and , so , , and , hence .
6. Conclusions
This paper analyzes and compares two types of Nakamura’s fuzzy preference relations—( and )—two types of Kołodziejczyk’s fuzzy preference relations—( and )—and the counterparts of the Kołodziejczyk’s fuzzy preference relations—( and )—on a group of eight selected cases, with all the possible levels of overlap between two triangular fuzzy numbers and . First, for and we obtain that , . If , we have that for and for . Secondly, for and , we have that for and for . Furthermore, for and and for and . Thirdly, for test case 1, . For the test cases 3, 5 and 7, if , then and . For the test case 8, we have . For the test cases 2, 4 and 6, if , then and . These results provide insights into the decomposition and intersection of fuzzy numbers. Among the six fuzzy preference relations, the appropriate fuzzy preference relation can be chosen from the decision-maker’s perspective. Given this fuzzy preference relation, the final ranking of a set of alternatives is derived.
Worthy of future research is extending the analysis to other types of fuzzy numbers. First, the analysis can be easily extended to the trapezoidal fuzzy numbers. Second, for the hesitant fuzzy set lexicographical ordering method, Liu et al. [
14] modified the method of Farhadinia [
15] and this was more reasonable in more general cases. Recently, Alcantud and Torra [
16] provided the necessary tools for the hesitant fuzzy preference relations. Thus, the analysis of hesitant fuzzy preference relations is a subject of considerable ongoing research.