A General Zero Attraction Proportionate Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification
Abstract
:1. Introduction
2. Past Works on NMCC and PNMCC Algorithms
2.1. NMCC Algorithm
2.2. PNMCC Algorithm
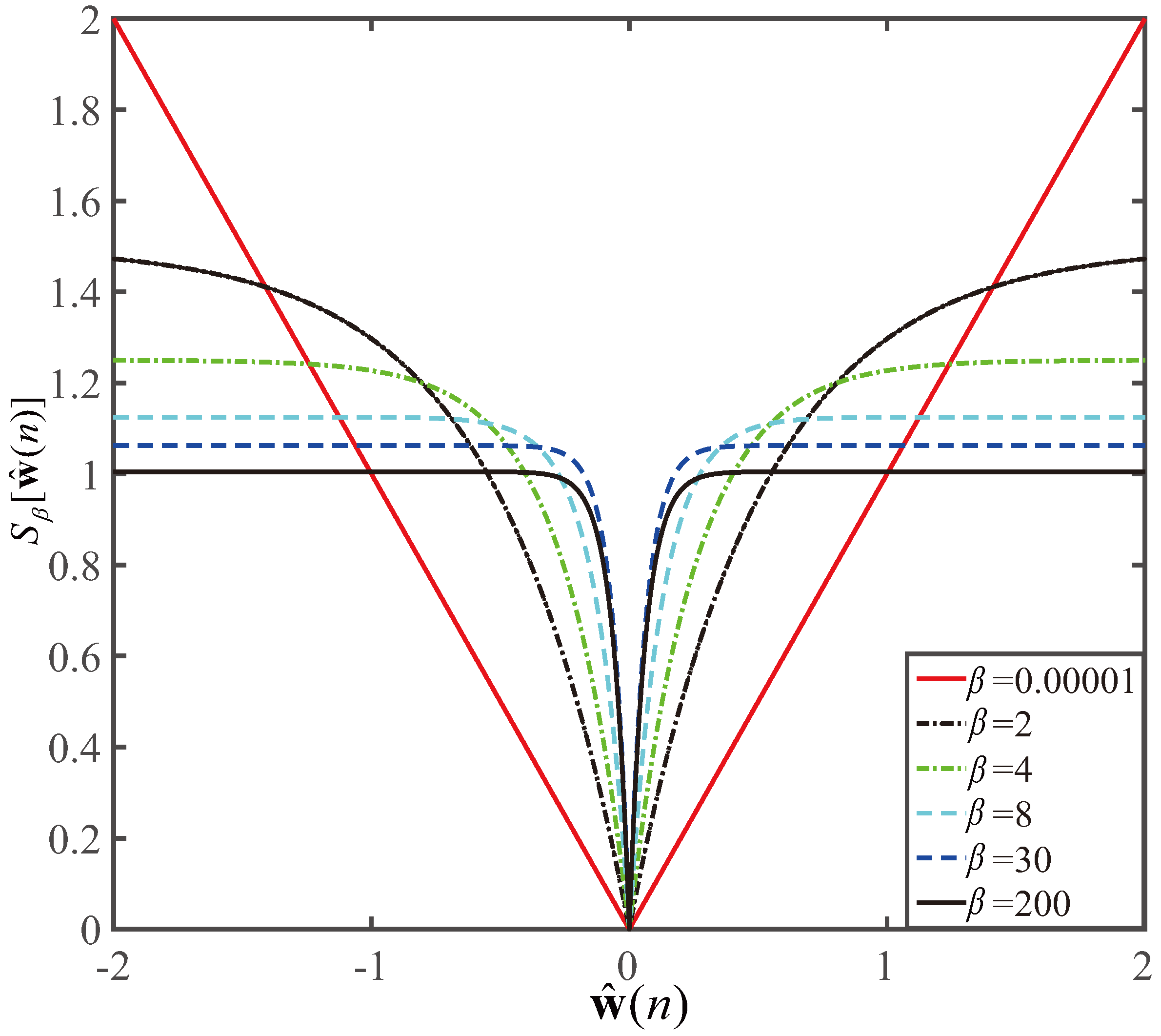
3. Proposed GZA-PNMCC Algorithm
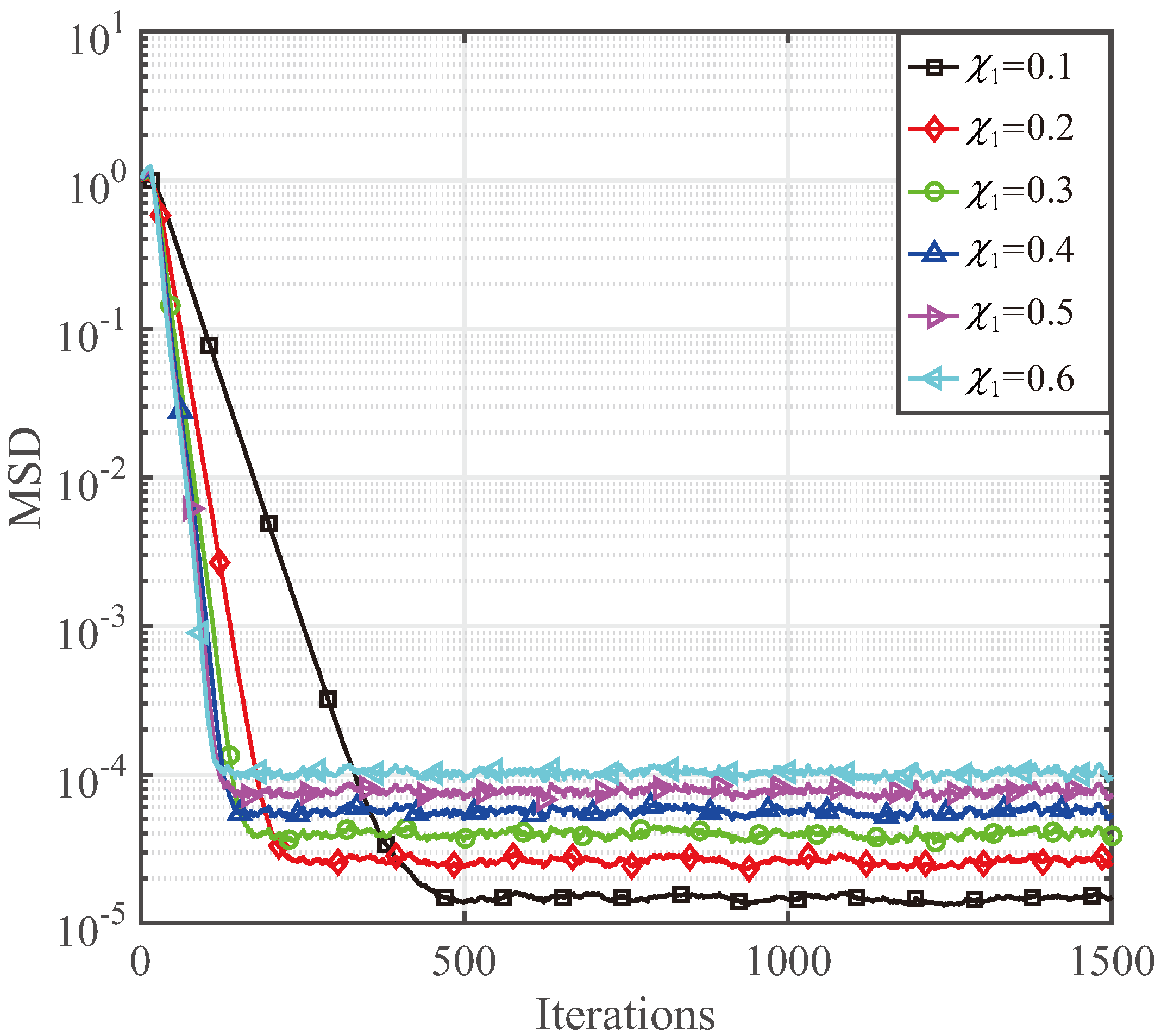
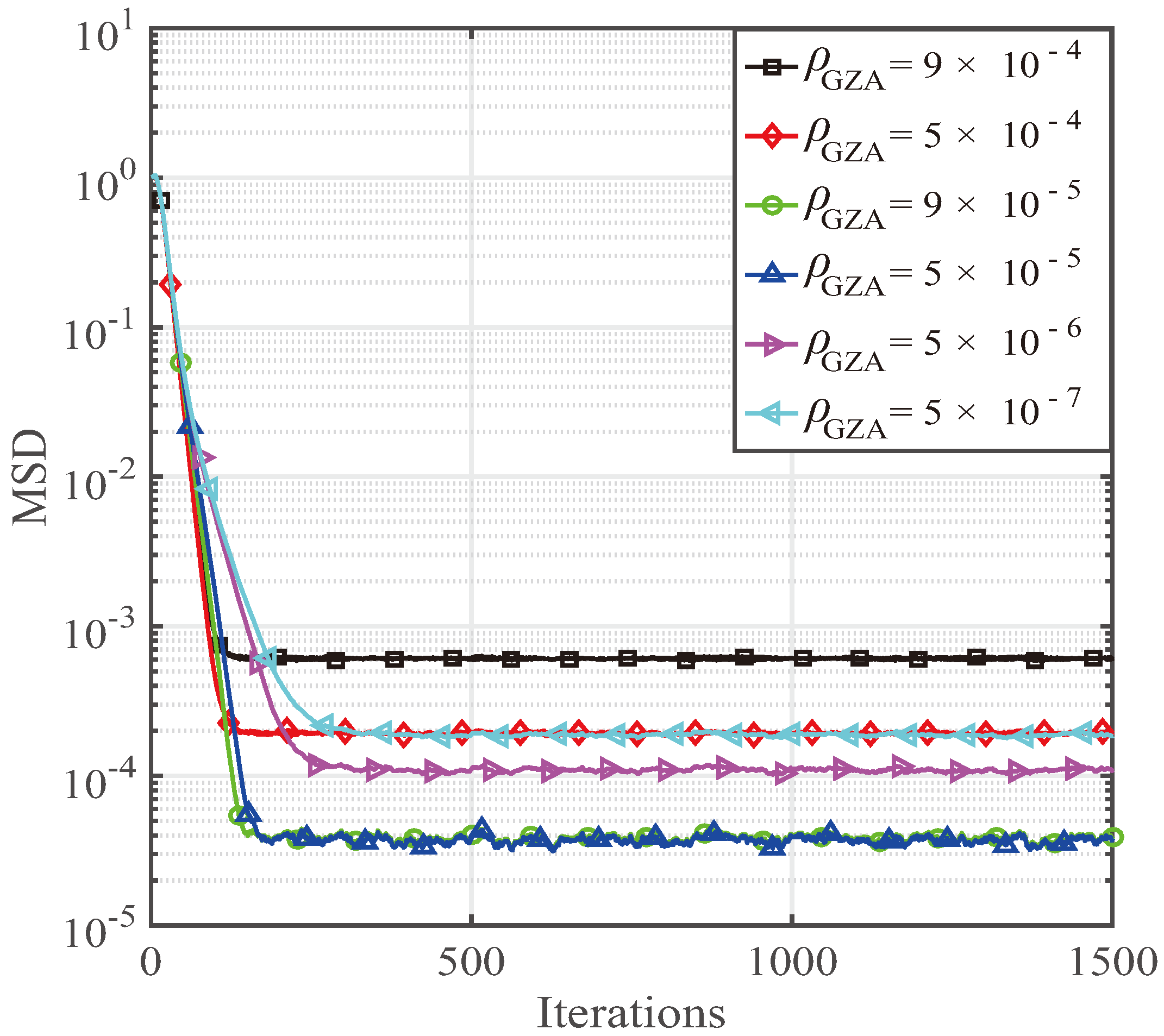
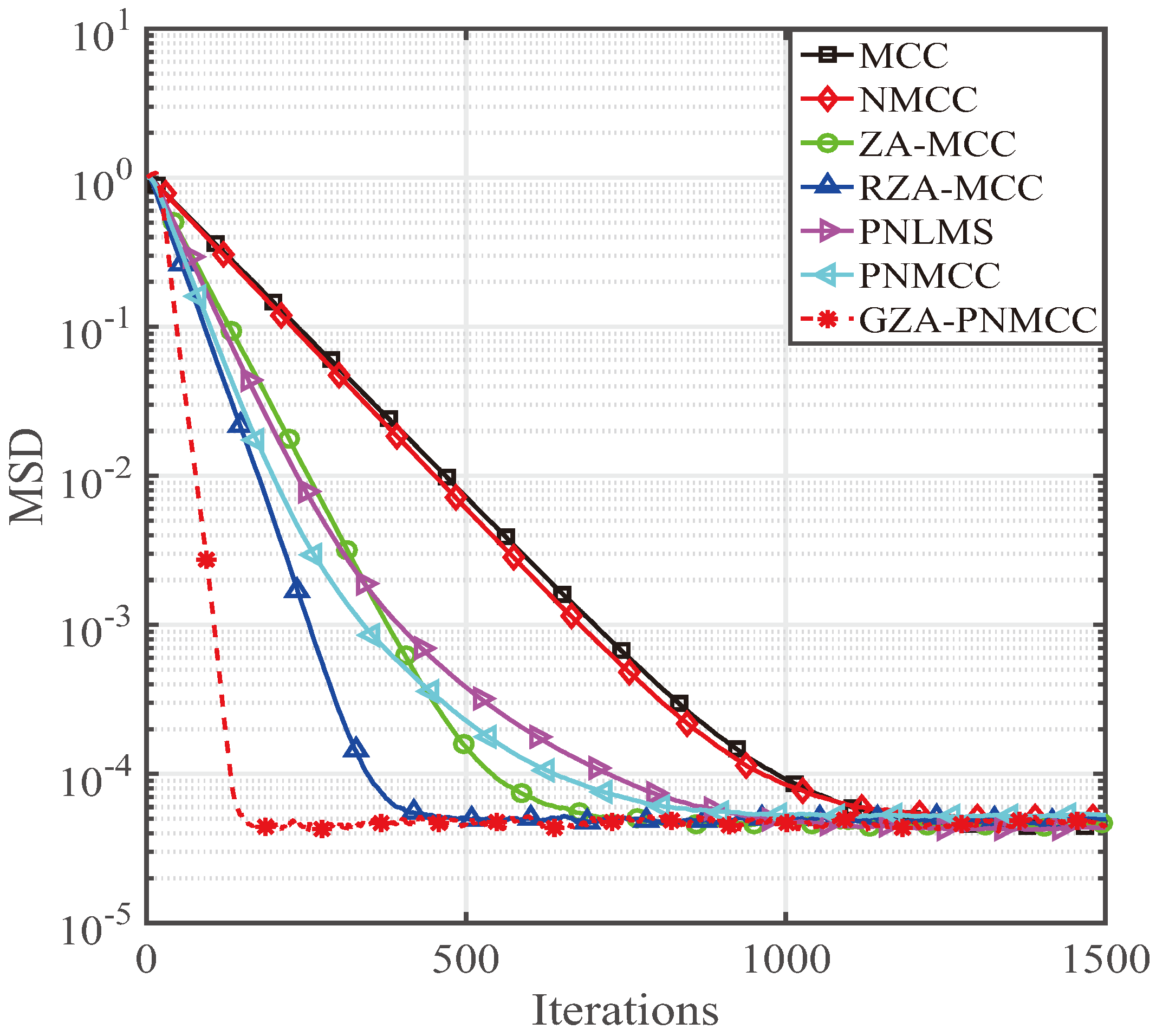
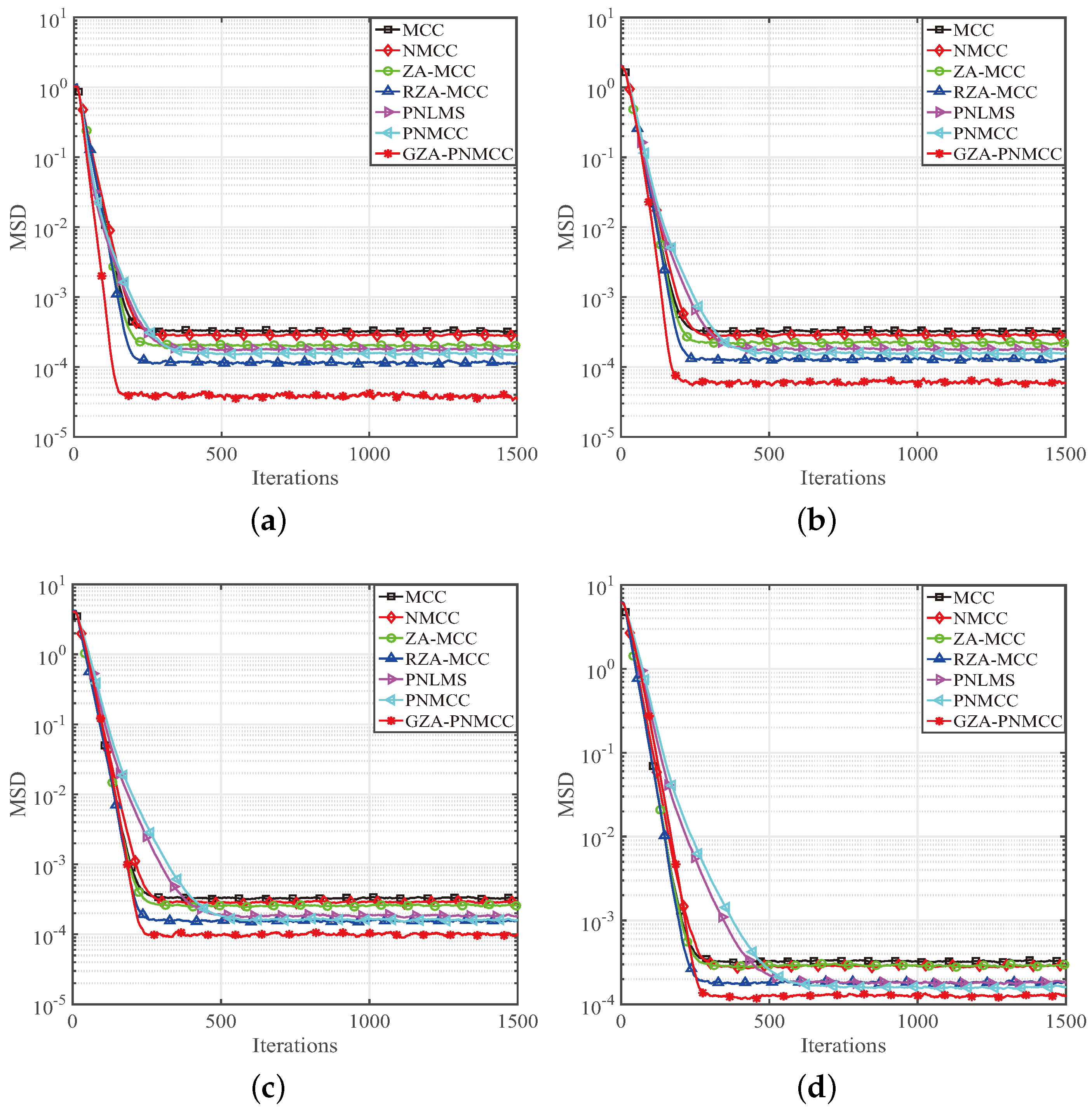
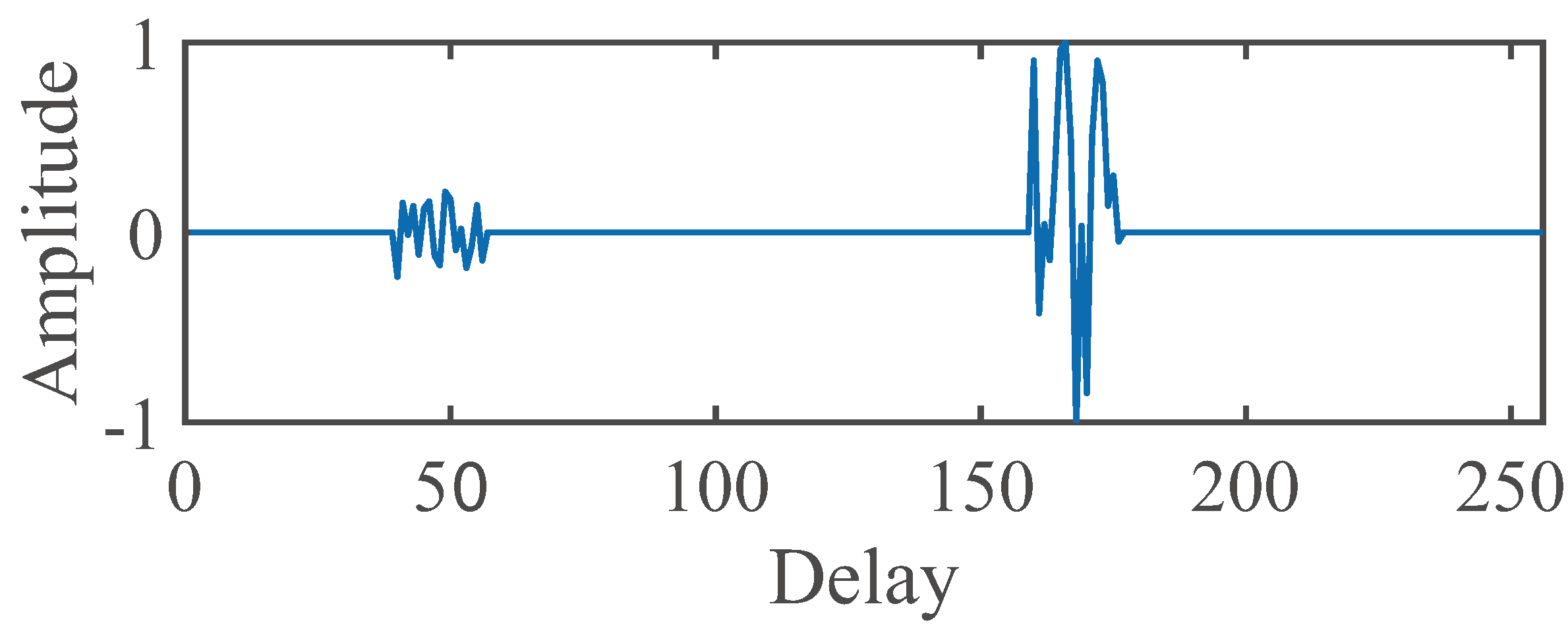
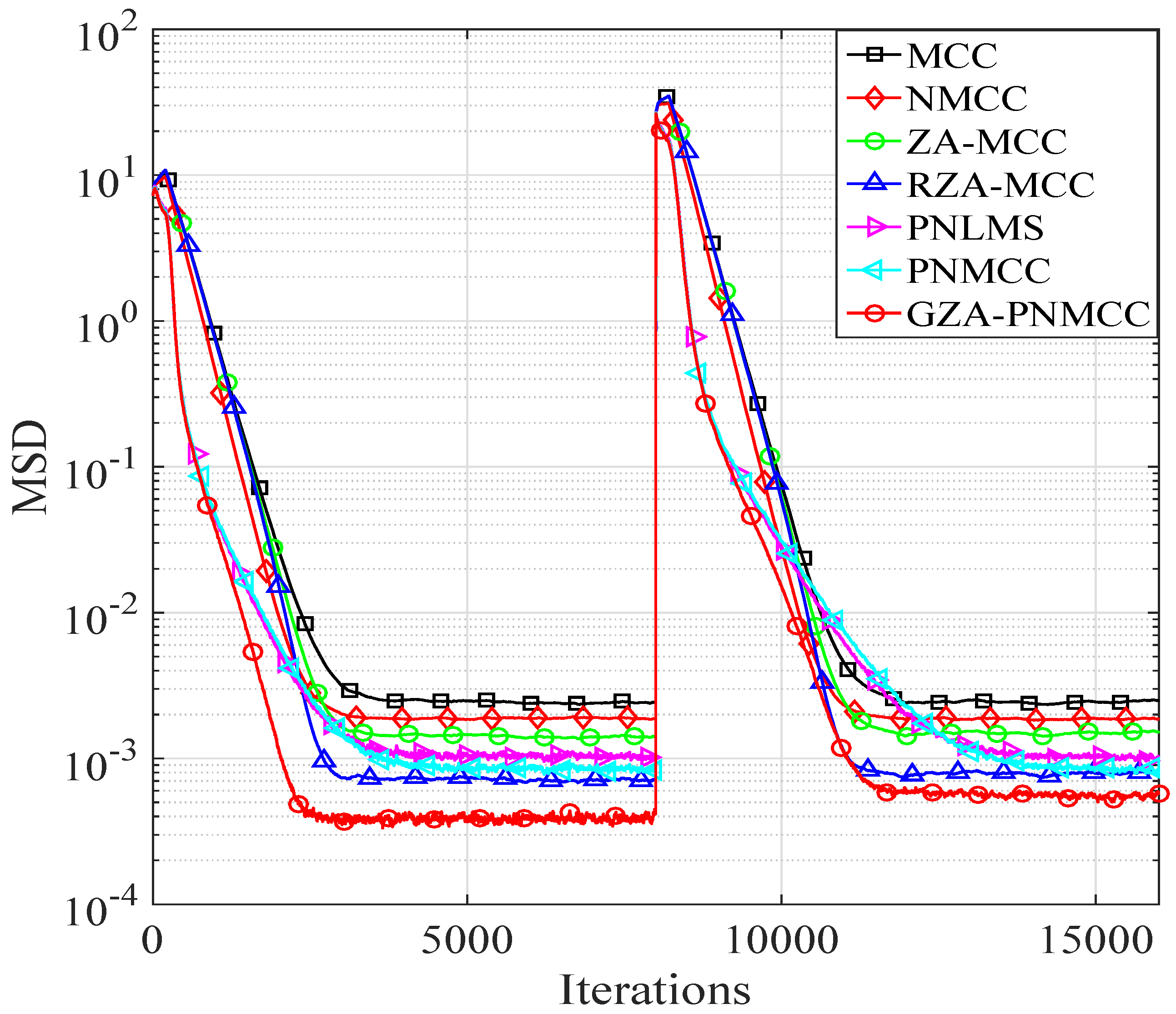
4. Behavior of the Proposed GZA-PNMCC Algorithm
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Khong, A.W.H.; Naylor, P.A. Efficient use of sparse adaptive filters. In Proceedings of the Fortieth Asilomar Conference on Signals, Systems and Computers (ACSSC ’06), Pacific Grove, CA, USA, 29 October–1 November 2006; pp. 1375–1379. [Google Scholar]
- Paleologu, C.; Benesty, J.; Ciochina, S. Sparse Adaptive Filters for Echo Cancellation; Morgan & Claypool: San Rafael, CA, USA, 2010. [Google Scholar]
- Rodger, J.A. Toward reducing failure risk in an integrated vehicle health maintenance system: A fuzzy multi-sensor data fusion Kalman filter approach for IVHMS. Expert Syst. Appl. 2012, 139, 9821–9836. [Google Scholar] [CrossRef]
- Murakami, Y.; Yamagishi, M.; Yukawa, M.; Yamada, I. A sparse adaptive filtering using time-varying soft-thresholding techniques. In Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010; pp. 3734–3737. [Google Scholar]
- Li, Y.; Hamamura, M. Zero-attracting variable-step-size least mean square algorithms for adaptive sparse channel estimation. Int. J. Adapt. Control Signal Process. 2015, 29, 1189–1206. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, Y.; Hero, A.O., III. Sparse LMS for system identification. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ’09), Taipei, Taiwan, 19–24 April 2009; pp. 3125–3128. [Google Scholar]
- Wang, Y.; Li, Y.; Yang, R. Sparse adaptive channel estimation based on mixed controlled l2 and lp-norm error criterion. J. Frankl. Inst. 2017, 354, 7215–7239. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Sparse least mean mixed-norm adaptive filtering algorithms for sparse channel estimation applications. Int. J. Commun. Syst. 2017, 30, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y. Sparse multi-path channel estimation using norm combination constrained set-membership NLMS algorithms. Wirel. Commun. Mob. Comput. 2017, 2017, 8140702. [Google Scholar] [CrossRef]
- Li, Y.; Jin, Z.; Wang, Y. Adaptive channel estimation based on an improved norm constrained set-membership normalized least mean square algorithm. Wirel. Commun. Mob. Comput. 2017, 2017, 8056126. [Google Scholar]
- Duttweiler, D.L. Proportionate normalized least-mean-squares adaptation in echo cancelers. IEEE Trans. Speech Audio Process. 2000, 8, 508–518. [Google Scholar] [CrossRef]
- Naylor, P.A.; Cui, J.; Brookes, M. Adaptive algorithms for sparse echo cancellation. Signal Process. 2009, 86, 1182–1192. [Google Scholar] [CrossRef]
- Cotter, S.F.; Rao, B.D. Sparse channel estimation via matching pursuit with application to equalization. IEEE Trans. Commun. 2002, 50, 374–377. [Google Scholar] [CrossRef]
- Gui, G.; Peng, W.; Adachi, F. Improved adaptive sparse channel estimation based on the least mean square algorithm. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 3105–3109. [Google Scholar]
- Arenas, J.; Figueiras-Vidal, A.R. Adaptive combination of proportionate filters for sparse echo cancellation. IEEE Trans. Audio Speech Lang. Process. 2009, 17, 1087–1098. [Google Scholar] [CrossRef]
- Nekuii, M.; Atarodi, M. A fast converging algorithm for network echo cancellation. IEEE Signal Process. Lett. 2004, 11, 427–430. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Norm-adaption penalized least mean square/fourth algorithm for sparse channel estimation. Signal Process. 2016, 128, 243–251. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Wang, S. Low-complexity non-uniform penalized affine projection algorithm for sparse system identification. Circuits Syst. Signal Process. 2016, 35, 1611–1624. [Google Scholar] [CrossRef]
- Stojanovic, M.; Freitag, L.; Johnson, M. Channel-estimation-based adaptive equalization of underwater acoustic signals. In Proceedings of the OCEANS ’99 MTS/IEEE, Riding the Crest into the 21st Century, Seattle, WA, USA, 13–16 September 1999; pp. 985–990. [Google Scholar]
- Pelekanakis, K.; Chitre, M. Comparison of sparse adaptive filters for underwater acoustic channel equalization/estimation. In Proceedings of the 2010 IEEE International Conference on Communication Systems (ICCS), Singapore, 17–19 November 2010; pp. 395–399. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Sparse-aware set-membership NLMS algorithms and their application for sparse channel estimation and echo cancelation. AEU Int. J. Electron. Commun. 2016, 70, 895–902. [Google Scholar] [CrossRef]
- Gui, G.; Mehbodniya, A.; Adachi, F. Least mean square/fourth algorithm for adaptive sparse channel estimation. In Proceedings of the 2013 IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 296–300. [Google Scholar]
- Vuokko, L.; Kolmonen, V.M.; Salo, J.; Vainikainen, P. Measurement of large-scale cluster power characteristics for geometric channel models. IEEE Trans. Antennas Propagat. 2007, 55, 3361–3365. [Google Scholar] [CrossRef]
- Radecki, J.; Zilic, Z.; Radecka, K. Echo cancellation in IP networks. In Proceedings of the 45th Midwest Symposium on Circuits and Systems, Tulsa, OK, USA, 4–7 August 2002; pp. 219–222. [Google Scholar]
- Cui, J.; Naylor, P.A.; Brown, D.T. An improved IPNLMS algorithm for echo cancellation in packet-switched networks. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ’04), Montreal, QC, Canada, 17–21 May 2004. [Google Scholar]
- Widrow, B.; Stearns, S.D. Adaptive Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1985. [Google Scholar]
- Wang, Y.; Li, Y. Norm penalized joint-optimization NLMS algorithms for broadband sparse adaptive channel estimation. Symmetry 2017, 9, 133. [Google Scholar] [CrossRef]
- Haykin, S. Adaptive Filter Theory; Prentice Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Li, Y.; Hamamura, M. An improved proportionate normalized least-mean-square algorithm for broadband multipath channel estimation. Sci. World J. 2014, 2014, 572969. [Google Scholar] [CrossRef] [PubMed]
- Benesty, J.; Gay, S.L. An improved PNLMS algorithm. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Orlando, FL, USA, 13–17 May 2002; Volume II, pp. 1881–1884. [Google Scholar]
- Gay, S.L. An efficient, fast converging adaptive filter for network echo cancellation. In Proceedings of the 32nd Asilomar Conference on Signals and System for Computing, Pacific Grove, CA, USA, 1–4 November 1998; Volume 1, pp. 394–398. [Google Scholar]
- Liu, W.F.; Pokharel, P.P.; Principe, J.C. Correntropy: Properties and applications in non-Gaussian signal processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y. Sparse SM-NLMS algorithm based on correntropy criterion. Electron. Lett. 2016, 52, 1461–1463. [Google Scholar] [CrossRef]
- Chen, B.; Principe, J.C. Maximum correntropy estimation is a smoothed MAP estimation. IEEE Signal Process. Lett. 2012, 19, 491–494. [Google Scholar] [CrossRef]
- Chen, B.; Xing, L.; Liang, J.; Zheng, N.; Principe, J.C. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 2014, 21, 880–884. [Google Scholar]
- Zhao, S.; Chen, B.; Principe, J.C. Kernel adaptive filtering with maximum correntropy criterion. In Proceedings of the 2011 International Joint Conference on Neural Networks (IJCNN), San Jose, CA, USA, 31 July–5 August 2011; pp. 2012–2017. [Google Scholar]
- Chen, B.; Xing, L.; Zhao, H.; Zheng, N.; Principe, J.C. Generalized correntropy for robust adaptive filtering. IEEE Trans. Signal Process. 2016, 64, 3376–3387. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Zhao, H.; Zheng, N.; Principe, J.C. Convergence of a fixed-point algorithm under maximum correntropy criterion. IEEE Signal Process. Lett. 2015, 22, 1723–1727. [Google Scholar] [CrossRef]
- Singh, A.; Principe, J.C. Using correntropy as a cost function in linear adaptive filters. In Proceedings of the International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 2950–2955. [Google Scholar]
- Hadded, D.B.; Petraglia, M.R.; Petraglia, A. A unified approach for sparsity-aware and maximum correntropy adaptive filters. In Proceedings of the 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; pp. 170–174. [Google Scholar]
- Ma, W.; Qu, H.; Gui, G.; Xu, L.; Zhao, J.; Chen, B. Maximum correntropy criterion based sparse adaptive filtering algorithms for robust channel estimation under non-Gaussian environments. J. Frankl. Inst. 2015, 352, 2708–2727. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Albu, F.; Yang, R. Group-constrained maximum correntropy criterion algorithms for estimating sparse mix-noised channels. Entropy 2017, 19, 432. [Google Scholar] [CrossRef]
- Wu, Z.; Peng, S.; Chen, B.; Zhao, H.; Principe, J.C. Proportionate minimum error entropy algorithm for sparse system identification. Entropy 2015, 17, 5995–6006. [Google Scholar] [CrossRef]
- Salman, M.S. Sparse leaky-LMS algorithm for system identification and its convergence analysis. Int. J. Adapt. Control Signal Process. 2014, 28, 1065–1072. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Yang, R.; Albu, F. A soft parameter function penalized normalized maximum correntropy criterion algorithm for sparse system identification. Entropy 2017, 19, 45. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Yang, R. A sparsity-aware proportionate normalized maximum correntropy criterion algorithm for sparse system identification in non-gaussian environment. In Proceedings of the 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; pp. 246–250. [Google Scholar]
- Hoyer, P.O. Non-negative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2001, 49, 1208–1215. [Google Scholar]
- Huang, Y.; Benesty, J.; Chen, J. Acoustic MIMO Signal Processing; Springer: Berlin, Germany, 2006. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Wang, Y.; Albu, F.; Jiang, J. A General Zero Attraction Proportionate Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification. Symmetry 2017, 9, 229. https://doi.org/10.3390/sym9100229
Li Y, Wang Y, Albu F, Jiang J. A General Zero Attraction Proportionate Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification. Symmetry. 2017; 9(10):229. https://doi.org/10.3390/sym9100229
Chicago/Turabian StyleLi, Yingsong, Yanyan Wang, Felix Albu, and Jingshan Jiang. 2017. "A General Zero Attraction Proportionate Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification" Symmetry 9, no. 10: 229. https://doi.org/10.3390/sym9100229
APA StyleLi, Y., Wang, Y., Albu, F., & Jiang, J. (2017). A General Zero Attraction Proportionate Normalized Maximum Correntropy Criterion Algorithm for Sparse System Identification. Symmetry, 9(10), 229. https://doi.org/10.3390/sym9100229





