Some Invariants of Jahangir Graphs
Abstract
:1. Introduction
2. Main Results
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
3. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rücker, G.; Rücker, C. On topological indices, boiling points, and cycloalkanes. J. Chem. Inf. Comput. Sci. 1999, 39, 788–802. [Google Scholar] [CrossRef]
- Klavzar, S.; Gutman, I. A comparison of the Schultz molecular topological index with the Wiener index. J. Chem. Inf. Comput. Sci. 1996, 36, 1001–1003. [Google Scholar] [CrossRef]
- Brückler, F.M.; Došlić, T.; Graovac, A.; Gutman, I. On a class of distance-based molecular structure descriptors. Chem. Phys. Lett. 2011, 503, 336–338. [Google Scholar] [CrossRef]
- Deng, H.; Yang, J.; Xia, F. A general modeling of some vertex-degree based topological indices in benzenoid systems and phenylenes. Comput. Math. Appl. 2011, 61, 3017–3023. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F. The Clar covering polynomial of hexagonal systems I. Discret. Appl. Math. 1996, 69, 147–167. [Google Scholar] [CrossRef]
- Gutman, I. Some properties of the Wiener polynomials. Graph Theory Notes N. Y. 1993, 125, 13–18. [Google Scholar]
- Deutsch, E.; Klavzar, S. M-Polynomial, and degree-based topological indices. Iran. J. Math. Chem. 2015, 6, 93–102. [Google Scholar]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-polynomial and related topological indices of Nanostar dendrimers. Symmetry 2016, 8, 97. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-Polynomial and Degree-Based Topological Indices of Polyhex Nanotubes. Symmetry 2016, 8, 149. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Nizami, A.R.; Kang, S.M. Some Computational Aspects of Triangular Boron Nanotubes. Symmetry 2016, 9, 6. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Shahzadi, Z.; Kang, S.M. Some invariants of circulant graphs. Symmetry 2016, 8, 134. [Google Scholar] [CrossRef]
- Lourdusamy, A.; Jayaseelan, S.S.; Mathivanan, T. On pebbling Jahangir graph. Gen. Math. Notes 2011, 5, 42–49. [Google Scholar]
- Mojdeh, M.A.; Ghameshlou, A.N. Domination in Jahangir Graph J2,m. Int. J. Contemp. Math. Sci. 2007, 2, 1193–1199. [Google Scholar] [CrossRef]
- Ali, K.; Baskoro, E.T.; Tomescu, I. On the Ramsey number of Paths and Jahangir, graph J3,m. In Proceedings of the 3rd International Conference on 21st Century Mathematics, Lahore, Pakistan, 4–7 March 2007.
- Farahani, M.R. Hosoya Polynomial and Wiener Index of Jahangir graphs J2,m. Pac. J. Appl. Math. 2015, 7, 221–224. [Google Scholar]
- Farahani, M.R. The Wiener Index and Hosoya polynomial of a class of Jahangir graphs J3,m. Fundam. J. Math. Math. Sci. 2015, 3, 91–96. [Google Scholar]
- Wang, S.; Farahani, M.R.; Kanna, M.R.; Jamil, M.K.; Kumar, R.P. The Wiener Index and the Hosoya Polynomial of the Jahangir Graphs. Appl. Comput. Math. 2016, 5, 138–141. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Dobrynin, A.A.; Entringer, R.; Gutman, I. Wiener index of trees: Theory and applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Gutman, I.; Polansky, O.E. Mathematical Concepts in Organic Chemistry; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Randic, M. Characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Bollobás, B.; Erdős, P. Graphs of extremal weights. Ars Comb. 1998, 50, 225–233. [Google Scholar] [CrossRef]
- Amic, D.; Bešlo, D.; Lucic, B.; Nikolic, S.; Trinajstic, N. The vertex-connectivity index revisited. J. Chem. Inf. Comput. Sci. 1998, 38, 819–822. [Google Scholar] [CrossRef]
- Hu, Y.; Li, X.; Shi, Y.; Xu, T.; Gutman, I. On molecular graphs with smallest and greatest zeroth-order general Randic index. MATCH Commun. Math. Comput. Chem. 2005, 54, 425–434. [Google Scholar]
- Caporossi, G.; Gutman, I.; Hansen, P.; Pavlović, L. Graphs with maximum connectivity index. Comput. Biol. Chem. 2003, 27, 85–90. [Google Scholar] [CrossRef]
- Li, X.; Gutman, I. Mathematical Aspects of Randic-Type Molecular Descriptors; University of Kragujevac and Faculty of Science Kragujevac: Kragujevac, Serbia, 2006. [Google Scholar]
- Kier, L.B.; Hall, L.H. Molecular Connectivity in Chemistry and Drug Research; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Kier, L.B.; Hall, L.H. Molecular Connectivity in Structure-Activity Analysis; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Randić, M. On history of the Randić index and emerging hostility toward chemical graph theory. MATCH Commun. Math. Comput. Chem. 2008, 59, 5–124. [Google Scholar]
- Randić, M. The connectivity index 25 years after. J. Mol. Graph. Model. 2001, 20, 19–35. [Google Scholar] [CrossRef]
- Nikolić, S.; Kovačević, G.; Miličević, A.; Trinajstić, N. The Zagreb indices 30 years after. Croat. Chem. Acta 2003, 76, 113–124. [Google Scholar]
- Gutman, I.; Das, K.C. The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem. 2004, 50, 83–92. [Google Scholar]
- Das, K.C.; Gutman, I. Some properties of the second Zagreb index. MATCH Commun. Math. Comput. Chem. 2004, 52, 103–112. [Google Scholar]
- Trinajstic, N.; Nikolic, S.; Milicevic, A.; Gutman, I. On Zagreb indices. Kem. Ind. 2010, 59, 577–589. [Google Scholar]
- Huang, Y.; Liu, B.; Gan, L. Augmented Zagreb Index of Connected Graphs. MATCH Commun. Math. Comput. Chem. 2012, 67, 483–494. [Google Scholar]
- Furtula, B.; Graovac, A.; Vukičević, D. Augmented Zagreb index. J. Math. Chem. 2010, 48, 370–380. [Google Scholar] [CrossRef]
- Shirdel, G.H.; Pour, H.R.; Sayadi, A.M. The hyper-Zagreb index of graph operations. Iran. J. Math. Chem. 2013, 4, 213–220. [Google Scholar]
- Ghorbani, M.; Azimi, N. Note on multiple Zagreb indices. Iran. J. Math. Chem. 2012, 3, 137–143. [Google Scholar]

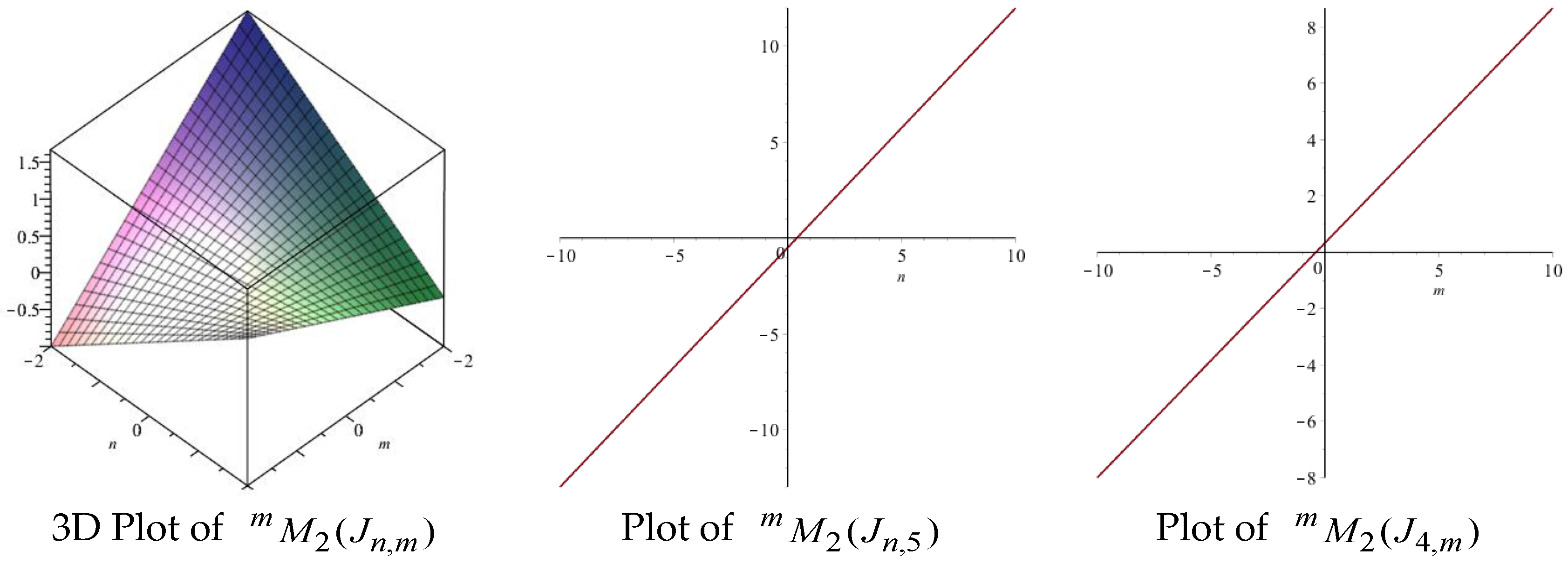
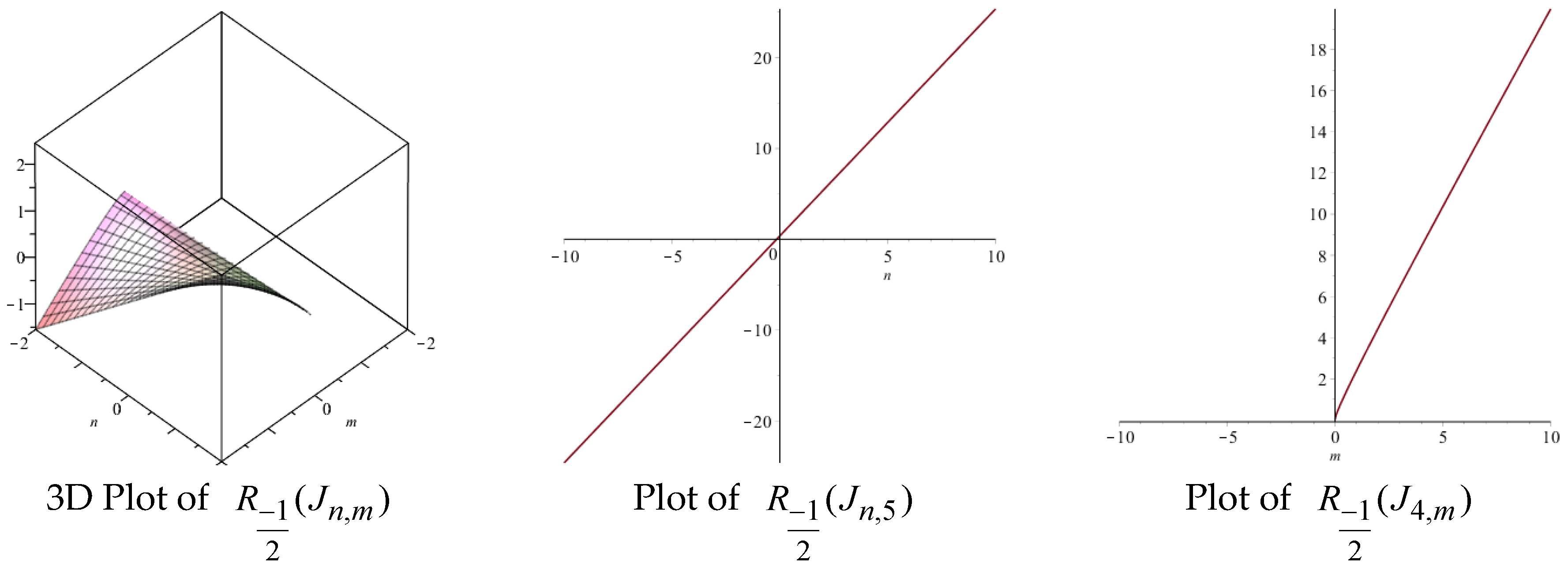
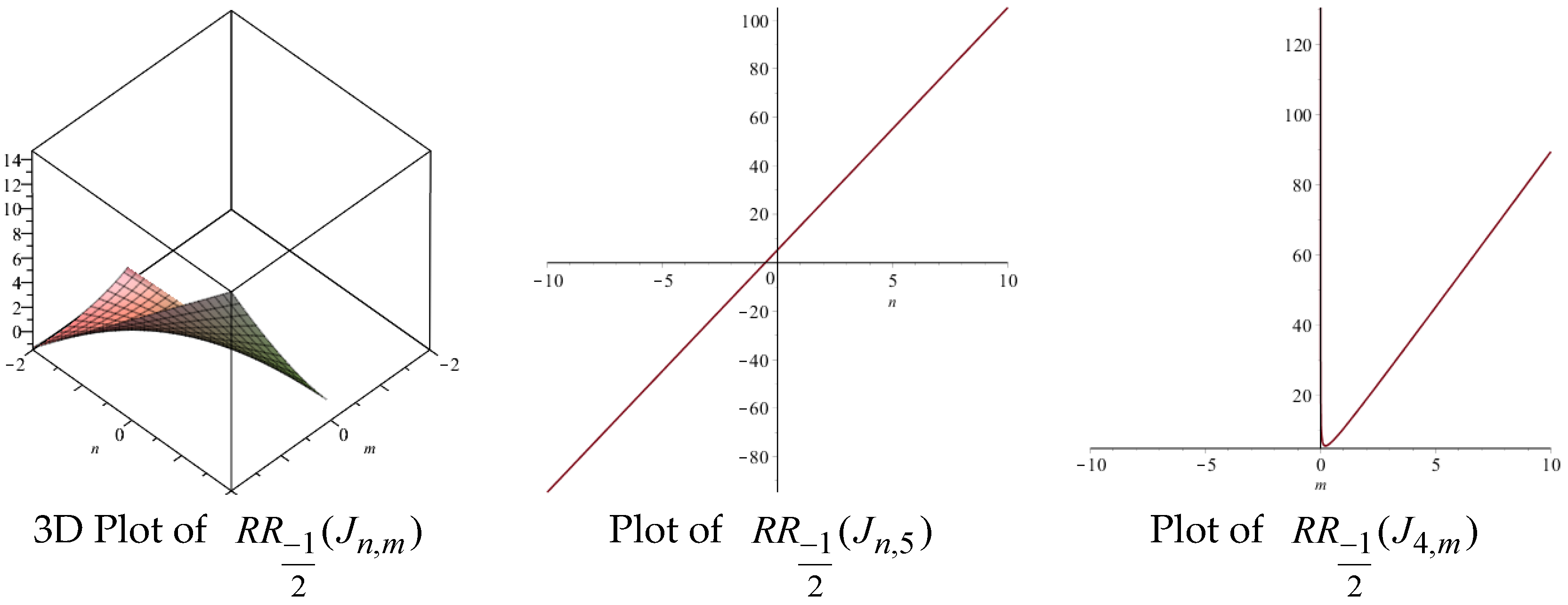
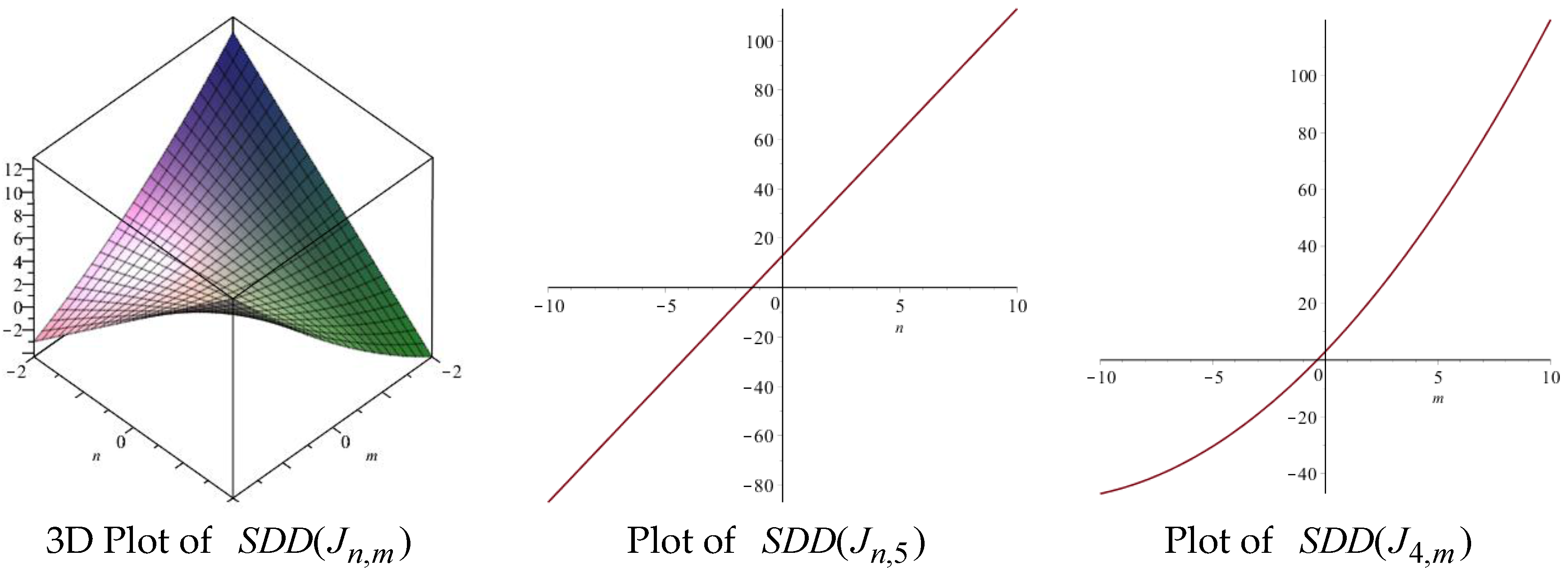

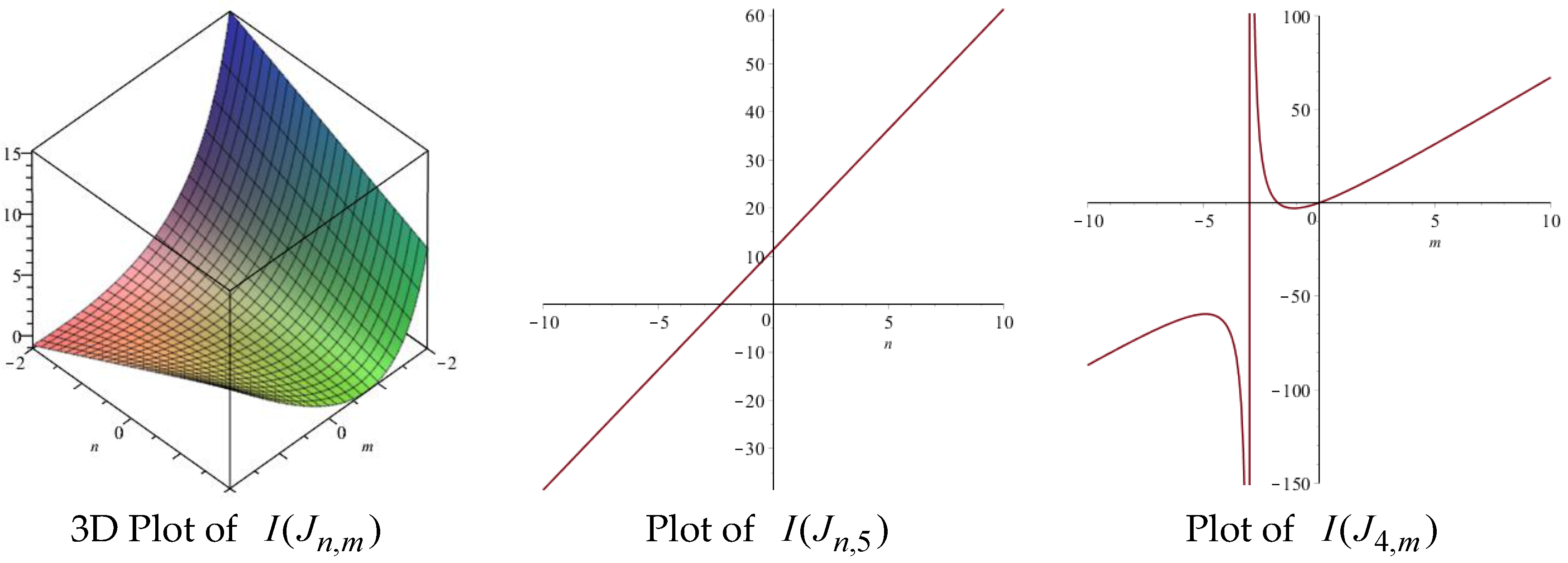
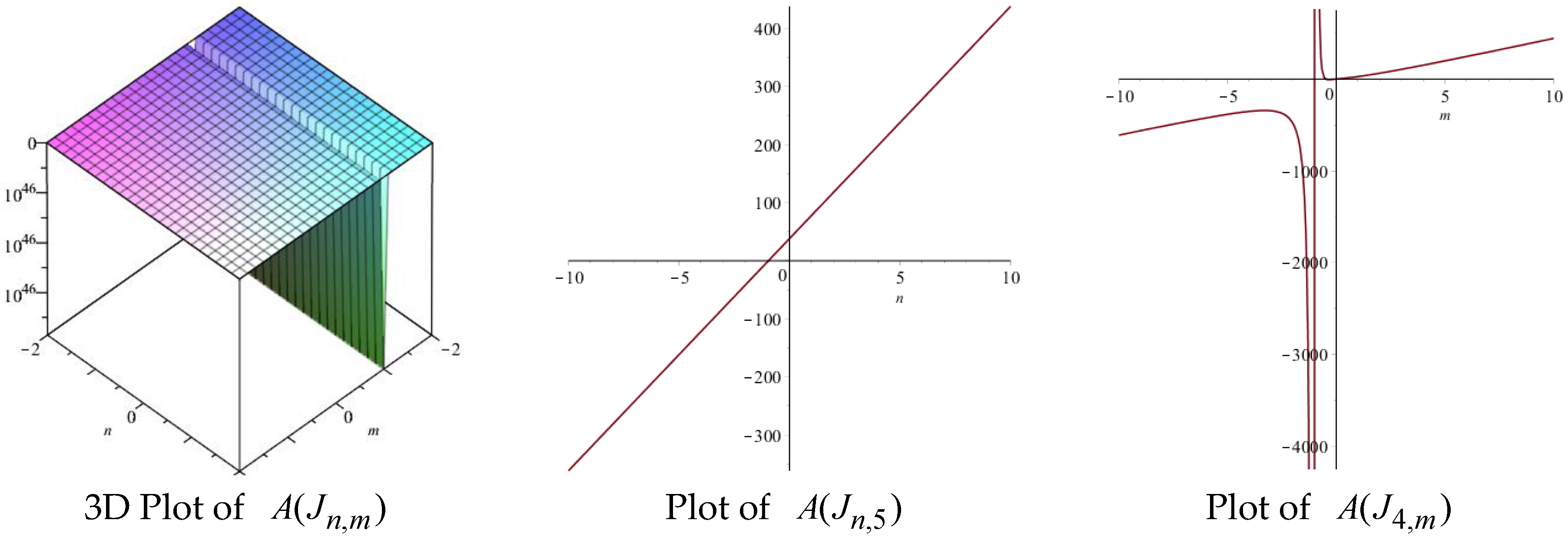
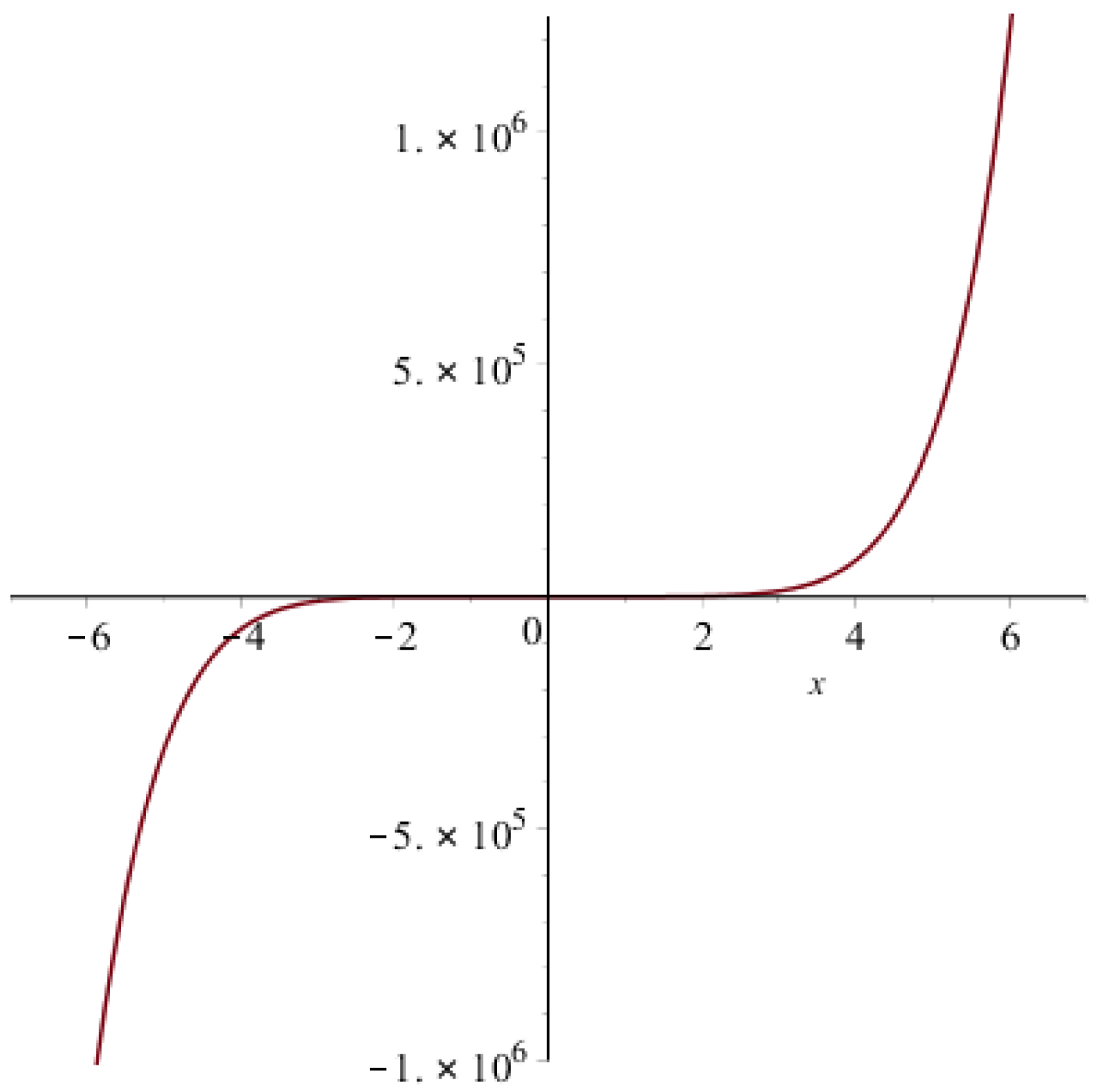
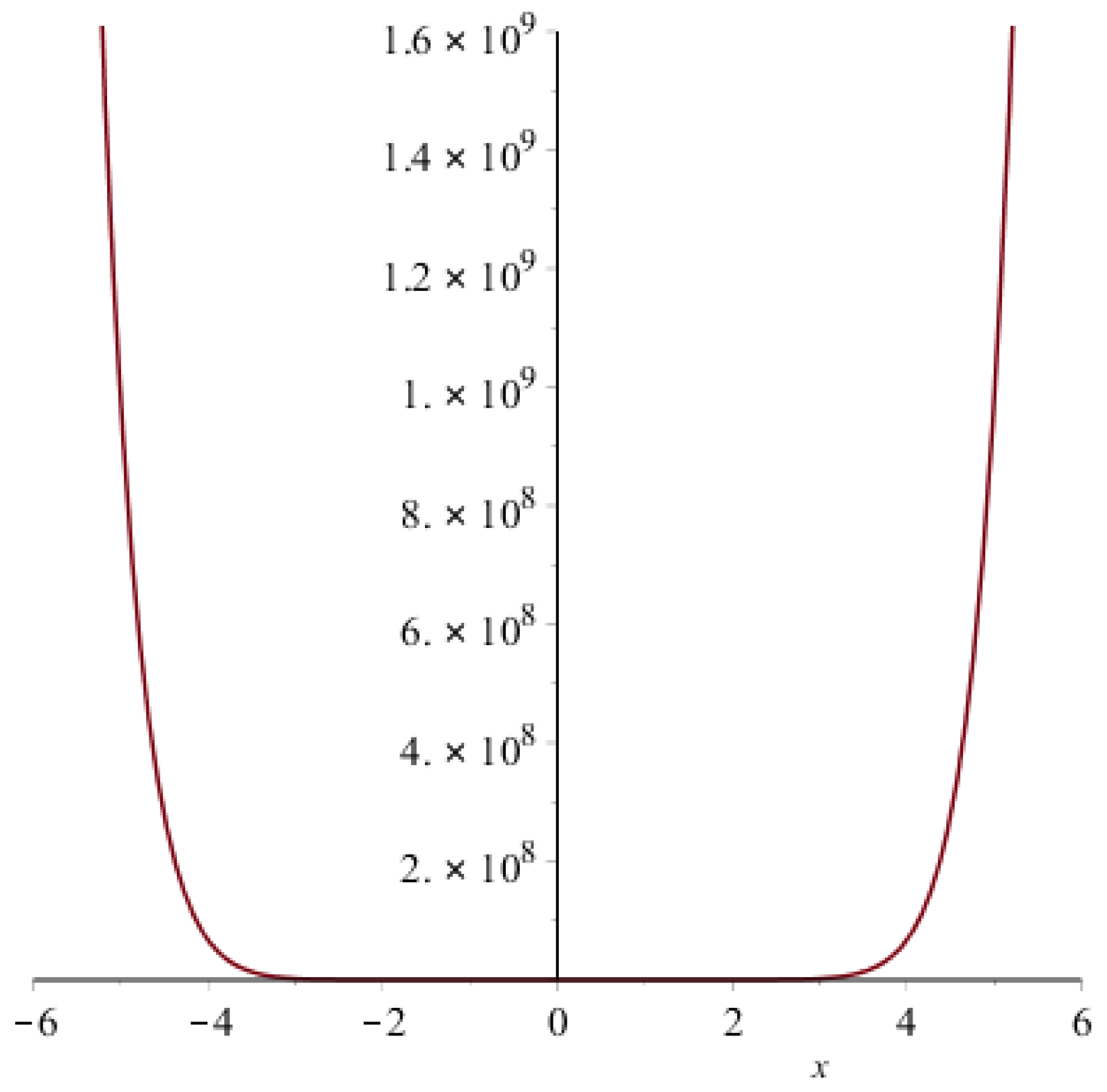

| Topological Index | Derivation from |
|---|---|
| First Zagreb | |
| Second Zagreb | |
| Second Modified Zagreb | |
| Inverse Randic | |
| General Randic | |
| Symmetric Division Index | |
| Harmonic Index | |
| Inverse sum Index | |
| Augmented Zagreb Index |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munir, M.; Nazeer, W.; Kang, S.M.; Qureshi, M.I.; Nizami, A.R.; Kwun, Y.C. Some Invariants of Jahangir Graphs. Symmetry 2017, 9, 17. https://doi.org/10.3390/sym9010017
Munir M, Nazeer W, Kang SM, Qureshi MI, Nizami AR, Kwun YC. Some Invariants of Jahangir Graphs. Symmetry. 2017; 9(1):17. https://doi.org/10.3390/sym9010017
Chicago/Turabian StyleMunir, Mobeen, Waqas Nazeer, Shin Min Kang, Muhammad Imran Qureshi, Abdul Rauf Nizami, and Youl Chel Kwun. 2017. "Some Invariants of Jahangir Graphs" Symmetry 9, no. 1: 17. https://doi.org/10.3390/sym9010017
APA StyleMunir, M., Nazeer, W., Kang, S. M., Qureshi, M. I., Nizami, A. R., & Kwun, Y. C. (2017). Some Invariants of Jahangir Graphs. Symmetry, 9(1), 17. https://doi.org/10.3390/sym9010017