A (1 + 2)-Dimensional Simplified Keller–Segel Model: Lie Symmetry and Exact Solutions. II
Abstract
:1. Introduction
2. Lie Symmetry of the Cauchy Problem
3. Application of Lie Symmetry for Constructing Exact Solutions of Cauchy Problems
3.1. Exact Solutions of the (1 + 1)-Dimensional Cauchy Problem
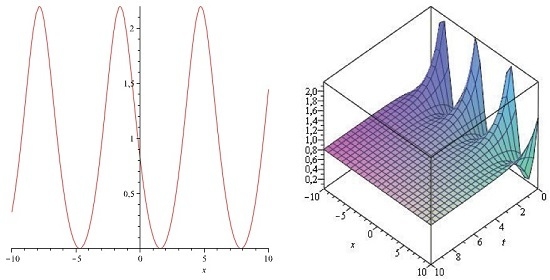
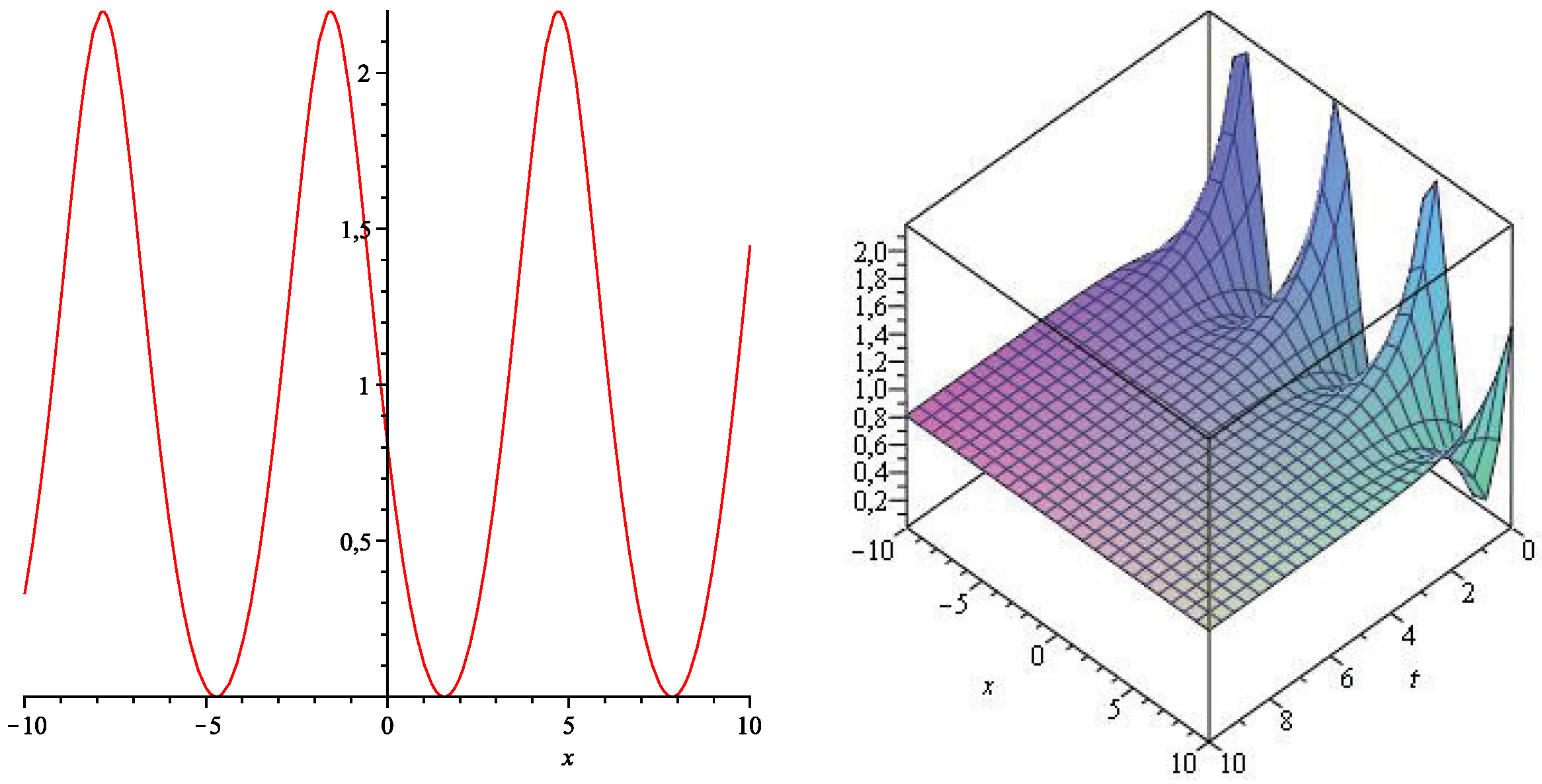
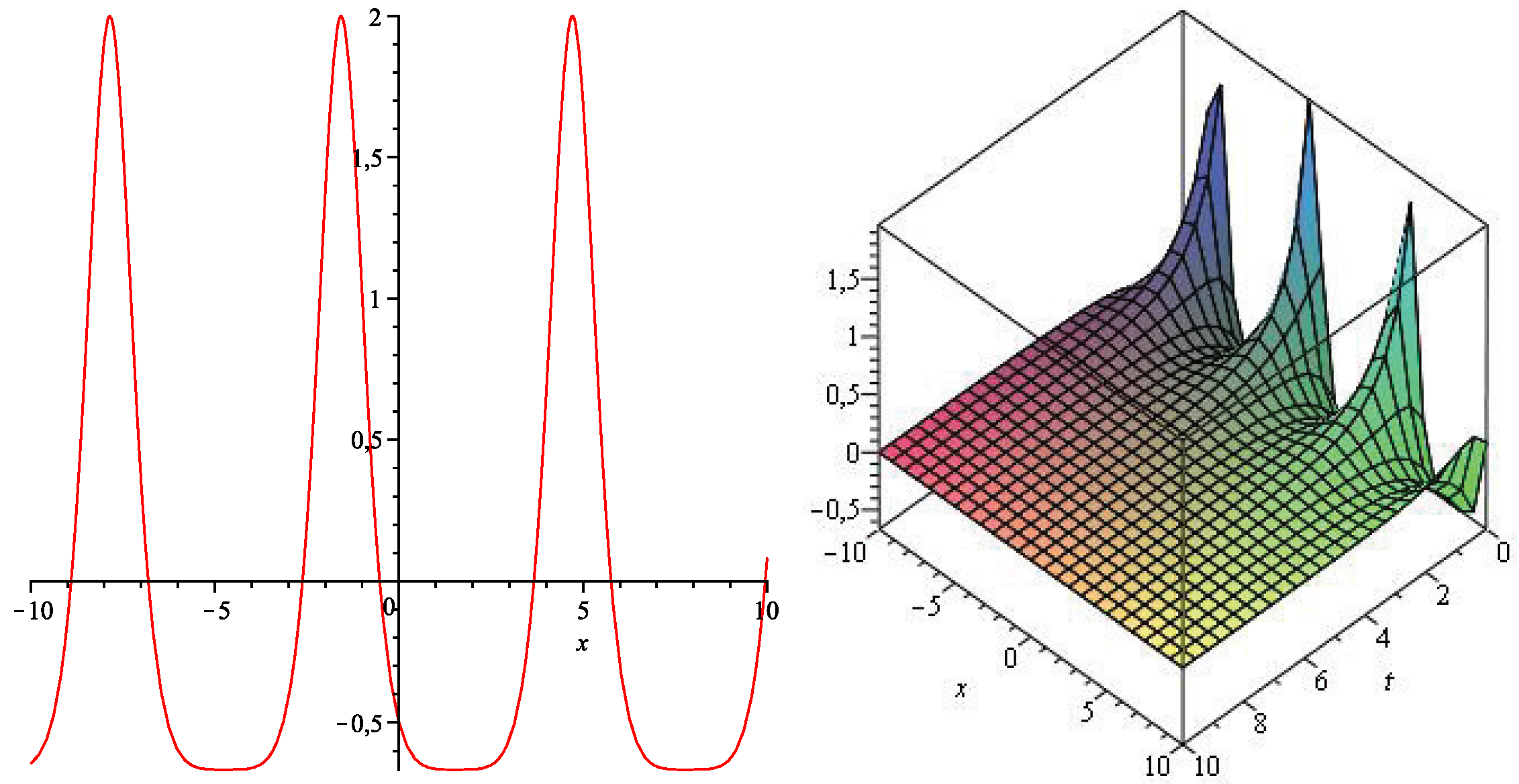
3.2. Reduction and Exact Solutions of (1 + 2)-Dimensional Cauchy Problem
4. Lie Symmetry of the Neumann Problems
4.1. Neumann Problem on the Strip
4.2. Neumann Problem on Interior/Exterior of a Circle
5. Exact Solutions of the Neumann Problem
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lie, S. Uber integration durch bestimmte integrale von einer Klasse lineare partiellen differentialgleichungen. Arch. Math. 1881, 8, 328–368. [Google Scholar]
- Engel, F.; Heegaard, P. Gesammelte Abhandlungen, Band 3; Benedictus Gotthelf Teubner: Leipzig, Germany, 1922. [Google Scholar]
- Bluman, G.W.; Anco, S.C. Symmetry and Integration Methods for Differential Equations; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: Berlin, Germany, 1989. [Google Scholar]
- Fushchych, W.I.; Shtelen, W.M.; Serov, M.I. Symmetry Analysis and Exact Solutions of Equations of Nonlinear Mathematical Physics; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Ovsiannikov, L.V. The Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Cherniha, R.; Kovalenko, S. Lie symmetries and reductions of multi-dimensional boundary value problems of the Stefan type. J. Phys. A Math. Theor. 2011, 44. [Google Scholar] [CrossRef]
- Cherniha, R.; Kovalenko, S. Lie symmetries of nonlinear boundary value problems. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 71–84. [Google Scholar] [CrossRef]
- Cherniha, R.; King, J.R. Lie and conditional symmetries of a class of nonlinear (1 + 2)-dimensional boundary value problems. Symmetry 2015, 7, 1410–1435. [Google Scholar] [CrossRef]
- Abd-el Malek, M.B.; Amin, A.M. Lie group method for solving the generalized Burgers’, Burgers’-KdV and KdV equations with time-dependent variable coefficients. Symmetry 2015, 7, 1816–1830. [Google Scholar] [CrossRef]
- Didovych, M. A (1 + 2)-dimensional simplified Keller–Segel model: Lie symmetry and exact solutions. Symmetry 2015, 7, 1463–1474. [Google Scholar] [CrossRef]
- Keller, E.K.; Segel, L.A. Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 1970, 26, 399–415. [Google Scholar] [CrossRef]
- Keller, E.K.; Segel, L.A. Traveling bands of chemotactic bacteria: A theoretical analysis. J. Theor. Biol. 1971, 30, 235–248. [Google Scholar] [CrossRef]
- Horstmann, D. From 1970 until present: The Keller–Segel model in chemotaxis and its consequences. Jahresber. Deutsch. Math.-Verein 2013, 105, 103–165. [Google Scholar]
- Calvez, V.; Dolak-Strub, Y. Asymptotic behavior of a two-dimensional Keller–Segel model with and without density control. Math. Model. Biol. Syst. 2007, 2, 323–329. [Google Scholar]
- Nagai, T. Convergence to self-similar solutions for a parabolic-elliptic system of drift-diffusion type in R2. Adv. Differ. Equ. 2011, 9, 839–866. [Google Scholar]
- Nagai, T. Global existence and decay estimates of solutions to a parabolic-elliptic system of drift-diffusion type in R2. Differ. Integral Equ. 2011, 1, 29–68. [Google Scholar]
- Hopf, E. The partial differential equation Ut + UUx = μUxx. Comm. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Burgers, J.M. The Nonlinear Diffusion Equation; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1973. [Google Scholar]
- Bateman, H.; Erdelyi, A. Tables of Integral Transforms; McGraw-Hill Book Company: New York, NY, USA, 1954. [Google Scholar]
- Cherniha, R. New non-Lie ansatze and exact solutions of nonlinear reaction-diffusion-convection equations. J. Phys. A Math. 1998, 31, 8179–8198. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Galaktionov, V.A.; Kurdyumov, S.P.; Mikhailov, A.P. Blow-up in quasilinear parabolic equations. In de Gruyter Expositions in Mathematics; Walter de Gruyter & Co.: Berlin, Germany, 1995; Volume 19. [Google Scholar]
- Bluman, G.W. Application of the general similarity solution of the heat equation to boundary value problems. Q. Appl. Math. 1974, 31, 403–415. [Google Scholar] [CrossRef]
| MAI | ||
|---|---|---|
| 1 | ∀ | with |
| with | ||
| with | ||
| 2 | 0 | with |
| with | ||
| with | ||
| 3 | with | |
| with | ||
| with | ||
| 4 | with | |
| with | ||
| with |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cherniha, R.; Didovych, M. A (1 + 2)-Dimensional Simplified Keller–Segel Model: Lie Symmetry and Exact Solutions. II. Symmetry 2017, 9, 13. https://doi.org/10.3390/sym9010013
Cherniha R, Didovych M. A (1 + 2)-Dimensional Simplified Keller–Segel Model: Lie Symmetry and Exact Solutions. II. Symmetry. 2017; 9(1):13. https://doi.org/10.3390/sym9010013
Chicago/Turabian StyleCherniha, Roman, and Maksym Didovych. 2017. "A (1 + 2)-Dimensional Simplified Keller–Segel Model: Lie Symmetry and Exact Solutions. II" Symmetry 9, no. 1: 13. https://doi.org/10.3390/sym9010013
APA StyleCherniha, R., & Didovych, M. (2017). A (1 + 2)-Dimensional Simplified Keller–Segel Model: Lie Symmetry and Exact Solutions. II. Symmetry, 9(1), 13. https://doi.org/10.3390/sym9010013