Lorentz Transformations from Intrinsic Symmetries
Abstract
:1. Introduction
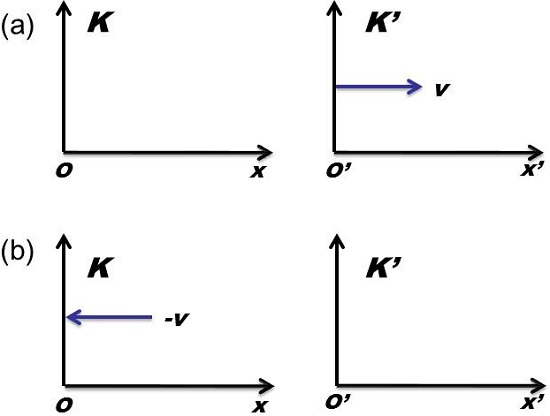
2. Derivation of the Lorentz Transformation
3. Discussion
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Einstein, A. Zur elecktrodynamik bewegter korper. Ann. Phys. (Leipzig) 1905, 17, 891–921. (In German) [Google Scholar] [CrossRef]
- Von Ignatowsky, W.A. Einige allgemeine bemerkungen zum relativitatsprinzip. Verh. Deutch. Phys. Ges. 1910, 12, 788–796. (In German) [Google Scholar]
- Frank, P.; Rothe, H. Uber die transformation der raumzeitkoordinaten von ruhenden auf bewegte systeme. Ann. Phys. (Leipzig) 1911, 34, 825–855. (In German) [Google Scholar] [CrossRef]
- Pauli, W. Theory of Relativity; Pergamon: London, UK, 1958. [Google Scholar]
- Arzelies, H. Relativistic Kinematics; Pergmon: New York, NY, USA, 1966. [Google Scholar]
- Lee, A.R.; Kalotas, T.M. Lorentz transformations from the first postulate. Am. J. Phys. 1975, 43, 434–437. [Google Scholar] [CrossRef]
- Lėvy-Leblond, J.-M. One more derivation of the Lorentz transformation. Am. J. Phys. 1976, 44, 271–277. [Google Scholar] [CrossRef]
- Poincaré, H. On the Dynamics of the Electron. Comptes Rendus 1905, 140, 1504–1508. (In French) [Google Scholar]
- Berzi, V.; Gorini, V. Reciprocity principle and the Lorentz transformations. J. Math. Phys. 1969, 10, 1518–1524. [Google Scholar] [CrossRef]
- Bacry, H.; Lėvy-Leblond, J.-M.J. Possible kinematics. Math. Phys. 1968, 9, 1605–1614. [Google Scholar] [CrossRef]
- Eisenberg, L.J. Necessity of the linearity of relativistic transformations between inertial systems. Am. J. Phys. 1967, 35. [Google Scholar] [CrossRef]
- Baird, L.C. Linearity of the Lorentz transformation. Am. J. Phys. 1976, 44, 167–171. [Google Scholar] [CrossRef]
- Einstein, A. The Principle of Relativity; Methuen: London, UK, 1923. [Google Scholar]
- Einstein, A. The Meaning of Relativity; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Liberati, S. Tests of Lorentz invariance: A 2013 update. Class. Quantum Gravity 2013, 30. [Google Scholar] [CrossRef]
- Mattingly, D. Modern tests of Lorentz invariance. Living Rev. Relativ. 2005, 8. [Google Scholar] [CrossRef]
- Kostelecky, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef]
- Cohen, A.G.; Glashow, S.L. Very special relativity. Phys. Rev. Lett. 2006, 97, 021601. [Google Scholar] [CrossRef] [PubMed]
- Gibbons, G.W.; Gomis, J.; Pope, C.N. Generla Very special relativity is Finsler geometry. Phys. Rev. D 2007, 76, 081701. [Google Scholar] [CrossRef]
- Bogoslovsky, G.Y. Lorentz symmetry violation without violation of relativistic symmetry. Phys. Lett. A 2006, 350, 5–10. [Google Scholar] [CrossRef]
- Hill, J.M.; Cox, B.J. Einstein’s special relativity beyond the speed of light. Proc. R. Soc. A 2012, 468. [Google Scholar] [CrossRef]
- Brennich, H. Süssmann’s deduction of Lorentz group. Z. Naturforschung 1969, 24, 1853–1854. [Google Scholar]
- Rindler, W. Essential Relativity; Springer: New York, NY, USA, 1977. [Google Scholar]
- Süssmann, G. A purely kinematical derivation of the Lorentz group. Opt. Commun. 2000, 179, 479–483. [Google Scholar] [CrossRef]
- Field, J.H. Space–time exchange invariance: Special relativity as a symmetry principle. Am. J. Phys. 2001, 69, 569–575. [Google Scholar] [CrossRef]
- Friedman, Y.; Gofman, Y. Relativistic linear spacetime transformations based on symmetry. Found. Phys. 2002, 32, 1717–1736. [Google Scholar] [CrossRef]
- Einstein, A. Relativity: The Special and General Theory; Lawson, R.W., Translator; Crown: New York, NY, USA, 1961; Appendix I; pp. 115–120. [Google Scholar]
- Miller, A.I. Albert Einstein’s Special Relativity: Emergence (1905) and Early Interpretation (1905–1911); Addison-Wesley: Reading, MA, USA, 1981; pp. 207–219. [Google Scholar]
- Martinez, A.A. Kinematic subtleties in Einstein’s first derivation of the Lorentz transformations. Am. J. Phys. 2004, 72, 790–798. [Google Scholar] [CrossRef]
- Rynasiewicz, R. The optics and electrodynamics of ‘On the electrodynamics of moving bodies’. Ann. Phys. (Leipzig) 2005, 14 (Suppl. S1), 38–57. [Google Scholar] [CrossRef]
- Mermin, N.D. Relativity without light. Am. J. Phys. 1984, 52, 119–124. [Google Scholar] [CrossRef]
- Schwartz, H.M. Deduction of the general Lorentz transformations from a set of necessary assumptions. Am. J. Phys. 1984, 52, 346–350. [Google Scholar] [CrossRef]
- Singh, S. Lorentz transformations in Mermin’s relativity without light. Am. J. Phys. 1986, 54, 183–184. [Google Scholar] [CrossRef]
- Schwartz, H.M. A simple new approach to the deduction of the Lorentz transformations. Am. J. Phys. 1985, 53, 1007–1008. [Google Scholar] [CrossRef]
- Lucas, J.R.; Hodgson, P.E. Space Time and Electromagnetism; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Field, J.H. A new kinematic derivation of the Lorentz transformation and the particle description of light. Helv. Phys. Acta 1997, 70, 542–564. [Google Scholar]
- Coleman, B. A dual first-postulate basis for special relativity. Eur. J. Phys. 2003, 24, 301–313. [Google Scholar] [CrossRef]
- Wigner, E.P. On unitary representations of the inhomogeneous Lorentz group. Ann. Math. 1939, 40, 149–204. [Google Scholar] [CrossRef]
- De Lange, O.L. Comment on “Space–time exchange invariance: Special relativity as a symmetry principle,” by J.H. Field [Am. J. Phys. 69 (5), 569–575 (2001)]. Am. J. Phys. 2002, 70, 78–79. [Google Scholar] [CrossRef]
- Field, J.H. Space–time symmetry is broken. Fund. J. Mod. Phys. 2015, 8, 25–34. [Google Scholar]
- Field, J.H. Differential equations, Newton’s laws of motion and relativity. Fund. J. Mod. Phys. 2015, 8, 147–162. [Google Scholar]
- Süssmann, G. Foundation of Lorentzian groups on symmetry-assumptions and relativity-assumptions alone. Z. Naturforschung 1969, 24, 495–498. [Google Scholar]
- Fowles, G.R. Self-inverse form of the Lorentz transformation. Am. J. Phys. 1977, 45, 675–676. [Google Scholar] [CrossRef]
- Cook, R.J. Comment on “Self-inversion form of the Lorentz transformation”. Am. J. Phys. 1979, 47, 117–118. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chao, S.D. Lorentz Transformations from Intrinsic Symmetries. Symmetry 2016, 8, 94. https://doi.org/10.3390/sym8090094
Chao SD. Lorentz Transformations from Intrinsic Symmetries. Symmetry. 2016; 8(9):94. https://doi.org/10.3390/sym8090094
Chicago/Turabian StyleChao, Sheng D. 2016. "Lorentz Transformations from Intrinsic Symmetries" Symmetry 8, no. 9: 94. https://doi.org/10.3390/sym8090094
APA StyleChao, S. D. (2016). Lorentz Transformations from Intrinsic Symmetries. Symmetry, 8(9), 94. https://doi.org/10.3390/sym8090094