Modeling Bottom-Up Visual Attention Using Dihedral Group D4 †
Abstract
:1. Introduction
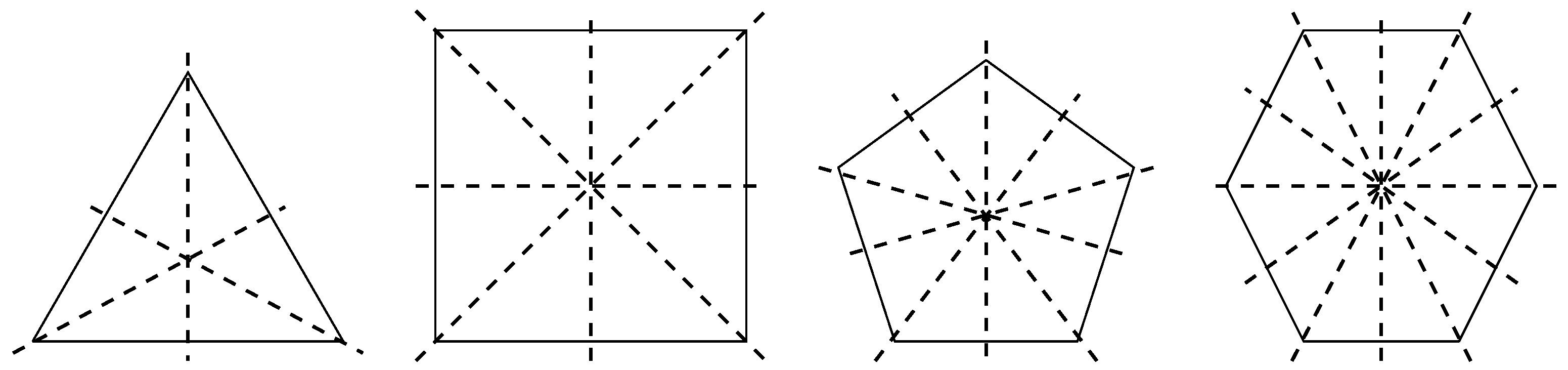
2. Theory
- (i)
- G must be closed under , that is for every pair of elements in G, we must have that is again an element in G.
- (ii)
- The operation must be associative, that is for all elements in G, we must have that:
- (iii)
- There is an element e in G, called the identity element, such that for all , we have that:
- (iv)
- For every element g in G, there is an element in G, called the inverse of g, such that:
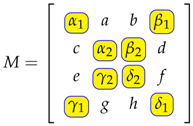
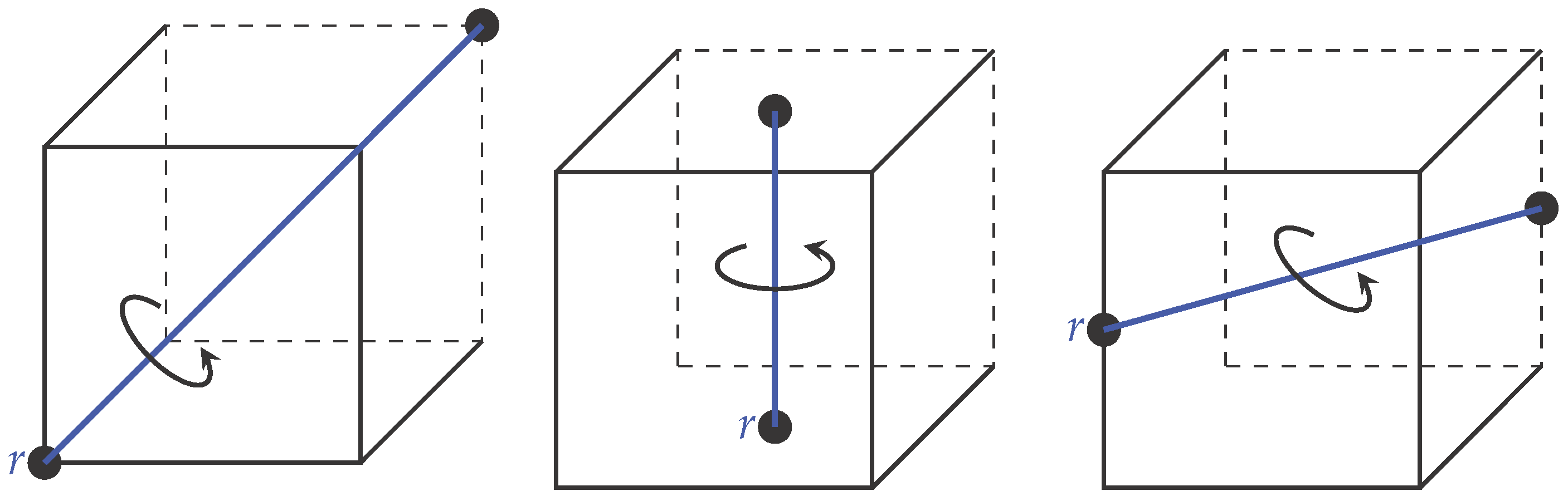
The Group
3. Method
3.1. Background
3.2. Fast Implementation of the Group Operations
3.3. De-Correlation of Color Image Channels
3.4. Implementation of the Algorithm
4. Comparing Different Saliency Models
4.1. Center-Bias
4.2. Shuffled Metric
4.3. Dataset
4.4. Saliency Models
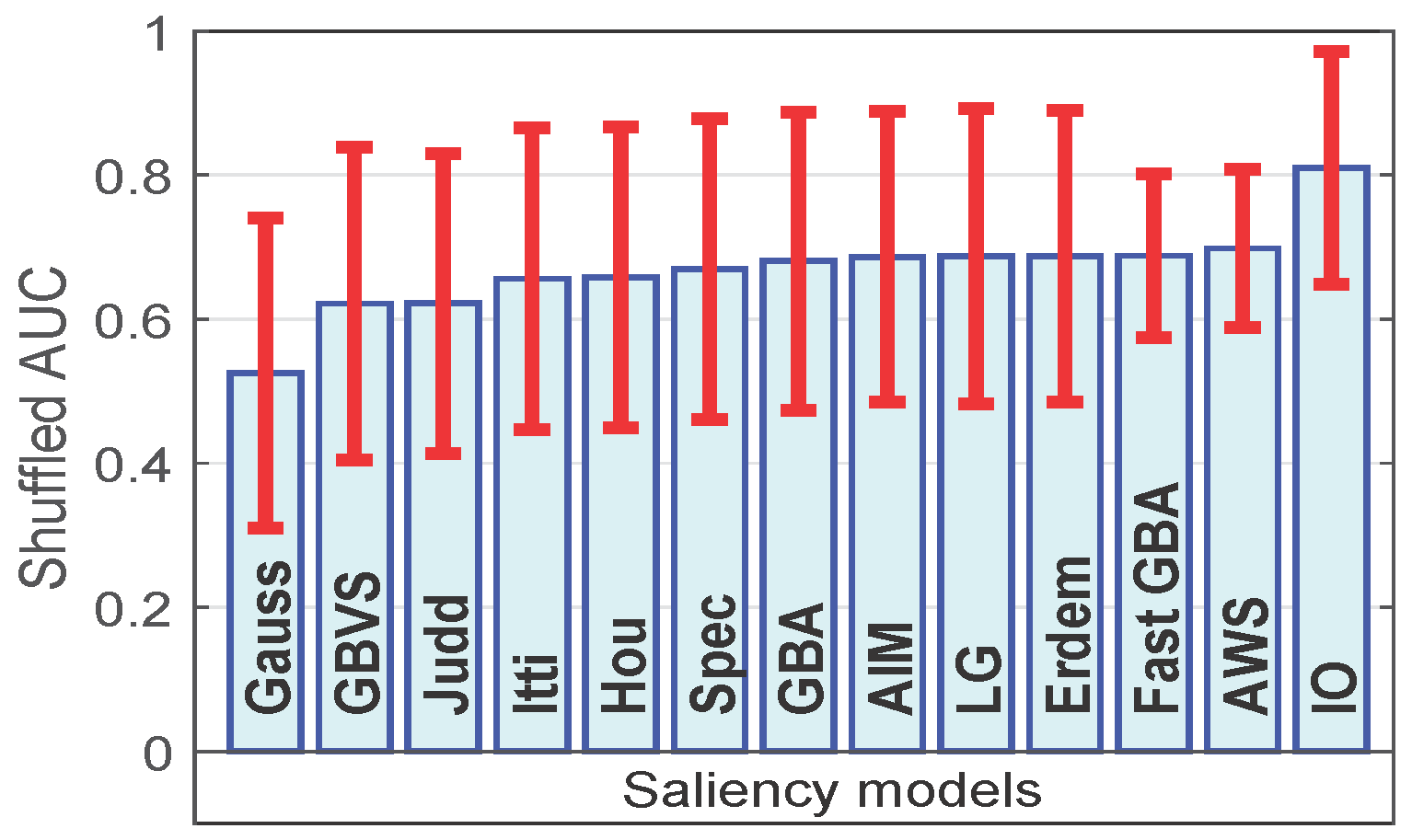
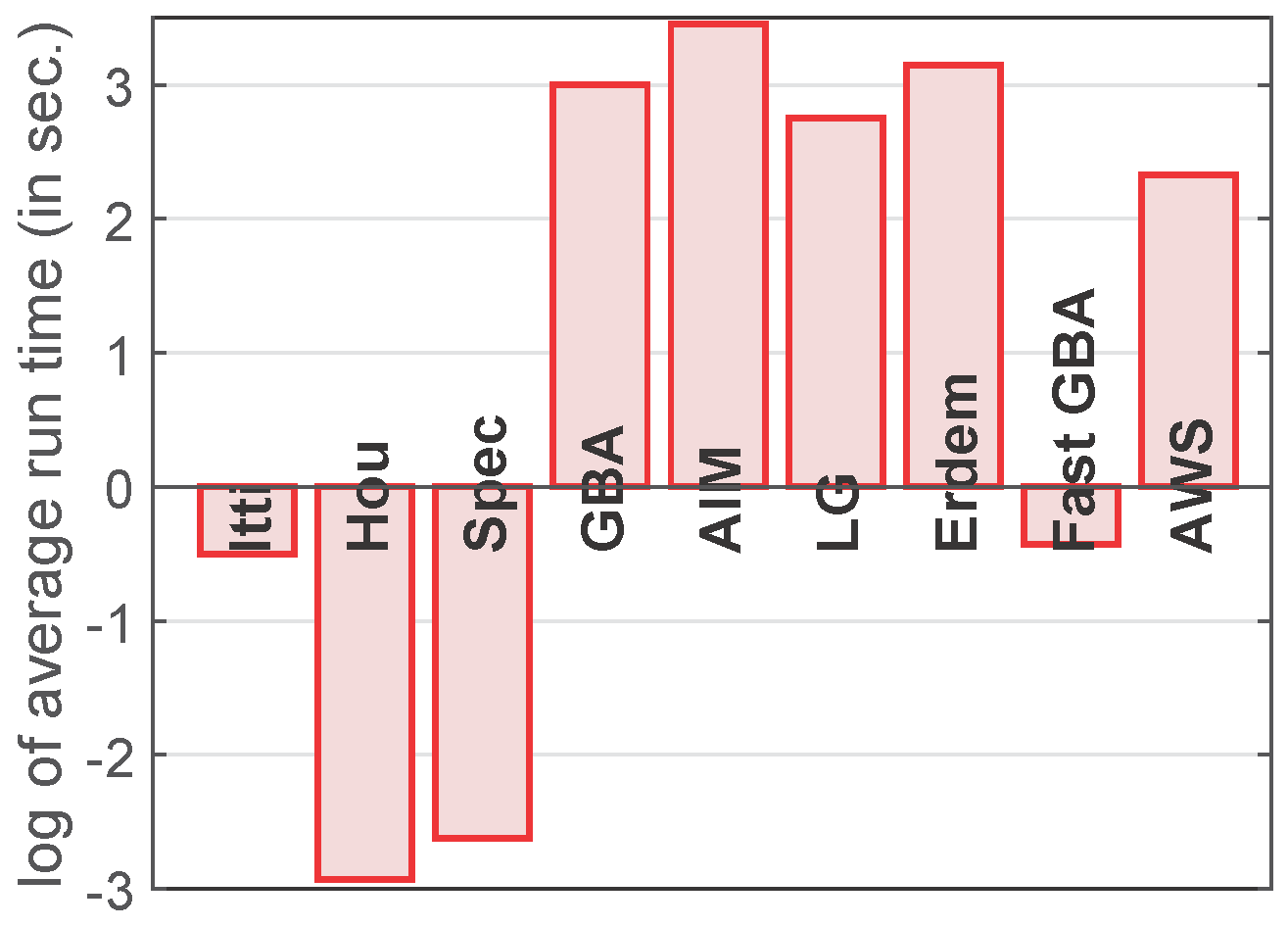
4.5. Ranking among the Saliency Models
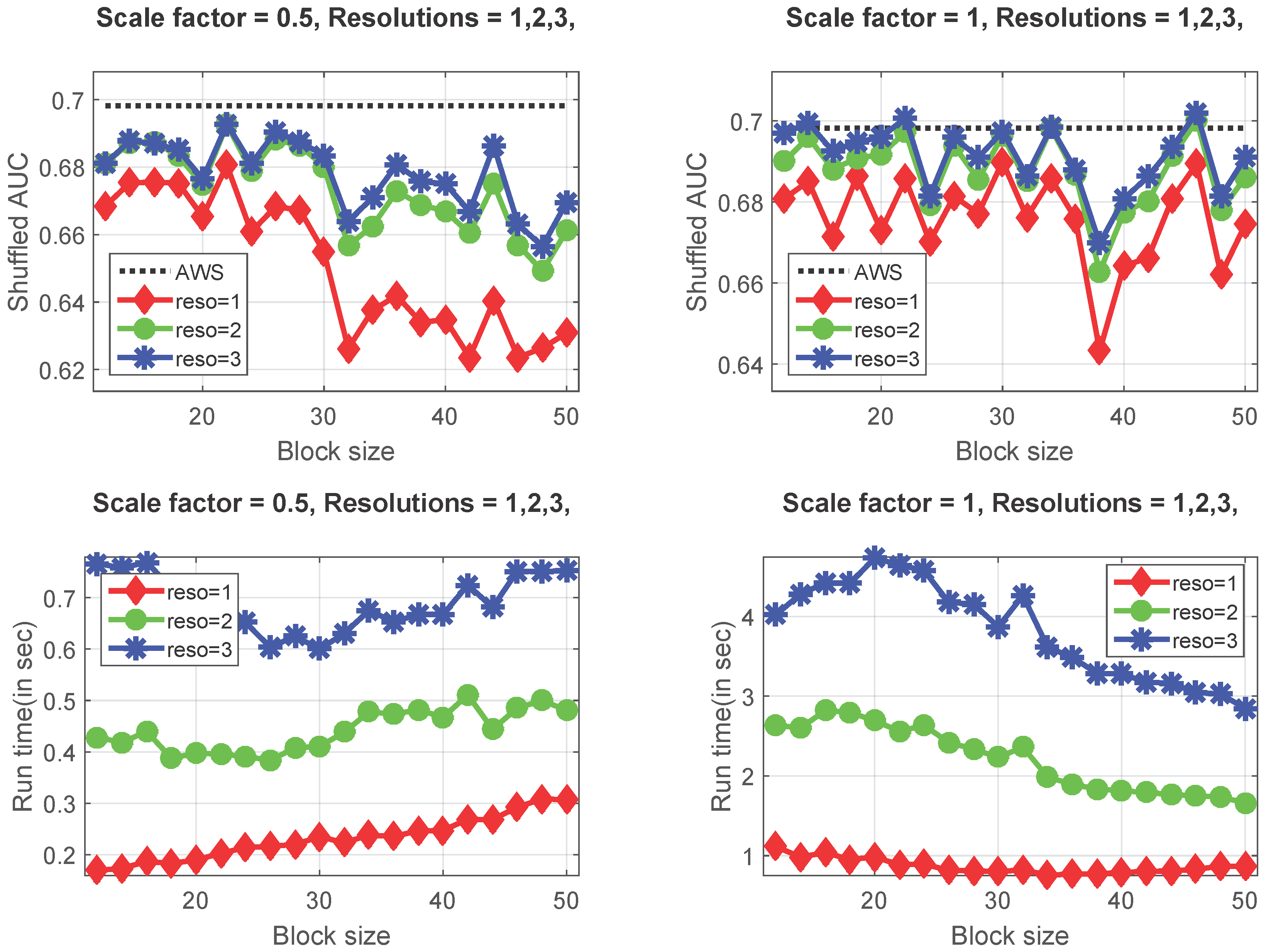
4.6. Optimizing the Proposed Fast GBA Model
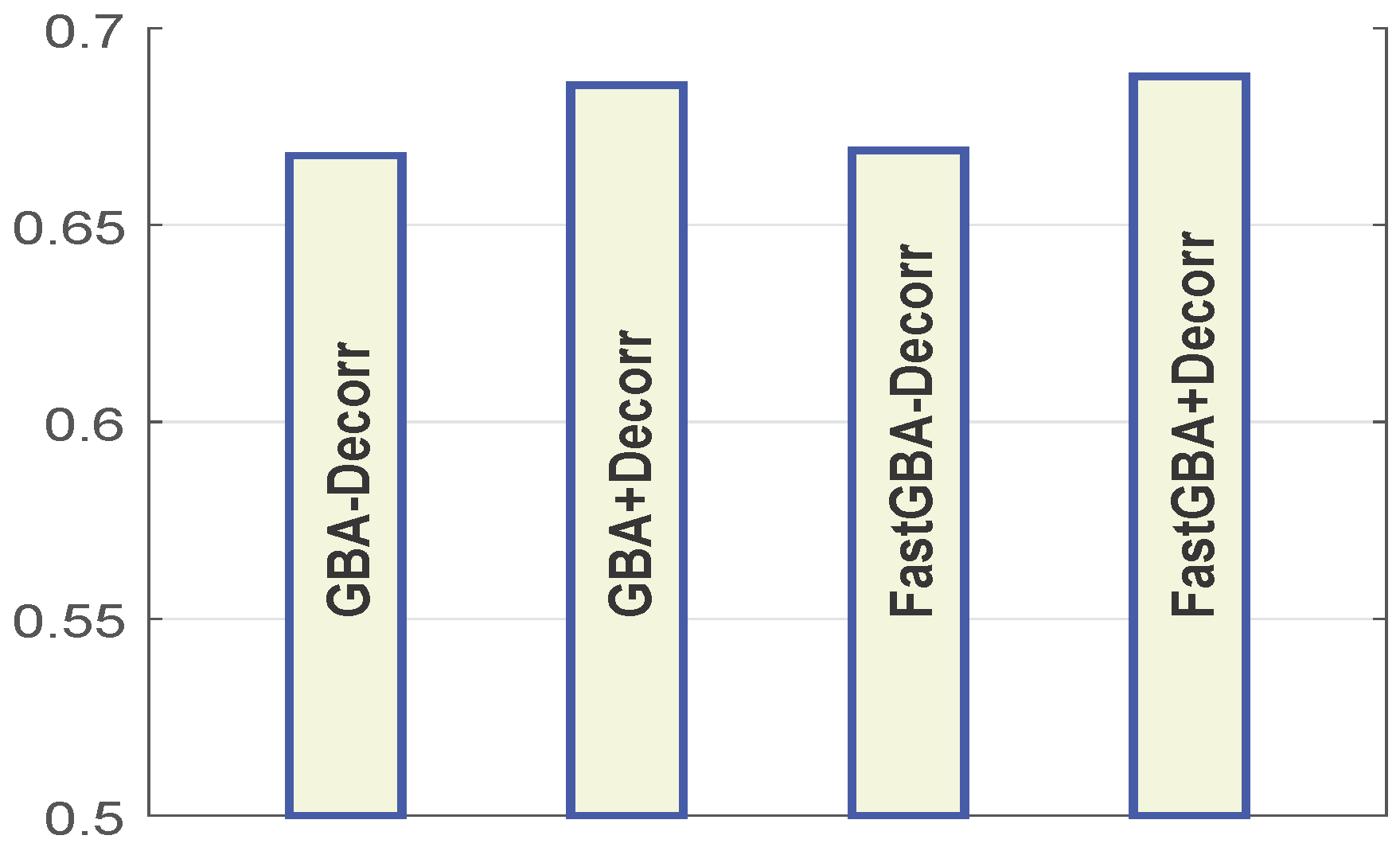
4.7. Impact of De-Correlation on the Performance of the Proposed Fast GBA Model
5. Future Work
6. Conclusions
Conflicts of Interest
References
- Suder, K.; Worgotter, F. The control of low-level information flow in the visual system. Rev. Neurosci. 2000, 11, 127–146. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Yang, M.H. Top-down visual saliency via joint CRF and dictionary learning. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 2296–2303.
- He, S.; Lau, R.W.; Yang, Q. Exemplar-Driven Top-Down Saliency Detection via Deep Association. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016.
- Koch, C.; Ullman, S. Shifts in selective visual attention: Towards the underlying neural circuitry. Hum. Neurobiol. 1985, 4, 219–227. [Google Scholar] [PubMed]
- Itti, L. Automatic Foveation for Video Compression Using a Neurobiological Model of Visual Attention. IEEE Trans. Image Process. 2004, 13, 1304–1318. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.X.; Lisin, D.A. Image Compression based on Visual Saliency at Individual Scales. In Proceedings of the 5th International Symposium on Advances in Visual Computing Part I, Las Vegas, NV, USA, 30 November–2 December 2009; pp. 157–166.
- Alsam, A.; Rivertz, H.; Sharma, P. What the Eye Did Not See—A Fusion Approach to Image Coding. In Advances in Visual Computing; Bebis, G., Boyle, R., Parvin, B., Koracin, D., Fowlkes, C., Wang, S., Choi, M.H., Mantler, S., Schulze, J., Acevedo, D., et al., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany; Heidelberg, Germany, 2012; Volume 7432, pp. 199–208. [Google Scholar]
- Alsam, A.; Rivertz, H.J.; Sharma, P. What the eye did not see–A fusion approach to image coding. Int. J. Artif. Intell. Tools 2013, 22, 1360014. [Google Scholar] [CrossRef]
- Siagian, C.; Itti, L. Biologically-Inspired Robotics Vision Monte-Carlo Localization in the Outdoor Environment. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007.
- Frintrop, S.; Jensfelt, P.; Christensen, H.I. Attentional Landmark Selection for Visual SLAM. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006.
- Kadir, T.; Brady, M. Saliency, Scale and Image Description. Int. J. Comput. Vis. 2001, 45, 83–105. [Google Scholar] [CrossRef]
- Feng, X.; Liu, T.; Yang, D.; Wang, Y. Saliency based objective quality assessment of decoded video affected by packet losses. In Proceedings of the 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 2560–2563.
- Ma, Q.; Zhang, L. Saliency-Based Image Quality Assessment Criterion. In Advanced Intelligent Computing Theories and Applications. With Aspects of Theoretical and Methodological Issues; Huang, D.S., Wunsch, D.C.I., Levine, D., Jo, K.H., Eds.; Lecture Notes in Computer Science; Springer: Berlin, Germany; Heidelberg, Germany, 2008; Volume 5226, pp. 1124–1133. [Google Scholar]
- El-Nasr, M.; Vasilakos, A.; Rao, C.; Zupko, J. Dynamic Intelligent Lighting for Directing Visual Attention in Interactive 3-D Scenes. IEEE Trans. Comput. Intell. AI Games 2009, 1, 145–153. [Google Scholar] [CrossRef]
- Rosenholtz, R.; Dorai, A.; Freeman, R. Do predictions of visual perception aid design? ACM Trans. Appl. Percept. 2011, 8, 12:1–12:20. [Google Scholar] [CrossRef]
- Judd, T.; Ehinger, K.; Durand, F.; Torralba, A. Learning to predict where humans look. In Proceedings of the 2009 IEEE International Conference on Computer Vision (ICCV), Kyoto, Japan, 27 September–4 October 2009; pp. 2106–2113.
- Breazeal, C.; Scassellati, B. A Context-Dependent Attention System for a Social Robot. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Stockholm, Sweden, 31 July–6 August 1999; pp. 1146–1153.
- Ajallooeian, M.; Borji, A.; Araabi, B.; Ahmadabadi, M.; Moradi, H. An application to interactive robotic marionette playing based on saliency maps. In Proceedings of the 18th IEEE International Symposium on Robot and Human Interactive Communication, Toyama, Japan, 27 September–2 October 2009; pp. 841–847.
- Itti, L.; Koch, C. A saliency-based search mechanism for overt and covert shifts of visual attention. Vis. Res. 2000, 40, 1489–1506. [Google Scholar] [CrossRef]
- Liu, T.; Sun, J.; Zheng, N.N.; Tang, X.; Shum, H.Y. Learning to Detect A Salient Object. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 18–23 June 2007.
- Achanta, R.; Estrada, F.; Wils, P.; Süsstrunk, S. Salient region detection and segmentation. In Proceedings of the 6th International Conference on Computer Vision Systems, Santorini, Greece, 12–15 May 2008; pp. 66–75.
- Erdem, E.; Erdem, A. Visual saliency estimation by nonlinearly integrating features using region covariances. J. Vis. 2013, 13, 1–20. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Lau, R.W.H.; Liu, W.; Huang, Z.; Yang, Q. SuperCNN: A Superpixelwise Convolutional Neural Network for Salient Object Detection. Int. J. Comput. Vis. 2015, 115, 330–344. [Google Scholar] [CrossRef]
- Alsam, A.; Sharma, P.; Wrålsen, A. Asymmetry as a Measure of Visual Saliency. Lecture Notes in Computer Science (LNCS); Springer-Verlag Berlin Heidelberg: Berlin, Germany; Heidelberg, Germany, 2013; Volume 7944, pp. 591–600. [Google Scholar]
- Alsam, A.; Sharma, P.; Wrålsen, A. Calculating saliency using the dihedral group D4. J. Imaging Sci. Technol. 2014, 58, 10504:1–10504:12. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C.; Niebur, E. A Model of Saliency-Based Visual Attention for Rapid Scene Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Garcia-Diaz, A.; Fdez-Vidal, X.R.; Pardo, X.M.; Dosil, R. Saliency from hierarchical adaptation through decorrelation and variance normalization. Image Vis. Comput. 2012, 30, 51–64. [Google Scholar] [CrossRef]
- Dummit, D.S.; Foote, R.M. Abstract Algebra, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Lenz, R. Using representations of the dihedral groups in the design of early vision filters. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP-93), Minneapolis, MN, USA, 27–30 April 1993; pp. 165–168.
- Lenz, R. Investigation of Receptive Fields Using Representations of the Dihedral Groups. J. Vis. Commun. Image Represent. 1995, 6, 209–227. [Google Scholar] [CrossRef]
- Foote, R.; Mirchandani, G.; Rockmore, D.N.; Healy, D.; Olson, T. A wreath product group approach to signal and image processing. I. Multiresolution analysis. IEEE Trans. Signal Process. 2000, 48, 102–132. [Google Scholar] [CrossRef]
- Chang, W.Y. Image Processing with Wreath Products. Master’s Thesis, Harvey Mudd College, Claremont, CA, USA, 2004. [Google Scholar]
- Lenz, R.; Bui, T.H.; Takase, K. A group theoretical toolbox for color image operators. In Proceedings of the IEEE International Conference on Image Processing, Genoa, Italy, 11–14 September 2005; Volume 3, pp. 557–560.
- Sharma, P. Evaluating visual saliency algorithms: Past, present and future. J. Imaging Sci. Technol. 2015, 59, 50501:1–50501:17. [Google Scholar] [CrossRef] [Green Version]
- Tatler, B.W.; Baddeley, R.J.; Gilchrist, I.D. Visual correlates of fixation selection: Effects of scale and time. Vis. Res. 2005, 45, 643–659. [Google Scholar] [CrossRef] [PubMed]
- Tatler, B.W. The central fixation bias in scene viewing: Selecting an optimal viewing position independently of motor biases and image feature distributions. J. Vis. 2007, 7, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Tseng, P.H.; Carmi, R.; Cameron, I.G.M.; Munoz, D.P.; Itti, L. Quantifying center bias of observers in free viewing of dynamic natural scenes. J. Vis. 2009, 9, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Tong, M.H.; Marks, T.K.; Shan, H.; Cottrell, G.W. SUN: A Bayesian framework for saliency using natural statistics. J. Vis. 2008, 8, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, T. ROC Graphs with Instance-Varying Costs. Pattern Recognit. Lett. 2004, 27, 882–891. [Google Scholar] [CrossRef]
- Bruce, N.D.B.; Tsotsos, J.K. Saliency Based on Information Maximization. In Proceedings of the Neural Information Processing Systems conference (NIPS 2005), Vancouver, BC, Canada, 5–10 December 2005; pp. 155–162.
- Hou, X.; Zhang, L. Saliency Detection: A Spectral Residual Approach. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8.
- Schauerte, B.; Stiefelhagen, R. Predicting Human Gaze using Quaternion DCT Image Signature Saliency and Face Detection. In Proceedings of the IEEE Workshop on the Applications of Computer Vision (WACV), Breckenridge, CO, USA, 9–11 January 2012.
- Harel, J.; Koch, C.; Perona, P. Graph-Based Visual Saliency. In Proceedings of Neural Information Processing Systems (NIPS); MIT Press: Cambridge, MA, USA, 2006; pp. 545–552. [Google Scholar]
- Borji, A.; Itti, L. Exploiting Local and Global Patch Rarities for Saliency Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 18–20 June 2012; pp. 1–8.
- Borji, A.; Sihite, D.N.; Itti, L. Quantitative Analysis of Human-Model Agreement in Visual Saliency Modeling: A Comparative Study. IEEE Trans. Image Process. 2013, 22, 55–69. [Google Scholar] [CrossRef] [PubMed]
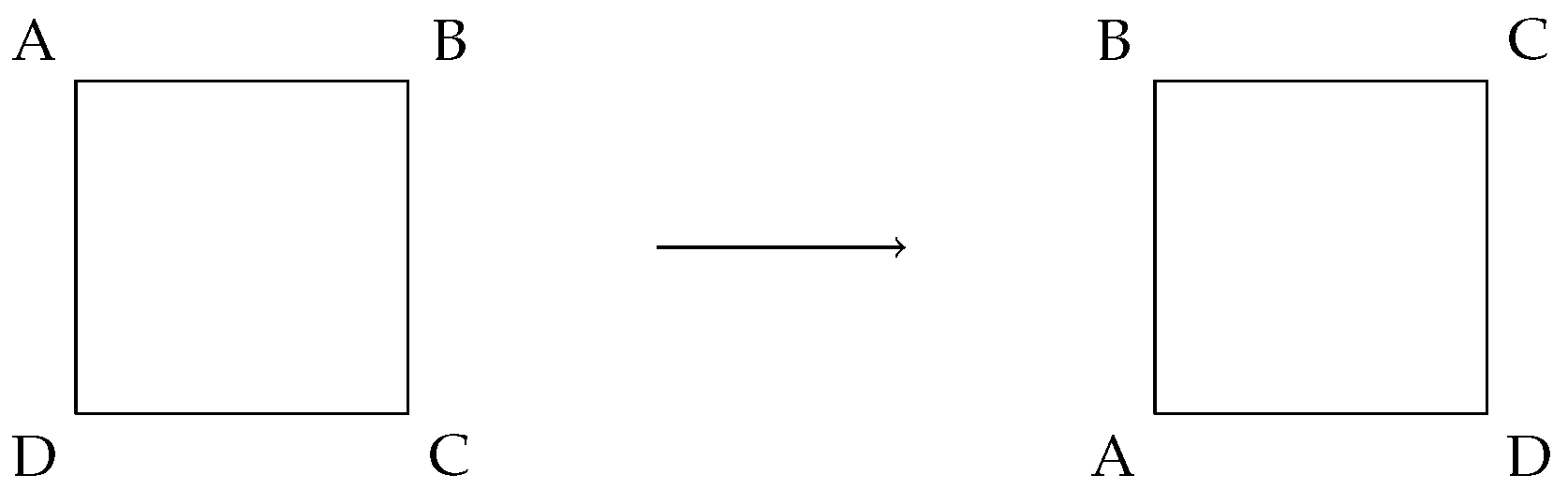



© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, P. Modeling Bottom-Up Visual Attention Using Dihedral Group D4. Symmetry 2016, 8, 79. https://doi.org/10.3390/sym8080079
Sharma P. Modeling Bottom-Up Visual Attention Using Dihedral Group D4. Symmetry. 2016; 8(8):79. https://doi.org/10.3390/sym8080079
Chicago/Turabian StyleSharma, Puneet. 2016. "Modeling Bottom-Up Visual Attention Using Dihedral Group D4" Symmetry 8, no. 8: 79. https://doi.org/10.3390/sym8080079
APA StyleSharma, P. (2016). Modeling Bottom-Up Visual Attention Using Dihedral Group D4. Symmetry, 8(8), 79. https://doi.org/10.3390/sym8080079





