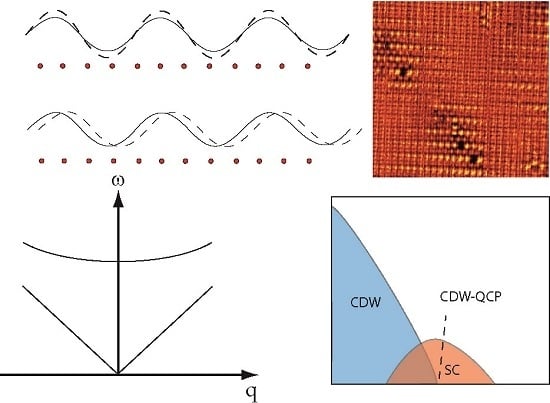
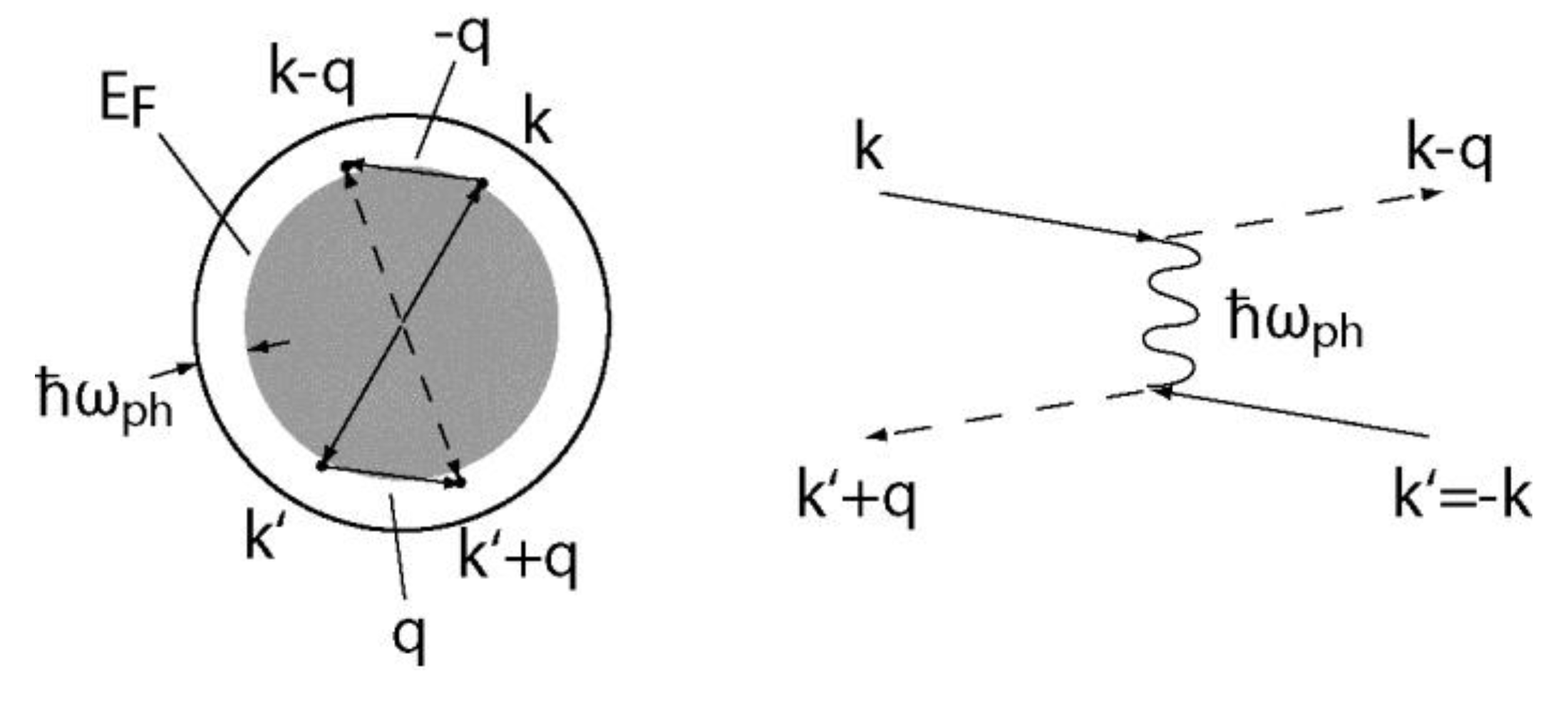
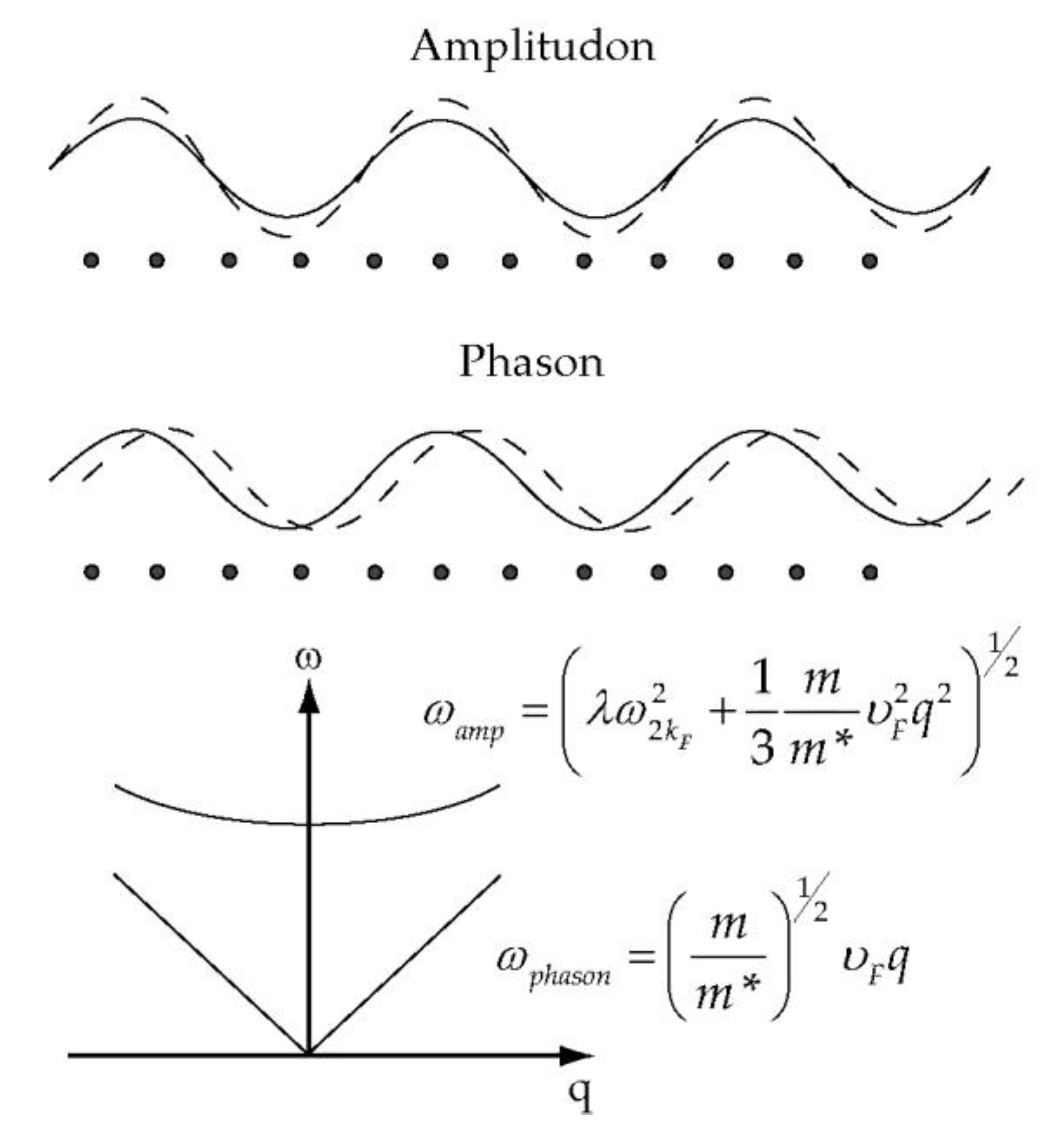
Fluctuating Charge Order: A Universal Phenomenon in Unconventional Superconductivity?
Abstract
:1. Introduction
2. The 122 Iron Pnictides
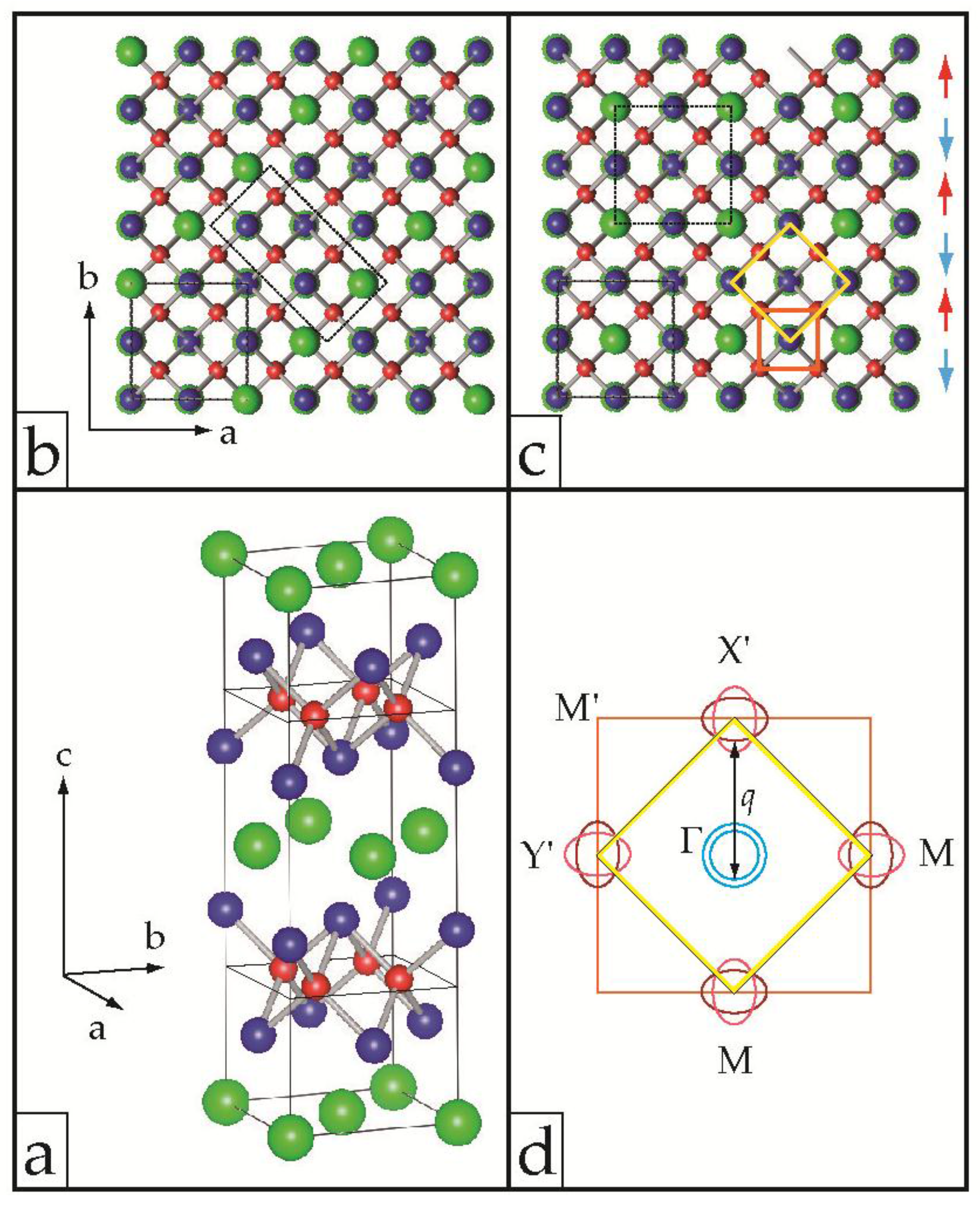
2.1. The 122 Cleavage Surfaces
2.2. The Order–Order Phase Transition
2.3. The Fermi Topology of 122 Fe Pnictides
3. Charge Order in Cuprates and Other Unconventional Superconductors
4. Experimental Considerations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ARPES | Angle-resolved photoelectron spectroscopy |
| BCS | Bardeen-Cooper-Schrieffer |
| BZ | Brillouin zone |
| CDW | Charge density wave |
| DFT | Density functional theory |
| DOS | Density of states |
| FS | Fermi surface |
| ML | Monolayer |
| SBZ | Surface Brillouin zone |
| SDW | Spin density wave |
| STM | Scanning tunneling microscopy |
| STS | Scanning tunneling spectroscopy |
| YBCO | Yttrium barium cuprate |
References
- Grosso, G.; Parravicini, G. Solid State Physics; Elsevier Academic Press: Oxford, UK, 2014. [Google Scholar]
- Giamarchi, T. Quantum Physics in One Dimension; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Torchinsky, D.H.; Mahmood, F.; Bollinger, A.T.; Božović, I.; Gedik, N. Fluctuating charge-density waves in a cuprate superconductor. Nat. Mater. 2013, 12, 387–391. [Google Scholar] [CrossRef] [PubMed]
- Grüner, G. Density Waves in Solids; Perseus Publishing: Cambridge, MA, USA, 1994. [Google Scholar]
- Wang, F.; Lee, D.-H. The electron-pairing mechanism of iron-based superconductors. Science 2011, 332, 200–204. [Google Scholar] [CrossRef] [PubMed]
- Castellani, C.; di Castro, C.; Grilli, M. Non-fermi-liquid behavior and d-wave superconductivity near the charge-density-wave quantum critical point. Z. Phys. B Condens. Matter 1996, 103, 137–144. [Google Scholar] [CrossRef]
- Castellani, C.; di Castro, C.; Grilli, M. Singular quasiparticle scattering in the proximity of charge instabilities. Phys. Rev. Lett. 1995, 75, 4650–4653. [Google Scholar] [CrossRef] [PubMed]
- Croft, T.P.; Lester, C.; Senn, M.S.; Bombardi, A.; Hayden, S.M. Charge density wave fluctuations in La2−xSrxCuO4 and their competition with superconductivity. Phys. Rev. B 2014, 89, 224513. [Google Scholar] [CrossRef]
- Thampy, V.; Dean, M.P.M.; Christensen, N.B.; Steinke, L.; Islam, Z.; Oda, M.; Ido, M.; Momono, N.; Wilkins, S.B.; Hill, J.P. Rotated stripe order and its competition with superconductivity in La1.88Sr0.12CuO4. Phys. Rev. B 2014, 90, 100510. [Google Scholar] [CrossRef]
- Noack, R.M.; Scalapino, D.J.; Scalettar, R.T. Charge-density-wave and pairing susceptibilities in a two-dimensional electron-phonon model. Phys. Rev. Lett. 1991, 66, 778–781. [Google Scholar] [CrossRef] [PubMed]
- Zhai, H.; Wang, F.; Lee, D.-H. Antiferromagnetically driven electronic correlations in iron pnictides and cuprates. Phys. Rev. B 2009, 80, 064517. [Google Scholar] [CrossRef]
- Yin, Y.; Zech, M.; Williams, T.L.; Wang, X.F.; Wu, G.; Chen, X.H.; Hoffman, J.E. Scanning tunneling spectroscopy and vortex imaging in the iron pnictide superconductor BaFe1.8Co0.2As2. Phys. Rev. Lett. 2009, 102, 097002. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Xia, Y.; Wray, L.; Qian, D.; Gomes, K.K.; Yazdani, A.; Chen, G.F.; Luo, J.L.; Wang, N.L.; Hasan, M.Z. Experimental determination of the microscopic origin of magnetism in parent iron pnictides. Available online: https://arxiv.org/abs/0812.2289 (acessed on 6 June 2016).
- Massee, F.; de Jong, S.; Huang, Y.; Kaas, J.; van Heumen, E.; Goedkoop, J.B.; Golden, M.S. Cleavage surfaces of the BaFe2−xCoxAs2 and FeySe1−xTex superconductors: A combined STM plus LEED study. Phys. Rev. B 2009, 80, 140507. [Google Scholar] [CrossRef]
- Zhang, H.; Dai, J.; Zhang, Y.; Qu, D.; Ji, H.; Wu, G.; Wang, X.F.; Chen, X.H.; Wang, B.; Zeng, C.; et al. √2 × √2 structure and charge inhomogeneity at the surface of superconducting BaFe2−xCoxAs2 (x = 0–0.32). Phys. Rev. B 2010, 81, 104520. [Google Scholar] [CrossRef]
- Nascimento, V.B.; Li, A.; Jayasundara, D.R.; Xuan, Y.; O’Neal, J.; Pan, S.; Chien, T.Y.; Hu, B.; He, X.B.; Li, G.; et al. Surface geometric and electronic structures of BaFe2As2(001). Phys. Rev. Lett. 2009, 103, 076104. [Google Scholar] [CrossRef] [PubMed]
- Niestemski, F.C.; Nascimento, V.B.; Hu, B.; Plummer, E.W.; Gillett, J.; Sebastian, S.; Wang, Z.; Madhavan, V. Unveiling the atomic and electronic structure at the surface of the parent pnictide SrFe2As2. Available online: http://arxiv.org/abs/0906.2761 (acessed on 6 June 2016).
- Li, G.; He, X.; Li, A.; Pan, S.H.; Zhang, J.; Jin, R.; Sefat, A.S.; McGuire, M.A.; Mandrus, D.G.; Sales, B.C.; et al. BaFe2As2 surface domains and domain walls: Mirroring the bulk spin structure. Available online: http://arxiv.org/abs/1006.5907 (acessed on 6 June 2016).
- Hoffman, J.E. Spectroscopic scanning tunneling microscopy insights into Fe-based superconductors. Rep. Prog. Phys. 2011, 74, 124513. [Google Scholar] [CrossRef]
- Cordin, M.; Amann, P.; Menzel, A.; Bertel, E.; Baranov, M.; Diehl, S.; Redinger, J.; Franchini, C. Comment on “Cleavage surfaces of the BaFe2−xCoxAs2 and FeySe1−xTex superconductors: A combined STM plus LEED study”. Phys. Rev. B 2012, 86, 167401. [Google Scholar] [CrossRef]
- Gao, M.; Ma, F.; Lu, Z.-Y.; Xiang, T. Surface structures of ternary iron arsenides AFe2As2 (A = Ba, Sr, or Ca). Phys. Rev. B 2010, 81, 193409. [Google Scholar] [CrossRef]
- Gu, J.; Sim, W.S.; King, D.A. Vibrational-entropy-driven order-order phase transition at monolayer coverage: CO on Co{10-10}. J. Chem. Phys. 1997, 107, 5613–5616. [Google Scholar] [CrossRef]
- Cordin, M.; Lechner, B.A.J.; Amann, P.; Menzel, A.; Bertel, E.; Franchini, C.; Zucca, R.; Redinger, J.; Baranov, M.; Diehl, S. Phase transitions driven by competing interactions in low-dimensional systems. EPL 2010, 92, 26004. [Google Scholar] [CrossRef]
- Bertel, E. Quasi-critical fluctuations: A novel state of matter? J. Nanopart. Res. 2013, 15, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Deisl, C.; Swamy, K.; Memmel, N.; Bertel, E.; Franchini, C.; Schneider, G.; Redinger, J.; Walter, S.; Hammer, L.; Heinz, K. (3 × 1)-Br/Pt(110) structure and the charge-density-wave-assisted c(2 × 2) to (3 × 1) phase transition. Phys. Rev. B 2004, 69, 195405–195413. [Google Scholar] [CrossRef]
- Rice, T.M.; Scott, G.K. New mechanism for a charge-density-wave instability. Phys. Rev. Lett. 1975, 35, 120. [Google Scholar] [CrossRef]
- Amann, P.; Cordin, M.; Braun, C.; Lechner, B.A.J.; Menzel, A.; Bertel, E.; Franchini, C.; Zucca, R.; Redinger, J.; Baranov, M.; et al. Electronically driven phase transitions in a quasi-one-dimensional adsorbate system. Eur. Phys. J. B 2010, 75, 15–22. [Google Scholar] [CrossRef]
- Minca, M.; Penner, S.; Dona, E.; Menzel, A.; Bertel, E.; Brouet, V.; Redinger, J. Surface resonances on transition metals as low-dimensional model systems. N. J. Phys. 2007, 9, 386–399. [Google Scholar] [CrossRef]
- Cordin, M.; Lechner, B.A.J.; Duerrbeck, S.; Menzel, A.; Bertel, E.; Redinger, J.; Franchini, C. Experimental observation of defect pair separation triggering phase transitions. Sci. Rep. 2014, 4, 4110. [Google Scholar] [CrossRef] [PubMed]
- Zabolotnyy, V.B.; Evtushinsky, D.V.; Kordyuk, A.A.; Inosov, D.S.; Koitzsch, A.; Boris, A.V.; Sun, G.L.; Lin, C.T.; Knupfer, M.; Büchner, B.; et al. Fermi surface of Ba1−xKxFe2As2 as probed by angle-resolved photoemission. Phys. C Superconduct. 2009, 469, 448–451. [Google Scholar] [CrossRef]
- Borisenko, S.V.; Zabolotnyy, V.B.; Kordyuk, A.A.; Evtushinsky, D.V.; Kim, T.K.; Morozov, I.V.; Follath, R.; Büchner, B. One-sign order parameter in iron based superconductor. Symmetry 2012, 4, 251–264. [Google Scholar] [CrossRef]
- Kordyuk, A.A.; Zabolotnyy, V.B.; Evtushinsky, D.V.; Yaresko, A.N.; Büchner, B.; Borisenko, S.V. Electronic band structure of ferro-pnictide superconductors from ARPES experiment. J. Superconduct. Novel Magnet. 2013, 26, 2837–2841. [Google Scholar] [CrossRef]
- Kondo, T.; Fernandes, R.M.; Khasanov, R.; Liu, C.; Palczewski, A.D.; Ni, N.; Shi, M.; Bostwick, A.; Rotenberg, E.; Schmalian, J.; et al. Unexpected fermi-surface nesting in the pnictide parent compounds BaFe2As2 and CaFe2As2 revealed by angle-resolved photoemission spectroscopy. Phys. Rev. B 2010, 81, 060507. [Google Scholar] [CrossRef]
- De Jong, S.; van Heumen, E.; Thirupathaiah, S.; Huisman, R.; Massee, F.; Goedkoop, J.B.; Ovsyannikov, R.; Fink, J.; Dürr, H.A.; Gloskovskii, A.; et al. Droplet-like fermi surfaces in the anti-ferromagnetic phase of EuFe2As2, an Fe-pnictide superconductor parent compound. EPL 2010, 89, 27007. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, G.; Meng, J.; Zhang, W.; Liu, H.; Zhao, L.; Jia, X. High resolution angle-resolved photoemission spectroscopy on Cu-based and Fe-based high-Tc superconductors. Phys. Status Solidi A 2010, 207, 2674–2692. [Google Scholar] [CrossRef]
- Evtushinsky, D.V.; Kordyuk, A.A.; Zabolotnyy, V.B.; Inosov, D.S.; Kim, T.K.; Büchner, B.; Luo, H.; Wang, Z.; Wen, H.-H.; Sun, G.; et al. Propeller-like low temperature fermi surface of Ba1−xKxFe2As2 from magnetotransport and photoemission measurements. J. Phys. Soc. Jpn. 2011, 80, 023710. [Google Scholar] [CrossRef]
- Zabolotnyy, V.B.; Inosov, D.S.; Evtushinsky, D.V.; Koitzsch, A.; Kordyuk, A.A.; Sun, G.L.; Park, J.T.; Haug, D.; Hinkov, V.; Boris, A.V.; et al. (π,π) electronic order in iron arsenide superconductors. Nature 2009, 457, 569–572. [Google Scholar] [CrossRef] [PubMed]
- Fink, J.; Charnukha, A.; Rienks, E.D.L.; Liu, Z.H.; Thirupathaiah, S.; Avigo, I.; Roth, F.; Jeevan, H.S.; Gegenwart, P.; Roslova, M.; et al. Non-fermi-liquid scattering rates and anomalous band dispersion in ferropnictides. Phys. Rev. B 2015, 92, 201106. [Google Scholar] [CrossRef]
- Johannes, M.D.; Mazin, I.I. Fermi surface nesting and the origin of charge density waves in metals. Phys. Rev. B 2008, 77, 165135. [Google Scholar] [CrossRef]
- Faraggi, M.N.; Zubizarreta, X.; Arnau, A.; Silkin, V.M. On the stability of the electronic system in transition metal dichalcogenides. J. Phys. Condens. Matter 2016, 28, 184004. [Google Scholar] [CrossRef] [PubMed]
- Mazin, I.I.; Kimber, S.A.J.; Argyriou, D.N. Quasiparticle interference in antiferromagnetic parent compounds of iron-based superconductors. Phys. Rev. B 2011, 83, 052501. [Google Scholar] [CrossRef]
- Song, C.-L.; Zhang, H.-M.; Zhong, Y.; Hu, X.-P.; Ji, S.-H.; Wang, L.; He, K.; Ma, X.-C.; Xue, Q.-K. Observation of double-dome superconductivity in potassium-doped FeSe thin films. Phys. Rev. Lett. 2016, 116, 157001. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.R.; Zhang, C.F.; Ning, H.L.; Li, W.; Chen, L.; Jia, T.; Hashimoto, M.; Lu, D.H.; Shen, Z.-X.; Zhang, Y. Simultaneous emergence of superconductivity, inter-pocket scattering and nematic fluctuation in potassium-coated FeSe superconductor. Available online: http://arxiv.org/abs/1512.02526 (acessed on 6 June 2016).
- Blanco-Canosa, S.; Frano, A.; Loew, T.; Lu, Y.; Porras, J.; Ghiringhelli, G.; Minola, M.; Mazzoli, C.; Braicovich, L.; Schierle, E.; et al. Momentum-dependent charge correlations in YBa2Cu3O6+d superconductors probed by resonant X-ray scattering: Evidence for three competing phases. Phys. Rev. Lett. 2013, 110, 187001. [Google Scholar] [CrossRef] [PubMed]
- Da Silva Neto, E.H.; Aynajian, P.; Frano, A.; Comin, R.; Schierle, E.; Weschke, E.; Gyenis, A.; Wen, J.; Schneeloch, J.; Xu, Z.; et al. Ubiquitous interplay between charge ordering and high-temperature superconductivity in cuprates. Science 2014, 343, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, W.A.; Kampf, A.P.; Bulut, S. Charge order in the pseudogap phase of cuprate superconductors. N. J. Phys. 2015, 17, 013025. [Google Scholar] [CrossRef]
- Ghiringhelli, G.; Le Tacon, M.; Minola, M.; Blanco-Canosa, S.; Mazzoli, C.; Brookes, N.B.; De Luca, G.M.; Frano, A.; Hawthorn, D.G.; He, F.; et al. Long-range incommensurate charge fluctuations in (Y,Nd)Ba2Cu3O6+x. Science 2012, 337, 821–825. [Google Scholar] [CrossRef] [PubMed]
- Comin, R.; Frano, A.; Yee, M.M.; Yoshida, Y.; Eisaki, H.; Schierle, E.; Weschke, E.; Sutarto, R.; He, F.; Soumyanarayanan, A.; et al. Charge order driven by fermi-arc instability in Bi2Sr2−xLaxCuO6+δ. Science 2014, 343, 390–392. [Google Scholar] [CrossRef] [PubMed]
- Comin, R.; Sutarto, R.; da Silva Neto, E.H.; Chauviere, L.; Liang, R.; Hardy, W.N.; Bonn, D.A.; He, F.; Sawatzky, G.A.; Damascelli, A. Superconductivity. Broken translational and rotational symmetry via charge stripe order in underdoped YBa2Cu3O6+y. Science 2015, 347, 1335–1339. [Google Scholar] [CrossRef] [PubMed]
- Da Silva Neto, E.H.; Comin, R.; He, F.; Sutarto, R.; Jiang, Y.; Greene, R.L.; Sawatzky, G.A.; Damascelli, A. Charge ordering in the electron-doped superconductor Nd2−xCexCuO4. Science 2015, 347, 282–285. [Google Scholar] [CrossRef] [PubMed]
- Blackburn, E.; Chang, J.; Hücker, M.; Holmes, A.T.; Christensen, N.B.; Liang, R.; Bonn, D.A.; Hardy, W.N.; Rütt, U.; Gutowski, O.; et al. X-ray diffraction observations of a charge-density-wave order in superconducting ortho-II YBa2Cu3O6.54 single crystals in zero magnetic field. Phys. Rev. Lett. 2013, 110, 137004. [Google Scholar] [CrossRef] [PubMed]
- Kohsaka, Y.; Taylor, C.; Fujita, K.; Schmidt, A.; Lupien, C.; Hanaguri, T.; Azuma, M.; Takano, M.; Eisaki, H.; Takagi, H.; et al. An intrinsic bond-centered electronic glass with unidirectional domains in underdoped cuprates. Science 2007, 315, 1380–1385. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Mayaffre, H.; Krämer, S.; Horvatić, M.; Berthier, C.; Hardy, W.N.; Liang, R.; Bonn, D.A.; Julien, M.-H. Incipient charge order observed by NMR in the normal state of YbBa2Cu3Oy. Nat. Commun. 2015, 6, 6438. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.H.; Buchholz, M.; Trabant, C.; Chang, C.F.; Komarek, A.C.; Heigl, F.; Zimmermann, M.V.; Cwik, M.; Nakamura, F.; Braden, M.; et al. Charge stripe order near the surface of 12-percent doped La2−xSrxCuO4. Nat. Commun. 2012, 3, 1023. [Google Scholar] [CrossRef] [PubMed]
- Fine, B.V. Comment on “broken translational and rotational symmetry via charge stripe order in underdoped YBa2Cu3O6+y”. Science 2016, 351, 235. [Google Scholar] [CrossRef] [PubMed]
- Comin, R.; Sutarto, R.; Neto, E.H.D.S.; Chauviere, L.; Liang, R.; Hardy, W.N.; Bonn, D.A.; He, F.; Sawatzky, G.A.; Damascelli, A. Response to comment on “Broken translational and rotational symmetry via charge stripe order in underdoped YBa2Cu3O6+y”. Science 2016, 351, 235. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Chubukov, A.V. Enhancement of superconductivity at the onset of charge-density-wave order in a metal. Phys. Rev. B 2015, 92, 125108. [Google Scholar] [CrossRef]
- Soshi, I.; Motoharu, I. Possibility of charge density wave transition in a SrPt2Sb2 superconductor. J. Phys. Condens. Matter 2016, 28, 165702. [Google Scholar]
- Kiss, T.; Yokoya, T.; Chainani, A.; Shin, S.; Hanaguri, T.; Nohara, M.; Takagi, H. Charge-order-maximized momentum-dependent superconductivity. Nat. Phys. 2007, 3, 720–725. [Google Scholar] [CrossRef]
- Dressel, M. Quantum criticality in organic conductors? Fermi liquid versus non-fermi-liquid behaviour. J. Phys. Condens. Matter 2011, 23, 293201. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.H.P.; Xu, H.C.; Chen, C.; Huang, Z.C.; Lou, X.; Pu, Y.J.; Song, Q.; Xie, B.P.; Abdel-Hafiez, M.; Chareev, D.A.; et al. Anomalous correlation effects and unique phase diagram of electron-doped FeSe revealed by photoemission spectroscopy. Nat. Commun. 2016, 7, 10840. [Google Scholar] [CrossRef] [PubMed]

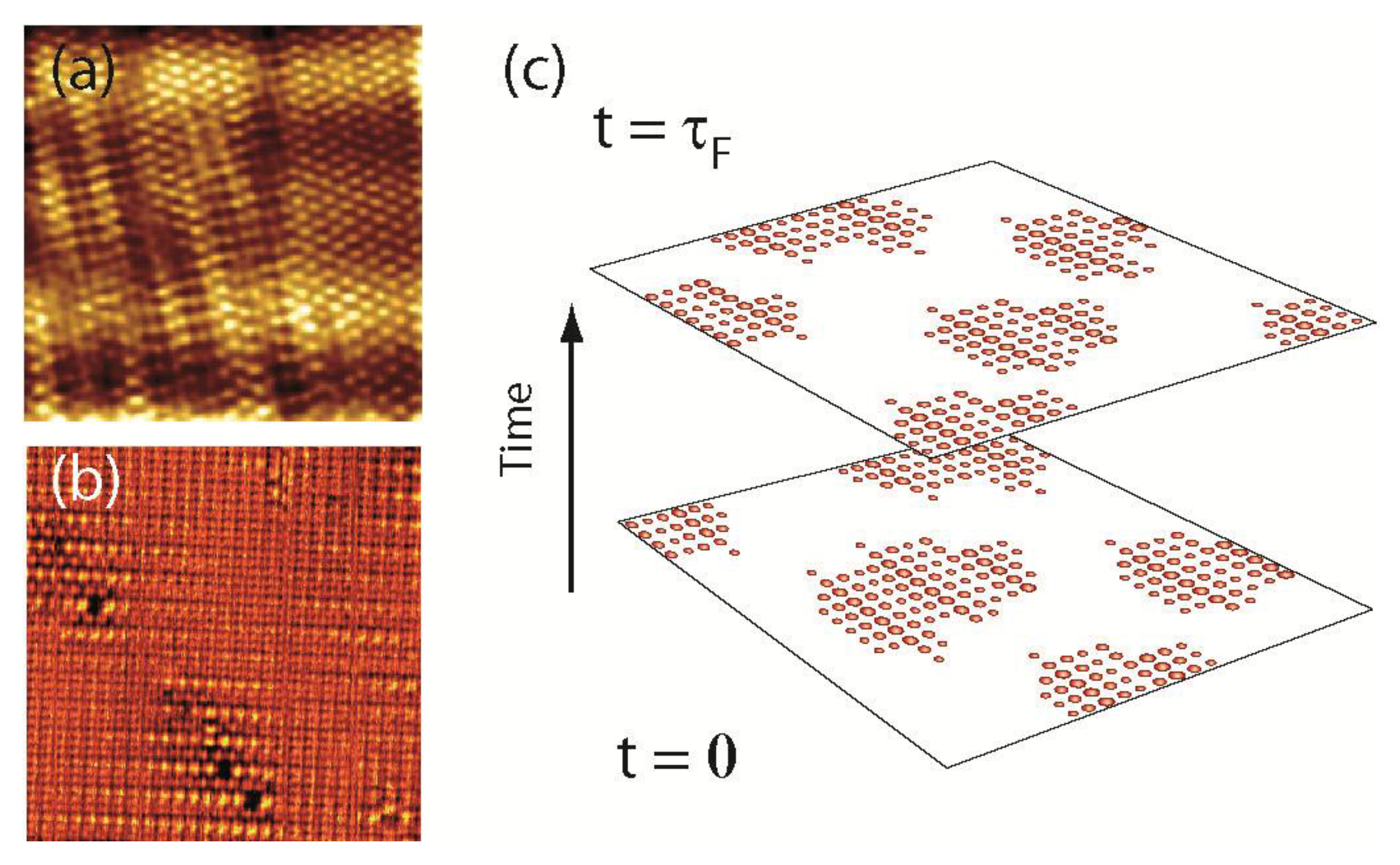
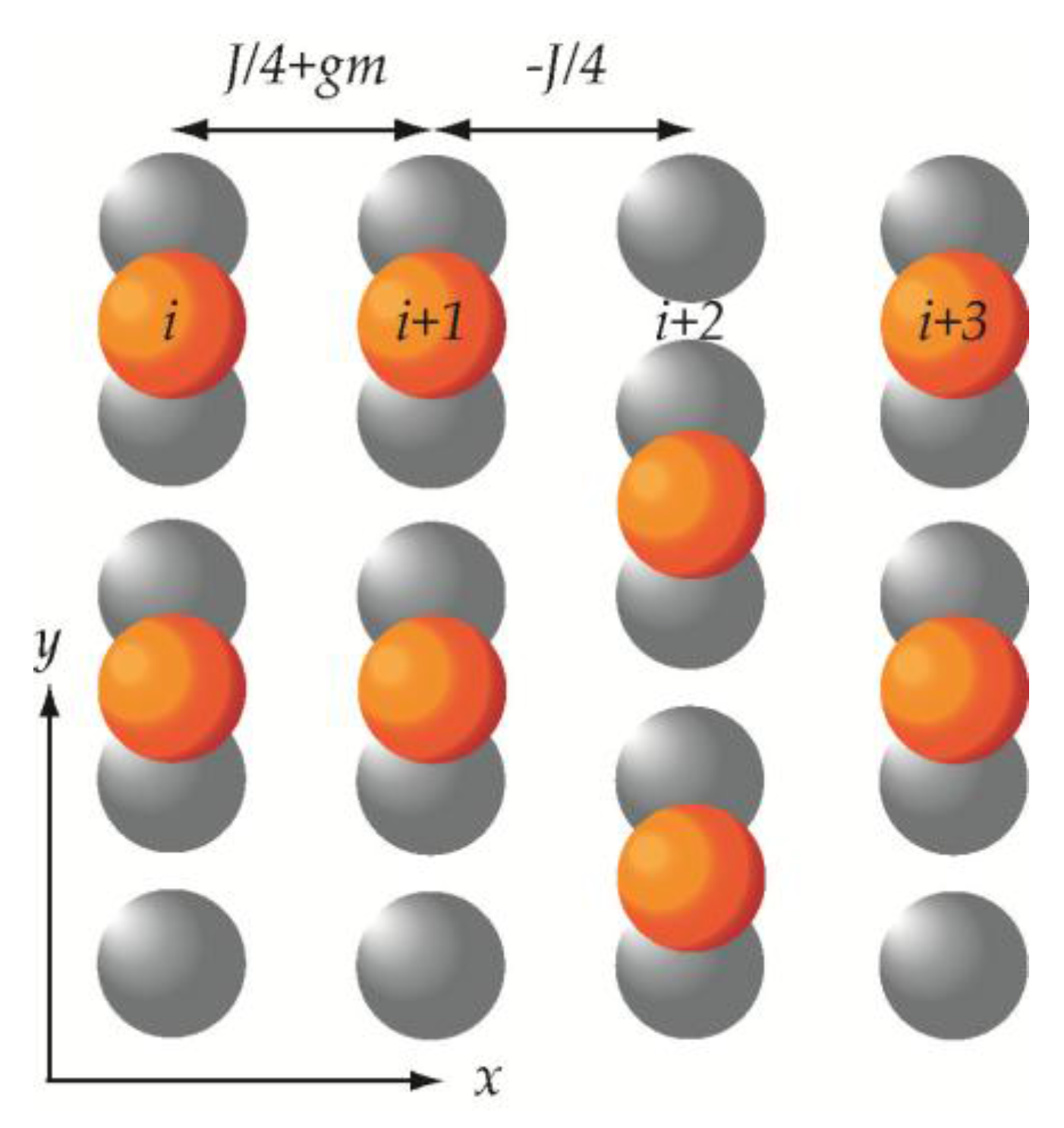

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertel, E.; Menzel, A. Fluctuating Charge Order: A Universal Phenomenon in Unconventional Superconductivity? Symmetry 2016, 8, 45. https://doi.org/10.3390/sym8060045
Bertel E, Menzel A. Fluctuating Charge Order: A Universal Phenomenon in Unconventional Superconductivity? Symmetry. 2016; 8(6):45. https://doi.org/10.3390/sym8060045
Chicago/Turabian StyleBertel, Erminald, and Alexander Menzel. 2016. "Fluctuating Charge Order: A Universal Phenomenon in Unconventional Superconductivity?" Symmetry 8, no. 6: 45. https://doi.org/10.3390/sym8060045
APA StyleBertel, E., & Menzel, A. (2016). Fluctuating Charge Order: A Universal Phenomenon in Unconventional Superconductivity? Symmetry, 8(6), 45. https://doi.org/10.3390/sym8060045