Bézier Triangles with G² Continuity across Boundaries

Abstract

PN (point-normal) triangles are cubic Bézier triangles which meet at their edges to surface a triangular mesh, but this only achieves $G^0$ continuity. We define blending regions that span the edges shared by adjacent pairs of triangular domains and blend the corresponding Bézier triangles using a univariate blending function formulated in terms of barycentric coordinates. This produces $G^2$ continuity across boundaries while preserving $G^1$ continuity at vertices. The sharpness of the blends can be controlled locally by varying the extent of these blending regions. We demonstrate the effectiveness of our technique by showing several modeling examples.

1. Introduction

Constructing a smooth surface over a triangular mesh is an important topic in geometric modeling and computer graphics. Over recent decades, a variety of techniques for this problem have been proposed [1,2,3,4,5].

The curved point-normal (PN) triangle [2,3] is one of the more practical approaches to generating a surface over a triangular mesh. A type of cubic Bézier triangle [6], called a PN triangle, is created for each triangle in the mesh, using the mesh vertices and normal vectors. A surface is then formed by the set of PN triangles, which share a common tangent plane ($G^1$ continuity) at each vertex. However, while the edges of adjacent triangles are concurrent, the tangent planes do not necessarily coincide, resulting in only $G^0$ continuity. This makes PN triangles less applicable to the wide range of geometric modeling and graphics applications. To overcome this limitation, Fünfzig et al. [3] introduced PNG1 triangles, which are similar to PN triangles, but their control points are blended pairwise to produce a surface with full $G^1$ continuity. In general, blending control points is suitable for generating a smooth surface, but it would be quite difficult to create the sharp features such as darts, creases and corners using this approach.

In this paper, we aim to generate a smooth surface with $G^2$ continuity while producing sharp features in desired regions. For this, we extend PN triangles and construct a blending region around the common boundary of two adjacent Bézier triangles, which are then linearly blended. Compared to the previous approaches, our method has the strength to handle smoothness and sharpness simultaneously. Figure 1 shows the main stages in this technique.

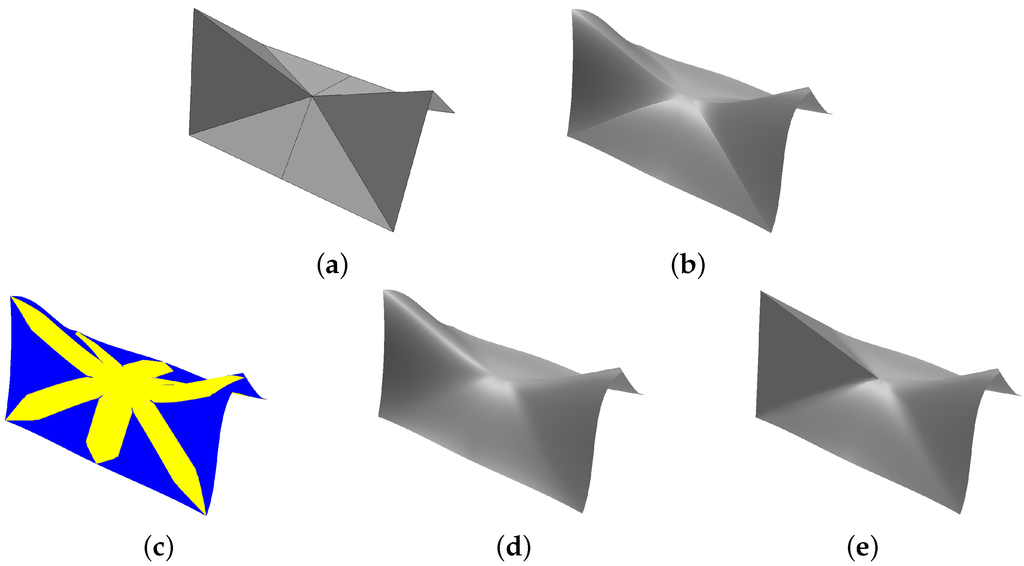
Figure 1. Blending of Bézier triangles: (a) A given triangular mesh; (b) Cubic Bézier triangles with $G^0$ continuity; (c) Blending regions (in yellow) between adjacent triangles; (d) A smoothly blended surface; (e) A blended surface with sharp features.

The main contributions of this paper can be summarized as follows:

• A simple technique for generating a smooth surface with $G^2$ continuity over a triangular mesh.
• Surface construction using a simple linear blending of two Bézier triangles rather than a manifold.
• Interactive control of the blending region on each Bézier triangle allows sharp features such as darts, corners and creases to be created in a controlled manners.

The rest of this paper is organized as follows. In Section 2, we briefly review some related recent work on the surfacing of triangular meshes, and in Section 3, we explain how to construct a PN triangle on each triangle of a mesh. The blending of PN triangles is then described in Section 4, and various examples are given in Section 5. In Section 6, we conclude the paper and suggest some future research.

2. Related Work

Vlachos et al. [2] introduced point-normal (PN) triangles for surfacing a triangular mesh. On each triangle of a mesh, they create a cubic Bézier triangle using vertices and normals from the mesh. Adjacent triangles share an edge but not the tangent planes along that edge. Thus, this method is restricted to generating a $G^0$-continuous surface. Nevertheless, they achieve the appearance of visual smoothness by introducing an auxiliary set of quadratic Bézier triangles from which smoothly varying normals can be computed. Fünfzig et al. [3] extended the PN triangle to the PNG1 triangle which has tangent-plane continuity across triangle boundaries. A PNG1 triangle is constructed by blending each Bézier triangle with the three neighbors that share its edges.

Blending techniques are widely used in geometric modeling. Vida et al. [7] survey the parametric blending of curves and surfaces. Depending on the number of surfaces to be blended, various approaches have been proposed. Choi and Ju [8] used a rolling ball to generate a tubular surface with $G^1$-continuous contact to the adjacent surfaces. This technique can be made more flexible by varying the radius of the ball [9].

Hartmann [10] showed how to construct $G^n$ parametric blending surfaces by specifying a blending region on each surface to be blended, using two curves, and reparameterizing the region with common parameters. A univariate blending function is then constructed using one of three common parameters to create a smooth blend. Song and Wang [11] extended this method by reparameterizing the blending regions automatically.

A more general blending scheme was introduced by Grim and Hughes [12]. Starting with a control mesh of arbitrary topology, they construct a manifold structure consisting of charts and transition functions. A smooth surface is then constructed by combining geometries on overlapping charts using a blending function. Cotrina and Pla [13] described a similar algorithm for constructing $C^k$-continuous surfaces with B-spline boundary curves, which can be viewed as a generalized B-spline surface. This approach was subsequently generalized by Cotrina et al. [14] to produce three different types of surfaces. However, these techniques require complicated transition functions between overlapping charts.

Ying and Zorin [15] created smooth surfaces of arbitrary topology by constructing charts in the complex plane and combining them with simple transition functions. This approach provides both $C^{\infty }$ continuity and local control of the surface. However, the resulting surfaces are not piecewise polynomial or rational. Recently, Vecchia et al. [4] overcame this limitation. They constructed piecewise-rational surfaces of arbitrary topology and smoothness from triangular meshes. The transition functions between overlapping charts were then obtained by subchart parameterization, and geometries on each chart were blended. This method was subsequently extended to produce sharp features such as creases, corners or cusps [5].

The work that we have briefly reviewed in this section has demonstrated that the application of a blending function to overlapping surfaces is a flexible way to create blends. However, the need for charts which can accommodate many different topologies makes these techniques difficult to implement, and can also offer obstacles to control. Our technique is much simpler because blending is restricted to easily identified regions spanning pairs of triangles which share an edge. Nevertheless, like other techniques, our method is able to produce sharp features when these are required.

3. Cubic Bézier Triangles

On each triangle of the given mesh, we construct a cubic Bézier triangle $\mathbf{b}(u,v,w)$ of the following form:

$$\begin{array}{ccc}\hfill \mathbf{b}(u,v,w)& =& \sum _{i+j+k=3}{\mathbf{b}}_{ijk}\frac{3!}{i!j!k!}{u}^i{v}^j{w}^k,u+v+w=1,\hfill \end{array}$$

(1)

where $(u,v,w)$ are barycentric coordinates in a triangular domain and ${\mathbf{b}}_{ijk}$ are control-points (see Figure 2).

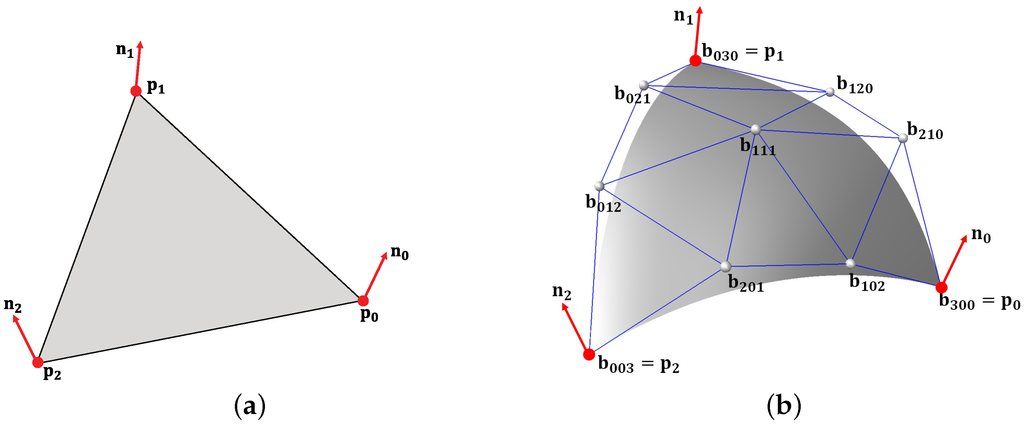
Figure 2. (a) A cubic Bézier triangle; (b) Constructed on a triangle.

The control-points of a cubic Bézier triangle are determined from its vertices ${\mathbf{p}}_1,{\mathbf{p}}_2$ and ${\mathbf{p}}_3$, and the corresponding normals ${\mathbf{n}}_1,{\mathbf{n}}_2$ and ${\mathbf{n}}_3$ as follows:

$$\begin{array}{c}{\mathbf{b}}_{300}={\mathbf{p}}_1,{\mathbf{b}}_{030}={\mathbf{p}}_2,{\mathbf{b}}_{003}={\mathbf{p}}_3\hfill \\ {\mathbf{b}}_{210}=(2{\mathbf{p}}_1+{\mathbf{p}}_2-w_{12}{\mathbf{n}}_1)/3\hfill \\ {\mathbf{b}}_{120}=(2{\mathbf{p}}_2+{\mathbf{p}}_1-w_{21}{\mathbf{n}}_2)/3\hfill \\ {\mathbf{b}}_{021}=(2{\mathbf{p}}_2+{\mathbf{p}}_3-w_{23}{\mathbf{n}}_2)/3\hfill \\ {\mathbf{b}}_{012}=(2{\mathbf{p}}_3+{\mathbf{p}}_2-w_{32}{\mathbf{n}}_3)/3\hfill \\ {\mathbf{b}}_{102}=(2{\mathbf{p}}_3+{\mathbf{p}}_1-w_{31}{\mathbf{n}}_3)/3\hfill \\ {\mathbf{b}}_{201}=(2{\mathbf{p}}_1+{\mathbf{p}}_3-w_{13}{\mathbf{n}}_1)/3\hfill \\ {\mathbf{b}}_{111}=E+(E-V)/2\hfill \end{array},$$

(2)

where $w_{ij}=({\mathbf{p}}_j-{\mathbf{p}}_i)·{\mathbf{n}}_i$, $E=({\mathbf{b}}_{210}+{\mathbf{b}}_{120}+{\mathbf{b}}_{021}+{\mathbf{b}}_{012}+{\mathbf{b}}_{102}+{\mathbf{b}}_{201})/6$ and $V=({\mathbf{p}}_1+{\mathbf{p}}_2+{\mathbf{p}}_3)/3$. Figure 3b shows cubic Bézier triangles constructed from a triangular mesh in Figure 3a. We have already explained that this surface has $G^1$ continuity at triangle vertices, but only $G^0$ continuity across triangle edges.

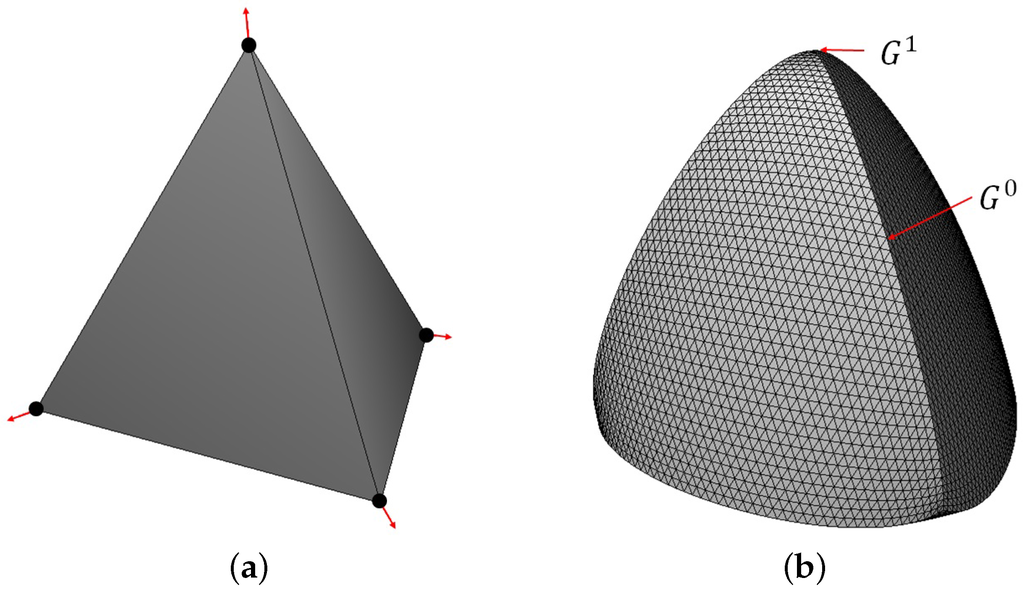
Figure 3. (a) A triangular mesh; (b) Surface of cubic Bézier triangles.

4. Smooth Blending of Bézier Triangles

4.1. Barycentric Coordinates with Respect to Different Triangular Domains

We will now show how to blend two Bézier triangles to achieve $G^2$ continuity across their boundaries. Figure 4 shows four domain triangles $T_i$, $i=0,1,2,3$ with vertices $({\mathbf{a}}_i,{\mathbf{b}}_i,{\mathbf{c}}_i)$. We subdivide the domain triangle $T_0$ into three subdomains $T_{01},T_{02}$ and $T_{03}$. If a point $\mathbf{u}$ has the barycentric coordinates $(u,v,w)$ with respect to $T_0=({\mathbf{a}}_0,{\mathbf{b}}_0,{\mathbf{c}}_0)$, then the subdomain where it lies can be identified by its smallest coordinate:

$$\left\{\begin{array}{c}\mathbf{u}\in T_{01}\text{if}u\text{is}\text{the}\text{smallest}\text{coordinate}\hfill \\ \mathbf{u}\in T_{02}\text{if}v\text{is}\text{the}\text{smallest}\text{coordinate}\hfill \\ \mathbf{u}\in T_{03}\text{if}w\text{is}\text{the}\text{smallest}\text{coordinate}\hfill \end{array}.\right.$$

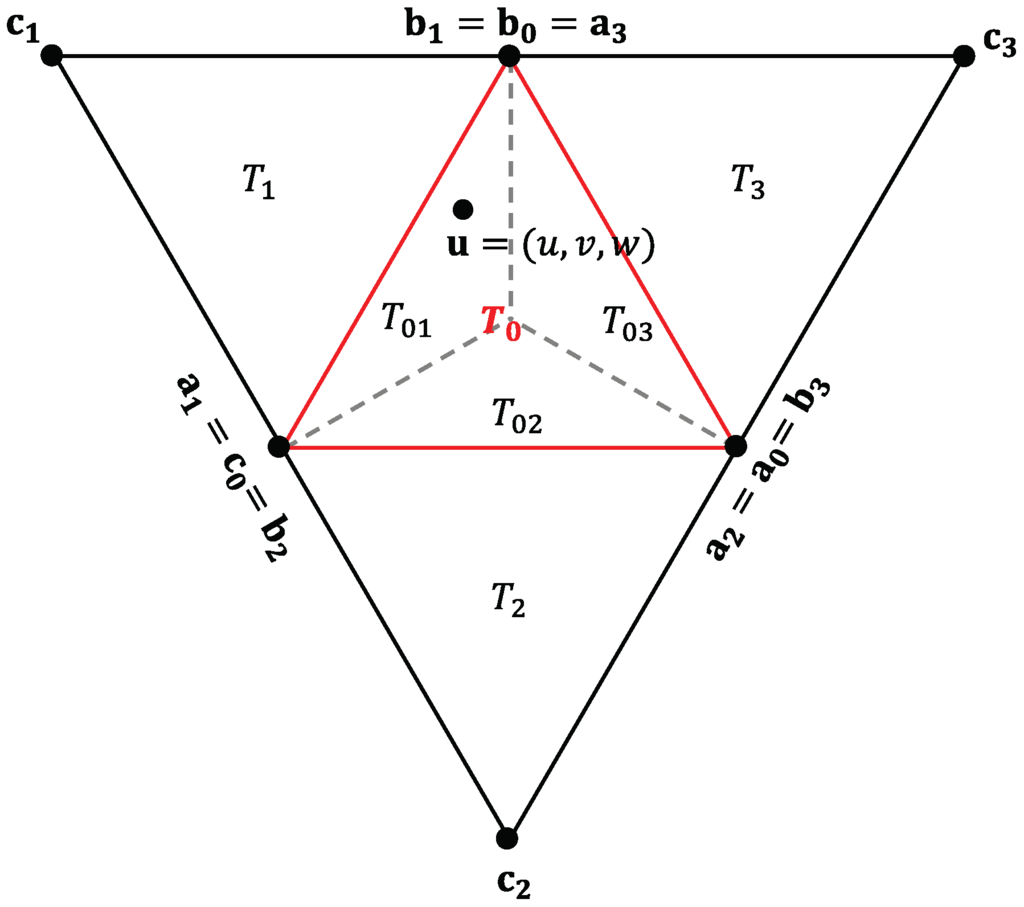
Figure 4. Four domain triangles $T_0,T_1,T_2$ and $T_3$, and the three subdomains $T_{01},T_{02}$ and $T_{03}$.

If $\mathbf{u}$ lies in $T_{01}$, then we blend the two Bézier triangles ${\mathbf{b}}_0(u,v,w)$ and ${\mathbf{b}}_1(u_1,v_1,w_1)$, defined on $T_0$ and $T_1$ respectively, where $(u_1,v_1,w_1)$ are the barycentric coordinates of $\mathbf{u}$ with respect to $T_1$. For a point in $T_{02}$, we blend ${\mathbf{b}}_0(u,v,w)$ and ${\mathbf{b}}_2(u_2,v_2,w_2)$, and similarly for points in $T_{03}$. Based on the ratios of the lengths in Figure 5, the barycentric coordinates $(u_i,v_i,w_i)$ of $\mathbf{u}$ with respect to $T_i$, $i=1,2,3$ can be expressed as follows:

$$\begin{array}{c}(u_1,v_1,w_1)=(1-v,1-w,-u)\hfill \\ (u_2,v_2,w_2)=(1-w,1-u,-v)\hfill \\ (u_3,v_3,w_3)=(1-u,1-v,-w)\hfill \end{array}.$$

(3)

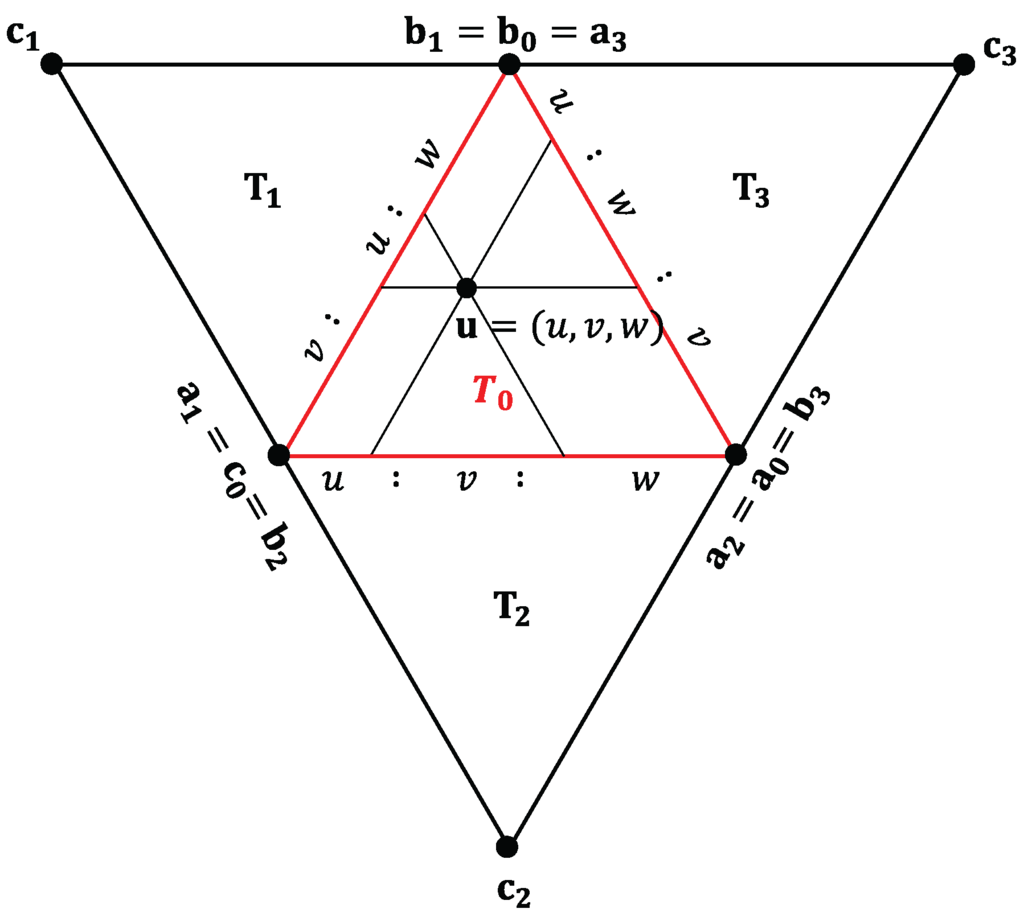
Figure 5. Ratios of lengths that determine the barycentric coordinates $(u,v,w)$ [6].

For example, the barycentric coordinates $(u,v,w)$ of ${\mathbf{c}}_0$ with respect $T_0$ are $(0,0,1)$ and its coordinates $(u_1,v_1,w_1)$ with respect to $T_1$ are $(1-v,1-w,-u)=(1,0,0)$. These coordinate systems serve the same purpose as the charts used to find transition functions in manifold-based approaches, but our method is much simpler.

4.2. Defining Blending Regions

Now, we can define a blending region between two adjacent Bézier triangles. Given a point $\mathbf{u}$ in $T_{02}$, as shown in Figure 6, we can define two vectors $\mathbf{a}$ and $\mathbf{b}$ as follows:

$$\mathbf{a}=\mathbf{u}-{\mathbf{c}}_0=(u,v,w-1),\mathbf{b}={\mathbf{a}}_0-{\mathbf{c}}_0=(1,0,-1).$$

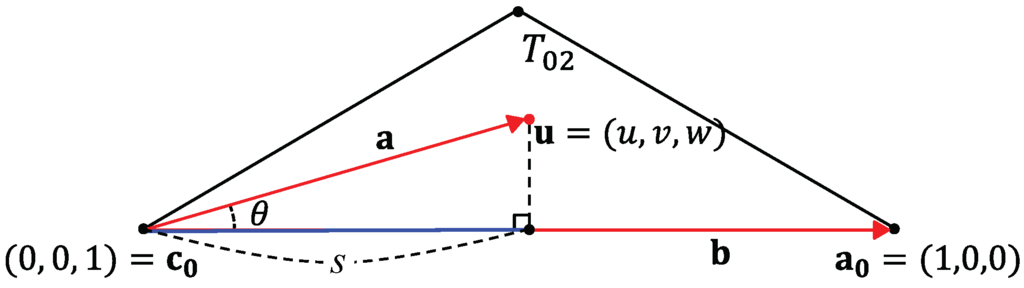
Figure 6. Projected length of ($\mathbf{a}$) on to ($\mathbf{b}$).

Note that the barycentric coordinates of a vector require that all coordinates add to 0. We now find the length s of $\mathbf{a}$ projected on to $\mathbf{b}$, which can be expressed as follows:

$$s=\parallel \mathbf{a}\parallel cos\theta =\frac{\mathbf{a}·\mathbf{b}}{\parallel \mathbf{b}\parallel }=\frac{u-w+1}{\sqrt{2}},$$

where $0\le s\le \sqrt{2}$.

Let $h(>0)$ be a user-specified constant for controlling the extent of the blending region $r\left(s\right)$, which can then be parameterized in terms of s as follows:

$$r\left(s\right)=\left\{\begin{array}{cc}s/\sqrt{3}& (0<s<1.5h)\hfill \\ \\ \sqrt{h^2-{(2h-s)}^2}& (1.5h\le s<2h)\hfill \\ \\ h& (2h\le s<\sqrt{2}-2h)\hfill \\ \\ \sqrt{h^2-{(s-\sqrt{2}+2h)}^2}& (\sqrt{2}-2h\le s<\sqrt{2}-1.5h)\hfill \\ \\ (\sqrt{2}-s)/\sqrt{3}& (\sqrt{2}-1.5h\le s<\sqrt{2})\hfill \end{array}.\right.$$

Figure 7a shows the blending region of the subdomain $T_{02}$ in gray. The dark gray circular segments of radius h give this region a smooth boundary. The maximum value of h is $\sqrt{2}/4$, when the two circular segments fuse into one ($2h=\sqrt{2}-2h$).

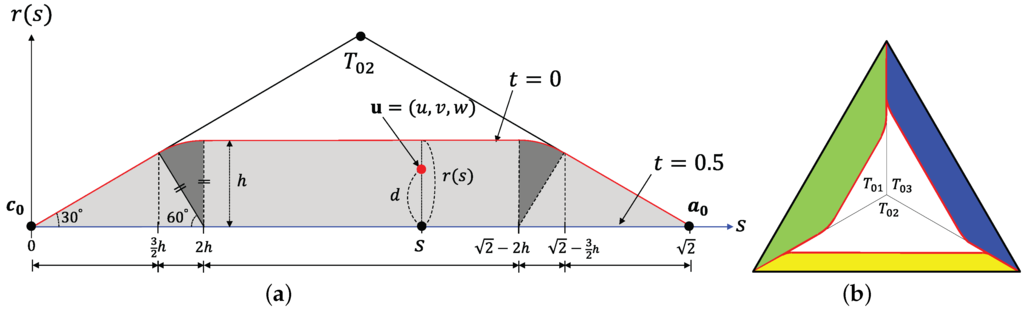
Figure 7. (a) Parameterization of a blending region; (b) Different blending regions.

We can now introduce a blending parameter t, defined as follows:

$$t=\left\{\begin{array}{cc}0.5\times (1-d/r\left(s\right))& \text{for}d\le r\left(s\right)\hfill \\ 0& \text{for}d>r\left(s\right)\hfill \end{array},\right.$$

(4)

where $d=\sqrt{{\parallel \mathbf{a}\parallel }^2-s^2}=\sqrt{u^2+v^2+{(w-1)}^2-s^2}$ is the distance between $\mathbf{u}$ and $\overline{{\mathbf{c}}_0{\mathbf{a}}_0}$. Thus, t is 0 outside the blending region, and it varies from 0 to $0.5$ inside the blending region, as shown in Figure 7a. In our method, we can define different blending regions on each edge of a domain triangle by using different values of the user-specified h, as shown in Figure 7b. Sharp edges can easily be created by degenerate case ($h=0$).

4.3. Blending Bézier Triangles

Finally, we blend pairs of adjacent Bézier triangles which share a common boundary. We again consider a point $\mathbf{u}=(u,v,w)$ in $T_{02}$, with barycentric coordinates $(u_2,v_2,w_2)$ with respect to $T_2$. A point on the blending surface $S(u,v,w)$ can now be obtained by linearly blending two points ${\mathbf{p}}_0={\mathbf{b}}_0(u,v,w)$ and ${\mathbf{p}}_2={\mathbf{b}}_2(u_2,v_2,w_2)$ on the corresponding Bézier triangles, as follows:

$$S(u,v,w)=(1-\alpha \left(t\right)){\mathbf{p}}_0+\alpha \left(t\right){\mathbf{p}}_2,$$

(5)

where $\alpha \left(t\right)$ is a blending function in terms of the parameter t determined by Equation (4). Note that $S(u,v,w)$ reverts to ${\mathbf{b}}_0(u,v,w)$ outside the blending region (the white area in Figure 7b).

Depending on the choice of $\alpha \left(t\right)$ in Equation (5), we can achieve different continuity across the edges of Bézier triangles. For $G^k$ continuity, the blending function $\alpha \left(t\right)$ should satisfy the following conditions:

$$\left\{\begin{array}{c}\alpha \left(0\right)=1\hfill \\ \alpha \left(1\right)=0\hfill \\ {\alpha }^{\prime }\left(0\right)={\alpha }^{\prime \prime }\left(0\right)=\cdots ={\alpha }^k\left(0\right)=0\hfill \\ {\alpha }^{\prime }\left(1\right)={\alpha }^{\prime \prime }\left(1\right)=\cdots ={\alpha }^k\left(1\right)=0\hfill \end{array}.\right.$$

In this paper, we achieve $G^2$ continuity across the edges of Bézier triangles by choosing the blending function shown in Figure 8 and formulated as follows:

$$\alpha \left(t\right)=-6t^5+15t^4-10t^3+1(0\le t\le 1).$$

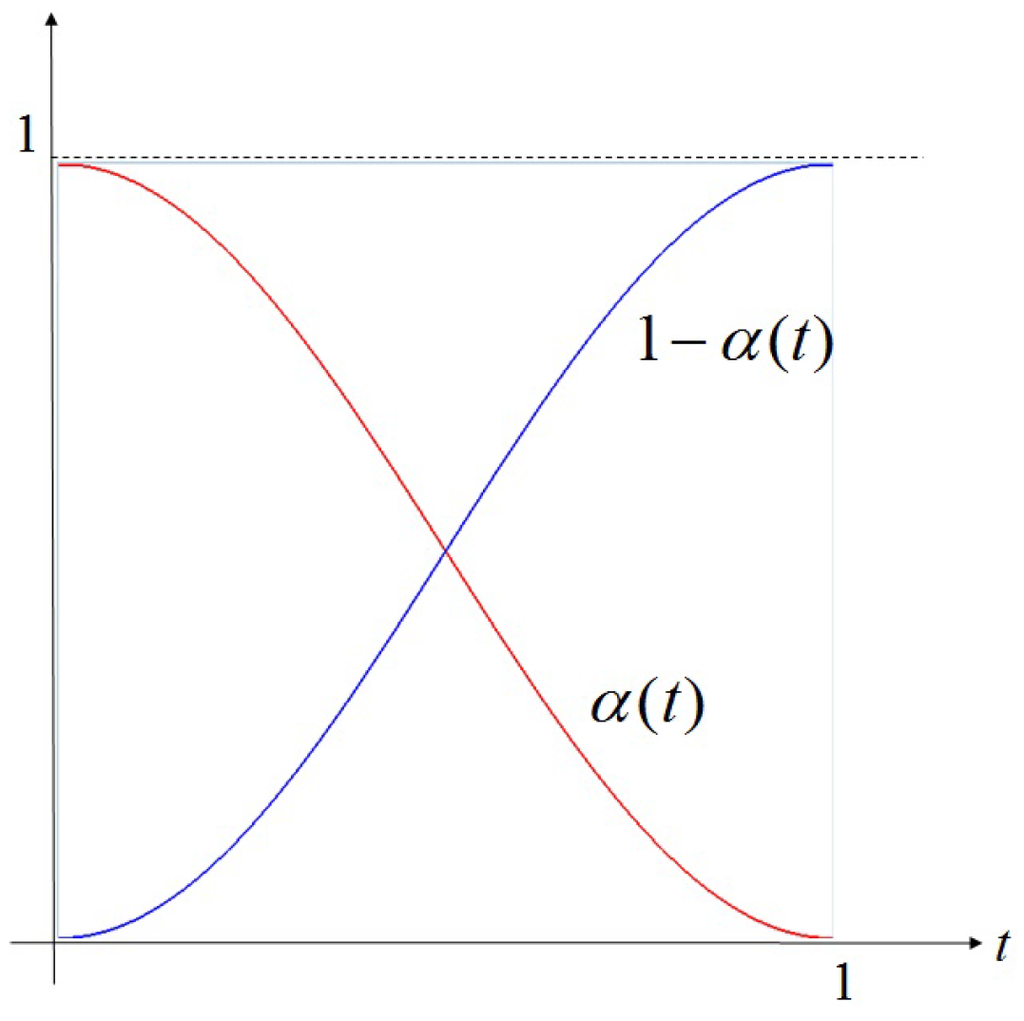
Figure 8. Quintic blending function $\alpha \left(t\right)$.

Singularities remain at the vertices of the Bézier triangles, where only $G^1$ continuity is achieved.

5. Experimental Results

We implemented our technique in C++ on a PC with an Intel Core i7 2.00GHz CPU with 8GB of main memory and an Intel(R) Iris Pro Graphics 5200. Figure 9 shows example blends on the mesh of Figure 3a with extents corresponding to $h=.106$ and $h=.212$, and their different blending results are shown in Figure 9b,d, respectively. If we set $h=0$, we obtain the PN triangles of Figure 3b.

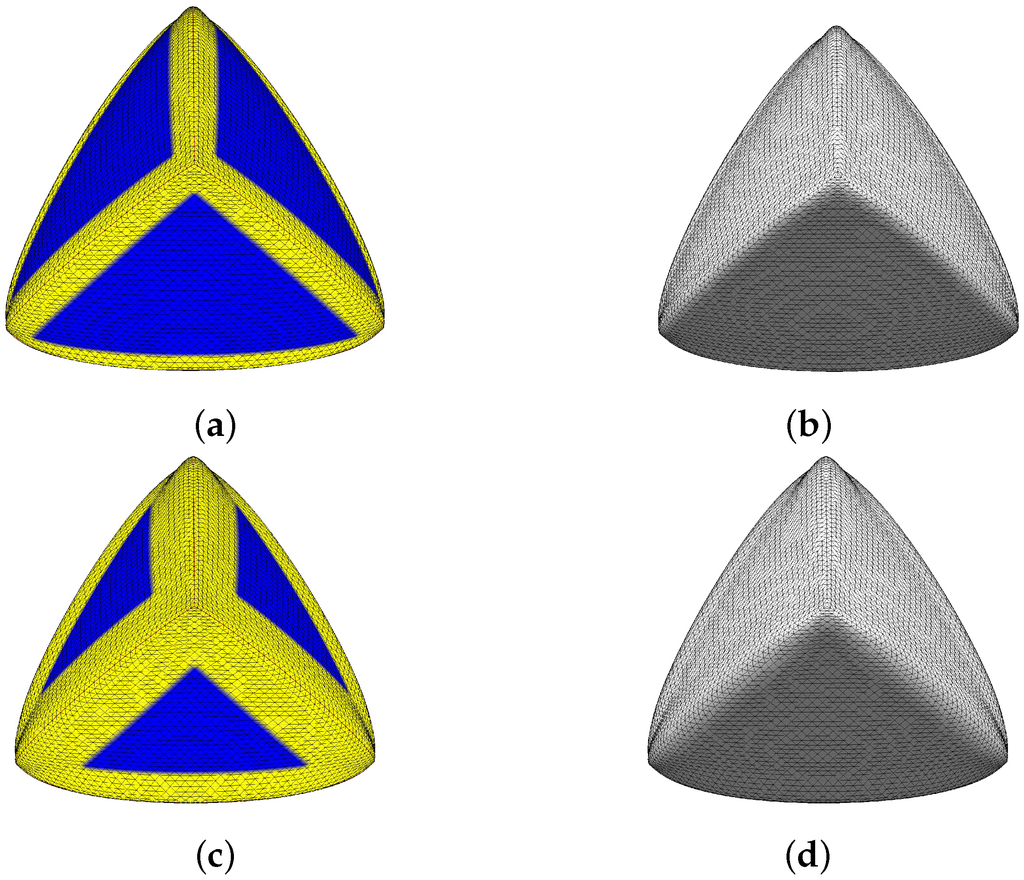
Figure 9. Blended triangles with (b) $h=.106$ and (d) $h=.212$. (blending regions are shown in yellow in (a),(c)).

Figure 10 shows a stellated dodecahedron surfaced by our method. Bézier triangles in Figure 10d join smoothly, whereas Figure 10b shows $G^0$ continuity between adjacent ones. Planar Bézier triangles can be used to construct surfaces with large flat areas as well as various sharp features, as shown in Figure 11.

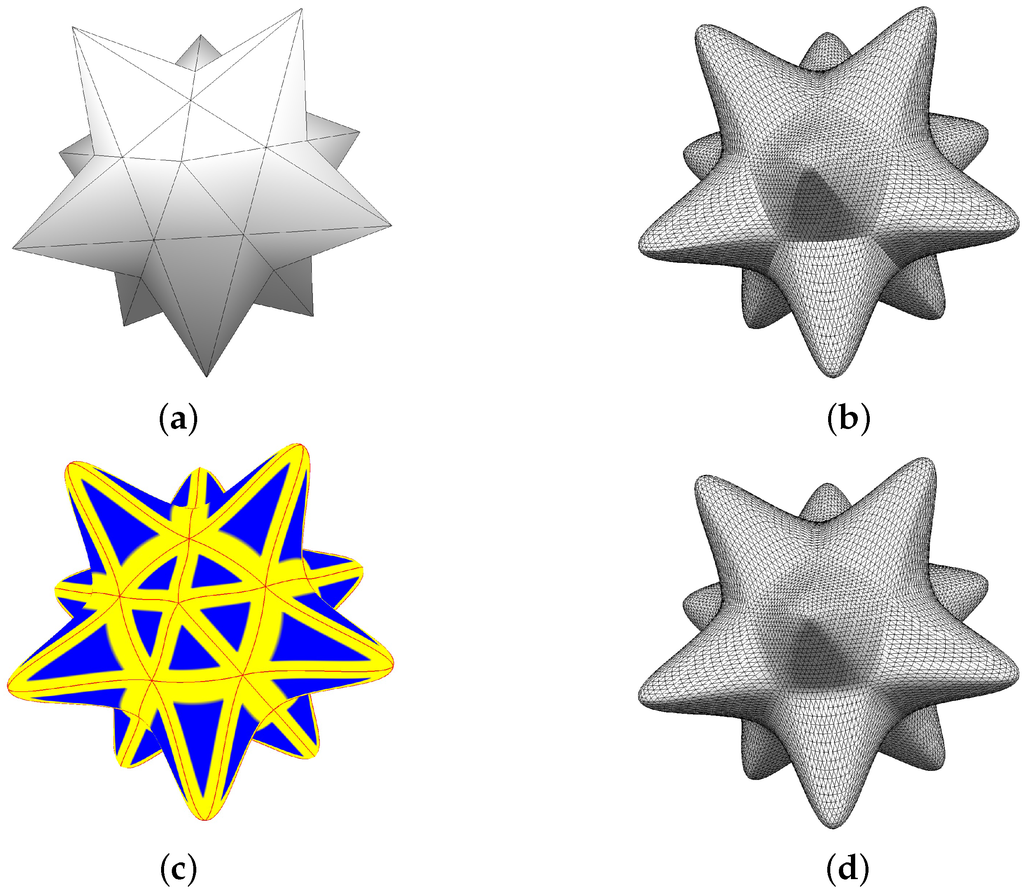
Figure 10. (a) A stellated dodecahedron; (b) Surfaced by PN triangles; (c),(d) Using our method (blend regions are shown in yellow in (c)).

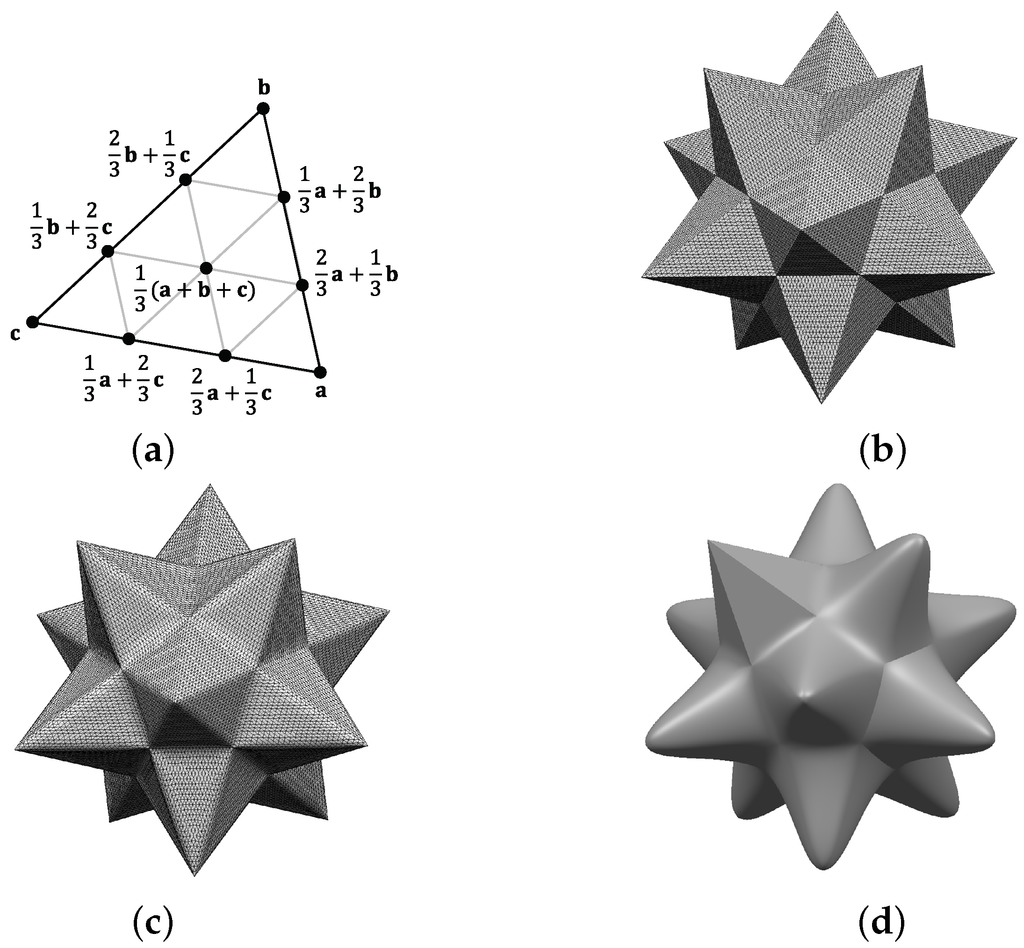
Figure 11. Planar Bézier triangles (defined using the scheme shown in (a)) produce (b) on object with flat faces ($h=0$), which can be (c) blended by setting $h=.106$. (d) Different values of h produces a variety of darts, crease and corners.

Figure 12a–d show more examples of creating sharp features. Figure 12b shows the result of blending Bézier triangles defined on each triangle of a given mesh in Figure 11a. Figure 11c shows the blending regions with different extents and planar Bézier triangles. Finally, the resulting sharp features are shown in Figure 11d.

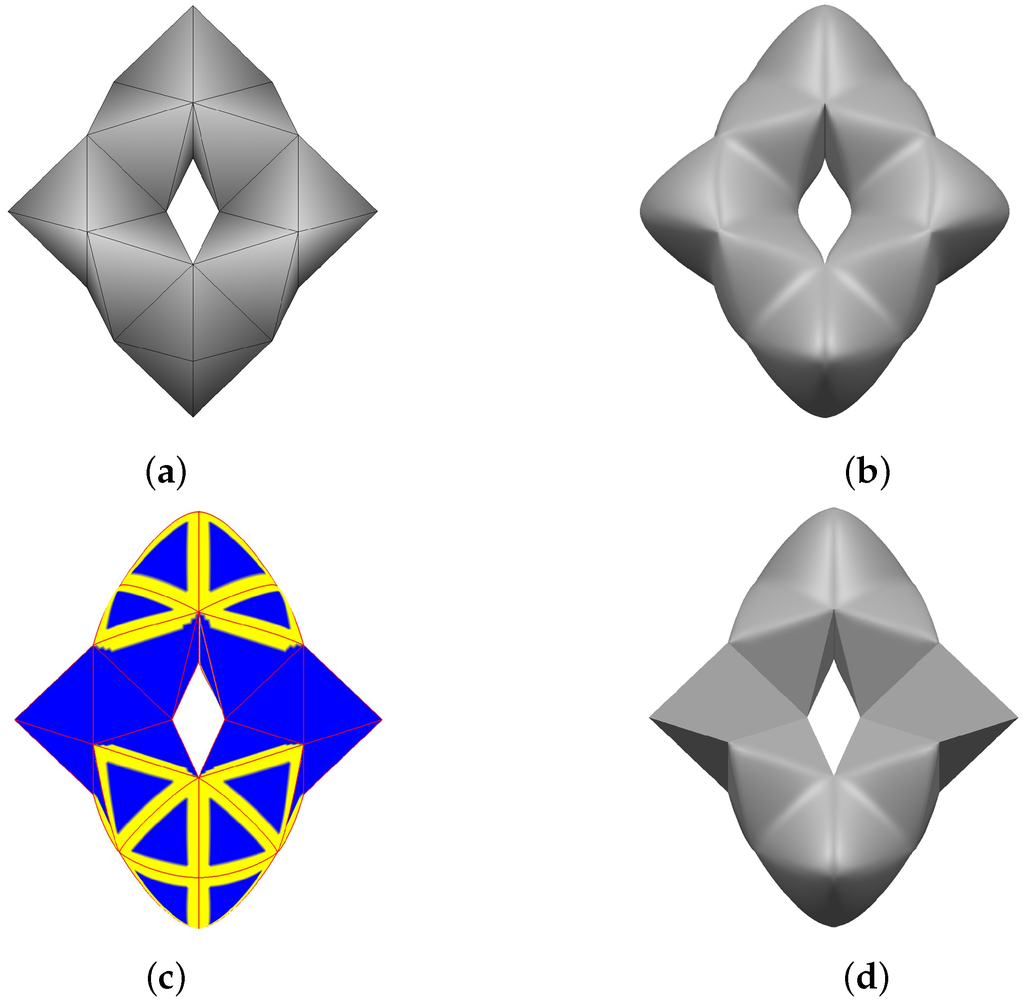
Figure 12. (a) A different geometry surfaced by Bézier triangles (b), and (c) Blending regions with different extents, and (d) Sharp features generated by blending different types of Bézier triangles.

Figure 13 shows various examples including non-symmetric objects. The first column shows the benchmark models also used in [2] and the second column shows the geometries generated by PN triangles, where Bézier triangles are joined with only $G^0$ continuity. Finally, smooth surfaces generated by our method are shown in the last column.

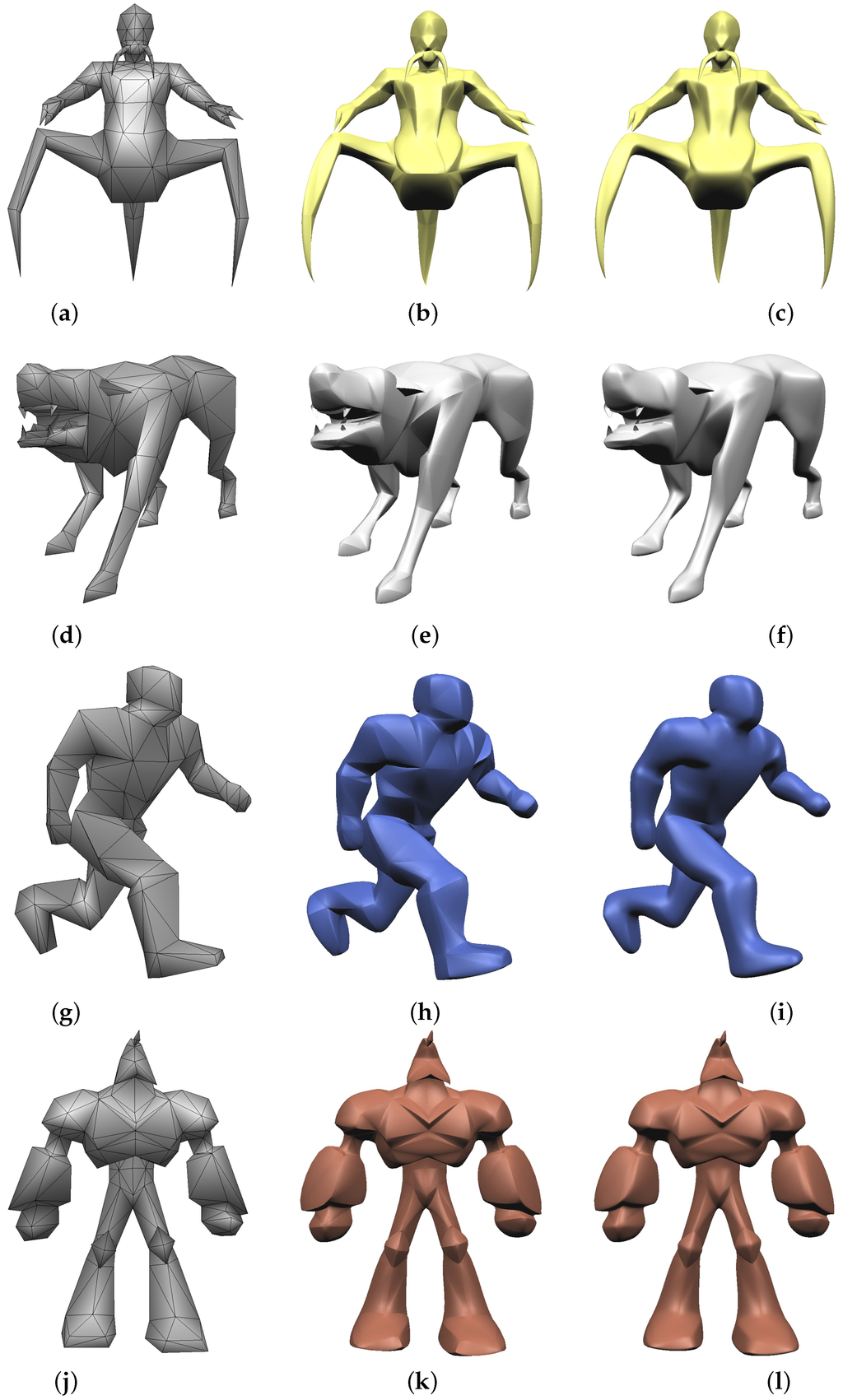
Figure 13. Comparison with PN triangles: (a), (d), (g), (h): control meshes; (b), (e), (h), (k): PN triangles with $G^0$ continuity; (c), (f), (i), (l): smooth surfaces with $G^2$ continuity.

6. Conclusions

We have shown how to construct a blending surface over a triangular mesh using Bézier triangles with improved continuity. We create blending regions that span the edges shared by pairs of triangles, using relative coordinates formulated in terms of ratios of barycentric coordinates. Using a blending function with second-order continuity at this edges, we obtain a surface with $G^1$ continuity at the corner points of Bézier triangles and $G^2$ continuity across the edges of the Bézier triangles. We can represent sharp features by controlling the blending regions of individual Bézier triangles and introducing planar Bézier triangles. In experimental results, we demonstrated the effectiveness of our technique by constructing several blending surfaces with or without sharp features.

The blending function employed in the current implementation is somewhat restricted to generating various blending effects. However, our technique can easily be extended by introducing blending functions with higher continuity or additional controllability [10]. We are also examining ways of increasing the geometric continuity at the vertices of Bézier triangles.