On Center, Periphery and Average Eccentricity for the Convex Polytopes

Abstract

A vertex v is a peripheral vertex in G if its eccentricity is equal to its diameter, and periphery $P\left(G\right)$ is a subgraph of G induced by its peripheral vertices. Further, a vertex v in G is a central vertex if $e\left(v\right)=rad\left(G\right)$, and the subgraph of G induced by its central vertices is called center $C\left(G\right)$ of $G.$ Average eccentricity is the sum of eccentricities of all of the vertices in a graph divided by the total number of vertices, i.e., $avec\left(G\right)=\{\frac{1}{n}\sum e_G\left(u\right);u\in V\left(G\right)\}.$ If every vertex in G is central vertex, then $C\left(G\right)=G$, and hence, G is self-centered. In this report, we find the center, periphery and average eccentricity for the convex polytopes.

1. Introduction

In the facility location problem, we select a site according to some standard judgment. For example, if we want to find out the exact location for an emergency facility, such as a fire station or a hospital, we reduce the distance between that facility and the area where the emergency happens, and if we are to decide the position for a service facility, like a post office, power station or employment office, we try to reduce the traveling time of all people who have been living in that district. In the construction of a railway line, a pipeline and a superhighway, we will reduce the distance of the constructing unit for the people living in that area. All of these situations illustrate the concept of centrality but each of these three examples deals with different types of centers. Nowadays, centrality questions are being studied with the help of distance and graphs. We shall observe that many kinds of centers are helpful in facility location problems.

The most important and fundamental concept that extends to the whole of graph theory is distance. The distance is applicable in many fields, such as graph operation, extremal problems on connectivity, diameter and isomorphism testing. The theme of distance is used to check the symmetry of graphs. It also provides a base for many useful graph parameters, like radius, diameter, metric dimension, eccentricity, center and periphery, etc.

The eccentricity of the vertices in G has a fundamental importance. Recently, many indices related to eccentricity have been derived, i.e., eccentric connectivity index, adjacent eccentric sum index, Wiener index and eccentric distance sum [1]. The center and periphery is also based on minimum and maximum eccentricity, respectively. W.Goddard and O. R. Oellermann in [2] have shown that if G is an undirected graph, then,

$$rad\left(G\right)\le diam\left(G\right)\le 2rad\left(G\right)$$

They also examined the radius and diameter of certain families of graphs in the same paper, as follows:

• $rad\left(K_n\right)=diam\left(K_n\right)=1$ for $n\ge 2,$
• $rad\left(C_n\right)=diam\left(C_n\right)=\frac{n}{2},$
• $rad\left(K_{m,n}\right)=diam\left(K_{m,n}\right)=2$ if m and n is at least two,
• $rad\left(P_n\right)=\frac{n-1}{2}$, $diam\left(P_n\right)=n-1.$

This implies that complete graphs $K_n$ for $n\ge 2$, complete bipartite graphs $K_{m,n}$ where $m,n\ge 2$ and all cycles are self-centered. Jordan [3] determined the diameter of a tree. Bela Bollobas [4] discussed the diameter of random graphs. The radius and diameter of a bridge graph are determined by Martin Farber in [5]. More general results were presented by V. Klee and D. Larman [6] and Bela Bollobas [4]. B. Hedman determined the sharp bounds for the diameter of the clique graph $K\left(G\right)$ in terms of the diameter of G. The idea of self-centered graphs is presented and elaborated by Ando, Akiyama and Avis individually [7]. These self-centered graphs are extensively studied in [7,8,9,10,11]. The extremal size of a connected self-centered graph with p vertices and r radius is explained by F. Buckely [12]. The center in maximal outer planar graphs is demonstrated by A. Proskurowski in [13]. Hedetniemi [14] has shown that every graph is the center of some graph. The center of graph G is the full graph if and only if $rad\left(G\right)=diam\left(G\right)$ [15]. F. Buckely and F. Harary [16] gave the concept of average eccentricity. Average eccentricity is the sum of eccentricities of all of the vertices in a graph divided by the total number of vertices, i.e.,

$$avec\left(G\right)=\frac{1}{n}\sum _{u\in V\left(G\right)}{e}_G\left(u\right).$$

The upper bounds of average eccentricity are determined by P. Dankelman, W. Goddard and C.S. Swart [17]. Average eccentricity is most important in communication networks. The average eccentricity of Sierpinski graphs $S_n^p$ is determined by Andreas, M. Hinz and Daniele Parisse [18]. Since 1980, the average eccentricity has had a great roll as a molecular descriptor in mathematical chemistry. This is attributed to V.A. Skorobogatov and A.A. Dobrynin [19]. For more details, please see [20,21,22] and the references therein.

Definition 1.

For a connected graph G, the eccentricity $e\left(v\right)$ of a vertex v is its distance to a vertex farthest from v. Thus,

$$e\left(v\right)=Max\left\{d\right(u,v):u\in V(G\left)\right\}.$$

Definition 2.

The radius $rad\left(G\right)$ of G is the minimum eccentricity among all vertices of G.

Definition 3.

The diameter $diam\left(G\right)$ of G is the maximum eccentricity among all vertices of G.

Definition 4.

Average eccentricity is the sum of eccentricities of all of the vertices in a graph divided by the total number of vertices, i.e.,

$$avec\left(G\right)=\frac{1}{n}\sum _{u\in V\left(G\right)}{e}_G\left(u\right).$$

Definition 5.

A vertex u is eccentric to a vertex v if $d(u,v)=e\left(v\right)$.

Definition 6.

A vertex v is a peripheral vertex in G if its eccentricity is equal to its diameter, and periphery $P\left(G\right)$ is a subgraph of G induced by its peripheral vertices. Further, a vertex v in G is a central vertex if $e\left(v\right)=rad\left(G\right)$, and the subgraph of G induced by its central vertices is called center $C\left(G\right)$ of G. If every vertex in G is a central vertex, then $C\left(G\right)=G$, and hence, G is self-centered.

In the present report, we discuss the center, periphery and average eccentricity for families of convex polytope graphs, $A_n$, $S_n$ and $T_n$.

2. The Center and Periphery for Convex Polytope $A_n$

In this section, we determine the center and periphery for convex polytope $A_n$.

Definition 7.

The graph of convex polytope (double antiprism) $A_n$ can be obtained from the graph of convex polytope $R_n$ by adding new edges $b_{i+1}{c}_i$, i.e.,

$$V\left(A_n\right)=V\left(R_n\right)\mathrm{and}E\left(A_n\right)=E\left(R_n\right)\cup \{b_{i+1}{c}_i:1\le i\le n\}.$$

Theorem 1.

For the family of convex polytope $A_n$, $n=2k$, $Cen\left(A_n\right)$ and Per $\left(A_n\right)$ are subgraphs induced by the vertices $(b_1,b_2,\dots ,b_{2k})$ and $\{a_i\cup c_i:1\le i\le 2k\}$, respectively.

Proof. 

For all even values of n, select a vertex $a_1$ on the cycle $(a_1{a}_2{a}_3\dots a_i\dots a_{2k})$. Then:

$$d(a_1,a_i)=i-1,1\le i\le k+1$$

(1)

when $i=k+2$, $d(a_1,a_i)=k-1$ and for $i=2k$, $d(a_1,a_i)=1.$

In addition, for every value of i within $k+2$ to $2k$, $d(a_1,a_i)$ must lie between $k-1$ and one, i.e.,

$$d(a_1,a_i)=2k+1-i;k+2\le i\le 2k.$$

Thus, to find the vertices farthest from $a_1$ in $A_n$, consider only $1\le i\le k+1$.

As each $a_i$ is adjacent to $b_i$, $b_{i-1}$ and each $b_i$ adjacent to $c_i,c_{i-1}$, therefore, (1) implies,

$$d(a_1,b_i)=i,1\le i\le k$$

$$d(a_1,c_i)=i+1,1\le i\le k$$

For $k+1\le i\le 2k$, consider the cycle $(b_1{b}_2\dots b_{k+1}\dots b_i\dots b_{2k})$. In this cycle, the distance between $b_i$ and $b_{2k}$ is $2k-i$, and $b_{2k}$ is adjacent to $a_1$, therefore, the distance between $a_1$ and $b_i$ is $2k-i+1$.

$$d(a_1,b_i)=2k-i+1,k+1\le i\le 2k.$$

Now, consider the cycle $(c_1{c}_2\dots c_{k+1}\dots c_i\dots c_{2k})$. The distance between $c_i$ and $c_{2k-1}$ is $2k-1-i$ and the vertex $c_{2k-1}$ is adjacent to $b_{2k}$ and $b_{2k}$ adjacent to $a_1$. It shows,

$$d(a_1,c_i)=2k-i+1,k+1\le i\le 2k-1.$$

For $i=2k$, $d(a_1,c_i)=2$.

Hence, $c_k$ is a vertex farthest from $a_1$.

$$e\left(a_1\right)=k+1$$

(2)

Thus, the eccentricity of each vertex on inner cycle $(a_1{a}_2{a}_3\dots a_i\dots a_{2k})$ is $k+1$.

In the same way, take cycle $(b_1{b}_2\dots b_i\dots .b_{2k})$; the distance between $b_1$ and $b_i$ in this cycle is,

$$d(b_1,b_i)=i-1;1\le i\le k+1$$

(3)

Each $b_i$ is adjacent to $a_i$ and $a_{i+1}$. Therefore,

$$d(b_1,a_1)=1,(b_1,a_2)=1$$

For $3\le i\le k+1$, consider the path $b_1\to a_2\to a_3\to \dots \to a_i$. Then, the distance between $a_i$ and $a_2$ is $i-2$. $a_2$ is also adjacent to $b_1$. Therefore, the distance between $b_1$ and $a_i$ is as follows,

$$d(b_1,a_i)=i-1,3\le i\le k+1$$

For $k+2\le i\le 2k$, consider the cycle $(a_1{a}_2\dots a_{k+2}\dots a_i\dots a_{2k})$. The distance between $a_i$ and $a_{2k}$ is $2k-i$. Further, $a_{2k}$ is adjacent to $a_1$ and $a_1$ adjacent to $b_1$. Therefore, the distance between $b_1$ and $a_i$ is $2k-i+2$.

$$d(b_1,a_i)=2k-i+2,k+2\le i\le 2k$$

Further, $b_i$ is also adjacent to $c_i$ and $c_{i-1}$; it follows from (3):

$$d(b_1,c_i)=i,1\le i\le k$$

For $k+1\le i\le 2k$, consider the cycle $(c_1{c}_2\dots c_{k+1}\dots c_i\dots c_{2k})$. The distance between $c_i$ and $c_{2k}$ is $2k-i$, where $c_{2k}$ is also adjacent to $b_1$. Therefore,

$$d(b_1,c_i)=2k-i+1,k+1\le i\le 2k$$

Hence, $b_{k+1}$, $a_{k+1}$ and $c_k$ are the vertices farthest from $b_1$. Therefore:

$$e\left(b_1\right)=k,$$

(4)

Hence, each vertex on the middle cycle $(b_1{b}_2\dots b_i\dots .b_{2k})$ has eccentricity k.

Further, to find out the eccentricity of the vertices on the outer cycle $(c_1{c}_2\dots c_i\dots c_{2k})$, choose a vertex $c_1$ on this cycle. The distance between $c_1$ and $c_i$ is $i-1$.

$$d(c_1,c_i)=i-1,$$

(5)

Each $c_i$ is adjacent to $b_i$ and $b_{i+1}$, i.e.,

$$d(c_1,b_1)=1,$$

(6)

For $3\le i\le k+1$, consider the path $c_1\to b_2\to b_3\to \dots \to b_i$. The distance between $b_2$ and $b_i$ is $i-2$. As $b_2$ is adjacent to $c_1$, therefore, $c_1$ and $b_i$ has the following distance,

$$d(c_1,b_i)=i-1,3\le i\le k+1$$

For $k+2\le i\le 2k$, consider the cycle $(b_1{b}_2\dots b_{k+2}\dots b_i\dots b_{2k})$. The distance between $b_i$ and $b_{2k}$ is $2k-i$. As $b_{2k}$ is adjacent to $b_1$ and $b_1$ adjacent to $c_1$, therefore, the distance between $c_1$ and $b_i$ is $2k-i+2$.

$$d(c_1,b_i)=2k-i+2,k+2\le i\le 2k.$$

Each $b_i$ is also adjacent to $a_i$ and $a_{i+1}$, using the result of (6),

$$d(c_1,a_1)=2,d(c_1,a_2)=2$$

For $3\le i\le k+2$, consider the path $c_1\to b_2\to b_3\to \dots \to b_{i-1}\to a_i$. In this path, the distance between $b_2$ and $b_{i-1}$ is $i-3$. $b_{i-1}$ is adjacent to $a_i$ and $b_2$ adjacent to $c_1$. Therefore, the distance between $c_1$ and $a_i$ is $i-1$.

$$d(c_1,a_i)=i-1,3\le i\le k+2$$

For $k+3\le i\le 2k$, consider the cycle $(a_1{a}_2\dots a_{k+2}\dots a_i\dots a_{2k})$. The distance between $a_i$ and $a_{2k}$ is $2k-i$. $a_{2k}$ is adjacent to $a_1$, $a_1$ adjacent to $b_1$ and $b_1$ adjacent to $c_1$. Therefore, the distance between $c_1$ and $a_i$ is $2k-i+3$.

$$d(c_1,a_i)=2k-i+3,k+3\le i\le 2k$$

This shows that $a_{k+1}$ is a vertex farthest from $c_1$. Therefore:

$$e\left(c_1\right)=k+1.$$

(7)

Therefore, (2), (4) and (7) imply,

$$diam\left(A_n\right)=k+1=\frac{n}{2}+1.$$

and:

$$rad\left(A_n\right)=k=\frac{n}{2}.$$

Consequently, Cen$\left(A_n\right)$ is a subgraph induced by vertices $(b_1,b_2,\dots ,b_{2k})$, while the set of vertices $\{a_1,a_2,\dots ,a_{2k},c_1,c_2,\dots ,c_{2k}\}$ is the peripheral vertices. Therefore, the periphery of $A_n$ is the subgraph induced by all of these vertices. ☐

Theorem 2.

For the family of convex polytope $A_n$, n is odd.

$$Cen\left(A_n\right)=Per\left(A_n\right)=A_n.$$

Proof. 

Consider, $n=2k+1$ $k\ge 2$. Select vertex $a_1$ on the cycle $(a_1{a}_2{a}_3\dots a_i\dots a_{2k+1})$. By using this,

$$d(a_1,a_i)=i-1,1\le i\le k+1$$

(8)

while i increases from $k+2$ to $2k+1$, $d(a_1,a_i)$ reduces from k to one.

$$d(a_1,a_i)=2k+2-i,k+2\le i\le 2k+1$$

Thus, to find the vertices farthest from $a_1$ in $A_n$, we have to take only those values of i that lie between one and $k+1$.

As each $a_i$ is adjacent to $b_i$, $b_{i-1}$ and each $b_i$ adjacent to $c_i,c_{i-1}$, therefore, (8) implies,

$$d(a_1,b_i)=i,1\le i\le k+1$$

$$d(a_1,c_i)=1+i,1\le i\le k$$

For $k+2\le i\le 2k+1$, consider the cycle $(b_1{b}_2\dots b_{k+1}\dots b_i\dots b_{2k+1})$. In this cycle, the distance between $b_i$ and $b_{2k+1}$ is $2k+1-i$, and $b_{2k+1}$ is adjacent to $a_1$. Therefore, the distance between $a_1$ and $b_i$ is $2k-i+2$.

$$d(a_1,b_i)=2k-i+2,k+2\le i\le 2k+1.$$

Now, consider the cycle $(c_1{c}_2\dots c_{k+1}\dots c_i\dots c_{2k+1})$. The distance between $c_i$ and $c_{2k}$ is $2k-i$. The vertex $c_{2k}$ is adjacent to $b_{2k+1}$ and $b_{2k+1}$ adjacent to $a_1$. It shows that the distance between $a_1$ and $c_i$ is $2k-i+2$.

$$d(a_1,c_i)=2k-i+2,k+1\le i\le 2k.$$

For $i=2k+1$, $d(a_1,c_i)=2$.

Hence, $c_k$ and $b_{k+1}$ are the vertices farthest from $a_1$. Therefore:

$$e\left(a_1\right)=k+1$$

(9)

Thus, the eccentricity of each vertex on inner cycle $(a_1{a}_2{a}_3\dots a_i\dots a_{2k+1})$ is $k+1$.

Similarly as above, the vertices $b_1$ and $b_i$ on cycle $(b_1{b}_2\dots b_i\dots .b_{2k+1})$ have the distance as,

$$d(b_1,b_i)=i-1,1\le i\le k+1$$

(10)

Each $b_i$ is adjacent to $a_i$ and $a_{i+1}$. Therefore,

$$d(b_1,a_1)=1,(b_1,a_2)=1$$

For $3\le i\le k+2$, consider the path $b_1\to a_2\to a_3\to \dots \to a_i$. Then, the distance between $a_i$ and $a_2$ is $i-2$. $a_2$ is also adjacent to $b_1$. Therefore, the distance between $b_1$ and $a_i$ is $i-1$, i.e.,

$$d(b_1,a_i)=i-1,3\le i\le k+2$$

For $k+3\le i\le 2k+1$, consider the cycle $(a_1{a}_2\dots a_{k+3}\dots a_i\dots a_{2k+1})$. The distance between $a_i$ and $a_{2k+1}$ is $2k-i+1$. Further, $a_{2k+1}$ is adjacent to $a_1$, and $a_1$ is adjacent to $b_1$. Therefore, the distance between $b_1$ and $a_i$ is $2k-i+3$.

$$d(b_1,a_i)=2k-i+3,k+3\le i\le 2k+1$$

Further, $b_i$ is also adjacent to $c_i$ and $c_{i-1}$; it follows from (10):

$$d(b_1,c_i)=i,1\le i\le k+1$$

For $k+2\le i\le 2k+1$, consider the cycle $(c_1{c}_2\dots c_{k+2}\dots c_i\dots c_{2k+1})$. The distance between $c_i$ and $c_{2k+1}$ is $2k+1-i$. $c_{2k+1}$ is also adjacent to $b_1$. Therefore,

$$d(b_1,c_i)=2k+2-i,k+2\le i\le 2k+1$$

Hence, $a_{k+2}$ and $c_{k+1}$ are the vertices farthest from $b_1$. Therefore:

$$e\left(b_1\right)=k+1.$$

(11)

Hence, each vertex on the middle cycle $(b_1{b}_2\dots b_i\dots .b_{2k+1})$ has eccentricity $k+1$.

Further, to find out the eccentricity of the vertices on the outer cycle $(c_1{c}_2\dots c_i\dots c_{2k+1})$, choose a vertex $c_1$ on this cycle. The distance between $c_1$ and $c_i$ is $i-1$.

$$d(c_1,c_i)=i-1,1\le i\le k+1$$

(12)

Each $c_i$ is adjacent to $b_i$ and $b_{i+1}$. Therefore,

$$d(c_1,b_1)=1,d(c_1,b_2)=1$$

(13)

For $3\le i\le k+2$, consider the path $c_1\to b_2\to b_3\to \dots \to b_i$. The distance between $b_2$ and $b_i$ is $i-2$. As $b_2$ is adjacent to $c_1$, therefore, the distance between $c_1$ and $b_i$ is $i-1$.

$$d(c_1,b_i)=i-1,3\le i\le k+2$$

For $k+3\le i\le 2k+1$, consider the cycle $(b_1{b}_2\dots b_{k+3}\dots b_i\dots b_{2k+1})$. The distance between $b_i$ and $b_{2k+1}$ is $2k+1-i$. As $b_{2k+1}$ is adjacent to $b_1$ and $b_1$ adjacent to $c_1$, therefore, the distance between $c_1$ and $b_i$ is $2k-i+3$.

$$d(c_1,b_i)=2k-i+3,k+3\le i\le 2k+1.$$

Each $b_i$ is also adjacent to $a_i$ and $a_{i+1}$, using the result of (13):

$$d(c_1,a_1)=2,d(c_1,a_2)=2$$

For $3\le i\le k+2$, consider the path $c_1\to b_2\to b_3\to \dots \to b_{i-1}\to a_i$. In this path, the distance between $b_2$ and $b_{i-1}$ is $i-3$. $b_{i-1}$ is adjacent to $a_i$, and $b_2$ is adjacent to $c_1$. Therefore, the distance between $c_1$ and $a_i$ is $i-1$.

$$d(c_1,a_i)=i-1,3\le i\le k+2$$

For $k+3\le i\le 2k$, consider the cycle $(a_1{a}_2\dots a_{k+3}\dots a_i\dots a_{2k+1})$. The distance between $a_i$ and $a_{2k+1}$ is $2k+1-i$. $a_{2k+1}$ is adjacent to $a_1$ and $a_1$ adjacent to $b_1$. In addition, $b_1$ is adjacent to $c_1$. Therefore, the distance between $c_1$ and $a_i$ is $2k-i+4$.

$$d(c_1,a_i)=2k-i+4,k+3\le i\le 2k+1$$

This shows that $a_{k+2}$ and $b_{k+2}$ are the vertices farthest from $c_1$. Therefore:

$$e\left(c_1\right)=k+1.$$

(14)

Consequently, (9), (11) and (14) show the smallest, In addition, the greatest eccentricity of these vertices is $k+1$. Therefore:

$$diam\left(A_n\right)=rad\left(A_n\right)=k+1=\frac{n-1}{2}+1=\frac{n+1}{2}.$$

Implies:

$$\mathrm{Cen}\left(A_n\right)=\mathrm{Per}\left(A_n\right)=A_n.$$

Hence, the family of $A_n$ is self-centered for odd values of n. ☐

2.1. Average Eccentricity for Convex Polytope $A_n$

Here, we also are concerned with calculating the average eccentricity for the graph of convex polytope $A_n$. The average eccentricity of any graph can be calculated by dividing the sum of the eccentricities of all of the vertices to the total number of vertices $\left(\stackrel{`}{n}\right)$. There are three circles in the graph of convex polytope $A_n$, and each circle consists of n vertices. Therefore, $A_n$ has a total of $3n$ vertices; it follows,

$$avec\left(A_n\right)=\frac{1}{n}\sum _{u\in V\left(G\right)}{e}_{G}u$$

(15)

By Theorem 1:

$$\begin{array}{ccc}\hfill avec\left(A_n\right)& =& \frac{1}{3\times \left(\stackrel{`}{n}\right)}[n\times \{e\left(a_1\right)+e\left(b_1\right)+e\left(c_1\right)\}]\hfill \\ & =& \frac{1}{3\times n}[n\times \{(k+1)+\left(k\right)+(k+1)\}]=k+\frac{2}{3}=\frac{n}{2}+\frac{2}{3}.\hfill \end{array}$$

and by Theorem 2,

$$\begin{array}{ccc}\hfill avec\left(A_n\right)& =& \frac{1}{3\times n}[n\times \left\{3(k+1)\right]\hfill \\ & =& k+1=\frac{n-1}{2}+1=\frac{n+1}{2}.\hfill \end{array}$$

Therefore, we have the following result:

$$avec\left(A_n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{n+1}{2}},\hfill & \mathrm{if}n=2k+1;\hfill \\ {\displaystyle \frac{n}{2}}+{\displaystyle \frac{2}{3}},\hfill & \mathrm{if}n=2k.\hfill \end{array}\right.$$

2.2. Illustration

Consider the graph of $A_8$. We have labeled each of its vertices by its eccentricities. The center and periphery are shown in Figure 1 and Figure 2.

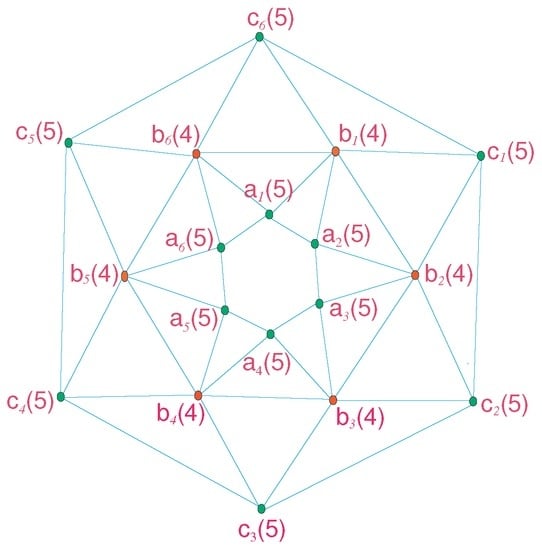
Figure 1. The graph of convex polytope $A_8$.

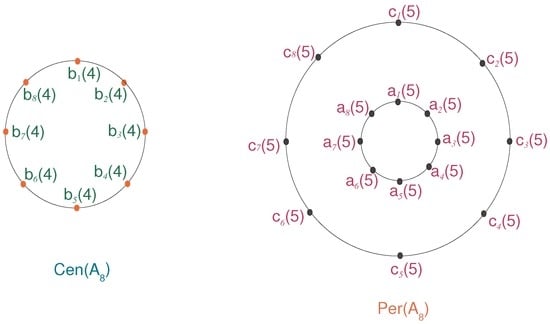
Figure 2. Centrality in the graph of convex polytope $A_8$.

3. The Center and Periphery for Convex Polytope $S_n$

Here, we examine the center and periphery for convex polytope $S_n$.

Definition 8.

The graph of convex polytope (double antiprism) $S_n$ can be obtained from the graph of convex polytope $Q_n$ by adding new edges $c_i{c}_{i+1}$, i.e.,

$$V\left(S_n\right)=V\left(Q_n\right)andE\left(S_n\right)=E\left(Q_n\right)\cup \{c_i{c}_{i+1}:1\le i\le n\}.$$

For our convenience, we identify the cycle induced by the vertices $(a_1,a_2,\dots ,a_n)$, $(b_1,b_2,\dots ,b_n)$, $(c_1,c_2,\dots ,c_n)$ and $(d_1,d_2,\dots ,d_n)$ as the inner cycle, interior cycle, exterior cycle and outer cycle, respectively.

Theorem 3.

For the family of convex polytope $S_n$, when n is even, we have:

$$diam\left(S_n\right)=\frac{n}{2}+1.$$

$$rad\left(S_n\right)=\frac{n}{2}+2.$$

Proof. 

Suppose, $n=2k$, $k\ge 2$. Consider the cycle $(a_1{a}_2\dots .a_i\dots a_{2k})$. Here, the eccentricity of only one vertex, i.e., $a_1$, is determined, and due to the symmetry of the graph, all other vertices have the same eccentricity as $a_1$ on this cycle. Using this cycle,

$$d(a_1,a_i)=i-1,1\le i\le k+1.$$

(16)

For $k+2\le i\le 2k$, $d(a_1,a_i)$ varies from $k-1$ to one, i.e.,

$$d(a_1,a_i)=2k-i+1,k+2\le i\le 2k.$$

Thus, to identify a vertex at maximum distance from $a_1$ in $S_n$, take only $1\le i\le k+1$.

As each $a_i$ is adjacent to $b_i$, therefore,

$$d(a_1,b_i)=i,1\le i\le k+1.$$

(17)

For $k+2\le i\le 2k$, take the interior cycle $(b_1{b}_2\dots b_{k+2}\dots b_i\dots b_{2k})$. In this cycle, the vertices $b_i$ and $b_{2k}$ are at a distance $2k-i$. Further, $b_{2k}$ is adjacent to $b_1$ and $b_1$ adjacent to $a_1$. Therefore, The distance between $a_1$ and $b_i$ is $2k-i+2$.

$$d(a_1,b_i)=2k-i+2,k+2\le i\le 2k.$$

Each $b_i$ is adjacent to $c_i$ and $c_{i-1}$, by using (17),

$$d(a_1,c_i)=i+1,1\le i\le k.$$

(18)

For $k+1\le i\le 2k$, consider the exterior cycle $(c_1{c}_2\dots c_{k+1}\dots c_i\dots c_{2k})$. The vertices $c_i$ and $c_{2k}$ are at a distance $2k-i$. As $c_{2k}$ is adjacent to $b_1$ and $b_1$ adjacent to $a_1$, therefore, $a_1$ and $c_i$ are at a distance $2k-i+2$.

$$d(a_1,c_i)=2k-i+2,k+1\le i\le 2k.$$

$c_i$ is also adjacent to $d_i$, so (18) implies,

$$d(a_1,d_i)=i+2,1\le i\le k.$$

For $k+1\le i\le 2k$, the vertices $d_i$ and $d_{2k}$ are at a distance $2k-i$ in the outer cycle $(d_1{d}_2\dots d_{k+1}\dots d_i\dots d_{2k})$. As $d_{2k}$ is adjacent to $c_{2k}$, $c_{2k}$ adjacent to $b_1$ and $b_1$ adjacent to $a_1$, therefore, $a_1$ and $d_i$ are at a distance $2k-i+3$.

$$d(a_1,d_i)=2k-i+3k+1\le i\le 2k.$$

Therefore, $e\left(a_1\right)=k+2$.

In the same manner as above, we calculate the eccentricity of $b_1$ in the cycle $(b_1{b}_2\dots b_i\dots b_{2k})$. The distance between $b_1$ and $b_i$ in this cycle is,

$$d(b_1,b_i)=i-1,1\le i\le k+1.$$

(19)

and,

$$d(b_1,b_i)=2k+1-i,k+2\le i\le 2k.$$

Therefore, we only take values of i between one and $k+1$. As each $b_i$ is adjacent to $c_i$ and $c_{i-1}$, using (19),

$$d(b_1,c_i)=i,1\le i\le k.$$

(20)

For $k+1\le i\le 2k$, consider the cycle $(c_1{c}_2\dots c_{k+2}\dots c_i\dots c_{2k})$. The distance between $c_i$ and $c_{2k}$ is $2k-i$. Since, $c_{2k}$ is adjacent to $b_1$. Thus,

$$d(b_1,c_i)=2k-i+1,k+1\le i\le 2k.$$

Each $c_i$ is also adjacent to $d_i$. Therefore, (20) shows,

$$d(b_1,d_i)=i+1,1\le i\le k.$$

For $k+1\le i\le 2k$, consider the cycle $(d_1{d}_2\dots d_i\dots d_{2k})$. The distance between $d_i$ and $d_{2k}$ is $2k-i$. As $d_{2k}$ is adjacent to $c_{2k}$ and $c_{2k}$ adjacent to $b_1$, therefore,

$$d(b_1,d_i)=2k-i+2,k+1\le i\le 2k.$$

$b_i$ is also adjacent to $a_i$, i.e.,

$$d(b_1,a_i)=i,1\le i\le k+1.$$

For $k+2\le i\le 2k$, consider the cycle $(a_1,a_2\dots a_{k+2}\dots a_i\dots a_{2k})$. The distance between the vertices $a_i$ and $a_{2k}$ is $2k-i$. As $a_{2k}$ is adjacent to $a_1$, $a_1$ adjacent to $b_1$, therefore,

$$d(b_1,a_i)=2k-i+2,k+2\le i\le 2k.$$

As, $d_k$ and $a_{k+1}$ are farthest from $b_1,$ therefore, $e\left(b_1\right)=k+1$. Next, the distance between $c_1$ and $c_i$ in the cycle $(c_1{c}_2\dots c_i\dots c_{2k})$ is $i-1$.

$$d(c_1,c_i)=i-1,1\le i\le k+1.$$

(21)

Additionally, for $k+2\le i\le 2k$,

$$d(c_1,c_i)=2k-i+1,k+2\le i\le 2k$$

Each $c_i$ is adjacent to $d_i$, from (21):

$$d(c_1,d_i)=i,1\le i\le k+1.$$

For $k+2\le i\le 2k$, the vertices $d_i$ and $d_{2k}$ are at a distance $2k-i$ in the cycle $(d_1{d}_2\dots d_{k+2}\dots d_i\dots d_{2k})$. The vertex $d_{2k}$ is adjacent to $d_1$ and $d_1$ adjacent to $c_1$. Therefore,

$$d(c_1,d_i)=2k-i+2,k+2\le i\le 2k.$$

Each $c_i$ is adjacent to $b_i$ and $b_{i+1}$; Equation (17) implies,

$$d(c_1,b_1)=1,d(c_1,b_2)=1.$$

(22)

For $3\le i\le k+1$, $b_2$ and $b_i$ are at a distance $i-2$ in the path $c_1\to b_2\to b_3\to \dots \to b_i$. Again, $b_2$ is adjacent to $c_1$; thus, we have:

$$d(c_1,b_i)=i-1,3\le i\le k+1.$$

(23)

For $k+2\le i\le 2k$, consider the cycle $(b_1{b}_2\dots b_{k+2}\dots b_i\dots b_{2k})$. The distance between $b_i$ and $b_{2k}$ is $2k-i$ in this cycle. As, $b_{2k}$ is adjacent to $b_1$, $b_1$ adjacent to $c_1$. Therefore,

$$d(c_1,b_i)=2k-i+2,k+2\le i\le 2k.$$

Since $b_i$ is adjacent to $a_i$, it follows from (22) that:

$$d(c_1,a_1)=2,d(c_1,a_2)=2$$

For $3\le i\le k+1$, $b_i$ and $b_2$ are at a distance $i-2$ in the path $c_1\to b_2\to b_3\to \dots \to b_i\to a_i$. The vertex $b_i$ is adjacent to $a_i$ and $b_2$ adjacent to $c_1$. Therefore,

$$d(c_1,a_i)=i,3\le i\le k+1.\dots \left(23\right)$$

For $k+2\le i\le 2k$, the distance between $a_i$ and $a_{2k}$ is $2k-i$ in the cycle $(a_1{a}_2\dots a_{k+2}\dots a_i\dots a_{2k})$. $a_{2k}$ is again adjacent to $a_1$, $a_1$ adjacent to $b_1$ and $b_1$ adjacent to $c_1$. For that reason,

$$d(c_1,a_i)=2k-i+3,k+2\le i\le 2k.$$

Consequently, $d_{k+1}$ and $a_{k+1}$ are farthest from $c_1$. Therefore, $e\left(c_1\right)=k+1$.

Next, take a vertex $d_1$ on the outer cycle. In this cycle $(d_1{d}_2\dots d_i\dots d_{2k})$,

$$d(d_1,d_i)=i-1,1\le i\le k+1.$$

(24)

Additionally,

$$d(d_1,d_i)=2k-i+1,k+2\le i\le 2k.$$

In addition, each $d_i$ is adjacent to $c_i$,

$$d(d_1,c_i)=i,1\le i\le k+1.$$

For $k+2\le i\le 2k$, take a cycle $(c_1,c_2\dots c_{k+2}\dots c_i\dots c_{2k})$. The vertices $c_i$ and $c_{2k}$ are at a distance $2k-i$ in this cycle. In addition, $c_{2k}$ is adjacent to $c_1$ and $c_1$ adjacent to $d_1$. Then,

$$d(d_1,c_i)=2k-i+2,k+2\le i\le 2k.$$

Each $c_i$ is adjacent to $b_i$ and $b_{i+1}$. i.e., $d(d_1,b_1)=2$ and:

$$d(d_1,b_2)=2.$$

(25)

For $3\le i\le k+1$, the vertices $b_2$ and $b_i$ are at a distance $i-2$ in the path $d_1\to c_1\to b_2\to b_3\to \dots \to b_i$. $b_2$ is adjacent to $c_1$ and $c_1$ adjacent to $d_1$ in $S_n$. Therefore,

$$d(d_1,b_i)=i,3\le i\le k+1,$$

(26)

For $k+2\le i\le 2k$, the vertices $b_i$ and $b_{2k}$ are at distance $2k-i$ in the cycle $(b_1,b_2\dots b_{k+2}\dots b_i\dots b_{2k})$. $b_{2k}$ is adjacent to $b_1$, $b_1$ adjacent to $c_1$ and $c_1$ adjacent to $d_1$; for this,

$$d(d_1,b_i)=2k-i+3,k+2\le i\le 2k.$$

In addition, $b_i$ is adjacent to $a_i$. This implies from (25),

$$d(d_1,a_1)=3,d(d_1,a_2)=3.$$

For $3\le i\le k+1$, the vertices $b_2$ and $b_i$ are at a distance $i-2$ in the path $d_1\to c_1\to b_2\to b_3\to \dots \to b_i\to a_i$. $b_i$ is adjacent to $a_i$, $b_2$ adjacent to $c_1$ and $c_1$ adjacent to $d_1$ in $S_n$. Therefore,

$$d(d_1,a_i)=i+1,3\le i\le k+1.$$

For $k+2\le i\le 2k$, consider the cycle $(a_1,a_2\dots a_{k+2}\dots a_i\dots a_{2k})$. The vertices $a_i$ and $a_{2k}$ are at a distance $2k-i$ in this cycle. $a_{2k}$ is adjacent to $a_1$, $a_1$ adjacent to $b_1$, $b_1$ adjacent to $c_1$ and $c_1$ adjacent to $d_1$. As a result,

$$d(d_1,a_i)=2k-i+4,k+2\le i\le 2k.$$

Consequently,

$$e\left(d_1\right)=k+2.$$

Thus, it is concluded that maximum eccentricity among all of the vertices of $S_n$ is $k+2$, and the minimum eccentricity is $k+1$.

Therefore

$$diam\left(S_n\right)=k+2=\frac{n}{2}+2.$$

$$rad\left(S_n\right)=k+1=\frac{n}{2}+1.$$

☐

The following corollary is straightforward.

Corollary 1.

The center and periphery for the family of convex polytope $\left(S_n\right)$, when n is even, are subgraphs induced by all of the central vertices $\{b_1,b_2,\dots ,b_i,\dots ,b_{2k},c_1,c_2,\dots .,c_i,\dots ,c_{2k}\}$ and peripheral vertices $\{a_1,a_2,\dots ,a_i,\dots ,a_{2k},d_1,d_2,\dots ,d_i,\dots ,d_{2k}\}$ of $S_n$, respectively.

Now, we find out the radius and diameter of $S_n$, when n is odd.

Theorem 4.

When n is odd, the family of convex polytope $S_n$ has the radius and diameter as,

$$diam\left(S_n\right)=\frac{n-1}{2}+3,$$

$$rad\left(S_n\right)=\frac{n-1}{2}+2.$$

Proof. 

Let $n=2k+1$, $k\ge 2$. Consider the cycle $(a_1{a}_2\dots .a_i\dots a_{2k+1})$, and select a vertex $a_1$ in it. It is clear that,

$$d(a_1,a_i)=i-1,1\le i\le k+1$$

$$d(a_1,a_i)=2k+2-i,k+2\le i\le 2k+1,$$

(27)

Thus, the equations above lead to the proof including only $1\le i\le k+1$ in order to find a vertex having the greatest distance from $a_1$ in $S_n$. Since each $a_i$ is adjacent to $b_i$, therefore, (27) implies that:

$$d(a_1,b_i)=i,1\le i\le k+1.$$

(28)

For $k+2\le i\le 2k+1$, the vertices $b_i$ and $b_{2k+1}$ are at a distance $2k-i+1$ in the cycle $(b_1{b}_2\dots b_{k+2}\dots b_i\dots b_{2k+1})$. $b_{2k+1}$ is adjacent to $b_1$ and $b_1$ adjacent to $a_1$. Therefore, The distance between $a_1$ and $b_i$ is $2k-i+3$.

$$d(a_1,b_i)=2k+3-i,k+2\le i\le 2k+1.$$

Again, each $b_i$ is adjacent to $c_i$ and $c_{i-1}$, by using (28).

$$d(a_1,c_i)=i+1,1\le i\le k+1.$$

(29)

For $k+2\le i\le 2k+1$, the distance between the vertices $c_i$ and $c_{2k+1}$ is $2k+1-i$ in the cycle $(c_1{c}_2\dots c_{k+1}\dots c_i\dots c_{2k+1})$. Since, $c_{2k+1}$ is adjacent to $b_1$ and $b_1$ adjacent to $a_1$, therefore, $a_1$ and $c_i$ are at a distance $2k-i+3$.

$$d(a_1,c_i)=2k-i+3,k+2\le i\le 2k+1.$$

In addition, $c_i$ is adjacent to $d_i$, therefore, (29) shows,

$$d(a_1,d_i)=i+2,1\le i\le k+1.$$

For $k+2\le i\le 2k+1$, the vertices $d_i$ and $d_{2k+1}$ are at a distance $2k+1-i$ in the cycle $(d_1{d}_2\dots d_{k+1}\dots d_i\dots d_{2k+1})$. In addition, $d_{2k+1}$ is adjacent to $c_{2k+1}$, $c_{2k+1}$ adjacent to $b_1$ and $b_1$ adjacent to $a_1$. Therefore, $a_1$ and $d_i$ are at a distance $2k-i+4$.

$$d(a_1,d_i)=2k-i+4,k+2\le i\le 2k+1.$$

As a result, $d_{k+1}$ is farthest from $a_1$; therefore, $e\left(a_1\right)=k+3$.

In order to find out the eccentricity of the vertices on the cycle $(b_1{b}_2\dots b_i\dots b_{2k+1})$, the distance between $b_1$ and $b_i$ in this cycle is $i-1$.

$$d(b_1,b_i)=i-1,1\le i\le k+1.$$

(30)

In addition,

$$d(b_1,b_i)=2k-i+2,k+2\le i\le 2k+1.$$

Further, each $b_i$ is adjacent to $c_i$ and $c_{i-1}$, therefore, (30) shows,

$$d(b_1,c_i)=i,1\le i\le k+1.$$

(31)

For $k+2\le i\le 2k+1$, consider the cycle $(c_1{c}_2\dots c_{k+2}\dots c_i\dots c_{2k+1})$. The distance between $c_i$ and $c_{2k+1}$ is $2k-i+1$. Since, $c_{2k+1}$ is adjacent to $b_1$, thus,

$$d(b_1,c_i)=2k-i+2,k+2\le i\le 2k+1.$$

Each $c_i$ is also adjacent to $d_i$. It is shown from (31),

$$d(b_1,d_i)=i+1,1\le i\le k+1.$$

For $k+2\le i\le 2k+1$, consider the cycle $(d_1{d}_2\dots d_i\dots d_{2k+1})$. The distance between $d_i$ and $d_{2k+1}$ is $2k-i+1$. As $d_{2k+1}$ is adjacent to $c_{2k+1}$ and $c_{2k+1}$ adjacent to $b_1$, therefore,

$$d(b_1,d_i)=2k-i+3,k+2\le i\le 2k+1.$$

$b_i$ is also adjacent to $a_i$, i.e.,

$$d(b_1,a_i)=i,1\le i\le k+1.$$

For $k+2\le i\le 2k+1$, consider the cycle $(a_1{a}_2\dots a_{k+2}\dots a_i\dots a_{2k+1})$. The vertices $a_i$ and $a_{2k+1}$ is $2k+1-i$. As $a_{2k+1}$ is adjacent to $a_1$, $a_1$ adjacent to $b_1$, therefore,

$$d(b_1,a_i)=2k-i+3,k+2\le i\le 2k+1.$$

Since, $d_{k+1}$ is a vertex farthest from $b_1,$ therefore, $e\left(b_1\right)=k+2$.

Next, the distance between $c_1$ and $c_i$ in the cycle $(c_1{c}_2\dots c_i\dots c_{2k+1})$ is,

$$d(c_1,c_i)=i-1,1\le i\le k+1.$$

(32)

Additionally,

$$d(c_1,c_i)=2k-i+2,k+2\le i\le 2k+1.$$

Each $c_i$ is adjacent to $d_i$, from (32):

$$d(c_1,d_i)=i,1\le i\le k+1.$$

For $k+2\le i\le 2k+1$, the vertices $d_i$ and $d_{2k+1}$ are at a distance $2k+1-i$ in the cycle $(d_1{d}_2\dots d_{k+2}\dots d_i\dots d_{2k+1})$. The vertex $d_{2k+1}$ is adjacent to $d_1$ and $d_1$ adjacent to $c_1$. Therefore,

$$d(c_1,d_i)=2k-i+3,k+2\le i\le 2k+1.$$

Each $c_i$ is adjacent to $b_i$ and $b_{i+1}$; Equation (28) implies,

$$d(c_1,b_1)=1,d(c_1,b_2)=1.$$

(33)

For $3\le i\le k+2$, $b_2$ and $b_i$ are at a distance $i-2$ in the path $c_1\to b_2\to b_3\to \dots \to b_i$. Again, $b_2$ is adjacent to $c_1$; thus, we have:

$$d(c_1,b_i)=i-1,3\le i\le k+2.$$

(34)

For $k+3\le i\le 2k+1$, consider the cycle $(b_1{b}_2\dots b_{k+1}\dots b_i\dots b_{2k+1})$. The distance between $b_i$ and $b_{2k+1}$ is $2k+1-i$ in this cycle. As $b_{2k+1}$ is adjacent to $b_1$ and $b_1$ adjacent to $c_1$, therefore,

$$d(c_1,b_i)=2k-i+3,k+3\le i\le 2k+1.$$

Since $b_i$ is adjacent to $a_i$, it follows from (33) that:

$$d(c_1,a_1)=2,d(c_1,a_2)=2$$

For $3\le i\le k+2$, $b_i$ and $b_2$ are at a distance $i-2$ in the path $c_1\to b_2\to b_3\to \dots \to b_i\to a_i$.

The vertex $b_i$ is adjacent to $a_i$, $b_2$ adjacent to $c_1$. Therefore,

$$d(c_1,a_i)=i,3\le i\le k+2.$$

For $k+3\le i\le 2k+1$, the distance between $a_i$ and $a_{2k+1}$ in the cycle $(a_1{a}_2\dots a_{k+2}\dots a_i\dots a_{2k+1})$. $a_{2k+1}$ is again adjacent to $a_1$, $a_1$ adjacent to $b_1$ and $b_1$ adjacent to $c_1$. For that reason,

$$d(c_1,a_i)=2k-i+4,k+3\le i\le 2k+1.$$

Consequently, $a_{k+2}$ is a vertex farthest from $c_1$. Therefore, $e\left(c_1\right)=k+2$.

Next, take a vertex $d_1$ on the outer cycle. In this cycle, $(d_1{d}_2\dots d_i\dots d_{2k+1})$,

$$d(d_1,d_i)=i-1,1\le i\le k+1.$$

(35)

$d(d_1,d_i)$ starts to decrease for $k+2\le i\le 2k+1$ as,

$$d(d_1,d_i)=2k-i+2,k+2\le i\le 2k+1.$$

Each $d_i$ is adjacent to $c_i$,

$$d(d_1,c_i)=i,1\le i\le k+1.$$

For $k+2\le i\le 2k+1$, take a cycle $(c_1{c}_2\dots c_{k+2}\dots c_i\dots c_{2k+1})$. The vertices $c_i$ and $c_{2k+1}$ are at a distance $2k+1-i$ in this cycle. In addition, $c_{2k+1}$ is adjacent to $c_1$ and $c_1$ adjacent to $d_1$. Then,

$$d(d_1,c_i)=2k-i+3,k+2\le i\le 2k+1.$$

Each $c_i$ is adjacent to $b_i$ and $b_{i+1}$, i.e., $d(d_1,b_1)=2$ and

$$d(d_1,b_2)=2.$$

(36)

For $3\le i\le k+2$, the vertices $b_2$ and $b_i$ are at a distance $i-2$ in the path $d_1\to c_1\to b_2\to b_3\to \dots \to b_i$. $b_2$ is adjacent to $c_1$ and $c_1$ adjacent to $d_1$ in $S_n$. Therefore,

$$d(d_1,b_i)=i,3\le i\le k+2.$$

(37)

For $k+3\le i\le 2k+1$, consider the cycle $(b_1{b}_2\dots b_{k+2}\dots b_i\dots b_{2k+1})$. The vertices $b_i$ and $b_{2k+1}$ are $2k+1-i$. $b_{2k+1}$ is adjacent to $b_1$, $b_1$ adjacent to $c_1$ and $c_1$ adjacent to $d_1$; for this,

$$d(d_1,b_i)=2k-i+4,k+3\le i\le 2k+1.$$

In addition, $b_i$ is adjacent to $a_i$. Therefore, (36) implies,

$$d(d_1,a_1)=,d(d_1,a_2)=3.$$

For $3\le i\le k+2$, the vertices $b_2$ and $b_i$ are at a distance $i-2$ in the path $d_1\to c_1\to b_2\to b_3\to \dots \to b_i\to a_i$. $b_i$ is adjacent to $a_i$, $b_2$ adjacent to $c_1$ and $c_1$ adjacent to $d_1$ in $S_n$. Therefore,

$$d(d_1,a_i)=i+1,3\le i\le k+2.$$

For $k+3\le i\le 2k+1$, consider the cycle $(a_1{a}_2\dots a_{k+2}\dots a_i\dots a_{2k+1})$. The vertices $a_i$ and $a_{2k+1}$ are $2k+1-i$. $a_{2k+1}$ is adjacent to $a_1$, $a_1$ adjacent to $b_1$, $b_1$ adjacent to $c_1$ and $c_1$ adjacent to $d_1$. As a result,

$$d(d_1,a_i)=2k-i+5,k+3\le i\le 2k+1.$$

This means,

$$e\left(d_1\right)=k+3.$$

It shows that the maximum and minimum eccentricity among all of the vertices of $S_n$ are $k+3$ and $k+2$, respectively. Therefore:

$$diam\left(S_n\right)=k+3=\frac{n-1}{2}+3.$$

$$rad\left(S_n\right)=k+2=\frac{n-1}{2}+2.$$

☐

Thus, we can summarize the above results as,

Corollary 2.

The center for the family of convex polytope $S\left(n\right)$ is a subgraph induced by all of the vertices of the interior and exterior cycles, and the periphery is the subgraphs induced by all of the peripheral vertices $\{a_1,a_2,\dots ,a_i,\dots ,a_{2k},d_1,d_2,\dots ,d_i,\dots ,d_{2k}\}$ of $S_n$, respectively.

3.1. Average Eccentricity for Convex Polytopes $S_n$

Here, the average eccentricity for the family of $S_n$ is being determined. The graph of $S_n$ consist of four major circles, and there are n vertices in each circle. Therefore, the total number of vertices in $S_n$ (i.e., $\acute{n}$) is $4n$; it follows,

$$avec\left(S_n\right)=\frac{1}{\acute{n}}\sum _{u\in V\left(G\right)}{e}_{G}u$$

By Theorem 3:

$$\begin{array}{ccc}\hfill avec\left(S_n\right)& =& \frac{1}{4\times \left(\acute{n}\right)}[n\times \{e\left(a_1\right)+e\left(b_1\right)+e\left(c_1\right)+e\left(d_1\right\}]\hfill \\ & =& \frac{1}{4\times n}[n\times \{(k+2)+(k+1)+(k+1)+(k+2)\}]\hfill \\ & =& \frac{1}{4\times n}[2n\times \{(k+2)+(k+1)\}]\hfill \\ & =& \frac{1}{2}\left[2k+3\right]\hfill \\ & =& k+\frac{3}{2}\hfill \\ & =& \frac{n+3}{2}.\hfill \end{array}$$

and by Theorem 4,

$$\begin{array}{ccc}\hfill avec\left(S_n\right)& =& \frac{1}{4\times n}[n\times \{(k+3)+(k+2)+(k+2)+(k+3)\}]\hfill \\ & =& \frac{1}{4\times n}[2n\times \{(k+3)+(k+2)\}]\hfill \\ & =& \frac{1}{2}\left[2k+5\right]\hfill \\ & =& k+\frac{5}{2}\hfill \\ & =& \frac{n-1}{2}+\frac{5}{2}\hfill \\ & =& \frac{n+4}{2}.\hfill \end{array}$$

Therefore, we have the following result:

$$avec\left(S_n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{n+3}{2}},\hfill & \mathrm{for}\mathrm{all}\mathrm{even}\mathrm{values}\mathrm{of}n\hfill \\ {\displaystyle \frac{n+4}{2}},\hfill & \mathrm{for}\mathrm{all}\mathrm{odd}\mathrm{values}\mathrm{of}n.\hfill \end{array}\right.$$

3.2. Illustration

Consider the graph of $S_6$. Its center and periphery are shown in Figure 3 and Figure 4.

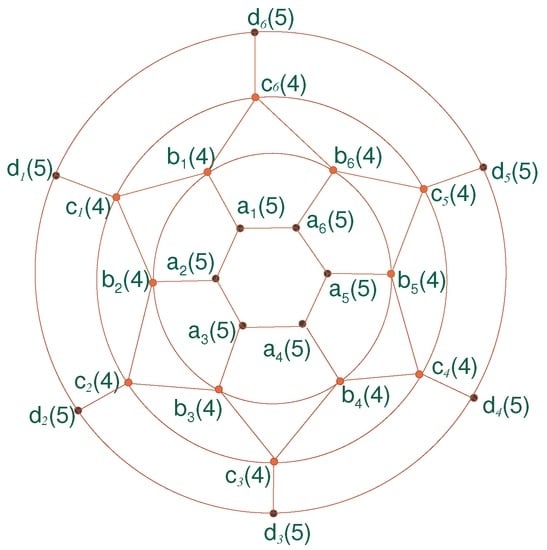
Figure 3. The graph of convex polytope $S_6$.

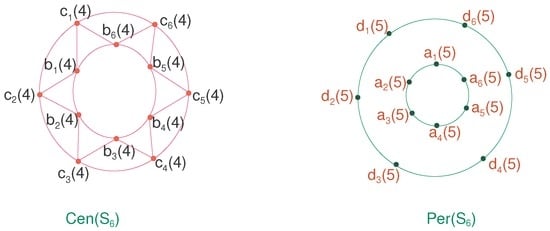
Figure 4. Centrality for $S_6$.

4. The Center and Periphery for Convex Polytopes $T_n$

Here, we established the center and periphery for $T_n$ and show that $T_n$ is not self-centered.

Definition 9.

The graph of convex polytope $T_n$ can be obtained from the graph of convex polytope $Q_n$ by adding new edges . It consist of three-sided faces, five-sided faces and n-sided faces. $a_{i+1}{b}_i$, i.e., $V\left(T_n\right)=V\left(Q_n\right)$ and $E\left(T_n\right)=E\left(Q_n\right)\bigcup \{a_{i+1}{b}_i:1\le i\le n\}.$

This section begins with the following theorem on $T_n$.

Theorem 5.

The diameter for the family of convex polytope $T_n$ is,

$$diam\left(T_n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{n}{2}}+2,\hfill & forn=2k;\hfill \\ {\displaystyle \frac{n-1}{2}}+2,\hfill & forn=2k+1.\hfill \end{array}\right.$$

In addition, its radius,

$$rad\left(T_n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{n}{2}}+1,\hfill & forntobeeven;\hfill \\ {\displaystyle \frac{n+1}{2}},\hfill & forntobeodd.\hfill \end{array}\right.$$

Proof. 

Consider, $n=2k$, $k\ge 2$. Choose take cycle $(a_1{a}_2\dots a_i\dots a_{2k})$. In this cycle:

$$d(a_1,a_i)=i-1,1\le i\le k+1.$$

(38)

For $k+2\le i\le 2k$, the distance between $a_1$ and $a_i$ decreases from $k-1$ to one, i.e.,

$$d(a_1,a_i)=2k-i+1,k+2\le i\le 2k.$$

Therefore, we must considered $1\le i\le k+1$ in order to find the distance of a vertex $a_1$ from a vertex farthest from it in $T_n$.

In the graph of $T_n$, each $a_i$ is adjacent to $b_i$ and $b_{i-1}$; thus, (38) implies,

$$d(a_1,b_i)=i,1\le i\le k.$$

(39)

For $k+1\le i\le 2k$, the vertices $b_i$ and $b_{2k}$ are at a distance $2k-i$ in the cycle $(b_1{b}_2\dots b_{k+1}\dots b_i\dots b_{2k})$. In addition, $b_{2k}$ is adjacent to $a_1$. Therefore, The distance between $a_1$ and $b_i$ is $2k-i+1$.

$$d(a_1,b_i)=2k-i+1k+1\le i\le 2k.$$

Further, each $b_i$ is adjacent to $c_i$ and $c_{i-1}$, using (39).

$$d(a_1,c_1)=2,d(a_1,c_{2k})=2$$

for $2\le i\le k$, consider path $a_1\to b_1\to b_2\to \dots \to b_i\to c_i$. The distance between $b_1$ and $b_i$ is $i-1$. Each $b_i$ is adjacent to $c_i$ and $b_1$ adjacent to $a_1$. Therefore,

$$d(a_1,c_i)=i+1,2\le i\le k.$$

(40)

Next, for $k+1\le i\le 2k-1$, consider the cycle $(b_1{b}_2\dots b_{i+1}\dots b_{2k})$. The vertices $b_{2k}$ and $b_{i+1}$ are at a distance $2k-i-1$. Further, $b_{2k}$ is adjacent to $a_1$ and $b_{i+1}$ adjacent to $c_i$. Therefore,

$$d(a_1,c_i)=2k-i+1,k+1\le i\le 2k-1.$$

$c_i$ is also adjacent to $d_i$. Therefore, (40) implies

$$d(a_1,d_i)=i+2,1\le i\le k.$$

For $k+1\le i\le 2k$, the vertices $d_i$ and $d_{2k}$ are at a distance $2k-i$ in the cycle $(d_1{d}_2\dots d_i\dots d_{2k})$. In addition, each $d_{2k}$ is adjacent to $c_{2k}$, $c_{2k}$ adjacent to $b_1$ and $b_1$ adjacent to $a_1$; therefore,

$$d(a_1,d_i)=2k+3-i,k+1\le i\le 2k.$$

Hence, $d_k$ is a vertex at the largest distance from $a_1$. Therefore, $e\left(a_1\right)=k+2$.

Next, continue this for cycle $(b_1{b}_2\dots b_i\dots b_{2k})$; we choose a vertex $b_1$, such that,

$$d(b_1,b_i)=i-1,1\le i\le k+1.$$

(41)

The distance between $b_1$ and $b_i$ decreases from $k-1$ to one, when i increases from $k+2$ to $2k$.

$$d(b_1,b_i)=2k-i+1,k+2\le i\le 2k.$$

In addition, each $b_i$ is adjacent to $a_i$ and $a_{i+1}$.

$$d(b_1,a_1)=1,d(b_1,a_2)=1$$

and when $3\le i\le k+1$, consider the path $b_1\to a_2\to a_3\to \dots \to a_i$. $a_2$ and $a_i$ are at a distance $i-2$ in this path, and $a_2$ is adjacent to $b_1$; therefore,

$$d(b_1,a_i)=i-1,3\le i\le k+1.$$

For $k+2\le i\le 2k$, consider the cycle $(a_1{a}_2\dots a_{k+2}\dots a_i\dots a_{2k})$. The distance between $a_i$ and $a_{2k}$ is $2k-i$. As $a_{2k}$ is adjacent to $a_1$ and $a_1$ adjacent to $b_1$, therefore,

$$d(b_1,a_i)=2k-i+2,k+2\le i\le 2k.$$

In addition, $b_i$ is adjacent to $c_i$ and $c_{i-1}$; using (41), we have:

$$d(b_1,c_i)=i,1\le i\le k.$$

(42)

For $k+1\le i\le 2k$, consider the path $b_1\to b_{2k}\to b_{2k-1}\to \dots \to b_{i+1}\to c_i.$ The distance between $b_{2k}$ and $b_{i+1}$ is $2k-i-1$. Further, $b_{2k}$ is adjacent to $b_1$. In addition, $b_{i+1}$ is adjacent to $c_i$. Therefore, the distance between $b_1$ and $c_i$ is $2k-i+1$.

$$d(b_1,c_i)=2k-i+1,k+1\le i\le 2k$$

Further, $c_i$ is adjacent to $d_i$; hence, (42) shows,

$$d(b_1,d_i)=i+1,1\le i\le k.$$

For $k+1\le i\le 2k$, the vertices $d_i$ and $d_{2k}$ are at a distance $2k-i$ in the cycle $(d_1{d}_2\dots d_{k+2}\dots d_i\dots d_{2k})$. The vertex $d_{2k}$ is adjacent to $c_{2k}$ and $c_{2k}$ adjacent to $b_1$. Therefore,

$$d(b_1,d_i)=2k-i+2,k+1\le i\le 2k.$$

Hence, $d_k$ is a vertex farthest from $b_1$. Therefore, $e\left(b_1\right)=k+1$

Next, to find out the eccentricity of the vertices $\{c_i,1\le i\le 2k\}$, take a vertex $c_1$ among all $c_i$’s, and each $c_i$ is adjacent to $b_i$, $b_{i+1}$, i.e.,

$$d(c_1,b_1)=1,,d(c_1,b_2)=1$$

and when $3\le i\le k+1$, consider the path $c_1\to b_2\to b_3\to \dots \to b_i$. $b_2$ and $b_i$ are at distance $i-2$, and again, $b_2$ is adjacent to $c_1$; thus, we have:

$$d(c_1,b_i)=i-1,3\le i\le k+1.$$

(43)

For $k+2\le i\le 2k$, consider the cycle $(b_1{b}_2\dots b_{k+2}\dots b_i\dots b_{2k})$. The distance between $b_i$ and $b_{2k}$ is $2k-i$ in this cycle. As $b_{2k}$ is adjacent to $b_1$ and $b_1$ adjacent to $c_1$, therefore,

$$d(c_1,b_i)=2k-i+2,k+2\le i\le 2k.$$

Moreover, $b_i$ is adjacent to $a_i$ and $a_{i+1}$; it follows from (43) that:

$$d(c_1,a_1)=2,d(c_1,a_2)=2,d(c_1,a_3)=2$$

For $4\le i\le k+2$, $a_i$ and $a_2$ are at a distance $i-3$ in the path $c_1\to b_2\to a_3\to \dots \to a_i$. Furthermore, $a_2$ is adjacent to $b_2$ and $b_2$ adjacent to $c_1$. Thus,

$$d(c_1,a_i)=i-1,4\le i\le k+2.$$

(44)

For $k+3\le i\le 2k$, the distance between $a_i$ and $a_{2k}$ in the cycle $(a_1{a}_2\dots a_{k+3}\dots a_i\dots a_{2k})$ is $2k-i$, and $a_{2k}$ is adjacent to $a_1$, $a_1$ adjacent to $b_1$ and $b_1$ adjacent to $c_1$. For that reason,

$$d(c_1,a_i)=2k-i+3,k+3\le i\le 2k.$$

Again, $c_i$ is adjacent to $d_i$. Hence,

$$d(c_1,d_i)=i,1\le i\le k+1$$

For $k+2\le i\le 2k$, the vertices $d_{2k}$ and $d_i$ are at a distance $2k-i$ in the cycle $(d_1{d}_2\dots d_{k+2}\dots d_i\dots d_{2k})$, and $d_{2k}$ is adjacent to $d_1$ and $d_1$ adjacent to $c_1$ in $T_n$. Therefore,

$$d(c_1,d_i)=2k-i+2,k+2\le i\le 2k$$

In order to find the distance between $c_1$ and $c_i,1\le i\le k+1$, consider the path $c_1\to b_2\to b_3\dots \to b_i\to c_i$. The distance between $b_2$ and $b_i$ is i-2, and $b_i$ is adjacent to $c_i$ and $b_2$ adjacent to $c_1$. Therefore,

$$d(c_1,c_i)=i,1\le i\le k+1.$$

For more values of i, $d(c_1,c_i)$ begins to reduce as,

$$d(c_1,c_i)=2k-i+2,k+2\le i\le 2k$$

This means that $a_{k+2}$, $c_{k+1}$ and $d_{k+1}$ are the vertices farthest from $c_1$. Therefore, $e\left(c_1\right)=k+1$.

Now, we find the eccentricities of the vertices on the cycle $(d_1{d}_2\dots d_i\dots d_{2k})$. In this cycle,

$$d(d_1,d_i)=i-1,1\le i\le k+1.$$

For $k+2\le i\le 2k$, the distance between $d_1$ and $d_i$ decreases from $k-1$ to one.

$$d(d_1,d_i)=2k+1-i,k+2\le i\le 2k.$$

As $d_i$ adjacent to $c_i$:

$$d(d_1,c_i)=i,1\le i\le k+1.$$

(45)

When i increases from $k+2$ to $2k$, the distance between $d_i$ and $d_{2k}$ is $2k-i$ in the cycle $(d_1{d}_2\dots d_{k+2}\dots d_i\dots d_{2k})$. In addition, $d_{2k}$ is adjacent to $d_1$ and $d_i$ adjacent to $c_i$. Thus,

$$d(d_1,c_i)=2k-i+2,k+2\le i\le 2k.$$

As each $c_i$ is adjacent to $b_i$, $b_{i+1}$.

$$d(d_1,b_1)=2,d(d_1,b_2)=2,$$

(46)

For $3\le i\le k+1$, consider a path $d_1\to c_1\to b_2\to b_3\to \dots \to b_i$. $b_2$ and $b_i$ are at a distance $i-2$, and $b_2$ is adjacent to $c_1$ and $c_1$ adjacent to $d_1$ in $T_n$. Therefore,

$$d(d_1,b_i)=i,3\le i\le k+1$$

For $k+2\le i\le 2k$, consider the cycle $(b_1{b}_2\dots b_{k+2}\dots b_i\dots b_{2k})$. The distance between the vertices $b_i$ and $b_{2k}$ is $2k-i$. $b_{2k}$ is adjacent to $b_1$, $b_1$ adjacent to $c_1$ and $c_1$ adjacent to $d_1$; for that reason,

$$d(d_1,b_i)=2k-i+3,k+2\le i\le 2k.$$

In addition, $b_i$ is adjacent to $a_i$ and $a_{i+1}$. Therefore, (46) implies,

$$d(d_1,a_1)=3,d(d_1,a_2)=3,d(d_1,a_3)=3$$

For $4\le i\le k+2$, the vertices $a_3$ and $a_i$ are at a distance $i-3$ in the path $d_1\to c_1\to b_2\to a_3\to a_4\to \dots \to a_i$. Further, $a_3$ is adjacent to $b_2$, $b_2$ adjacent to $c_1$ and $c_1$ adjacent to $d_1$ in $T_n$. Therefore,

$$d(d_1,a_i)=i,4\le i\le k+2.$$

For $k+3\le i\le 2k$, consider the cycle $(a_1{a}_2\dots a_{k+3}\dots a_i\dots a_{2k})$. The distance between the vertices $a_i$ and $a_{2k}$ is $2k-i$. $a_{2k}$ is adjacent to $a_1$ and $a_1$ adjacent to $b_1$. Further, $b_1$ adjacent to $c_1$ and $c_1$ adjacent to $d_1$. As a result,

$$d(d_1,a_i)=2k-i+4,k+3\le i\le 2k.$$

This shows that $a_{k+2}$ is at the highest distance from $d_1$. Therefore, $e\left(d_1\right)=k+2$.

Thus, it is concluded that the maximum eccentricity among all of the vertices of $T_n$ is $k+2$, and $k+1$ is the minimum eccentricity. Therefore, diam$\left(T_n\right)$ = $k+2$ = $\frac{n}{2}+2$.

$$rad\left(T_n\right)=k+1=\frac{n}{2}+1.$$

For odd n, the proof is analogous to the case discussed above and omitted. ☐

Corollary 3.

The center of $T_n$, when n is even, is the subgraph induced by the central vertices $\{b_i\cup c_i:1\le i\le n\},$ while the periphery is the subgraph induced by the vertices of inner and outer cycles.

4.1. Average Eccentricity for Convex Polytopes $T_n$

There are four circles in the graph of $T_n$, and each circle has n vertices. The average eccentricity for the graph of convex polytope $T_n$ can be found out by dividing sum of eccentricities of all vertices on each circle to its total number of vertices. Therefore,

$$avec\left(T_n\right)=\frac{1}{\acute{n}}\sum _{u\in V\left(G\right)}{e}_{G}u$$

By Theorem 5:

$$\begin{array}{ccc}\hfill avec\left(T_n\right)& =& \frac{1}{4\times n}[n\times \{(k+2)+(k+1)+(k+1)+(k+2)]\hfill \\ & =& \frac{1}{4\times n}[2n\times \{(k+2)+(k+1)\}]=\frac{1}{2}\left[2k+3\right]=k+\frac{3}{2}=\frac{n+3}{2}.\hfill \end{array}$$

and by Theorem 5,

$$\begin{array}{ccc}\hfill avec\left(T_n\right)& =& \frac{1}{4\times n}[n\times \{(k+2)+(k+2)+(k+1)+(k+2)\}]\hfill \\ & =& \frac{1}{4\times n}[3n\times (k+2)+n\times (k+1)]=\frac{1}{4}\left[4k+7\right]=\frac{1}{4}[4\left(\frac{n-1}{2}\right)+7]=\frac{n}{2}+\frac{5}{4}.\hfill \end{array}$$

Therefore, we get the following immediate result:

$$avec\left(T_n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{n}{2}}+{\displaystyle \frac{5}{4}},\hfill & \mathrm{if}n=2k+1;\hfill \\ {\displaystyle \frac{n+3}{2}},\hfill & \mathrm{if}n=2k.\hfill \end{array}\right.$$

4.2. Illustration

Consider the graph $T_6$. The center and periphery for $T_6$ are shown in Figure 5 and Figure 6.

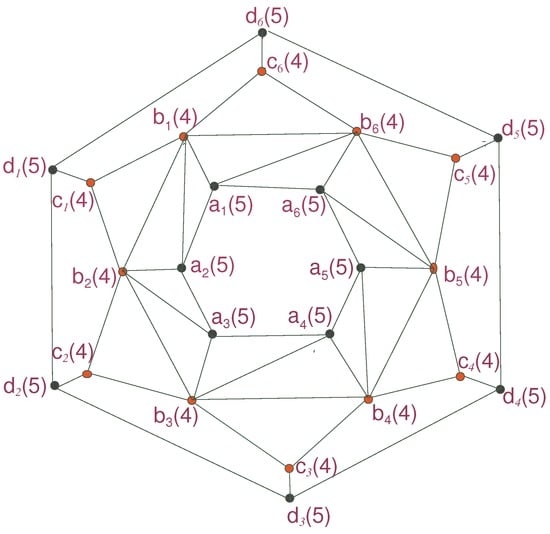
Figure 5. The graph of convex polytope $T_6$.

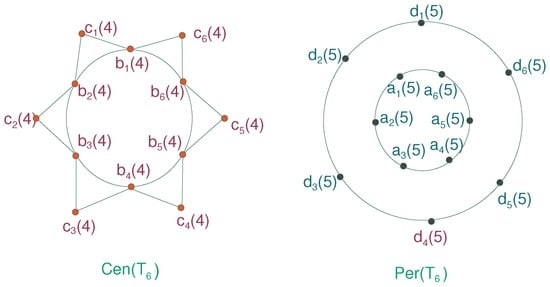
Figure 6. Centrality for $T_6$.

5. Concluding Remarks

In summary, we have studied the center and periphery of three types of families of convex polytopes via finding a subgraph induced by central and peripheral vertices. The predetermined facts about the eccentricity, radius and diameter of graphs play an important role in order to find the center and periphery for specific families of graphs; the average eccentricity of the above families of graphs has also been demonstrated.

6. Open Problems

This paper consist of the center and periphery for families of convex polytope graphs. This is an open problem for new researchers to find the center and periphery for others families of graphs, such as the corona product, composition product and lexicographic product of families of graphs.