A New Bayesian Edge-Linking Algorithm Using Single-Target Tracking Techniques
Abstract
:1. Introduction
2. Motivation (Idea)
3. Mathematical Background
3.1. Gaussian Markov Random Field
3.2. Circular State Space Model
3.3. Data Association for Single-Object Tracking
4. Proposed Approach
4.1. Improved Posterior with Marginalization of the EPs
4.2. Approach Based on the Metropolis–Hastings Algorithm
4.3. Gibbs Sampler-Based Approach
| Algorithm 1 Gibbs sampler-based approach. | |
| 1: | Let be a vector with non-negative integers s.t. for all . |
| 2: | for to do |
| 3: | for to T do |
| 4: | for to do |
| 5: | and make from the . |
| 6: | end for |
| 7: | Calculate the posterior |
| 8: | Draw a sample from the conditional posterior by |
| 9: | end for |
| 10: | Reconstruct using and find the best configuration with the MAP estimate. |
| 11: | end for |
4.4. Variational Bayes Using Mean-Field Approximation with Pseudo-Integration
| Algorithm 2 Variational Bayes approach. |
| 1: Let be a vector with non-negative integers s.t. for all . |
| 2: Set for all . |
| 3: Reconstruct using , and set . |
| 4: while (convergence) do |
| 5: . |
| 6: for to T do |
| 7: for to do |
| 8: , and make from . |
| 9: end for |
| 10: Calculate for all . |
| 11: Update for all . |
| 12: Normalize the updated distribution, . |
| 13: Obtain , and update . |
| 14: end for |
| 15: Reconstruct using , and find the best configuration using the MAP estimate. |
| 16: end while |
4.5. Variance Estimation Using Markov Chain Monte Carlo
5. Results
5.1. Noise-Free Image
5.2. Images with Occlusion
5.3. Image Segmentation with Varying Noise Levels
5.4. Application to More Complicated Raw Images
6. Discussion
7. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Marginalized Posterior
Appendix A.2. MATLAB Source Code
References
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 2nd ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 2001. [Google Scholar]
- Lebrun, M.; Buades, A.; Morel, J. A Nonlocal Bayesian Image Denoising Algorithm. SIAM J. Imaging Sci. 2013, 6, 1665–1688. [Google Scholar] [CrossRef]
- Yoon, J.W. Statistical denoising scheme for single molecule fluorescence microscopic images. Biomed. Signal Proc. Control 2014, 10, 11–20. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Marr, D.; Hildreth, E. Theory of Edge Detection. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1980, 207, 187–217. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Meyer, F.; Beucher, S. Morphological segmentation. J. Vis. Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
- Shih, F.Y.; Cheng, S. Adaptive mathematical morphology for edge linking. Inf. Sci. 2004, 167, 9–21. [Google Scholar] [CrossRef]
- Cook, G.W.; Delp, E.J. Multiresolution sequential edge linking. In Proceedings of the 1995 International Conference on Image Processing (ICIP), Washington, DC, USA, 23–26 October; IEEE: New York, NY, USA, 1995; pp. 41–44. [Google Scholar]
- Casadei, S.; Mitter, S.K. A hierarchical approach to high resolution edge contour reconstruction. In Proceedings of the 1996 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR ’96), San Francisco, CA, USA, 18–20 June 1998; IEEE: New York, NY, USA, 1998; pp. 149–154. [Google Scholar]
- Herout, A.; Dubská, M.; Havel, J. Review of Hough Transform for Line Detection. In Real-Time Detection of Lines and Grids; SpringerBriefs in Computer Science; Springer: London, UK, 2013; pp. 3–16. [Google Scholar]
- Farag, A.A.; Delp, E.J. Edge linking by sequential search. Pattern Recognit. 1995, 28, 611–633. [Google Scholar] [CrossRef]
- Hancock, E.R.; Kittler, J. Edge-labeling using dictionary-based relaxation. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 165–181. [Google Scholar] [CrossRef]
- Christmas, W.J.; Kittler, J.; Petrou, M. Structural matching in computer vision using probabilistic relaxation. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 749–764. [Google Scholar] [CrossRef]
- Feng, J.; Shi, Y.; Zhou, J. Robust and Efficient Algorithms for Separating Latent Overlapped Fingerprints. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1498–1510. [Google Scholar] [CrossRef]
- Mirmehdi, M.; Petrou, M. Segmentation of color textures. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 142–159. [Google Scholar] [CrossRef]
- Akinlar, C.; Chome, E. PEL: A Predictive Edge Linking algorithm. J. Vis. Commun. Image Represent. 2016, 36, 159–171. [Google Scholar] [CrossRef]
- Yang, X.; Liu, H.; Latecki, L.J. Contour-based object detection as dominant set computation. Pattern Recognit. 2012, 45, 1927–1936. [Google Scholar] [CrossRef]
- Jevtic, A.; Melgar, I.; Andina, D. Ant based edge linking algorithm. In Industrial Electronics, 35th Annual Conference of IEEE Industrial Electronics; IEEE: New York, NY, USA, 2009; pp. 3353–3358. [Google Scholar]
- Wang, Z.; Zhang, H. Edge linking using geodesic distance and neighborhood information. In Proceedings of the IEEE/ASME International Conference on, Advanced Intelligent Mechatronics (AIM 2008), Xi’an, China, 2–5 July 2008; IEEE: New York, NY, USA, 2008; pp. 151–155. [Google Scholar]
- Ghita, O.; Whelan, P.F. Computational approach for edge linking. J. Electron. Imaging 2002, 11, 479–485. [Google Scholar] [CrossRef]
- Isard, M.; Blake, A. Contour Tracking by Stochastic Propagation of Conditional Density; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1, pp. 343–356. [Google Scholar]
- Isard, M.; Blake, A. A mixed-state Condensation tracker with automatic model-switching. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 7 January 1998; IEEE: New York, NY, USA, 1998; pp. 107–112. [Google Scholar]
- Isard, M.; Blake, A. A smoothing filter for Condensation. In Proceedings of the 5th European Conference Computer Vision, Freiburg, Germany, 2–6 June 1998; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1, pp. 767–781. [Google Scholar]
- Zhang, S.; Zhou, H.; Jiang, F.; Li, X. Robust Visual Tracking Using Structurally Random Projection and Weighted Least Squares. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 1749–1760. [Google Scholar] [CrossRef]
- Zhou, H.; Taj, M.; Cavallaro, A. Target Detection and Tracking With Heterogeneous Sensors. IEEE J. Sel. Top. Signal Proc. 2008, 2, 503–513. [Google Scholar] [CrossRef]
- Lim, J.; Zitnick, C.L.; Dollár, P. Sketch Tokens: A Learned Mid-level Representation for Contour and Object Detection. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013.
- Marimont, D.; Rubner, Y. A probabilistic framework for edge detection and scale selection. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 7 January 1998; IEEE: New York, NY, USA, 1998; pp. 207–214. [Google Scholar]
- Gulshan, V.; Rother, C.; Criminisi, A.; Blake, A.; Zisserman, A. Geodesic Star Convexity for Interactive Image Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010.
- Veksler, O. Star shape prior for graph-cut image segmentation. In Proceedings of the 10th European Conference on Computer Vision (ECCV), Marseille, France, 12–18 October 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 454–467. [Google Scholar]
- Oh, S.; Russell, S.J.; Sastry, S. Markov Chain Monte Carlo Data Association for Multi-Target Tracking. IEEE Trans. Autom. Control 2009, 54, 481–497. [Google Scholar]
- Chen, S.; Cremers, D.; Radke, R.J. Image Segmentation with One Shape Prior - A Template-based Formulation. Image Vis. Comput. 2012, 30, 1032–1042. [Google Scholar] [CrossRef]
- Barker, S.; Rayner, P. Unsupervised image segmentation using Markov random field models. Pattern Recognit. 2000, 33, 587–602. [Google Scholar] [CrossRef]
- Celeux, G.; Forbes, F.; Peyrard, N. EM-Based Image Segmentation Using Potts Models with External Field; Rapport de Recherche RR-4456; INRIA: Le Chesnay, France, 2002. [Google Scholar]
- Brault, P.; Mohammad-Djafari, A. Unsupervised Bayesian wavelet domain segmentation using Potts-Markov random field modeling. J. Electron. Imaging 2005, 14, 043011. [Google Scholar]
- Rue, H.; Syversveen, A.R. Bayesian object recognition with Baddeley’s delta loss. Adv. Appl. Probab. 1988, 30, 64–88. [Google Scholar] [CrossRef]
- Chen, S.; Radke, R. Level set segmentation with both shape and intensity priors. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 27 September–4 October 2009; IEEE: New York, NY, USA, 2009; pp. 763–770. [Google Scholar]
- Rue, H.; Held, L. Gaussian Markov Random Fields: Theory and Applications; Monographs on Statistics and Applied Probability; Chapman & Hall: London, UK, 2005; Volume 104. [Google Scholar]
- Fan, A.; Fisher, J., III; Wells, W., III; LEvitt, J.; Willsky, A. MCMC Curve Sampling for Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2007; pp. 477–485. [Google Scholar]
- Chang, J.; Fisher, J.W., III. Efficient MCMC Sampling with Implicit Shape Representations. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011.
- Zhou, H.; Li, X.; Sadka, A.H. Nonrigid Structure-From-Motion From 2-D Images Using Markov Chain Monte Carlo. IEEE Trans. Multimed. 2012, 14, 168–177. [Google Scholar] [CrossRef]
- Panagiotakis, C.; Papadakis, H.; Grinias, E.; Komodakis, N.; Fragopoulou, P.; Tziritas, G. Interactive image segmentation based on synthetic graph coordinates. Pattern Recognit. 2013, 46, 2940–2952. [Google Scholar] [CrossRef]
- Cortés, X.; Serratosa, F. An interactive method for the image alignment problem based on partially supervised correspondence. Expert Syst. Appl. 2015, 42, 179–192. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A Database of Human Segmented Natural Images and its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics. In Proceedings of the 8th International Conference on Computer Vision, Dallas, TX, USA, 7–14 July 2001; IEEE: New York, NY, USA, 2001; Volume 2, pp. 416–423. [Google Scholar]
- Matlab code for Bayesian Edge-Linking Algorithms Using Single-Target Tracking Techniques. Available online: https://drive.google.com/file/d/0BwXUlJkl6zjeMGN3LU1RVzdiR0E (accessed on 15 November 2016).
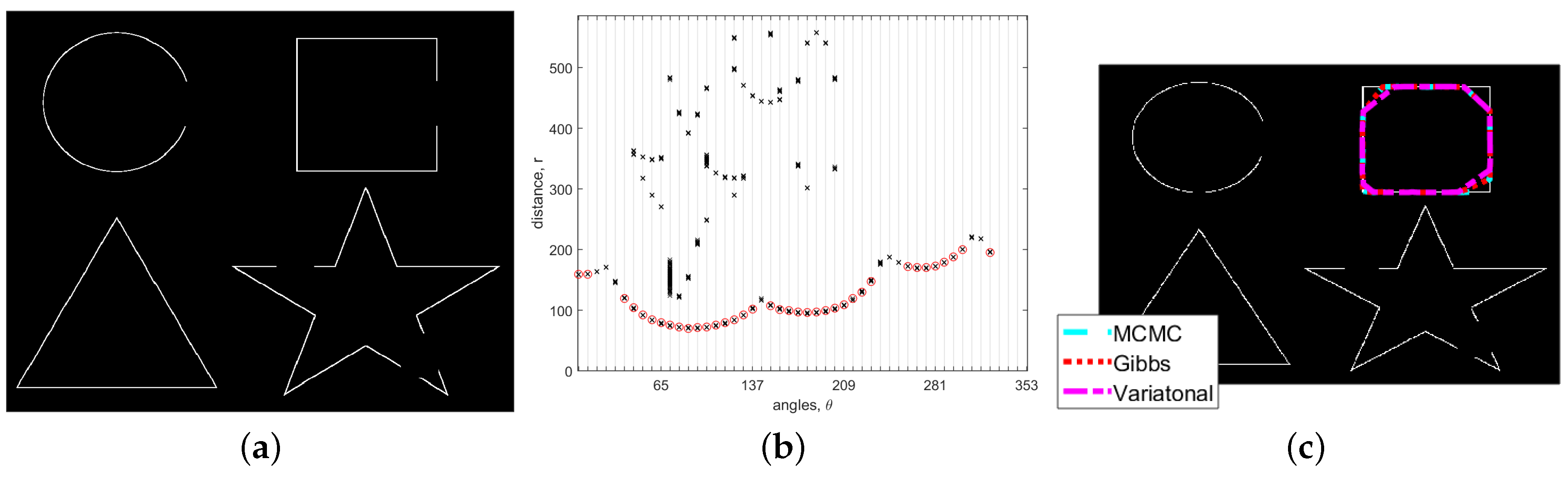


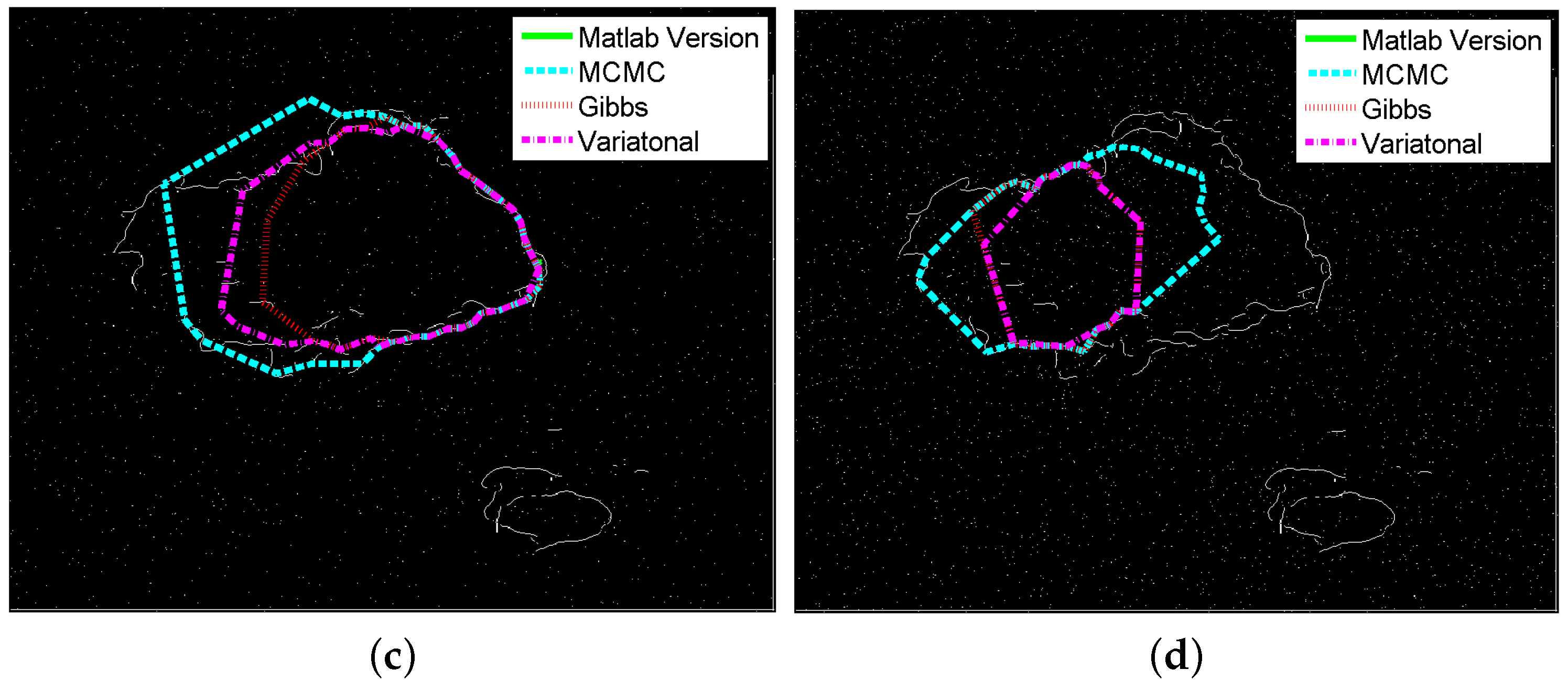

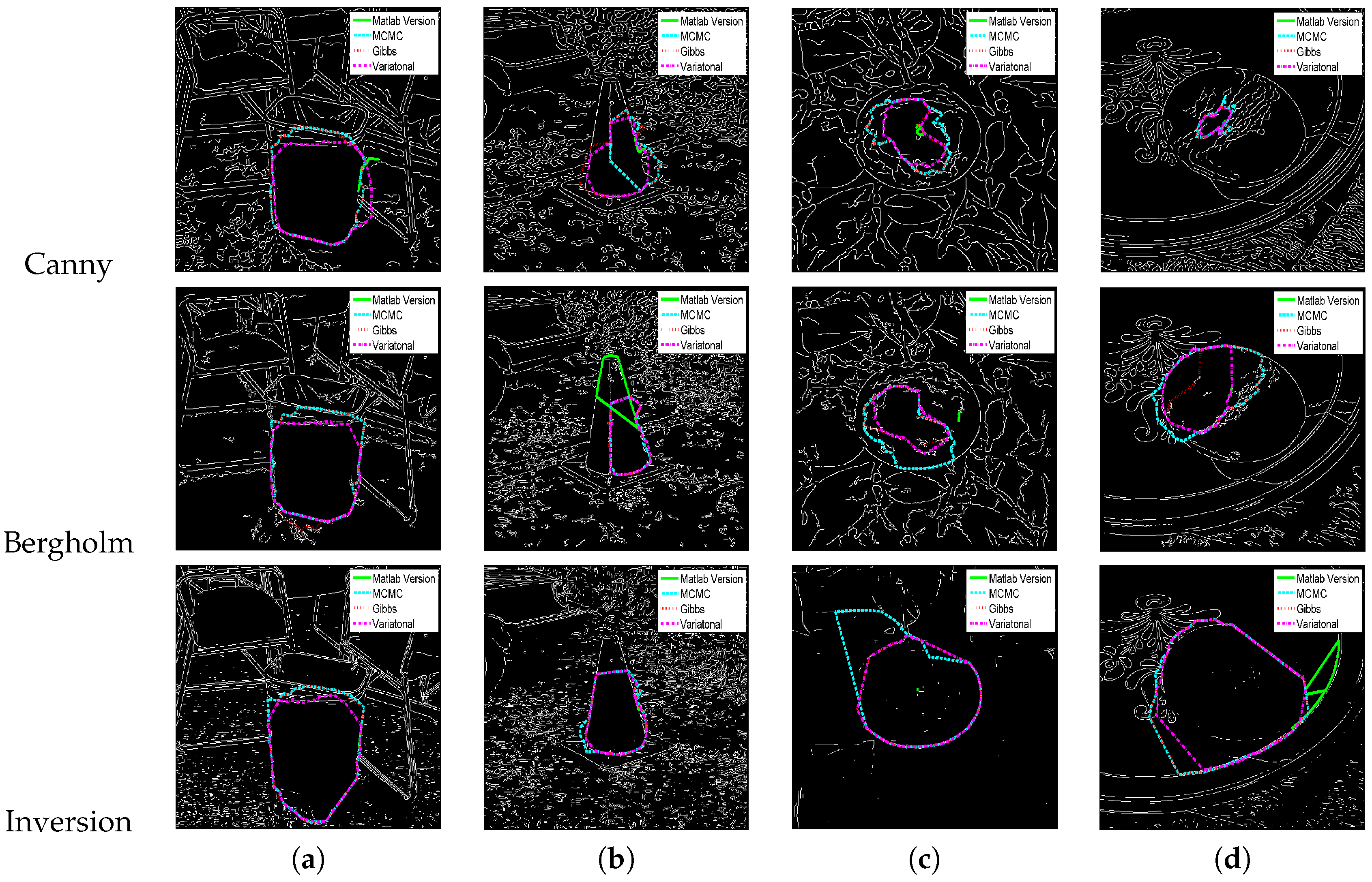
| Overlapping Rate (Average ± Std) | ||||
| MATLAB | MCMC | Gibbs | VB | |
| 0 | 0.77 0.10 | |||
| 0.76 0.08 | ||||
| 0.72 0.15 | ||||
| 0.64 0.14 | ||||
| Execution Time (Average ± Std) | ||||
| MATLAB | MCMC | Gibbs | VB | |
| 0 | ||||
| Image | Execution Time | |||
|---|---|---|---|---|
| MATLAB | MCMC | Gibbs | VB | |
| (a) | 1.7519 | 405.45 | 371.02 | 13.751 |
| (b) | 2.1913 | 447.51 | 525.08 | 19.322 |
| (c) | 1.5243 | 355.21 | 434.16 | 9.8595 |
| (d) | 1.7146 | 359.09 | 450.6 | 10.566 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, J.W. A New Bayesian Edge-Linking Algorithm Using Single-Target Tracking Techniques. Symmetry 2016, 8, 143. https://doi.org/10.3390/sym8120143
Yoon JW. A New Bayesian Edge-Linking Algorithm Using Single-Target Tracking Techniques. Symmetry. 2016; 8(12):143. https://doi.org/10.3390/sym8120143
Chicago/Turabian StyleYoon, Ji Won. 2016. "A New Bayesian Edge-Linking Algorithm Using Single-Target Tracking Techniques" Symmetry 8, no. 12: 143. https://doi.org/10.3390/sym8120143
APA StyleYoon, J. W. (2016). A New Bayesian Edge-Linking Algorithm Using Single-Target Tracking Techniques. Symmetry, 8(12), 143. https://doi.org/10.3390/sym8120143





