Comparing Bayesian and Maximum Likelihood Predictors in Structural Equation Modeling of Children’s Lifestyle Index
Abstract
:1. Introduction
- First moment properties of raw individual observations are mainly used in statistical techniques, thus making the techniques much simpler than second moment properties of the sample covariance matrix. Hence, B-SEM is easier to apply in more complex states.
- Direct latent variable estimation is possible, which simplifies the process of obtaining factor score estimates compared to classical regression methods.
- As manifest variables are directly modeled with their latent variables using familiar regression functions, B-SEM provides a more direct interpretation. It can also use common methods of regression modeling, such as residual and outlier analyses in conducting statistical analysis.
2. Theoretical Background of Maximum Likelihood-Structural Equation Modeling (ML-SEM) and Bayesian-SEM (B-SEM)
2.1. ML-SEM
- (a)
- is a matrix that represents factor loadings from modeling the regressions of on .
- (b)
- is a vector with normal distribution and is representative of the constructs (latent variables). are identically independent, have no correlation with , and have normal distribution . To modify the exogenous and endogenous latent variables’ association, is partitioned into , where and are and vector variables, respectively, with latent structures.
- (c)
- is a random vector with distribution that represents the error measurement.
- (a)
- is an matrix of structural parameters representing the relationships among endogenous latent variables. This matrix is assumed to have zeroes in the diagonal elements.
- (b)
- is an matrix of regression parameters relating both exogenous and endogenous latent variables, and is a vector of disturbances.
- (c)
- is an error term presumed to have distribution, where is a diagonal covariance matrix and this vector is uncorrelated with .
2.2. B-SEM
- is the number of categories for ;
- and represent the threshold levels associated with .
- is the inverse standardized normal distribution;
- is the total number of cases;
- is the number of cases in the th category.
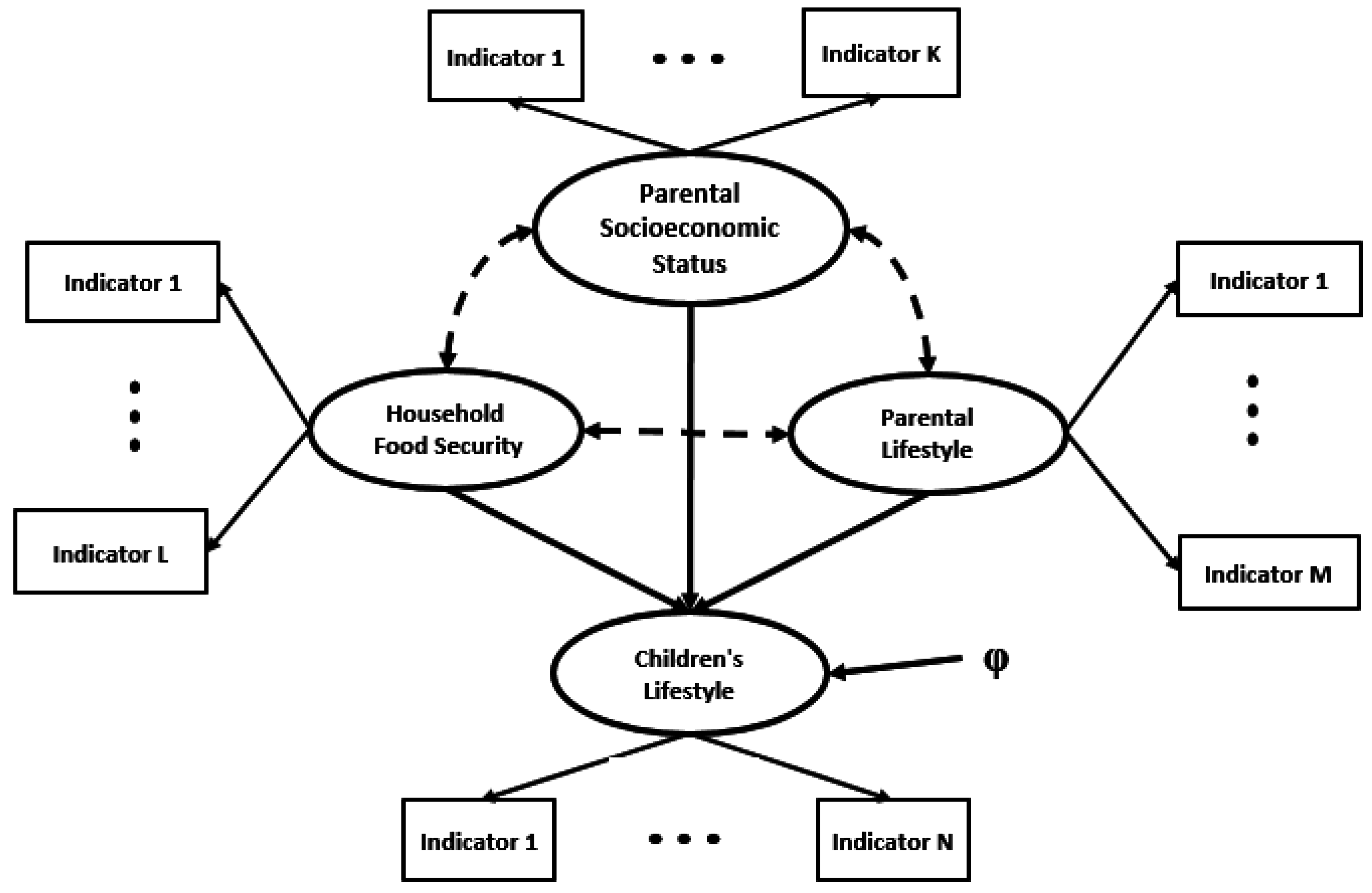
2.3. Modeling Description
3. Materials and Methods
3.1. Data Structure
3.2. Ethics Statement
3.3. Sampling
4. Results
- Prior I: Unknown loadings in are all made equal to 0.35, and the measures corresponding to are .
- Prior II: The hyperparameter values are considered half of the values in prior I.
- Prior III: The hyperparameter values are considered a quarter of the values in prior I.
- Prior IV: The hyperparameter values are considered double the values in prior I.
- is the coefficient of parental socioeconomic status indicator;
- is the coefficient of household food security indicator;
- is the coefficient of parental lifestyle indicator.
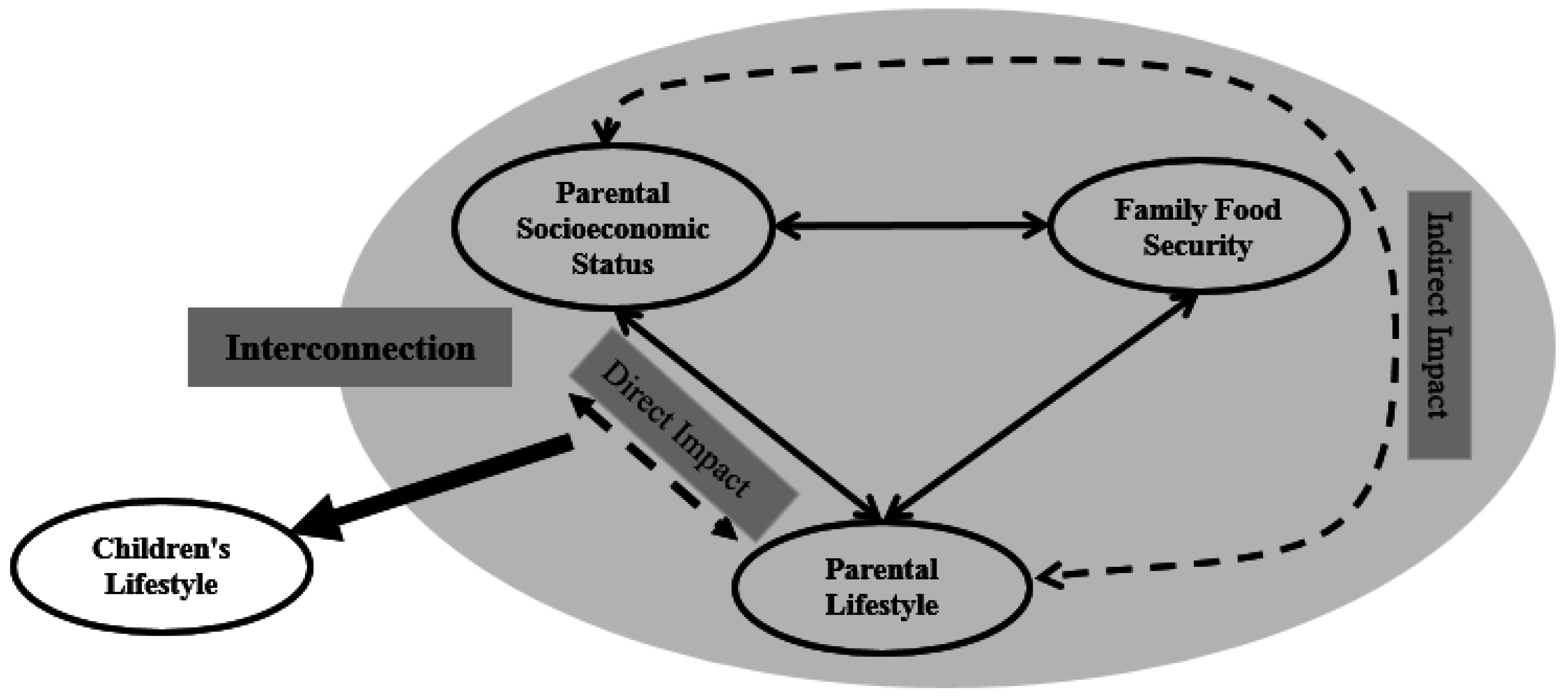
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brown, J.E.; Broom, D.H.; Nicholson, J.M.; Bittman, M. Do working mothers raise couch potato kids? Maternal employment and children’s lifestyle behaviours and weight in early childhood. Soc. Sci. Med. 2010, 70, 1816–1824. [Google Scholar] [CrossRef] [PubMed]
- Okubo, H.; Miyake, Y.; Sasaki, S.; Tanaka, K.; Murakami, K.; Hirota, Y. Dietary patterns in infancy and their associations with maternal socio-economic and lifestyle factors among 758 Japanese mother-child pairs: The Osaka maternal and child health study. Matern. Child Nutr. 2014, 10, 213–225. [Google Scholar] [CrossRef] [PubMed]
- Veldhuis, L.; Vogel, I.; van Rossem, L.; Renders, C.M.; HiraSing, R.A.; Mackenbach, J.P.; Raat, H. Influence of maternal and child lifestyle-related characteristics on the socioeconomic inequality in overweight and obesity among 5-year-old children; the “Be Active, Eat Right” Study. Int. J. Environ. Res. Public Health 2013, 10, 2336–2347. [Google Scholar] [CrossRef] [PubMed]
- Mangrio, E.; Wremp, A.; Moghaddassi, M.; Merlo, J.; Bramhagen, A.C.; Rosvall, M. Antibiotic use among 8-month-old children in Malmö, Sweden-in relation to child characteristics and parental sociodemographic, psychosocial and lifestyle factors. BMC Pediatr. 2009, 9, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Ek, A.; Sorjonen, K.; Nyman, J.; Marcus, C.; Nowicka, P. Child behaviors associated with childhood obesity and parents’ self-efficacy to handle them: Confirmatory factor analysis of the lifestyle behavior checklist. Int. J. Behav. Nutr. Phys. Acta 2015, 12, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Chi, D.L.; Masterson, E.E.; Carle, A.C.; Mancl, L.A.; Coldwell, S.E. Socioeconomic status, food security, and dental caries in US children: Mediation analyses of data from the National Health and Nutrition Examination Survey, 2007–2008. Am. J. Public Health 2014, 104, 860–864. [Google Scholar] [CrossRef] [PubMed]
- Ishida, R. Impacts of beautiful natural surroundings on happiness: Issues of environmental disruption, food, water security and lifestyle in modern times. Br. J. Med. Med. Res. 2015, 9, 1–6. [Google Scholar] [CrossRef]
- Ullman, J.B. Structural equation modeling: Reviewing the basics and moving forward. J. Personal. Assess. 2006, 87, 35–50. [Google Scholar] [CrossRef]
- Lee, S.Y. Structural Equation Modeling: A Bayesian Approach 2007, 1st ed.; John Wiley & Sons: West Sussex, UK, 2007; pp. 24–25. [Google Scholar]
- Olsson, U.H.; Foss, T.; Troye, S.V.; Howell, R.D. The performance of ML, GLS, and WLS estimation in structural equation modeling under conditions of misspecification and nonnormality. Struct. Equ. Model. 2000, 7, 557–595. [Google Scholar] [CrossRef]
- Bashir, M.K.; Schilizzi, S. Food security policy assessment in the Punjab, Pakistan: Effectiveness, distortions and their perceptions. Food Secur. 2015, 7, 1071–1089. [Google Scholar] [CrossRef]
- Wan Mohamed Radzi, C.W.J.B.; Salarzadeh Jenatabadi, H.; Hasbullah, M.B. Firm Sustainability Performance Index Modeling. Sustainability 2015, 7, 16196–16212. [Google Scholar] [CrossRef]
- Scheines, R.; Hoijtink, H.; Boomsma, A. Bayesian estimation and testing of structural equation models. Psychometrika 1999, 64, 37–52. [Google Scholar] [CrossRef]
- Lee, S.Y.; Song, X.Y. Evaluation of the Bayesian and maximum likelihood approaches in analyzing structural equation models with small sample sizes. Multivar. Behav. Res. 2004, 39, 653–686. [Google Scholar] [CrossRef] [PubMed]
- Dunson, D.B. Bayesian latent variable models for clustered mixed outcomes. J. R. Stat. Soc. Ser. B Stat. Methodol. 2000, 62, 355–366. [Google Scholar] [CrossRef]
- Lovaglio, P.G.; Boselli, R. Simulation studies of structural equation models with covariates in a redundancy analysis framework. Qual. Quant. 2015, 49, 881–890. [Google Scholar] [CrossRef]
- Lovaglio, P.G.; Vittadini, G. Structural equation models in a redundancy analysis framework with covariates. Multivar. Behav. Res. 2014, 49, 486–501. [Google Scholar] [CrossRef] [PubMed]
- Cho, S.J.; Preacher, K.J.; Bottge, B.A. Detecting intervention effects in a cluster-randomized design using multilevel structural equation modeling for binary responses. Appl. Psychol. Meas. 2015, 39, 627–642. [Google Scholar] [CrossRef]
- Scherer, R.; Gustafsson, J.E. Student assessment of teaching as a source of information about aspects of teaching quality in multiple subject domains: An application of multilevel bifactor structural equation modeling. Front. Psychol. 2015, 6, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Song, X.Y.; Lee, S.Y. A maximum likelihood approach for multisample nonlinear structural equation models with missing continuous and dichotomous data. Struct. Equ. Model. 2006, 13, 325–351. [Google Scholar] [CrossRef]
- Lee, S.Y.; Ho, W.T. Analysis of multisample identified and non-identified structural equation models with stochastic constraints. Comput. Stat. Data Anal. 1993, 16, 441–453. [Google Scholar] [CrossRef]
- Rabe-Hesketh, S.; Skrondal, A.; Pickles, A. Generalized multilevel structural equation modeling. Psychometrika 2014, 69, 167–190. [Google Scholar] [CrossRef]
- Yang, Y.; Green, S.B. Evaluation of structural equation modeling estimates of reliability for scales with ordered categorical items. Methodology 2015, 11, 23–34. [Google Scholar] [CrossRef]
- Wedel, M.; Kamakura, W.A. Factor analysis with (mixed) observed and latent variables in the exponential family. Psychometrika 2011, 66, 515–530. [Google Scholar] [CrossRef]
- Finch, W.H. Modeling nonlinear structural equation models: A comparison of the two-stage generalized additive models and the finite mixture structural equation model. Struct. Equ. Model. 2015, 22, 60–75. [Google Scholar] [CrossRef]
- Wall, M.M.; Amemiya, Y. Estimation for polynomial structural equation models. J. Am. Stat. Assoc. 2000, 95, 929–940. [Google Scholar] [CrossRef]
- Bollen, K.A. Latent variables in psychology and the social sciences. Annu. Rev. Psychol. 2002, 53, 605–634. [Google Scholar] [CrossRef] [PubMed]
- Flora, D.B.; Curran, P.J. An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychol. Methods 2004, 9, 466–491. [Google Scholar] [CrossRef] [PubMed]
- Evans, M.; Moshonov, H. Checking for prior-data conflict. Bayesian Anal. 2006, 1, 893–914. [Google Scholar] [CrossRef]
- Muthén, B.; Asparouhov, T. Bayesian structural equation modeling: A more flexible representation of substantive theory. Psychol. Methods 2012, 17, 313–335. [Google Scholar] [CrossRef] [PubMed]
- Evans, M. Measuring statistical evidence using relative belief. Comput. Struct. Biotechnol. J. 2016, 14, 91–96. [Google Scholar] [CrossRef] [PubMed]
- Yanuar, F.; Ibrahim, K.; Jemain, A.A. Bayesian structural equation modeling for the health index. J. Appl. Stat. 2013, 40, 1254–1269. [Google Scholar] [CrossRef]
- Bickel, G.; Nord, M.; Price, C.; Hamilton, W.; Cook, J. Guide to Measuring Household Food Security in the United States; USDA, Food and Nutrition Services: Alexandria, VA, USA, 2000.
- Nakayama, K.; Yamaguchi, K.; Maruyama, S.; Morimoto, K. The relationship of lifestyle factors, personal character, and mental health status of employees of a major Japanese electrical manufacturer. Environ. Health Prev. 2001, 5, 144–149. [Google Scholar] [CrossRef] [PubMed]
- Health Research Ethics Authority (HREA). Available online: http://www.hrea.ca/Ethics-Review-Required.aspx (accessed on 22 January 2016).
- Mullen, M.R.; Milne, G.R.; Doney, P.M. An international marketing application of outlier analysis for structural equations: A methodological note. J. Int. Market. 1995, 3, 45–62. [Google Scholar]
- Argyris, C.; Schön, D.A. Organizational learning: A theory of action perspective. Reis 1997, 77, 345–348. [Google Scholar] [CrossRef]
- Schoot, R.; Kaplan, D.; Denissen, J.; Asendorpf, J.B.; Neyer, F.J.; Aken, M.A. A gentle introduction to Bayesian analysis: Applications to developmental research. Child Dev. 2014, 85, 842–860. [Google Scholar] [CrossRef] [PubMed]
- Van Wesel, F. Priors & Prejudice: Using Existing Knowledge in Social Science Research. Ph.D. Thesis, Utrecht University, Utrecht, The Netherlands, January 2011. [Google Scholar]
- Rietbergen, C.; Klugkist, I.; Janssen, K.J.; Moons, K.G.; Hoijtink, H.J. Incorporation of historical data in the analysis of randomized therapeutic trials. Contemp. Clin. Trials 2011, 32, 848–855. [Google Scholar] [CrossRef] [PubMed]
- Garthwaite, P.H.; Kadane, J.B.; O’Hagan, A. Statistical methods for eliciting probability distributions. J. Am. Stat. Assoc. 2005, 100, 680–701. [Google Scholar] [CrossRef]
- Van Erp, S.; Mulder, J.; Oberski, D.L. Prior sensitivity analysis in default Bayesian structural equation modeling. In Proceedings of the 31th International Organisation of Pension Supervisors (IOPS) Summer Conference, Enschede, The Netherlands, 9–10 June 2016.
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis, 2nd ed.; Chapman & Hall/Chemical Rubber Company (CRC): Boca Raton, FL, USA, 2004; p. 189. [Google Scholar]




| Observation Number | Mahalanobis D-Squared | p1 | p2 |
|---|---|---|---|
| 36 | 22.56 | 0.0016 | 0.0084 |
| 88 | 20.31 | 0.0067 | 0.0091 |
| 92 | 18.92 | 0.0092 | 0.0104 |
| 134 | 36.58 | 0.0116 | 0.0124 |
| 228 | 32.71 | 0.0231 | 0.0178 |
| 256 | 30.08 | 0.0854 | 0.0364 |
| 372 | 28.19 | 0.0932 | 0.0392 |
| 411 | 25.44 | 0.1589 | 0.0421 |
| 444 | 19.76 | 0.2876 | 0.0482 |
| Characteristics | Percentage | Characteristics | Percentage |
|---|---|---|---|
| Gender: | Average hours per day of using technology: | ||
| Boy | 45.60% | Less than one hour per day | 13.20% |
| Girl | 54.40% | 1 to 2 h per day | 15.70% |
| School grades: | 3 to 4 h per day | 40.70% | |
| Grade 1 | 14.20% | More than 4 h per day | 30.70% |
| Grade 2 | 16.80% | Physical activities in a week: | |
| Grade 3 | 16.60% | None | 44.20% |
| Grade 4 | 16.30% | 1 or 2 times per week | 28.40% |
| Grade 5 | 17.30% | 3 or 4 times per week | 19.70% |
| Grade 6 | 18.80% | More than 4 times per week | 7.70% |
| Study at home: | Average sleeping hours in a day: | ||
| Less than one hour per day | 21.10% | Less than 7 h per day | 5.80% |
| 1 to 2 h per day | 29.40% | Between 7 and 8 h per day | 22.20% |
| 3 to 4 h per day | 33.10% | Between 8 and 9 h per day | 56.30% |
| More than 4 h per day | 16.40% | More than 9 h per day | 15.70% |
| Characteristics | Father (%) | Mother (%) | Characteristics | Father (%) | Mother (%) |
|---|---|---|---|---|---|
| Age: | Smoking Habit: | ||||
| Less than or equal 30 years old | 18.5% | 21.6% | Smoker | 66.6% | 23.8% |
| Between 31and 40 years old | 36.2% | 25.1% | Quitted | 15.7% | 13.7% |
| Between 41 and 50 years old | 22.1% | 28.4% | Non-smoker | 17.7% | 62.5% |
| More than 50 years old | 23.2% | 24.9% | Physical exercise: | ||
| Education: | None | 54.4% | 33.6% | ||
| Less than High School | 11.3% | 9.5% | 1 or 2 times in a week | 27.7% | 38.7% |
| High school | 19.8% | 6.7% | 3 or 4 times per week | 14.8% | 11.2% |
| Diploma | 37.7% | 41.9% | More than 4 times in a week | 3.1% | 16.5% |
| Bachelor | 29.1% | 33.1% | Working hours in a day: | ||
| Master or PhD | 2.1% | 8.8% | More than 14 hours per day | 26.7% | 8.2% |
| Income: | 9–14 hours per day | 62.8% | 73.5% | ||
| Less than RMB2000 per month | 11.7% | 20.6% | Less than 9 hours per day | 10.5% | 18.3% |
| RMB2001-RMB3000 per month | 22.6% | 24.5% | Average sleeping hours in a day: | ||
| RMB3001-RMB4000 per month | 33.9% | 22.1% | Less than 7 hours per day | 55.4% | 61.9% |
| RMB4001-RMB5000 per month | 19.9% | 17.3% | Between 7 to 8 hours per day | 27.9% | 30.0% |
| More than RMB5000 per month | 11.9% | 15.5% | More than 8 hours per day | 16.7% | 8.1% |
| Work experience: | Drinking Alcohol Habit: | ||||
| No work experience | 0.00% | 0.00% | Less than one time per month | 3.2% | 10.6% |
| Less than 5 years | 7.4% | 19.2% | 1 time per month | 4.5% | 22.7% |
| 5-10 years | 12.9% | 21.7% | 2 to 3 times per month | 16.1% | 32.1% |
| 11-15 years | 36.6% | 26.6% | 1 time per week | 16.7% | 28.2% |
| 16-20 years | 32.8% | 23.6% | 2 to 3 times per week | 39.5% | 6.4% |
| More than 20 years | 10.3% | 8.9% | 4 to 6 times per week | 18.7% | 0.00% |
| Every day | 1.3% | 0.00% |
| Parameter Description | Factor Loading |
|---|---|
| Parental Socioeconomic | |
| Mother’s age | 0.43 |
| Father’s age | 0.38 |
| Mother’s education | 0.74 |
| Father’s education | 0.39 |
| Mother’s income | 0.43 |
| Father’s income | 0.68 |
| Mother’s work experience | 0.06 |
| Father’s work experience | 0.05 |
| Parents’ marriage length | 0.82 |
| Parental Lifestyle | |
| Mother’s drinking alcohol | 0.36 |
| Father’s drinking alcohol | 0.73 |
| Mother’s smoking habit | 0.48 |
| Father’s smoking habit | 0.41 |
| Mother’s physical exercises | 0.21 |
| Father’s physical exercises | 0.09 |
| Mother’s working hours | 0.76 |
| Father’s working hours | 0.88 |
| Mother’s average sleeping hours | 0.83 |
| Father’s average sleeping hours | 0.71 |
| Household Food Security | |
| Worry about running out of food | 0.73 |
| Do not have money: household | 0.82 |
| Cannot afford to eat balanced meals: household | 0.93 |
| Cut down food portions: household | 0.12 |
| Do not eat the whole day: adults | 0.98 |
| Do not have money: children | 0.04 |
| Cannot afford to eat balanced meals: children | 0.25 |
| Cannot afford enough food: children | 0.82 |
| Skip a meal: children | 0.24 |
| Children’s Lifestyle | |
| Technology use | 0.92 |
| Hours of study at home | 0.73 |
| Child’s physical exercise | 0.49 |
| Child’s sleep amount | 0.68 |
| School grade | 0.46 |
| Prior I | Prior II | Prior III | Prior IV | |||||
|---|---|---|---|---|---|---|---|---|
| Parameter | Estimate | STD | Estimate | STD | Estimate | STD | Estimate | STD |
| θ1 | 0.561 | 0.021 | 0.555 | 0.033 | 0.549 | 0.069 | 0.584 | 0.121 |
| θ2 | 0.493 | 0.088 | 0.461 | 0.097 | 0.452 | 0.102 | 0.503 | 0.201 |
| θ3 | 0.203 | 0.096 | 0.192 | 0.051 | 0.180 | 0.091 | 0.221 | 0.138 |
| θ13 | 0.739 | 0.108 | 0.721 | 0.101 | 0.598 | 0.027 | 0.751 | 0.102 |
| θ16 | 0.683 | 0.112 | 0.677 | 0.109 | 0.655 | 0.111 | 0.686 | 0.138 |
| θ19 | 0.822 | 0.087 | 0.816 | 0.078 | 0.801 | 0.098 | 0.852 | 0.203 |
| θ22 | 0.733 | 0.039 | 0.730 | 0.035 | 0.722 | 0.069 | 0.763 | 0.093 |
| θ27 | 0.763 | 0.109 | 0.755 | 0.099 | 0.743 | 0.106 | 0.771 | 0.126 |
| θ28 | 0.883 | 0.119 | 0.844 | 0.081 | 0.822 | 0.077 | 0.896 | 0.119 |
| θ29 | 0.827 | 0.044 | 0.814 | 0.041 | 0.759 | 0.036 | 0.834 | 0.66 |
| θ210 | 0.711 | 0.066 | 0.697 | 0.057 | 0.666 | 0.051 | 0.723 | 0.107 |
| θ31 | 0.734 | 0.029 | 0.726 | 0.026 | 0.669 | 0.039 | 0.742 | 0.127 |
| θ32 | 0.822 | 0.071 | 0.816 | 0.064 | 0.798 | 0.061 | 0.831 | 0.104 |
| θ33 | 0.928 | 0.191 | 0.909 | 0.161 | 0.852 | 0.170 | 0.832 | 0.206 |
| θ35 | 0.981 | 0.058 | 0.921 | 0.052 | 0.832 | 0.048 | 0.883 | 0.067 |
| θ38 | 0.816 | 0.161 | 0.799 | 0.152 | 0.764 | 0.143 | 0.802 | 0.188 |
| Relation | Estimated Coefficients | |
|---|---|---|
| ML-SEM | B-SEM | |
| Parental socioeconomic → Children’s life style | 0.549 * | 0.561 * |
| Household food security → Children’s life style | 0.198 | 0.203 |
| Parental lifestyle → Children’s life style | 0.488 * | 0.493 * |
| Parental socioeconomic ↔ Parental lifestyle | 0.508 * | 0.513 * |
| Parental socioeconomic ↔ Household food security | 0.519 * | 0.521 * |
| Household food security ↔ Parental lifestyle | 0.611 * | 0.637 * |
| Name of Index | Formula | ML-SEM Value | B-SEM Value |
|---|---|---|---|
| MAPE | 0.094 | 0.088 | |
| RMSE | 0.091 | 0.051 | |
| MSE | 0.128 | 0.105 | |
| R2 | 0.601 | 0.761 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radzi, C.W.J.b.W.M.; Hui, H.; Salarzadeh Jenatabadi, H. Comparing Bayesian and Maximum Likelihood Predictors in Structural Equation Modeling of Children’s Lifestyle Index. Symmetry 2016, 8, 141. https://doi.org/10.3390/sym8120141
Radzi CWJbWM, Hui H, Salarzadeh Jenatabadi H. Comparing Bayesian and Maximum Likelihood Predictors in Structural Equation Modeling of Children’s Lifestyle Index. Symmetry. 2016; 8(12):141. https://doi.org/10.3390/sym8120141
Chicago/Turabian StyleRadzi, Che Wan Jasimah bt Wan Mohamed, Huang Hui, and Hashem Salarzadeh Jenatabadi. 2016. "Comparing Bayesian and Maximum Likelihood Predictors in Structural Equation Modeling of Children’s Lifestyle Index" Symmetry 8, no. 12: 141. https://doi.org/10.3390/sym8120141
APA StyleRadzi, C. W. J. b. W. M., Hui, H., & Salarzadeh Jenatabadi, H. (2016). Comparing Bayesian and Maximum Likelihood Predictors in Structural Equation Modeling of Children’s Lifestyle Index. Symmetry, 8(12), 141. https://doi.org/10.3390/sym8120141







