Next Article in Journal / Special Issue
Organocatalytic Asymmetric α-Chlorination of 1,3-Dicarbonyl Compounds Catalyzed by 2-Aminobenzimidazole Derivatives
Previous Article in Journal
Structural Properties and Biological Prediction of ({[(1E)-3-(1H-Imidazol-1-yl)-1-phenylpropylidene] amino}oxy)(4-methylphenyl)methanone: An In Silico Approach
Previous Article in Special Issue
Cyclodextrins in Asymmetric and Stereospecific Synthesis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Symmetry
Volume 8
Issue 1
10.3390/sym8010002
symmetry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Natural Abundance Isotopic Chirality in the Reagents of the Soai Reaction †

by
Béla Barabás
1,
Róbert Kurdi
2 and
Gyula Pályi
3,*
1
Institute of Mathematics, Budapest University of Technology and Economics, Egry J. u. 1, H-1111 Budapest, Hungary
2
Institute of Environmental Engineering, University of Pannonia, Egyetem u. 10, H-8200 Veszprém, Hungary
3
Department of Life Sciences, University of Modena and Reggio Emilia, Via Campi 103, I-41125 Modena, Italy
*
Author to whom correspondence should be addressed.
†
Some parts of the this paper have been presented at the 3rd International Symposium on the Soai Reactionand Related Topic, Fels˝omocsolád, Hungary, 2–5 September 2015; Abstracts, p. 26.
Symmetry 2016, 8(1), 2; https://doi.org/10.3390/sym8010002
Submission received: 20 November 2015 / Revised: 16 December 2015 / Accepted: 21 December 2015 / Published: 8 January 2016
(This article belongs to the Special Issue Asymmetric Catalysis)
Browse Figures
Versions Notes

Abstract

:
Isotopic chirality influences sensitively the enantiomeric outcome of the Soai asymmetric autocatalysis. Therefore magnitude and eventual effects of isotopic chirality caused by natural abundance isotopic substitution (H, C, O, Zn) in the reagents of the Soai reaction were analyzed by combinatorics and probability calculations. Expectable enantiomeric excesses were calculated by the Pars–Mills equation. It has been found that the chiral isotopic species formed by substitution in the otherwise achiral reagents provide enantiomeric excess (e.e.) levels that are higher than the sensitivity threshold of the Soai autocatalysis towards chiral induction. Consequently, possible chiral induction exerted by these e.e. values should be taken into account in considerations regarding the molecular events and the mechanism of the chiral induction in the Soai reaction.

1. Introduction

Effects caused by isotopic substitution have been broadly investigated and applied in analytical, organic and biological chemistry [1,2,3,4,5,6,7]. Studies, however, concerning the effects of chirality caused by isotopic substitution, especially on the natural abundance level, are much less numerous [8,9,10,11]. This can be due to the simple fact that elements occurring in typical organic syntheses or biochemistry (H, C, N, O, S) show highly imbalanced natural abundance distributions in favor of the lighter isotopes, or occur as a single isotope (P) [12]. Consequently, “statistical” chirality [13] caused by the substitution with the heavier isotope in otherwise achiral (isotopically prochiral) molecules (groups) appeared to be negligible. This situation changed radically with the discovery of the asymmetric autocatalysis (Soai reaction) in 1995 [14,15].
The Soai reaction shows extreme sensitivity towards the chiral induction exerted by even very low quantities both of the autocatalyst [16,17,18,19,20,21,22,23,24] and of added (enantiomerically pure or enriched) “foreign” chiral molecules [25,26,27,28,29,30,31]. It has also been proved experimentally that such inductor molecules may include enantiomers of simple chiral organic compounds with chirality due only to stable isotopic substitution [32,33,34,35,36,37,38,39]. The sensitivity towards any chiral additive, or even a very small excess of the product results in the capacity of this reaction to produce very high enantiomeric excess from infinitesimally low one. The fundamental significance of this aspect of the Soai reaction in studies concerning the origin(s) of biological chirality has also been discussed [40].
In the present study, we analyzed extension and eventual consequences of isotopic chirality occurring by natural abundance quantities of stable isotopes in the reagents of the Soai reaction.

2. Results and Discussion

The reagents of the most efficient variant [17] of the Soai reaction include an N-heterocyclic aldehyde, 4-[2-(tert.-butyl)ethynyl]pyrimidylaldehyde (1), di(iso-propyl)zinc (2) and the autocatalyst, which is the alkylation product of 1 by 2, leading to the secondary alcohol (3), as shown in Figure 1 [41,42]. These molecules are formed from H, C, N, O and Zn, which are present in nature as mixtures of their stable isotopes; the H, C, N, and O with dominance of the lighter nuclei, while Zn as a more equable mixture of five isotopes [12] (Table S1). As can be seen from the structures in Figure 1, the “isotopically prochiral” groups in compounds 1–3 are the tert.-Bu group in 1 and 3, as well as the iso-Pr group in compounds 2 and 3. These groups consist of H and C, thus the isotopic substitution by these elements will be analyzed here. N is not included in our analysis, even if a very recent study has shown that chirality caused (only) by N-isotopes can control the enantiomeric outcome of the Soai reaction [43]. Some fragments of hypothetic intermediates [44,45,46] of the Soai autocatalysis show chiral arrangement of the Zn atoms. One of these fragments, the structure of which has been essentially supported by X-ray crystallography [47], will also be included in the present study.
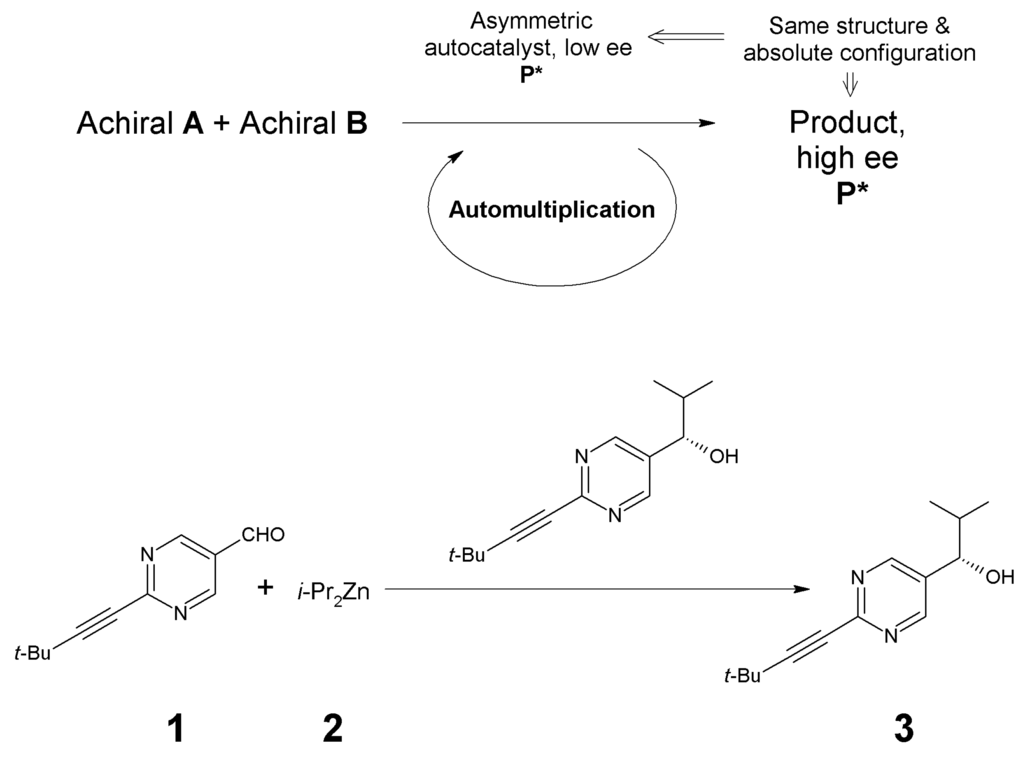
Symmetry 08 00002 g001 1024
Figure 1. The Soai reaction [37,38,39,41,42] (with the most efficient substrate).
Figure 1. The Soai reaction [37,38,39,41,42] (with the most efficient substrate).
Symmetry 08 00002 g001

2.1. The Tert.-Butyl Group

The tertiary-butyl group in compounds 1 and 3 is a highly symmetric species. Therefore, it needs at least two different substituents on at least two of its methyl groups for the generation of a center of chirality on the central C atom. Because of the presence of three identic (methyl) groups in this functionality, the number of possible isotopically substituted derivatives amounts to 112 (Supporting Materials 1) if the isotopic substitution in the central carbon atom is neglected, and 224 if this is taken into account. Because of the necessity of (at least) double isotopic substitution for obtaining a chiral isotopomer, the probabilities of the formation of such structures with natural abundance 2H and/or 13C substituents is very low. Only four combinations (from 112) have probability >10−8. The sum of the probabilities is 1.027 × 10−5, deriving mostly from species with one 13C substitution.
We calculated the expectable enantiomeric excesses (e.e.50%, %) with the Pars–Mills equation [40,48] (with 50% confidence, see also Supporting Materials 2) for sample sizes that could appear in usual micropreparative work (ranging from millimol to femtomol) (Table 1).
Table
Table 1. Expectable enantiomeric excesses in the t-Bu group.
Table 1. Expectable enantiomeric excesses in the t-Bu group.
Sample Sizee.e.50%
millimol8.60 × 10−7
micromole2.72 × 10−5
nanomol8.60 × 10−4
picomol2.72 × 10−2
femtomol8.60 × 10−1
These data show that even if the expectable e.e. values are very low, according to experimental evidence [16,17,18,19,20] and theoretical considerations [21,22,23,24], the isotope chirality in the tert.-butyl group in compounds 1 and/or 3 could influence the outcome of the most sensitive variant of the Soai reaction, however, taking into regard that it is separated from the pyrimidyl unit by the rigid C2 moiety, and thus from the decisive molecular events around the new stereocenter, this option appears as scarcely probable, but cannot be excluded.

2.2. The Iso-Propyl Group(s)

The i-Pr groups appear in two of the reactants: 2 and 3. There is, however, both quantitative and qualitative differences between these structures. Compound 2 contains two i-Pr groups, in organometallic bond, while autocatalyst 3 contains only one i-Pr moiety, linked by covalent C(sp3)–C(sp3) bond to the newly formed center of chirality. This is a fundamental difference, especially from the viewpoint that in 2 the i-Pr groups are present before the C–C bond making it an alkylation step, while the i-Pr group in 3 represent a final stage; that is, the stage when the fate of the asymmetry of the critical carbon atom has already been decided. On the other hand, compound 3 appears as autocatalyst in the subsequent cycle(s) of the reaction in intermediate(s), the structure of which is actually known only from theoretical studies [44,45,46,47,49]
The analysis of the eventual role of isotopically chiral i-Pr group(s) will be deduced step-by-step starting with the methyl group.
For commodity, let us define the probabilities (P) on the basis of the natural abundances [12] as follows: P(12C) = p = 0.98889, P(13C) = q = 0.01111, P(1H) = u = 0.999844 and P(2D) = v = 0.000156. Thus
p1 = P(12C1H3) = pu3p5 = P(13C1H3) = qu3
p2 = P(12C1H22D) = 3pu2vp6 = P(13C1H22D) = 3qu2v
p3 = P(12C1H2D2) = 3puv2p7 = P(13C1H2D2) = 3quv2
p4 = P(12C2D3) = pv3p8 = P(13C2D3) = qv3
amounting to eight cases, with ∑pi = 1 (i = 1–8). These cases, obviously, provide no chirality.
The iso-propyl group containing two methyl groups, gives 8 × 8 = 64 cases if the possible carbon or hydrogen isotope substitution in the central CH group is disregarded; if only the 12C/13C or 1H/2D exchange is taken into account, the number of cases is 2 × 64 = 128, while both of these exchanges yield 2 × 128 = 256 cases. We shall calculate below on the basis of 128 cases.
The probabilities of these cases are the products of the individual probabilities:
p × pi × pj and q × pi × pj, where i = 1,2,…,8 and j = 1,2,…,8. If i = j, the i-Pr group becomes symmetric, which are 16 cases from 128, leaving 112 as asymmetric cases. From these, obviously, 56 are of R and 56 of S configuration. The sum of the probabilities of the symmetric (achiral) cases is ∑(p × pi2 + q × pi2) = 0.977131 (since i = j in the symmetric cases).
The probability of the remaining 112 chiral cases is Pchiral = 1 – 0.977131 = 0.022869. The abundance of the symmetric species with central 12C is thus 0.98889 × 0.977131 = 0.96627566, while with central 13C it is 0.01111 × 0.977131 = 0.01085593 and the sum of these (as it should be) equals 0.977131.
Consequently, the sum of the abundances of the 56S and 56R species is 0.022869 ≈ 2.3%.
The actual alkylation reagent, 2, of the Soai reaction, however, contains two iso-propyl groups. This generates 128 × 128 = 16,384 cases if only the 12C/13C exchange possibility on the central (CH) carbon is considered; if the 1H/2D exchange is also taken into account, this increases the number of cases to 4 × 128 × 128 = 65,536. We shall use the former number (128) in the following calculations.
We can approach the problem from two viewpoints:
(i)
Each (of the two) i-Pr groups can be symmetric “internally”. In this case, each i-Pr group provides 16 (8 + 8) symmetric cases. Altogether, these are 162 = 256 cases. In the calculations with only one i-Pr group, we have seen that this leads to ∑(p × pi2 + q × pi2) = 0.977131 probability. The probability of that both i-Pr groups are of “internal” symmetry is the square of this value, 0.9771312 = 0.954785. This is then the probability of the achiral cases. Consequently, the probability of the chiral cases, which are 16,384 – 256 = 16,128 structures, is Pchiral = 1 – 0.954785 = 0.045215 ≈ 4.5%.
(ii)
If the symmetry between the two i-Pr groups is considered, this requires a “corresponding pair” to each of the configurations in one of the groups: 64 cases to each of the 64 combinations in one i-Pr, that is 642 = 4096, with “unique” CH group, or 1282 = 16,384 with one isotope exchange in the methylene group, or 2562 = 65,536, if both C and H exchange is considered. In more explicit terms, Pachiral = ∑[(p × pi × pj)2 + (q × pi × pj)2] = p2∑(pi × pj)2 + q2∑(pi × pj)2 = (p2 + q2) ∑(pi × pj)2, which is numerically for the above mentioned (one isotope exchange in the CH group) case: 0.978 × 0.9771312 = 0.93380 ≈ 93.4%.
Consequently, while 128 cases are achiral, and 16,384 – 128 = 16,256 structures are chiral, but the overwhelming majority of abundance is on the side of the achiral structures.
The probability of the chiral cases is Pchiral = 1 – 0.93380 = 0.06620 ≈ 6.6%.
The expectable enantiomeric excesses according to the Pars-Mills equation [40,48] (with 50% confidence, see also Supporting Materials 2) are as follows (Table 2).
Table
Table 2. Expectable enantiomeric excesses for cases (i) and (ii).
Table 2. Expectable enantiomeric excesses for cases (i) and (ii).
Case (i)Case (ii)
p = 0.045215p = 0.06662
Sample sizee.e.50%Sample sizee.e.50%
millimol1.29595 × 10−8millimol1.07 × 10−8
micromole4.09814 × 10−7micromole3.39 × 10−7
nanomol1.29595 × 10−5nanomol1.07 × 10−5
picomol4.09814 × 10−4picomol3.39 × 10−4
femtomol1.29595 × 10−2femtomol1.07 × 10−2
All supposed intermediates of the Soai reaction, however, contain two kinds (both C-bound and Zn-bound) i-Pr groups and more of these, than in the reagents shown in Figure 1. We analyzed a relatively simple one, compound No. 4, according to the numbering in reference [44] (S-E4), shown in Figure 2. We considered that variant of the i-Pr groups, where only 1H/2D or 12C/13C exchange occurs in the central CH groups. In this case, the number of all possibilities is 1284 = 268,435,456. Several of these structures are “degenerated” (equivalent to each other).
The number of the chiral structures deriving from S-E4 can be deduced as follows:
(a)
Chirality caused by the Zn-bound i-Pr groups, and only by these. The number of the Zn-bound cases is 1282, subtracting the number of the symmetric cases and multiplying the rest with the number of the symmetric cases of the C-bound i-Pr groups we obtain: (1282 – 162) × 128 = 2,064,384. The probability of the symmetric (achiral) cases is the same, which was calculated above for case (i) of the instance where only the internal symmetry of two i-Pr groups was considered: 0.9771312 = 0.954785 ≈ 95.5%, while for the chiral cases (1 − 0.954785) = 0.045215 ≈ 4.5%.
(b)
Chirality is caused by C-bound i-Pr groups, and only by these. In this case, each of the C-bound 128 i-Pr groups can be paired with 127 different configurations, choosing achiral Zn-bond partners we obtain 128 × 127 × 162 = 4,161,536 chiral cases. The probability of the C-bound achiral cases according to this approach is: 0.93380 ≈ 93.4%, and of the chiral cases (1 − 0.93380) = 0.06620 ≈ 6.6%.
(c)
If the combination of both the chirality of the Zn-bound and the C-bound structures (i-Pr groups) is considered, the number of the chiral cases amounts: (1282 − 162) × 128 × 127 = 262,176,768. The probability of this case equals 0.00300 because the probability of chirality in case (a) is 0.045215 and in case (b) is 0.06620, thus the probability of joint event equals 0.045215 × 0.06620 = 0.00300.
Hence the probability of the chiral cases all together is P∑ = 04222 + 0.06320 + 0.00300 = 0.10842 ≈ 10.8%.
We can get the same result if we consider that the probability of the achiral structures in this set-up is the product of the achiral probabilities in cases (a) and (b): 0.954785 × 0.93380 = 0.891572 ≈ 89.2%, while for the probability of the chiral structures we obtain P∑ = (1 − 0.891572) = 0.108428 ≈ 10.8%.
(d)
The number of the achiral cases is 128 for the C-bound structures and 16 × 16 = 256 for the Zn-bound ones. Thus the total number of the achiral cases is 128 × 256 = 32,768.
The sum of the number of chiral structures, from cases (a), (b) and (c) equals 268,402,688. This number plus the number of the achiral structures from case (d) gives exactly 268,435,456, as calculated from pure combinatorial considerations.
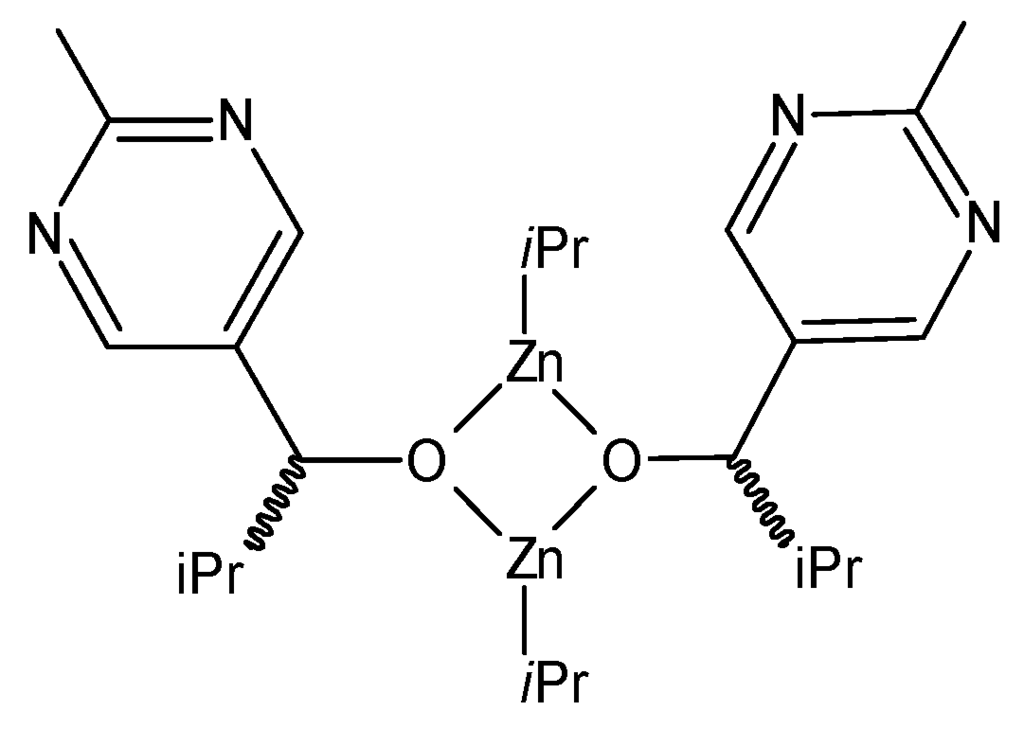
Symmetry 08 00002 g002 1024
Figure 2. Schematic structure of the dimeric intermediate of the Soai reaction, according to Schiaffino and Ercolani [44] (S-E4).
Figure 2. Schematic structure of the dimeric intermediate of the Soai reaction, according to Schiaffino and Ercolani [44] (S-E4).
Symmetry 08 00002 g002
It should be noted that this number of combinations corresponds approximately to the number of molecules in an ~0.45 femtomol size sample, approaching to a situation, where only for statistical reasons not all of the possibilities can be “materialized”, similarly to the case described by Eschenmoser for “statistical origin” of DNA [50].
It is remarkable that the huge numbers of possible chiral combinations generate only a fairly low percentage of chiral components (corresponding to the low probability values), while the large majority of components are of achiral structure. This, obviously, is due to the asymmetric natural abundance of the isotopes of H and C. However, even so, the percentages of expected enantiomeric excesses are much higher than the experimentally documented sensitivity threshold of the Soai reaction [16,17,18,19,20,37,38,39,41,42].
These results can be controlled by calculations on a somewhat different way, as shown in Supporting Materials 3. The result is exactly the same.
We also calculated for compound S-E4, with the Pars–Mills equation (with 50% confidence, see also Supporting Materials 2) the expectable e.e.50% values from sample sizes ranging from millimol to femtomol, for the chiral fraction of the molecules (Table 3):
Table
Table 3. Expectable enantiomeric excesses for S-E4.
Table 3. Expectable enantiomeric excesses for S-E4.
Sample Sizee.e.50% (%)
millimol8.36900 × 10−9
micromole2.64651 × 10−7
nanomol8.36900 × 10−6
picomol2.64651 × 10−4
femtomol8.36900 × 10−3
The expectable e.e. values for cases (a), (b) and (c) are separately listed in Supporting Materials 4.
It should be mentioned that the symmetries of compound S-E4 are valid only if the isotopic composition of the central O2Zn2 ring is disregarded. At the present level of our calculations we did so.

2.3. Zinc Isotopic Chirality?

Zinc is present in nature as a mixture of five stable isotopes, which are distributed much more evenly than those of H or C (see Table S1). It appeared therefore challenging to identify (eventual) structural features in the polymetallic intermediates hypothesized for the Soai reaction [44,45,46] where the chirality is caused by spatial distribution of Zn isotopes. The most striking structural element of this kind was found in the number 9 intermediate suggested by Schiaffino and Ercolani [44] (S-E9), as shown in Figure 3A. In this substructure, four Zn atoms and four O atoms form a virtual cube-like polyhedron, as shown in Figure 3B. Interestingly this hypothetical structural element also appears in the X-ray structure of the “enantiomeric” model compound of the Soai autocatalysis, reported very recently by Matsumoto et al. [47].
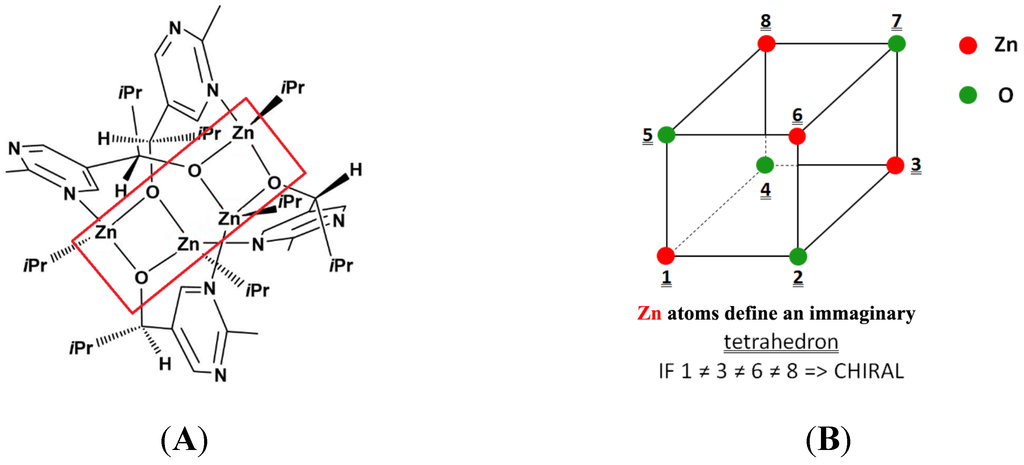
Symmetry 08 00002 g003 1024
Figure 3. (A) Schematic structure of a tetrameric intermediate of the Soai reaction according to Schiaffino and Ercolani [44] (S-E9) and (B) schematic structure of the O4Zn4 “twisted cube” fragment in compound S-E9.
Figure 3. (A) Schematic structure of a tetrameric intermediate of the Soai reaction according to Schiaffino and Ercolani [44] (S-E9) and (B) schematic structure of the O4Zn4 “twisted cube” fragment in compound S-E9.
Symmetry 08 00002 g003
The possibilities of developing chiral structure(s) in the O4Zn4 “cube” of compound S-E9 can be deduced as follows.
Simple case (all O atoms are regarded equal, or isotopic differences in these O atoms are disregarded). This approach enables calculating the contribution of the metal atoms to chirality.
In this case, chirality develops if all four Zn atoms are different isotopes, which are thus on the points of an imaginary tetrahedron centered in the center of the “cube”. Let us denote 64Zn as a, 65Zn as b, 66Zn as c, 67Zn as d, and 68Zn or 70Zn as e (we shall later use similar notation for oxygen isotopes: 16O u, 17O v, and 18O w).
Under these conditions, 10 chiral cases can evolve: abcd two times (since one point is a and the other three can be bcd or bdc), similarly abce, abde, acde or bcde all two times. Taking into regard the natural abundances, one obtains for the sum of the probabilities of all chiral cases P∑ = 0.002530375 ≈ 0.25%.
Utilizing the Pars–Mills equation [40,48] for calculation of the expected enantiomeric excesses (with 50% confidence, see also Supporting Materials 2), we obtain (Table 4).
Table
Table 4. Expectable enantiomeric excesses in the O4Zn4 “cube” (simple case).
Table 4. Expectable enantiomeric excesses in the O4Zn4 “cube” (simple case).
Sample Sizee.e.50% (%)
millimol5.47817 × 10−8
micromole1.73235 × 10−6
nanomol5.47817 × 10−5
picomol1.73235 × 10−3
femtomol5.47817 × 10−2
Complex case (isotopes of the oxygen atoms are considered). This situation can be approached by the following partial calculations:
(i)
The “cube” contains four different Zn isotopes, no matter which oxygen isotopes are present. This is equal to the “simple” case. The “cube” is chiral, 10 structures can be identified, the sum of the probabilities is P(i) = 0.002530375 = 0.2530375 ≈ 0.25%.
(ii)
Three different Zn isotopes in the “cube”; that is to say, within the four Zn atoms, two are of the same isotope. The two equal isotopes are placed in any case on one of the diagonals of one of the faces. Let us turn the cube in such position that the two equal isotopes occupy positions 1 and 3 (Figure 3b). Taking into regard that Zn has five isotopes, this results in 60 cases. If only the Zn atoms are regarded, this situation results in a symmetry plane in plane [2-6-8-4]. The “cube” becomes chiral if this symmetry is destroyed by putting different O isotopes to positions 5 and 7. Let us now consider the possibilities given by the three different O isotopes. This results in 54 additional cases coupled with each of the 60 cases derived from combinations of the Zn isotopes. Thus. the total number of chiral structures is 60 × 54 = 3240. The highest probability is provided by the combination (aabc + uuuw). This taken two times gives P(ii) = 1.10662 × 10−5 ≈ 0.0011%.
(iii)
Two different Zn isotopes, pairwise, that is 2 + 2 equal Zn isotopes, aabb and so on. This gives 10 cases, considering the three O isotopes, one obtains 36 additional possibilities for each of the Zn-derived 10, thus the total number of combinations is 10 × 36 = 360. The most probable case is the combination (aabb + uuww) two times, which gives P(iii) = 1.53122 × 10−7 ≈ 0.000015%.
(iv)
Two different Zn isotopes in the manner that three Zn isotopes are equal, that is the structure is of aaab type, which gives 20 cases, which is of relatively high symmetry; this can be spoiled in 54 ways for each structure, giving a total of 20 × 54 = 1080 cases. The highest probability is at the (aaab + uuuw) combination, taken two times P(iv) = 1.31637 × 10−4 ≈ 0.013%.
(V)
If all Zn atoms are of the same isotope, a “fourth” O isotope would be needed to obtain chiral structure, which is impossible, providing, consequently 0 cases and 0 probability.
The total number of chiral structures is 4690. The sum of the probabilities of these structures is P∑(i)–(iv) = 0.002672827 ≈ 0.27%.
It should be noted, that the majority (0.25% from 0.27%, that is 92.6%!) of the amount (probability) of these 4690 chiral structures comes from the variations in the distribution of the metal isotopes (“simple” case, or case (i), 10 structures) obviously because of the more even distribution of the natural abundances of these isotopes.
We calculated with the Pars–Mills equation [40,48] (see also Supporting Materials 2) the expectable enantiomeric excesses for reasonable microchemical sample sizes (Table 5).
Table
Table 5. Expectable enantiomeric excesses in the O4Zn4 “cube” (complex case).
Table 5. Expectable enantiomeric excesses in the O4Zn4 “cube” (complex case).
Sample Sizee.e.50% (%)
millimol5.33019 × 10−8
micromole1.68555 × 10−6
nanomol5.33019 × 10−5
picomol1.68555 × 10−3
femtomol5.33019 × 10−2
Similar to the probability dates, the expectable e.e. levels also show only a slight difference between the “simple” and the “complex” treatment.
It is an interesting feature of the mechanistic picture elaborated by Schiaffino and Ercolani [44] for the Soai reaction that some (3 of 7) of the intermediates suggested by these authors contain Zn atoms with four different substituents of deformed tetrahedral geometry. This means that these Zn atoms are chiral. To the best of our knowledge this aspect of the Schiaffino–Ercolani mechanism has not yet been discussed . We shall come back to this point in a forthcoming publication. The last two intermediates of this mechanism (2 of 7, one of these is the compound S-E9 discussed above, see also Supporting Materials 5), contain such Zn atoms, which are linked to two different ligands and to two oxygen atoms of equal “chemical environment”. These Zn atoms become chiral only if the two O atoms are different isotopes. Since all four Zn atoms in the intermediate S-E9 are of this kind, we analyzed this aspect too.
The probability of the evolution of a stereocenter on one of the Zn atoms can easily be calculated on the basis of the natural abundances of O (Table S1). The probability of achiral combinations is Pachiral = 0.995190 ≈ 99.5%, while that of the chiral ones is Pchiral = 1 – Pachiral = 0.0048099 ≈ 0.5%. The probability that one of the four zinc atoms in the imaginary “cube” becomes chiral is: P”cube” = 4 × Pchiral = 0.01924 ≈ 2%. The probability that all four Zn atoms in the “cube” become chiral is, however, very low: 1.37 × 10−4%. Whether mutual induction effects are influencing the configuration of these Zn atoms is not yet (?) clear.
The Pars–Mills [40,48] (see also Supporting Materials 2) equation for these probabilities, in reasonable microchemical sample size ranges, gives the following expectable enantiomeric excesses (Table 6).
Table
Table 6. Expectable enantiomeric excesses deriving from Zn atoms, chiral by O isotopes.
Table 6. Expectable enantiomeric excesses deriving from Zn atoms, chiral by O isotopes.
Sample Sizee.e.50% (%, one Zn)e.e.50 % (%, four Zn)
millimol3.97338 × 10−81.98669 × 10−8
micromole1.25649 × 10−66.28247 × 10−7
nanomol3.97338 × 10−51.98669 × 10−5
picomol1.25649 × 10−36.28247 × 10−4
femtomol3.97338 × 10−21.98669 × 10−2

3. Conclusions

It has been demonstrated by simple combinatorial/stochastic calculations that, in aldehyde, in the organometallic reagent, as well as in the autocatalyst of the Soai reaction, excess chiral structures can be present. The quantity of these structures in the usual range of micropreparative laboratory practice, from millimol to femtomol sample sizes, could reach such levels, which are higher than the sensitivity threshold of the asymmetric autocatalysis towards chiral induction, demonstrated experimentally [16,17,18,19,20] and evaluated theoretically [21,22,23,24]. In the relevant literature, however, no experimental or theoretical effort has been published earlier that deals with this problem.
The mechanism of the fascinating Soai autocatalysis is not yet known by direct experimental evidence. Reasonable theoretical efforts at the elucidation of the structure of the possible intermediates have been published on the basis of “first principles” and other calculations [44,45,46,49], as well as kinetic/calorimetric/spectroscopic measurements [51,52] (only to mention the most cited ones). Very recently, even realistically designed and prepared model compounds could be crystallized and studied by X-ray crystallography [47]. Several possible intermediates of fairly complicated structures have been proposed. We analyzed two of these structures, S-E4 and S-E9. The first compound (S-E4) has shown an incredible richness of possible chiral structures by 1H/2D and/or 12C/13C exchange, leading to fairly high levels of isotopically chiral components (up to ~11%). The second structure (S-E9) shows possibility for statistical chirality, generated by different Zn isotopes. If our hypothesis holds, this would be the first case where chirality due to different Zn isotopes evolved.
It appears reasonable to us that our results with the 1H/2D, 12C/13C, oxygen or Zn isotope-generated chirality can be controlled experimentally, by preparative (product chirality distribution) or chiroptical techniques. Obviously, model experiments with enantiomerically enriched isotopically chiral reagents could also be involved, particularly for the cases of 1H/2D or 12C/13C problems.
A challenging (experimental) feature of the absolute enantioselective synthesis variant of the Soai autocatalysis [16,18,20] might be in contact with the results of the present study regarding 1H/2D and/or 12C/13C exchange generated chirality. This feature is that, at sufficiently high number of parallel experiments (84) [20], a clear tendency of systematic preference for the S-enantiomer in the product was detected [53]. This observation has not yet been suitably explained. Excess statistical isotope chirality in (one or more of) the reagents may be one of the possible reasons how the distribution degeneracy of the product enantiomers is violated, without supposing charge/parity generated energy differences between the product (or intermediate) enantiomers [54].
The e.e.50% values, calculated by the Pars–Mills equation [40,48] (SM2) demonstrated an important fact, which is also evident from the mathematical structure of this formula, in samples where the percentual quantity of the chiral species is higher, the expectable enantiomeric excess is lower at a given sample size. This is in good agreement with the previously discussed idea about the exceptional role of the first [22,24,55,56,57,58] or very few [59,60,61,62] chiral molecules in achiral-to-chiral reactions, as inductors of chirality in the product.
Possibilities of chirality centered on Zn, or evolving in Zn-containing structural segments of the intermediates of the Soai autocatalysis were also detected by calculations. These elements of asymmetry may play an important role in the induction of chirality of the Soai reaction, especially in early stages of the molecular events. The results of the calculations show that the statistically evolving chirality reaches higher levels than the sensitivity threshold of the asymmetric autocatalysis towards induction of chirality. These results should also be taken into account in mechanistic speculations of other organo-zinc mediated C–C bond coupling reactions [63].
Rationalization of the available experimental results identify the Soai reaction as a highly exergonic enantioselective reaction network coupled to a heterochiral system that destabilizes the racemic composition [59]. The decisive point is most likely a kinetically controlled situation in closed systems (as many of the experimental realizations of the Soai autocatalysis), or a stationary state in open systems (modeled by the successive additions in some of the Soai reactions). The stochastic sign distribution between different experiments in the absolute asymmetric synthesis variant of the Soai autocatalysis may be (possibly in part) attributed to statistical isotope chirality effects, as shown in the present paper [54].

Supplementary Materials

Supporting material is available online at https://www.mdpi.com/2073-8994/8/1/2/s1.

Acknowledgments

The Authors acknowledge valuable discussions with Luciano Caglioti (Rome, Italy) and interesting additional ideas received from one of the anonymous Referees incorporated in the discussion [54].

Author Contributions

B.B.: Deduction of the necessary mathematical formalism and great part of the computer calculations. R.K.: Literature research and evaluation, computer calculations, editing the manuscript. G.P.: Formulation of the problem to be solved, selection of the methods and final evaluation of the results. Preparation of the draft of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References and Notes

  1. Arigoni, D.; Eliel, E.L. Chirality Due to the Presence of Hydrogen Isotopes at Noncyclic Positions. Top. Stereochem. 1969, 4, 127–243. [Google Scholar]
  2. Leach, A.G.; Houk, K.N. Diels Alder and Ene Reactions of Singlet Oxygen, Nitroso Compounds and Triazolinediones: Transition States and Mechanisms from Contemporary Theory. Chem. Commun. 2002, 1243–1255. [Google Scholar] [CrossRef]
  3. Galimov, E.N. Isotope Organic Geochemistry. Org. Geochem. 2006, 37, 1200–1262. [Google Scholar] [CrossRef]
  4. Zhou, Y.; Shan, Y.; Zhang, L.; Zhang, Y. Recent Advances in Stable Isotope Labeling Based Techniques for Proteome Relative Quantification. J. Chromatogr. A 2014, 1365, 1–11. [Google Scholar] [CrossRef] [PubMed]
  5. Gentile, N.; Siegwolf, R.T.W.; Esseiva, P.; Doyle, S.; Zollinger, K.; Delémont, O. Isotope Ratio Mass Spectrometry as a Tool for Source Inference in Forensic Science: A Critical Review. Forensic Sci. Int. 2015, 251, 139–158. [Google Scholar] [CrossRef] [PubMed]
  6. Umpleby, A.M. (Hormone Measurement Guidelines) Tracing Lipid Metabolism: The Value of Stable Isotopes. J. Endocrinol. 2015, 226, G1–G10. [Google Scholar] [CrossRef] [PubMed]
  7. Hyodo, F. Use of Stable Carbon and Nitrogen Isotopes in Insect Ecology. Entomol. Sci. 2015, 18, 295–312. [Google Scholar] [CrossRef]
  8. Horeau, A.; Nouaille, A.; Mislow, K. Secondary Deuterium Isotope Effects in Asymmetric Syntheses and Kinetic Resolutions. J. Am. Chem. Soc. 1965, 87, 4957–4958. [Google Scholar] [CrossRef]
  9. Pracejus, H. Steric Isotope Effects as Cause of a Catalytic Asymmetric Synthesis. Tetrahedron Lett. 1966, 7, 3809–3813. [Google Scholar] [CrossRef]
  10. Green, M.M.; Park, J.-W.; Sato, T.; Lifson, S.; Selinger, R.L.B.; Selinger, J.V. The Macromolecular Route to Chiral Amplification. Angew. Chem. Int. Ed. 1999, 38, 3138–3154. [Google Scholar] [CrossRef]
  11. Cantekin, S.; Balkende, D.W.R.; Smudlers, M.M.J.; Palmans, A.R.A.; Meijer, E.W. The Effect of Isotopic Substitution on the Chirality of a Self-assembled Helix. Nat. Chem. 2011, 3, 42–46. [Google Scholar] [CrossRef] [PubMed]
  12. Griffith, H. Stable Isotopes; BIOS Sci Publisher Ltd.: Oxford, UK, 1998. [Google Scholar]
  13. Caglioti, L.; Hajdu, C.; Holczknecht, O.; Zékány, L.; Zucchi, C.; Micskei, K.; Pályi, G. The Concept of Racemates and the Soai Reaction. Viva Orig. 2006, 34, 62–80. [Google Scholar]
  14. Soai, K.; Shibata, T.; Morioka, H.; Choji, K. Asymmetric Autocatalysis and the Amplification of Enantiomeric Excess of a Chiral Molecule. Nature 1995, 378, 767–768. [Google Scholar] [CrossRef]
  15. Shibata, T.; Morioka, H.; Hayase, T.; Choji, K.; Soai, K. Highly Enantioselective Catalytic Asymmetric Automultiplication of Chiral Pyrimidyl Alcohol. J. Am. Chem. Soc. 1996, 118, 471–472. [Google Scholar] [CrossRef]
  16. Soai, K.; Shibata, T.; Kowata, Y. Asymmetric Synthesis of Enantioenriched Alkanol by Spontaneous Asymmetric Synthesis. Japan Kokai Tokkyo Koho 9,268,179, 1997. [Google Scholar]
  17. Shibata, T.; Yonekubo, S.; Soai, K. Practically Perfect Asymmetric Autocatalysis with (2-Alkynyl-5-pyrimidyl)alkanols. Angew. Chem. Int. Ed. 1999, 38, 659–661. [Google Scholar] [CrossRef]
  18. Soai, K.; Sato, I.; Shibata, T.; Komiya, S.; Hayashi, M.; Matsueda, Y.; Imamura, H.; Hayase, T.; Morioka, H.; Tabira, H.; Yamamoto, J.; Kowata, Y. Asymmetric Synthesis of Pyrimidyl Alkanol without Adding Chiral Substances by the Addition of Diisopropylzinc to Pyrimidine-5-carboxaldehyde in Conjunction with Asymmetric Autocatalysis. Tetrahedron Asymmetry 2003, 14, 185–188. [Google Scholar] [CrossRef]
  19. Sato, I.; Urabe, H.; Ishiguro, S.; Shibata, T.; Soai, K. Amplification of Chirality from Extremely Low Level to Greater than 99.5% ee. Angew. Chem. Int. Ed. 2003, 42, 315–317. [Google Scholar] [CrossRef] [PubMed]
  20. Kawasaki, T.; Suzuki, K.; Shimizu, M.; Ishikawa, K.; Soai, K. Spontaneous Absolute Asymmetric Synthesis in the Presence of Achiral Silica Gel in Conjunction with Asymmetric Autocatalysis. Chirality 2006, 18, 479–482. [Google Scholar] [CrossRef] [PubMed]
  21. Micskei, K.; Maioli, M.; Zucchi, C.; Caglioti, L.; Pályi, G. Generalization Possibilities of Autocatalytic Absolute Enantioselective Synthesis. Tetrahedron Asymmetry 2006, 17, 2960–2962. [Google Scholar] [CrossRef]
  22. Caglioti, L.; Micskei, K.; Pályi, G. Chirality of the Very First Molecule in Absolute Enantioselective Synthesis. Viva Orig. 2007, 35, 82–84. [Google Scholar]
  23. Micskei, K.; Rábai, G.; Gál, E.; Caglioti, L.; Pályi, G. Oscillatory Symmetry Breaking in the Soai Reaction. J. Phys. Chem. B 2008, 112, 9196–9200. [Google Scholar] [CrossRef] [PubMed]
  24. Caglioti, L.; Micskei, K.; Pályi, G. First Molecules, Biological Chirality, Origin(s) of Life. Chirality 2011, 23, 65–68. [Google Scholar] [CrossRef] [PubMed]
  25. Sato, I.; Osanai, S.; Kadowaki, K.; Sugiyama, T.; Shibata, T.; Soai, K. Asymmetric Autocatalysis of Pyrimidyl Alkanol Induced by Optically Active 1,1’-Binaphthyl an Atropisomeric Hydrocarbon Generated from Spontaneous Resolution on Crystallization. Chem. Lett. 2002, 168–169. [Google Scholar] [CrossRef]
  26. Sato, I.; Ohno, A.; Aoyama, Y.; Kasahara, T.; Soai, K. Asymmetric Autocatalysis Induced by Chiral Hydrocarbon [2,2]-Paracyclophanes. Org. Biomol. Chem. 2003, 1, 244–246. [Google Scholar] [CrossRef] [PubMed]
  27. Kawasaki, T.; Tanaka, H.; Tsutsumi, T.; Kasahara, T.; Sato, I.; Soai, K. Chiral Discrimination of Cryptochiral Saturated Quaternary and Tertiary Hydrocarbons by Asymmetric Autocatalysis. J. Am. Chem. Soc. 2006, 128, 6032–6033. [Google Scholar] [CrossRef] [PubMed]
  28. Kawasaki, T.; Hatase, K.; Fujii, Y.; Jo, K.; Soai, K.; Pizzarello, S. The Distribution of Chiral Asymmetry in Meteorites: An Investigation Using Asymmetric Autocatalytic Chiral Sensors. Geochim. Cosmochim. Acta 2006, 70, 5395–5402. [Google Scholar] [CrossRef]
  29. Kawasaki, T.; Suzuki, K.; Licandro, E.; Bossi, A.; Maiorana, S.; Soai, K. Enantioselective Synthesis Induced by Tetrathia-[7]-helicenes in Conjunction with Asymmetric Autocatalysis. Tetrahedron Asymmetry 2006, 17, 2050–2053. [Google Scholar] [CrossRef]
  30. Sato, I.; Ohgo, Y.; Igarashi, H.; Nishiyama, D.; Kawasaki, T.; Soai, K. Determination of Absolute Configurations of Amino Acids by Asymmetric Autocatalysis of 2-Alkynylpyrimidyl Alkanol as a Chiral Sensor. J. Organomet. Chem. 2007, 692, 1783–1787. [Google Scholar] [CrossRef]
  31. Shibata, T.; Iwahashi, K.; Kawasaki, T.; Soai, K. Chiral Secondary Alcohol-induced Asymmetric Autocatalysis: Correalation between the Absolute Configuration of the Chiral Initiators and the Product. Tetrahedron Asymmetry 2007, 18, 1759–1762. [Google Scholar] [CrossRef]
  32. Sato, I.; Omiya, D.; Saito, T.; Soai, K. Highly Enantioselective Synthesis Induced by Chiral Primary Alcohols Due to Deuterium Substitution. J. Am. Chem. Soc. 2000, 122, 11739–11740. [Google Scholar] [CrossRef]
  33. Kawasaki, T.; Shimizu, M.; Nishiyama, D.; Ito, M.; Ozawa, H.; Soai, K. Asymmetric Autocatalysis Induced by Meteoritic Amino Acids with Hydrogen Isotope Chirality. Chem. Commun. 2009, 4396–4398. [Google Scholar] [CrossRef] [PubMed]
  34. Kawasaki, T.; Matsumura, Y.; Tsutsumi, T.; Suzuki, K.; Ito, M.; Soai, K. Asymmetric Autocatalysis Tiggered by Carbon Isotope (13C/12C) Chirality. Science 2009, 324, 492–495. [Google Scholar] [CrossRef] [PubMed]
  35. Kawasaki, T.; Okano, Y.; Suzuki, E.; Takano, S.; Oji, S.; Soai, K. Asymmetric Autocatalysis Tiggered by Chiral Isotopomer Arising from Oxygen Isotope Substitution. Angew. Chem. Int. Ed. 2011, 50, 8131–8133. [Google Scholar] [CrossRef] [PubMed]
  36. Matsumoto, A.; Oji, S.; Takano, S.; Tada, K.; Kawasaki, T.; Soai, K. Asymmetric Autocatalysis Tiggered by Oxygen Isotopically Chiral Glycerin. Org. Biomol. Chem. 2013, 11, 2928–2931. [Google Scholar] [CrossRef] [PubMed]
  37. Kawasaki, T.; Soai, K. Asymmetric Induction Arising from Enantiomerically Enriched Carbon-13 Isotopomers and Highly Selective Chiral Discrimination by Asymmeric Autocatalysis. Bull. Chem. Soc. Jpn. 2011, 84, 879–892. [Google Scholar] [CrossRef]
  38. Kawasaki, T.; Soai, K. Asymmetric Autocatalysis Tiggered by Chiral Crystals Formed from Achiral Compounds and Chiral Isotopomers. Isr. J. Chem. 2012, 52, 582–590. [Google Scholar] [CrossRef]
  39. Soai, K.; Kawasaki, T.; Matsumoto, A. The Origins of Homochirality Examined Using Asymmetric Autocatalysis. Chem. Record 2014, 14, 70–83. [Google Scholar] [CrossRef] [PubMed]
  40. Barabás, B.; Caglioti, L.; Micskei, K.; Zucchi, C.; Pályi, G. Isotope Chirality and Asymmetric Autocatalysis: A Possible Entry to Biological Chirality. Orig. Life Evol. Biosph. 2008, 38, 317–327. [Google Scholar] [CrossRef] [PubMed]
  41. Soai, K.; Kawasaki, T. Asymmetric Autocatalysis—Discovery and the State of the Art. In The Soai Reaction and Related Topic; Pályi, G., Zucchi, C., Caglioti, L., Eds.; Artestampa—Accademia Nazionale di Scienze, Lettere e Arti: Modena, Italy, 2012; pp. 9–34. [Google Scholar]
  42. Soai, K.; Kawasaki, T.; Matsumoto, A. Asymmetric Autocatalysis of Pyrimidyl Alkanol and Its Application to the Study on the Origin of Homochirality. Acc. Chem. Res. 2014, 47, 3643–3654. [Google Scholar] [CrossRef] [PubMed]
  43. Ozaki, H.; Tada, K.; Harada, S.; Ayugase, T.; Ozawa, H.; Kawasaki, T.; Matsumoto, A.; Soai, K. Asymmetric Autocatalysis Tiggered by Nitrogen Isotope Chirality. In Proceedings of the 3rd International Symposium on the Soai Reaction and Related Topic, Felsőmocsolád (H), Hungary, 2–5 September 2015; pp. 24–25.
  44. Schiaffino, L.; Ercolani, G. Unraveling the Mechanism of the Soai Asymmetric Autocatalytic Reaction by First-Principles Calculations: Induction and Amplification of Chirality by Self-Assembly of Hexamolecular Complexes. Angew. Chem. Int. Ed. 2008, 47, 6832–6835. [Google Scholar] [CrossRef] [PubMed]
  45. Schiaffino, L.; Ercolani, G. Mechanism of the Asymmetric Autocatalytic Soai Reaction Studied by Density Functional Theory. Chem. Eur. J. 2010, 16, 3147–3156. [Google Scholar] [CrossRef] [PubMed]
  46. Schiaffino, L.; Ercolani, G. Mechanistic Insights into the Soai Reaction from Formal Kinteics and Density Functional Theory Calculations. In The Soai Reaction and Related Topic; Pályi, G., Zucchi, C., Caglioti, L., Eds.; Artestampa—Accademia Nazionale di Scienze, Lettere e Arti: Modena, Italy, 2012; pp. 331–346. [Google Scholar]
  47. Matsumoto, A.; Abe, T.; Hara, A.; Tobita, T.; Sasagawa, T.; Kawasaki, T.; Soai, K. Crystal structure of the Isopropylzinc Alkoxide of Pyrimidyl Alkanol: Mechanistic Insights for Asymmetric Autocatalysis with Amplification of Enantiomeric Excess. Angew. Chem. Int. Ed. 2015, 54, 15218–15221. [Google Scholar] [CrossRef] [PubMed]
  48. Mills, W.H. Some Aspects of Stereochemistry. Chem. Ind. (Lond.) 1932, 750–759. [Google Scholar] [CrossRef]
  49. Gridnev, I.D.; Vorobiev, A.Kh.; Raskatov, J.A. Role of Oligomerization in the Soai Reaction: Structures, Energies, Possible Reactivity. In The Soai Reaction and Related Topic; Pályi, G., Zucchi, C., Caglioti, L., Eds.; Artestampa—Accademia Nazionale di Scienze, Lettere e Arti: Modena, Italy, 2012; pp. 79–122. [Google Scholar]
  50. Micura, R.; Bolli, M.; Eschenmoser, A. Pyranosyl-RNA: Chiroselective Self-assembly of Base Sequences by Ligative Oligomerization of Tetranucleotide-2‘,3‘-cyclophospates (with a Commentary Concerning the Origin of Biomolecular Homochirality). Chem. Biol. 1997, 4, 309–320. [Google Scholar]
  51. Quaranta, M.; Gehring, T.; Odell, B.; Brown, J.M.; Blackmond, J.M. Unusual Inverse Temperature Dependence on Reaction Rate in the Asymmetric Autocatalytic Alkylation of Pyrimidyl Aldehydes. J. Am. Chem. Soc. 2010, 132, 15104–15107. [Google Scholar] [CrossRef] [PubMed]
  52. Stiller, J.; Tse, E.S.Y.; Schlageter, M.; Gehring, T. Systematic and Mechanistic Studies on the Soai Reaction Using 2-(1--Adamantylethynyl)pyrimidyne-5-carbaddehyde. In The Soai Reaction and Related Topic; Pályi, G., Zucchi, C., Caglioti, L., Eds.; Artestampa—Accademia Nazionale di Scienze, Lettere e Arti: Modena, Italy, 2012; pp. 53–78. [Google Scholar]
  53. Barabás, B.; Caglioti, L.; Zucchi, C.; Maioli, M.; Gál, E.; Micskei, K.; Pályi, G. Violation of Distribution Symmetry in Statistical Evaluation of Absolute Enantioselective Synthesis. J. Phys. Chem. B 2007, 111, 11506–11510. [Google Scholar] [CrossRef] [PubMed]
  54. Ideas taken from the comments of one of the anonymous Referees of the present paper.
  55. Fuss, W. Does Life Originate from a Single Molecule? Chirality 2009, 21, 299–304. [Google Scholar] [CrossRef] [PubMed]
  56. Fuss, W. Biological Homochirality as a Result of a Single Event. Colloids Surf. B Biointerface 2009, 74, 498–503. [Google Scholar] [CrossRef] [PubMed]
  57. Morneau, B.N.; Kubala, J.M.; Barratt, C.; Schwartz, P.M. Analysis of a Chemical Model System Leading to Chiral Symmetry Breaking: Implications for the Evolution of Homochirality. J. Math. Chem. 2014, 52, 268–282. [Google Scholar] [CrossRef]
  58. Pavlov, V.A.; Klabunovski, E.I. Homochirality Origin in Nature: Possible Versions. Curr. Org. Chem. 2014, 18, 93–114. [Google Scholar] [CrossRef]
  59. Pályi, G.; Micskei, K.; Zékány, L.; Caglioti, L. Racemates and the Soai Reaction. Magyar Kém. Lapja 2005, 60, 17–24. [Google Scholar]
  60. Maioli, M.; Micskei, K.; Zucchi, C.; Caglioti, L.; Pályi, G. Evolution of Chirality in Consecutive Asymmetric Autocatalytic Reaction Cycles. J. Math. Chem. 2008, 43, 1505–1515. [Google Scholar] [CrossRef]
  61. Barabás, B.; Tóth, J.; Pályi, G. Stochastic Aspects of Asymmetric Autocatalysis and Absolute Asymmetric Synthesis. J. Math. Chem. 2010, 48, 457–489. [Google Scholar] [CrossRef]
  62. Caglioti, L.; Pályi, G. Single Chiral Molecule as Possible Starting Element of Complex Chiral Systems. Rend. Lincei Sci. Fis. Nat. 2013, 24, 191–196. [Google Scholar] [CrossRef]
  63. Bauer, T. Enantioselective Dialkylzinc-mediated Alkynylation, Arylation and Alkenylation of Carbonyl Groups. Coord. Chem. Rev. 2015, 299, 83–150. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Barabás, B.; Kurdi, R.; Pályi, G. Natural Abundance Isotopic Chirality in the Reagents of the Soai Reaction. Symmetry 2016, 8, 2. https://doi.org/10.3390/sym8010002

AMA Style

Barabás B, Kurdi R, Pályi G. Natural Abundance Isotopic Chirality in the Reagents of the Soai Reaction. Symmetry. 2016; 8(1):2. https://doi.org/10.3390/sym8010002

Chicago/Turabian Style

Barabás, Béla, Róbert Kurdi, and Gyula Pályi. 2016. "Natural Abundance Isotopic Chirality in the Reagents of the Soai Reaction" Symmetry 8, no. 1: 2. https://doi.org/10.3390/sym8010002

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop