Anonymous Multi-Receiver Identity-Based Authenticated Encryption with CCA Security

Abstract

In a multi-receiver encryption system, a sender chooses a set of authorized receivers and sends them a message securely and efficiently, as the message is well encrypted and only one ciphertext corresponding to the message is generated no matter how many receivers the sender has chosen. It can be applied to video conferencing systems, pay-per-view channels, remote education, and so forth. Due to privacy considerations, an authorized receiver may not expect that his identity is revealed. In 2010, anonymous multi-receiver identity-based (ID-based) encryption was first discussed, and furthermore, many works on the topic have been presented so far. Unfortunately, we find that all of those schemes fail to prove the chosen ciphertext attacks (CCA) security in either confidentiality or anonymity. In this manuscript, we propose the first anonymous multi-receiver ID-based authenticated encryption scheme with CCA security in both confidentiality and anonymity. In the proposed scheme, the identity of the sender of a ciphertext can be authenticated by the receivers after a successful decryption. In addition, the proposed scheme also is the first CCA-secure one against insider attacks. Moreover, only one pairing computation is required in decryption.

1. Introduction

Multi-receiver encryption makes it possible for a sender to compute and transmit only one ciphertext corresponding to a message for multiple receivers. It greatly decreases communication cost, so that it is popular among some advanced services, such as video conferencing, pay-per-view TV [1,2,3] and remote education. In order to prevent unauthorized access, messages are encrypted, and the encryption keys change every session. When a new member joins the communication group, the system will assign a long-term key to him, and the key will be revoked once the member leaves the group. The system must deal with key management effectively. Another important issue in such services is the authentication of the sender, which can guarantee the source and legality of the digital products. Many researchers focused on this topic and have proposed interesting results [4,5,6].

In 2001, Boneh and Franklin [7] first proposed an ID-based encryption scheme from the Weil pairing. In 2005, Du et al. [6] presented an ID-based broadcast encryption scheme for key distribution. They used matrix operations for encryption and decryption. In 2005, Wang and Wu [5] proposed an ID-based multicast encryption scheme, which has a key generation center and a group center. No users need any computation during the rekeying process. However, the sender must be the group center. In the same year, Baek et al. [4] proposed a multi-receiver ID-based encryption scheme along with a formal definition and security model for this kind of scheme. They proved the security in the selective ID model using random oracles [8]. Their second scheme was employed in the REACT technique proposed by Okamoto and Pointcheval [9].

In some situations, such as ordering sensitive TV programs, the customers may expect that their identities are not revealed. In consideration of protecting users’ privacy, Fan et al. [10] first introduced the concept of anonymous mutli-receiver ID-based encryption (AMRIBE) in 2010. They also proposed a multi-receiver ID-based encryption scheme using Lagrange interpolating polynomials in order to achieve anonymity for every receiver such that nobody knows who the receivers are except the sender. However, Chien [11] pointed out that Fan et al.’s scheme does not hold the anonymity. An attacker can identify the identity of a receiver. Chien indicated that the security model defined in [10] does not cover all of the multi-receiver environments. Additionally, he also proposed an improved AMRIBE scheme.

Recently, many results of AMRIBE have been proposed [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. After examining these results, however, we find that none of them satisfies the CCA (chosen ciphertext attacks) security in both confidentiality and anonymity. A major reason is that they are vulnerable to the insider attacks in anonymity, that is a selected receiver, called an insider, can derive the identities of the other receivers selected by the sender in those schemes.

Therefore, in view of the aforementioned reasons, we propose a novel type of multi-receiver encryption called anonymous multi-receiver identity-based authenticated encryption (AMRIBAE). A concrete encryption scheme has also been proposed, which achieves the CCA security in both confidentiality and anonymity, such that it is immune to not only outsider (i.e., unselected receiver) but insider attacks, as well. Let t be the number of the selected receivers of a ciphertext. In our scheme, even if the unselected receivers collude with any $(t-1)$ selected receivers, the anonymity of the non-colluding selected receiver is still preserved. Furthermore, we also prove that the proposed scheme achieves sender authentication, i.e., the identity of the sender of a ciphertext can be confirmed by the selected receivers. In addition, we provide complete proofs with problem reduction to formally demonstrate the CCA security. Furthermore, our scheme is decryption efficient due to only one pairing computation.

Anonymous Multi-Receiver ID-Based Encryption vs. Anonymous Dynamic Broadcast ID-Based Encryption

In [32], Delerablée et al. introduced the concept of dynamic broadcast encryption. In a dynamic broadcast encryption system, a sender can arbitrarily select some or all of the users who have enrolled in the system as the receivers of a ciphertext that he or she is about to generate, and it is unnecessary for the system to re-compute the private keys of the enrolled users whenever a new user joins the system. A multi-receiver encryption system can also achieve this; however, a non-dynamic broadcast encryption system cannot. In a non-dynamic system, all of the enrolled users should be the receivers of every ciphertext in the system, that is the receiver set contains all enrolled users, and it is always fixed for every ciphertext. In addition, the receiver set should be determined before private key generation, which will imply that the private keys of all enrolled users must be re-computed whenever a new user joins the non-dynamic system. Although a non-dynamic broadcast encryption scheme [33,34,35] might not be as flexible as a dynamic one, those schemes usually provide shorter ciphertext or constant-size ciphertext. Besides, in an ID-based encryption system, the identities of the users also act as their public keys, which will largely simplify the management of the public keys as compared to a non-ID-based one, such as [36].

This research will aim at anonymous multi-receiver ID-based encryption, which can be regarded as anonymous dynamic broadcast ID-based encryption. In this manuscript, we will discuss dynamic and ID-based schemes [10,11,14,16,18,19,20,21,23,25,26,27,28,29,31] and compare them to our work.

2. Related Works

In order to protect users’ privacy, Fan et al. [10] first introduced anonymous multi-receiver identity-based encryption (AMRIBE) in 2010. Their scheme was constructed by using Lagrange interpolating polynomials. However, it cannot achieve anonymity against outside and inside attackers. The cryptanalysis on Fan et al.’s scheme [10] has been presented in [11,13,25].

In 2012, Wang et al. proposed an AMRIBE scheme [25] by improving Fan et al.’s scheme. Unfortunately, their scheme did not achieve anonymity against inside attackers. The cryptanalysis on Wang et al.’s scheme [25] has been shown in [17,29]. In the same year, Tseng et al. proposed an AMRIBE scheme and claimed that their scheme is CCA secure in both confidentiality and anonymity [21,22]. However, we found that they demonstrated the security without considering all possible attackers. In the proof of the security, they assume that the attacker must compute the symmetric encryption/decryption key corresponding to the challenge ciphertext before it wins the CCA game. That is to say, the proof does not cover the type of attackers that win the CCA game, but have not computed the key of the challenge ciphertext. The details are shown in the Appendix.

In 2013, Zhang and Takagi proposed two AMRIBE schemes [31]. They designed a deployment in an e-mail delivery system and provided some experimental results. However, their first scheme cannot achieve anonymity against inside attackers [28], and they did not provide any security proof for their second scheme. Besides, Zhang and Mao proposed an improved AMRIBE scheme [28] based on Zhang et al.’s scheme [31] in 2013. They claimed that their scheme has the CCA security. However, we have found some mistakes in their security proofs due to the inconsistency between a hash function and the hash oracle corresponding to the function, where the details are shown in the Appendix.

In 2014, there were three AMRIBE schemes [23,26,27] proposed by Tseng et al., Wang and Zhang et al., respectively. Nevertheless, we have found some mistakes in their security proof, and the details are shown in the Appendix.

The other works [11,12,14,16,18,19,20,29] either have the CPA (chosen plaintext attacks) security only or have not provided the proof for the security. The security of all of the above schemes has been summarized in Section 6 Table 3.

3. Preliminaries

In this section, we define anonymous multi-receiver ID-based authenticated encryption and review some hard problems and assumptions. In addition, we propose a modified decisional bilinear Diffie–Hellman (DBDH) assumption, called the M-DBDH assumption, and prove that the assumption holds if the 1-weak decisional bilinear Diffie–Hellman inversion (1-wDBDHI) problem is hard.

Definition 1. An anonymous multi-receiver identity-based authenticated encryption (AMRIBAE) scheme consists of the following algorithms:

-

Setup is an algorithm that takes as input a security parameter l. It returns a master secret key $msk$ and system parameters $params$.

-

KeyExtract is an algorithm that takes as input $params$, $msk$ and a user’s identity $I{D}_i\in {\{0,1\}}^{*}$ and then returns the secret key $d_i$ of the user.

-

Encrypt is an algorithm that takes as input $params$, a message M, the identity $I{D}_s$ of the sender, the private key $d_s$ of the sender and an identity set $\{I{D}_1,I{D}_2,\cdots ,I{D}_t\}$ and returns a ciphertext C. We write $C=Encrypt(params,I{D}_s,I{D}_1,I{D}_2,\cdots ,I{D}_t,M,d_s)$.

-

Decrypt is an algorithm that takes as input $params$, a ciphertext C and the secret key $d_i$ of user $I{D}_i$ and returns a message M. We write $M=Decrypt(params,C,d_i)$.

Let $G_1$ and $G_2$ be two cyclic groups of prime order q, P be a generator of $G_1$ and $e:G_1\times G_1\to G_2$ be a bilinear mapping.

Definition 2 (The Bilinear Diffie–Hellman (BDH) Problem). Given $(P,aP,bP,cP)$ for some random $a,b,c\in {\mathbb{Z}}_q^{*}$, compute $e{(P,P)}^{abc}$.

Definition 3 (The Decisional Bilinear Diffie–Hellman (DBDH) Problem). Given $(P,aP,bP,cP,Z)$ for some random $a,b,c\in {\mathbb{Z}}_q^{*}$ and $Z{\in }_R\{e{(P,P)}^{abc},Y{\in }_R{G}_{2}e{(P,P)}^{abc}\}$, decide if $Z=e{(P,P)}^{abc}$.

Definition 4 (The DBDH Assumption [7]). Define that an algorithm $\mathcal{A}$ with output $\beta \in \{0,1\}$ has advantage ϵ in solving the DBDH problem if:

$$\left|Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{abc})=1]-Pr[\mathcal{A}(P,aP,bP,cP,Z)=1]\right|\ge ϵ$$

where $a,b,c{\in }_R{\mathbb{Z}}_q^{*}$ and $Z{\in }_R\{e{(P,P)}^{abc},Y{\in }_R{G}_{2}e{(P,P)}^{abc}\}$. We say that the DBDH assumption holds if no polynomial-time algorithm has a non-negligible advantage in solving the DBDH problem.

Definition 5 (The l-Weak Decisional Bilinear Diffie–Hellman Inversion (l-wDBDHI) Problem [37]).

Given $(P,Y,cP,Z)$, where $Z{\in }_R\{e{(P,P)}^{b^{l+1}c},Y{\in }_R{G}_{2}e{(P,P)}^{abc}\}$ and $Y=(bP,b^{2}P,\cdots ,b^{l}P)$, decide if $Z=e{(P,P)}^{b^{l+1}c}$.

Definition 6 (The l-Weak Decisional Bilinear Diffie–Hellman Inversion (l-wDBDHI) Assumption [37]).

Define that an algorithm $\mathcal{A}$ with output $\beta \in \{0,1\}$ has advantage ϵ in solving the l-wDBDHI problem if:

$$\left|Pr[\mathcal{A}(P,Y,cP,e{(P,P)}^{b^{l+1}c})=1]-Pr[\mathcal{A}(P,Y,cP,Z)=1]\right|\ge ϵ.$$

We say that the l-wDBDHI assumption holds if there exists no polynomial-time adversary that has a non-negligible advantage in solving the l-wDBDHI problem.

Definition 7 (The Modified Decisional Bilinear Diffie–Hellman (M-DBDH) Problem). Given $(P,aP,bP,cP,e{(P,P)}^{b^{2}c},Z)$ for some random $a,b,c\in {\mathbb{Z}}_q^{*}$ and $Z{\in }_R\{e{(P,P)}^{abc},Y{\in }_R{G}_{2}e{(P,P)}^{abc}\}$, decide if $Z=e{(P,P)}^{abc}$. Define that an algorithm $\mathcal{A}$ with output $\beta \in \{0,1\}$ has advantage ϵ in solving the M-DBDH problem if:

$$\left|Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1]-Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},Z)=1]\right|\ge ϵ$$

where $a,b,c{\in }_R{\mathbb{Z}}_q^{*}$ and $Z{\in }_R\{e{(P,P)}^{abc},Y{\in }_R{G}_{2}e{(P,P)}^{abc}\}$.

Theorem 8. No polynomial-time algorithm has a non-negligible advantage in solving the M-DBDH problem if the 1-wDBDHI assumption holds.

Proof. If there exists a polynomial-time algorithm $\mathcal{A}$ with non-negligible advantage ϵ in solving the M-DBDH problem, then we can construct a polynomial-time algorithm $\mathcal{B}$ with non-negligible advantage in solving the 1-wDBDHI problem as follows. Given a 1-wDBDHI instance $(P,bP,cP,Z)$, $\mathcal{B}$ forms an M-DBDH instance via the following operations:

• Randomly choose $a\in Z_q^{*}$, and compute $aP$.
• Compute $Z_1=e{(bP,cP)}^a$.
• Set the M-DBDH instance as $(P,aP,bP,cP,Z,Z_1)$, and input it into $\mathcal{A}$.

Let β be the output of $\mathcal{A}$. $\mathcal{B}$ will confirm that $Z=e{(P,P)}^{b^{2}c}$ by outputting one as the answer of the 1-wDBDHI instance if $\beta =1$; otherwise, $\mathcal{B}$ will output zero.

Since:

$$\left|Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1]-Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},W)=1]\right|\ge ϵ$$

where $W{\in }_R\{e{(P,P)}^{abc},X{\in }_R{G}_{2}e{(P,P)}^{abc}\}$,

$$|Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1]-\frac{1}{2}|$$

$$\ge \left|Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1]-Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},W)=1]\right|\ge ϵ.$$

Let $T{\in }_R\{e{(P,P)}^{b^{2}c},X{\in }_R{G}_{2}e{(P,P)}^{abc}\}$. Thus, we have that:

$$|Pr[\mathcal{B}(P,bP,cP,e{(P,P)}^{b^{2}c})=1]-Pr[\mathcal{B}(P,bP,cP,T)=1]|$$

$$=\left|Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1]\right.$$

$$-(\frac{1}{2}Pr[\mathcal{B}(P,bP,cP,e{(P,P)}^{b^{2}c})=1]$$

$$\left.+\frac{1}{2}Pr[\mathcal{B}(P,bP,cP,X)=1])\right|$$

$$=|\frac{1}{2}Pr[\mathcal{A}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1]-\frac{1}{4}|\ge \frac{ϵ}{2}.$$

It turns out that the polynomial-time algorithm $\mathcal{B}$ has a non-negligible advantage $\frac{ϵ}{2}$ in solving the 1-wDBDH problem. ☐

Definition 9 (The M-DBDH Assumption). We say that the M-DBDH assumption holds if no polynomial-time algorithm has non-negligible advantage in solving the M-DBDH problem.

By Theorem 8, the M-DBDH assumption holds.

4. Our Scheme

In this section, we will present an anonymous multi-receiver identity-based authenticated encryption scheme with provable CCA security in both confidentiality and anonymity against not only outsider, but also insider attacks. Our scheme can be viewed as a key encapsulation mechanism. The notations used in the proposed scheme are defined in Table 1.

Table 1. The notations.

Notation	Meaning
$G_1$	a cyclic additive group of prime order q
$G_2$	a cyclic multiplicative group of prime order q
e	a bilinear mapping; $e:G_1\times G_1\to G_2$
P	a generator of $G_1$
KGC	the key generation center
$P_{pub}$	the public key of KGC
M	a message
$I{D}_i$	the identity of user i
$Q_i$	the hashed value of $I{D}_i$
$d_i$	the private key of $I{D}_i$

Table 1. The notations.

Notation	Meaning
$G_1$	a cyclic additive group of prime order q
$G_2$	a cyclic multiplicative group of prime order q
e	a bilinear mapping; $e:G_1\times G_1\to G_2$
P	a generator of $G_1$
KGC	the key generation center
$P_{pub}$	the public key of KGC
M	a message
$I{D}_i$	the identity of user i
$Q_i$	the hashed value of $I{D}_i$
$d_i$	the private key of $I{D}_i$

The proposed scheme is described as follows.

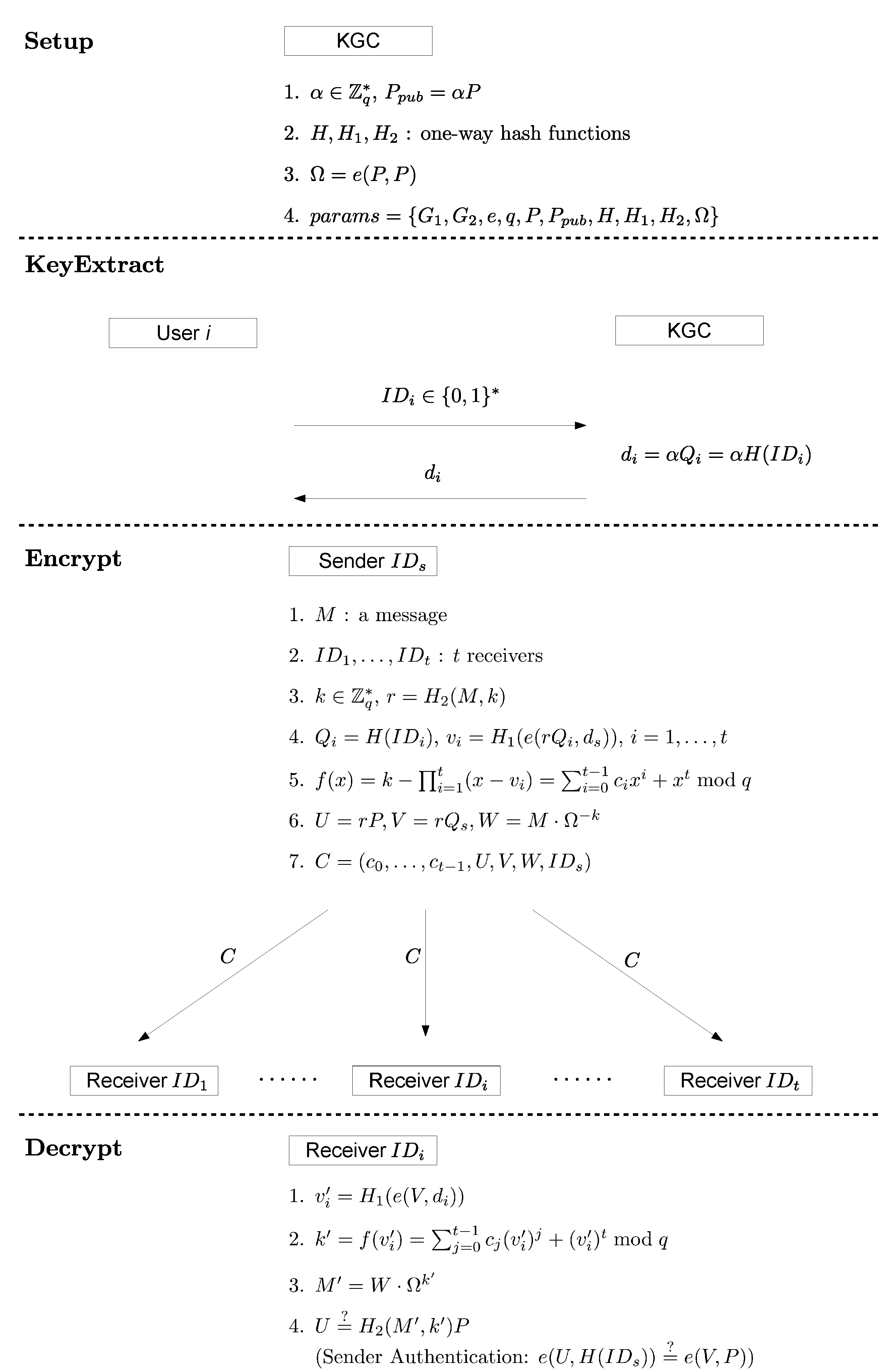
• Setup
  The key generation center (KGC) performs the following operations:

  • Choose an integer $\alpha \in {\mathbb{Z}}_q^{*}$ randomly as the master secret key, and set $P_{pub}=\alpha P$.
  • Choose three cryptographic one-way hash functions, $H:{\{0,1\}}^{*}\to G_1$, $H_1:G_2\to {\mathbb{Z}}_q^{*}$, and $H_2:{\{0,1\}}^{*}\times {\mathbb{Z}}_q^{*}\to {\mathbb{Z}}_q^{*}$.
  • Compute $\Omega =e(P,P)$.
  • Publish the system parameters $params=\{G_1,G_2,e,q,P,P_{pub},H,H_1,H_2,\Omega \}$ and keep the master key α secret.
• KeyExtract
  When user i joins the system, KGC will compute $Q_i=H\left(I{D}_i\right)$ and the private key $d_i=\alpha Q_i$ of the user, and then, KGC will send $d_i$ to user i in a secure manner.
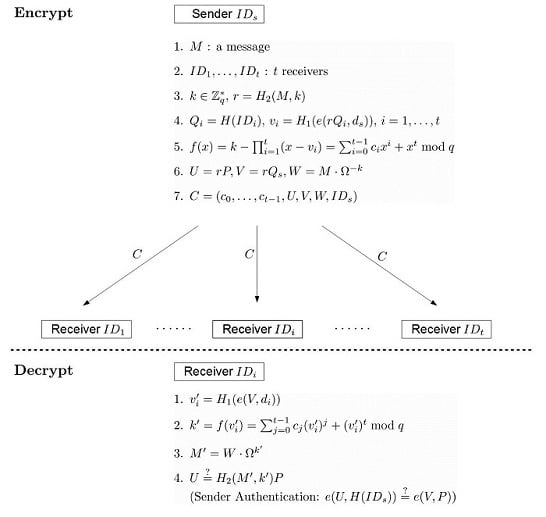
• Encrypt
  A sender, say $I{D}_s$, produces the ciphertext of a message by performing the following steps:

  • Choose a message $M\in G_2$, and select a set of t receivers $\{I{D}_1,\cdots ,I{D}_t\}$.
  • Choose $k\in {\mathbb{Z}}_q^{*}$ at random, and compute $r=H_2(M,k)$.
  • For $i=1$ to t, compute $Q_i=H\left(I{D}_i\right)$ and $v_i=H_1\left(e(r{Q}_i,d_s)\right)$.
  • Compute ${\displaystyle f\left(x\right)=k-\prod _{i=1}^t(x-v_i)=\sum _{i=0}^{t-1}{c}_i{x}^i+x^{t}modq}$.
  • Compute $U=rP,V=r{Q}_s$ and $W=M·{\Omega }^{-k}$.
  • Set the ciphertext $C=(c_0,c_1,\cdots ,c_{t-1},U,V,W,I{D}_s)$.
• Decrypt
  After receiving the ciphertext $C=(c_0,c_1,\cdots ,c_{t-1},U,V,W,I{D}_s)$, a selected receiver, say $I{D}_i$, can decrypt C as follows.

  • Compute $v_i^{\prime }=H_1\left(e(V,d_i)\right)$.
  • Compute ${\displaystyle k^{\prime }=f\left(v_i^{\prime }\right)=\sum _{j=0}^{t-1}{c}_j{\left(v_i^{\prime }\right)}^j+{\left(v_i^{\prime }\right)}^{t}modq}$.
  • Compute $M^{\prime }=W·{\Omega }^{k^{\prime }}$.
  • Accept $M^{\prime }$ if $U=H_2(M^{\prime },k^{\prime })P$. If the receiver wants to authenticate the identity of the sender, he can check whether $e(U,H\left(I{D}_s\right))=e(V,P)$.

The proposed scheme also is illustrated in Figure 1, and the correctness is demonstrated as follows.

$$\begin{array}{cc}{v}_i^{\prime }& =H_1\left(e(V,d_i)\right)\hfill \\ & =H_1\left(e(r{Q}_s,\alpha Q_i)\right)\hfill \\ & =H_1\left(e(r{Q}_i,\alpha Q_s)\right)\hfill \\ & =H_1\left(e(r{Q}_i,d_s)\right)\hfill \\ & =v_i\hfill \end{array}$$

and

$$k^{\prime }=f\left(v_i^{\prime }\right)=f\left(v_i\right)=k.$$

Thus, the selected receiver $I{D}_i$ can successfully recover the message by computing $M^{\prime }=W·{\Omega }^{k^{\prime }}=W·{\Omega }^k=M$, so that $U=H_2(M,k)P=H_2(M^{\prime },k^{\prime })P$.

After successfully recovering the message, we have $e(V,d_i)=(rH\left(I{D}_s^{\prime }\right),\alpha Q_i)=e(r{Q}_i,\alpha Q_s)=e(r{Q}_i,d_s)$ for some identity $I{D}_s^{\prime }$, which convinces the receiver that the ciphertext is encrypted with the private key of $I{D}_s^{\prime }$. Additionally, the equation $e(U,H\left(I{D}_s\right))=e(V,P)$ can guarantee that $V=r{Q}_s=rH\left(I{D}_s\right)$, which means $I{D}_s^{\prime }=I{D}_s$. This feature makes it possible for the receivers to authenticate the sender of the ciphertext they received. Besides, according to [38], in an anonymous multi-receiver encryption scheme, the length of a ciphertext will at least linearly grow with the number of the receivers. Thus, the ciphertext length of our scheme might be optimal in the aspect of [38].

Figure 1. The proposed anonymous multi-receiver identity-based authenticated encryption (AMRIBAE) scheme.

Figure 1. The proposed anonymous multi-receiver identity-based authenticated encryption (AMRIBAE) scheme.

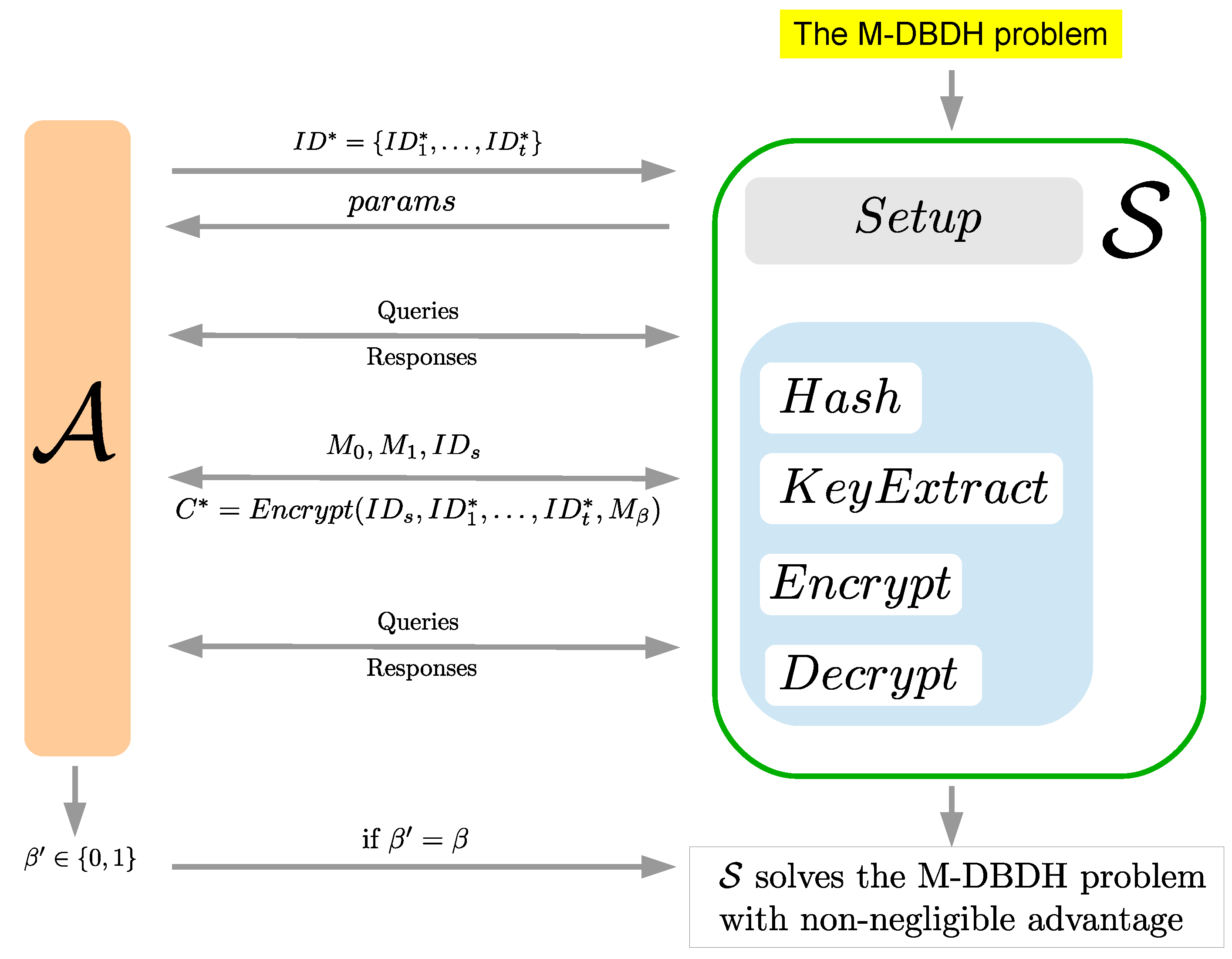
5. Security Models and Proofs

In this section, we will define the security models and the security notions for anonymous multi-receiver identity-based authenticated encryption. The security notions are the “indistinguishability of encryptions under selective multi-ID, chosen-ciphertext attacks” (IND-sMID-CCA) and the “anonymous indistinguishability of encryptions under selective multi-ID, chosen-ciphertext attacks” (Anon-sMID-CCA). We then will prove that our proposed scheme is provably CCA secure in confidentiality and anonymity against insider and outsider attacks.

Definition 10 (The IND-sMID-CCA Game). Let $\mathcal{A}$ be a polynomial-time attacker. $\mathcal{A}$ interacts with a simulator $\mathcal{S}$ in the following game.

Initialization. $\mathcal{A}$ chooses a set of identities $I{D}^{*}=\{I{D}_1^{*},I{D}_2^{*},\cdots ,I{D}_t^{*}\}$ and sends $I{D}^{*}$ to $\mathcal{S}$.

Setup. $\mathcal{S}$ runs the Setup algorithm to generate $params$ and $msk$. $\mathcal{S}$ then sends $params$ to $\mathcal{A}$.

Phase 1. $\mathcal{A}$ issues the following queries.

-

Hash query: $\mathcal{S}$ operates hash functions on the inputs given by $\mathcal{A}$ and returns the hashed values.

-

KeyExtract ($I{D}_i$): $\mathcal{A}$ sends an identity $I{D}_i$ to $\mathcal{S}$ and $\mathcal{S}$ returns the private key of $I{D}_i$ where KeyExtract ($I{D}_j$) cannot be queried if $I{D}_j\in I{D}^{*}$.

-

Encrypt ($I{D}_s,I{D}_1,\cdots ,I{D}_u,M$): $\mathcal{A}$ sends a sender’s identity $I{D}_s$, a receiver set $\{I{D}_1,\cdots ,I{D}_u\}$ and a message M to $\mathcal{S}$. $\mathcal{S}$ returns a ciphertext C to $\mathcal{A}$.

-

Decrypt ($C,I{D}_i$): $\mathcal{A}$ sends an identity $I{D}_i$ and a ciphertext C to $\mathcal{S}$, and $\mathcal{S}$ returns the message M.

Challenge. $\mathcal{A}$ submits a sender’s identity $I{D}_s$ and $(M_0,M_1)$ to $\mathcal{S}$, with restrictions that $M_0,M_1$ are two distinct messages of the same length, $I{D}_s\in I{D}^{*}$, and KeyExtract ($I{D}_s$) has not been queried before. $\mathcal{S}$ then randomly chooses $\beta \in \{0,1\}$ and generates $C^{*}$ = Encrypt $(I{D}_s,I{D}_1^{*},\cdots ,I{D}_t^{*},M_{\beta })$. Finally, $\mathcal{S}$ sends $C^{*}$ to $\mathcal{A}$.

Phase 2. $\mathcal{A}$ issues the queries defined in Phase 1, excluding the Decrypt queries with $C=C^{*}$ and $I{D}_i\in I{D}^{*}$ and the query KeyExtract ($I{D}_s$).

Guess. Finally, $\mathcal{A}$ outputs ${\beta }^{\prime }\in \{0,1\}$ and wins the game if ${\beta }^{\prime }=\beta$.

The advantage of $\mathcal{A}$ winning the game is defined as:

$${\mathbf{Adv}}^{IND-sMID-CCA}\left(\mathcal{A}\right)=\left|Pr[{\beta }^{\prime }=\beta ]-\frac{1}{2}\right|.$$

An anonymous multi-receiver identity-based authenticated encryption scheme is said to be IND-sMID-CCA secure if there exists no polynomial-time attacker that can win the IND-sMID-CCA game with non-negligible advantage. The model of this game is shown in Figure 2.

Figure 2. The indistinguishability of encryptions under selective multi-ID, chosen-ciphertext attacks (IND-sMID-CCA) game.

Figure 2. The indistinguishability of encryptions under selective multi-ID, chosen-ciphertext attacks (IND-sMID-CCA) game.

Definition 11 (The Anon-sMID-CCA Game). Let $\mathcal{A}$ be a polynomial-time attacker. $\mathcal{A}$ interacts with a simulator $\mathcal{S}$ in the following game.

Initialization. $\mathcal{A}$ chooses two identities $\{I{D}_0^{*},I{D}_1^{*}\}$ and sends them to $\mathcal{S}$.

Setup. $\mathcal{S}$ runs the Setup algorithm to generate $params$ and $msk$. $\mathcal{S}$ then sends $params$ to $\mathcal{A}$.

Phase 1. $\mathcal{A}$ issues the following queries.

-

Hash query: $\mathcal{S}$ operates hash functions on the inputs given by $\mathcal{A}$ and returns the hashed values.

-

KeyExtract ($I{D}_i$): $\mathcal{A}$ sends an identity $I{D}_i$ to $\mathcal{S}$, and $\mathcal{S}$ returns the private key of $I{D}_i$ where neither KeyExtract ($I{D}_0^{*}$) nor KeyExtract ($I{D}_1^{*}$) can be queried.

-

Encrypt ($I{D}_s,I{D}_1,\cdots ,I{D}_u,M$): $\mathcal{A}$ sends a sender’s identity $I{D}_s$, a receiver set $\{I{D}_1,\cdots ,I{D}_u\}$ and a message M to $\mathcal{S}$. $\mathcal{S}$ returns a ciphertext C to $\mathcal{A}$.

-

Decrypt ($C,I{D}_i$): $\mathcal{A}$ sends an identity $I{D}_i$ and a ciphertext C to $\mathcal{S}$, and $\mathcal{S}$ returns the message M.

Challenge. $\mathcal{A}$ submits a sender’s identity $I{D}_s$, a message M and a set of identities $\{I{D}_2,I{D}_3,\cdots ,I{D}_t\}$ to $\mathcal{S}$ with restrictions that $I{D}_s\{I{D}_0^{*},I{D}_1^{*}\}$ and KeyExtract ($I{D}_s$) has not been queried before. $\mathcal{S}$ then randomly chooses $\beta \in \{0,1\}$ and generates $C^{*}$ = Encrypt $(I{D}_s,I{D}_{\beta }^{*},I{D}_2,\cdots ,I{D}_t,M)$. Finally, $\mathcal{S}$ sends $C^{*}$ to $\mathcal{A}$.

Phase 2. $\mathcal{A}$ issues the queries defined in Phase 1, excluding Decrypt ($C^{*},I{D}_0^{*}$), Decrypt ($C^{*},I{D}_1^{*}$) and KeyExtract ($I{D}_s$).

Guess. Finally, $\mathcal{A}$ outputs ${\beta }^{\prime }\in \{0,1\}$ and wins the game if ${\beta }^{\prime }=\beta$.

The advantage of $\mathcal{A}$ winning the game is defined as:

$${\mathbf{Adv}}^{Anon-sMID-CCA}\left(\mathcal{A}\right)=\left|Pr[{\beta }^{\prime }=\beta ]-\frac{1}{2}\right|.$$

An anonymous multi-receiver identity-based authenticated encryption scheme is said to be Anon-sMID-CCA secure if there exists no polynomial-time attacker that can win the Anon-sMID-CCA game with non-negligible advantage. The model of this game is shown in Figure 3.

Note that there is a restriction that KeyExtract ($I{D}_s$) cannot be queried in both the IND-sMID-CCA game and the ANON-sMID-CCA game. This is to model that the adversary cannot collude with the sender, since the confidentiality and the anonymity will be meaningless when the collusion happens.

Figure 3. The anonymous (Anon)-sMID-CCA game.

Figure 3. The anonymous (Anon)-sMID-CCA game.

Definition 12 (The Sender Authentication Game). Let $\mathcal{A}$ be a polynomial-time attacker. $\mathcal{A}$ interacts with a simulator $\mathcal{S}$ in the following game.

Initialization. $\mathcal{A}$ chooses two identities $\{I{D}_s^{*},I{D}_R^{*}\}$ and sends them to $\mathcal{S}$.

Setup. $\mathcal{S}$ runs the Setup algorithm to generate $params$ and $msk$. $\mathcal{S}$ then sends $params$ to $\mathcal{A}$.

Phase 1. $\mathcal{A}$ issues the following queries.

-

Hash query: $\mathcal{S}$ operates hash functions on the inputs given by $\mathcal{A}$ and returns the hashed values.

-

KeyExtract ($I{D}_i$): $\mathcal{A}$ sends an identity $I{D}_i$ to $\mathcal{S}$ and $\mathcal{S}$ returns the private key of $I{D}_i$ where neither KeyExtract ($I{D}_s^{*}$) nor KeyExtract ($I{D}_R^{*}$) can be queried.

-

Encrypt ($I{D}_s,I{D}_1,\cdots ,I{D}_u,M$): $\mathcal{A}$ sends a sender’s identity $I{D}_s$, a receiver set $\{I{D}_1,\cdots ,I{D}_u\}$ and a message M to $\mathcal{S}$. $\mathcal{S}$ returns a ciphertext C to $\mathcal{A}$.

-

Decrypt ($C,I{D}_i$): $\mathcal{A}$ sends an identity $I{D}_i$ and a ciphertext C to $\mathcal{S}$, and $\mathcal{S}$ returns the message M.

Forgery. $\mathcal{A}$ outputs a ciphertext $C^{*}$ with restrictions that the sender is $I{D}_s^{*}$ and $I{D}_R^{*}$ is one of the receivers, and $C^{*}$ was not outputted by querying the Encrypt oracle. $\mathcal{A}$ wins the game if $C^{*}$ is a valid ciphertext.

The advantage of $\mathcal{A}$ winning the game is defined as:

$${\mathbf{Adv}}^{SA}\left(\mathcal{A}\right)=Pr[Decrypt(C,I{D}_R^{*})\ne \perp ].$$

An anonymous multi-receiver identity-based authenticated encryption scheme is said to satisfy sender authentication if there exists no polynomial-time attacker that can win the sender authentication game with non-negligible advantage. The model of this game is shown in Figure 4.

Figure 4. The sender authentication game.

Figure 4. The sender authentication game.

Theorem 13. (Confidentiality) The proposed AMRIBAE scheme is IND-sMID-CCA secure in the random oracle model if the M-DBDH assumption holds.

Proof. The basic concept of the proof is a proof by contradiction. Assume that the proposed scheme is not IND-sMID-CCA secure, i.e., there exists a polynomial-time adversary $\mathcal{A}$ that wins the IND-sMID-CCA game with non-negligible advantage. Then, we will construct a polynomial-time algorithm $\mathcal{S}$ that has non-negligible advantage in solving the M-DBDH problem.

First, $\mathcal{S}$ is given $<q,G_1,G_2,e,P,aP,bP,cP,e{(P,P)}^{b^{2}c},Z>$, which is an instance of the M-DBDH problem. $\mathcal{S}$ simulates the game for $\mathcal{A}$ as follows:

Initialization. $\mathcal{A}$ outputs a target identity set $I{D}^{*}=\{I{D}_1^{*},\cdots ,I{D}_t^{*}\}$.

Setup. $\mathcal{S}$ sets $P_{pub}=cP$, computes $\Omega =e(P,P)$ and outputs $\{G_1,G_2,e,q,P,P_{pub},H,H_1,H_2,\Omega \}$ as the public parameters where $H,H_1$ and $H_2$ are three random oracles controlled by $\mathcal{S}$.

Phase 1. $\mathcal{S}$ maintains H-list, $H_1$-list and $H_2$-list to store the results of querying $H,H_1$ and $H_2$, respectively. In this phase, $\mathcal{A}$ can issue the following queries:

-

H-query:

This oracle takes an identity $I{D}_j\in {\{0,1\}}^{*}$ as input. If there exists a record $(I{D}_j,Q_j,q_j)$ in H-list, return $Q_j$. Otherwise, do the following:

• Randomly select $q_j\in {\mathbb{Z}}_q^{*}$.
• If $I{D}_j\in I{D}^{*}$, compute $Q_j=q_j\left(bP\right)$; else $Q_j=q_{j}P$.
• Return $Q_j$, and add $(I{D}_j,Q_j,q_j)$ into H-list.

-

$H_1$-query:

This oracle takes $X_j$ as input, where $X_j\in G_2$. If there exists a record $(X_j,v_j)$ in $H_1$-list, return $v_j$. Otherwise, do the following:

• Randomly choose $v_j\in {\mathbb{Z}}_q^{*}$.
• Add $(X_j,v_j)$ to $H_1$-list.
• Return $v_j$.

-

$H_2$-query:

This oracle takes $M_j\in G_2$ and an integer $k_j\in {\mathbb{Z}}_q^{*}$ as input. If there exists a record $(M_j,k_j,r_j,U_j)$ in $H_2$-list, return $r_j$. Otherwise, do the following:

• Randomly choose $r_j\in {\mathbb{Z}}_q^{*}$, and compute $U_j=r_{j}P$.
• Add $(M_j,k_j,r_j,U_j)$ to $H_2$-list.
• Return $r_j$.

-

KeyExtract:

This oracle takes an identity $I{D}_j$ as input. Call $H\left(I{D}_j\right)$ and retrieve $q_j$ from H-list. Then, $\mathcal{S}$ does the following:

-

If $I{D}_j\in I{D}^{*}$, return “reject”.

-

Otherwise, compute $d_j=q_j\left(cP\right)$ and return $d_j$.

-

Encrypt:

This oracle takes $u+1$ identities $(I{D}_s,I{D}_1,\cdots ,I{D}_u)$ and a message M as input. Upon receiving an Encryptquery, $\mathcal{S}$ does the following:

• Choose $k,r\in {\mathbb{Z}}_q^{*}$ at random, and set $H_2(M,k)=r$.
• For $i=1$ to u,

  -

  if $I{D}_{s}I{D}^{*}$, compute $v_i=H_1\left(e{(Q_i,d_s)}^r\right)$, where $d_s$ is the private key of the sender $I{D}_s$;

  -

  if $I{D}_s\in I{D}^{*}$ and $I{D}_{i}I{D}^{*}$, compute $v_i=H_1\left(e{(d_i,Q_s)}^r\right)$, where $d_i$ is the private key of the receiver $I{D}_i$;

  -

  if $I{D}_s,I{D}_i\in I{D}^{*}$, compute $v_i=H_1\left({\left(e{(P,P)}^{b^{2}c}\right)}^{r{q}_s{q}_i}\right)$.

• Compute ${\displaystyle f\left(x\right)=k-\prod _{i=1}^u(x-v_i)=\sum _{i=0}^{u-1}{c}_i{x}^i+x^{u}modq}$.
• Compute $U=rP,V=r{Q}_s,$ and $W=M·e{(P,P)}^{-k}$.
• Set the ciphertext $C=(c_0,c_1,\cdots ,c_{u-1},U,V,W,I{D}_s)$, and return C.

-

Decrypt:

This oracle takes an identity $I{D}_j$ and a ciphertext C as input. Upon receiving a Decryptquery, denoted by Decrypt$(C,I{D}_j)$ where $C=(c_0,\cdots ,c_{u-1},U,V,W,I{D}_s)$, $\mathcal{S}$ does the following:

• Search $H_2$-list to get $(M_i,k_i,r_i,U_i)$ with $U_i=U$. If not found, return “reject”.
• Search H-list to get $(I{D}_s,Q_s,q_s)$ with $e(U,Q_s)=e(P,V)$. If not found, return “reject”.
• This step can be separated into three cases:

  -

  if $I{D}_{s}I{D}^{*}$, compute $v_j=H_1\left(e{(Q_j,d_s)}^{r_i}\right)$;

  -

  if $I{D}_s\in I{D}^{*}$ and $I{D}_{j}I{D}^{*}$, compute $v_j=H_1\left(e{(d_j,Q_s)}^{r_i}\right)$;

  -

  if $I{D}_s,I{D}_j\in I{D}^{*}$, compute $v_j=H_1\left({\left(e{(P,P)}^{b^{2}c}\right)}^{r_i{q}_s{q}_j}\right)$.

• Compute $k=c_0+c_1{v}_j+\cdots +c_{u-1}{v}_j^{u-1}+v_j^{u}modq$.
• Check whether $k_i=k$ and $M_i=W·{\Omega }^k$ or not. If not, return “reject”. Otherwise, return $M_i$.

Challenge. $\mathcal{A}$ sends $(M_0,M_1)$ and a sender’s identity $I{D}_s$ to $\mathcal{S}$, with restrictions that $M_0,M_1$ are two distinct messages with the same length, $I{D}_s\in I{D}^{*}$, and KeyExtract ($I{D}_s$) has never been queried. $\mathcal{S}$ performs the following operations:

• Choose $\beta \in \{0,1\}$ randomly.
• For $i=1$ to t, call $H\left(I{D}_i^{*}\right)$, and retrieve $q_i^{*}$ from H-list.
• Call $H\left(I{D}_s\right)$, and retrieve $q_s$ from H-list.
• Choose $k\in {\mathbb{Z}}_q^{*}$, and set $U^{*}=aP$ and $V^{*}=q_s\left(aP\right)$.
• For $i=1$ to t, compute $v_i=H_1\left(Z^{q_i^{*}{q}_s}\right)$.
• Compute ${\displaystyle f\left(x\right)=k-\prod _{i=1}^t(x-v_i)=\sum _{i=0}^{t-1}{c}_i{x}^i+x^{t}modq}$ and $W^{*}=M_{\beta }·{\Omega }^{-k}$.
• Set the ciphertext $C^{*}=(c_0,c_1,\cdots ,c_{t-1},U^{*},V^{*},W^{*},I{D}_s)$, and send $C^{*}$ to $\mathcal{A}$.

Phase 2. $\mathcal{A}$ makes queries as those in Phase 1. However, if $\mathcal{A}$ issues a Decrypt query with input $C=C^{*}$ and $I{D}_i\in I{D}^{*}$ or the query KeyExtract ($I{D}_s$), $\mathcal{S}$ will return “reject”.

Guess. Finally, $\mathcal{A}$ outputs ${\beta }^{\prime }\in \{0,1\}$. If ${\beta }^{\prime }=\beta$, then $\mathcal{S}$ outputs one. Otherwise, $\mathcal{S}$ randomly chooses $\overline{\beta }\in \{0,1\}$ and outputs $\overline{\beta }$.

If $Z=e{(P,P)}^{abc}$, then $Z^{q_i^{*}{q}_s}=e{(P,P)}^{abc{q}_i^{*}{q}_s}=e{(q_i^{*}\left(bP\right),q_s\left(cP\right))}^a=e{(Q_i^{*},d_s)}^a$ for $i=1$ to t. Therefore, $C^{*}$ is a correct ciphertext. Otherwise, Z is an element randomly chosen in $G_2$. As the construction above, $\mathcal{S}$ correctly simulates the IND-sMID-CCA game. If $\mathcal{A}$ wins the IND-sMID-CCA game with non-negligible advantage, at least ϵ, $*Pr[{\beta }^{\prime }=\beta ]-\frac{1}{2}\ge ϵ$ under a correct simulation of the game, i.e., $|Pr[\mathcal{A}(\Omega )={\beta }^{\prime }=\beta ]-\frac{1}{2}\ge ϵ$, where Ω is a correct AMRIBAE scheme. Thus, we have that:

$$\left|Pr\right[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1]$$

$$=Pr[\mathcal{A}(\Omega )=\beta ]+\frac{1}{2}(1-Pr[\mathcal{A}(\Omega )=\beta ])$$

$$=\frac{1}{2}Pr[\mathcal{A}(\Omega )=\beta ]+\frac{1}{2}$$

and

$$Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},Z)=1]$$

$$=\frac{1}{2}Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1]$$

$$+\frac{1}{2}Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},X{\in }_R{G}_{2}e{(P,P)}^{abc})=1]$$

$$=\frac{1}{2}(\frac{1}{2}Pr[\mathcal{A}(\Omega )=\beta ]+\frac{1}{2})+\frac{1}{2}(\frac{1}{2}+\frac{1}{2}·\frac{1}{2})$$

$$=\frac{1}{4}Pr[\mathcal{A}(\Omega )=\beta ]+\frac{5}{8}.$$

We can obtain:

$$\left|Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1]-Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},Z)=1]\right|$$

$$=|\frac{1}{4}Pr[\mathcal{A}(\Omega )=\beta ]-\frac{1}{8}=\frac{1}{4}|Pr[\mathcal{A}(\Omega )=\beta ]-\frac{1}{2}|\ge \frac{ϵ}{4}.$$

Therefore, $\mathcal{S}$ solves the M-DBDH problem with non-negligible advantage $\frac{ϵ}{4}$ within polynomial time. ☐

Theorem 13 ensures the CCA security of confidentiality against the outside attackers (unselected receivers). In confidentiality, no inside attackers exist (selected receivers), because every selected receiver can decrypt the ciphertext.

Theorem 14. (Anonymity) The proposed AMRIBAE scheme is Anon-sMID-CCA secure in the random oracle model if the M-DBDH assumption holds.

Proof. Assume that the proposed scheme is not Anon-sMID-CCA secure, that is there exists a polynomial-time adversary $\mathcal{A}$ that wins the Anon-sMID-CCA game with non-negligible advantage. We will construct a polynomial-time algorithm $\mathcal{S}$ that has non-negligible advantage in solving the M-DBDH problem.

First, $\mathcal{S}$ is given $<q,G_1,G_2,e,P,aP,bP,cP,e{(P,P)}^{b^{2}c},Z>$, which is an instance of the M-DBDH problem. $\mathcal{S}$ simulates the game for $\mathcal{A}$ as follows:

Initialization. $\mathcal{A}$ outputs a target identity set $I{D}^{*}=\{I{D}_0^{*},I{D}_1^{*}\}$.

Setup. $\mathcal{S}$ sets $P_{pub}=cP$, computes $\Omega =e(P,P)$ and outputs $\{G_1,G_2,e,q,P,P_{pub},H,H_1,H_2,\Omega \}$ as the public parameters, where $H,H_1$ and $H_2$ are three random oracles controlled by $\mathcal{S}$.

Phase 1. $\mathcal{S}$ maintains H-list, $H_1$-list and $H_2$-list to store the results of querying $H,H_1$ and $H_2$, respectively. In this phase, $\mathcal{A}$ can issue the H, $H_1$, $H_2$, KeyExtract, Encrypt and Decrypt queries. The simulations are the same as those in the proof of Theorem 13.

Challenge. $\mathcal{A}$ sends a message M, $t-1$ receivers’ identities $\{I{D}_2,I{D}_3,\cdots ,I{D}_t\}$ and a sender’s identity $I{D}_s$ to $\mathcal{S}$ with restrictions that $I{D}_s\in I{D}^{*}$ and KeyExtract ($I{D}_s$) has never been queried. $\mathcal{S}$ does the following:

• Choose $\beta \in \{0,1\}$ randomly.
• For $i=2$ to t, call $H\left(I{D}_i\right)$, and retrieve $q_i$ from H-list.
• Call $H\left(I{D}_{\beta }^{*}\right)$, and retrieve $q_{\beta }^{*}$ from H-list.
• Call $H\left(I{D}_s\right)$, and retrieve $q_s$ from H-list.
• Choose $k\in {\mathbb{Z}}_q^{*}$, and set $U^{*}=aP$ and $V^{*}=q_s\left(aP\right)$.
• For $i=2$ to t, compute $v_i=H_1\left(e(q_i{U}^{*},q_s\left(cP\right))\right)$.
• Compute $v_{\beta }=H_1\left(Z^{q_{\beta }^{*}{q}_s}\right)$.
• Compute ${\displaystyle f\left(x\right)=k-(x-v_{\beta })\prod _{i=2}^t(x-v_i)=\sum _{i=0}^{t-1}{c}_i{x}^i+x^{t}modq}$ and $W^{*}=M·{\Omega }^{-k}$.
• Set the ciphertext $C^{*}=(c_0,c_1,\cdots ,c_{t-1},U^{*},V^{*},W^{*},I{D}_s)$ and send $C^{*}$ to $\mathcal{A}$.

Phase 2. $\mathcal{A}$ makes queries as those in Phase 1. However, if $\mathcal{A}$ issues a Decrypt query with input $C=C^{*}$ and $I{D}_i\in I{D}^{*}$ or KeyExtract ($I{D}_s$), $\mathcal{S}$ will return “reject”.

Guess. Finally, $\mathcal{A}$ outputs ${\beta }^{\prime }\in \{0,1\}$. If ${\beta }^{\prime }=\beta$, then $\mathcal{S}$ outputs one. Otherwise, $\mathcal{S}$ randomly chooses $\overline{\beta }\in \{0,1\}$ and outputs $\overline{\beta }$.

If $Z=e{(P,P)}^{abc}$, then $Z^{q_{\beta }^{*}{q}_s}=e{(P,P)}^{abc{q}_{\beta }^{*}{q}_s}=e{(q_{\beta }^{*}\left(bP\right),q_s\left(cP\right))}^a=e{(Q_{\beta }^{*},d_s)}^a$ for $\beta \in \{0,1\}$. Therefore, $C^{*}$ is a correct ciphertext. Otherwise, Z is an element randomly chosen in $G_2$. As the construction above, $\mathcal{S}$ correctly simulates the Anon-sMID-CCA game. If $\mathcal{A}$ wins the game with non-negligible advantage at least ϵ, $*Pr[{\beta }^{\prime }=\beta ]-\frac{1}{2}\ge ϵ$ under a correct simulation of the game, i.e., $*Pr[\mathcal{A}(\Omega )={\beta }^{\prime }=\beta ]-\frac{1}{2}\ge ϵ$, where Ω is a correct AMRIBAE scheme. Thus, we have that:

$$\left|Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},e{(P,P)}^{abc})=1-Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{b^{2}c},Z)=1]\right|$$

$$=|(\frac{1}{2}Pr[\mathcal{A}(\Omega )=\beta ]+\frac{1}{2})-(\frac{1}{4}Pr[\mathcal{A}(\Omega )=\beta ]+\frac{5}{8})|$$

$$=|\frac{1}{4}Pr[\mathcal{A}(\Omega )=\beta ]-\frac{1}{8}|=\frac{1}{4}|Pr[\mathcal{A}(\Omega )=\beta ]-\frac{1}{2}|\ge \frac{ϵ}{4}.$$

Therefore, $\mathcal{S}$ solves the M-DBDH problem with non-negligible advantage $\frac{ϵ}{4}$ within polynomial time. ☐

Theorem 14 guarantees the CCA security of anonymity against both the outside attackers (unselected receivers) and the inside attackers (selected receivers) in the proposed scheme. In other words, even if an adversary compromises with any $t-1$ receivers, the anonymity of the remaining receiver is still preserved in the proposed scheme. In this proof, we do not cover the following extreme case. Assume that the total number of users in the system is N. The extreme case occurs when a user (sender) encrypts a message for other $N-2$ selected users (receivers), so that there would be only one unselected user, and this unselected user can no doubt figure out the identities of the $N-2$ receivers.

Theorem 15. (Sender authentication) The proposed AMRIBAE scheme satisfies sender authentication in the random oracle model if the DBDH assumption holds.

Proof. Assume that there exists a polynomial-time adversary $\mathcal{A}$ that wins the sender authentication game with non-negligible advantage. Then, we will construct a polynomial-time algorithm $\mathcal{S}$ that has non-negligible advantage in solving the DBDH problem.

First, $\mathcal{S}$ is given $<q,G_1,G_2,e,P,aP,bP,cP,Z>$, which is an instance of the DBDH problem. $\mathcal{S}$ simulates the game for $\mathcal{A}$ as follows:

Initialization. $\mathcal{A}$ outputs an identity set $I{D}^{*}=\{I{D}_s^{*},I{D}_R^{*}\}$.

Setup. $\mathcal{S}$ sets $P_{pub}=cP$, computes $\Omega =e(P,P)$ and outputs $\{G_1,G_2,e,q,P,P_{pub},H,H_1,H_2,\Omega \}$ as the public parameters, where $H,H_1$ and $H_2$ are three random oracles controlled by $\mathcal{S}$.

Phase 1. $\mathcal{S}$ maintains H-list, $H_1$-list and $H_2$-list to store the results of querying $H,H_1$ and $H_2$, respectively. In this phase, $\mathcal{A}$ can issue the following queries:

-

H-query:

This oracle takes an identity $I{D}_j\in {\{0,1\}}^{*}$ as input. If there exists a record $(I{D}_j,Q_j,q_j)$ in H-list, return $Q_j$. Otherwise, do the following:

• Randomly select $q_j\in {\mathbb{Z}}_q^{*}$.
• If $I{D}_j=I{D}_s^{*}$, compute $Q_j=q_j\left(aP\right)$; else if $I{D}_j=I{D}_R^{*}$, compute $Q_j=q_j\left(bP\right)$; else $Q_j=q_{j}P$.
• Return $Q_j$ and add $(I{D}_j,Q_j,q_j)$ into H-list.

-

The simulation of $H_1$-query and $H_2$-query are the same as those in the proof of Theorem 13.

-

KeyExtract:

This oracle takes an identity $I{D}_j$ as input. Call $H\left(I{D}_j\right)$, and retrieve $q_j$ from H-list. Then, $\mathcal{S}$ does the following:

-

If $I{D}_j\in I{D}^{*}$, return “reject”.

-

Otherwise, compute $d_j=q_j\left(cP\right)$, and return $d_j$.

-

Encrypt:

This oracle takes $u+1$ identities $(I{D}_s,I{D}_1,\cdots ,I{D}_u)$ and a message M as input. Upon receiving an Encrypt query, $\mathcal{S}$ does the following:

• Choose $k,r\in {\mathbb{Z}}_q^{*}$ at random, and set $H_2(M,k)=r$.
• For $i=1$ to u,

  -

  if $I{D}_s\in I{D}^{*}$, compute $v_i=H_1\left(e{(Q_i,d_s)}^r\right)$, where $d_s$ is the private key of the sender $I{D}_s$;

  -

  if $I{D}_s\in I{D}^{*}$ and $I{D}_i\in I{D}^{*}$, compute $v_i=H_1\left(e{(d_i,Q_s)}^r\right)$, where $d_i$ is the private key of the receiver $I{D}_i$;

  -

  if $I{D}_s,I{D}_i\in I{D}^{*}$, compute $v_i=H_1\left(Z^{r{q}_s{q}_i}\right)$.

• Compute ${\displaystyle f\left(x\right)=k-\prod _{i=1}^u(x-v_i)=\sum _{i=0}^{u-1}{c}_i{x}^i+x^{u}modq}$.
• Compute $U=rP,V=r{Q}_s$ and $W=M·{\Omega }^{-k}$.
• Set the ciphertext $C=(c_0,c_1,\cdots ,c_{u-1},U,V,W,I{D}_s)$, and return C.

-

Decrypt:

This oracle takes an identity $I{D}_j$ and a ciphertext C as input. Upon receiving a Decrypt query, denoted by Decrypt $(C,I{D}_j)$, where $C=(c_0,\cdots ,c_{u-1},U,V,W,I{D}_s)$, $\mathcal{S}$ does the following:

• Search $H_2$-list to get $(M_i,k_i,r_i,U_i)$ with $U_i=U$. If not found, return “reject”.
• Search H-list to get $(I{D}_s,Q_s,q_s)$ with $e(U,Q_s)=e(P,V)$. If not found, return “reject”.
• This step can be separated into three cases:

  -

  if $I{D}_s\in I{D}^{*}$, compute $v_j=H_1\left(e{(Q_j,d_s)}^{r_i}\right)$;

  -

  if $I{D}_s\in I{D}^{*}$ and $I{D}_j\in I{D}^{*}$, compute $v_j=H_1\left(e{(d_j,Q_s)}^{r_i}\right)$;

  -

  if $I{D}_s,I{D}_j\in I{D}^{*}$, compute $v_j=H_1\left(Z^{r_i{q}_s{q}_j}\right)$.

• Compute $k=c_0+c_1{v}_j+\cdots +c_{u-1}{v}_j^{u-1}+v_j^{u}modq$.
• Check whether $k_i=k$ and $M_i=W·{\Omega }^k$ or not. If not, return “reject”. Otherwise, return $M_i$.

Forgery. Finally, $\mathcal{A}$ outputs $C^{*}=(c_0,c_1,\cdots ,c_{t-1},U^{*},V^{*},W^{*},I{D}_s^{*})$, where $C^{*}$ was not outputted by querying the Encrypt oracle. Then, $\mathcal{S}$ performs the following.

• Search $H_2$-list to get $(M_i,k_i,r_i,U_i)$ with $U_i=U^{*}$.
• Call $H\left(I{D}_s^{*}\right)$ and $H\left(I{D}_R^{*}\right)$ to retrieve $q_s^{*}$ and $q_R^{*}$ from H-list.
• Compute $v=H_1\left(Z^{q_s^{*}{q}_R^{*}{r}_i}\right)$.
• Compute $k=c_0+c_{1}v+\cdots +c_{t-1}{v}^{t-1}+v^{t}modq$.
• Check whether $k_i=k$ and $M_i=W·{\Omega }^k$ or not. If it is, $\mathcal{A}$ wins the game.

$\mathcal{S}$ outputs 1 if $\mathcal{A}$ wins the game. Otherwise, $\mathcal{S}$ outputs 0. Assume $\mathcal{A}$ wins the game with a non-negligible advantage at least ϵ under a correct simulation. To analyze the advantage of solving the DBDH problem, we define the following events.

• $E_1$: The game has been correctly simulated.
• $E_2$: $\mathcal{A}$ wins the game.

Then, we have that:

$$Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{abc})=1]$$

$$=Pr[E_1\wedge E_2]=Pr\left[E_1\right]Pr\left[E_2\right|E_1]$$

$$\ge 1·ϵ=ϵ$$

and

$$\left|Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{abc})=1]-Pr[\mathcal{S}(P,aP,bP,cP,Z)=1]\right|$$

$$=|\frac{1}{2}Pr[\mathcal{S}(P,aP,bP,cP,e{(P,P)}^{abc})=1]|\ge \frac{1}{2}ϵ.$$

Therefore, $\mathcal{S}$ solves the DBDH problem with non-negligible advantage $\frac{ϵ}{2}$ within polynomial time. ☐

Theorem 15 guarantees that the proposed scheme satisfies sender authentication. In other words, even if an adversary compromises with any $t-1$ receivers, the adversary cannot impersonate a sender to send a valid ciphertext.

6. Comparisons

In this section, we compare the proposed scheme to [10,11,14,16,18,19,20,21,23,25,26,27,28,29] and [31] in performance and security. According to [39,40,41] and [42], we can obtain that $T_p\approx 5T_e$, $T_s\approx 29T_m$, $T_e\approx 240T_m$, $T_h\approx 23T_m$ and $T_a\approx 0.12T_m$, shown in Table 2, which summarizes the comparison in the computation cost of encryption/decryption and the ciphertext length for multiple receivers. Especially, our scheme is efficient in decryption.

The security comparison is shown in Table 3. The schemes of [11,29] and the second scheme of [31] lack the proofs for confidentiality and anonymity. The scheme [19] did not provide the proof for anonymity, but it is CPA secure in confidentiality. The schemes [14,16,18] and [20] are CPA secure in both confidentiality and anonymity, where the proof of [20] is under a standard model. The scheme [10] is CCA secure in confidentiality, but it is not with anonymity, which has been indicated in [11,13,25]. The scheme of [25] and the first scheme of [31] are CCA secure in confidentiality and anonymity against outsider attacks; however, the authors of [17,29] and [28], respectively, have shown that they are not with anonymity against insider attacks. In addition, we demonstrate that there exist some problems in the proofs of the schemes [21,22,23,26,27,28], where the details are shown in the Appendix. Our scheme is the first one that can achieve the CCA security under the random oracle model against outside attackers and inside attackers simultaneously. The confidentiality and anonymity of our scheme have been formally proven in Section 5.

Table 2. Performance comparison.

	Encryption Cost	Decryption Cost	Ciphertext Length
[10]	$(2t+3)T_h+2t{T}_m+(t^2+2)T_s$	$4T_h+(t+2)T_s$
	$+(t^2-t)T_a+t{T}_{poly}+T_p+T_e$	$+t{T}_a+2T_p$	$(t+2)u+w$
	$\approx (29t^2+48t+1567)T_m+t{T}_{poly}$	$\approx (29t+2550)T_m$
[11]	$(2t+1)T_h+(t+1)T_s+t{T}_p$	$t{T}_h+t{T}_s+t{T}_p$	$(t+2)u+w$
	$\approx (1275t+52)T_m$	$\approx 1252t{T}_m$
[25]	$(2t+3)T_h+2t{T}_m+(2t^2+t+1)T_s$	$4T_h+(2t+2)T_s$
	$+2(t^2-t)T_a+t{T}_{poly}+T_p+t{T}_e$	$+2t{T}_a+2T_p$	$(2t+2)u+w$
	$\approx (58t^2+317t+1298)T_m+t{T}_{poly}$	$\approx (58t+2550)T_m$
[21]	$(t+1)T_h+2T_s+t{T}_p+T_{poly}$	$T_h+t{T}_m+T_p$	$t\left|q\right|+u+w$
	$\approx (1223t+1223)T_m+T_{poly}$	$\approx (t+1223)T_m$
[18]	$(t+2)T_s+(t+1)T_p+T_{CRT}$	$T_p$	$t\left|q\right|+2u+w$
	$\approx (1229t+1258)T_m+T_{CRT}$	$\approx 1200T_m$
[16]	$t{T}_h+(t+1)T_e+(2t+5)T_s+(t+1)T_e$	$T_h+T_e+t(2T_p+T_e+T_s)$	$(t+2)u+w$
	$\approx (1251t+1585)T_m$	$\approx (2669t+1223)T_m$
[29]	$(2t+4)T_h+2t{T}_m+(t^2+t+1)T_s$	$4T_h+(t+1)T_s$
	$+2(t^2-t)T_a+t{T}_{poly}+T_p+t{T}_e$	$+t{T}_a+2t{T}_p$	$(2t+2)u+w$
	$\approx (29t^2+317t+1233)T_m+t{T}_{poly}$	$\approx (2429t+121)T_m$
[31]-Scheme 1	$(t+1)T_h+2t{T}_e+2T_s$	$(t+1)T_h+T_s$
	$+t{T}_a+2t{T}_p$	$+T_a+2T_p$	$(t+2)u+w$
	$\approx (1703t+1281)T_m$	$\approx (23t+2452)T_m$
[31]-Scheme 2	$(t+1)T_h+2t{T}_e+2T_s$	$(t+1)T_h+T_s$
	$+t{T}_a+2t{T}_p$	$+T_a+2T_p$	$(t+2)u+w$
	$\approx (1703t+1281)T_m$	$\approx (23t+2452)T_m$
[14]	$(2t+1)T_h+(3t+2)T_s$
	$+T_e+n{T}_a$	$t(T_p+T_a+T_h)$	$(t+1)v+w$
	$\approx (133t+1281)T_m$	$\approx 1223t{T}_m$
[19]	$t{T}_h+t^2{T}_m+(t+4)T_s$	$T_h+T_{poly}$
	$+(t+1)T_e+T_{poly}$	$+2T_a+(t+1)T_s+4T_p$	$(t+3)u+v$
	$\approx (t^2+1252t+1316)T_m$	$\approx (29t+4852)T_m+T_{poly}$
[28]	$(2t+1)T_h+(t+1)T_m$
	$+t{T}_e+(2t+2)T_s$	$(t+1)T_h+(t+1)T_p+t{T}_s$	$(t+2)u+w$
	$\approx (1305t+82)T_m$	$\approx (1252t+1223)T_m$
[20]	$t{T}_h+(t+1)T_m+(t^2+1)T_s$	$T_h+T_m+T_e$
	$+(t^2-t)\left|ID\right|T_a+T_e+t{T}_{poly}$	$+t{T}_a+t{T}_s+2T_p$	$(t+1)u+v$
	$\approx (29t^2+24t+270)T_m+t{T}_{poly}$	$\approx (29t+2664)T_m$
[23]	$(3t+1)T_h+2T_s+t{T}_p$	$2T_h+T_e$	$(t+1)u+\left|q\right|+w$
	$\approx (1269t+81)T_m$	$\approx 1246T_m$
[27]	$(2t+2)T_h+4T_s+t{T}_p+T_{poly}$	$3T_h+t{T}_m+3T_p+T_s+T_a$	$t\left|q\right|+3u+\left|ID\right|$
	$\approx (1246t+162)T_m+T_{poly}$	$\approx (t+3698)T_m$
[26]	$(t+2)T_h+(t+2)T_s+t{T}_p$	$4T_h+t{T}_s+T_e$	$(t+2)u+w$
	$\approx (1252t+104)T_m$	$\approx (29t+1292)T_m$
Ours	$(2t+1)T_h+4T_s+t{T}_p+T_{poly}$	$2T_h+t{T}_m+T_p+T_s$	$t\left|q\right|+2u+v$
	$\approx (1246t+139)T_m+T_{poly}$	$\approx (t+1275)T_m$

•T_p: the cost of a pairing operation; •T_h: the cost of a hash operation; •T_m: the cost of a modular multiplication in ${\mathbb{Z}}_q^{*}$; •T_e: the cost of a modular exponentiation in ${\mathbb{Z}}_q^{*}$; •T_s: the cost of a scalar multiplication in an additive group or an exponentiation in a multiplicative group; •T_a: the cost of an addition in an additive group or a multiplication in a multiplicative group; •T_poly: the cost of constructing a polynomial; •T_CRT: the cost of applying the Chinese remainder theorem; •t: the number of receivers; •|ID|: the bit length of an identity; •q: a large prime; •u: the bit length of an element in an additive group; •v: the bit length of an element in a multiplicative group; •w: the bit length of a symmetric encryption key.

Table 2. Performance comparison.

	Encryption Cost	Decryption Cost	Ciphertext Length
[10]	$(2t+3)T_h+2t{T}_m+(t^2+2)T_s$	$4T_h+(t+2)T_s$
	$+(t^2-t)T_a+t{T}_{poly}+T_p+T_e$	$+t{T}_a+2T_p$	$(t+2)u+w$
	$\approx (29t^2+48t+1567)T_m+t{T}_{poly}$	$\approx (29t+2550)T_m$
[11]	$(2t+1)T_h+(t+1)T_s+t{T}_p$	$t{T}_h+t{T}_s+t{T}_p$	$(t+2)u+w$
	$\approx (1275t+52)T_m$	$\approx 1252t{T}_m$
[25]	$(2t+3)T_h+2t{T}_m+(2t^2+t+1)T_s$	$4T_h+(2t+2)T_s$
	$+2(t^2-t)T_a+t{T}_{poly}+T_p+t{T}_e$	$+2t{T}_a+2T_p$	$(2t+2)u+w$
	$\approx (58t^2+317t+1298)T_m+t{T}_{poly}$	$\approx (58t+2550)T_m$
[21]	$(t+1)T_h+2T_s+t{T}_p+T_{poly}$	$T_h+t{T}_m+T_p$	$t\left|q\right|+u+w$
	$\approx (1223t+1223)T_m+T_{poly}$	$\approx (t+1223)T_m$
[18]	$(t+2)T_s+(t+1)T_p+T_{CRT}$	$T_p$	$t\left|q\right|+2u+w$
	$\approx (1229t+1258)T_m+T_{CRT}$	$\approx 1200T_m$
[16]	$t{T}_h+(t+1)T_e+(2t+5)T_s+(t+1)T_e$	$T_h+T_e+t(2T_p+T_e+T_s)$	$(t+2)u+w$
	$\approx (1251t+1585)T_m$	$\approx (2669t+1223)T_m$
[29]	$(2t+4)T_h+2t{T}_m+(t^2+t+1)T_s$	$4T_h+(t+1)T_s$
	$+2(t^2-t)T_a+t{T}_{poly}+T_p+t{T}_e$	$+t{T}_a+2t{T}_p$	$(2t+2)u+w$
	$\approx (29t^2+317t+1233)T_m+t{T}_{poly}$	$\approx (2429t+121)T_m$
[31]-Scheme 1	$(t+1)T_h+2t{T}_e+2T_s$	$(t+1)T_h+T_s$
	$+t{T}_a+2t{T}_p$	$+T_a+2T_p$	$(t+2)u+w$
	$\approx (1703t+1281)T_m$	$\approx (23t+2452)T_m$
[31]-Scheme 2	$(t+1)T_h+2t{T}_e+2T_s$	$(t+1)T_h+T_s$
	$+t{T}_a+2t{T}_p$	$+T_a+2T_p$	$(t+2)u+w$
	$\approx (1703t+1281)T_m$	$\approx (23t+2452)T_m$
[14]	$(2t+1)T_h+(3t+2)T_s$
	$+T_e+n{T}_a$	$t(T_p+T_a+T_h)$	$(t+1)v+w$
	$\approx (133t+1281)T_m$	$\approx 1223t{T}_m$
[19]	$t{T}_h+t^2{T}_m+(t+4)T_s$	$T_h+T_{poly}$
	$+(t+1)T_e+T_{poly}$	$+2T_a+(t+1)T_s+4T_p$	$(t+3)u+v$
	$\approx (t^2+1252t+1316)T_m$	$\approx (29t+4852)T_m+T_{poly}$
[28]	$(2t+1)T_h+(t+1)T_m$
	$+t{T}_e+(2t+2)T_s$	$(t+1)T_h+(t+1)T_p+t{T}_s$	$(t+2)u+w$
	$\approx (1305t+82)T_m$	$\approx (1252t+1223)T_m$
[20]	$t{T}_h+(t+1)T_m+(t^2+1)T_s$	$T_h+T_m+T_e$
	$+(t^2-t)\left|ID\right|T_a+T_e+t{T}_{poly}$	$+t{T}_a+t{T}_s+2T_p$	$(t+1)u+v$
	$\approx (29t^2+24t+270)T_m+t{T}_{poly}$	$\approx (29t+2664)T_m$
[23]	$(3t+1)T_h+2T_s+t{T}_p$	$2T_h+T_e$	$(t+1)u+\left|q\right|+w$
	$\approx (1269t+81)T_m$	$\approx 1246T_m$
[27]	$(2t+2)T_h+4T_s+t{T}_p+T_{poly}$	$3T_h+t{T}_m+3T_p+T_s+T_a$	$t\left|q\right|+3u+\left|ID\right|$
	$\approx (1246t+162)T_m+T_{poly}$	$\approx (t+3698)T_m$
[26]	$(t+2)T_h+(t+2)T_s+t{T}_p$	$4T_h+t{T}_s+T_e$	$(t+2)u+w$
	$\approx (1252t+104)T_m$	$\approx (29t+1292)T_m$
Ours	$(2t+1)T_h+4T_s+t{T}_p+T_{poly}$	$2T_h+t{T}_m+T_p+T_s$	$t\left|q\right|+2u+v$
	$\approx (1246t+139)T_m+T_{poly}$	$\approx (t+1275)T_m$

•T_p: the cost of a pairing operation; •T_h: the cost of a hash operation; •T_m: the cost of a modular multiplication in ${\mathbb{Z}}_q^{*}$; •T_e: the cost of a modular exponentiation in ${\mathbb{Z}}_q^{*}$; •T_s: the cost of a scalar multiplication in an additive group or an exponentiation in a multiplicative group; •T_a: the cost of an addition in an additive group or a multiplication in a multiplicative group; •T_poly: the cost of constructing a polynomial; •T_CRT: the cost of applying the Chinese remainder theorem; •t: the number of receivers; •|ID|: the bit length of an identity; •q: a large prime; •u: the bit length of an element in an additive group; •v: the bit length of an element in a multiplicative group; •w: the bit length of a symmetric encryption key.

Table 3. Properties comparison. CPA, chosen plaintext attack.

	Confidentiality	Anonymity		SecurityModel	Sender Authentication
		Outsider	Insider
[10]	CCA	△	△	ROM	No
[11]	–	–	–	–	No
[25]	CCA	CCA	△	ROM	No
[21,22]	△	△	△	ROM	No
[18]	CPA	CPA	CPA	ROM	No
[29]	–	–	–	–	No
[16]	CPA	CPA	CPA	ROM	No
[31]-Scheme 1	CCA	CCA	△	ROM	No
[31]-Scheme 2	–	–	–	–	No
[14]	CPA	CPA	CPA	ROM	No
[19]	CPA	–	–	ROM	No
[28]	△	△	△	ROM	No
[20]	CPA	CPA	CPA	STD	No
[23]	△	△	△	ROM	No
[27]	△	△	△	ROM	Yes
[26]	–	△	△	ROM	No
Ours	CCA	CCA	CCA	ROM	Yes

△: the authors claimed that their scheme is CCA secure, but it has some security flaws or there exist some problems in the security proofs.

Table 3. Properties comparison. CPA, chosen plaintext attack.

	Confidentiality	Anonymity		SecurityModel	Sender Authentication
		Outsider	Insider
[10]	CCA	△	△	ROM	No
[11]	–	–	–	–	No
[25]	CCA	CCA	△	ROM	No
[21,22]	△	△	△	ROM	No
[18]	CPA	CPA	CPA	ROM	No
[29]	–	–	–	–	No
[16]	CPA	CPA	CPA	ROM	No
[31]-Scheme 1	CCA	CCA	△	ROM	No
[31]-Scheme 2	–	–	–	–	No
[14]	CPA	CPA	CPA	ROM	No
[19]	CPA	–	–	ROM	No
[28]	△	△	△	ROM	No
[20]	CPA	CPA	CPA	STD	No
[23]	△	△	△	ROM	No
[27]	△	△	△	ROM	Yes
[26]	–	△	△	ROM	No
Ours	CCA	CCA	CCA	ROM	Yes

△: the authors claimed that their scheme is CCA secure, but it has some security flaws or there exist some problems in the security proofs.

7. Conclusions

In consideration of privacy preservation, Fan et al. first introduced the concept of anonymous multi-receiver identity-based encryption in 2010. Many works on the topic have been proposed recently. It is an interesting topic and worthy of study in both practical and theoretical aspects, because customers always pay much attention to their privacy in modern societies.

However, there is no anonymous multi-receiver identity-based encryption scheme proposed in the literature that possesses complete CCA security. In order to cope with the problem, we have proposed a new anonymous multi-receiver identity-based encryption scheme, which is provably CCA secure in both confidentiality and anonymity against not only outside attackers, but also inside attackers. Furthermore, the proposed scheme has also achieved sender authentication. All of the properties of our scheme are guaranteed based on the DBDH assumption and the M-DBDH assumption, whose hardness has been proven in this paper.