Effects of Initial Symmetry on the Global Symmetry of One-Dimensional Legal Cellular Automata

Abstract

To examine the development of pattern formation from the viewpoint of symmetry, we applied a two-dimensional discrete Walsh analysis to a one-dimensional cellular automata model under two types of regular initial conditions. The amount of symmetropy of cellular automata (CA) models under regular and random initial conditions corresponds to three Wolfram’s classes of CAs, identified as Classes II, III, and IV. Regular initial conditions occur in two groups. One group that makes a broken, regular pattern formation has four types of symmetry, whereas the other group that makes a higher hierarchy pattern formation has only two types. Additionally, both final pattern formations show an increased amount of symmetropy as time passes. Moreover, the final pattern formations are affected by iterations of base rules of CA models of chaos dynamical systems. The growth design formations limit possibilities: the ratio of developing final pattern formations under a regular initial condition decreases in the order of Classes III, II, and IV. This might be related to the difference in degree in reference to surrounding conditions. These findings suggest that calculations of symmetries of the structures of one-dimensional cellular automata models are useful for revealing rules of pattern generation for animal bodies.

1. Introduction

Animals have many kinds of pattern formation. Leopards living in closed habitats, such as forests, have a frequency of stripes that is much higher, more irregular, and more complex than those living in open habitats [1]. These body patterns reflect adaptations to the surrounding environment and, thus, pattern formation is substantially related to the conservation of species [1]. When we observe pattern formation, we read “texture”, which includes shape, among other factors. Texture is measured by terms including spectrum, entropy, and fractal dimension [2,3]. The method of measurement combining entropy and symmetry, the two-dimensional discrete Walsh analysis, can be applied to analyses of two-dimensional surfaces [3,4,5]. In previous studies, the two-dimensional discrete Walsh analysis has been used in theoretical studies with one-dimensional legal cellular automata. As a result, studies have revealed the theoretical process of pattern formation, which reduces entropy and increases specific symmetry (self-organization) [4], and the real biological process of pattern formation, which reduces entropy and increases specific symmetry. They have also revealed that the real biological process has phase transitions, as seen in calculations with the two-dimensional Ising model [5]. However, the calculations in previous studies [3,4,5] always start with the condition of a random state. Pattern formation of a biological or animal surface does not necessarily start from such a random state, but rather from a regular state. Thus, clarifying the theoretical process of regular pattern formation has the possibility of revealing general features and the real biological process of pattern formation.

The purpose of this study was to clarify the theoretical process of pattern formation, starting from a regular state. We applied a two-dimensional discrete Walsh analysis to one-dimensional legal cellular automata.

The structure of this paper is as follows. In Section 2, we explain the method of analysis and data on one-dimensional legal cellular automata (CAs). In Section 3, we explain the data of the regular initial conditions. In Section 4, we briefly review the discrete Walsh analysis for calculating the symmetry and symmetropy of CA patterns. In Section 5, we describe and discuss the results and consider the symmetry relationships between the initial conditions and final patterns. Section 6 provides our conclusions.

2. Methods

The Discrete Walsh Analysis

We briefly outline the discrete Walsh analysis here (Figure 1). For details of the mathematical procedures, see previous studies [3,4,6]. The Walsh function $wal\left(r,x\right)$ of order $r$ and argument $x$ can be represented over the interval $0\le x<1$ as follows:

$$wal(r,x)={\prod }_{i=0}^{m-1}\text{sgn}\left[{\left(\text{cos}{2}^i\text{π}x\right)}^{ri}\right]$$

(1)

where $r_i=0 \text{or} 1$, $r={\sum }_{i=0}^{m-1}{r}_i{2}^i$, and $m$ is the smallest positive integer such that $2^m>r$. Dyadic addition of non-negative integers r and s is defined as $r\oplus s={\sum }_{i=0}^f\left|r_i-s_i\right|2^i$, where $r={\sum }_{i=0}^f{r}_i{2}^i$ and $s={\sum }_{i=0}^f{s}_i{2}^i$. Consequently, the product of the two Walsh functions is given by $wal\left(r,x\right)wal\left(s,x\right)=wal(r\oplus s,x)$. From this calculation, the Walsh function can be shown to form an orthonormal set. In this case, we can define a Walsh transform, similar to a Fourier transform.

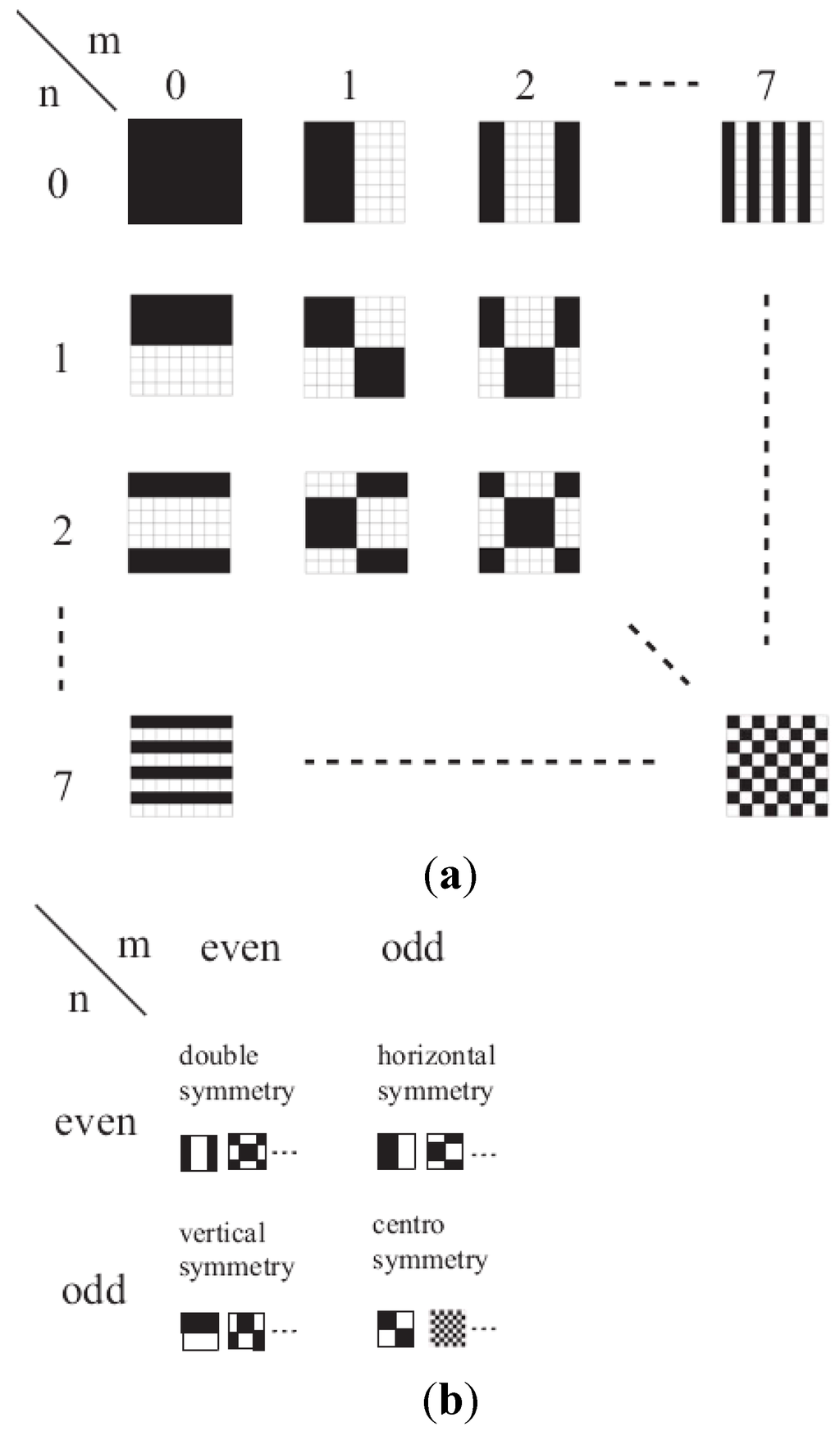
Figure 1. (a) Examples of the two-dimensional discrete Walsh functions for $m=n=8$. Black represents +1, and white represents –1; and (b) four types of symmetry in terms of the discrete Walsh function.

Figure 1. (a) Examples of the two-dimensional discrete Walsh functions for $m=n=8$. Black represents +1, and white represents –1; and (b) four types of symmetry in terms of the discrete Walsh function.

The two-dimensional discrete Walsh function can be represented in matrix form as $\left[W_{mn}\left(i, j\right)\right]$, where $W_{mn}\left(i, j\right)$ is the amount of the (m,n)th -order Walsh function in the ith row cell in the jth column.

This pattern can be written as $\left[x_{ij}\right]$, where $x_{ij}$ is the amount of the gray level in the $i^{th}$ row cell in the jth column and $i,j=0,1,\dots ,N-1.$ If just two gray levels exist, for example, “black” and “white”, then $x_{ij}$ is typically represented by 1 and 0, respectively (Figure 1a). The two-dimensional discrete Walsh transform of the pattern $\left[x_{ij}\right]$ is given by:

$$a_{mn}=\frac{1}{N^2}{\displaystyle \sum }_{i=0}^{N-1}{\displaystyle \sum }_{j=0}^{N-1}{x}_{ij}{W}_{mn}\left(i, j\right)$$

(2)

where $m,n=0,1,\dots ,N-1.$ The functions $a_{mn}$ and ${\left(a_{mn}\right)}^2$ are the two-dimensional Walsh spectrum and power spectrum, respectively.

The Walsh power spectrum can be normalized as follows:

$$P_{mn}=\frac{{\left(a_{mn}\right)}^2}{K}$$

(3)

where $K={\sum }_{m=0}^{N-1}{\sum }_{n=0}^{N-1}{\left(a_{mn}\right)}^2-{\left(a_{00}\right)}^2$. In this case, we obtain:

$${{\displaystyle \sum }}^{\text{}}{P}_{mn}=1$$

(4)

where the sum is taken over all ordered pairs $\left(m,n\right)$ for $0\le m, n\le N-1$, except for $\left(m,n\right)=\left(0,0\right)$.

The spatial pattern is considered as an information source, consisting of dot patterns. The dot patterns emitted from the source are assumed to occur with the corresponding probabilities given by Equation (4).

Next, we consider the information entropy resulting from the symmetry of the pattern. Because the two-dimensional Walsh functions can be easily divided into four types of symmetry (Figure 1b), Equation (4) can be rewritten as:

$${\displaystyle \sum }_{i=1}^4{P}_i=1$$

(5)

where vertical symmetric component:

$$P_1={\displaystyle \sum }_{m=\text{even},n=\text{odd}}{P}_{mn}$$

(6)

horizontal symmetric component:

$$P_2={\displaystyle \sum }_{m=\text{odd},n=\text{even}}{P}_{mn}$$

(7)

centro symmetric component:

$$P_3={\displaystyle \sum }_{m=\text{odd},n=\text{odd}}{P}_{mn}$$

(8)

and double symmetric component:

$$P_4={\displaystyle \sum }_{m=\text{even},n=\text{even}}{P}_{mn}$$

(9)

When the spatial pattern is regarded as an information source consisting of four types of symmetry, the corresponding probabilities are given by Equations (6)–(9). Applying the entropy function from information theory to these four symmetric components, we obtain:

$$S=-{\displaystyle \sum }_{i=1}^4{P}_i{\text{log}}_2{P}_i$$

(10)

As shown in Equations (5) and (10), $S$ ranges from 0 to 2 bits. Since this entropy relates to the symmetry, it is called the “symmetropy” [6]. The symmetropy can be considered as a quantitative and objective measure of symmetry. If the amount of a certain component is larger than the amounts of the other three components, then the pattern is rich in symmetry related to the particular component. In this case, Equation (10) shows that $S$ decreases. Conversely, if the amounts of the four components are almost equal to one another, then the pattern is poor in symmetry, and $S$ increases. Previous studies have concentrated on symmetry [4]. Following this idea, in this study, we measured the symmetry of the initial condition and the final pattern to examine the effects on final patterns of the initial condition of symmetry in CA patterns.

3. Calculations

For simplicity, this paper uses only “classical” CAs according to the Wolfram classification [7]; that is, the one-dimensional legal CA that obeys the 32 possible legal totalistic rules. The totalistic rules involve nearest and next nearest neighbors, and each cell has two possible colors: white (0) or black (1). In addition, because the total number of neighborhoods of five cells is equal to 2⁵, we can obtain the 32 possible legal totalistic rules. Wolfram [7,8] discovered that, although the patterns obtained with different rules differed in detail, they appeared to fall into four qualitative classes:

• Class I: fixed point (rules 0, 4, 16, 32, 36, 48, 54, 60, and 62) (Figure 2a).
• Class II: periodic (rules 8, 24, 40, 56, and 58) (Figure 2b).
• Class III: chaotic (rules 2, 6, 10, 12, 14, 18, 22, 26, 28, 30, 34, 38, 42, 44, 46, and 50) (Figure 2c).
• Class IV: complex (rules 20, 52) (Figure 2d).

Figure 2. Examples of final patterns in each class. (a) is an example of Class I, (b) of Class II, (c) Class III, and (d) is an example of Class IV.

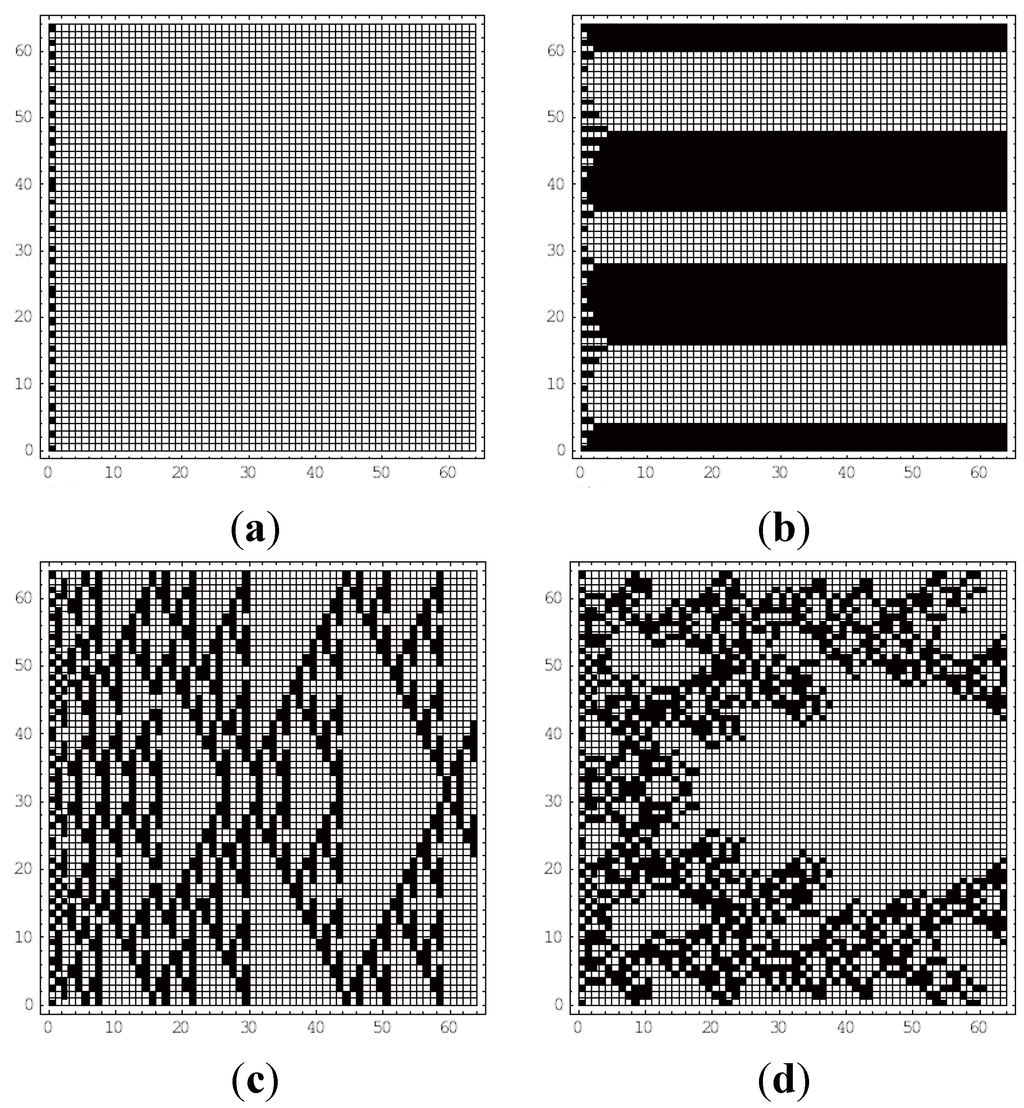
Figure 2. Examples of final patterns in each class. (a) is an example of Class I, (b) of Class II, (c) Class III, and (d) is an example of Class IV.

In this paper, we do not use all codes in class I because the patterns are trivial. We measure the initial condition (2⁶ × 1) and the final pattern. The number of cells is 2⁶ × 2⁶ because, to measure the number of symmetries, this number of cells is the minimum needed [4]. In the present study, we can use only two kinds of initial condition, horizontal symmetry and double symmetry, because we consider n = 2 in the discrete Walsh function W_mn (as in Figure 3).

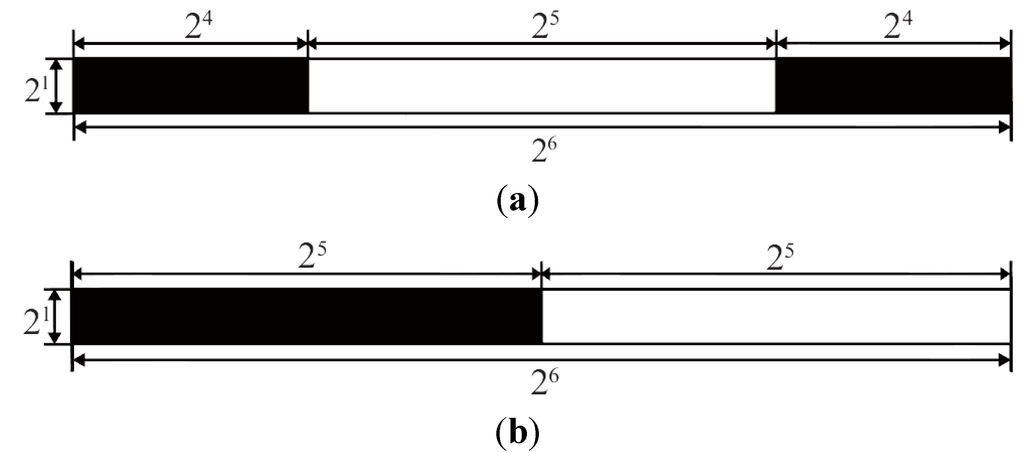
Figure 3. An example of initial symmetry. (a) Double Symmetry is one example of $D{S}_0$, and (b) Horizontal Symmetry is one example of $H{S}_0$. In this study, the initial condition was limited to n = 2 because 2¹ = 2 = n. Thus, (a) shows the case of m = even, and (b) shows the case of m = odd.

Figure 3. An example of initial symmetry. (a) Double Symmetry is one example of $D{S}_0$, and (b) Horizontal Symmetry is one example of $H{S}_0$. In this study, the initial condition was limited to n = 2 because 2¹ = 2 = n. Thus, (a) shows the case of m = even, and (b) shows the case of m = odd.

First, we run two types of regular initial conditions; the horizontal symmetry with 32 conditions, abbreviated as $H{S}_0$, and the double symmetry with 31 conditions, abbreviated as $D{S}_0$. Then, under each initial condition, the amounts of symmetry were averaged for each class. We compared this result with the random initial condition in [4], abbreviated as $R{a}_0$. Then, for each initial condition, we compared the relationship between the amount of symmetry in the initial condition and that in the final pattern. The method can be extended to 2D cellular automata, but requires a large number of analysis.

4. Results

4.1. Class

Figure 4 shows the amount of symmetropy for the three initial conditions ($R{a}_0$, $D{S}_0$ and $H{S}_0$) and the amount of symmetropy in each initial condition for the final patterns. The results show that under all initial conditions, the numbers of symmetries of the CA patterns correspond to three qualitative classes of CAs, identified as Classes II, III, and IV, according to Wolfram’s original classification [7,8]. Additionally, the result of the measurement of symmetropy under regular and random initial conditions shows a relational expression: Class II < Class IV < Class III. In all classes, the amount of symmetropy under $R{a}_0$ is larger than that under $D{S}_0$ and $H{S}_0$. In $R{a}_0$, the amount of symmetropy of all classes decreased as time passed. In contrast, in $D{S}_0$ and $H{S}_0$, the amount of symmetropy of all classes increased as time passed. Thus, the final patterns of the regular initial condition ($D{S}_0$ and $H{S}_0$) are more regular than those of the random initial conditions ($R{a}_0$).

4.2. Four Types of Symmetry

Figure 4 shows increases or decreases in the amount of symmetry for four kinds of symmetries in initial conditions and in final patterns. In $H{S}_0$, Classes II, III, and IV have all of the four kinds of symmetries: vertical symmetry, horizontal symmetry, centro symmetry, and double symmetry. However, in $D{S}_0$, Classes II, III, and IV have only two kinds of symmetries: vertical symmetry and double symmetry (Figure 4).

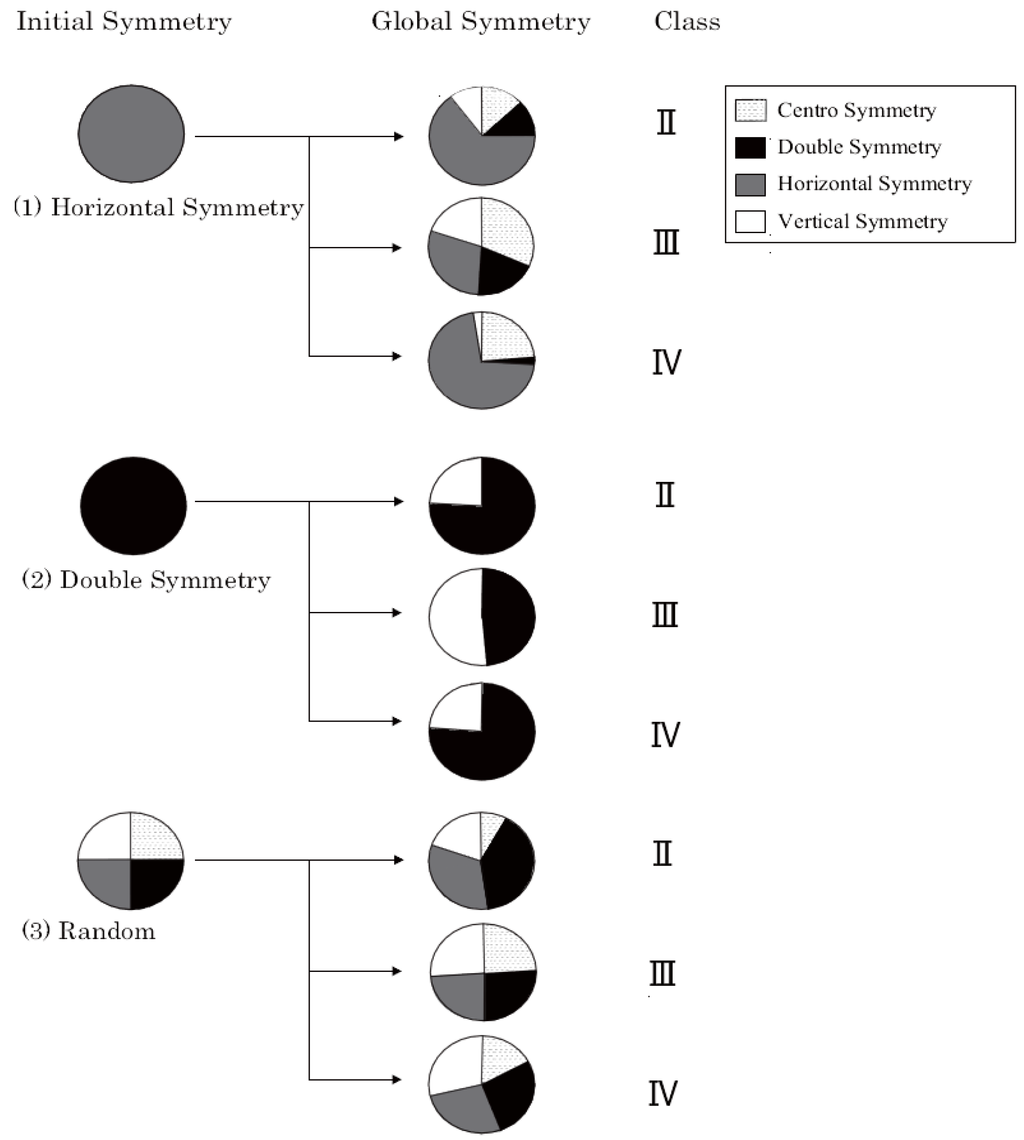
Figure 4. Pie charts of the three types of initial condition ($H{S}_0$, $D{S}_0$ and $R{a}_0$). For $H{S}_0$ and $R{a}_0$, all classes have all four types of symmetry: vertical symmetry, horizontal symmetry, centro symmetry, and double symmetry. In contrast, $D{S}_0$ with all classes had two types of symmetry: vertical symmetry and double symmetry. Regarding vertical symmetry and double symmetry, the relational expression was $H{S}_0$ < $R{a}_0$ < $D{S}_0$, and regarding horizontal symmetry and centro symmetry, it was $D{S}_0$ < $R{a}_0$ < $H{S}_0$.

Figure 4. Pie charts of the three types of initial condition ($H{S}_0$, $D{S}_0$ and $R{a}_0$). For $H{S}_0$ and $R{a}_0$, all classes have all four types of symmetry: vertical symmetry, horizontal symmetry, centro symmetry, and double symmetry. In contrast, $D{S}_0$ with all classes had two types of symmetry: vertical symmetry and double symmetry. Regarding vertical symmetry and double symmetry, the relational expression was $H{S}_0$ < $R{a}_0$ < $D{S}_0$, and regarding horizontal symmetry and centro symmetry, it was $D{S}_0$ < $R{a}_0$ < $H{S}_0$.

In $D{S}_0$, two kinds of symmetries, double symmetry and vertical symmetry, developed globally in the final formations. The design developed by $D{S}_0$ has a complicated pattern that lined up with a regular pattern (Figure 5a,b). Development was accompanied by a large increase in the amount of vertical symmetry. Thus, vertical symmetry contributed to the development of the spatial direction of the final patterns, whereas the double symmetry of $D{S}_0$ was preserved. In contrast, the design developed by $H{S}_0$ has all four kinds of symmetry (Figure 4), and the horizontal symmetry of $H{S}_0$ was not preserved.

Figure 5. Examples of final patterns with regular initial conditions. (a,b) belong to $D{S}_0$, and (c,d) belong to $H{S}_0$.

Figure 5. Examples of final patterns with regular initial conditions. (a,b) belong to $D{S}_0$, and (c,d) belong to $H{S}_0$.

4.3. The Ratio of Final Formation

The ratios of developed final patterns in each Class for ${\text{DS}}_0,{\text{Ra}}_0,{\text{and HS}}_0$ are shown in Table 1. The ratio of developed of final patterns is calculated by dividing the number of final pattern formation for each class (periodic or chaotic or complex) by a product of the number of initial condition (if $H{S}_0$: 32, if $D{S}_0$: 31) and the total number of classes (the sum rules of periodic, chaotic and complex: 23). For example, in the case of $H{S}_0$’s periodic in Table 1, the ratio of periodic is 12 is calculated from 89, 32, and 23 for the numbers of final pattern formation, initial condition, and the sum rules of periodic, chaotic and complex, respectively. The ratio of 12 is obtained as: 89(final patterns)/32rules/23(number of classes) × 100. According to Yamazaki et al. [4], $R{a}_0$ made final patterns using every rule and class; the ratio of formation was 100%. In contrast, for $D{S}_0\text{ and }H{S}_0$, the ratio of formation is less than 50% for all classes, and the developing final pattern ratios are 12% for Class II, 43%–44% for Class III, and 6% for Class IV (Table 1).

Table 1. The rate of final patterns of $D{S}_0$ and $H{S}_0$.

Class	Horizontal Symmetry	Double Symmetry	Random
Periodic	12	12	100×
Chaotic	43	44	100×
Complex	6	6	100×

Table 1. The rate of final patterns of $D{S}_0$ and $H{S}_0$.

Class	Horizontal Symmetry	Double Symmetry	Random
Periodic	12	12	100×
Chaotic	43	44	100×
Complex	6	6	100×

In all classes, the rate of the forming pattern of $R{a}_0$ was larger than that of $D{S}_0$ and $H{S}_0$. Comparing $D{S}_0$ with $H{S}_0$, the rate of forming patterns of class III was larger than that of class II and class IV; also, in each class, the two types of $D{S}_0$ and $H{S}_0$ had the same rates. Data indicated by asterisks are from [4].

5. Discussion

5.1. Class

For all classes, the amount of symmetry for $H{S}_0$ is larger than that for $D{S}_0$, and the final pattern formations of $D{S}_0$ have a higher hierarchy than $H{S}_0$; in contrast, the final pattern formations of $H{S}_0$ had more broken regularity than $H{S}_0$ (Figure 5c,d). This result is interpreted as the double symmetry having a higher amount of symmetry than the horizontal symmetry, because $D{S}_0$ has an axis of symmetry with space and time, whereas $H{S}_0$ has an axis of symmetry with time alone.

From the measurement of symmetropy, developed pattern formations of $H{S}_0$ and $D{S}_0$ have many types of symmetries that predominate as time passes. This result corresponds to the viewpoint of the Curie Symmetry Principle [4]. In contrast, the developed pattern formations of $R{a}_0$ show a situation in which one type of symmetry was predominant as time passed [4]; this result does not correspond to the viewpoint of the Curie Symmetry Principle [4]. Here, it is shown that the theoretical process of pattern formation reduced entropy and increased specific symmetry [4,5]; however, this process has been examined only from $R{a}_0$ [4,5]. In this study, the final pattern formations from regular initial conditions did not reduce entropy and increased specific symmetry. Thus, the Curie Symmetry Principle cannot be used to evaluate the proxy of pattern formation.

The final pattern formation of $D{S}_{0 }$ is composed of the same scale forms, to stand in a line (Figure 5a,b). The pattern formations are supposed to be affected by “iteration” of the base rules of CAs, and this result is correlated with the previous studies, such as [9] that shows that the Walsh transform allows one to compute the correlation between the inputs and the outputs of the iterations of a cellular automaton. Generally, as systems are put under greater stress, the observed states lose symmetry and gain in complexity (both spatial and temporal). However, as the systems are further stressed, states with more symmetries and more structures appear. Moreover, symmetries and chaos—patterns and disorder—can coexist naturally within the same simple mathematical framework [10]. In this study, the natural coexistence of symmetry and chaos (iteration of CAs) is found in the final pattern formation of $D{S}_0$; this means a simple mathematical framework of a one-dimensional legal cellular automata. Complicated structure pattern formations are developed by a simple model; thus, the quantity of information needed to describe an object may be more than that needed to prescribe it. Thus, under an initial condition of strong regularity, theoretical phenomena revealed occurrences of iterations with regularity, and the concepts of the theoretical phenomena could be helpful to interpret the process and the circumstance of biological patterns with higher-complexity structures.

5.2. Four Types of Symmetry

For all classes, the amount of symmetropy for $H{S}_0$ is larger than that for $D{S}_0$ (Figure 4), because $H{S}_0$ has four types of symmetry, while $D{S}_0$ has only two types (Figure 4). This result coincides with that the final pattern of $H{S}_0$, which shows steady state decay, and that of $D{S}_0$, which shows switching of a steady state to a hierarchy.

$H{S}_0$ has four types of symmetry: vertical, double, horizontal, and centro symmetries. $D{S}_0$ has only two types: vertical and double symmetries. These results show that double and vertical symmetries are the basic ones for forming patterns, and whether they form random or regular patterns is affected by the amount of horizontal and centro symmetries. The direction of each symmetry shows that (1) vertical symmetry has an axis of symmetry with space, (2) horizontal symmetry has an axis of symmetry with time, (3) double symmetry has an axis of symmetry with space and time, and (4) centro symmetry has an axis of symmetry with space and time. Thus, combinations of double and vertical symmetries, which are the basic symmetries of pattern forming, have axes of symmetries with space and time. In contrast, the combination of horizontal and centro symmetries is a supplemental one, for pattern formation. Thus, the basic and supplemental symmetries have balance with space and time. Additionally, the initial condition constrains the combination of symmetries (the analysis decided the symmetry direction): vertical and double symmetries versus horizontal and centro symmetries.

We compared the amounts of the four types of symmetries among $D{S}_0,R{a}_0,\text{and }H{S}_0$. The amount of vertical symmetry and double symmetry increased in the order $H{S}_0<R{a}_0<D{S}_0$, except for Class II’s vertical symmetry. Additionally, the amount of horizontal symmetry and centro symmetry increased in the order $D{S}_0<R{a}_0<H{S}_0$.

In regular and random initial conditions, Class III has equal amount of symmetries of the different types of symmetries, but Classes II and IV have different amounts. Here, we explain biological patterns from these results. The organisms’ developed pattern formations can select the amounts of two types of symmetry (horizontal and centro) according to the circumstances, because both horizontal and centro symmetries have symmetry axes related to “time”. Here, time is related to the future. Thus, the combination of symmetries with wide varieties, as in this study, may provide the opportunity for understanding how to develop pattern formation (heredity or circumstances), and may be able to manage pattern formation, and to predict the future.

5.3. The Ratio of Final Formation

The growth design formations are limited in $H{S}_0$ and $D{S}_0$, but there is no limit in $R{a}_0$ (Table 1). This means the variability of symmetries of $R{a}_0$ is larger than that of $H{S}_0$ and $D{S}_0$. The numbers of developed final pattern rules for $H{S}_0$ and $D{S}_0$ are almost equal in every class, because the numbers of initial conditions are almost the same; 32 for $H{S}_0$ and 31 for $D{S}_0$, and most of the $H{S}_0$ rules correspond to $D{S}_0$ ones.

The rules that did not develop final patterns under regular initial conditions need larger amounts and more symmetries. The ratio of rules developing final patterns to those with no developing final patterns was calculated for each Class (Table 1). The ratio of rules that developed final patterns under the regular initial condition decreased in the order of Class III, Class II, and Class IV. Thus, Class III does not need more of the amounts and types of symmetries, whereas Class IV requires much more in the way of amounts and many types of symmetries, and Class II requires moderate amounts and types of symmetry. We explain biological patterns from these theories. Class III is not influenced by circumstances, and allows easy development of final patterns, which means heredity. On the other hand, Class IV is influenced by circumstances, and Class II by circumstances and heredity. Animals having Class III biological patterns may select the circumstances by themselves, because their biological patterns are interpreted as genetic characteristics. The animals having Class IV biological patterns may adapt themselves to circumstances, because their biological patterns are interpreted as acquired characteristics. The animals having Class II biological patterns may be able to select a circumstance by themselves and may be able to adapt themselves to a circumstance, because their biological patterns are interpreted as random genetic characteristics and random circumstances. They may take an unplanned survival strategy.

Here, we discuss living animals. Although clams appear in Class III [11], their shell patterns are in heredity [12]. Additionally, the habitat of clams is decided by the height of ground level and drying time within 1 day, which has no relationship with pattern formation [13]. This might be supported by the hypothesis “The animals having Class III biological pattern formation may select circumstance by themselves, because their biological patterns are interpreted as genetic characters”. However, Neritina, a typical shellfish, appears in Classes II and IV [11]; their shell design pattern formation has been found along the structure of the growth lines [14]. Thus, Neritina may be affected by the circumstances around them. In addition, their shell patterns have been found to be of color bands [14]; thus, Neritina may have been affected by circumstance and heredity.

6. Conclusions

We examined the structure of one-dimensional legal cellular automata from the viewpoint of symmetry to reveal the rules of animals’ pattern generation. The following conclusions are derived. (1) Under all regular and random initial conditions, a relational expression, Class II <Class IV <Class III, was seen. In all classes, the pattern formation with regular initial conditions was more regular than that with random initial conditions. (2) We compared the pattern formation made with two types of regular initial conditions. The final pattern formations of $H{S}_0$, which have more broken regularity, have four types of symmetries, whereas that of $D{S}_0$ has only two types of symmetries, which are of a higher hierarchy. Both regular initial conditions show situations in which many types of symmetry predominated as time passed. We showed that when pattern formation develops, amounts of symmetries and types of symmetries do not always decrease. (3) We found that growth design formations have limited possibilities with regular initial conditions; the results of calculating the ratio of developing final patterns decreases in the order of Class III, Class II, and Class IV.