Computing with Colored Tangles
Abstract
:1. Introduction
1.1. What Is a Tangle Machine Computation?
- Idempotence: for all and for all . Thus, x cannot concoct any new information from itself.
- Reversibility: The map , which maps each color to a corresponding color , is a bijection for all . In particular, if for some and for some , then . Thus, the input x of a computation may uniquely be reconstructed from the output together with the program .
- Distributivity: For all and for all :This is the main property. It says that carrying out a computation on an output gives the same result as carrying out that computation both on the input x and also on the state y and then combining these as . In the context of information, this is a no double counting property [4].
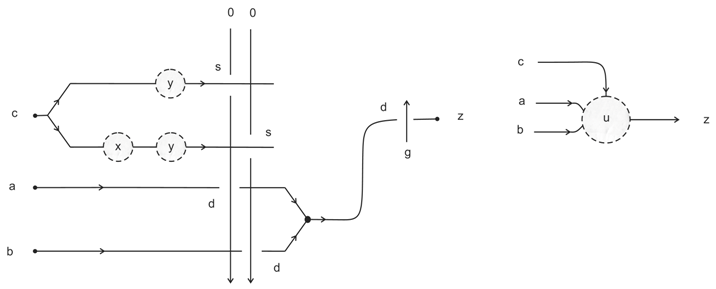
- Whereas the alphabet of a classical Turing machine is discrete (usually just zero and one and maybe two), the alphabet Q of a tangle machine can be any set, discrete or not. Two values of Q may be chosen to represent zero and one, while the rest may represent something else, perhaps electric signals.
- Whereas a Turing machine computation is sequential with each step depending only on the state of the read/write head and on the scanned signal, a tangle machine computation is instantaneous and is dictated by an oracle. Time plays no role in a tangle machine computation.
- A tangle machine computation may or may not be deterministic (colors may represent random variables and not their realizations), and it may or may not be bounded (contain a bounded number of interactions). Quandles and tangle machines are flexible enough to admit several different interpretations. In this paper, we use tangle machines to realize both logic gates (deterministic, composing perhaps unbounded computations) and interactive proof computations (probabilistic, bounded size).
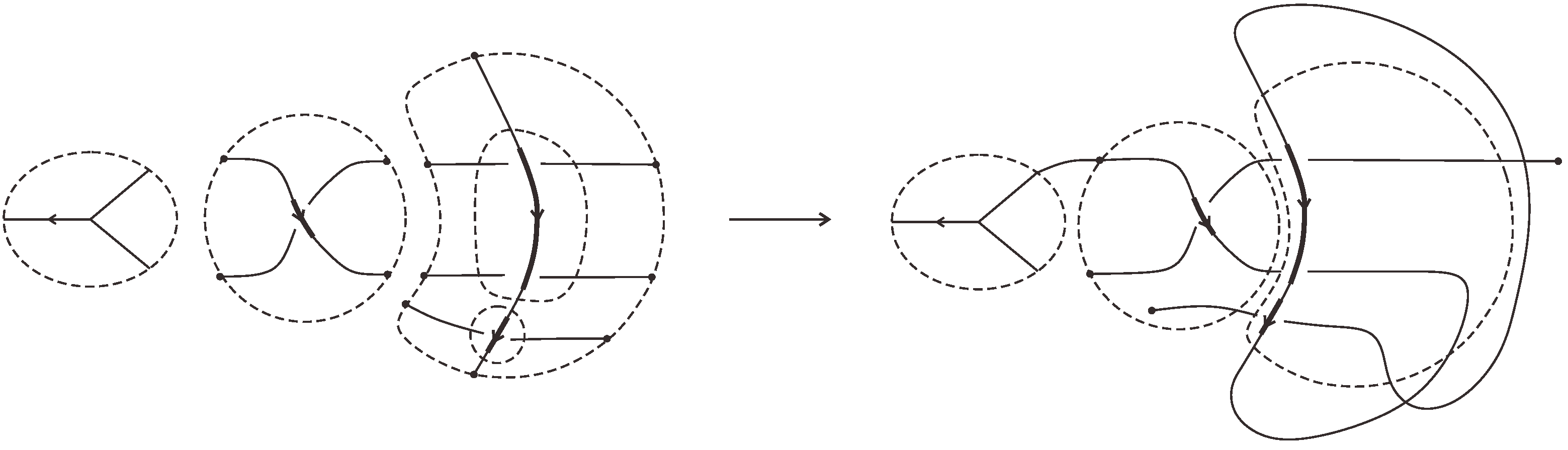
- A tangle machine is flexible. There is a natural and intuitive set of local moves relating bisimilar tangle machine computations (Section 10).
- A tangle machine representation is abstract. A tangle machine computation takes place on the level of information itself, with no reference to time. The axioms of a quandle have intrinsic interpretation in terms of the preservation and non-redundancy of information.
1.2. Results
1.3. Other Low Dimensional Topological Approaches to Computation
1.4. Contents of This Paper
2. Models of Computation
2.1. Turing Machines
- Σ is a finite set of symbols called the alphabet, which contains a “blank” symbol.
- is a finite set of “machine states” with and being, respectively, the initial and final (halting) states.
- is a transition function.
2.2. Computable Functions and Decidable Languages
2.3. Interactive Proof
2.4. Probabilistically-Checkable Proofs
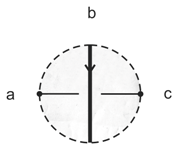
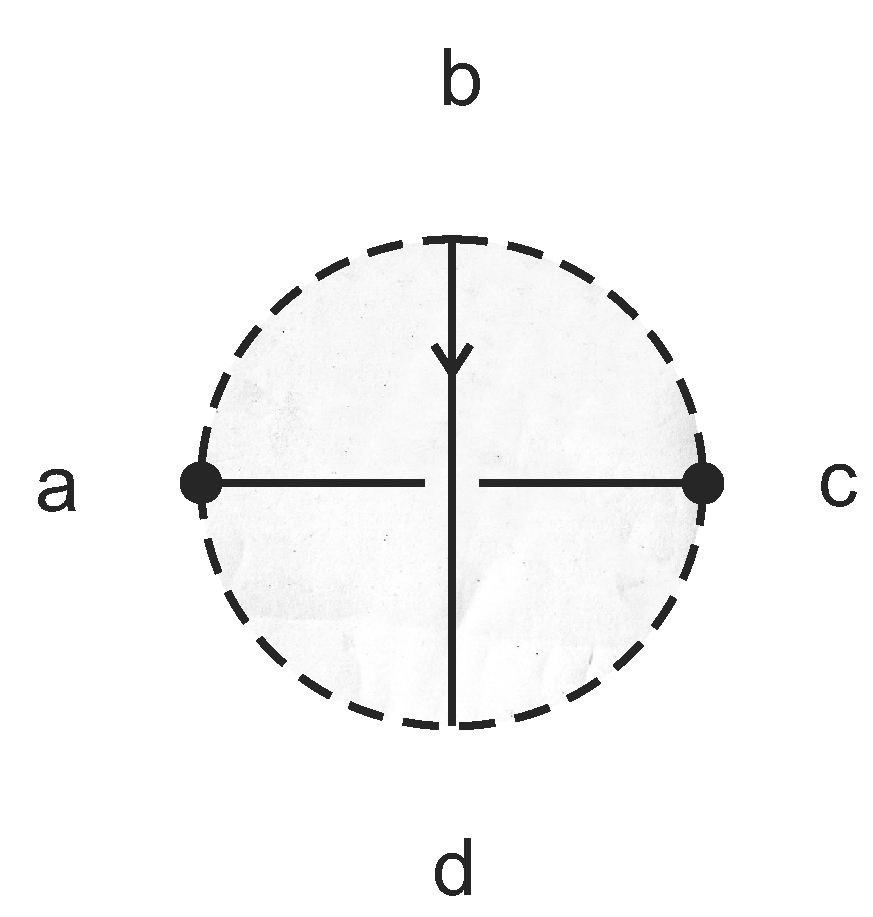
3. Tangle Machines
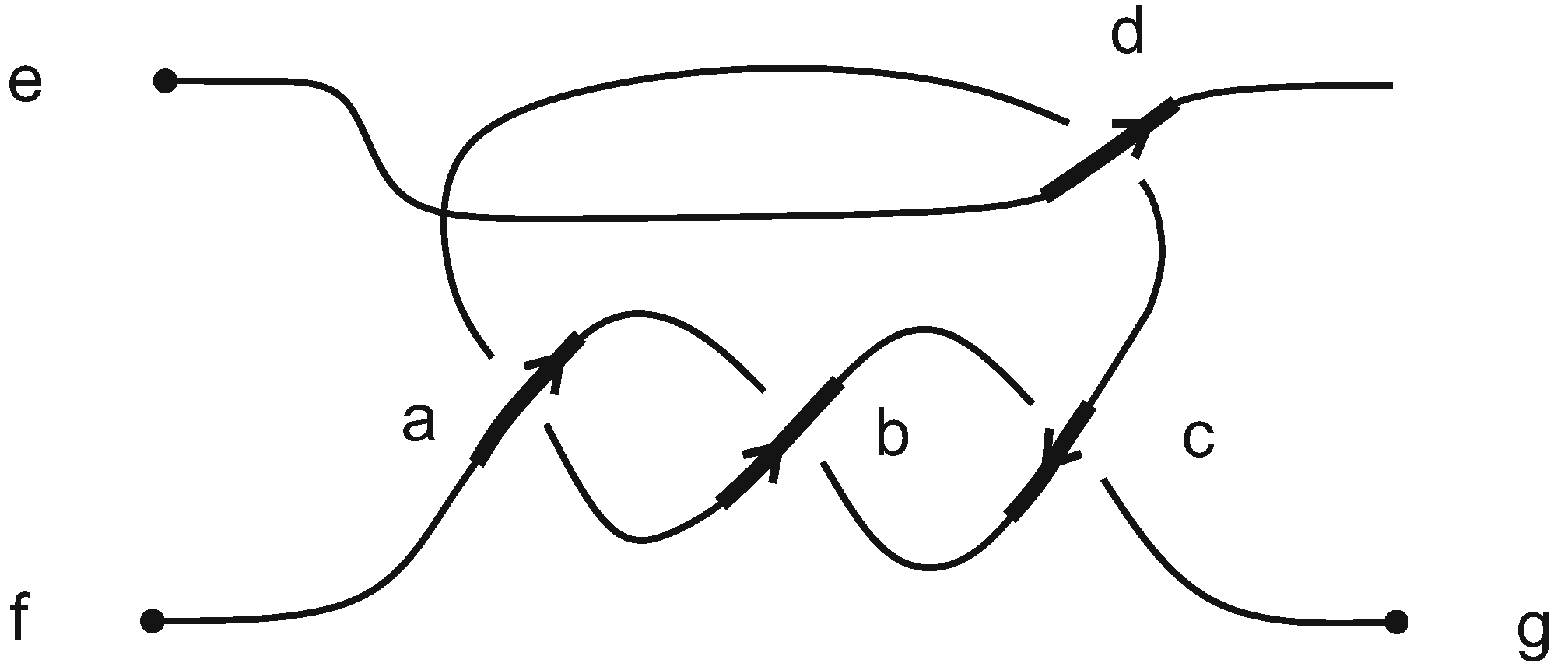
3.1. Without Colors

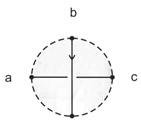
3.2. Colors
- Idempotence: for all and for all .
- Reversibility: The map , which maps each color to a corresponding color , is a bijection for all . In particular, if for some and for some , then .
- Distributivity: For all and for all :
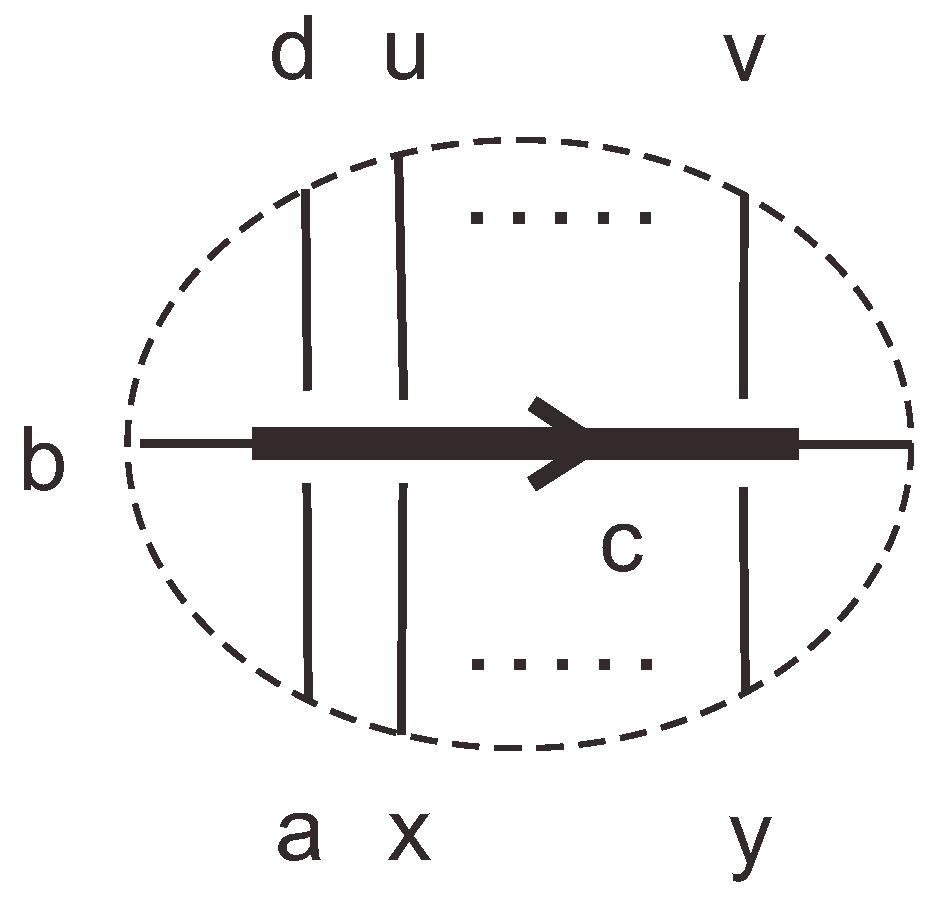
3.3. With Colors
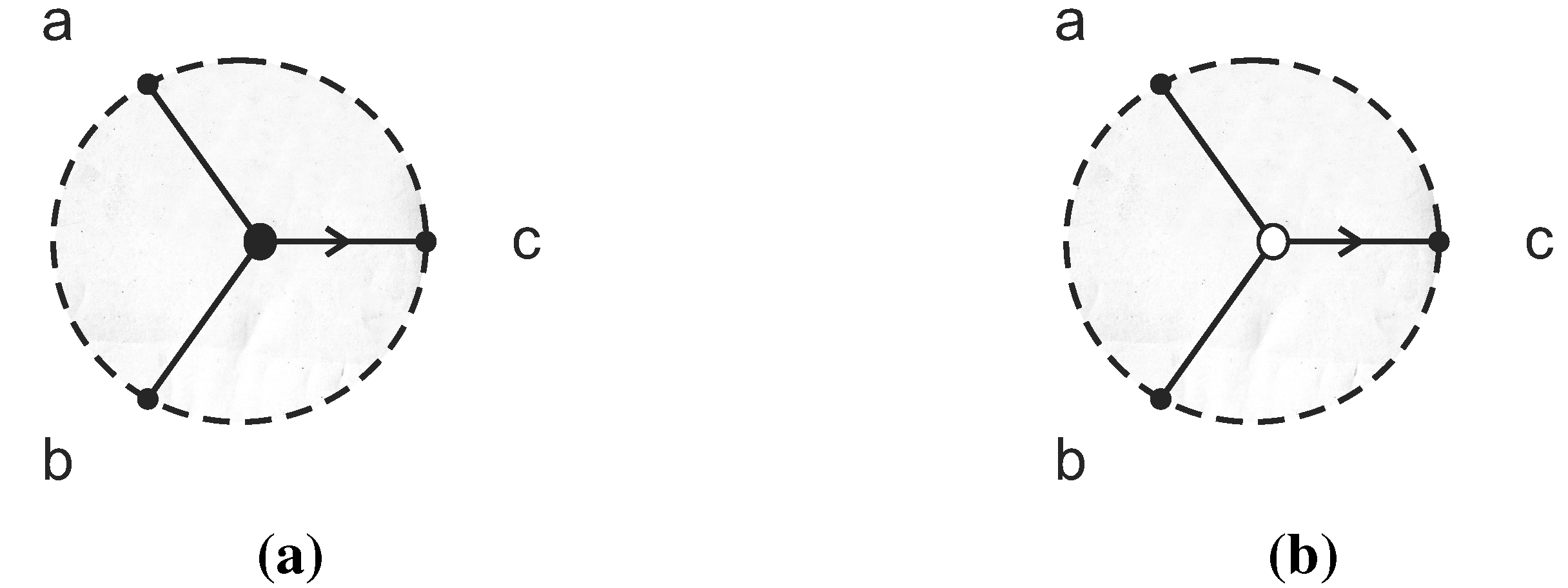
- 1.
- A choice of a set of input registers in M.
- 2.
- A choice of a set of output registers in M with .
- 3.
- A coloring ϱ of all agents in M (and an assignment of either max or min to each wye).
- 4.
- A coloring of all registers in .
- 5.
- A unique (oracle) determination of a coloring of all registers in . If does not uniquely determine , the computation cannot take place.
4. Tangle Machines Are Turing Complete
4.1. Quagma Approach

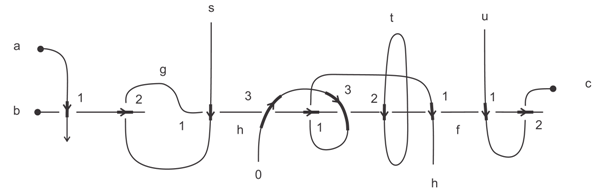
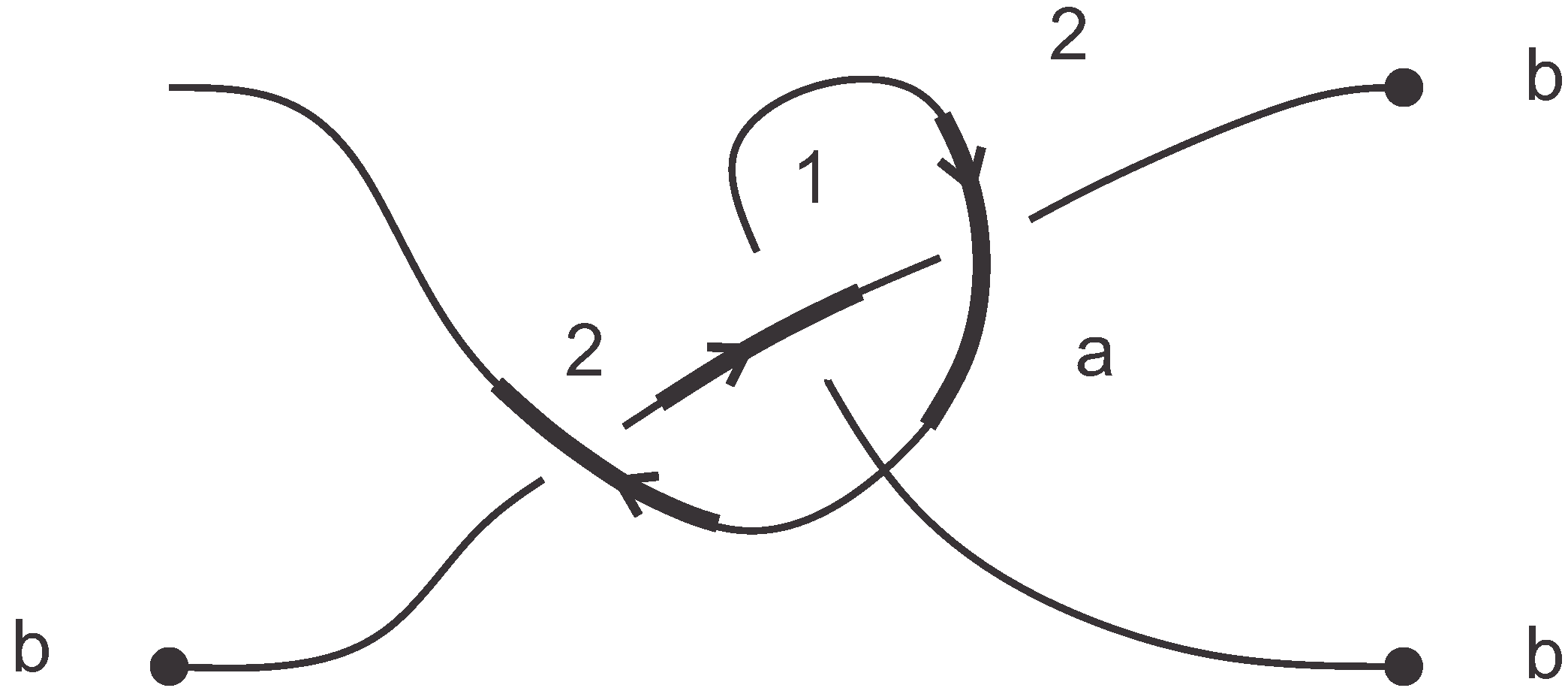
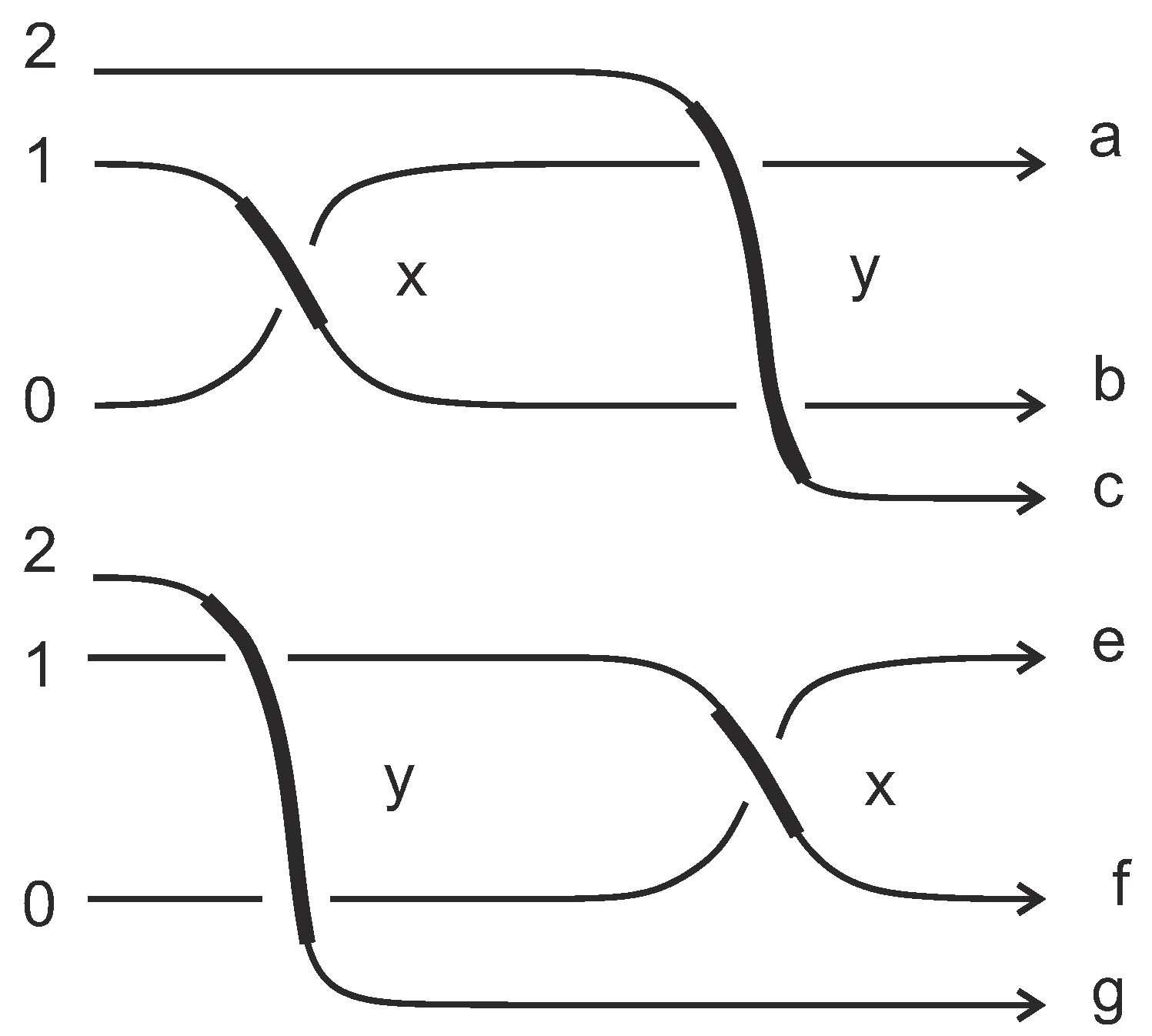
4.2. Wye Approach
4.3. Nonabelian Simple Group Approach
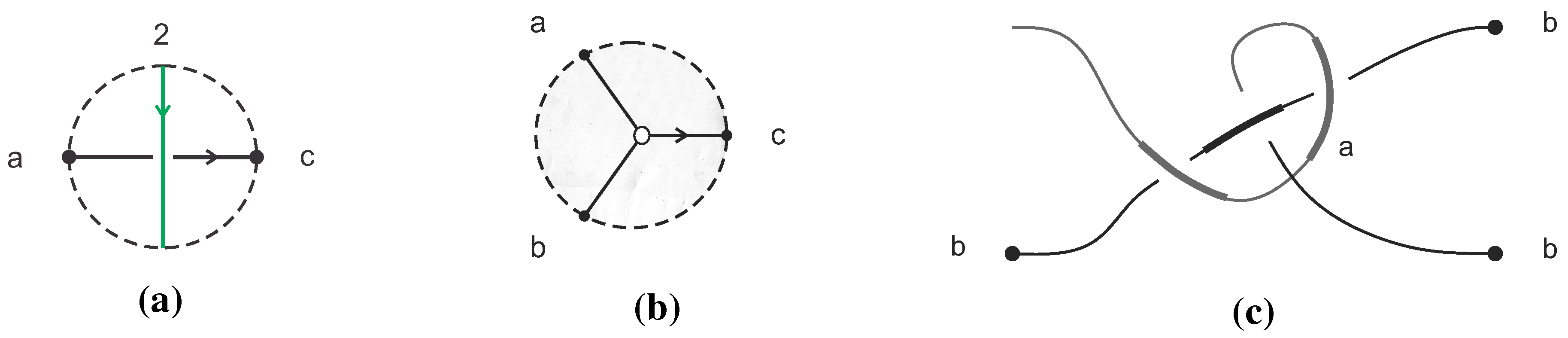
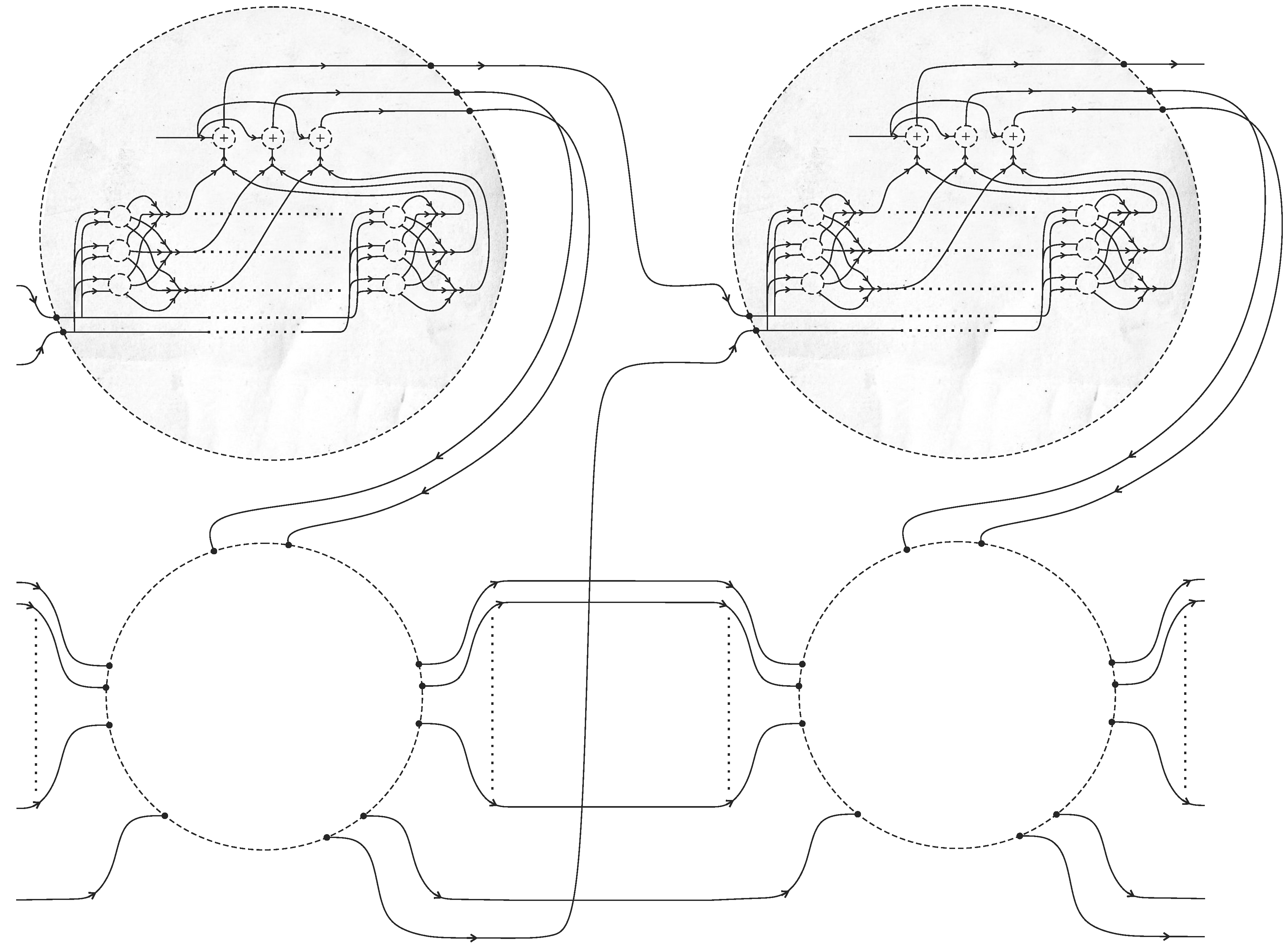
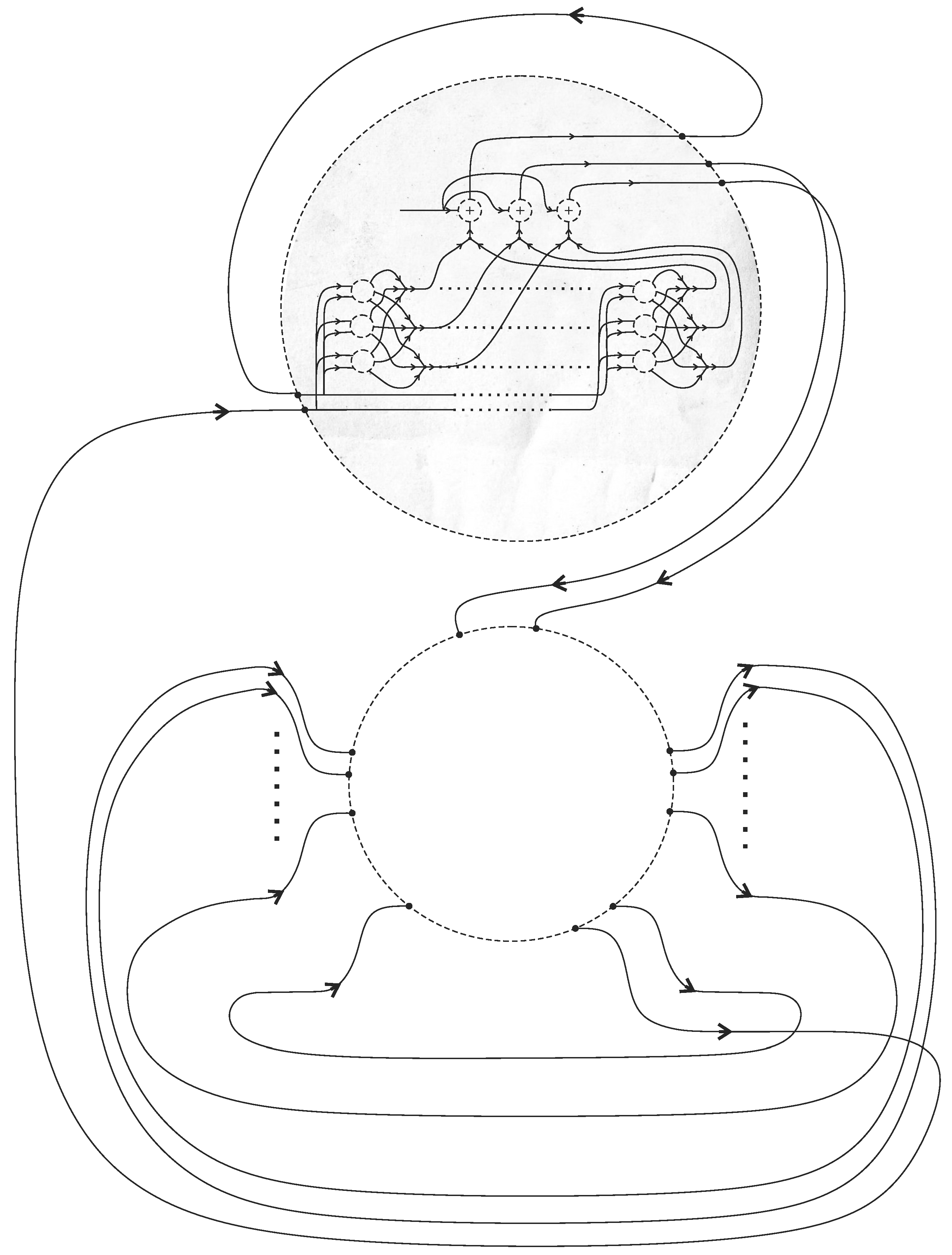
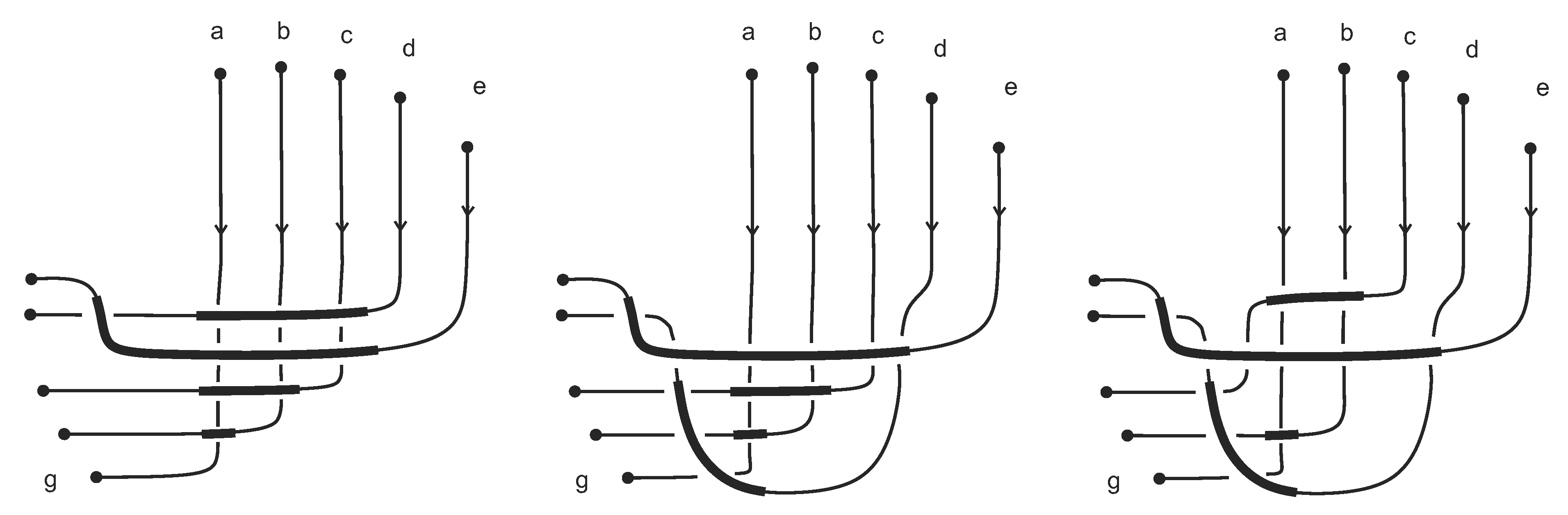
5. Turing Machine Simulation
5.1. Turing Tangle Machine
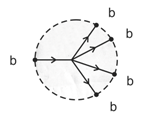
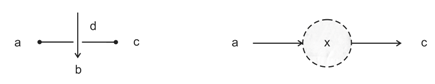
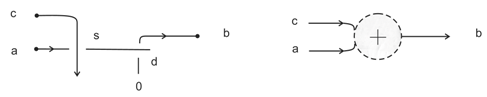
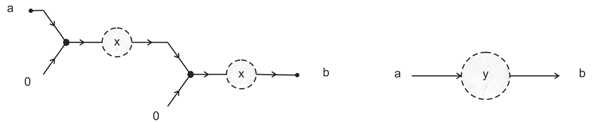
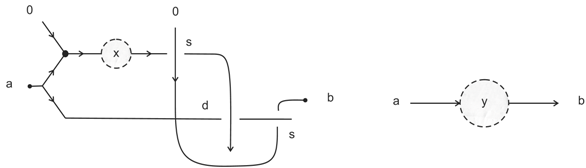
- Selector Depending on the color c of a control strand, either x or y emerges as the output, z. To be precise, if , and if .where s is an arbitrary constant whose value is greater than two.
- Mask-generating machine This sub-machine is shown in Figure 9. Its input registers are a register colored by an integer , called a pointer, and a sequence of colored registers together, called a mask. Its output registers are a register colored p, and one register colored zero for all other input colored registers, except for a single register colored one in the p-th position of the output.
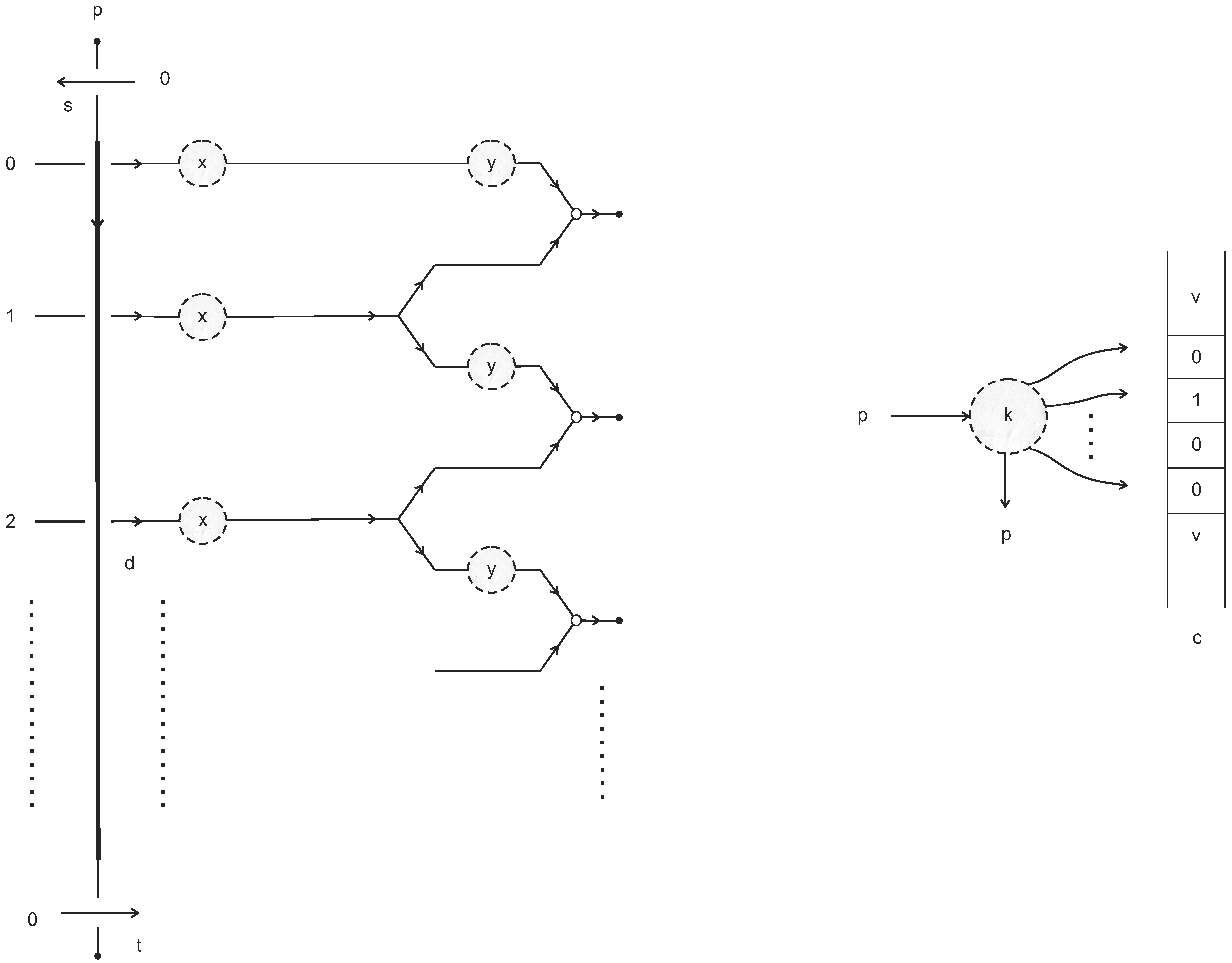
5.2. Finite Control

5.3. Memory Unit and One-Step Computation
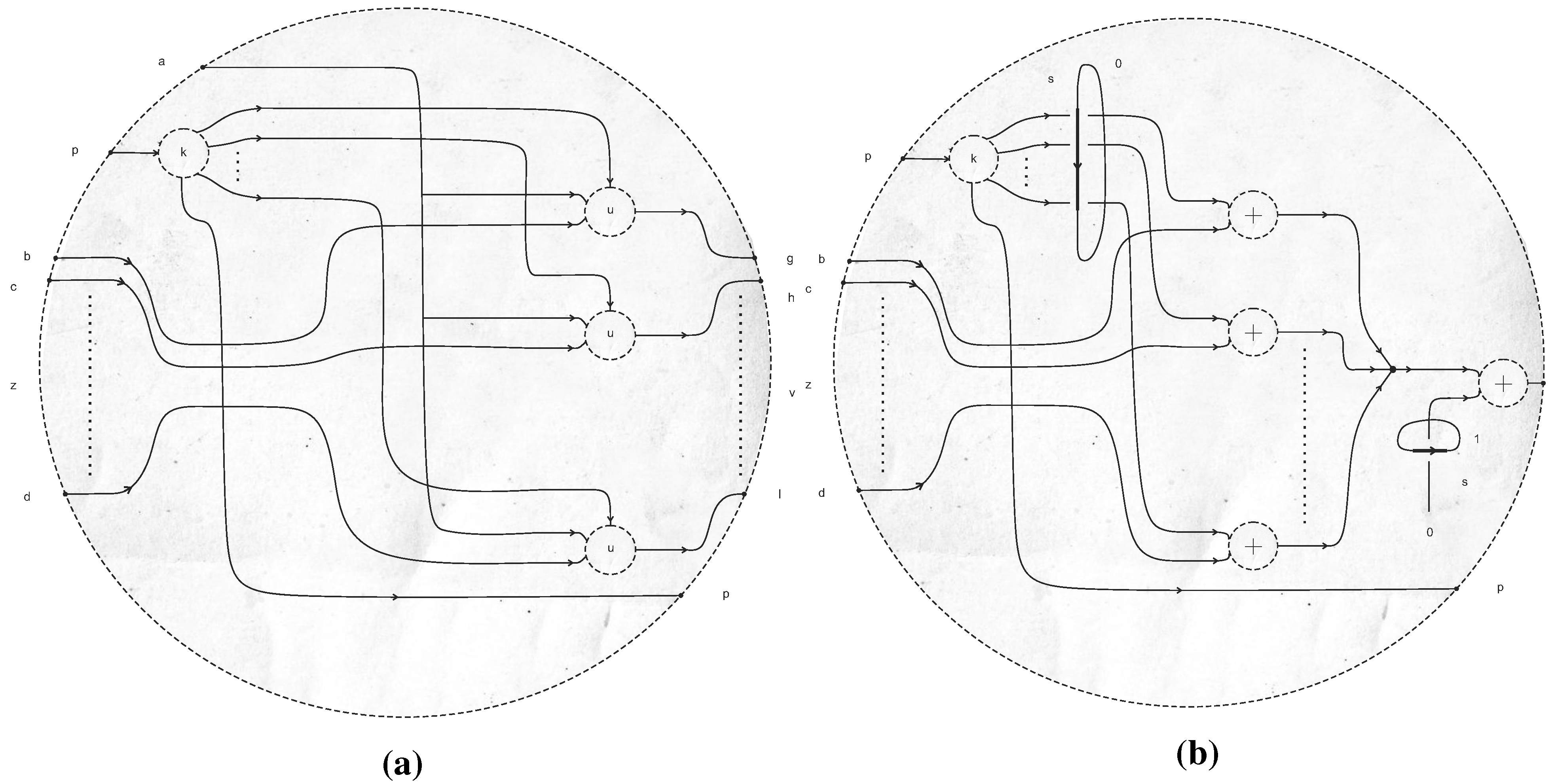
- An integer pointer register colored , indicating the current head position.
- A finite, possibly unbounded set of registers, each of which represents a single (memory) cell on a tape. These tape registers are colored .
- A pair of registers colored correspondingly by a pair instructions , where a denotes the symbol to be written in the current cell to which the head points (which is numbered ), and ϵ denotes the (possibly zero) increment to be added to , so that .
- The updated pointer .
- A finite, possibly unbounded set of registers whose colors have been all passed unchanged, except for a single cell whose content may have been modified.
- A strand colored by , the content of the cell to which the head points in its new location
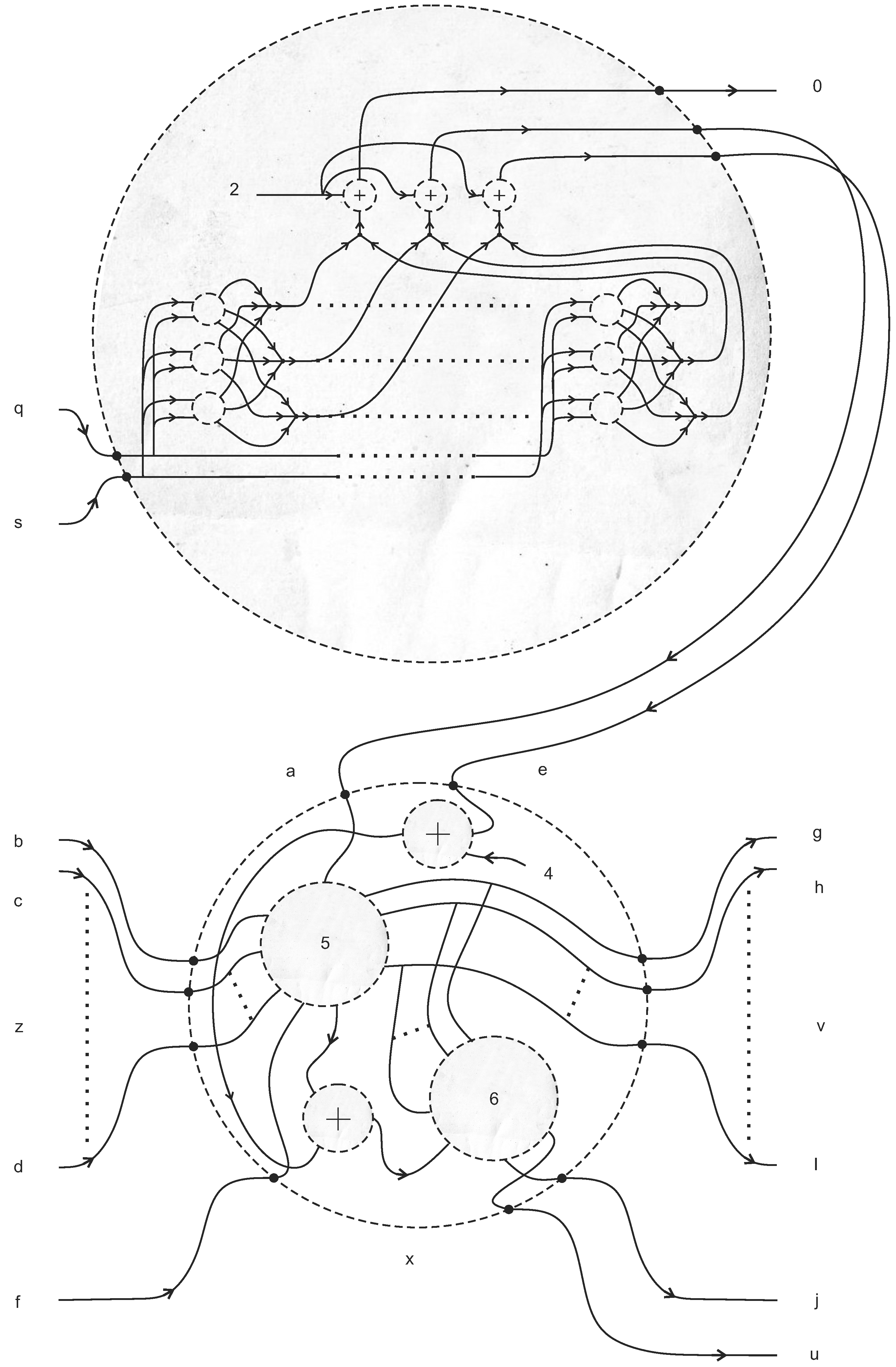
5.4. Halting
6. Interactive Proofs: Distribution of Knowledge by Deformation
6.1. Deformation of a Single Interaction
6.2. Statistics of Beliefs and Interactions
6.3. Expressive Power of a Network: The Class BraidIP
6.4. Braid of Beliefs
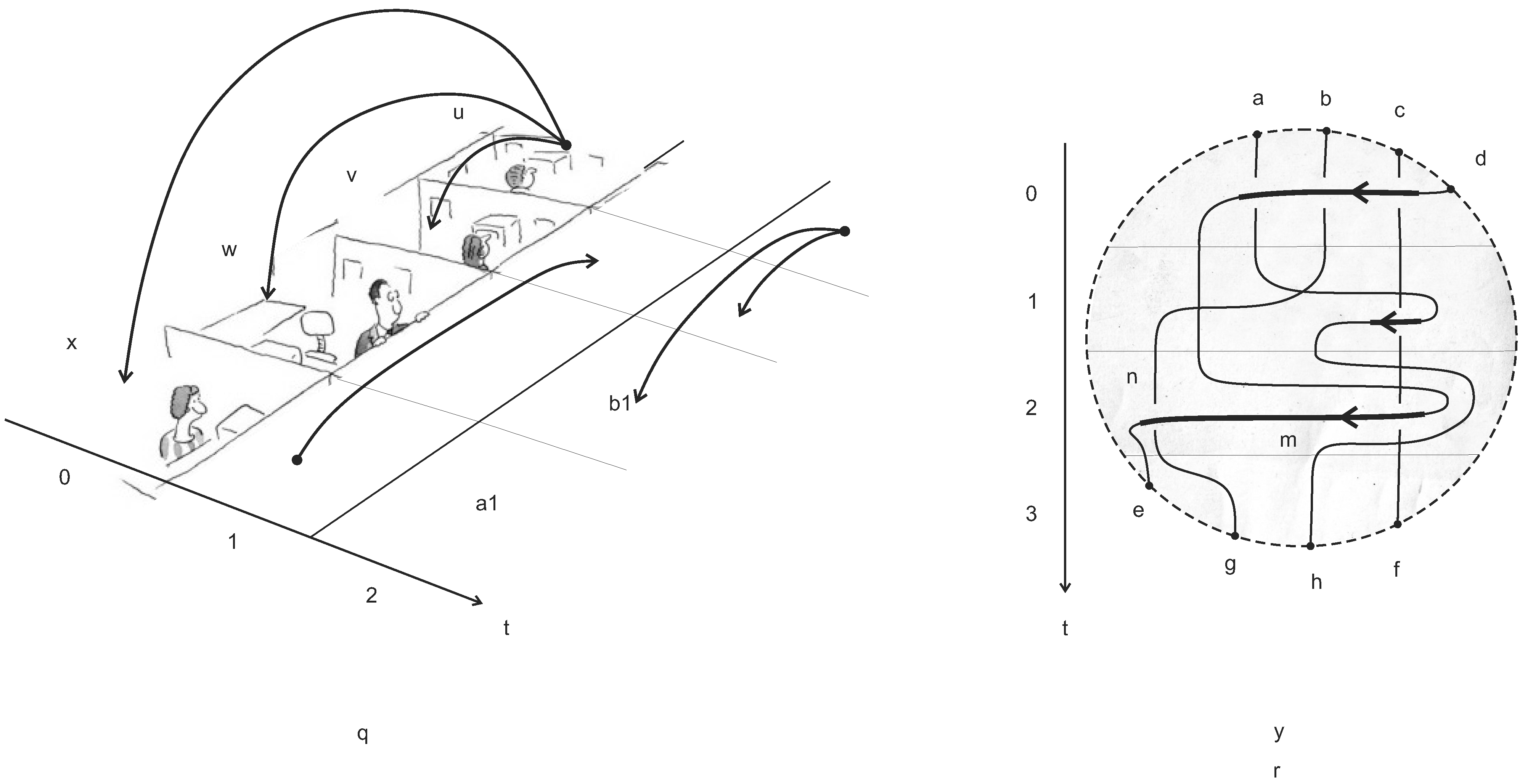
6.5. An Example

| Description | IP system | Deformed IP system |
| Participants | Verifier, prover | Many verifiers (patient), verifier (agent), prover |
| Verifier “state of mind” | Accept/reject | Belief true/false |
| Conclusion | Verifier decides accept/reject | If the two verifiers do not agree, then the patient may change her belief. |
| Completeness, soundness | c, s | cδ, sδ |
7. Deformation of an IP System
7.1. Two Approaches to Deform IP
7.1.1. Agent and Patient as a Single Verifier
7.1.2. Verifiers Communicating Through a Noisy Channel
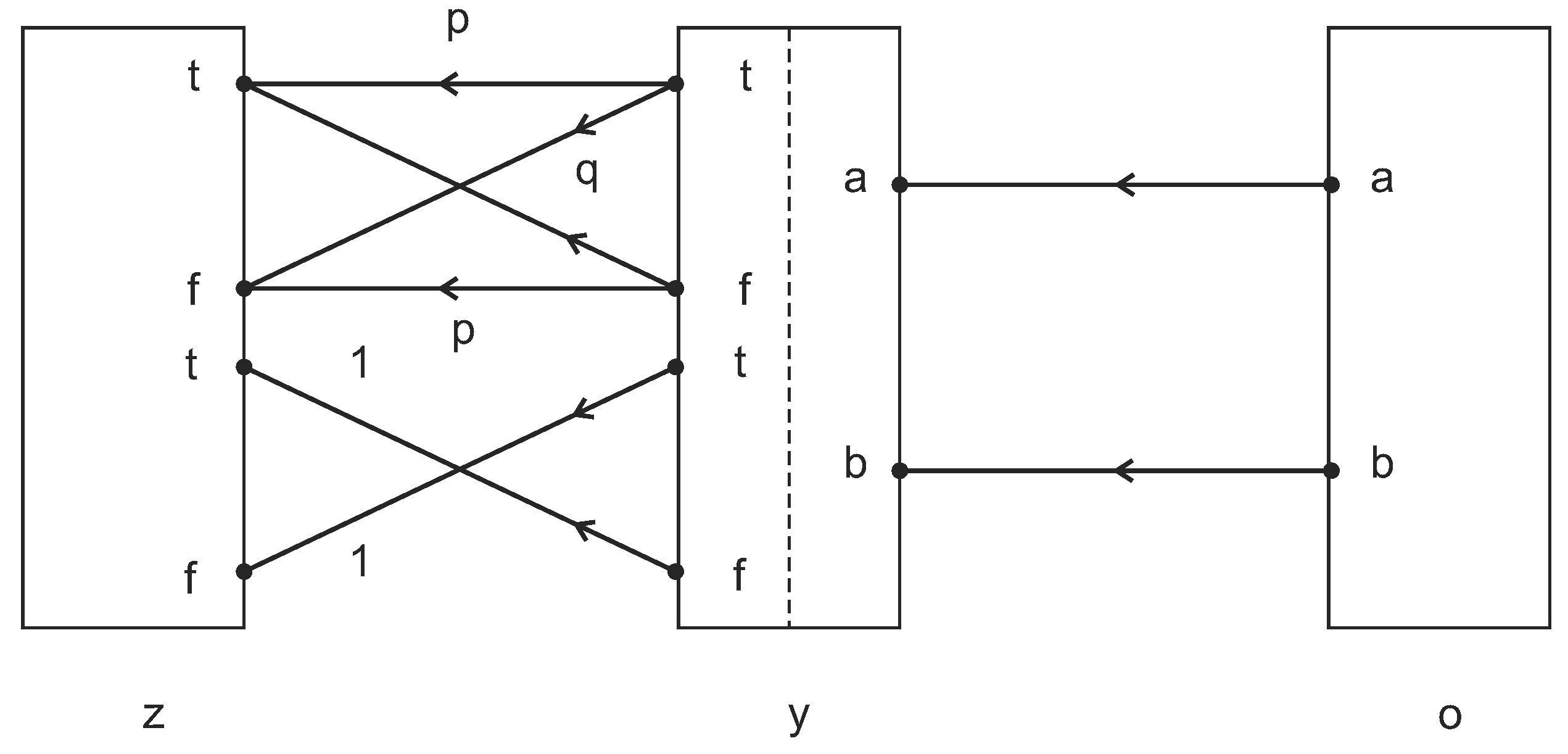
7.1.3. Further Metaphors for Deformed Interactions
7.2. Probabilistic Theorem Proving in Networks
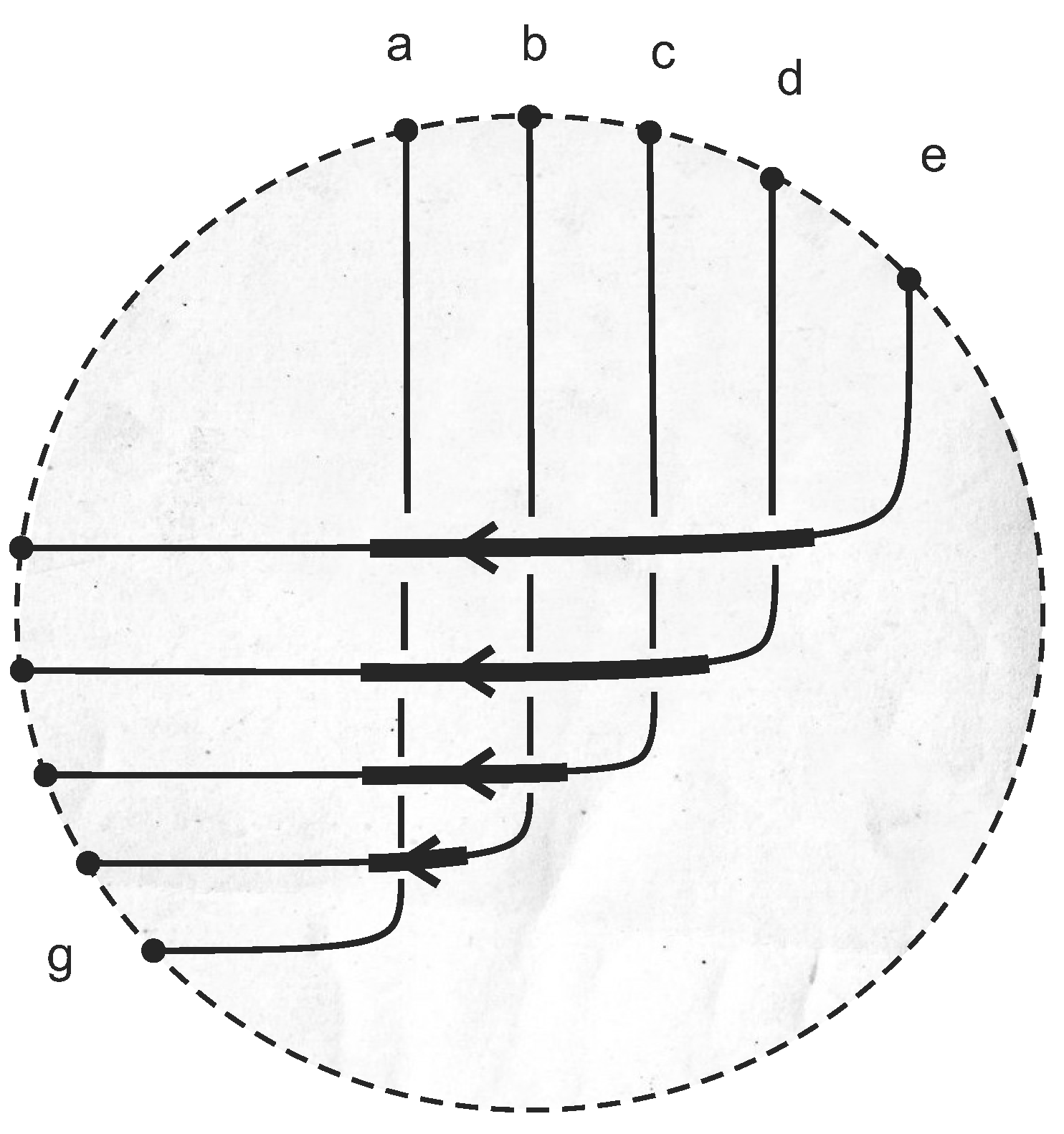
8. Efficient IP Strategies: Tangled IP
8.1. The Complexity Class TangIP
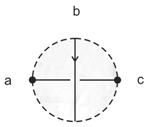
8.2. The Hopf–Chernoff Configuration

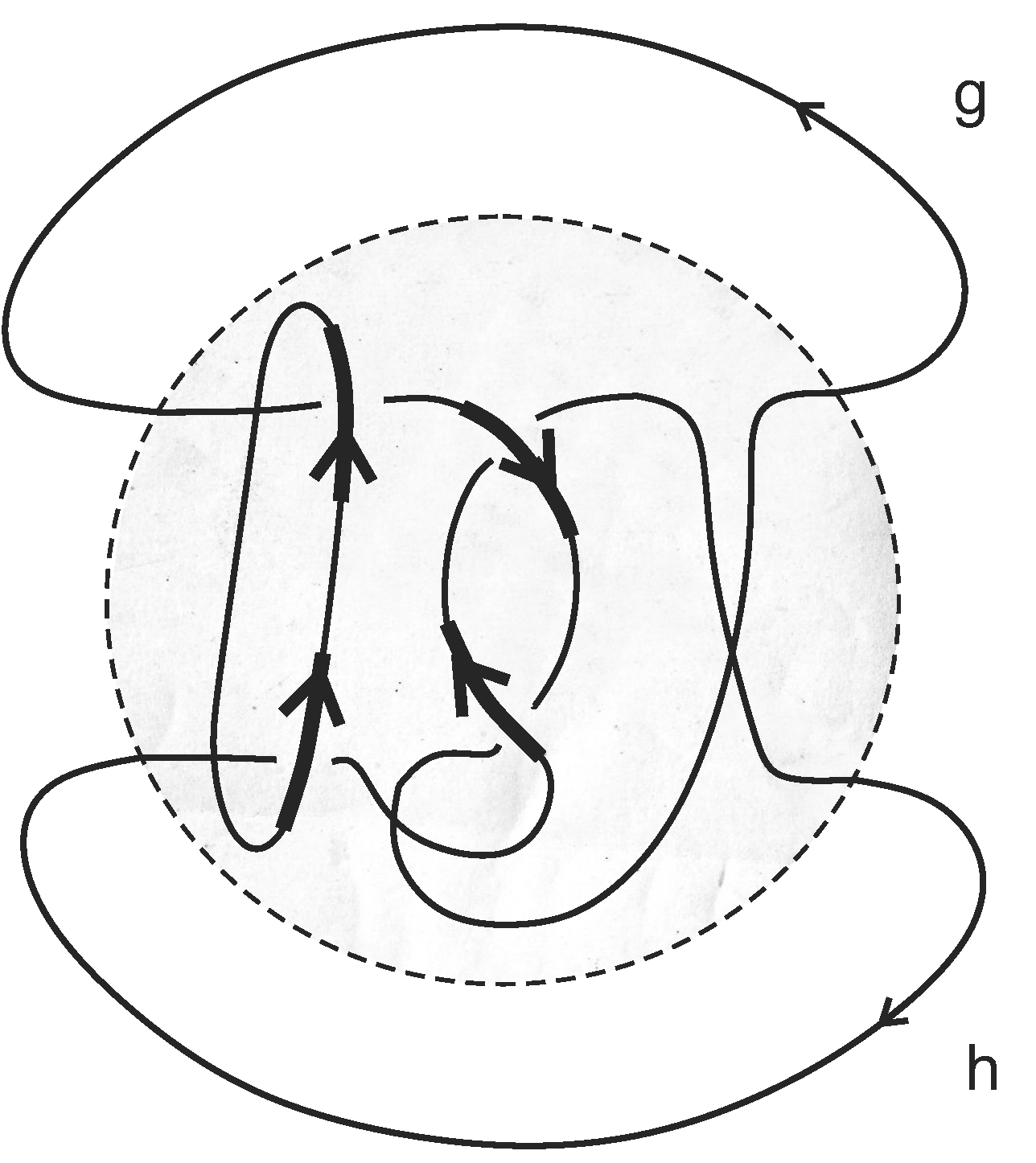
9. PCP Networks
- ∧⟶V flips a bit with probability .
- ∧⟶V flips a bit with probability δ.
- ∧ ⟶ V flips no bit.
- ∧ ⟶ V flips a bit.
9.1. A Better Than Classical PCP Verifier
- Choose input beliefs , , arbitrarily from . Assume , and fix δ.
- Let α be a Bernoulli distribution with parameter . Draw a belief from α for the top agent, and set the bottom agent to the negation of that belief. We color the bottom agent as , which equals α as a distribution, to diagrammatically signify what we are doing.
- Do the following for , where :
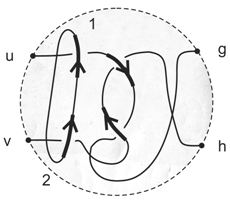
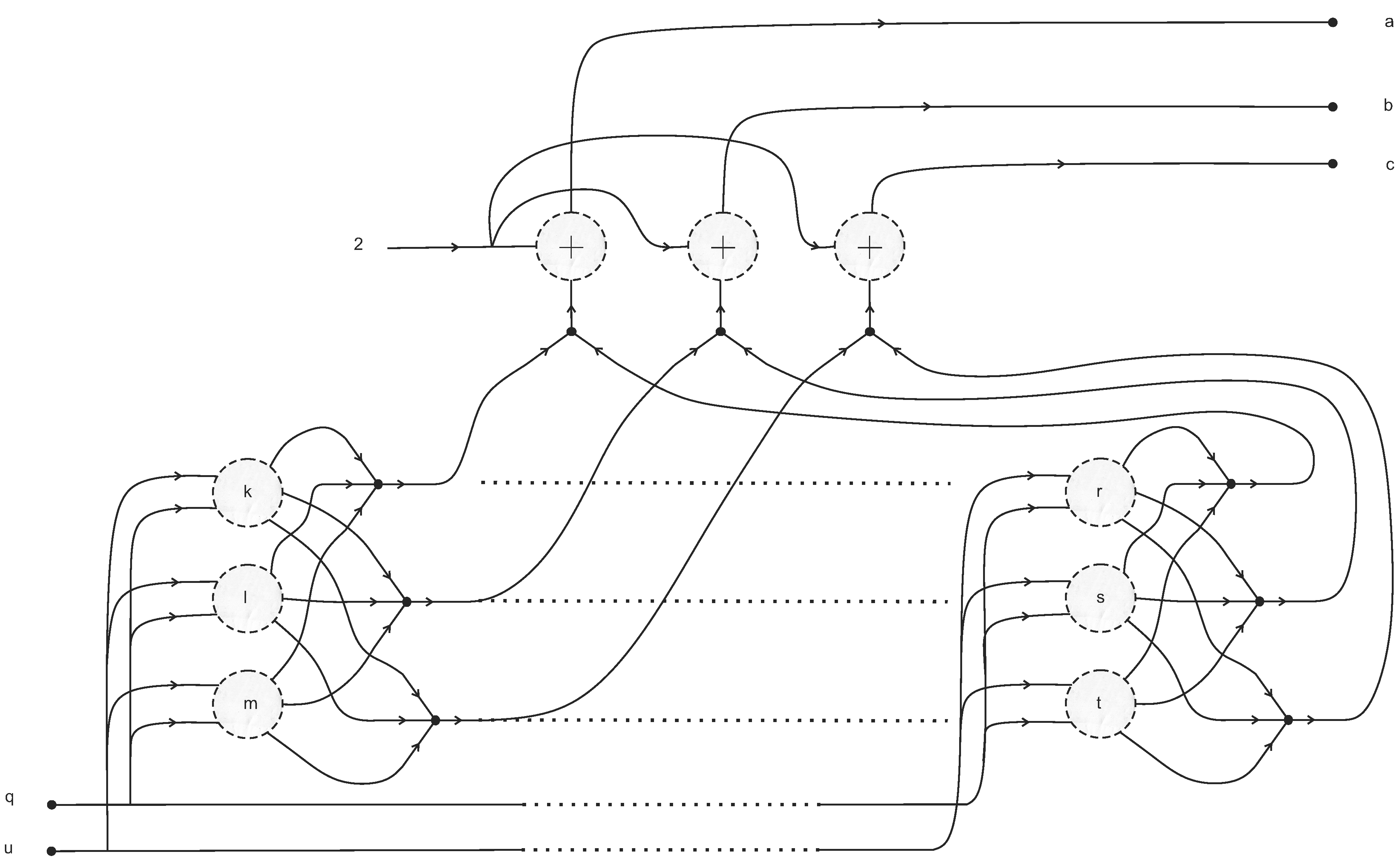
- Using the underlying deformed PCP verifier, perform the four interactions of the Hopf–Chernoff configuration to propagate the beliefs of the two verifiers from to according to the diagram below.
- Set , .
- If the patient belief in the output , then return ; otherwise, return .
- Completeness Assume that , and note that as , so does . In the limit where , note that by Equation (41), the Hopf–Chernoff swaps the beliefs α and , such that always and . Thus, Step (iv) of the algorithm concludes with .
- Soundness The soundness of the algorithm bounds the probability that in the case where . This probability is given by:Although not truly essential, the algorithm assumes . The conditional probabilities above can be bounded using Equation (41) as follows. Take and assume that . In this case, Equation (41) implies:On the other hand, letting , the same equation reads:This follows from the fact that the algorithm decides if irrespective of the beliefs themselves. For that reason, these equations coincide, though for different values of α and . Both describe a failure of the algorithm to decide . The theorem now follows from Equation (53)–(55).
10. Low-Dimensional Topology and Bisimulation
10.1. Equivalence
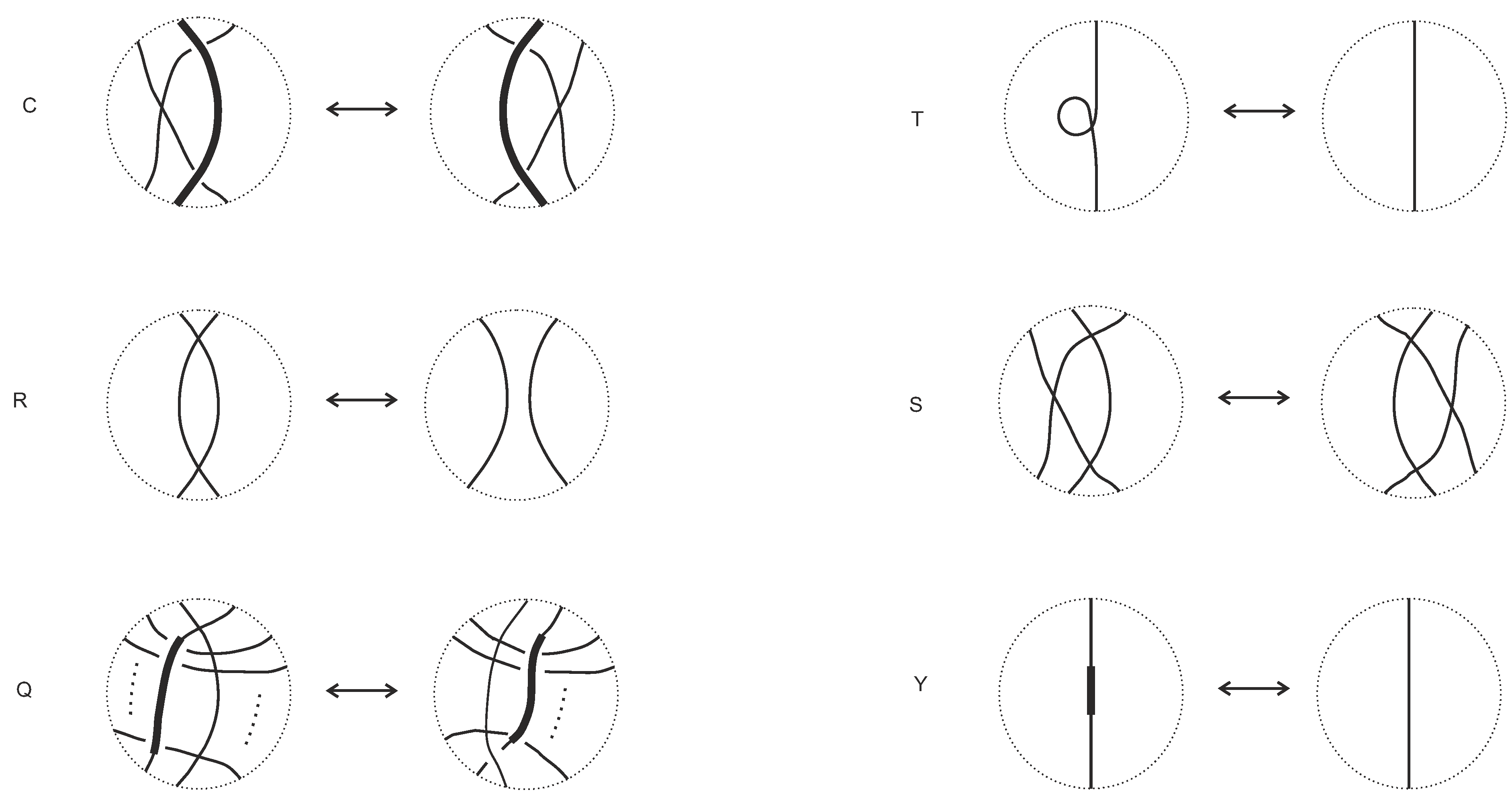
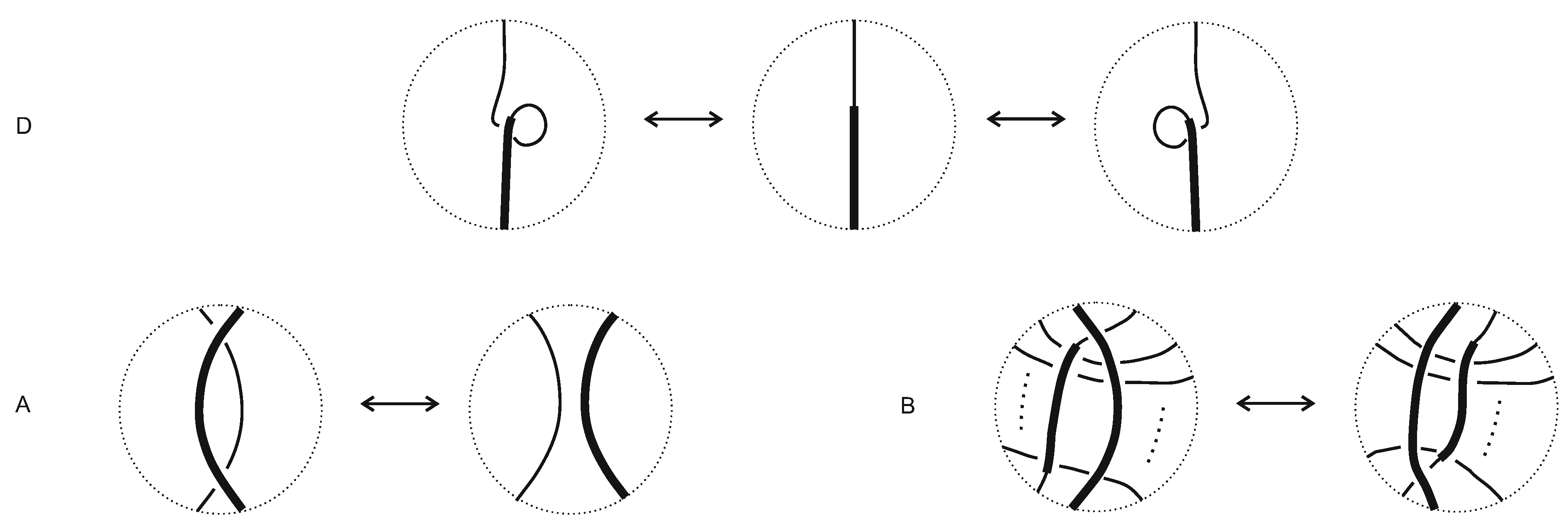
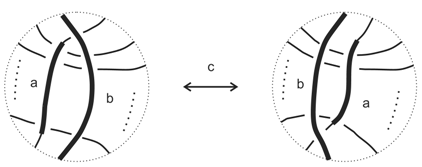
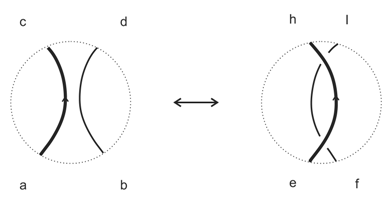
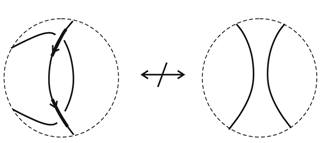
10.2. The Single Agent in R2 and R3
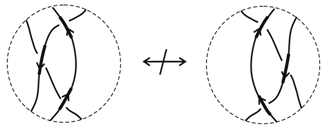
10.3. Zero Knowledge
- 1.
- There are no intermediate interactions in M that decide L.
- 2.
- There exists an equivalent machine , which decides L at one of its intermediate interactions.
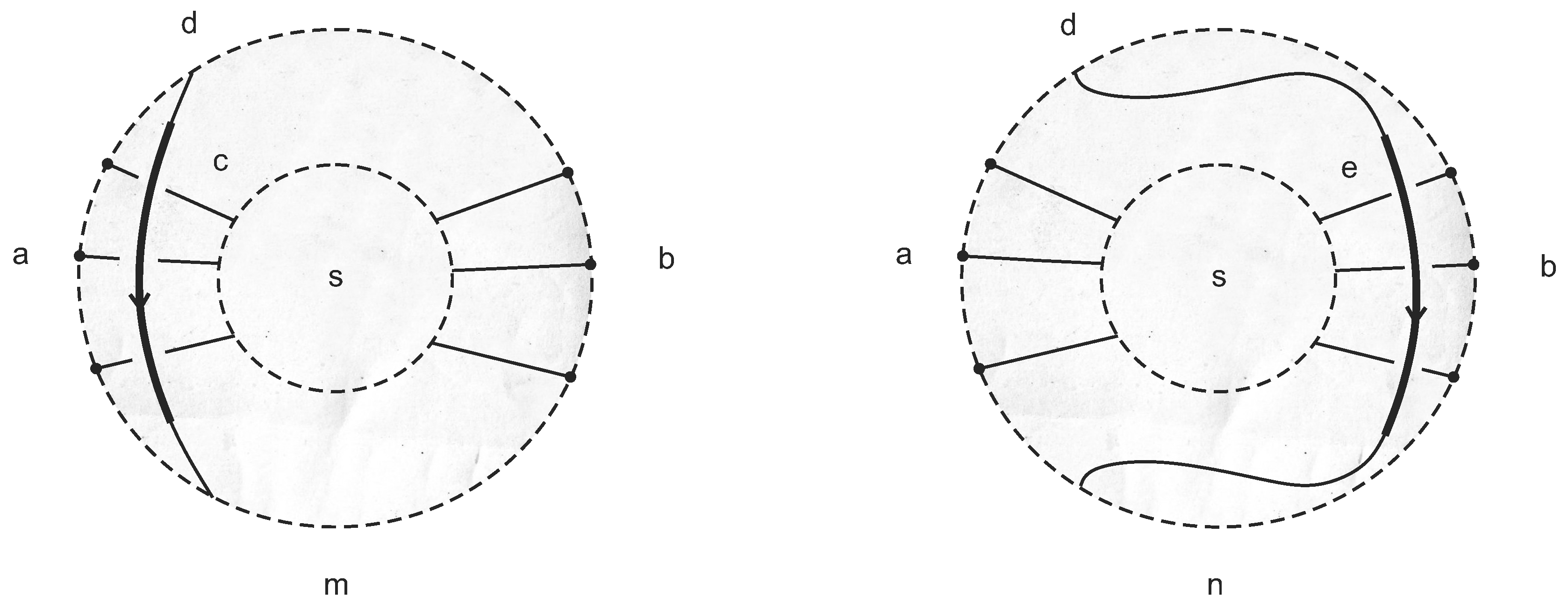
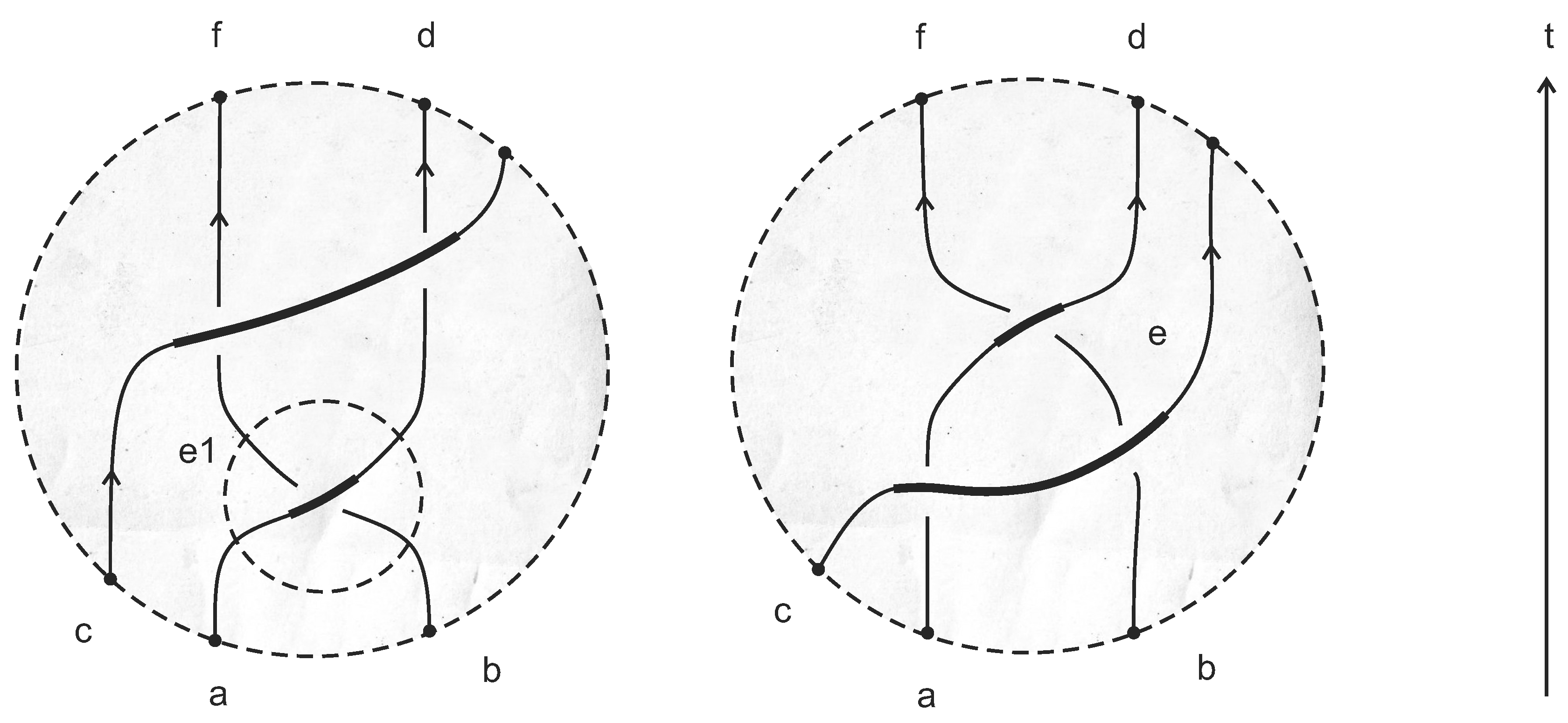
10.4. Example
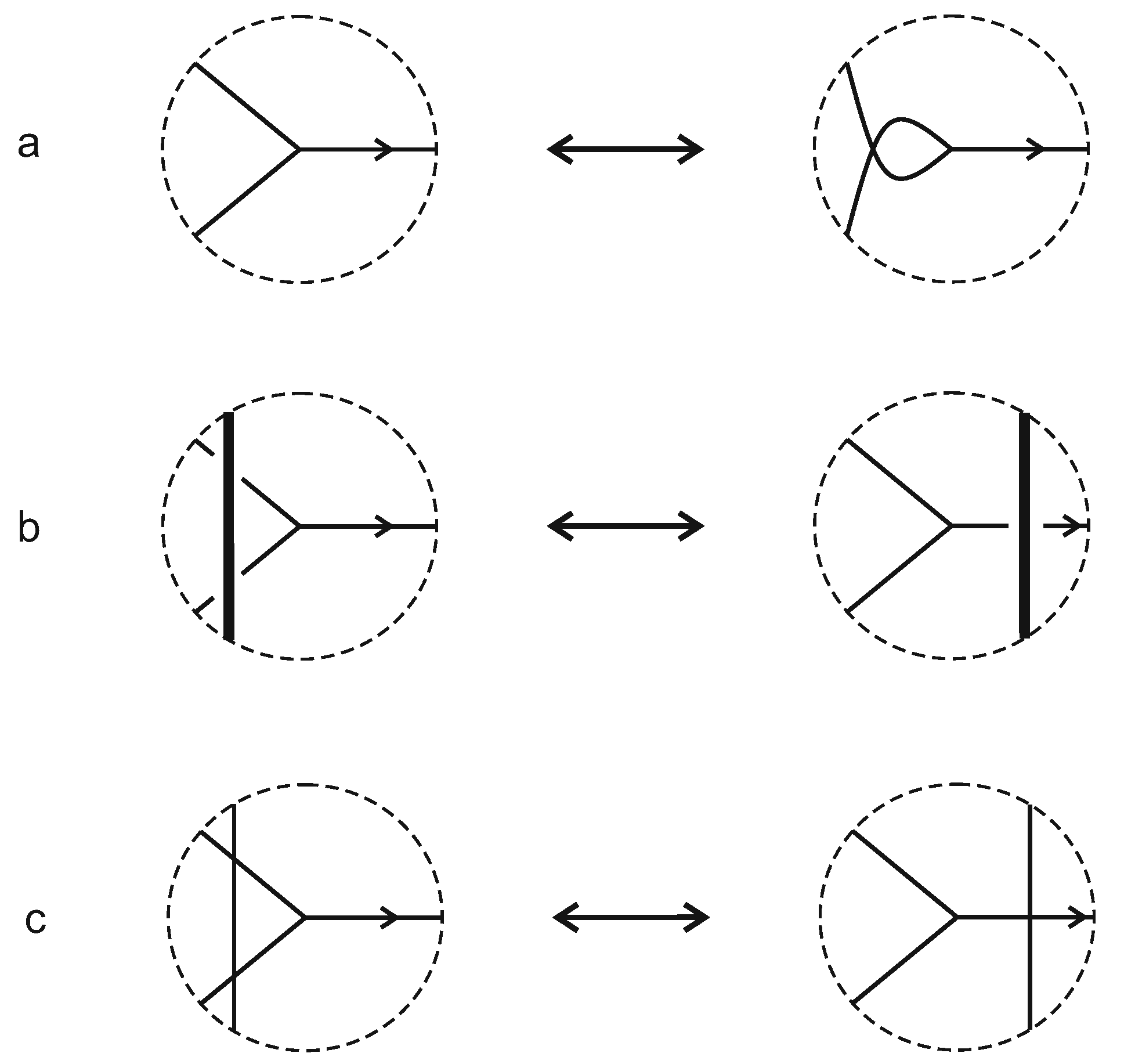
10.5. Equivalence for Machines with Wyes
11. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Carmi, A.Y.; Moskovich, D. Tangle machines. Proc. R. Soc. A 2015, 471. [Google Scholar] [CrossRef]
- Churchill, F.B. William Johannsen and the genotype concept. J. Hist. Biol. 1974, 7, 5–30. [Google Scholar] [CrossRef] [PubMed]
- Johannsen, W. The genotype conception of heredity. Am. Nat. 1911, 45, 129–159. [Google Scholar] [CrossRef]
- Carmi, A.Y.; Moskovich, D. Low dimensional topology of information fusion. In Proceedings of the 8th International Conference on Bio-inspired Information and Communications Technologies, Boston, MA, USA, 1–3 December 2014; pp. 251–258.
- Shamir, A. IP = PSPACE. J. ACM 1992, 39, 869–877. [Google Scholar] [CrossRef]
- Elhamdadi, M. Distributivity in Quandles and Quasigroups. In Algebra, Geometry and Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 2014; pp. 325–340. [Google Scholar]
- Peirce, C.S. On the algebra of logic. Am. J. Math. 1880, 3, 15–57. [Google Scholar] [CrossRef]
- Kauffman, L.H. Knot automata. In Proceedings of the Twenty-Fourth International Symposium on Multiple-Valued Logic, Boston, MA, USA, 25–27 May 1994; pp. 328–333.
- Kauffman, L.H. Knot logic. In Knots and Applications; Series of Knots and Everything 6; Kauffman, L., Ed.; World Scientific Publications: Singapore, 1995; pp. 1–110. [Google Scholar]
- Buliga, M.; Kauffman, L. GLC actors, artificial chemical connectomes, topological issues and knots. In Proceedings of the Fourteenth International Conference on the Synthesis and Simulation of Living Systems, New York, NY, USA, 30 July–2 August 2013; pp. 490–497.
- Meredith, L.G.; Snyder, D.F. Knots as processes: A new kind of invariant. 2010. Available online: http://arxiv.org/abs/1009.2107 (accessed on 17 July 2015).
- Kauffman, L.H.; Lomonaco, S.J., Jr. Braiding operators are universal quantum gates. New J. Phys. 2004, 6. [Google Scholar] [CrossRef]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Sarma, S.D. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083–1159. [Google Scholar] [CrossRef]
- Ogburn, R.W.; Preskill, J. Topological quantum computation. In Quantum Computing and Quantum Communications; Springer: Berlin, Germany, 1999; Volume 1509, pp. 341–356. [Google Scholar]
- Kitaev, A.Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Mochon, C. Anyons from nonsolvable finite groups are sufficient for universal quantum computation. Phys. Rev. A 2003, 67. [Google Scholar] [CrossRef]
- Alagic, G.; Jeffery, S.; Jordan, S. Circuit Obfuscation Using Braids. In Proceedings of the 9th Conference on the Theory of Quantum Computation, Communication and Cryptography, Singapore, 21–23 May 2014; Volume 27, pp. 141–160.
- Buliga, M. Computing with space: A tangle formalism for chora and difference. 2011. Available online: http://arxiv.org/abs/1103.6007 (accessed on 17 July 2015).
- Abramsky, S.; Coecke, B. Categorical quantum mechanics. In Handbook of Quantum Logic and Quantum Structures; Elsevier: Amsterdam, The Netherlands, 2009; Volume 2, pp. 261–323. [Google Scholar]
- Baez, J.; Stay, M. Physics, topology, logic and computation: A Rosetta stone. Lect. Notes Phys. 2011, 813, 95–172. [Google Scholar]
- Vicary, J. Higher Semantics for Quantum Protocols. In Proceedings of the 27th Annual ACM/IEEE Symposium on Logic in Computer Science, Los Alamitos, CA, USA, 25–28 June 2012; pp. 606–615.
- Roscoe, A.W. Consistency in distributed databases. In Oxford University Computing Laboratory Technical Monograph; Oxford University Press: Oxford, UK, 1990; Volume PRG-87. [Google Scholar]
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem. P. Lond. Math. Soc. Ser. 2 1937, 42, 230–265. [Google Scholar] [CrossRef]
- Turing, A.M. On computable numbers, with an application to the Entscheidungsproblem: A correction. P. Lond. Math. Soc. Ser. 2 1938, 43, 544–546. [Google Scholar] [CrossRef]
- Hopcroft, J.E.; Motwani, R.; Ullman, J.D. Introduction to Automata Theory, Languages, and Computation, 2nd ed.; Addison-Wesley: Reading, MA, USA, 2001. [Google Scholar]
- Goldwasser, S.; Micali, S.; Rackoff, C. The Knowledge complexity of interactive proof-systems. SIAM J. Comput. 1989, 18, 186–208. [Google Scholar] [CrossRef]
- Ben-Or, M.; Goldwasser, S.; Kilian, J.; Wigderson, A. Multi prover interactive proofs: How to remove intractability assumptions. In Proceedings of the 20th ACM Symposium on Theory of Computing, Chicago, IL, USA, 2–4 May 1988; pp. 113–121.
- Babai, L.; Fortnow, L.; Lund, C. Non-deterministic exponential time has two-prover interactive protocols. Comput. Complex. 1991, 1, 3–40. [Google Scholar] [CrossRef]
- Arora, S.; Safra, S. Probabilistic checking of proofs: A new characterization of NP. J. ACM 1998, 45, 70–122. [Google Scholar] [CrossRef]
- Moshkovitz, D.; Raz, R. Two-query PCP with subconstant error. J. ACM 2010, 57. [Google Scholar] [CrossRef]
- Arora, S.; Lund, C.; Motwani, R.; Sudan, M.; Szegedy, M. Proof verification and hardness of approximation problems. J. ACM 1998, 45, 501–555. [Google Scholar] [CrossRef]
- Håstad, J. Some optimal inapproximability results. J. ACM 1997, 48, 798–859. [Google Scholar] [CrossRef]
- Khot, S.; Saket, R. A 3-query non-adaptive PCP with perfect completeness. In Proceedings of the 21st IEEE Conference on Computational Complexity, Prague, Czech Republic, 16–20 July 2006; pp. 159–169.
- Zwick, U. Approximation algorithms for constraint satisfaction problems involving at most three variables per constraint. In Proceedings of the 9th ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, USA, 25–27 January 1998; pp. 201–210.
- Bar-Natan, D.; Dancso, S. Finite type invariants of w-knotted objects I: W-knots and the Alexander polynomial. 2014. Available online: http://arxiv.org/abs/1405.1956 (accessed on 17 July 2015).
- Kauffman, L.H. Virtual knot theory. Europ. J. Combinatorics 1999, 20, 663–690. [Google Scholar] [CrossRef]
- Clark, D.; Morrison, S.; Walker, K. Fixing the functoriality of Khovanov homology. Geom. Topol. 2009, 13, 1499–1582. [Google Scholar] [CrossRef]
- Buliga, M. Braided spaces with dilations and sub-riemannian symmetric spaces. In Geometry, Exploratory Workshop on Differential Geometry and Its Applications; Andrica, D., Moroianu, S., Eds.; Cluj Univ. Press: Cluj-Napoca, Romania, 2011; pp. 21–35. [Google Scholar]
- Ishii, A.; Iwakiri, M.; Jang, Y.; Oshiro, K. A G–family of quandles and handlebody-knots. Illinois J. Math. 2013, 57, 817–838. [Google Scholar]
- Przytycki, J.H. Distributivity versus associativity in the homology theory of algebraic structures. Demonstr. Math. 2011, 44, 823–869. [Google Scholar]
- Joyce, D. A classifying invariant of knots: The knot quandle. J. Pure Appl. Algebra 1982, 23, 37–65. [Google Scholar] [CrossRef]
- Abramsky, S. No-cloning in categorical quantum mechanics. In Semantic Techniques in Quantum Computation; Mackie, I., Gay, S., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 1–28. [Google Scholar]
- Krohn, K.; Maurer, W.D.; Rhodes, J. Realizing complex boolean functions with simple groups. Inform. Control 1966, 9, 190–195. [Google Scholar] [CrossRef]
- Barrington, D.A. Bounded-width polynomial-size branching programs recognize exactly those languages in NC1. J. Comput. System Sci. 1989, 38, 150–164. [Google Scholar] [CrossRef]
- Fredkin, E.; Toffoli, T. Conservative logic. Int. J. Theor. Phys. 1982, 21, 219–253. [Google Scholar] [CrossRef]
- Surowiecki, J. The Wisdom of Crowds: Why the Many Are Smarter Than the Few and How Collective Wisdom Shapes Business, Economies, Societies, and Nations; Random House LLC: New York, NY, USA, 2005. [Google Scholar]
- Arora, S.; Barak, B. Computational Complexity: A Modern Approach; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Goldreich, O. A short tutorial of zero-knowledge. 2010. in press. Available online: http://www.wisdom.weizmann.ac.il/ oded/zk-tut02.html (accessed on 17 July 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carmi, A.Y.; Moskovich, D. Computing with Colored Tangles. Symmetry 2015, 7, 1289-1332. https://doi.org/10.3390/sym7031289
Carmi AY, Moskovich D. Computing with Colored Tangles. Symmetry. 2015; 7(3):1289-1332. https://doi.org/10.3390/sym7031289
Chicago/Turabian StyleCarmi, Avishy Y., and Daniel Moskovich. 2015. "Computing with Colored Tangles" Symmetry 7, no. 3: 1289-1332. https://doi.org/10.3390/sym7031289
APA StyleCarmi, A. Y., & Moskovich, D. (2015). Computing with Colored Tangles. Symmetry, 7(3), 1289-1332. https://doi.org/10.3390/sym7031289