Conservation Laws and Exact Solutions of a Generalized Zakharov–Kuznetsov Equation
Abstract
: In this paper, we study a generalized Zakharov–Kuznetsov equation in three variables, which has applications in the nonlinear development of ion-acoustic waves in a magnetized plasma. Conservation laws for this equation are constructed for the first time by using the new conservation theorem of Ibragimov. Furthermore, new exact solutions are obtained by employing the Lie symmetry method along with the simplest equation method.1. Introduction
Many important phenomena and dynamic processes in physics, applied mathematics and engineering can be described by higher-dimensional extensions of the Korteweg–de Vries (KdV) equation. Zakharov and Kuznetsov successfully proposed one such model [1]. The Zakharov–Kuznetsov (ZK) equation given by:
This paper aims to study the generalized Zakharov–Kuznetsov (gZK) equation [4,8]:
It is of great importance to search for exact solutions of nonlinear partial differential equations (NPDEs), such as the gZK equation, because many physical phenomena are described by NPDEs. Although there is no unique method for finding exact solutions of NLPEs, a great deal of research work has been devoted to developing different methods to solve NLPEs. Some of the methods found in the literature include the inverse scattering transform method [9], Darboux transformation [10], Hirota’s bilinear method [11], Bäcklund transformation [12], the multiple exp-function method [13], the (G′/G)-expansion method [14], the sine-cosine method [15], the F -expansion method [16], the exp-function expansion method [17] and the Lie symmetry method [18,19].
There is no doubt that in the study of differential equations, conservation laws play an important role. In fact, conservation laws describe physical conserved quantities, such as mass, energy, momentum and angular momentum, as well as charge and other constants of motion [20,21]. They have been used in investigating the existence, uniqueness and stability of solutions of nonlinear partial differential equations [22–24]. Furthermore, they have been used in the development and use of numerical methods [25,26]. Recently, conservation laws were used to obtain exact solutions of some partial differential equations [27–31]. Thus, it is essential to study the conservation laws of partial differential equations.
The paper is organized as follows: In Section 2, we derive conservation laws of (2) by employing the new conservation law theorem by Ibragimov [32]. In Section 3, we obtain exact solutions of (2) using Lie symmetry analysis and the simplest equation method [33–35]. Finally, concluding remarks are presented in Section 4.
2. Conservation Laws
In this section, the new conservation theorem by Ibragimov [32] will be used to construct conservation laws for (2). To use the conservation theorem by Ibragimov [32], we need to know the Lie point symmetries of (2). Thus, we first compute the symmetries of (2).
2.1. Lie Point Symmetries of (2)
The vector field:
Solving the above system of partial differential equations, one obtains the following four Lie point symmetries:
2.2. Application of the New Conservation Theorem
The gZK equation together with its adjoint equation are given by:
The third-order Lagrangian for the system of Equations (3a) and (3b) is given by:
We have the following four cases:
We first consider the Lie point symmetry X1 = ∂t of (2). Corresponding to this symmetry, the Lie characteristic functions are W1 = −ut. and W2 = −vt. Thus, by using the Ibragimov theorem [32], the components of the conserved vector associated with the symmetry X1 = ∂t are given by:
Likewise, the Lie point symmetry X2 = ∂x has the Lie characteristic functions W1 = −ux and W2 = −vx. Invoking Ibragimov’s theorem, we obtain the conserved vector, whose components are:
The Lie point symmetry X3 = ∂y has the Lie characteristic functions W1 = −u and W2 = −vy, and using Ibragimov’s theorem, the components of the conserved vector are:
Finally, the Lie point symmetry X4 = 3nt∂t + nx∂x + ny∂y − 2u∂u gives W1 = −(2u + 3ntut + nxux + nyuy) and W2 = (2 − 2n)v − 3ntvt − nxvx − nyvy, and so, the associated conserved vector has components:
3. Exact Solutions
In this section, we obtain exact solutions of (2) using firstly its Lie point symmetries and, secondly, by employing the simplest equation method.
3.1. Exact Solutions of (2) Using Its Lie Point Symmetries
First of all, we utilize the linear combination of the three translation symmetries, namely X = X1 + νX2 + X3, and reduce the gZK Equation (2) to a PDE in two independent variables. The associated Lagrange system is:
By considering θ as the new dependent variable and f and g as new independent variables, the gZK Equation (2) transforms to:
The combination Γ1 + kΓ2, of the two symmetries Γ1 and Γ2, for an arbitrary constant k, yields the two invariants:
The integration of (8) yields
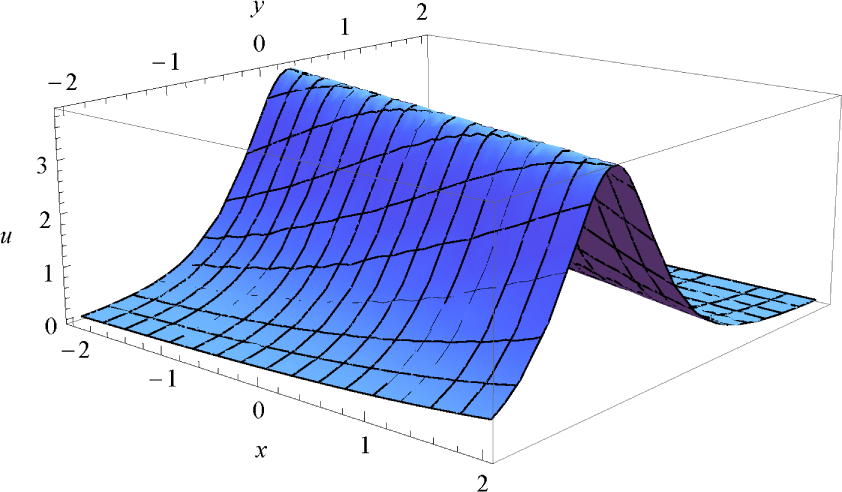
Note that (11) represents a non-topological soliton solution. A sketch of the solution (11) with n = 2, α = 2, k = 5, ν = 1, β = 1, t = 0 and C1 = 1 is given in Figure 1.
3.2. Exact Solutions of (2) Using the Simplest Equation Method
In this subsection, we use the simplest equation method [33–35] to solve the nonlinear third-order ODE (8) for n = 1, 2. The simplest equations that we use here are the Bernoulli equation:
The solution of Bernoulli Equation (12) we use here is given by:
3.2.1. Solutions of (2) Using the Bernoulli Equation as the Simplest Equation
n = 1
In this case, the balancing procedure yields M = 2 and solutions of (8) are of the form:
We insert this value of W (z) in (8). Then, using the Bernoulli Equation (12) and, thereafter, equating the coefficients of powers of Gi to zero, we obtain an algebraic system of five equations in terms of A0, A1, A2, namely:
With the aid of Maple, we solve the above system and obtain:
Therefore, the solution of (2), for n = 1 is given by:
n = 2
The balancing procedure yields M = 1, so the solutions of (8) take the form:
As before, substituting (17) into (8), we obtain the algebraic system of equations:
Therefore, the solutions of (2) for n = 2 are given by:
3.2.2. Solutions of (2) Using the Riccati Equation as the Simplest Equation
n = 1
For this case, the balancing procedure gives M = 2, and so, (14) becomes:
The insertion of this value of W (z) into (8) and making use of the Riccati Equation (13) yields the following algebraic system of equations in terms of A0, A1, A2:
The solution of the above system using Maple gives:
Consequently, the solutions of (2) are:
n = 2
The balancing procedure yields M = 1, so the solutions of (8) are of the form:
Substituting (22) into (8) and using the Riccati equation [36], we obtain the following algebraic system of equations:
Solving the above algebraic equations, one obtains:
Hence, we have the following solutions of (2) for n = 2:
4. Concluding Remarks
In this paper, we studied the generalized Zakharov–Kuznetsov Equation (2). We derived the conservation laws of this equation by using the new conservation theorem by Ibragimov. Moreover, the Lie point symmetries of (2) were obtained and were used in conjunction with the simplest equation method to obtain exact solutions of the generalized Zakharov–Kuznetsov equation. The solutions obtained here are new and more general than the ones obtained before in [4] and [8]. Furthermore, the importance of the conservation laws has been emphasized in the Introduction.
Acknowledgments
D.M.M. would like to thank the FRC of Faculty of Agriculture, Science and Technology, North-West University, Mafikeng Campus, and NRF of South Africa for their financial support. D.M.M. and C.M.K. thank Tanki Motsepa for helpful discussions.
Author Contributions
D.M.M. and C.M.K. worked together in the derivation of the mathematical results. Both authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zakharov, V.E.; Kuznetsov, E.A. On three-Dimensional solitons. Sov. Phys 1974, 39, 285–288. [Google Scholar]
- Munro, S.; Parkes, E.J. Stability of solitary-wave solutions to a modified Zakharov–Kuznetsov equation. J. Plasma Phys 2000, 64, 411–426. [Google Scholar]
- Munro, S.; Parkes, E.J. The derivation of a modified Zakharov–Kuznetsov equation and the stability of its solution. J. Plasma Phys 1999, 62, 305–317. [Google Scholar]
- Wazwaz, A.M. The extended tanh method for the Zakharo-Kuznetsov (ZK) equation, the modified ZK equation, and its generalized forms. Commun. Nonlinear Sci. Numer. Simul 2008, 13, 1039–1047. [Google Scholar]
- Wazwaz, A.M. Exact solutions with solitons and periodic structures for the Zakharov–Kuznetsov (ZK) equation and its modified form. Commun. Nonlinear Sci. Numer. Simul 2005, 10, 597–606. [Google Scholar]
- Moussa, M.H.M. Similarity solutions to non-linear partial differential equation of physical phenomena represented by the Zakharov–Kuznetsov equation. Int. J. Eng. Sci 2001, 39, 1565–1575. [Google Scholar]
- Peng, Y.Z. Exact travelling wave solutions for the Zakharov–Kuznetsov equation. Appl. Math. Comput 2008, 199, 397–405. [Google Scholar]
- El-Ganaini, S.I.; Travelling, Wave. Solutions of the Zakharov–Kuznetsov Equation with Power Law Nonlinearity. Int. J. Contemp. Math. Sci 2011, 6, 2353–2366. [Google Scholar]
- Ablowitz, M.J.; Clarkson, P.A. Soliton, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformation and Soliton; Springer: Berlin, Germany, 1991. [Google Scholar]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Gu, C.H. Soliton Theory and Its Application; Zhejiang Science and Technology Press: Zhejiang, China, 1990. [Google Scholar]
- Ma, W.X.; Huang, T.; Zhang, Y. A multiple exp-function method for nonlinear differential equations and its applications. Phys. Scr 2010, 82. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.; Zhang, J. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar]
- Wazwaz, M. The Tanh and Sine-Cosine Method for Compact and Noncompact Solutions of Nonlinear Klein Gordon Equation. Appl. Math. Comput 2005, 167, 1179–1195. [Google Scholar]
- Wang, M.; Li, X. Extended F− Expansion and Periodic Wave Solutions for the Generalized Zakharov Equations. Phys. Lett. A 2005, 343, 48–54. [Google Scholar]
- He, J.; Wu, X. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, Graduate Texts in Mathematics, 107, 2nd ed; Springer-Verlag: Berlin, Germany, 1993. [Google Scholar]
- Muatjetjeja, B.; Khalique, C.M. Benjamin-Bona-Mahony Equation with Variable Coefficients: Conservation Laws. Symmetry 2014, 6, 1026–1036. [Google Scholar]
- Bluman, G.W.; Cheviakov, A.F.; Anco, S.C. Applications of Symmetry Methods to Partial Differential Equations. In Applied Mathematical Sciences; Springer: New York, NY, USA, 2010; Volume 168. [Google Scholar]
- Muatjetjeja, B.; Khalique, C.M. Conservation Laws for a Variable Coefficient Variant Boussinesq System. Abstr. Appl. Anal 2014, 169694:1–169694:5. [Google Scholar]
- Lax, P.D. Integrals of nonlinear equations of evolution and solitary waves. Commun. Pure Appl. Math 1968, 21, 467–490. [Google Scholar]
- Benjamin, T.B. The stability of solitary waves. Proc. R. Soc. Lond. A 1972, 328, 153–183. [Google Scholar]
- Knops, R.J.; Stuart, C.A. Quasiconvexity and uniqueness of equilibrium solutions in nonlinear elasticity. Arch. Ration. Mech. Anal 1984, 86, 234–249. [Google Scholar]
- LeVeque, R.J. Numerical Methods for Conservation Laws; Birkhauser: Basel, Switherland, 1992. [Google Scholar]
- Godlewski, E.; Raviart, P.A. Numerical Approximation of Hyperbolic Systems of Conservation Laws; Springer: Berlin, Germany, 1996. [Google Scholar]
- Sjöberg, A. Double reduction of PDEs from the association of symmetries with conservation laws with applications. Appl. Math. Comput 2007, 184, 608–616. [Google Scholar]
- Muatjetjeja, B.; Khalique, C.M. Lie group classification for a generalised coupled Lane–Emden system in dimension one. East Asian J. Appl. Math 2014, 4, 301–311. [Google Scholar]
- San, S.; Yasar, E. On the Conservation Laws and Exact Solutions of a Modified Hunter–Saxton Equation. Adv. Math. Phys 2014, 349059:1–349059:6. [Google Scholar]
- Naz, R.; Ali, Z.; Naeem, I. Reductions and New Exact Solutions of ZK, Gardner KP, and Modified KP Equations via Generalized Double Reduction Theorem. Abstr. Appl. Anal. 201, 340564:1–340564:11.
- Tracina, R.; Bruzon, M.S.; Grandarias, M.L.; Torrisi, M. Nonlinear self-adjointness, conservation laws, exact solutions of a system of dispersive evolution equations. Commun. Nonlinear Sci. Numer. Simulat 2014, 19, 3036–3043. [Google Scholar]
- Ibragimov, N.H. A new conservation theorem. J. Math. Anal. Appl 2007, 333, 311–328. [Google Scholar]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitons Fractals 2005, 24, 1217–1231. [Google Scholar]
- Kudryashov, N.A. Exact solitary waves of the Fisher equation. Phys. Lett. A 2005, 342, 99–106. [Google Scholar]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul 2012, 17, 2248–2253. [Google Scholar]
- Khalique, C.M. On the Solutions and Conservation Laws of a Coupled Kadomtsev-Petviashvili Equation. J. Appl. Math 2013, 741780:1–741780:7. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mothibi, D.M.; Khalique, C.M. Conservation Laws and Exact Solutions of a Generalized Zakharov–Kuznetsov Equation. Symmetry 2015, 7, 949-961. https://doi.org/10.3390/sym7020949
Mothibi DM, Khalique CM. Conservation Laws and Exact Solutions of a Generalized Zakharov–Kuznetsov Equation. Symmetry. 2015; 7(2):949-961. https://doi.org/10.3390/sym7020949
Chicago/Turabian StyleMothibi, Dimpho Millicent, and Chaudry Masood Khalique. 2015. "Conservation Laws and Exact Solutions of a Generalized Zakharov–Kuznetsov Equation" Symmetry 7, no. 2: 949-961. https://doi.org/10.3390/sym7020949
APA StyleMothibi, D. M., & Khalique, C. M. (2015). Conservation Laws and Exact Solutions of a Generalized Zakharov–Kuznetsov Equation. Symmetry, 7(2), 949-961. https://doi.org/10.3390/sym7020949






