Abstract
Future communication networks would be required to deliver data on a far greater scale than is known to us today, thus mandating the maximal utilization of the available radio spectrum using cognitive radios. In this paper, we have proposed a novel cooperative spectrum sensing approach for cognitive radios. In cooperative spectrum sensing, the fusion center relies on reports of the cognitive users to make a global decision. The global decision is obtained by assigning weights to the reports received from cognitive users. Computation of such weights requires prior information of the probability of detection and the probability of false alarms, which are not readily available in real scenarios. Further, the cognitive users are divided into reliable and unreliable categories based on their weighted energy by using some empirical threshold. In this paper, we propose a method to classify the cognitive users into reliable, neutral and unreliable categories without using any pre-defined or empirically-obtained threshold. Moreover, the computation of weights does not require the detection, or false alarm probabilities, or an estimate of these probabilities. Reliable cognitive users are assigned the highest weights; neutral cognitive users are assigned medium weights (less than the reliable and higher than the unreliable cognitive users’ weights); and unreliable users are assigned the least weights. We show the performance improvement of our proposed method through simulations by comparing it with the conventional cooperative spectrum sensing scheme through different metrics, like receiver operating characteristic (ROC) curve and mean square error. For clarity, we also show the effect of malicious users on detection probability and false alarm probability individually through simulations.1. Introduction
Information and communication technologies have experienced phenomenal growth in the past fifteen years. This growth has spawned tools and services that have redefined how we communicate and interact with each other. Billions of users share petabytes of data in the form of pictures and videos through social networking sites and services, like Facebook, Twitter, WhatsApp, YouTube and numerous others. The scale of multimedia content that today’s communication technologies have to cater for can be gauged from the fact that on YouTube alone, 300 h of video is uploaded every minute, which is equivalent to 49 years of multimedia content every day [1]. We are practically living in the era of “Big Data”. The future, with the proliferation of the Internet of Things (IoT) and ubiquitous computing, will see an even greater surge in the generation, sharing and processing of data. The scale of data that future networks have to handle would pose diverse challenges, like security, privacy, radio spectrum scarcity, etc. Future communication networks would undoubtedly require the most efficient use and maximal utilization of the radio spectrum, which would be the predominant medium for most of the data communication.
The solution to the inherent problems of spectrum scarcity and spectrum under-utilization came in the shape of cognitive radio. Cognitive radio is a promising technology, which overcomes the spectrum scarcity and spectrum under-utilization by allowing the non-licensed users to use the licensed spectrum when it is not used by the licensed users [2,3]. Due to the less privileged status of the non-licensed or cognitive users, they are bound to leave the licensed spectrum instantly when the privileged or primary user (PU) needs the spectrum. This necessitates the cognitive user (CU) to have accurate and timely information of the spectrum’s utilization by the PU. This makes spectrum sensing one of the most important feature of the cognitive radios to protect the PU [4–6].
The sensing performance and reliability of a single CU highly deteriorates in an environment where the channel suffers from destructive effects, such as fading and shadowing or when the hidden terminal problem occurs. Therefore, cooperative spectrum sensing was proposed to overcome the channel destructive effects, to avoid the hidden terminal problem and to improve spectrum sensing performance [7,8]. In cooperative spectrum sensing, the location diversity of multiple CUs is exploited by their cooperation, which helps to detect even a weak primary signal and consequently improves the detection performance of the cognitive radio network, decreases interference to the PU caused by misdetection and increases the protection of the PU. The individual reports generated by CUs are forwarded to a central decision entity, usually called the fusion center (FC). The size of an individual CU’s report may be one bit (in the case of a hard decision), l bits (1 < l < m, in the case of a quantized decision) [9,10] or m bits (in the case of a soft decision). The fusion center computes the global decision by using weighted sum of the CUs’ reports.
However, the advantages of the cooperation are also accompanied by certain challenges. For example, the cooperation incurs potential security vulnerabilities. The security vulnerabilities can be exploited by different types of attacks that can be launched in a cognitive radio network, for example primary user emulation (PUE) attack, jamming disruption attack and spectrum sensing data falsification (SSDF) or Byzantine attack [11]. In this work, we consider the SSDF attack in which the malicious users send wrong sensing reports to the fusion center either to degrade the sensing performance of the network or to achieve their selfish greedy objectives.
The presence of the malicious user(s) in a cooperative environment severely degrades the sensing performance of the cognitive radio network [12]. A variety of approaches have been proposed in the literature [13–15] to restrict malicious users in different applications. In [15], the authors proposed an encrypted identification tag for the authentication of CUs and a reliability test for the detection of unreliable and malicious users. In [16], the authors proposed a distributed and lightweight method for the detection of intrusion in wireless sensor networks based on traffic monitoring and fuzzy inference system. Authentication-based security approaches are discussed in [17–19]. In [20], a cryptographic technique, like blind signature and electronic coin, is used to achieve mobility, reliability, anonymity and flexibility in a mobile wireless network. The weight-based cooperative spectrum sensing methods [21–23], where the weight coefficients of the CUs are computed using the Bayesian criterion or maximum likelihood ratio test, provide optimal detection performance. However, such methods, for the computation of weight coefficients, require prior knowledge of the PU’s steady-state probability, detection probability and false alarm probability or an estimate of these probabilities. Unfortunately, the prior unavailability of these probabilities in real scenarios makes such methods less practical. In [22], the authors use an empirical threshold to classify the CUs into reliable and unreliable categories.
In this work, we propose a simple method that classifies the CUs into reliable, neutral and unreliable categories with no need for any pre-defined or empirical threshold. Each category is assigned a different weight. The computation of weights for different CUs in a particular category is carried out similar to the technique presented in our previous work [15]. The reliable CUs get the highest weights, whereas the unreliable CUs are assigned the lowest weights. The weights of the neutral CUs lay in between the reliable and unreliable CUs’ weights. For the computation and assignment of weights to different CUs, our proposed approach does not require the detection and false alarm probabilities. The weight coefficients are computed and updated by the current observation of the CUs.
The rest of this paper is outlined as follows. The system model is described in Section 2. In Section 3, the proposed CU classification and weight computation are presented. Simulations results and a discussion are presented in Section 4. Finally, the paper is concluded in Section 5.
2. System Model
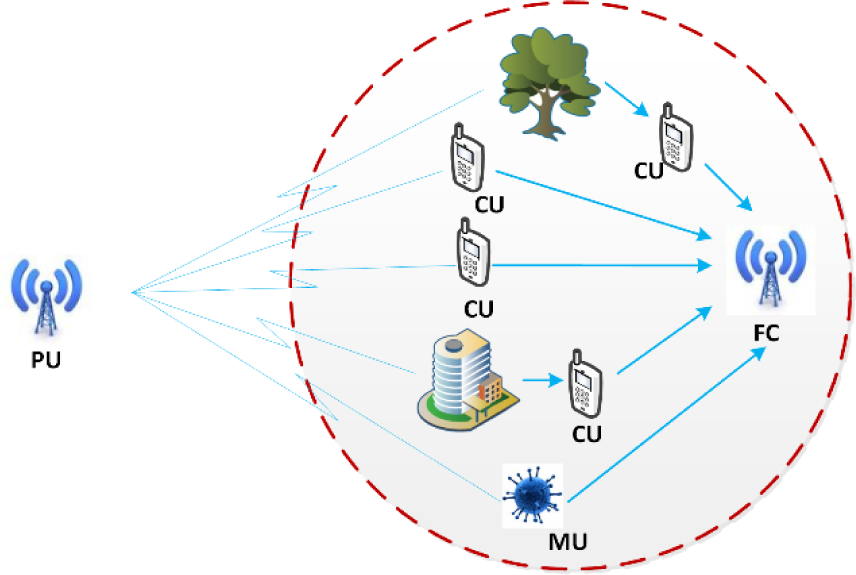
We consider a cognitive radio network as shown in Figure 1 that consists of N CUs, of which l CUs may experience fading or the shadowing effect and M (M << N) CUs are malicious users (MU). We assume three types of malicious users: always present (AP), always absent (AA) and always different (AD). In the first two types, malicious users always send a high or low signal, respectively, regardless of the actual status of the PU, whereas in the last type, the malicious user always sends an opposite signal of PU status. We assume an error-free common control channel between CU and FC. We use the soft fusion rule, where each CU reports its observation to the fusion center in m bits.
Detection of the primary signal by the CU is a binary hypothesis testing problem. The signal received by the i-th CU is given as:
The local observation of the i-th CU is denoted by Yi and is obtained using the energy detection technique [24] given as:
Since the fusion center receives local observations from the CUs, the local decision of the CUs is computed at the fusion center by applying the same energy threshold. The local decision of the i-th CU is denoted by DL,i and is given as below:
The energy threshold λ is assumed to be same for local and global decisions. In order to minimize the influence and bias of the i-th CU on global decision and weight assignments, the local decision and local observation of the i-th CU is skipped. The global decision computed by excluding the i-th CU observation/local decision is called partial global decision and is denoted by DG,i. Weighted observation of the CUs excluding the i-th CU is given as:
For simulation, we calculate the global probability of detection and the global probability of false alarms as follows:
In the above equation, H shows the real status of the PU and is a stream of ones and zeros, where one represents the presence of the PU and zero represents the absence of the PU. The represents the number of times that the condition in the subscript is satisfied.
3. Classification of the Cognitive Users and Weight Coefficients’ Computation
The fusion center classifies the CUs into three categories, i.e., reliable, neutral and unreliable, and assigns weights to each category as described in the subsections to follow.
3.1. Classification of the Cognitive Users
The CUs are classified into reliable, neutral and unreliable categories on the basis of local decisions, partial global decisions and global decisions, i.e., DL,i, DG,i and DG, as below.
3.1.1. Reliable Cognitive Users
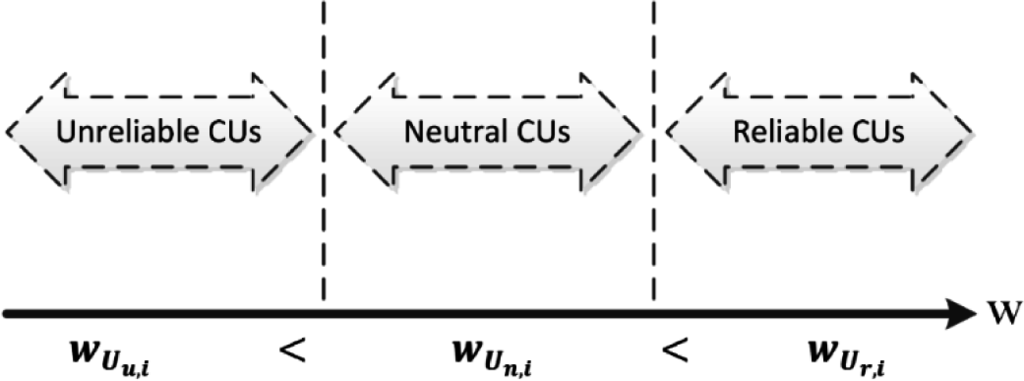
If the local decision of a CU is similar to the global decision, but is different from the partial global decision, this means that the CU is highly reliable and influential. This implies that the absence of such a CU produces a result that is different from the accurate result (global decision). Such CUs are classified as reliable users, and the CUs in this category are assigned the highest weight coefficients, as shown in Figure 3. The weight coefficient of each CU in this category is computed in Section 3.2.
The mathematical expression for reliable CUs can be expressed as below.
The set of reliable CUs and their observations (energy) are denoted by Ur and Er, respectively, and are given by the following expressions.
Let be the total number of reliable CUs, i.e., the size of Ur or Er.
3.1.2. Neutral Cognitive Users
If the local decision of a CU and partial global decision are equal to the global decision, then the CU is classified as a neutral user. The same partial global decision and global decision implies that the presence or absence of the CU has no impact on the decision and shows a neutral behavior in decision making. The weights assigned to neutral CUs will be less than the reliable CUs, but greater than the unreliable CUs. The mathematical expression for the neutral CUs is given as:
The set of neutral CUs and their observations (energy) are denoted by Un and En, respectively, and are given by:
Let be the total number of neutral CUs, i.e., a size of Un or En.
3.1.3. Unreliable Cognitive Users
If the local decision of a CU is different from the global decision, the CU is classified as an unreliable CU. The unreliable users are assigned the least weight coefficients. The mathematical expression for the unreliable CUs is given as:
The set of unreliable CUs and their observations are denoted by Uu and Eu, respectively, and are given as below:
Let be the total number of unreliable CUs, i.e., the size of Uu or Eu. The total number of CUs is the summation of reliable, neutral and unreliable CUs, as given by the following equation:
3.2. Weight Updating and Assignment
Depending on the type of CUs, different weights are assigned to them, as shown in Figure 3. The highest weights are assigned to the reliable CUs, whereas the lowest weights are assigned to the unreliable CUs. Neutral CUs are assigned weights that are less than the weights of the reliable CUs and greater than the weights of the unreliable CUs.
To compute the weight coefficients for the CUs, observations of the reliable, neutral and unreliable CUs (elements of Er, En and Eu) are sorted in ascending or descending order depending on the global decision, as follows:
The normalized weight coefficients of neutral CUs are given by Equations (27) and (28).
The normalized weight coefficients of unreliable CUs are given by Equations (29) and (30).
From the Equations (25)–(30), the weights of reliable, neutral and unreliable CUs are related as . Note that the maximum weight assigned to a neutral CU is less than the minimum weight of reliable CUs, and similarly, the maximum weight assigned to an unreliable CU is less than the minimum weight of neutral CUs. This relationship is shown, mathematically, below:
4. Simulation Results and Discussion
The performance effectiveness of our proposed approach is shown through simulations in this section. We compare our proposed approach with the conventional cooperative spectrum sensing scheme. Simulation parameters are summarized in Table 1. We observe the ROC, probability of detection, probability of false alarms and mean square error of our proposed approach and conventional CSS. The minimum detection probability and maximum false alarm probability of the system are set to 0.8 and 0.25, respectively.

Figure 4 shows the performance comparison of our proposed scheme and the conventional CSS scheme in terms of the ROC under the effect of zero, one and two malicious users (AD type). It is clear from the figure that as the number of malicious users increases, the detection performance of both schemes decreases. When there is no malicious user among the CUs, the gap between the performance curve of our proposed approach and the conventional CSS is minimum. In this case, our approach performs slightly better than conventional CSS. By introducing malicious users (i.e., one or two), the gap between our proposed and conventional CSS is increased due to the more severe effect by MUs on conventional CSS. Our proposed approach minimizes the effect of MUs by judiciously categorizing the CUs into reliable, neutral and unreliable categories and assigning them weights accordingly. The effect of malicious users is suppressed by assigning low weights to them, which makes our proposed approach more robust and efficient.
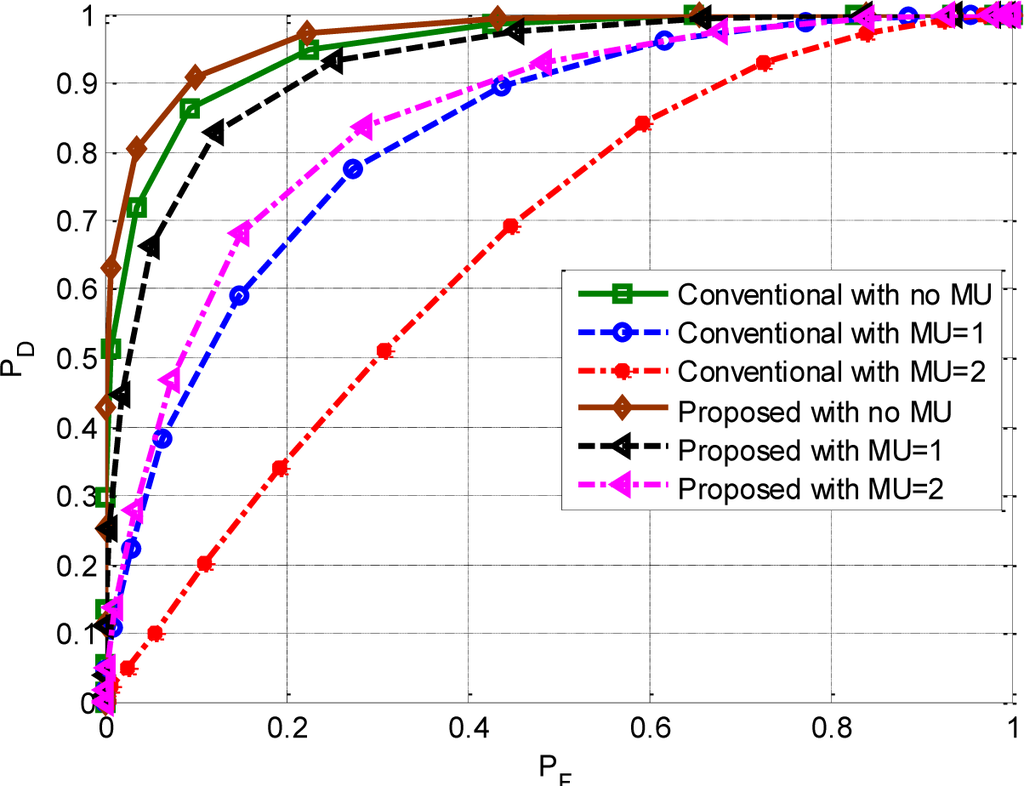
Figure 5 shows a comparison of the detection probability of our proposed scheme with the conventional CSS in the presence of no and three malicious users (one of each type), respectively. It is evident from the figure that the detection probability of conventional CSS drops to an unacceptable level (below 0.8) in the presence of malicious users, whereas the detection probability of our proposed approach maintains a stable and acceptable level (above 0.8) as the number of iterations increases after experiencing a slight initial degradation. The decreased detection probability occurs due to the presence of AF and AD types of malicious users on which conventional CSS has no control, whereas our proposed approach restricts them by properly placing in the unreliable category and assigning low weight coefficients.
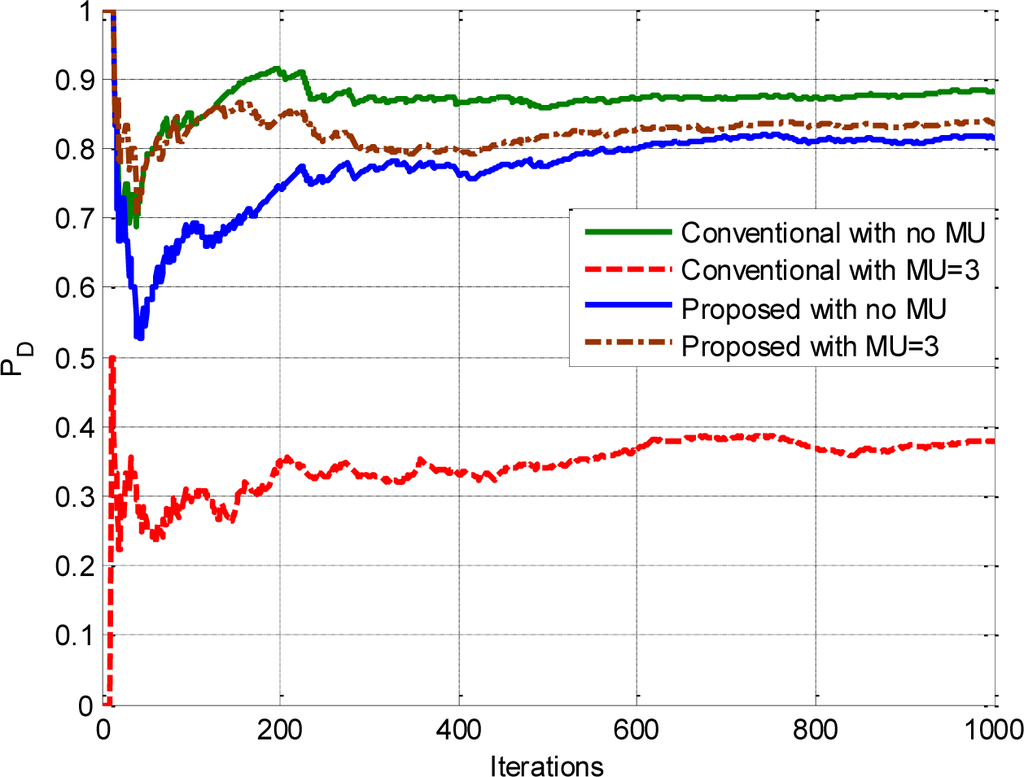
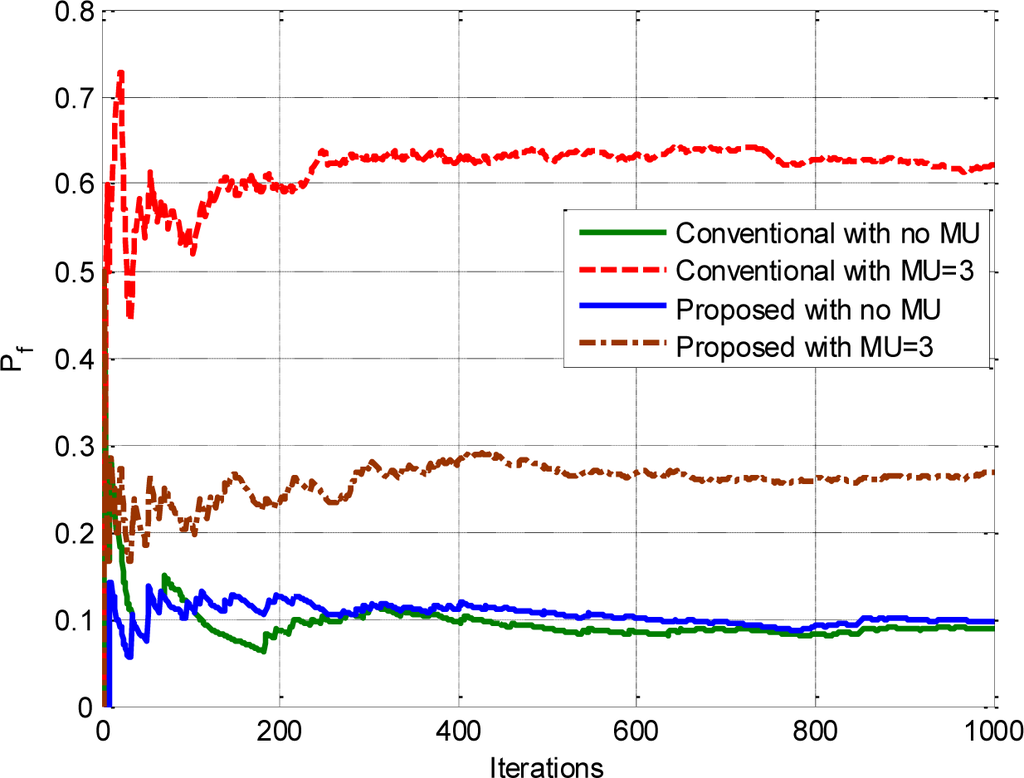
Figure 6 shows a comparison of the false alarm probability of our proposed approach with the conventional CSS in the presence of no and three malicious users (one of each type). It can be observed from the figure that when there are no malicious users, both schemes show similar false alarm probabilities, but when malicious users are introduced into the network, then our proposed scheme outperforms the conventional CSS scheme in terms of false alarm probability. The increased false alarm probability is due to the presence of AP and AD types of malicious users, which cannot be curtailed by conventional CSS, while our proposed approach restrains them by assigning low weight coefficients.
In Figure 7, we compare the mean square error (MSE) of our proposed approach with that of the conventional CSS. The mean squared error has statistical equivalence to the probability of error in detection. The probability of error can be described in terms of the global misdetection probability and the global false-alarm probability as follows:
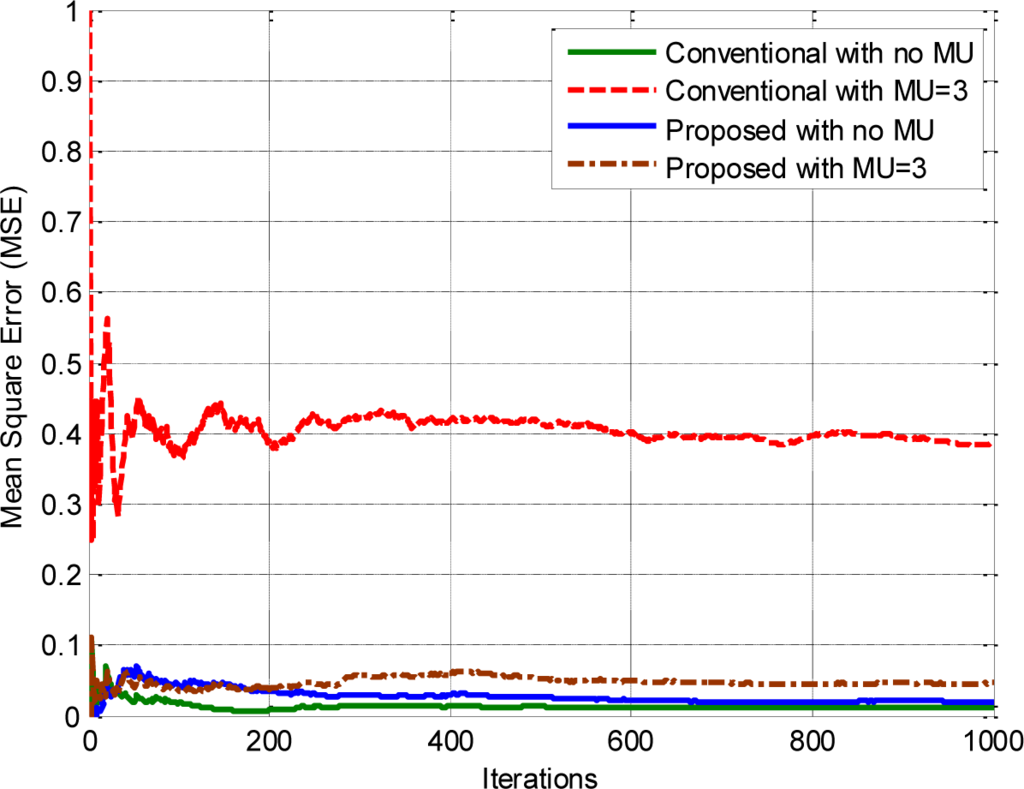
It can be observed from the figure that when the network is free of malicious users, both schemes show almost similar mean square error, but when malicious users are introduced into the network, then the error of conventional CSS becomes significantly greater than that of our proposed approach. The increased value of error in conventional CSS occurs due to high misdetection and high false alarm probabilities.
5. Conclusions
The unavailability of prior information of the detection and false alarm probabilities makes the schemes, which are based on these probabilities, less practical. In this paper, we proposed a simple, but efficient classification method that classifies the CUs into reliable, neutral and unreliable categories without requiring any empirical or pre-defined threshold for such classification. Malicious users are restricted by assigning the lowest weight, and the trustworthy CUs are encouraged by assigning higher weights accordingly. Weights are computed by the actual observation of the CUs, rather than detection and false alarm probabilities. The effectiveness of the proposed method of CUs’ classification and weight assignment has been demonstrated through simulations.
Acknowledgments
This work was supported by the National Research Foundation (NRF) of Korea funded by the MEST (Nos. NRF-2012R1A1A2038831 and NRF-2013R1A2A2A05004535).
Author Contributions
Both authors contributed substantively in order to materialize the concept of this work. The first author conceived of the idea of this work and designed the experiments. The second author supervised the research and helped with the experiments along with the analysis of the data. The article was written by the first author and revised and critically reviewed by the second author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- YouTube Product Statistics, Available online: http://www.youtube.com/yt/press/statistics.html (accessed on 22 March 2015).
- Mitola, J.; Maguire, G.Q., Jr. Cognitive radio: Making software radios more personal. IEEE Pers. Commun. 1999, 6, 13–18. [Google Scholar]
- Haykin, S. Cognitive radio: Brain-empowered wireless communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar]
- Habiba, U.; Islam, M.I.; Amin, M.R. Performance evaluation of the VoIP services of the cognitive radio system, based on DTMC. J. Inf. Process. Syst. 2014, 10, 119–131. [Google Scholar]
- Tasnina, A.T.; Akhter, S.; Islam, M.I.; Amin, M.R. Spectrum sensing and data transmission in a cognitive relay network considering spatial false alarms. J. Inf. Process. Syst. 2014, 10, 459–470. [Google Scholar]
- Khan, R.T.; Islam, M.I.; Amin, M.R. Traffic analysis of a cognitive radio network based on the concept of medium access probability. J. Inf. Process. Syst. 2014, 10, 602–617. [Google Scholar]
- Ghasemi, A.; Sousa, E.S. Collaborative spectrum sensing for opportunistic access in fading environments, Proceedings of 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN), Baltimore, MD, USA, 8–11 November 2005; pp. 131–136.
- Mishra, S.M.; Sahai, A.; Brodersen, R.W. Cooperative sensing among cognitive radios, Proceedings of IEEE International Conference on Communications (ICC’06), Istanbul, Turkey, 11–15 June 2006; pp. 1658–1663.
- Shah, H.A.; Usman, M.; Koo, I. Bioinformatics-Inspired Quantized Hard Combination-Based Abnormality Detection for Cooperative Spectrum Sensing in Cognitive Radio Networks. IEEE Sens. J 2014, 15, 2324–2334. [Google Scholar]
- Ma, J.; Zhao, G.; Li, Y. Soft combination and detection for cooperative spectrum sensing in cognitive radio networks. IEEE Trans. Wirel. Commun. 2008, 7, 4502–4507. [Google Scholar]
- Bhattacharjee, S.; Sengupta, S.; Chatterjee, M. Vulnerabilities in cognitive radio networks: A survey. Comput. Commun. 2013, 36, 1387–1398. [Google Scholar]
- Zeng, K.; Tang, Y. Impact of Misbehaviors in Cooperative Spectrum Sensing for Cognitive Radio Networks, Proceedings of 7th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM), Wuhan, China, 23–25 September 2011; pp. 1–4.
- Vu-Van, H.; Koo, I. A sequential cooperative spectrum sensing scheme based on cognitive user reputation. IEEE Trans. Consum. Electron. 2012, 58, 1147–1152. [Google Scholar]
- Kaligineedi, P.; Khabbazian, M.; Bhargava, V.K. Malicious user detection in a cognitive radio cooperative sensing system. IEEE Trans. Wirel. Commun. 2010, 9, 2488–2497. [Google Scholar]
- Usman, M.; Koo, I. Secure cooperative spectrum sensing for the cognitive radio network using non-uniform reliability. Sci. World J. 2014, 1–10. [Google Scholar]
- Ponomarchuk, Y.; Seo, D.-W. Intrusion detection based on traffic analysis and fuzzy inference system in wireless sensor networks. J. Converg. 2010, 1, 35–41. [Google Scholar]
- Singh, R.; Singh, P.; Duhan, M. An effective implementation of security based algorithmic approach in mobile ad hoc networks. Hum.-Centric Comput. Inf. Sci. 2014, 4, 1–14. [Google Scholar]
- Gnanaraj, J.W.K.; Ezra, K.; Rajsingh, E.B. Smart card based time efficient authentication scheme for global grid computing. Hum.-Centric Comput. Inf. Sci. 2013, 3, 1–14. [Google Scholar]
- Chung, Y.; Choi, S.; Won, D. Lightweight anonymous authentication scheme with unlinkability in global mobility networks. J. Converg. 2013, 4, 23–29. [Google Scholar]
- Peng, K. A secure network for mobile wireless service. J. Inf. Process. Syst. 2013, 9, 247–258. [Google Scholar]
- Chair, Z.; Varshney, P. Optimal data fusion in multiple sensor detection systems. IEEE Trans. Aerosp. Electron. Syst. 1986, 22, 98–101. [Google Scholar]
- Ansari, N.; Chen, J.G.; Zhang, Y.Z. Adaptive decision fusion for unequiprobable sources. IEE Proc. Radar Sonar Navig. 1997, 144, 105–111. [Google Scholar]
- Chen, L.; Wang, J.; Li, S. An adaptive cooperative spectrum sensing scheme based on the optimal data fusion rule, Proceedings of 4th International Symposium on Wireless Communication Systems (ISWCS), Trondheim, Norway, 17–19 October 2007; pp. 582–586.
- Urkowitz, H. Energy detection of unknown deterministic signals. Proc. IEEE 1967, 55, 523–531. [Google Scholar]
- Zhao, T.; Zhao, Y. A new cooperative detection technique with malicious user suppression, Proceedings of IEEE International Conference on Communications (ICC), Dresden, Germany, 14–18 June 2009; pp. 1–5.
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).