Abstract
The idea of construction of twin buildings is as old as architecture itself, and yet there is hardly any study emphasizing their specificity. Most frequently there are two objects or elements in an architectural composition of “twins” in which there may be various symmetry relations, mostly bilateral symmetries. The classification of “twins” symmetry in this paper is based on the existence of bilateral symmetry, in terms of the perception of an observer. The classification includes both, 2D and 3D perception analyses. We start analyzing a pair of twin buildings with projection of the architectural composition elements in 2D picture plane (plane of the composition) and we distinguish four 2D keyframe cases based on the relation between the bilateral symmetry of the twin composition and the bilateral symmetry of each element. In 3D perception for each 2D keyframe case there are two sub-variants, with and without a symmetry plane parallel to the picture plane. The bilateral symmetry is dominant if the corresponding symmetry plane is orthogonal to the picture plane. The essence of the complete classification is relation between the bilateral (dominant) symmetry of the architectural composition and the bilateral symmetry of each element of that composition.1. Introduction
Symmetry is one of the oldest visual, aesthetic, stylish and functional characteristics of architecture. When talking about symmetry in architecture, it primarily refers to the geometric symmetry. Until the modern and contemporary architecture, symmetry was a dominant and universal principle in the architecture of all civilizations. Modern architects have been trying to create distance from all previous historical styles and asymmetry has become acceptable as a new and unexplored field of design. Through postmodern and contemporary architecture symmetry gets new innovative interpretations and visualizations (see [1–3]). Symmetry is one of the fundamental principles of the universe and nature and can be found everywhere [4,5]. Symmetry from the universe and nature reflects in all kind of human creativity and science [6]. When once talking about one bridge, Benjamin said that symmetry evoked a form of affective neutrality [7].
The study of symmetries, patterns, and repetitions is the central topic of the book On Growth and Form [8]. Symmetry of an object exists until, after all geometrical transformations are applied, there is at least one unchanged feature or some property of that objects [8]. Asymmetry is the complete absence of any type of symmetry (see also [9–11]). Kim Williams distinguishes the seven most often used types of symmetry in architecture: bilateral symmetry, rotation and reflection, cylindrical symmetry, chiral symmetry, similarity symmetry, spiral or helical symmetry and translational symmetry. To achieve different types of symmetry, a variety of spatial transformations may be used as well as combinations thereof. Mitra and Pauly analyzed some of those transformations and their application in architectural design, Figure 1 [12].

Bilateral symmetry is one of the most common types of symmetry of architectural and urban form, where the halves of a composition mirror each other [13]. Bilateral symmetry in plane can be defined as an organizing system that reflects either a plan, or elevation around a central line or axis [14]. Often, instead of bilateral symmetry, it is called mirror symmetry [15]. “The popular of bilateral symmetry is probably an expression of our experience of nature, and in particular with our experience of our own bodies. As many cultures believe that God created man in His own image, architecture has in turn probably been created in the image of man” [13].
Almost all living creatures are essentially symmetrical and identical individuals (twins) are “symmetrical” to each other. Fascination with the phenomenon of “twins” was one of the main ideas in the architecture of all civilizations. In architectural buildings “twins” are usually characterized by bilateral (mirror) symmetry. We also consider chirality of building object and the chirality of the twin composition itself (Figure 2). Chirality is found in two objects that are each other’s mirror image and which cannot be superimposed, such as our hands [13,16,17]. Such objects usually have “left” and “right” form. Chiral object cannot possess bilateral symmetry itself as well as any other symmetry transformation, which change orientation of the figure. In two dimensions, every figure that possesses an axis of symmetry is achiral. In three dimensions, every object that possesses a plane of symmetry or a center of symmetry is achiral [18].
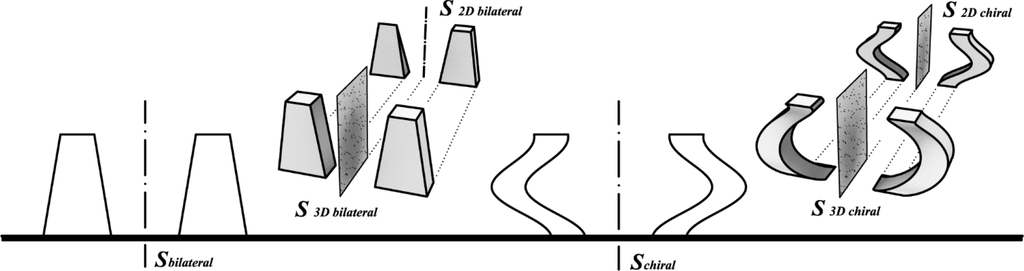
People have the ability to detect symmetry very fast, and this ability has been a topic of interest to psychologists and philosophers (e.g., [19]). More about human symmetry perception can be found in Tyler’s works (e.g., [20,21]). Humans are able to easily recognize bilateral symmetry (e.g., [22]) and they usually connect symmetry of an object with the existence of bilateral symmetry. About perception of chirality, Branndt said: “Studies in psychology of aesthetics have indeed addressed the issue of differences in the perception of left and right objects, and found that such differences do exist” [23].
2. Symmetry of Twins
Notion of symmetry has changed through history [9], but the essence of the idea and geometric settings of twin buildings remained the same. In this paper, symmetry of “twins” is analyzed in terms of contemporary interpretations of symmetry in architecture. Twin buildings, or towers, is architectonic composition of at least two similar elements (building objects), arranged in some geometric relation and placed to each other. This composition can be seen as one complex object. Symmetry relations among twin buildings are usually multiple or composite, in which some dominant type of symmetry can be noticed. We can distinguish the symmetry of each building element and the symmetry of the architectonic twin composition. We analyzed the twin composition having in mind that “twins” are usually characterized by bilateral symmetry. Classification is created from the point of view of an observer, who perceives architectural composition while standing in imaginary symmetry plane of that composition. The dominant (or primary) bilateral symmetry is symmetry of the composition orthogonal to the imaginary “plane of the twin composition”, while the bilateral self-symmetry of each building objects is secondary. For defining and analyzing different cases the following relation can be established:
Architecture is the image we see [24] and an architect’s ideas address the observer through that image, since perception of objects in space is based on 2D images view process. An observer is not able to see the complete architectural composition at once. The observer should stand near the imaginary symmetry plane [25] of the composition and to be in a position to have the possibility of symmetry perception. This position can be considered as twins symmetry keyframe of the observer’s visual perception. Such approach implies the existence of a mutually parallel plane of symmetry of architectonic twin composition and planes of symmetry of the building objects (intersection of symmetry planes is in the infinity).
Analyzing a pair of twin buildings, which is the most common in architecture practice, we start with an image view-projection of the architectural composition elements in (frontal) 2D view. These cases correspond to projection of parallel planes of symmetry, which are orthogonal to the frontal view. As a 2D image, the observer can notice mirror symmetry axes instead of a plane of symmetry, and we distinguish four 2D keyframe cases:
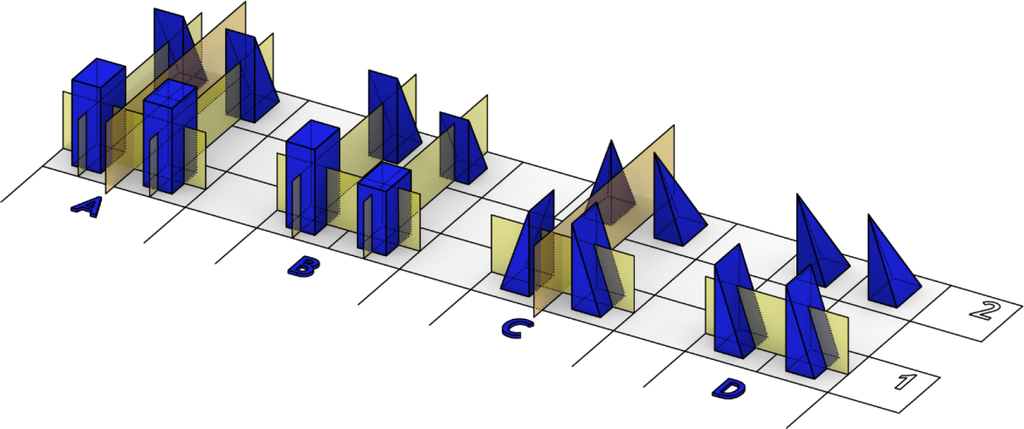
case A. Composition is bilaterally symmetric and the objects in the composition are bilaterally symmetric, too (Figure 3A).
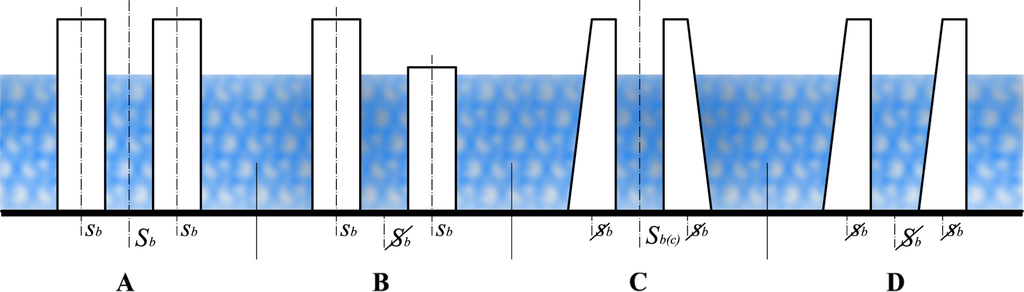 Figure 3. Twin towers in symmetry cases (A), (B), (C) and (D) (frontal view).
Figure 3. Twin towers in symmetry cases (A), (B), (C) and (D) (frontal view).case B. Composition is not bilaterally symmetric but each object in the composition is bilaterally symmetric (Figure 3B).
case C. Composition is bilaterally symmetric, but none of the objects in the composition is bilaterally symmetric (Figure 3C).
case D. Composition is not bilaterally symmetric and none of the objects in the composition is bilaterally symmetric too (Figure 3D).
Having only these 2D images in mind, we are not yet sure about the symmetry of the whole composition, but from the architectural point of view, we should have some impression. Very often, this view will match the dominant symmetry of the composition, not only in terms of symmetry planes, but also in terms of chirality. For example, an observer sees case D as a chiral composition of chiral objects. As we will see later, this does not have to be true, since there may be some other planes of symmetry, which are not visible to the observer or not dominant in the composition or in a single object. There are many examples of visually chiral in architecture [16,26], which is not chiral from the mathematical point of view.
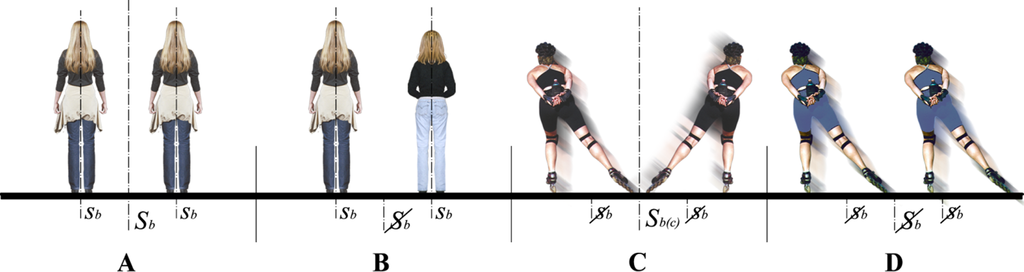
In terms of the geometry, the human body and the bodies of most living creatures are bilaterally symmetrical. Mobility does not interfere with the bilateral symmetry of the human body. Symmetry cases A and B in architecture are comparable with the geometrical symmetry of identical and fraternal twins at inaction. Symmetry case C is comparable with the geometrical symmetry of identical twins in motion and symmetry case D with symmetry of identical or fraternal twins in motion (Figure 4). Identical twins, standing next to one another, can be bilaterally symmetrical at inaction and chiral in motion. About this aspect of symmetry Hargittai said: “Different shapes have different symmetries, and the shapes that develop in nature and appear in human-made objects are closely related to motion. Humans and most, though not all, animals have a left side and a right side. Their bilateral symmetry is a consequence of their mode of motion” [15]. More about symmetries of non-rigid shapes (like human bodies) can be found in Raviv’s work in this field [27,28].
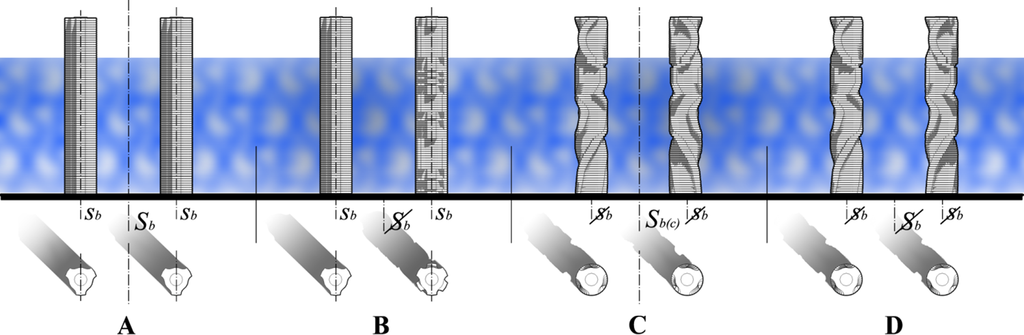
In contemporary architecture, the concept of dynamic architecture has been developed, where each floor of the tower rotates around vertical axes independently. Those buildings can be defined as non-rigid shapes in architecture. 3D model of David Fisher’s Dynamic tower in Dubai was used for the illustration shown in Figure 5. We can analyze the previously defined four cases of “twins” symmetry, shown through the motion of the floors.
As we said, classification of “twins” symmetry in this paper is based on the existence of bilateral symmetry, in terms of the perception of an observer, who is not always able to see a complete architectural composition, or at least, not at once. The observer should be in a position to have the possibility of perception of the necessary symmetries for the proposed classification. Sometimes, this approach results in a wrong perception. For example, in a complex twin composition in Figure 6, it is not easy to get the whole picture of the twin composition due to the diversity of the objects themselves, their symmetries and a well-chosen position of the objects in the composition. If the observer is moving around the building, he then perceives other geometric characteristics of architectural composition and its elements as well, and forms a complete picture of the existing symmetries.

Complete classification of twins’ symmetry must include both 2D and 3D perception behavior analysis, to exceed illusive perception. We will consider the concept of twin composition based on bilateral symmetry and chirality of the composition and of the building elements itself. All objects that are bilaterally symmetric are achiral, but there are achiral objects with other symmetries that render an object achiral (such as inversion symmetry), although these are less relevant to architecture [16].
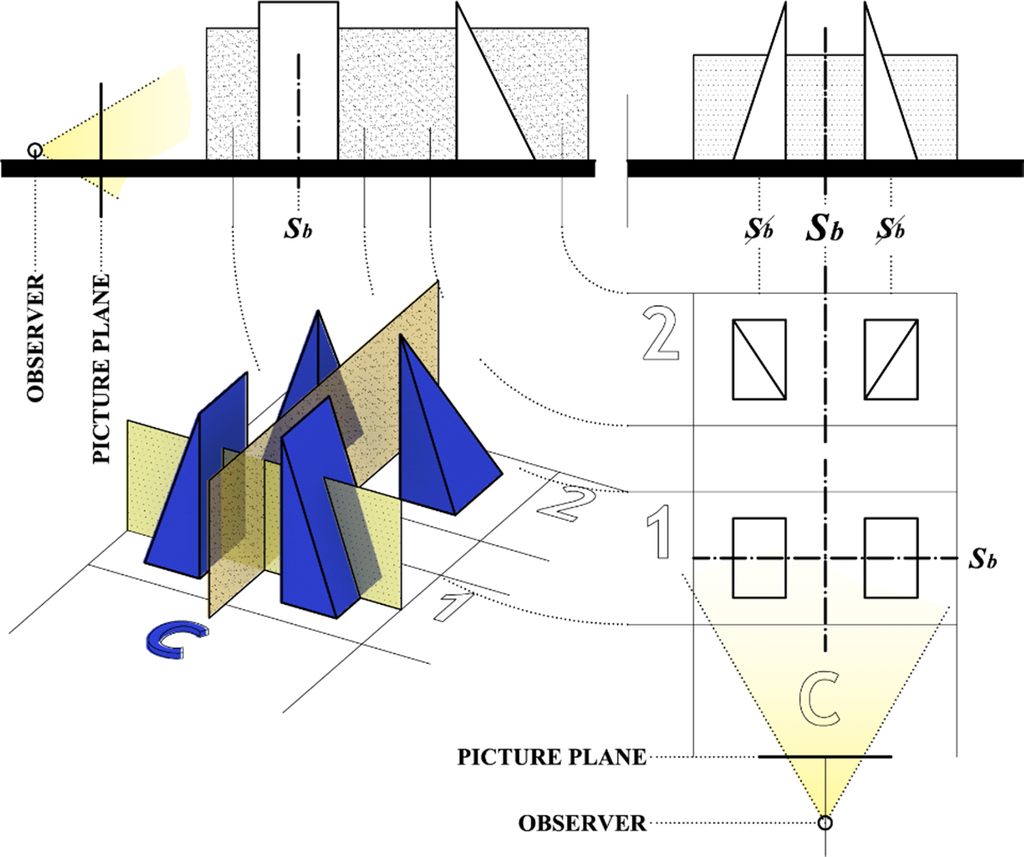
In Figure 7 the previous four 2D cases are shown in isometric view, together with the corresponding sub-variants. Here we represent only two sub-variants for each case, based on the existence of mutually orthogonal planes of symmetry. In each sub-variant in row number 1, common symmetry plane of architectural composition and of building objects exists. That plane is parallel with the observer’s starting picture plane. All these compositions are achiral. In all these cases the building units are achiral too, since all of them possess a symmetry plane. But notice that this symmetry plane is not the dominant symmetry of the twin composition, since it is in the plane of the twin composition. An observer is not able to notice the whole twin composition and this plane of symmetry at the same time. Similarly, cases B1 and D1 are more likely to be seen as a chiral composition then achiral, since the view where one can recognize the left and the right half of twin composition is parallel with the symmetry plane of the composition. Sub-variants in row number 2 do not posses this (frontal) symmetry plane. A2 and C2 twin composition are achiral, but mutually different, since in A2 building objects are achiral and in case C2 building objects are chiral. Cases B2 and D2 represent chiral twin composition, but in case B2 buildings objects are achiral and in case D2 they are chiral.
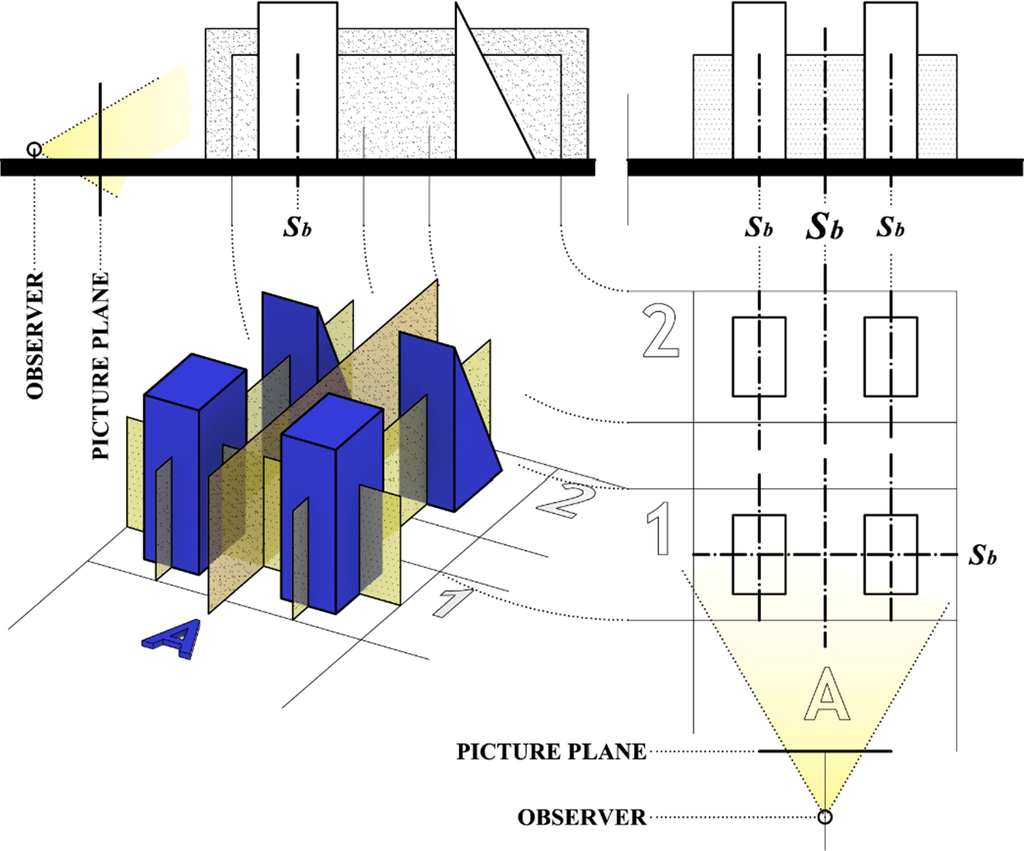
2.1. Case A
In this case there is an architectural twin composition that is bilaterally symmetric and each of the building objects is bilaterally symmetric too. Therefore, the composition is achiral as well as its building elements. The symmetry of the architectural composition is bilateral (Sb), as well as the symmetry of building objects (sb).
In 3D perception behavior there are two sub-variants, with (A1) and without (A2) symmetry plane parallel to the picture plane of the observer’s twins symmetry keyframe position. That plane is orthogonal to the dominant plane of symmetry of the whole (Figure 8). From the aspect of the dominant symmetry, case A in geometry of the composition-building parts can be described as bilaterally–bilateral symmetry in both sub-variants (and also as achiral-achiral).
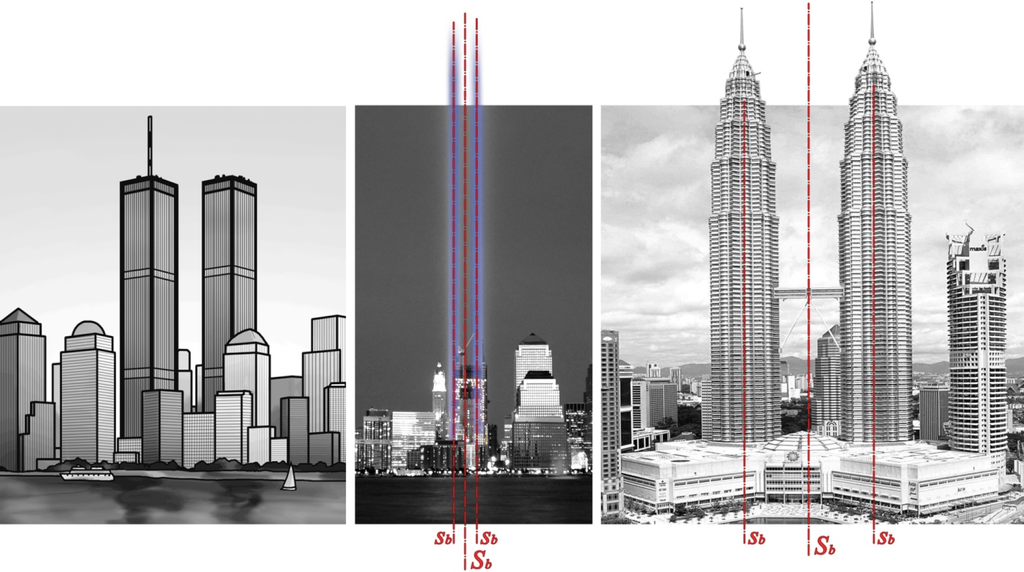
In addition to the bilateral symmetry, some other types of symmetry may be present, considering multiple symmetries characteristics of architecture. Light beams of the WTC memorial are bilaterally symmetrical to each other and each of them are bilaterally self-symmetrical (Figure 9). There is also cylindrical symmetry of each of the light beams. Similar examples are the Petronas Towers, shown in the same figure.
Most historical examples of the architectural composition of twin buildings are based on case A. These examples can be seen in all civilizations and through all styles of architecture. Figure 10 shows the twin elements of the gate of Kalemegdan fortress in Serbia, The Twin Pogoda temple in Taiyuan (China) and Trier Saint Peter’s cathedral in Germany.

The towers of Pagoda temple are identical twin buildings, Figure 10. Saint Peter’s Cathedral is the example of the complex symmetry case, which includes case A and case B, explained above. Two radial tower elements (in the corners of the Cathedral) are identical, with bilaterally–bilateral symmetry, but the composition of two prismatic steeples is not bilaterally symmetrical. In that case, there is none bilaterally–bilateral symmetry of two twin elements of the building.
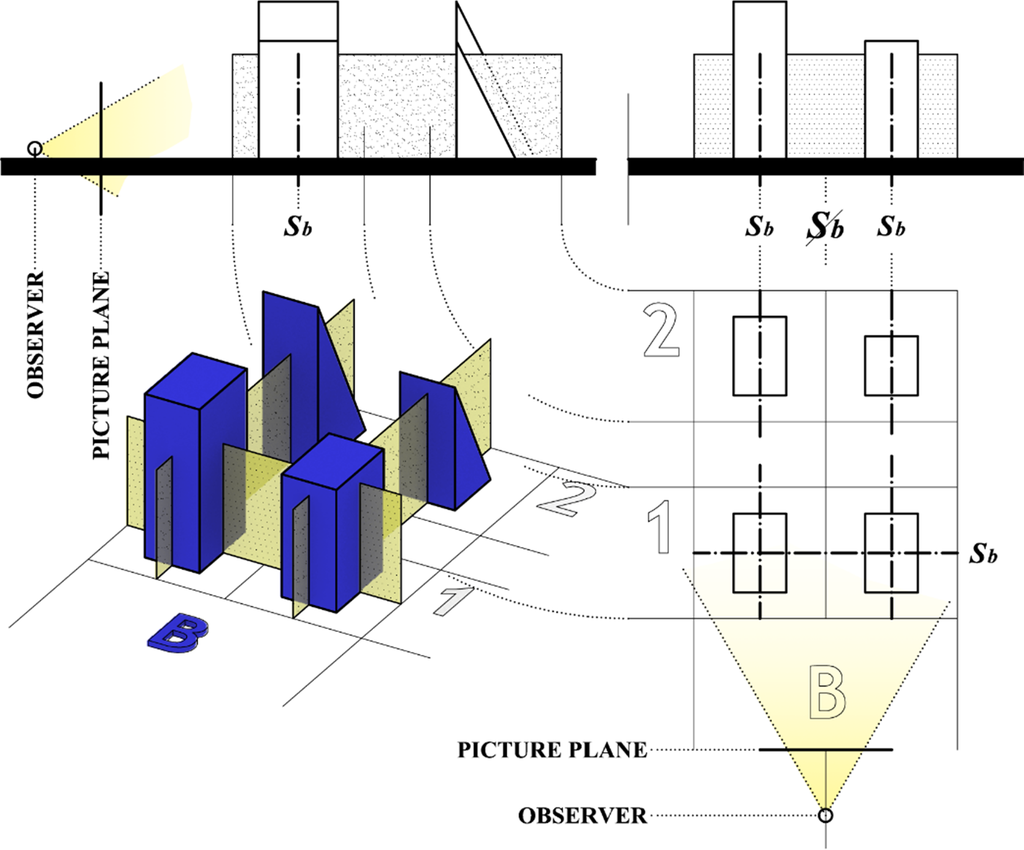
2.2. Case B
In this case there is an architectural composition of two buildings and each one is bilaterally self-symmetric with mutually parallel planes of symmetries, but architectural composition does not have the plane of symmetry parallel with those planes. Some other types of symmetry may be present. Their context and their purpose make them twin objects.
In 3D perception behavior there are two sub-variants, with and without a symmetry plane parallel to the picture plane of the observer’s twins symmetry keyframe position, Figure 11. In B1, that plane of symmetry is parallel to the plane of symmetry of the whole composition and does not have the role of the dominant symmetry. Case B in geometry of the twin buildings can be described, from the aspect of dominant symmetry as non-bilaterally–bilateral symmetry. From strictly geometric point of view, B1 is bilaterally–bilateral symmetry, and B2 is non bilaterally–bilateral symmetry. B1 is achiral composition, but for the observer it is rather visual chiral (because of the position of the mirror plane which is not easily visible), while each building object is achiral.
The Cathedral of Chartres in France has two bilaterally self-symmetrical towers, which are not mutually bilaterally symmetrical. The West gate of Belgrade in Serbia consists of two towers, similar structures, one of which is higher (Figure 12). In both examples, in their spatial structure bilateral self-symmetry of each part of the building exists. The symmetry of their architectural composition is not bilateral, but because of its structure, function and context can be considered as “twins”. Sometimes, this case of symmetry of “twins” is a part of complex symmetrical relations, like in the Cathedral shown in Figure 12.

Within this case we also recognize objects that are similar or simply scaled in order to produce more dynamic structures. Sometimes such objects are connected with elements that do not fit with any symmetry and very often are asymmetric, but this has no influence to the observer to see the composition as strongly symmetric.
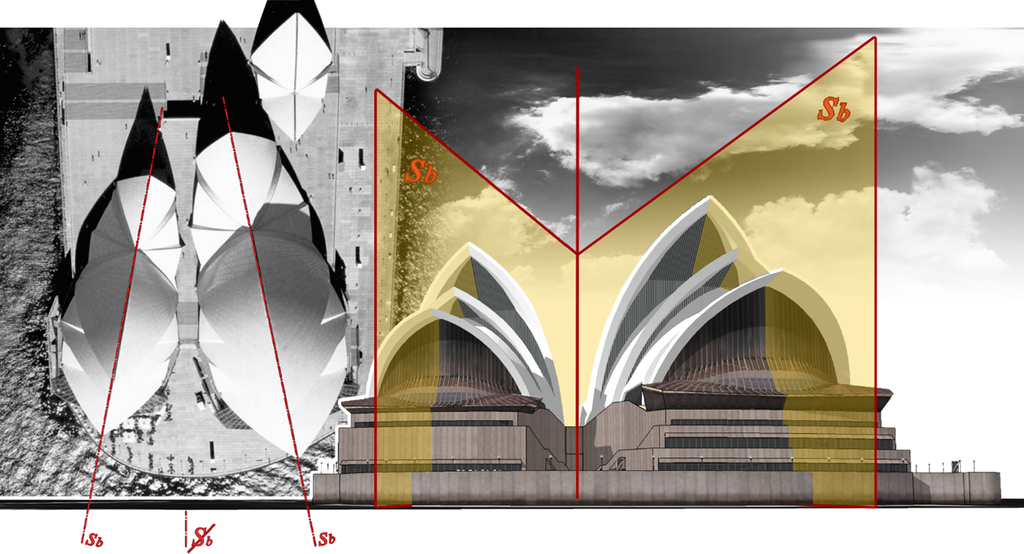
One of the specific examples of case B symmetry of “twins” is Sydney Opera House. The shells are segments of a sphere, thus similar in shape, while differing in size and inclination [13]. The extracted symmetries include reflections, as well as general similarities that involve uniform scaling, rotation, and translation. Each of two “twin” elements of Sydney Opera House is bilateral self-symmetrical, but in the geometrical composition of these elements bilateral similarity symmetry does not exist (Figure 13). Instead of that, rotational symmetry composed with scaling is presented. There is a third element of this structure, much smaller and in the background. It can be defined as a third twin element, but observer from the previously defined position cannot see all three of them at once.
2.3. Case C
In this case there is an architectural composition of two buildings or two parts of the same building, which are mutually mirror-symmetrical, but the building objects do not have a mirror plane parallel with the dominant mirror plane of the composition. The whole composition is mirror symmetric and achiral.
In 3D perception behavior there are two sub-variants, with and without symmetry plane parallel to the picture plane of the observer’s twins symmetry keyframe position, Figure 11. In case C1 each building object is achiral in 3D, but in case C2 these building objects are chiral in 3D (Figure 14). In both sub-variants, the twin composition is achiral, since there is at least one symmetry plane of the twin composition. Case C in geometry of the twin buildings from the aspect of dominant symmetry can be described as bilaterally–non-bilateral symmetry. From the strictly geometric point of view, C1 is bilaterally–bilateral symmetry, and C2 is bilaterally–non-bilateral symmetry.
Asymmetrical objects and symmetry breaking can be of a high interest for architects and viewers, introducing a new dynamical component. However, since in this paper we are interested only in twin compositions, there must be some noticeable symmetries or similarities among them. Very often, chiral objects in architecture are based on rotation and translation or scaling, so this produce spiral and helicoidal structures which have orientation, and twins chiral objects can be mirror reflected, so that the observer can easily notice two different orientations.
Since mirror reflection changes the orientation of an object, a chiral object does not possess bilateral (mirror) symmetry. In some cases building objects have bilateral self-symmetries, which the observer cannot perceive from the observation position lying in the reflection plane of the whole composition (case C1). An example is Bahrain WTC towers, where each of the towers has bilateral self-symmetry hidden from the observer standing in symmetry plane of the architectural composition. This is therefore an example of case C (C1) of symmetry of “twins”. Almaty Twin Towers in Kazakhstan are a typical example of the same case of “twins” symmetry (Figure 15).

2.4. Case D
In this case there is an architectural composition of two buildings, but there is no any dominant symmetry plane of the composition nor of the building objects, so there is no symmetry plane orthogonal to the plane of composition. Some other elements of symmetry (translation, rotation) may be present. This case of symmetry is characteristic of modern and especially contemporary architecture. In 3D perception behavior there are two sub-variants, with and without a symmetry plane parallel to the picture plane of observer’s twins symmetry keyframe position, Figure 16.
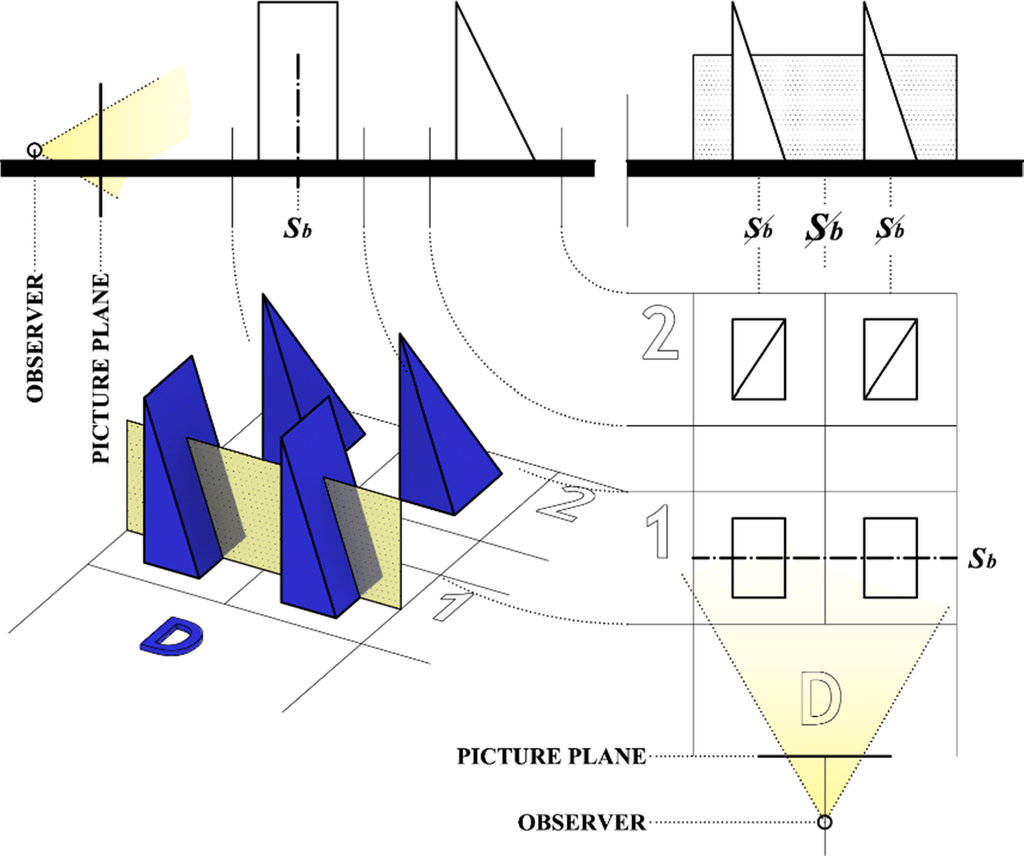
Case D in geometry of twin buildings can be described, from the aspect of dominant symmetry as non-bilaterally–non-bilateral symmetry. From the strictly geometric point of view, D1 is bilaterally–symmetry, and D2 is non-bilaterally–non-bilateral symmetry. D1 is achiral composition, but for the observer it is rather visually chiral (because of the position of the mirror plane which is not easily visible), while each building object is achiral.
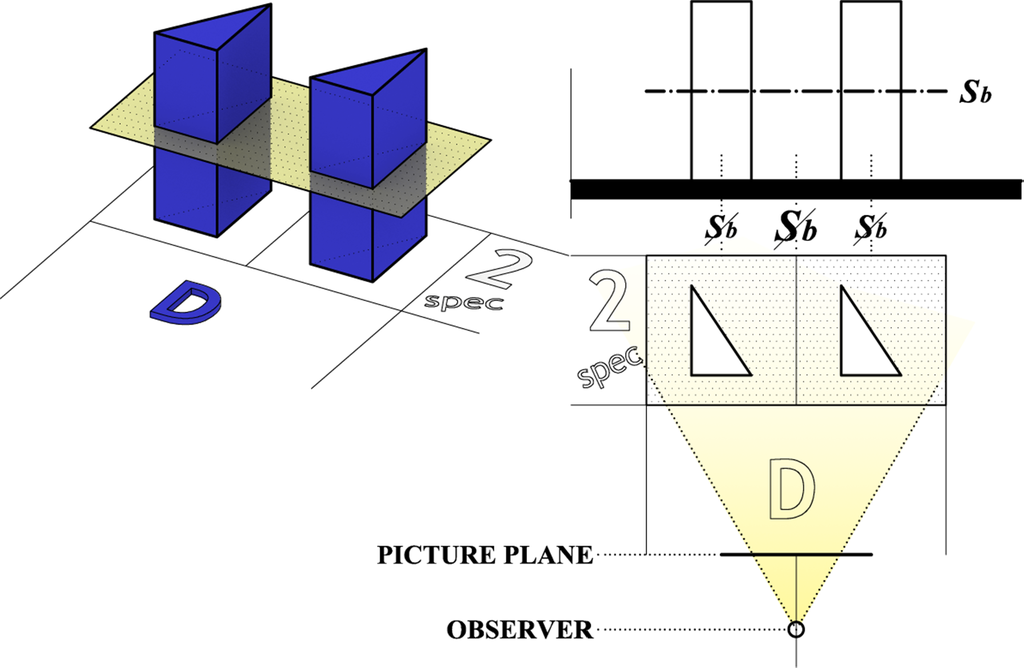
Figure 17 illustrates one more possibility of twin composition. There is a horizontal symmetry plane, which can be found in example shown in Figure 6—Azrieli Center in Tel Aviv, Israel. Horizontal symmetry plane may be mutual for all elements in an architectural composition. The role of such one plane of symmetry is to connect different building objects in a twin composition. Such a plane of symmetry is rarely used separately of the described cases. It can be considered as a special case of D2, where there are no other planes of symmetries, except for this one.
In Figure 18 shows contemporary examples of this case. There is the characteristic absence of building’s bilateral self-symmetry and bilateral symmetry of architectural composition, but in addition, there are twins that we call emphatic. Velo towers are maybe the best example of this assertion. “Kyssen” Towers in Gothenburg are competition entry for Scandinavia’s tallest skyscraper in Gothenburg. Two asymmetrical buildings are unequivocally “twins”. Hang Lung Plaza designed for Shenyang in China is a large commercial complex. Depending on the position of the observer, they could be observed as four pairs of “twins”, all of which can be classified as the case D. In many of these examples similarity between twins objects can be noticed. In this case the objects have only similarity symmetry, without any kind of bilateral symmetry of architectural composition or bilaterally self-symmetry. This concept of architectural design is the aesthetic characteristics of the largest number of contemporary architectural compositions of “twins”. Also it can be defined as contemporary and probably the future trend in architectural design.

3. Conclusions
The idea of construction of twin buildings is as old as architecture itself. Twin objects can exist as a complex unit with sub-units (buildings), or as elements of the same object. Frequently there are two objects or elements in architectural composition of “twins” which can be analyzed as a complex unit. In relation to the previous and considering the existence of bilateral symmetry (as the most frequent type of symmetry in architecture) and chirality, the authors have suggested a classification of “twins” symmetry. This classification is created from the point of view of an observer, who perceives architectural composition while standing in an imaginary symmetry plane of that composition, exactly as the designers planned. That position can be defined as the observer’s twins symmetry keyframe, with 2D perception behavior aspect. Some other symmetry relations may be present in a twin building architectural composition, which the observer can perceive when walking around the buildings. That is 3D perception behavior aspect. Complete classification of twins symmetry include both, 2D and 3D perception behavior analysis, to avoid illusive perception. Such analysis can distinguish four cases of the symmetry of “twins”, which are marked as cases A, B, C and D, with two sub-cases presented in this paper. The essence of these cases is the relation between bilateral symmetry of an architectural composition and bilateral symmetry of each element. That relation is based on the existence or non-existence of the dominant bilateral symmetry identified as:
case A. bilaterally–bilateral symmetry
case B. non-bilaterally–bilateral symmetry
case C. bilaterally–non-bilateral symmetry
case D. non-bilaterally–non-bilateral symmetry
Dominant (or primary) is the symmetry of a composition orthogonal to the imaginary plane of a twin composition, while self-symmetry of each building objects is secondary. Multiple cases can be found in the same architectural composition, which include symmetry relations of the parts of the buildings. Cases A and B were dominant in classical architecture and in the period of modern architecture, and case C and especially case D are characteristic of contemporary architecture. Figure 19 show examples of under construction and in progress projects, classified in the four cases.

Acknowledgments
The authors express their gratitude to the Ministry of Science and Technological Development of Serbia for providing partial support for this project (Grant No. 174012, Grant No. 33051 and Grant No. 36037).
The authors thanks David Avnir, Institute of Chemistry, The Hebrew University of Jerusalem, for useful comments and valuable remarks that considerably improved the paper.
Author Contributions
Contributions of the first author are development of the researching concept, classifications of “twins” symmetry and making original figures. Contributions of the second author are development of the researching concept, work on chirality in architecture and mathematical aspects of the research. Contributions of the third author are analyzing of the historical aspects of the “twins” symmetry research and supervision.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baglivo, J.A.; Graver, J.E. Incidence and Symmetry in Design and Architecture; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Hahn, A.J. Mathematical Excursions to the Worlds Great Buildings; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Moskal, G. Modern Buildings: Identifying Bilateral and Rotational Symmetry and Transformations; Rosen Classroom: New York, NY, USA, 2004. [Google Scholar]
- Lawson, B. The Language of Space; Architectural Press: Oxford, UK, 2001. [Google Scholar]
- Radovic, L.J.; Jablan, S. Visual Communication through Visual Mathematics. Filomat 2009, 23, 56–67. [Google Scholar]
- Jablan, S. Symmetry, Ornament and Modularity; Series on Knot and Everything; World Scientific Publishing: Singapore, 2002; Volume 30. [Google Scholar]
- Benjamin, A. Writing Art and Architecture; Re.Press: Melbourne, Australia, 2010. [Google Scholar]
- Thompson, D.W. On Growth and Form; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Renata, J.M. Symmetry Notion as a Universal Principle of Design. Arhitekturaiurbanizam 2008, 22–23, 85–97. [Google Scholar]
- Sabelli, H.; Lawandow, A.; Kopra, A.R.; Asymmetry, Symmetry. Beauty. Symmetry 2010, 2, 1591–1624. [Google Scholar]
- Vollers, K. Twist & Build: Creating Non-orthogonal Architecture; 010 Uitgeverij: Rotterdam, The Netherlands, 2001. [Google Scholar]
- Mitra, N.J.; Pauly, M. Symmetry for Architectural Design, Proceedings of the Advances in Architectural Geometry, Vienna, Austria, 15–16 September 2008.
- Williams, K. Symmetry in Architecture, Available online: http://www.mi.sanu.ac.rs/vismath/kim/index.html accessed on 9 February 2015.
- Farrelly, L. The Fundamentals of Architecture; AVA Publishing SA: Lausanne, Switzerland, 2007. [Google Scholar]
- Hargittai, M.; Hargittai, I. Visual Symmetry; World Scientific Publishing: Singapore, 2009. [Google Scholar]
- Avnir, D.; Huylebruck, D. On Left and Right: Chirality in Architecture. Nexus Netw. J 2013, 15, 171–182. [Google Scholar]
- Petitjean, M. Chirality in Metric Spaces. Symmetry Cult. Sci. 2010, 21, 27–36. [Google Scholar]
- Wagnière, G.H. On Chirality and the Universal Asymmetry: Reflections on Image and Mirror Image; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Beck, D.M.; Pinsk, M.A.; Kastner, S. Symmetry Perception in Humans and Macaques. Trends Cogn. Sci. 2005, 9, 405–406. [Google Scholar]
- Bars, I.; Terning, J. Symmetry and Perspective. In Extra Dimensions in Space and Time; Multiversal Journeys; Springer: New York, NY, USA, 2010; pp. 43–46. [Google Scholar]
- Tyler, C.W. Human Symmetry Perception and Its Computational Analysis; Taylor & Francis: Abingdon, UK, 2009. [Google Scholar]
- Treder, M.S. Behind the Looking-Glass: A Review on Human Symmetry Perception. Symmetry 2010, 2, 1510–1543. [Google Scholar]
- Branndt, J.; Mackavey, W. Left-right Confusion and the Perception of Bilateral Symmetry. Int. J. Neurosci. 1981, 12, 87–94. [Google Scholar]
- Tierney, T. Abstract Space Beneath the Media Surface; Taylor & Francis: Abingdon, UK, 2007. [Google Scholar]
- Todorović, D. Geometric and Perceptual Effects of the Location of the Observer Vantage Point for Linear-perspective Images. Perception 2005, 34, 521–544. [Google Scholar]
- Hargittai, I.; Hargittai, M. Symmetry: A Unifying Concept; Shelter Publications: Bolinas, CA, USA, 1994. [Google Scholar]
- Raviv, D. Symmetries of Non-rigid Shapes, Proceedings of the Workshop on Non-Rigid Registration and Tracking through Learning, Rio de Janeiro, Brazil, 14 October 2007.
- Raviv, D. Full and partial symmetries of non-rigid shapes. Int. J. Comput. Vis. 2010, 89, 18–39. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).