Abstract
A model is described that can be used to estimate the bulk polarization of large rotating meteoroids in the magnetic field of a neutron star. The results of this model are applicable to the Supernova Neutrino Amino Acid Processing model, which describes one possible way in which the amino acids, known in nearly all cases to exhibit supramolecular chirality, could have become enantiomeric.
1. Introduction
Analyses of inclusions in meteoritic carbonaceous chondrites [–] have shown that the molecules of life, especially the amino acids, are made in outer space. Furthermore, some of the amino acids so synthesized tend to have the left-handed chirality that is observed almost entirely in earthly amino acids.
It is generally accepted that if some mechanism can introduce an imbalance in the populations of the left- and right-handed forms of any amino acid [], successive synthesis or evolution of the molecules involving autocatalytic reactions can amplify this enantiomerism ultimately to produce a single form. What is not well understood, however, is the mechanism by which the initial imbalance is produced, and the means by which it always produces the left-handed chirality observed in the amino acids. This enigma has been discussed in numerous reviews in past years (see, e.g., [–]).
The energy states of the left- and right-handed forms have been shown, by detailed computations, to differ at most by infinitesimal amounts due to parity violation [,], so it would be difficult for thermal equilibrium to produce the imbalance. However, some evidence exists that electroweak parity-violating energy shifts could produce an enantiomeric excess if the molecules are in a gas-phase [].
Recent work [,] has suggested that the chirality of the amino acids could be established in the magnetic field of a nascent neutron star from a core-collapse supernova via processing by the neutrinos that would be emitted. This model, the Supernova Neutrino Amino Acid Processing model, or SNAAP model, not only appears to produce a small chiral imbalance, but always produces the same sign of the chirality.
Another suggested mechanism lies with the processing of a population of amino acids by circularly polarized light [–]; this could select one chirality over the other. However, this solution does not easily explain why the physical conditions that would select one form in one place would not select the other in a different location. Nonetheless [], a region as small as a planetary system could be processed by the output from a localized region of a single star so that all of the light could be of a single circular polarization, and this could explain the observed meteoritic and Earth’s results. Another problem with this model is that it must destroy large amounts of amino acids in order to produce significant enantiomerism [].
Another possibility [] invokes selective processing by some manifestation of the weak interaction, which does violate parity conservation, so it might perform a chiral selection. This idea was based on earlier work [,]. Mann et al. [] focused on the β-decay of 14C to produce the selective processing. However, it was not possible in that study to show how simple β-decay could produce chiral-selective molecular destruction. A modern update on this possibility [] does appear to produce some enantiomerism. Another suggestion [] assumed that neutrinos emitted by a core-collapse supernova would selectively process the carbon or the hydrogen in the amino acids to produce enantiomerism. This suggestion also did not explain how a predisposition toward one or the other molecular chirality could evolve from the neutrino interactions. A similar suggestion [] involves the effects of neutrinos from supernovae on molecular electrons. It was also suggested that the differences between ortho- and para-hydrogen pairs [] in the amino acids could produce a chiral selection. The possibility that dark matter or cosmological neutrinos could select enantiomers has also been studied [].
In this paper, we study the capability of the SNAAP model for selective destruction of one molecular chirality. This extends previous work [] to include the dynamical effects that would be produced on the amino acids that were included in meteoroids that were large enough to escape destruction by the supernova photons as they passed by a nascent neutron star. This model has many similarities to nuclear magnetic resonance, even though it is essentially classical. The study does show that the amino acids contained in a large meteoroid could undergo orientation from the magnetic field of the neutron star, subsequent chiral sub-state selection from the combination of that field and the rotation of the meteoroids, and finally chiral selection by the neutrinos emitted as the neutron star produced by a core-collapse supernova cools over its characteristic few second cooling time.
Section 2 reviews the SNAAP model. Section 3 presents the model by which we describe the chiral state selection and determines the resulting population imbalance. Section 4 estimates the magnitude of the enantiomeric excess that might be expected from this model, and Section 5 presents our conclusions.
2. The SNAAP Model
This model assumes that the neutrinos emitted from the nascent neutron star would interact with the amino acids that had been oriented by the neutron star’s magnetic field. These molecules would have to be contained in large meteoroids that happened to be passing by the star as it became a supernova, so that they could survive the high temperature environment existing near the star. The crucial interaction that destroys 14N, is
where
is an electron antineutrino and e+ is a positron. It was also assumed that some imbalance in the total angular momentum of the molecules would be achieved, perhaps by the Buckingham effect [,], so that the conversion of 14N to 14C would, because of a spin selection effect on the strength of the interaction, preferentially destroy one orientation compared with the other. The geometry of this situation is indicated in Figure 1, and the redistribution of the magnetic sub-state populations of the molecules is indicated in Figure 2.
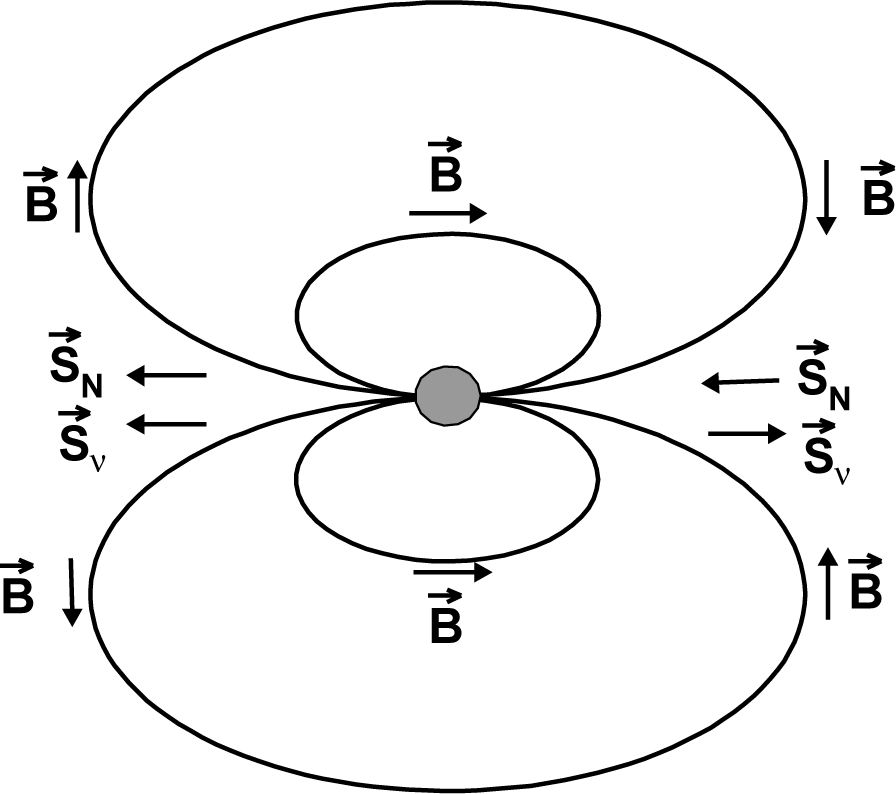
Figure 1.
Magnetic field around a neutron star, indicated by B, directions of the antineutrino spins, indicated by
, and the alignment direction of the 14N, indicated by
[,]. Courtesy of the International Journal of Molecular Sciences and Springer Publishing.
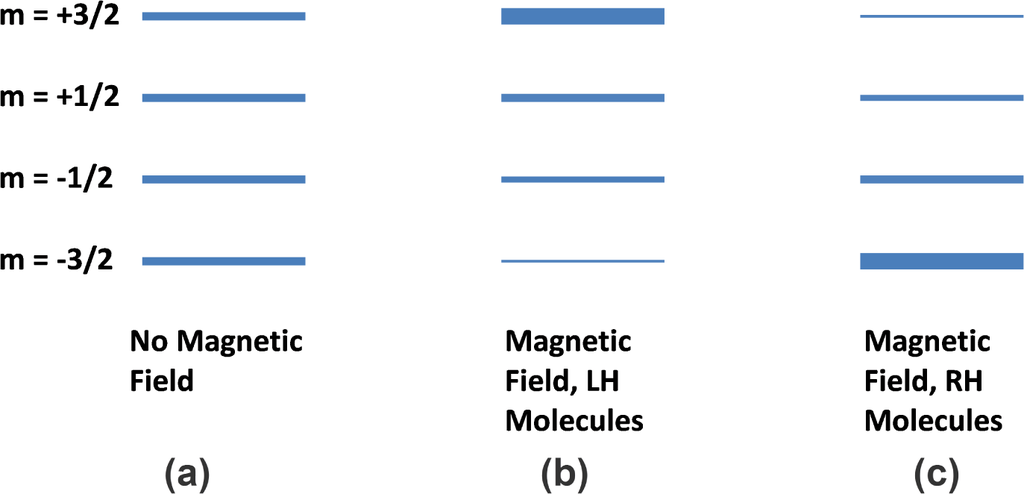
Figure 2.
Populations of the different magnetic sub-states for an atom having angular momentum
in a zero magnetic field (a), and for left-handed molecules (b) and right-handed molecules (c) in the presence of an external magnetic field. The thickness of the line indicates the magnitude of the population of each sub-state [,]. Courtesy of the International Journal of Molecular Sciences and Springer Publishing.
The strength of the neutrino interactions that destroy the 14N depends on the orientation of the neutrino’s spin with that of the 14N, as well as conservation of angular momentum. This is indicated by Equations (2) and (3). The 14N atom has a spin of 1, in units of Planck’s constant divided by 2π, whereas the
and the e+ each have spins of
. The 14C atom has a spin of zero.
In Equation (2), the anti-aligned case, the two spin vectors on the left-hand side of the equation can add up to
and can equal the sum of the spin vectors on the right-hand side. In Equation (3), the aligned case, the two spin vectors on the left-hand side of the equation add up to
and cannot equal the spin vector sum on the right-hand side without an additional unit of angular momentum, indicated by the question mark. This must come from the wave function of the νe or the e+, and it is known [] to inhibit the destruction of 14N in the aligned case with respect to the anti-aligned case by about an order of magnitude.
We expect that the alignment of the nuclear spin in the neutron star’s magnetic field will result in a slight enantiomeric excess. The hyperfine interaction will couple the nuclear and electronic spins and has been well studied in stellar environments [,]. Then, while the relationship is non-trivial for complex molecules, the molecular chirality can be shown to be related the electron angular momentum []. Thus, this would select one chirality on each side of the neutron star. Although the effects on the two sides of the star would come close to cancelling out if the neutrino fluxes were the same on both sides, that has been shown not to be the case in the strong magnetic field of a neutron star [–], hence one of the chiral states would then be selected.
Although the cross section for the neutrino-14N interaction is tiny, roughly 10−40 cm2, this will produce an enantiomeric excess of about a part in 106 in this model []. This is comparable to or greater than that achieved in other models, although direct comparison is difficult. As with any model of chirality selection, amplification, presumably by autocatalysis [–], which has been demonstrated to occur in laboratory experiments [–], is required to produce the order-of-a-few percent magnitudes of the enantiomeric excess observed in the meteorites, and the homochirality observed on Earth.
Additional details of the SNAAP model are discussed in [] and [].
3. Dynamical Model of Chiral State Selection
The vectors that are relevant to this model are shown in Figure 3. These include the magnetic field vector, the molecular total angular momentum vector, and the vector that characterizes the rotation of the meteoroid in which the molecules are contained. Clearly the orientation of the rotation vector of the meteoroid, ω, is random with respect to the direction of the magnetic field, B, and the orientation of the molecules within the meteoroid is random with respect to the direction of ω. Thus any dynamical description of the effects associated with molecular sub-state reorientation needs to average over the directions of two of the vectors with respect to that of the magnetic field. A Monte Carlo code was written, and the averages performed, not only over the directions, but over the magnitude of the magnetic field B as well.
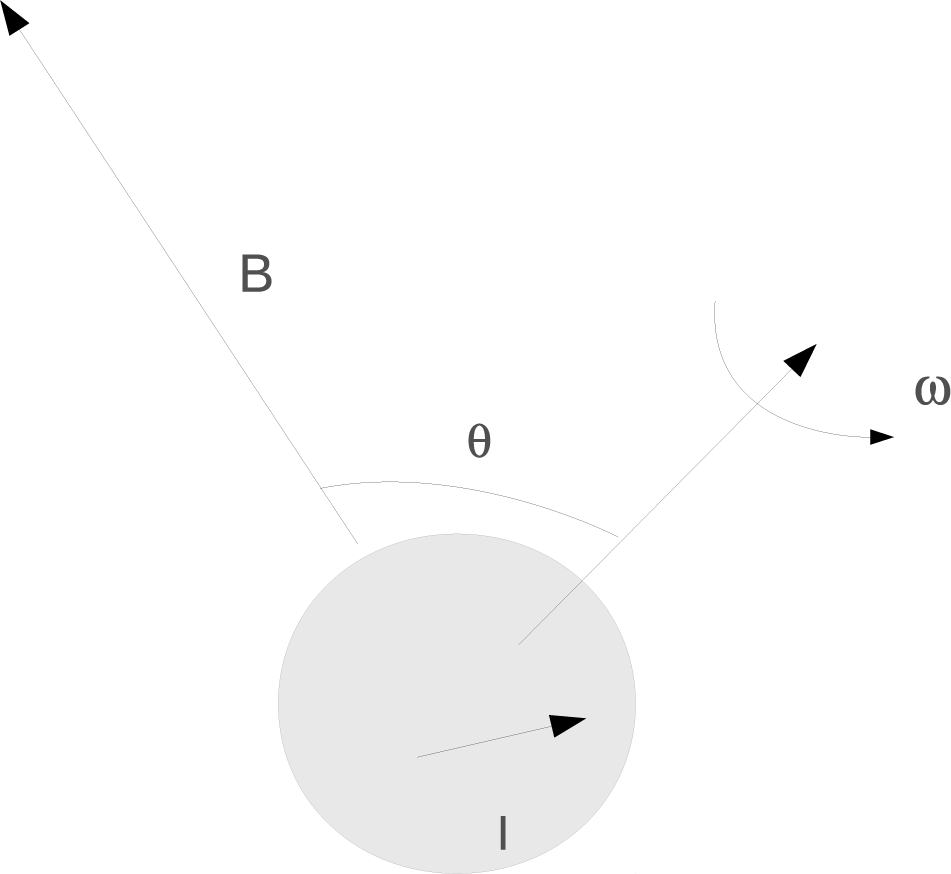
Figure 3.
The vectors relevant to the dynamical model of chiral state selection in the SNAAP model. B is the magnetic field vector, I is the total spin of the molecule, and ω is the vector that characterizes the rotation of the meteoroid in which the molecules are contained.
The quantity calculated by the Monte Carlo code is the bulk polarization of the meteoroid, M, which results from the interaction between the magnetic field of the nascent neutron star and the rotation of the meteoroid. This is similar to that from nuclear magnetic resonance, in which the slight imbalance in magnetic sub-state distribution in thermal equilibrium is shifted by a radiofrequency signal as the magnetic field passes through the value at which the energy difference between the sub-states is resonant. In the present model, the shift is not due to a resonant condition, but rather to an adiabatic transition between the chiral states that results from the interaction between the magnetic field of the neutron star and the rotating total angular momentum of each molecule.
The bulk polarization of the molecules trapped in a meteoroid will depend on the strength of the star’s field at the meteoroid’s location, the gyromagnetic ratio of the molecule γ, the meteoroid’s angular speed, and the orientation of the angular velocity vector with respect to the magnetic field. In the reference frame of the meteoroid, the magnetic field has a component parallel to the angular velocity vector and a component perpendicular to this vector, with the perpendicular component rotating at the angular frequency of the meteoroid. The polarization is well-established in this condition []. For a population of polarized states with a rotating component of a magnetic field, the magnetization vector is given by the Bloch Equation []:
where the bulk magnetization
is initiated in the external magnetic field for a material with number density n and magnetic moment μ. The relaxation time, TR, corresponds to the damping time constant during which a magnetized medium returns to a state of random orientation. The last term in Equation (4) corresponds to the torque on the magnetic moment from the medium’s motion in the external magnetic field.
For a material of non-zero magnetic moment in an external magnetic field B○, the angular momentum vector will precess about the magnetic field axis with the precession frequency ω○ = γB○. The rotation of the meteoroid in the magnetic field induces an NMR-like situation in which a rotating magnetic field B1 exists about a stationary magnetic field B○ in the reference frame of the meteoroid. In the case of an additional field B1 perpendicular to the external field and rotating about B○ with a frequency ω, the precession frequency about this field vector is defined as ω1 = γB1. Equation (4) can then be solved by assuming a rotating reference frame in which B1 is stationary.
We start with a simplified model in which the medium is assumed to be rotating at constant angular speed in the magnetic field from a central neutron star. For this situation, the time spent in the magnetic field is assumed to be much longer than the relaxation time. For this reason, we can take the stationary solution of the bulk magnetization:
from which the average magnetization of a population of molecules can be written in component form:
where Δω = ω − ω○. In Equation (6), the maximum polarization in the z direction, defined to be parallel to the field B○, will occur for a large Δω corresponding to a large difference in the perpendicular field rotation rate and the precession frequency about the parallel field. This corresponds to a minimum in the x and y components of the bulk magnetization. The overall polarization angle ϕ with respect to B○ is given by:
The parallel and perpendicular components of the magnetic field are determined by the angle between the meteoroid’s angular velocity vector and the magnetic field produced by the neutron star:
where θ is the angle between the angular velocity vector of the meteoroid and the local field vector of the neutron star Bns at the location of the meteoroid. The rotation rate of B⊥ about B|| is equal to the angular speed of the meteoroid in the stellar field. Equation (6) shows that there is an interdependence of Δω and ω1.
In order to examine this interdependence, we performed several Monte Carlo simulations of meteoroids in the vicinity of a neutron star’s (dipole) magnetic field to simulate a spatial distribution of meteoroids with varying angular speeds and orientations relative to the external dipole field. Ideally, meteoroids in polar orbits will be most significantly affected as the neutrino spin vectors are aligned with the magnetic field in the neutron star’s polar region. In this way, the average bulk polarization angle is determined using Equation (7).
For each simulation, meteoroids were assumed to be distributed evenly in a volume of space about the neutron star with random angular orientations and velocities. Several cases, listed in Table 1, were studied. In each case, the volume distribution of meteoroids was assumed to be flat, as was the angular speed. For each sample in the Monte Carlo calculation, the components of the magnetization were calculated along with the polarization angle.

Table 1.
Model parameters used in this study.
These calculations have ignored the effects of thermalization. If such effects were important they would produce a competition between the thermalization lifetime and the time associated with producing the sub-state imbalance, which is the order of the inverse of the meteoroid rotation time. The lifetimes of the chiral states of the amino acids at the temperatures of outer space have been found to be hundreds of years or even much longer [], even at the relatively high temperatures assumed in that study. Thus we have assumed the thermalization times to be infinite.
4. Results
The calculated polarization distributions corresponding to the different sets of physical parameters indicated in Table 1 are shown in Figures 4–8. The angular orientation of the meteoroid’s rotation axis with respect to the polar field of the neutron star was assumed flat in this model.
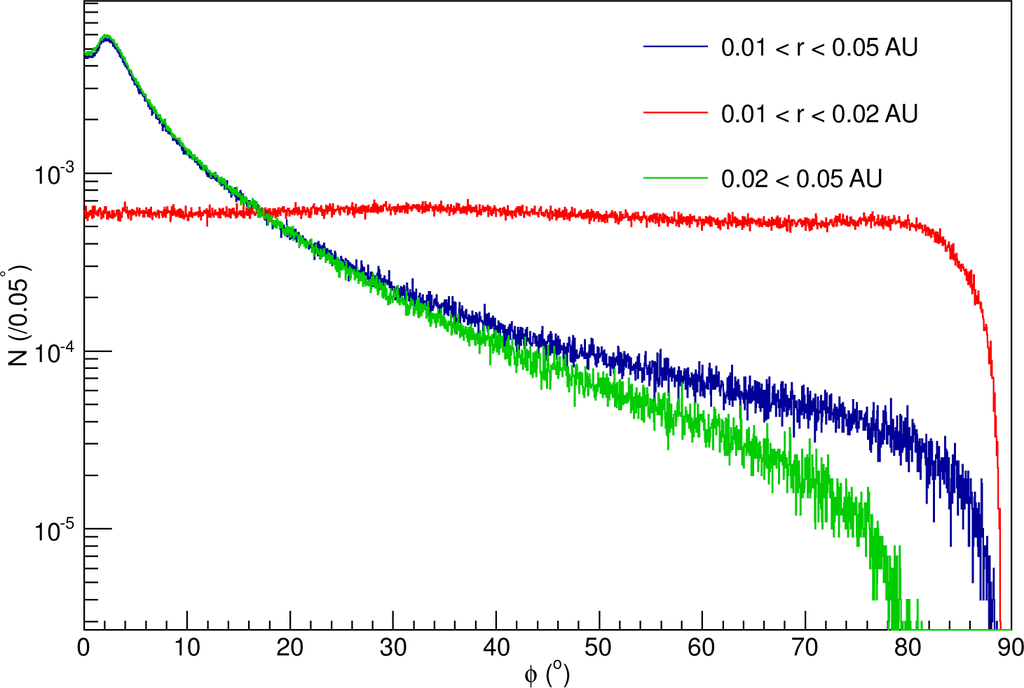
Figure 4.
Polarization angle distributions for Models A, B and C. This figure compares the polarization distribution for various meteoroid radial ranges.
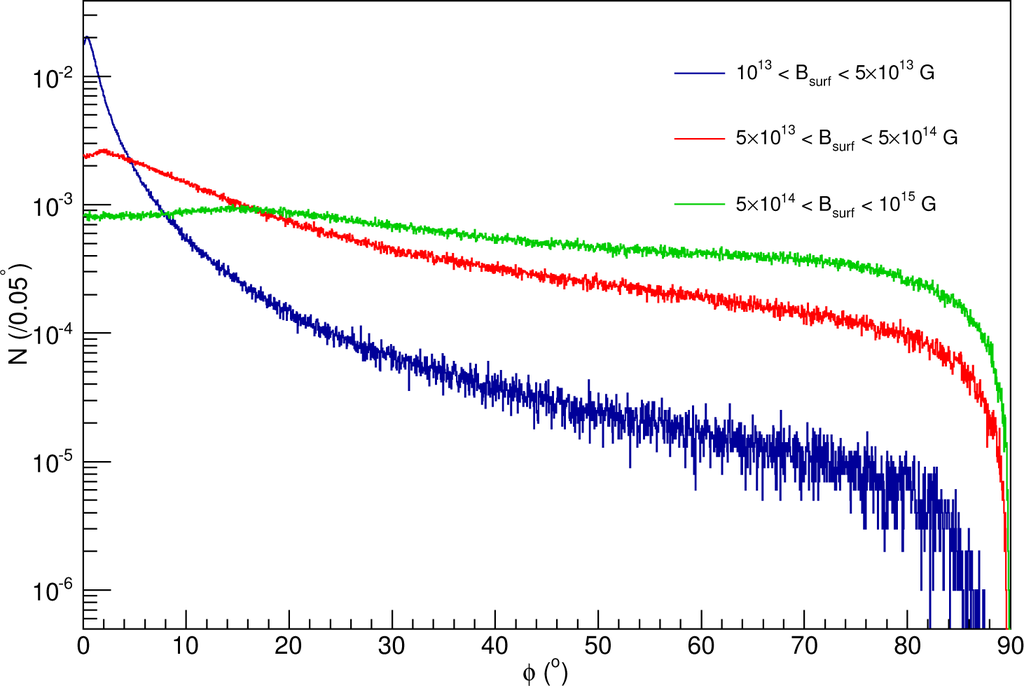
Figure 8.
Polarization distribution for Models K, L and M. In this figure, the polarization distributions are compared for evolutionary models with a range of neutron star surface magnetic fields.
Figure 4 shows the results of Models A, B and C, in which the meteoroids are uniformly distributed in increasingly incremented radial regions as indicated in Table 1. The angular speed of the meteoroid in each event varies uniformly between 0 and 10 rad s−1. The distribution of polarization with respect to the stellar magnetic field vector is shown for these models in the figure. The bulk polarization is seen to increase dramatically with radius. For the random orientation of the meteoroid rotational velocity vectors, the value of the precession frequency ω1 about the perpendicular component of the magnetic field in the meteoroid’s reference frame decreases as well, resulting in a smaller perpendicular component of magnetization and a larger parallel component (Equation (6)).
While one may conclude that larger radii are more important for this scenario, the neutrino fluence decreases with increasing radius, resulting in a reduced selective production effect. Likewise, as the field weakens, the overall polarization may be more susceptible to stochastic effects since the net torque of the external field is much weaker.
The effect of the angular speed of the meteoroid is shown in Figure 5. There the radius ranges from 0.01 and 0.05 astronomical units (AU). Each model is used to explore an increasingly larger range of angular speeds. Equation (6) shows that a quasi-resonant condition occurs in the magnetic field in the case where Δω = 0. For a time that is long compared with the relaxation time of the molecule, the difference in rotational frequency and the magnetic field resonance frequency increases, resulting in a larger polarization component parallel to the magnetic field vector and smaller perpendicular components of polarization. Thus a larger rotation speed will move the meteoroid farther out of the resonant region. The smallest amount of polarization in the z direction will result for values of Δω = 0, or for meteoroid rotation speeds equal to that of the molecular precession frequency of the local magnetic field. For a gyromagnetic ratio of 2 × 107 rad s−1 T−1 and a surface magnetic field of 1014 G, this would correspond to an angular speed of 5 rad s−1 at 0.025 AU. Thus, the effect of meteoroid rotation can be significant in reducing the overall polarization for small rotation rates. While the rotational rate distribution is assumed flat in this model, very likely the rotation rates are heavily weighted towards zero.
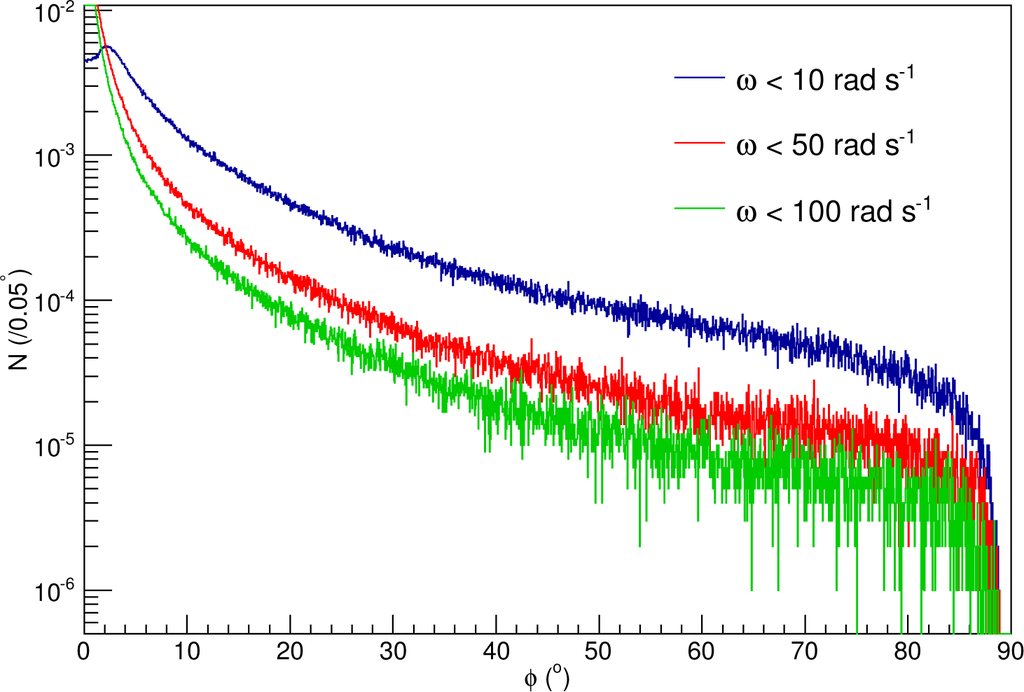
Figure 5.
Polarization distributions for Models A, D and E. This figure compares the polarization distribution for various meteoroid angular speeds.
The effect of the neutron star’s surface magnetic field is shown in Figure 6. Here, the surface field of the star is varied while a distribution of angular speeds and radii are simulated. While a higher field will exert a stronger initial torque on the molecules, the steady-state condition of the system for strong fields becomes more significantly affected by the randomly distributed perpendicular components of the field in the reference frame of the meteoroid. Then, the resonant precession frequency of the external field differs significantly from the angular speed of the meteoroid. The polarization distribution is then more strongly affected by the perpendicular components of the field.
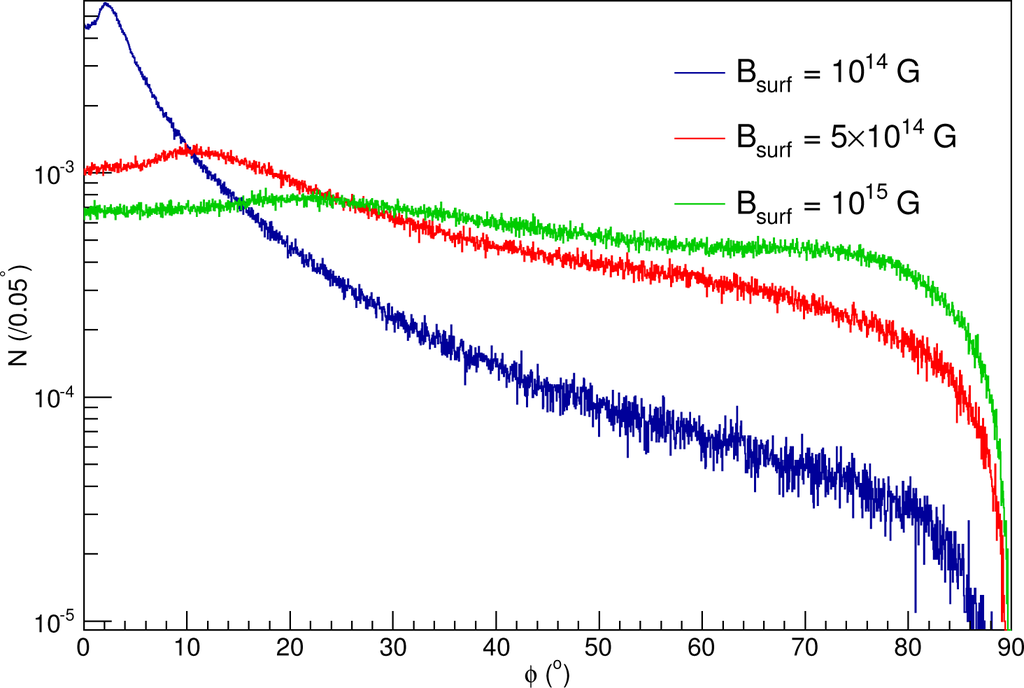
Figure 6.
Polarization distribution for Models A, F and G. This figure compares the polarization distribution for various neutron star surface magnetic fields.
The effects of increasing the molecular gyromagnetic ratios are similar to the effects of increasing the external magnetic fields. While a stronger gyromagnetic ratio will result in a larger external torque on the molecule’s magnetic moment, the torque from the effective field, with a significant contribution from a perpendicular component, will contribute to the overall molecular orientation. This is shown in Figure 7 for Models A, J and K. In the steady state, a smaller gyromagnetic ratio results in a smaller contribution from the random orientations of the angular speed vectors of the meteoroids, and the overall polarization is more randomly distributed. However, even for a fairly large gyromagnetic ratio of 5 × 107 rad s−1 T−1, there is a net polarization parallel to the local magnetic field.
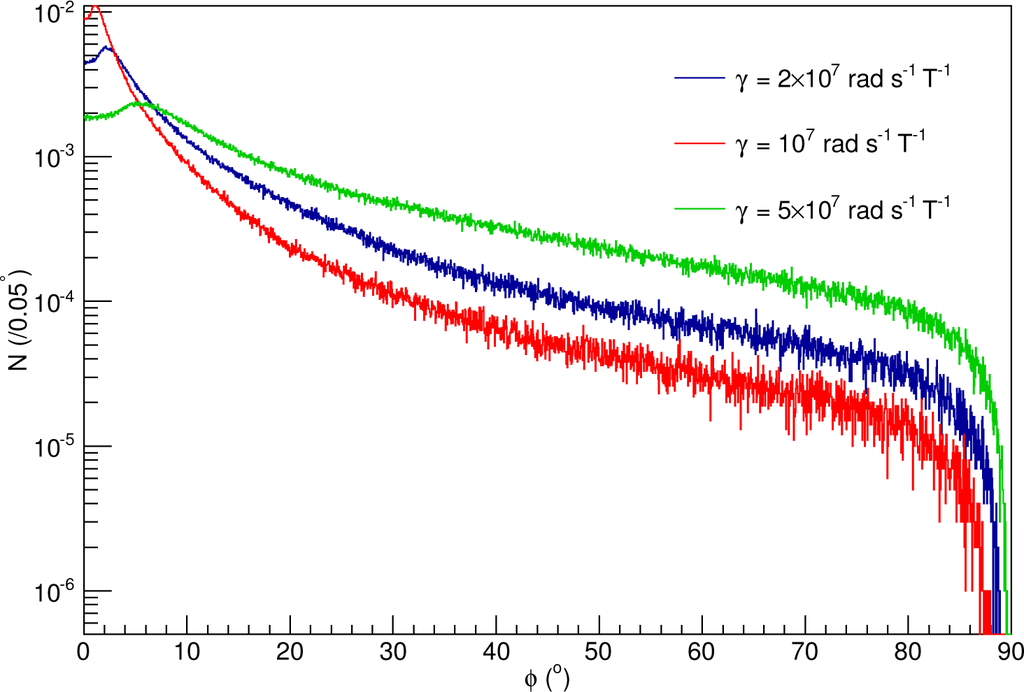
Figure 7.
Polarization distribution for Models A, H and J. This figure compares the polarization in this model for various molecular gyromagnetic ratios.
Finally, we examine the distribution of magnetic fields with Models K, L and M, the results of which are shown in Figure 8. The meteoroids were assumed to be constrained within a radius of 0.01 to 0.05 AU about a population of stars with a distribution of magnetic fields as shown in Table 1. As discussed previously, a stronger magnetic field will result in a loss of net polarization, so that Model M, with a distribution of larger magnetic fields, has a polarization distribution that is not as pronounced about zero degrees as in the case of Model L.
These particular models are interesting as they enable a more accurate estimate of the enantiomerism that could be produced in the SNAAP model than was done previously. In [], an estimated cross section for antineutrino conversion of 14N to 14C was made from the results of [], and it was assumed that the minimum distance from the nascent neutron star to the meteoroid that would permit survival of the meteoroid would be 0.01 AU. At that distance the estimated enantiomeric excess was 1 × 10−4 percent. However, implicit in that assumption was the estimate that the molecular polarization was 100 percent. We have calculated the fraction of the molecules that occur within 10 degrees of the direction of the magnetic field of the neutron star, as determined from our calculations, and the results are given as the right hand column in the table. These results range from very small values to nearly 100 percent. The very small values occur at the smallest radii, at which the magnetic field becomes so strong that the model probably breaks down anyway. At a radius of 2 AU, our estimate of the bulk polarization is about 50 percent, and the neutrino flux will have fallen off from the value used in the estimate of [] by a factor of 4. The result is that the estimated enantiomeric excess becomes 1 × 10−5 percent; one part in 107.
Does so low a value permit the SNAAP model to drive the ultimate homochirality of the Earth, or even the few percent enantiomeric excesses found in the meteoritic samples? The favored mechanism by which amplification could occur, autocatalysis, was originally suggested by Frank [], but has been elaborated since by others [–]. More significantly, it has been demonstrated experimentally [–], thus showing that autocatalysis does actually work. However, the minimum levels of enantiomeric excess in those experiments were fractions of a percent, several orders of magnitude larger than the value we estimate for the SNAAP model. However, existing experiments have not yet determined the lower limit for autocatalysis to prevail.
A qualitative evaluation of the optimal radius about the neutron star at which the polarization can occur can be made by examining the product of the neutrino flux and the average normalized polarization. This is described as the bulk polarization normalized to unity by subtracting this from π/4, which is the bulk polarization for a completely unpolarized medium.
The calculated polarization with respect to the magnetic field vector increases with radius while the neutrino flux decreases as r−2. Thus the product of the normalized polarization and 1/r2 will provide a rough idea of an optimal radius for which chiral selection occurs. This product is shown as a function of radius in Figure 9 for a surface field of 1014 G and γ = 2 × 107. We note, however, that this calculation does not account for the thermalization, the effects of which are difficult to estimate, since molecules buried in pockets of the meteoroid may be more immune to thermalization effects than those on the surface.
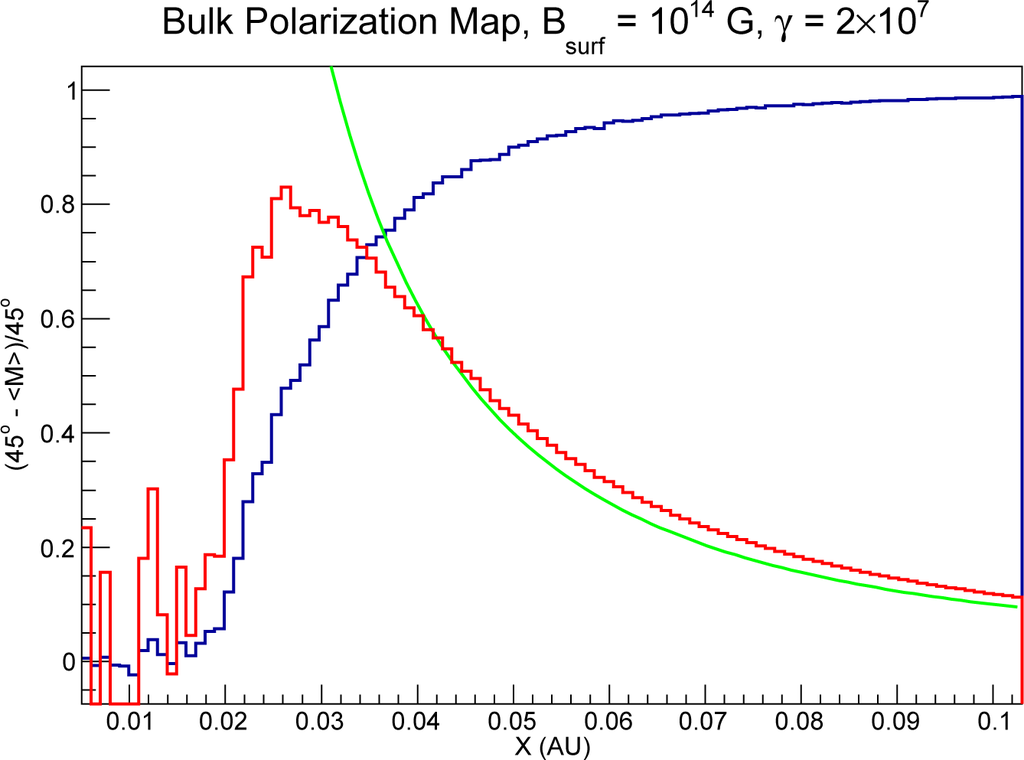
Figure 9.
Product of the normalized polarization and 1/r2 for a surface field strength of 1014G and γ = 2 × 107. The black line is the normalized polarization. The green line is the 1/r2 relationship, and the red line is the product of the two. Large fluctuations near 0 AU are statistical.
5. Discussion
In order for an effective production of an enantiomeric excess of polar atoms/molecules via the SNAAP model, three things are required, i.e., (1) a strong external magnetic field, (2) a species with a non-zero magnetic moment (gyromagnetic ratio), and (3) an external polarized weak interaction mechanism. All three of these are satisfied by introducing a meteoroid containing a molecular species that is not initially polarized with respect to the magnetic field in the vicinity of a nascent neutron star from a core-collapse supernova. The meteoroid acts as the substrate carrying the molecular or atomic species, and the neutron star provides both the external magnetic field and the polarized weak interaction in the form of selective destruction of the molecule via neutrinos, which are naturally polar since they have a definite helicity. The differential in interaction cross sections between the neutrino–nucleus collisions in which the reactants are aligned parallel or anti-parallel, together with the asymmetric emission of the neutrinos, provides a difference in the destruction of the polar molecule and thus creates an enantiomeric excess.
In the present paper, we have investigated the likelihood of atomic or molecular polarization via meteoroid passage in the vicinity of a nascent neutron star. The meteoroids in this model provide a mode of transport by which molecules are moved close enough to the neutron star surface to benefit from the intense neutrino flux from the cooling star, but sufficiently distant and/or large to avoid complete destruction from supernova photons. Molecular polarization is accomplished via the intense magnetic field. Molecules within the meteoroid are polarized, and the bulk polarization of the material has been calculated for several situations. Magnetic resonance conditions have been examined as natural precession frequencies of the molecular medium interact with the angular speed of the meteoroid.
The presented model assumes a sampling of meteoroids in a variety of conditions including rotation rate, magnetic field, distance from the neutron star, and angular declination with respect to the neutron star’s magnetic poles. Using this sampling in a Monte Carlo calculation, we have been able to determine a range of conditions for which the SNAAP model is most effective. While the average polarization in the presented samplings may favor a more pronounced polarization farther from the neutron star, we must also account for the fact that the neutrino interaction rate decreases dramatically with radius. Thus, the effect of increasing radius on polarization and neutrino reaction rate favors one condition while adversely affecting the other.
The final simulation in this study not only considered the effects of a population of meteoroids about a single star, but also the effects of various neutron star magnetic fields in a “galaxy wide” sampling to gain a perspective of the overall simulation. It is found that a net molecular polarization can be produced.
Of course, it is difficult to test the SNAAP model. However, one could envision bombarding amino acids contained in a strong magnetic field with neutrinos from, for example, the Spallation Neutron Source; such experiments were discussed in []. This would not provide a complete test of the model, but it would test the most basic features.
Confirmation of cosmic production of amino acid enantiomerism is crucial to the veracity of this or any other model that purports to explain how it is produced. Although the meteorites in which it has been observed are strongly suggestive, the data from the Rosetta mission and its lander Philae [], which at this writing are orbiting comet 67P/Churyumov–Gerasimenko, will establish whether enantiomerism is indeed created in the cosmos, and that the models describing the possible mechanisms must be given serious consideration. However, non-detection of enantiomerism will not necessarily reject these models. Glavin et al. [] found that the meteoritic enantiomerism depended critically on the amount of aqueous alteration that the material had undergone before it arrived on Earth. Perhaps the water is essential for the formation of the enantiomeric supramolecular assembly. Alternatively, it may provide a mobility necessary for molecular alignment in the magnetic field. It has also been suggested [,] that some molecule that is especially resistant to racemization, for example, alpha-dialkyl amino acids such as isovaline, could be formed by whatever process is responsible for producing its enantiomerism, and it could then transfer its asymmetry to other amino acids.
Perhaps Rosetta will reduce the parameter space in which we currently reside.
Acknowledgments
Michael Famiano’s work is supported by NSF grant #PHY-1204486 and #PHY-0855013. Both Michael Famiano’s and Richard Boyd’s work was supported by the NAOJ Visiting Professor program.
Author Contributions
Michael Famiano performed all the calculations the results from which are shown in the paper. He also coauthored the current paper, and was involved in all modifications in response to the reviewers comments, and in the explanations to the reviewers.
Richard Boyd is one of the original SNAAP model authors, and coauthored the current paper. He was involved in all modifications in response to the reviewers comments, and in the explanations to the reviewers.
Toshitaka Kajino is one of the original SNAAP model authors, and commented on several versions of the current paper.
Takashi Onaka is one of the original SNAAP model authors, and commented on several versions of the current paper.
Michael Famiano’s students, Sarah Hulbert and Katrina Koehler, both assisted in running calculations for the current model. They also generated figures and calculations spanning the parameter space covered by this model.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kvenvolden, K.; Lawless, J.; Pering, K.; Peterson, E.; Flores, J.; Ponnamperuma, C.; Kaplan, I.R.; Moore, C. Evidence for extraterrestrial amino-acids and hydrocarbons in the murchison meteorite. Nature 1970, 228, 923–926. [Google Scholar]
- Bada, J.L.; Cronin, J.R.; Ho, M.-S.; Kvenvolden, K.A.; Lawless, J.G.; Miller, S.L.; Oro, J.; Steinberg, S. On the reported optical activity of amino acids in the Murchison meteorite. Nature 1983, 1301, 494–496. [Google Scholar]
- Cronin, J.R.; Pizzarello, S. Enantiomeric excesses of meteoritic amino acids. Science 1997, 275, 951–955. [Google Scholar]
- Cronin, J.R.; Pizzarello, S.; Cruikshank, D.P. Meteorites and the Early Sola. System.; Kerridge, J.F., Matthews, M.S., Eds.; University of Arizona Press: Tucson, AZ, USA, 1998; pp. 819–857. [Google Scholar]
- Glavin, D.P.; Dworkin, J.P. Enrichment of the amino acid L-isovaline by aqueous alteration on CI and CM meteorite parent bodies. Proc. Natl. Acad. Sci. USA. 2009, 106, 5487–5492. [Google Scholar]
- Glavin, D.P.; Callahan, M.P.; Dworkin, J.P.; Elsila, J.E. The effects of parent body processes on amino acids in carbonaceous chondrites. Met. Plan. Sci. 2010, 45, 1948–1972. [Google Scholar]
- Hurd, C.D.K.; Blinova, A.; Simkus, D.N.; Huang, Y.; Tarozo, R.; O’D Alexander, C.M.; Gyngard, F.; Nittler, L.R.; Cody, G.D.; Fogel, M.L.; et al. Origin and evolution of prebiotic organic matter as inferred from the Tagish Lake Meteorite. Science 2011, 332, 1304–1307. [Google Scholar]
- Bonner, W. The origin and amplification of biomolecular chirality. Orig. Life Evol. Biosph. 1991, 21, 59–111. [Google Scholar]
- Barron, L.D. Chirality and Life. Space Sci. Rev. 2008, 135, 187–201. [Google Scholar]
- Frank, F. On spontaneous asymmetric synthesis. Biochim. Biophys. Acta. 1953, 11, 459–463. [Google Scholar]
- Mason, S.F. Origins of biomolecular handedness. Nature 1984, 311, 19–23. [Google Scholar]
- Kondepudi, D.K.; Nelson, G.W. Weak neutral currents and the origin of biomolecular chirality. Nature 1985, 314, 438–441. [Google Scholar]
- Gol’danskii, V.I.; Kuz’min, V.V. Spontaneous breaking of mirror symmetry in nature and the origin of life. Sov. Phys. Uspekhi. 1989, 32, 1–29. [Google Scholar]
- Boyd, R.N. Stardust, Supernovae and the Molecules o. Life.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Tranter, G.E.; MacDermott, A.J. Parity-violating energy differences between chiral conformations of tetrahydrofuran, a model system for sugars. Chem. Phys. Lett. 1986. [Google Scholar]
- Quack, M. How important is parity violation for molecular and biomolecular chirality? Angew. Chem. Int. Ed. 2002, 41, 4618–4630. [Google Scholar]
- MacDermott, A.J.; Fu, T.; Nakastuka, R.; Coleman, A.P.; Hyde, G.O. Parity-violating energy shifts of murchison L-amino acids are consistent with an electroweak origin of meteoric L-enantiomeric excesses. Orig. Life Evol. Biosph. 2009, 39, 459–478. [Google Scholar]
- Boyd, R.N.; Kajino, T.; Onaka, T. Supernovae and the chirality of the amino acids. Astrobiology 2010, 10, 561–568. [Google Scholar]
- Boyd, R.N.; Kajino, T.; Onaka, T. Supernovae, neutrinos, and the chirality of the amino acids. Int. J. Mol. Sci. 2011, 12, 3432–3444. [Google Scholar]
- Bailey, J.; Chrysostomou, A.; Hough, J.H.; Gledhill, T.M.; McCall, A.; Clark, S.; Menard, F.; Tamura, M. Circular polarization in star-formation regions: Implications for biomolecular homochirality. Science 1988, 281, 672–674. [Google Scholar]
- Takano, Y.; Takahashi, J.; Kaneko, T.; Marumo, K.; Kobayashi, K. Asymmetric synthesis of amino acid precursors in interstellar complex organics by circularly polarized light. Earth Planet. Sci. Lett. 2007, 254, 106–114. [Google Scholar]
- De Marcellus, P.; Meinert, C.; Nuevo, M.; Filippi, J.-J.; Danger, G.; Deboffle, D.; Nahon, L.; d’Hendecourt, L.L.S.; Meierhenrich, U.J. Non-racemic amino acid production by ultraviolet irradiation of achiral interstellar ice analogs with circularly polarized light. Astrophys. J. 2011, 727, L1–L6. [Google Scholar]
- Takahashi, J.-I.; Shinojima, H.; Seyama, M.; Ueno, Y.; Kaneko, T.; Kobayashi, K.; Mita, H.; Adachi, M.; Hosaka, M.; Katoh, M. Chirality emergence in thin solid films of amino acids by polarized light from synchrotron radiation and free electron laser. Int. J. Mol. Sci. 2009, 10, 3044–3064. [Google Scholar]
- Meinert, C.; Filippi, J.-J.; Nahon, L.; Hoffman, S.V.; d’Hendecourt, L.; de Marcellus, P.; Bredehoft, J.H.; Thiemann, W.H.-P.; Meierhenrich, U.J. Photochirogenesis: Photochemical models on the origin of biomolecular homochirality. Symmetry 2010, 2, 1055–1080. [Google Scholar]
- Meierhenrich, U.J.; Filippi, J.-J.; Meinert, C.; Bredehoft, J.H.; Takahashi, J.-I.; Nahon, L.; Jones, N.C.; Hoffman, S.V. Circular dichroism of amino acids in the vacuum-ultraviolet region. Angew. Chem. Int. Ed. 2002, 49, 7799–7802. [Google Scholar]
- Mann, A.K.; Primakoff, H. Chirality of electrons from beta-decay and the left-handed asymmetry of proteins. Orig. Life. 1981, 11, 255–265. [Google Scholar]
- Vester, F.; Ulbright, T.L.V.; Krauch, H. Optical activity and parity violation in beta-decay. Naturwissenschaften 1959, 46, 68–69. [Google Scholar]
- Ulbricht, T.L.V.; Vester, F. Attempts to induce optical activity with polarized-radiation. Tetrahedron 1962, 18, 629–637. [Google Scholar]
- Gusev, G.A.; Kobayashi, K.; Moiseenko, E.V.; Poluhina, N.G.; Saito, T.; Ye, T.; Tsarev, V.A.; Xu, J.; Huang, Y.; Zhang, G. Results of the second stage of the investigation of the radiation mechanism of chiral influence (RAMBAS-2 experiment). Orig. Life Evol. Biosph. 2008, 38, 509–515. [Google Scholar]
- Cline, D. Supernova antineutrino interactions cause chiral symmetry breaking and possibly homochiral biomaterials for life. Chirality 2005, 17, S234–S239. [Google Scholar]
- Bargueno, P.; de Tudela, R.P. The role of supernova neutrinos on molecular homochirality. Orig. Life Evol. Biosph. 2007, 37, 253–257. [Google Scholar]
- Shinitzky, M.; Elitzur, A.C. Ortho-Para spin isomers of the protons in the methylene group-possible implications for protein structure. Chirality 2006, 18, 754–756. [Google Scholar]
- Bargueno, P.; Dobado, A.; Gonzalo, I. Could dark matter or neutrinos discriminate between the enantiomers of a chiral molecule? Europhys. Lett. 2008, 82, 13002–13005. [Google Scholar]
- Buckingham, A.D. Chirality in NMR spectroscopy. Chem. Phys. Lett. 2004. [Google Scholar]
- Buckingham, A.D.; Fischer, P. Direct chiral discrimination in NMR spectroscopy. Chem. Phys. 2006, 324, 111–116. [Google Scholar]
- Boyd, R.N. An Introduction to Nuclea. Astrophysics.; The University of Chicago Press: Chicago, IL, USA, 2008; pp. 126–132. [Google Scholar]
- Berdyugina, S.V.; Solanki, S.K. The molecular Zeeman effect and diagnostics of solar and stellar magnetic fields I. Theoretical spectral patterns in the Zeeman regime. Astron. Astrophys. 2002, 385, 701–715. [Google Scholar]
- Berdyugina, S.V.; Braun, P.A.; Fluri, D.M.; Solanki, S.K. The molecular Zeeman effect and diagnostics of solar and stellar magnetic fields III. Theoretical spectral patterns in the Paschen-Back regime. Astron. Astrophys. 2005, 444, 947–960. [Google Scholar]
- Perez-Garcia, V.M.; Gonzalo, I.; Perez-Diaz, J.L. Theory of the stability of the quantum chiral state. Phys. Lett. A. 1992, 167, 377–382. [Google Scholar]
- Lai, D.; Qian, Y.-Z. Neutrino transport in strongly magnetized proto-neutron stars and the origin of pulsar kicks: The effect of asymmetric magnetic field topology. Astrophys. J. 1998, 505, 844–853. [Google Scholar]
- Horowitz, C.J.; Li, G. Cumulative parity violation in supernovae. Phys. Rev. Lett. 1998, 80. [Google Scholar] [CrossRef]
- Arras, P.; Lai, D. Neutrino-nucleon interactions in magnetized neutron-star matter: The effects of parity violation. Phys. Rev. D. 1999, 60, 043001:1–043001:28. [Google Scholar]
- Maruyama, T.; Kajino, T.; Yasutake, N.; Cheoun, M.-K.; Ryu, C.-Y. Asymmetric neutrino emission from magnetized proton-neutron star matter including hyperons in relativistic mean field theory. Phys. Rev. D. 2011, 83, 081303:1–081303:5. [Google Scholar]
- Soai, K.; Shibata, T.; Morioka, H.; Choji, K. Asymmetric autocatalysis and amplification of enantiomeric excess of a chiral molecule. Nature 1995, 378, 767–768. [Google Scholar]
- Soai, K.; Sato, I. Asymmetric autocatalysis and its application to chiral discrimination. Chirality 2002, 14, 548–554. [Google Scholar]
- Mathew, S.P.; Iwamura, H.; Blackmond, D.G. Amplification of enantiomeric excess in a proline-mediated reaction. Angew. Chem. Int. Ed. 2004, 43, 3317–3321. [Google Scholar]
- Breslow, R.; Levine, M.S. Amplification of enantiomeric concentrations under credible prebiotic conditions. Proc. Natl. Acad. Sci. USA. 2006, 103, 12979–12980. [Google Scholar]
- Bloch, F. Nuclear induction. Phys. Rev. 1946, 70. [Google Scholar] [CrossRef]
- Ehrenfreund, P.; Bernstein, M.P.; Dworkin, J.P.; Sandford, S.A.; Allamandola, L.J. The photostability of amino acids in space. Astrophys. J. 2001, 550, L95–L99. [Google Scholar]
- Fuller, G.M.; Haxton, W.C.; McLaughlin, G.C. Prospects for detecting neutrino flavor oscillations. Phys. Rev. D. 1999, 59, 085005:1–085005:15. [Google Scholar]
- Thiemann, W.H.-P.; Meierhenrich, U. ESA Mission ROSETTA will probe for chirality of cometary amino acids. Orig. Life Evol. Biosph. 2011, 31, 199–210. [Google Scholar]
- Pizzarello, S.; Weber, A.L. Prebiotic amino acids as asymmetric catalysts. Science 2004, 303, 1151–1152. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).