Abstract
Gestalt Algebra gives a formal structure suitable for describing complex patterns in the image plain. This can be useful for recognizing hidden structure in images. The work at hand refers to the laws of perceptual psychology. A manifold called the Gestalt Domain is defined. Next to the position in 2D it also contains an orientation and a scale component. Algebraic operations on it are given for mirror symmetry as well as organization into rows. Additionally the Gestalt Domain contains an assessment component, and all the meaning of the operations implementing the Gestalt-laws is realized in the functions giving this component. The operation for mirror symmetry is binary, combining two parts into one aggregate as usual in standard algebra. The operation for organization into rows, however, combines n parts into an aggregate, where n may well be more than two. This is algebra in its more general sense. For recognition, primitives are extracted from digital raster images by Lowe’s Scale Invariant Feature Transform (SIFT). Lowe’s key-point descriptors can also be utilized. Experiments are reported with a set of images put forth for the Computer Vision and Pattern Recognition Workshops (CVPR) 2013 symmetry contest.1. Introduction
“Gestalt” has many meanings in the German language. Leo [1] lists “shape, figure, form, build, conformation, design, guise, likeness, stature” and the word in its English use, which is mainly as a technical term of psychology. Perceiving a Gestalt—of a human, an arbitrary object, some piece of music or mathematic, even of a thought—means recognizing its structure and inner organization immediately, i.e., without cognitive efforts. Humans can do so, even if this inner structure is complicated and deep.
1.1. Gestalt Laws
Mirror Symmetry has long ago been identified as one of the strongest Gestalt law principles [2]. Another such classical law concerns good continuation and similarity. In order to be perceived as such Gestalt a finite number of otherwise similar parts should be positioned in equal spacing in a row. In [3] we also treat a third law of mutual organization of parts into an aggregate—the rotational symmetries—though these are not a dominant part of the classical Gestalt literature. For any of these organizational principles the following propositions may be stated: (1) The mutual organization in the image plain gives the aggregate (Gestalt) more meaning than just the sum of the meaning of its parts; (2) the parts of a Gestalt may again be Gestalten on a smaller scale, and so forth in a recursive way; (3) gestalt perception will still work well if the parts are displaced from the ideal configuration by moderate errors; (4) no Gestalt will ever fill the entire infinite plane, it will always only cover a limited region; (5) the Gestalt organization must not explain all structure or objects contained in its region, there may well be arbitrary clutter present between the part objects.
The investigation of Gestalt perception should not be biased by the structure of a given “input image” or camera type—i.e., a particular rectangular or hexagonal pixel raster. The main goal is to investigate the interrelations between parts and aggregates. This can be better done using continuous domains such as the 2D plane. It is well in the line of classic Gestalt literature to visualize the objects of interest as line drawings. However, for this work, simple dot patterns or lines are not sufficient. The objects of interest here also have a scale (i.e., size), an orientation, a rotational frequency and an assessment measure. So a specific way of drawing had to be invented.
1.2. Avoiding Hard Constraints
Mirror-symmetry can be seen as a property of a pair of objects, and good continuation in a row as property of an n-tuple of objects, respectively. Mathematically, it is best understood as a constraint relation (binary for mirror-symmetry, and n-ary for rows). Such relation can alternatively be given as characteristic function (again on pairs of objects, and on n-tuples of objects, respectively) yielding one if the constraint holds and zero otherwise. For imperfect symmetries—such as extracted from natural images or hand-drawn—tolerances are required. These are step-function parameters for the characteristic functions corresponding to the constraints. A good choice of such parameters will require extensive machine-learning. Representative data will be needed. Such parameters will also be a prospective error source leading to occasional recognition failure.
In this work such step-functions are replaced by continuous and analytic functions. They are defined on the same domain as the characteristic functions, and they also yield value one for perfect symmetric arrangement of the parts. For imperfect configurations they will give a continuous value between zero and one. They will be called “assessment functions”. Accordingly, each aggregate object will get an assessment measure describing numerically how symmetric it is.
Decisions are avoided. Any configuration (pair or n-tuple, respectively) forms a new aggregate (mirror or row). Such operation is always permitted. In mathematical terms this is called “algebraic closure”. Binary operations—such as the one for mirror-symmetry—are common in standard algebra. n-ary operations—such as the one for continuation in rows—are less common. They are being studied in universal algebra [4]. In Section 2 below the operations of such algebra and some of its properties are given.
1.3. Related Work
Classical Gestalt literature—such as [2]—tends to create evidence by making “experiments” with the reader by integrating figures of illusions etc. in their papers. Today more precise and quantitative results are obtained by experimenting with representative sets of subjects perceiving patterns rendered on a screen and measuring their saccades [5]. Gestalt algebra may contribute to such psychological work by providing means to properly render nested symmetries. Moreover, Gestalt algebra may benefit from such work through grounding and comparing it with human perception. Some authors from the machine vision community continue the classical Gestalt work by considering artificial neural net implementations of mirror symmetry in particular in comparison with physiological and psychological findings [6].
Picture grammars [7] or related formal syntactic structure for the generation and recognition of aggregated patterns have been popular in machine vision three decades ago. Still today syntactic structure is regarded as an option for recognition by some authors [8]. In 1997, Bienstock et al. proposed nested recursive Gestalt recognition where the assessment was based on minimum description length in a preliminary work [9]. However, to the best of our knowledge this interesting line of research has not been further pursued.
In the computer graphics community sophisticated syntactical work can be found aiming as well at the generation of plants, as the generation of man-made urban structure such as automatic generation of credible buildings [10]. Desolneux put forth a statistical model for Gestalt perception based on an a-contrario test using competing models for background and object groups [11]. Her theory has been applied to symmetry recognition with high success [12]. The use of orientations for symmetry recognition has been implemented by formulae quite similar to (5) already more than 20 years ago [13]. The mirroring of SIFT descriptors as utilized in Section 3 has been published by R. Ma [14].
1.4. Own Previous Work
We presented the definitions of the technical Section 2 of this contribution in [15]. Since then some changes and improvements have been made, including the third (rotational symmetry) operation and addition of the frequency domain, which is due to be published soon [3].
2. Gestalt Algebra
In this section a Gestalt will simply be an element of the manifold given in (1). The equations below give this manifold the extra structure of a generalized algebra. Using the operations given there, new Gestalten (aggregates) can be constructed from old Gestalten (parts). The following Sections 2.1 to 2.3 should be understood without considering an input image. They only explain what numerical attributes are given for the Gestalten and how a new aggregate-Gestalt is calculated given a pair or n-tupel of part-Gestalten. Section 2.4 briefly explains how these definitions can be used to render graphical images that exhibit mirror symmetries and/or repetitions in rows of controllable quality. Only for the last Section 2.5, an input image is considered. Here an extraction method is required to transform the image—given as pixel matrix—into a set of primitive Gestalten.
2.1. Gestalt Domain
Formula (1) defines a manifold—with a discrete component in third position and margins in fourth and fifth:
An element g∊G is referred to as Gestalt, and the whole set G as the Gestalt Domain. For convenience there are names for the components of the Gestalt domain: the position po(g)—in the 2D vectorspace, the orientation or(g)—in the additive circle group isomorph to SO(2), the frequency fr(g)—a positive integer, the scale sc(g)—which is greater zero, and the assessment as(g)—between zero and one.
Gestalten may be visualized as has been done in Figure 1. Thirty three random instances have been drawn using uniform distributed positions between zero and ten in both components, uniform distributed orientation, frequency drawn from round(1/rand) where rand is drawn uniformly between zero and one, uniform scale between zero and three, and uniform assessment. Position is displayed as center of a circle and scale as its diameter. Frequency comes as number of spokes in each wheel. Orientation is given as angle between the x-axis and the first spoke—transformation between the orientation component of the domain (between zero and one) and the display angle is by multiplying with 2π/fr(g). Assessment is given as grey tone such that good Gestalten (as(g) = 1) are black and bad Gestalten (as(g) close to zero) white. So the good ones are more salient, and the bad ones faint.
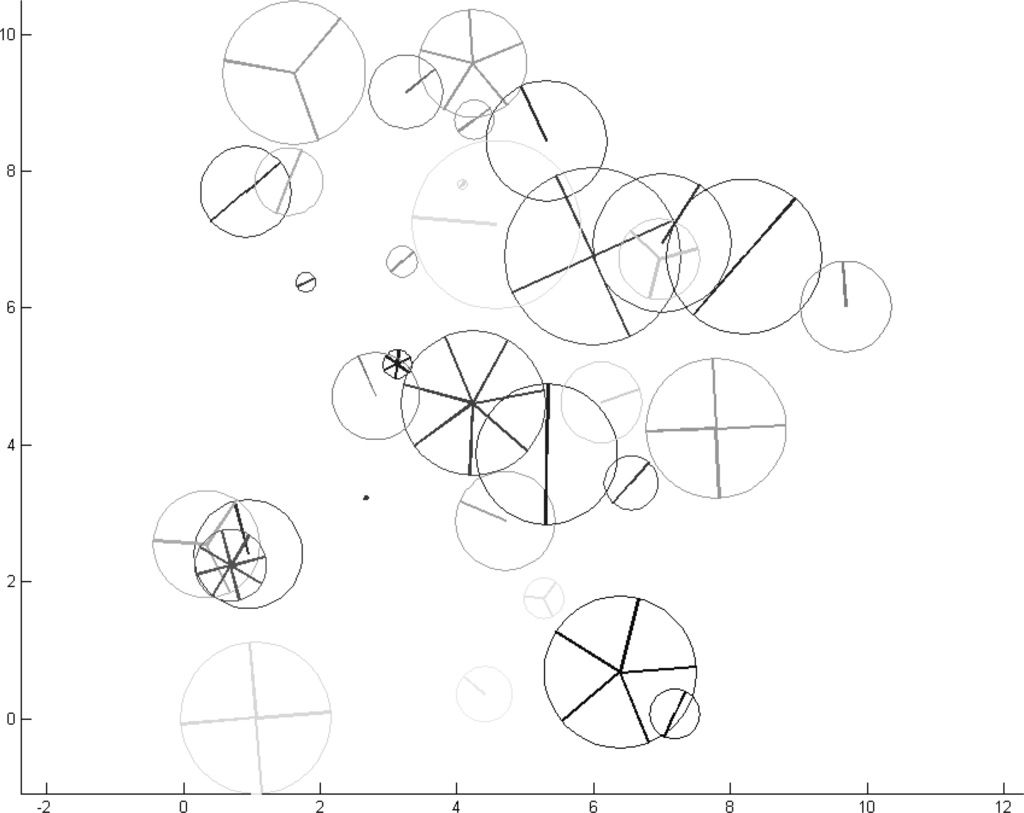
Figure 1 shows random Gestalten. Accordingly, a human subject will only perceive a bunch of clutter without any structure or organization. In the sections below, however, algebraic calculation rules will be given that yield new Gestalten out of given ones. Accordingly, human subjects will perceive aggregate-part order in the following figures.
2.2. Mirror Operation
A binary operation |: GxG → G is defined by
As common with binary operations the symbol is placed between the operands. Position is just the mid of the two parts. For the sake of algebraic closure arctan(x/0) = π/2 is artificially set. Thus, e.g., also g|g is defined. The factor 1/π properly scales the orientation for the frequency 2 which is constantly set so for mirror Gestalten. Of course negative outcomes o will be represented by 1 + o in the orientation domain. The scale of the aggregate is obtained as sum of the geometric mean of the scale of the parts plus their Euclidean distance.
These four components do capture little of what was intended in view of the laws presented in Section 1.1. Instead all that intent is built into the assessment component a| which is defined in Formulae (3)–(7): first definition step is setting a|(g|h) = 0 if fr(g) ≠ fr(h). Else a geometric mean is given
So that Gestalten which are too far apart are punished as well as Gestalten which are too close to each other. Optimal is a distance equal to the geometric mean of the scales of the parts. For this setting the positional component of the assessment function will equal one. The law of mirror symmetry is accounted for in the following preference on specific orientation settings:
Finally, another geometric mean transports some of the assessment of the parts to the aggregate:
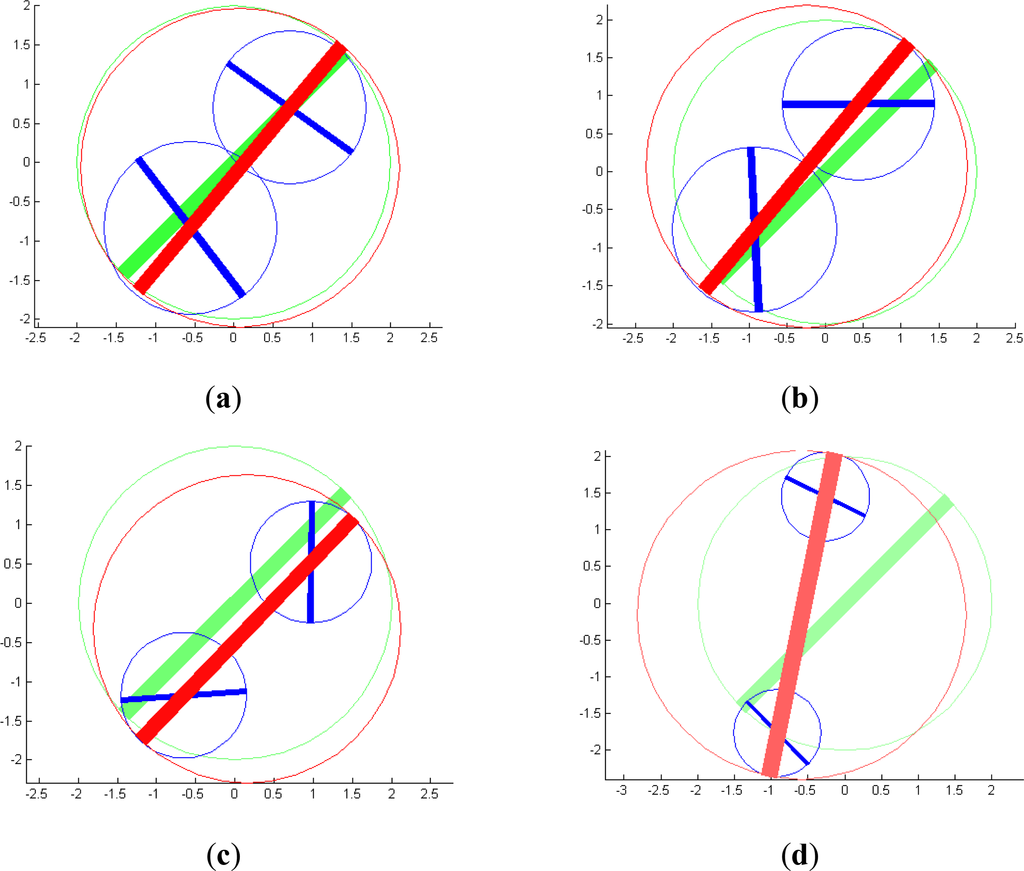
Figure 2 shows examples of the mirror operation | at work. Setting the green Gestalt fix, two blue parts of it are sampled using the assessment functions as distributions. For this the position components are set optimally and the scale is set to optimal half size. Then the orientation of one part is set uniformly at random and the other such that Equation (5) gives optimal a|,o = 1. Then position, orientation, and scale are disturbed by small random errors such that the functions a|,p, a|,o, and a|,s respectively are expected to be 1 − ∊, where ∊ is a small positive value. The assessment of the parts is set to one here. The red Gestalt is then obtained by using Equation (2) in its constructive (reducing and recognizing) way. The parts of the Figure 2a–d are made with rising ∊. Thus, both the green and the red Gestalt are becoming brighter, i.e., assessed worse. Also it is evident that with a small ∊ the reconstructed Gestalt matches the original one well, while with rising deviations they start drifting apart.
2.3. Row Forming Operation
A n-ary operation ∑: G, …, G → G is defined by
Such n-ary operations are a little unusual for standard algebra but well investigated in generalized algebra (e.g., [4]). The operation symbol is placed in front of the arguments. Position is again just the mid of the n parts. The same arctan version from Equation (2) is used here again. Moreover, the frequency is also constantly set to two. The scale of the aggregate is obtained as sum of the geometric mean of the scales of the parts scmid plus the Euclidean distance from the first to the last part’s position.
The intended meaning is again built into the assessment component a∑ which is defined in Formulae (9)–(13): first definition step is setting a|(∑g) = 0 if fr(gi) ≠ fr(gj) for any index pair (i, j) in the tuple. Else the assessment is again given as geometric mean:
Similarly, the orientations of the part Gestalten need to be averaged using
In analogy to Equations (6) and (7) uneven scales are punished and the assessments of the parts are transported into the aggregate by another geometric mean:
2.4. Rendering Complex Patterns by Use of Gestalt Algebra
Similar to the method used for Figure 2, more complex Gestalten can be obtained using operations successively. Formula (16) exemplarily gives the Gestalt Algebra term visualized in Figure 3.
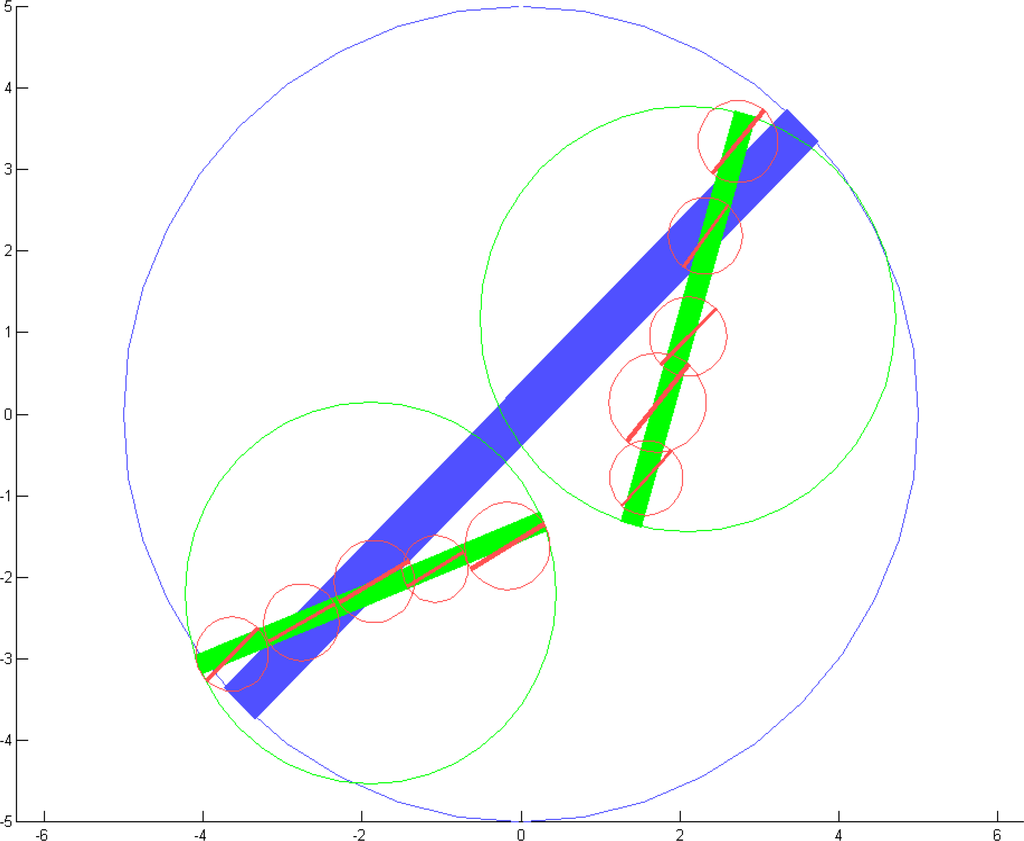
Here are some open issues of the theory. In order to obtain such nice symmetric outcomes, information must be transported from one part of the term to another, e.g., if g1 is decomposed as row of five members, then g2 should also be decomposed as row of five members. The mid-orientation component for h1 … h5 was of course drawn uniformly between zero and one, and then disturbed by an ∊-deviation. However, not so for h6 … h10. Here, the mid-orientation was obtained by combining the mid orientation of h1 … h5 with or(f) according to Formula (5). In other words: symmetry in the structure of the term should be rewarded—as well as symmetry over several levels of the term.
2.5. Searching and Clustering for Recognition
Given a set of primitive Gestalten (in list0) all combinations of these may be tested using the operations | and ∑, respectively. Most of the resulting new Gestalten will have zero or very small assessments. A threshold can control the search. Only those Gestalten with better assessments may enter list| or list∑, respectively. Then again the Gestalten in these lists can be tested with the operations and the best ones kept, yielding list||, list∑|, list|∑, and list∑∑, respectively. Additional evaluations of the type outlined in Section 2.4 are possible (but not yet implemented). The search may be continued until now good Gestalten are possible anymore (recall their scale is always becoming bigger), or terminated at any time. Output can be the best Gestalt in all lists only, or a set of the best few.
The search outlined above may lead to high computational effort—due to the combinatory growth of possibilities for n-ary operations such as ∑. This is avoided by greedily searching only “maximal meaningful elements” in the sense of the Desolneux theory [11]. Practically, this means that first only pairs are investigated (as with the binary operation |). Then, the rows are successively prolonged always adding only the best possible partner, until the row-Gestalt becomes worse in its assessment.
In order to add more robustness to the recognition process, the set of the best Gestalten resulting from the search can be clustered. This has been implemented for mirror Gestalten, again using a greedy search, seeded by the few very best. As yet, no clustering for row-Gestalten has been implemented.
3. Results
For the time being experiments on recognition are done with the trainings data of the “Symmetry in Real World Images” contest along with the CVPR 2013 [16]. Gestalt Algebra participated—but with rather mediocre success [17]. The main obstacle is how to connect the algebra to the image data. One option for extraction of primitive Gestalten from images is the well-known Scale-Invariant Feature Transform SIFT of D. Lowe [18]. As first step it constructs an image pyramid by successive Gaussian filtering, and storing also the difference-of-Gaussians images. In this scale-space structure it picks minima as well as maxima calling them key-points. A 300 kPixel image of normal content usually provides some hundred or thousand such key-points attributed with location and scale. Orientation comes with every key-point as direction of the brightness gradient between −π and π. Thus the frequency attribute is set to one for all such primitives. The SIFT implementations accept only instances where a certain “cornerness” surpasses a given threshold. They can thus be modified to also output an assessment with every key-point such that instances which are just above the accepting threshold get values close to zero, while the best one receives optimal value one. Figure 4b exemplarily shows the set of primitive Gestalten obtained from one of the animal images in the training set using the same convention as Figure 1.

SIFT has a second step in which local descriptors are extracted from the image at the particular location, scale, and orientation. To this end a 4 × 4 grid is scaled, rotated and shifted accordingly. In each cell of the grid a gradient orientation histogram is obtained with 8 bins. Thus the descriptor is a vector of 128 dimensions. For primitives obtained by SIFT this descriptor can be used for improving the recognition of symmetry—and Table 1 shows the gain thus achieved.

Of course there is a difference between the obvious clutters in Figure 1 and the kind-of-order in the 579 Gestalten of Figure 4b. However, it is immediately evident that automatic search for proper mirror-symmetric Gestalten on this primitive set is quite a challenge, while this is still one of the easier examples in the data. Note also that SIFT-Gestalten come here with frequency component set to one. Since frequency was not in the definitions of [15], it had to be set to two like for mirror and row Gestalten—so that even more information was lost which is retained now. This particular picture already contains structured symmetry, e.g., the ears of the animal give rise to local symmetries, which are combined into a symmetry of symmetries (much like the term (16)) fitting the ground-truth.
Table 1 gives some recognition figures. The method outlined in Section 2.5 achieves around 23% recognition rates and the performance was improved to 40% with the help of SIFT-descriptor matching for additional assessing the mirror Gestalten following [14]. Here, the success criteria of the CVPR competition were used, namely position correct within 10% of the image size and orientation of the mirror axis correct up to 10 degree. In the competition best recognition rates were higher, such as around 60%.
4. Conclusions
The state of theory in Gestalt Algebra is not quite mature as yet. There are yet only quite primitive results on closure and commutativity. Much work lies ahead. Practical achievements are limited as well. Other methods such as [12] achieved far better performance in the contest—with lower computational complexity. Yet, such approaches cannot capture the recursive (somehow syntactic) structure of symmetries of symmetries etc. Also, they apply different methods for mirror, row, and rotational symmetry recognition, while Gestalt Algebra gives a unified concept.
Conflicts of Interest
The author declares no conflict of interest.
References
- Leo Online Dictionary. Available online: http://www.leo.org/ (accessed on 13 February 2014).
- Wertheimer, M. Untersuchungen zur Lehre der Gestalt, M., II. Psychol. Forsch 1923, 4, 301–350. (In German). [Google Scholar]
- Michaelsen, E.; Yashina, V. Simple Gestalt Algebra. Pattern Recognit. Image Anal 2014. in press.. [Google Scholar]
- Malcev, A.I. Algebraic Systems; Nauka: Moscow, Russia, 1970; Springer: Berlin, Germany, 1973.
- Sassi, M.; Demeyer, M.; Wagemans, J. Peripheral Contour Grouping and Saccade Targeting: The Role of Mirror Symmetry. Symmetry 2014, 6, 1–22. [Google Scholar]
- Treder, M.S. Behind the Looking-Glass: A Review on Human Symmetry Perception. Symmetry 2010, 2, 1510–1543. [Google Scholar]
- Rosenfeld, A. Picture Languages; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Zhu, L.; Chen, Y.; Yuille, A. Unsupervised learning of probabilistic grammar-markov models for object categories. IEEE Trans. Pattern Recognit. Mach. Intell 2009, 31, 114–128. [Google Scholar]
- Bienstock, E.; Geman, S.; Potter, D. Compositionality MDL Priors, and Object Recognition. In Advances in Neural Information Processing Systems; Mozer, M.C., Jordan, M.I., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; pp. 838–844. [Google Scholar]
- Finkenzeller, D.; Bender, J. Semantic representation of complex building structures. In Proceedings of the Computer Graphics and Visualization (CGV 2008)—IADIS Multi Conference on Computer Science and Information Systems, Amsterdam, The Netherlands, 22–27 July 2008.
- Desolneux, A.; Moisan, L.; Morel, J.-M. Gestalt theory and computer vision. In Seeing, Thinking and Knowing; Carsetti, A., Ed.; Kluwer: Dordrecht, The Netherlands, 2004; pp. 71–101. [Google Scholar]
- Patraucean, V.; von Gioi, R.G.; Ovsjankov, M. Detection of Mirror-Symmetric Image Patches. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Portland, OR, USA, 23–28 June 2013.
- Reisfeld, D.; Wolfson, H.; Yeshurun, Y. Detection of Interest Points Using Symmetry. In Proceedings of the ICCV, Osaka, Japan, 4–7 December 1990; pp. 62–65.
- Ma, R.; Chen, J.; Su, Z. MI-SIFT: Mirror and inversion invariant generalization for sift descriptor. In Proceedings of the ACM International Conference on Image and Video Retrieval; ACM: New York, NY, USA, 2010; pp. 228–235. [Google Scholar]
- Michaelsen, E.; Muench, D.; Arens, M. Recognition of Symmetry Structure by Use of Gestalt Algebra. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Portland, OR, USA, 23–28 June 2013.
- Symmetry Detection from Real World Images—A Competition. Available online: http://vision.cse.psu.edu/research/symComp13/index.shtml (accessed on 14 February 2014).
- Liu, J.; Slota, G.; Zheng, G.; Wu, Z.; Park, M.; Lee, S.; Rauschert, I.; Liu, Y. Symmetry Detection from RealWorld Images Competition 2013: Summary and Results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Portland, OR, USA, 23–28 June 2013.
- Lowe, D.G. Object Recognition from Local Scale-invariant Features. In Proceedings of the International Conference on Computer Vision, Corfu, Greece; 1999; pp. 1150–1157. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).