Invisibility and PT Symmetry: A Simple Geometrical Viewpoint

Abstract

We give a simplified account of the properties of the transfer matrix for a complex one-dimensional potential, paying special attention to the particular instance of unidirectional invisibility. In appropriate variables, invisible potentials appear as performing null rotations, which lead to the helicity-gauge symmetry of massless particles. In hyperbolic geometry, this can be interpreted, via Möbius transformations, as parallel displacements, a geometric action that has no Euclidean analogy.

1. Introduction

The work of Bender and coworkers [1–6] has triggered considerable efforts to understand complex potentials that have neither parity ( ) nor time-reversal symmetry ( ), yet they retain combined invariance. These systems can exhibit real energy eigenvalues, thus suggesting a plausible generalization of quantum mechanics. This speculative concept has motivated an ongoing debate in several forefronts [7,8].

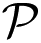
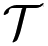
Quite recently, the prospect of realizing -symmetric potentials within the framework of optics has been put forward [9,10] and experimentally tested [11]. The complex refractive index takes on here the role of the potential, so they can be realized through a judicious inclusion of index guiding and gain/loss regions. These -synthetic materials can exhibit several intriguing features [12–14], one of which will be the main interest of this paper, namely, unidirectional invisibility [15–17].

In all these matters, the time-honored transfer-matrix method is particularly germane [18]. However, a quick look at the literature immediately reveals the different backgrounds and habits in which the transfer matrix is used and the very little cross talk between them.

To remedy this flaw, we have been capitalizing on a number of geometrical concepts to gain further insights into the behavior of one-dimensional scattering [19–26]. Indeed, when one think in a unifying mathematical scenario, geometry immediately comes to mind. Here, we keep going this program and examine the action of the transfer matrices associated to invisible scatterers. Interestingly enough, when viewed in SO(1, 3), they turn to be nothing but parabolic Lorentz transformations, also called null rotations, which play a crucial role in the determination of the little group of massless particles. Furthermore, borrowing elementary techniques of hyperbolic geometry, we reinterpret these matrices as parallel displacements, which are motions without Euclidean counterpart.

We stress that our formulation does not offer any inherent advantage in terms of efficiency in solving practical problems; rather, it furnishes a general and unifying setting to analyze the transfer matrix for complex potentials, which, in our opinion, is more than a curiosity.

2. Basic Concepts on Transfer Matrix

To be as self-contained as possible, we first briefly review some basic facts on the quantum scattering of a particle of mass m by a local complex potential V(x) defined on the real line ℝ [27–34]. Although much of the renewed interest in this topic has been fuelled by the remarkable case of symmetry, we do not use this extra assumption in this Section.

The problem at hand is governed by the time-independent Schrödinger equation

$$H\mathrm{\Psi }(x)=\left[-\frac{d^2}{d{x}^2}+U(x)\right]\mathrm{\Psi }(x)=\varepsilon \mathrm{\Psi }(x)$$

(1)

where ε = 2mE/ћ² and U(x) = 2mV(x)/ћ², E being the energy of the particle. We assume that U(x) → 0 fast enough as x → ±∞, although the treatment can be adapted, with minor modifications, to cope with potentials for which the limits U_± = lim_x→±∞ U(x) are different.

Since U(x) decays rapidly as |x| → ∞, solutions of (1) have the asymptotic behavior

$$\mathrm{\Psi }(x)=\{\begin{array}{ll}{A}_{+}{e}^{+\mathit{\text{ikx}}}+A_{-}{e}^{-\mathit{\text{ikx}}}\hfill & x\to -\infty \hfill \\ B_{+}{e}^{+\mathit{\text{ikx}}}+B_{-}{e}^{-\mathit{\text{ikx}}}\hfill & x\to \infty \hfill \end{array}$$

(2)

Here, k² = ε, A_± and B_± are k-dependent complex coefficients (unspecified, at this stage), and the subscripts + and — distinguish right-moving modes exp(+ikx) from left-moving modes exp(−ikx), respectively.

The problem requires to work out the exact solution of (1) and invoke the appropriate boundary conditions, involving not only the continuity of Ψ(x) itself, but also of its derivative. In this way, one has two linear relations among the coefficients A_± and B_±, which can be solved for any amplitude pair in terms of the other two; the result can be expressed as a matrix equation that translates the linearity of the problem. Frequently, it is more advantageous to specify a linear relation between the wave amplitudes on both sides of the scatterer, namely,

$$\left(\begin{array}{c}{B}_{+}\\ B_{-}\end{array}\right)=\text{M}\left(\begin{array}{c}{A}_{+}\\ A_{-}\end{array}\right)$$

(3)

M is the transfer matrix, which depends in a complicated way on the potential U(x). Yet one can extract a good deal of information without explicitly calculating it: let us apply (3) successively to a right-moving [(A₊ = 1, B₋ = 0)] and to a left-moving wave [(A₊ = 0, B₋ = 1)], both of unit amplitude. The result can be displayed as

$$\begin{array}{cc}\left(\begin{array}{c}{T}^{\ell }\\ 0\end{array}\right)=\text{M}\left(\begin{array}{c}1\\ R^{\ell }\end{array}\right),& \left(\begin{array}{c}{R}^r\\ 1\end{array}\right)=\text{M}\left(\begin{array}{c}0\\ T^r\end{array}\right),\end{array}$$

(4)

where T^ℓ,r and R^ℓ,r are the transmission and reflection coefficients for a wave incoming at the potential from the left and from the right, respectively, defined in the standard way as the quotients of the pertinent fluxes [35].

With this in mind, Equation (4) can be thought of as a linear superposition of the two independent solutions

$${\mathrm{\Psi }}_k^{\ell }(x)=\{\begin{array}{ll}{e}^{+\mathit{\text{ikx}}}+R^{\ell }(x)e^{-\mathit{\text{ikx}}}\hfill & x\to -\infty ,\hfill \\ T^{\ell }(k)e^{+\mathit{\text{ikx}}}\hfill & x\to \infty ,\hfill \end{array}{\mathrm{\Psi }}_k^r(x)=\{\begin{array}{ll}{T}^r(k)e^{-\mathit{\text{ikx}}}\hfill & x\to -\infty ,\hfill \\ e^{-\mathit{\text{ikx}}}+R^r(k)e^{+\mathit{\text{ikx}}}\hfill & x\to \infty ,\hfill \end{array}$$

(5)

which is consistent with the fact that, since ε > 0, the spectrum of the Hamiltonian (1) is continuous and there are two linearly independent solutions for a given value of ε. The wave function ${\mathrm{\Psi }}_k^{\ell }(x)$ represents a wave incident from −∞ [exp(+ikx)] and the interaction with the potential produces a reflected wave [R^ℓ(k) exp(−ikx)] that escapes to −∞ and a transmitted wave [T^ℓ(k) exp(+ikx)] that moves off to −∞. The solution ${\mathrm{\Psi }}_k^{\ell }(x)$ can be interpreted in a similar fashion.

Because of the Wronskian of the solutions (5) is independent of x, we can compute $W({\mathrm{\Psi }}_k^{\ell },{\mathrm{\Psi }}_k^r)={\mathrm{\Psi }}_k^{\ell }{\mathrm{\Psi }}_k^{r^{\prime }}-{\mathrm{\Psi }}_k^{{\ell }^{\prime }}{\mathrm{\Psi }}_k^r$ first for x → −∞ and then for x → ∞; this gives

$$\frac{i}{2k}W({\mathrm{\Psi }}_k^{\ell },{\mathrm{\Psi }}_k^r)=T^r(k)=T^{\ell }(k)\equiv T(k)$$

(6)

We thus arrive at the important conclusion that, irrespective of the potential, the transmission coefficient is always independent of the input direction.

Taking this constraint into account, we go back to the system (4) and write the solution for M as

$$\begin{array}{cccc}{M}_{11}(k)=T(k)-\frac{R^{\ell }(k)R^r(k)}{T(k)},& M_{12}(k)=\frac{R^r(k)}{T(k)},& M_{21}(k)=-\frac{R^{\ell }(k)}{T(k)},& M_{22}(k)=\frac{1}{T(k)}\end{array}$$

(7)

A straightforward check shows that det M = +1, so M ∊ SL(2, ℂ); a result that can be drawn from a number of alternative and more elaborate arguments [36].

One could also relate outgoing amplitudes to the incoming ones (as they are often the magnitudes one can externally control): this is precisely the scattering matrix, which can be concisely formulated as

$$\left(\begin{array}{c}{B}_{+}\\ A_{-}\end{array}\right)=\text{S}\left(\begin{array}{c}{A}_{+}\\ B_{-}\end{array}\right)$$

(8)

with matrix elements

$$\begin{array}{cccc}{S}_{11}(k)=T(k),& S_{12}(k)=R^r(k),& S_{21}(k)=R^{\ell }(k),& S_{22}(k)=T(k)\end{array}$$

(9)

Finally, we stress that transfer matrices are very convenient mathematical objects. Suppose that V₁ and V₂ are potentials with finite support, vanishing outside a pair of adjacent intervals I₁ and I₂. If M₁ and M₂ are the corresponding transfer matrices, the total system (with support I₁ U I₂) is described by

$$\text{M}={\text{M}}_1{\text{M}}_2$$

(10)

This property is rather helpful: we can connect simple scatterers to create an intricate potential landscape and determine its transfer matrix by simple multiplication. This is a common instance in optics, where one routinely has to treat multilayer stacks. However, this important property does not seem to carry over into the scattering matrix in any simple way [37,38], because the incoming amplitudes for the overall system cannot be obtained in terms of the incoming amplitudes for every subsystem.

3. Spectral Singularities

The scattering solutions (5) constitute quite an intuitive way to attack the problem and they are widely employed in physical applications. Nevertheless, it is sometimes advantageous to look at the fundamental solutions of (1) in terms of left- and right-moving modes, as we have already used in (2).

Indeed, the two independent solutions of (1) can be formally written down as [39]

$$\begin{array}{ll}{\mathrm{\Psi }}_k^{(+)}(x)\hfill & =e^{+\mathit{\text{ikx}}}+{\int }_x^{\infty }{K}_{+}(x,x^{\prime })e^{+ik{x}^{\prime }}d{x}^{\prime }\hfill \\ {\mathrm{\Psi }}_k^{(-)}(x)\hfill & =e^{-\mathit{\text{ikx}}}+{\int }_{-\infty }^x{K}_{-}(x,x^{\prime })e^{-ik{x}^{\prime }}d{x}^{\prime }\hfill \end{array}$$

(11)

The kernels K_±(x,x ′) enjoy a number of interesting properties. What matters for our purposes is that the resulting ${\mathrm{\Psi }}_k^{(\pm )}(x)$ are analytic with respect to k in ℂ₊ = {z ∊ ℂ| Imz > 0} and continuous on the real axis. In addition, it is clear that

$$\begin{array}{cccc}{\mathrm{\Psi }}_k^{(+)}(x)=e^{+\mathit{\text{ikx}}}& x\to \infty ,& {\mathrm{\Psi }}_k^{(-)}(x)=e^{-\mathit{\text{ikx}}}& x\to -\infty \end{array}$$

(12)

that is, they are the Jost functions for this problem [31].

Let us look at the Wronskian of the Jost functions $W({\mathrm{\Psi }}_k^{(-)},{\mathrm{\Psi }}_k^{(+)})$, which, as a function of k, is analytical in ℂ₊. A spectral singularity is a point k* ∊ ℝ₊ of the continuous spectrum of the Hamiltonian (1) such that

$$W({\mathrm{\Psi }}_{k_{*}}^{(-)},{\mathrm{\Psi }}_{k_{*}}^{(+)})=0$$

(13)

so ${\mathrm{\Psi }}_k^{(\pm )}(x)$ become linearly dependent at k* and the Hamiltonian is not diagonalizable. In fact, the set of zeros of the Wronskian is bounded, has at most a countable number of elements and its limit points can lie in a bounded subinterval of the real axis [40]. There is an extensive theory of spectral singularities for (1) that was started by Naimark [41]; the interested reader is referred to, e.g., Refs. [42–46] for further details.

The asymptotic behavior of ${\mathrm{\Psi }}_k^{\pm }(x)$ at the opposite extremes of ℝ with respect to those in (12) can be easily worked out by a simple application of the transfer matrix (and its inverse); viz,

$$\begin{array}{ll}{\mathrm{\Psi }}_k^{(-)}(x)\hfill & =M_{12}{e}^{+\mathit{\text{ikx}}}+M_{22}{e}^{-\mathit{\text{ikx}}}x\to \infty \hfill \\ {\mathrm{\Psi }}_k^{(+)}(x)\hfill & =M_{22}{e}^{+\mathit{\text{ikx}}}-M_{21}{e}^{-\mathit{\text{ikx}}}x\to -\infty \hfill \end{array}$$

(14)

Using ${\mathrm{\Psi }}_k^{\pm }(x)$ in (12) and (14), we can calculate

$$\frac{i}{2k}W({\mathrm{\Psi }}_k^{(-)},{\mathrm{\Psi }}_k^{(+)})=M_{22}(k)$$

(15)

Upon comparing with the definition (13), we can reinterpret the spectral singularities as the real zeros of M₂₂(k) and, as a result, the reflection and transmission coefficients diverge therein. The converse holds because M₁₂(k) and M₂₁(k) are entire functions, lacking singularities. This means that, in an optical scenario, spectral singularities correspond to lasing thresholds [47–49].

One could also consider the more general case that the Hamiltonian (1) has, in addition to a continuous spectrum corresponding to k ∊ ℝ₊, a possibly complex discrete spectrum. The latter corresponds to the square-integrable solutions of that represent bound states. They are also zeros of M₂₂(k), but unlike the zeros associated with the spectral singularities these must have a positive imaginary part [36].

The eigenvalues of S are

$$s_{\pm }=\frac{1}{M_{22}(k)}\left[1\pm \sqrt{1-M_{11}(k)M_{22}(k)}\right]$$

(16)

At a spectral singularity, s₊ diverges, while s_ → M₁₁(k)/2, which suggests identifying spectral singularities with resonances with a vanishing width.

4. Invisibility and Symmetry

As heralded in the Introduction, unidirectional invisibility has been lately predicted in materials. We shall elaborate on the ideas developed by Mostafazadeh [50] in order to shed light into this intriguing question.

The potential U(x) is called reflectionless from the left (right), if R^ℓ(k) = 0 and R^r(k) ≠ 0 [R^r(k) = 0 and R^ℓ(k) ≠ 0]. From the explicit matrix elements in (7) and (9), we see that unidirectional reflectionlessness implies the non-diagonalizability of both M and S. Therefore, the parameters of the potential for which it becomes reflectionless correspond to exceptional points of M and S [51,52].

The potential is called invisible from the left (right), if it is reflectionless from left (right) and in addition T(k) = 1. We can easily express the conditions for the unidirectional invisibility as

$$\begin{array}{lll}{M}_{12}(k)\ne 0,\hfill & M_{11}(k)=M_{22}(k)=1\hfill & (\text{left invisible})\hfill \\ M_{21}(k)\ne 0,\hfill & M_{11}(k)=M_{22}(k)=1\hfill & (\text{right invisible})\hfill \end{array}$$

(17)

Next, we scrutinize the role of -symmetry in the invisibility. For that purpose, we first briefly recall that the parity transformation “reflects” the system with respect to the coordinate origin, so that x ↦ −x and the momentum p ↦ − p. The action on the wave function is

$$\mathrm{\Psi }(x)\mapsto (P\mathrm{\Psi })(x)=\mathrm{\Psi }(-x)$$

(18)

On the other hand, the time reversal inverts the sense of time evolution, so that x ↦ x, p ↦ −p and i ↦ −i. This means that the operator implementing such a transformation is antiunitary and its action reads

$$\mathrm{\Psi }(x)\mapsto (T\mathrm{\Psi })(x)=\mathrm{\Psi }*(x)$$

(19)

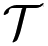
Consequently, under a combined transformation, we have

$$\mathrm{\Psi }(x)\mapsto (PT\mathrm{\Psi })(x)=\mathrm{\Psi }*(-x)$$

(20)

Let us apply this to a general complex scattering potential. The transfer matrix of the -transformed system, we denote by M^{( )}, fulfils

$$\left(\begin{array}{c}{A}_{+}^{*}\\ A_{-}^{*}\end{array}\right)={\text{M}}^{(PT)}\left(\begin{array}{c}{B}_{+}^{*}\\ B_{-}^{*}\end{array}\right)$$

(21)

Comparing with (3), we come to the result

$${\text{M}}^{(PT)}=({\text{M}}^{-1})*$$

(22)

and, because det M = 1, this means

$$\begin{array}{cccc}{M}_{11}\stackrel{PT}{\mapsto }{M}_{22}^{*},& M_{12}\stackrel{PT}{\mapsto }-M_{12}^{*},& M_{21}\stackrel{PT}{\mapsto }{M}_{21}^{*},& M_{22}\stackrel{PT}{\mapsto }{M}_{11}^{*},\end{array}$$

(23)

When the system is invariant under this transformation [M^{( )} = M], it must hold

$${\text{M}}^{-1}=\text{M}*$$

(24)

a fact already noticed by Longhi [48] and that can be also recast as [53]

$$Re\left(\frac{R^{\ell }}{T}\right)=Re\left(\frac{R^r}{T}\right)=0$$

(25)

This can be equivalently restated in the form

$$\begin{array}{cc}{\rho }^{\ell }-\tau =\pm \pi /2,& {\rho }^r-\tau =\pm \pi /2\end{array}$$

(26)

with τ = arg(T) and ρ_ℓ,r = arg(R_ℓ,r). Hence, if we look at the complex numbers R^ℓ, R^r, and T as phasors, Equation (26) tell us that R^ℓ and R^r are always collinear, while T is simultaneously perpendicular to them. We draw the attention to the fact that the same expressions have been derived for lossless symmetric beam splitters [54]: we have shown that they hold true for any -symmetric structure.

A direct consequence of (23) is that there are particular instances of -invariant systems that are invisible, although not every invisible potential is invariant. In this respect, it is worth stressing, that even ( -symmetric) potentials do not support unidirectional invisibility and the same holds for real ( -symmetric) potentials.

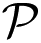
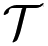
In optics, beam propagation is governed by the paraxial wave equation, which is equivalent to a Schrödinger-like equation, with the role of the potential played here by the refractive index. Therefore, a necessary condition for a complex refractive index to be invariant is that its real part is an even function of x, while the imaginary component (loss and gain profile) is odd.

5. Relativistic Variables

To move ahead, let us construct the Hermitian matrices

$$\text{X}=\left(\begin{array}{c}{X}_{+}\\ X_{-}\end{array}\right)\otimes \left(\begin{array}{cc}{X}_{+}^{*}& X_{-}^{*}\end{array}\right)=\left(\begin{array}{cc}{\left|X_{+}\right|}^2& X_{+}{X}_{-}^{*}\\ X_{+}^{*}{X}_{-}& {\left|X_{-}\right|}^2\end{array}\right)$$

(27)

where X_± refers to either A_± or B_±; i.e., the amplitudes that determine the behavior at each side of the potential. The matrices X are quite reminiscent of the coherence matrix in optics or the density matrix in quantum mechanics.

One can verify that M acts on X by conjugation

$${\text{X}}^{\prime }=MX{M}^{†}$$

(28)

The matrix X′ is associated with the amplitudes B_± and X with A_±.

Let us consider the set σ^μ = ( ,σ), with Greek indices running from 0 to 3. The σ^μ are the identity and the standard Pauli matrices, which constitute a basis of the linear space of 2 × 2 complex matrices. For the sake of covariance, it is convenient to define σ̃^μ = σ_μ = ( ,−σ), so that [55]

$$\text{Tr}({\tilde{\sigma }}^{\mu }{\sigma }_{\nu })=2{\delta }_{\nu }^{\mu }$$

(29)

and ${\delta }_{\nu }^{\mu }(\text{M})$ is the Kronecker delta. To any Hermitian matrix X we can associate the coordinates

$$x^{\mu }=\frac{1}{2}\text{Tr}(\text{X}{\tilde{\sigma }}^{\mu })$$

(30)

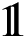
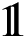
The congruence (28) induces in this way a transformation

$${x^{\prime }}^{\mu }={\mathrm{\Lambda }}_{\nu }^{\mu }(\text{M})x^{\nu }$$

(31)

where ${\mathrm{\Lambda }}_{\nu }^{\mu }(\text{M})$ can be found to be

$${\mathrm{\Lambda }}_{\nu }^{\mu }(\text{M})=\frac{1}{2}\text{Tr}({\tilde{\sigma }}^{\mu }\text{M}{\sigma }_{\nu }{\text{M}}^{†})$$

(32)

This equation can be solved to obtain M from Λ. The matrices M and −M generate the same Λ, so this homomorphism is two-to-one. The variables x^μ are coordinates in a Minkovskian (1+3)-dimensional space and the action of the system can be seen as a Lorentz transformation in SO(1, 3).

Having set the general scenario, let us have a closer look at the transfer matrix corresponding to right invisibility (the left invisibility can be dealt with in an analogous way); namely,

$$\text{M}=\left(\begin{array}{cc}1& R\\ 0& 1\end{array}\right)$$

(33)

where, for simplicity, we have dropped the superscript from R^r, as there is no risk of confusion. Under the homomorphism (32) this matrix generates the Lorentz transformation

$$\mathrm{\Lambda }(\text{M})=\left(\begin{array}{cccc}1+{\left|R\right|}^2/2& ReR& -ImR& -{\left|R\right|}^2/2\\ ReR& 1& 0& -ReR\\ -ImR& 0& 1& ImR\\ {\left|R\right|}^2/2& ReR& -ImR& 1-{\left|R\right|}^2/2\end{array}\right)$$

(34)

According to Wigner [56], the little group is a subgroup of the Lorentz transformations under which a standard vector s^μ remains invariant. When s^μ is timelike, the little group is the rotation group SO(3). If s^μ is spacelike, the little group are the boosts SO(1, 2). In this context, the matrix (34) is an instance of a null rotation; the little group when s^μ is a lightlike or null vector, which is related to E(2), the symmetry group of the two-dimensional Euclidean space [57].

If we write (34) in the form Λ(M) = exp(iN), we can easily work out that

$$\text{N}=\left(\begin{array}{cccc}0& ReR& -ImR& 0\\ ReR& 0& 0& -ReR\\ -ImR& 0& 0& ImR\\ 0& ReR& -ImR& 0\end{array}\right)$$

(35)

This is a nilpotent matrix and the vectors annihilated by N are invariant by Λ(M). In terms of the Lie algebra so(1, 3), N can be expressed as

$$\text{N}=ReR(K_1+J_2)-ImR(K_2+J_1)$$

(36)

where K_i generate boosts and J_i rotations (i = 1, 2, 3) [58]. Observe that the rapidity of the boost and the angle of the rotation have the same norm. The matrix N define a two-parameter Abelian subgroup.

Let us take, for the time being, Re R = 0, as it happens for -invariant invisibility. We can express K₂ + J₁ as the differential operator

$${\text{K}}_2+J_1\mapsto (x^2{\partial }_0+x^0{\partial }_2)+(x^2{\partial }_3-x^3{\partial }_2)=x^2({\partial }_0+{\partial }_3)+(x^0-x^3){\partial }_2$$

(37)

As we can appreciate, the combinations

$$\begin{array}{ccc}{x}^2,& x^0-x^3,& {\left(x^0\right)}^2-{\left(x^1\right)}^2-{\left(x^3\right)}^2\end{array}$$

(38)

remain invariant. Suppressing the inessential coordinate x², the flow lines of the Killing vector (37) is the intersection of a null plane, x⁰ − x³ = c₂ with a hyperboloid (x⁰)² − (x¹)² − (x³)² = c₃. The case c₃ = 0 has the hyperboloid degenerate to a light cone with the orbits becoming parabolas lying in corresponding null planes.

6. Hyperbolic Geometry and Invisibility

Although the relativistic hyperboloid in Minkowski space constitute by itself a model of hyperbolic geometry (understood in a broad sense, as the study of spaces with constant negative curvature), it is not the best suited to display some features.

Let us consider the customary tridimensional hyperbolic space ℍ³, defined in terms of the upper half-space {(x, y, z) ∊ ℝ³|z > 0}, equipped with the metric [59]

$$d{s}^2=\frac{\sqrt{d{x}^2+d{y}^2+d{z}^2}}{z}$$

(39)

The geodesics are the semicircles in ℍ³ orthogonal to the plane z = 0.

We can think of the plane z = 0 in R³ as the complex plane ℂ with the natural identification (x, y, z) ↦ w = x + iy. We need to add the point at infinity, so that ℂ̂ = ℂU ∞, which is usually referred to as the Riemann sphere and identify ℂ̂ as the boundary of ℍ³.

Every matrix M in SL(2, ℂ) induces a natural mapping in ℂ via Möbius (or bilinear) transformations [60]

$$w^{\prime }=\frac{M_{11}w+M_{12}}{M_{21}w+M_{22}}$$

(40)

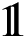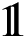Note that any matrix obtained by multiplying M by a complex scalar λ gives the same transformation, so a Möbius transformation determines its matrix only up to scalar multiples. In other words, we need to quotient out SL(2, ℂ) by its center { , − }: the resulting quotient group is known as the projective linear group and is usually denoted PSL(2, ℂ).

Observe that we can break down the action (40) into a composition of maps of the form

$$\begin{array}{ccc}w\mapsto w+\lambda ,& w\mapsto \lambda w,& w\mapsto -1/w\end{array}$$

(41)

with λ ∊ ℂ. Then we can extend the Mobius transformations to all ℍ³ as follows:

$$\begin{array}{ccc}(w,z)\mapsto (w+\lambda ,z),& (w,z)\mapsto (\lambda w,|\lambda |z),& (w,z)\mapsto \left(-\frac{w*}{\left|w^2\right|+z^2},\frac{z}{\left|w^2\right|+z^2}\right)\end{array}$$

(42)

The expressions above come from decomposing the action on ℂ̂ of each of the elements of PSL(2, ℂ) in question into two inversions (reflections) in circles in ℂ̂. Each such inversion has a unique extension to ℍ₃ as an inversion in the hemisphere spanned by the circle and composing appropriate pairs of inversions gives us these formulas.

In fact, one can show that PSL(2, ℂ) preserves the metric on ℍ₃. Moreover every isometry of ℍ₃ can be seen to be the extension of a conformal map of ℂ̂ to itself, since it must send hemispheres orthogonal to ℂ̂ to hemispheres orthogonal to ℂ̂, hence circles in ℂ̂ to circles in ℂ̂. Thus all orientation-preserving isometries of ℍ₃ are given by elements of PSL(2, ℂ) acting as above.

In the classification of these isometries the notion of fixed points is of utmost importance. These points are defined by the condition w′ = w in (40), whose solutions are

$$w_f=\frac{(M_{11}-M_{22})\pm \sqrt{{\left[\text{Tr}(\text{M})\right]}^2-4}}{2M_{21}}$$

(43)

So, they are determined by the trace of M. When the trace is a real number, the induced Mobius transformations are called elliptic, hyperbolic, or parabolic, according [Tr(M)]² is lesser than, greater than, or equal to 4, respectively. The canonical representatives of those matrices are [61]

$$\begin{array}{ccc}\underset{\text{elliptic}}{\underbrace{\left(\begin{array}{cc}{e}^{i\theta /2}& 0\\ 0& e^{-i\theta /2}\end{array}\right),}}& \underset{\text{hyperbolic}}{\underbrace{\left(\begin{array}{cc}{e}^{\xi /2}& 0\\ 0& e^{-\xi /2}\end{array}\right),}}& \underset{\text{parabolic}}{\underbrace{\left(\begin{array}{cc}1& \lambda \\ 0& 1\end{array}\right),}}\end{array}$$

(44)

while the induced geometrical actions are

$$\begin{array}{ccc}{w}^{\prime }=w{e}^{i\theta },& w^{\prime }=w{e}^{\xi },& w^{\prime }=w+\lambda \end{array}$$

(45)

that is, a rotation of angle θ (so fixes the axis z), a squeezing of parameter ξ (it has two fixed points in ℂ̂, no fixed points in ℍ₃, and every hyperplane in ℍ₃ that contains the geodesic joining the two fixed points in ℂ̂ is invariant); and a parallel displacement of magnitude λ, respectively. We emphasize that this later action is the only one without Euclidean analogy Indeed, in view of (33), this is precisely the action associated to an invisible scatterer. The far-reaching consequences of this geometrical interpretation will be developed elsewhere.

7. Concluding Remarks

We have studied unidirectional invisibility by a complex scattering potential, which is characterized by a set of invariant equations. Consequently, the -symmetric invisible configurations are quite special, for they possess the same symmetry as the equations.

We have shown how to cast this phenomenon in term of space-time variables, having in this way a relativistic presentation of invisibility as the set of null rotations. By resorting to elementary notions of hyperbolic geometry, we have interpreted in a natural way the action of the transfer matrix in this case as a parallel displacement.

We think that our results are yet another example of the advantages of these geometrical methods: we have devised a geometrical tool to analyze invisibility in quite a concise way that, in addition, can be closely related to other fields of physics.