Octahedral Systems
Call a
-uniform hypergraph on
a
colourful hypergraph. A colourful configuration defines a colourful hypergraph by taking hyperedges corresponding to colourful simplices containing
in their interior. We will call a colourful hypergraph that arises from a colourful configuration with
a
configuration hypergraph. Our strategy, following [
13], is to show that a particular configuration hypergraph whose hyperedges correspond to the colourful simplices containing
in a configuration cannot exist. The Colourful Carathéodory Theorem gives that any configuration hypergraph must satisfy:
Property 1. Every vertex of a configuration hypergraph belongs to at least one of its hyperedges.
Fix a colour i. We call a set t of d points that contains exactly one point from each other than an i-transversal. That is to say, an i-transversal t has and for . We call any pair of disjoint i-transversals an i-octahedron; these may or may not generate a cross-polytope, i.e., a d-dimensional octahedron, in the geometric sense that their convex hull is a cross-polytope with same coloured points never adjacent in the skeleton of the polytope.
A key property of colourful configurations is that for a fixed
i-octahedron Ω, the parity of the number of colourful simplices containing
formed using points from Ω and a point of colour
i does not depend on which point of colour
i is chosen. This is a topological fact that corresponds to the fact that
is either
inside or
outside the octahedron, see the
Octahedron Lemma of [
3] for a proof.
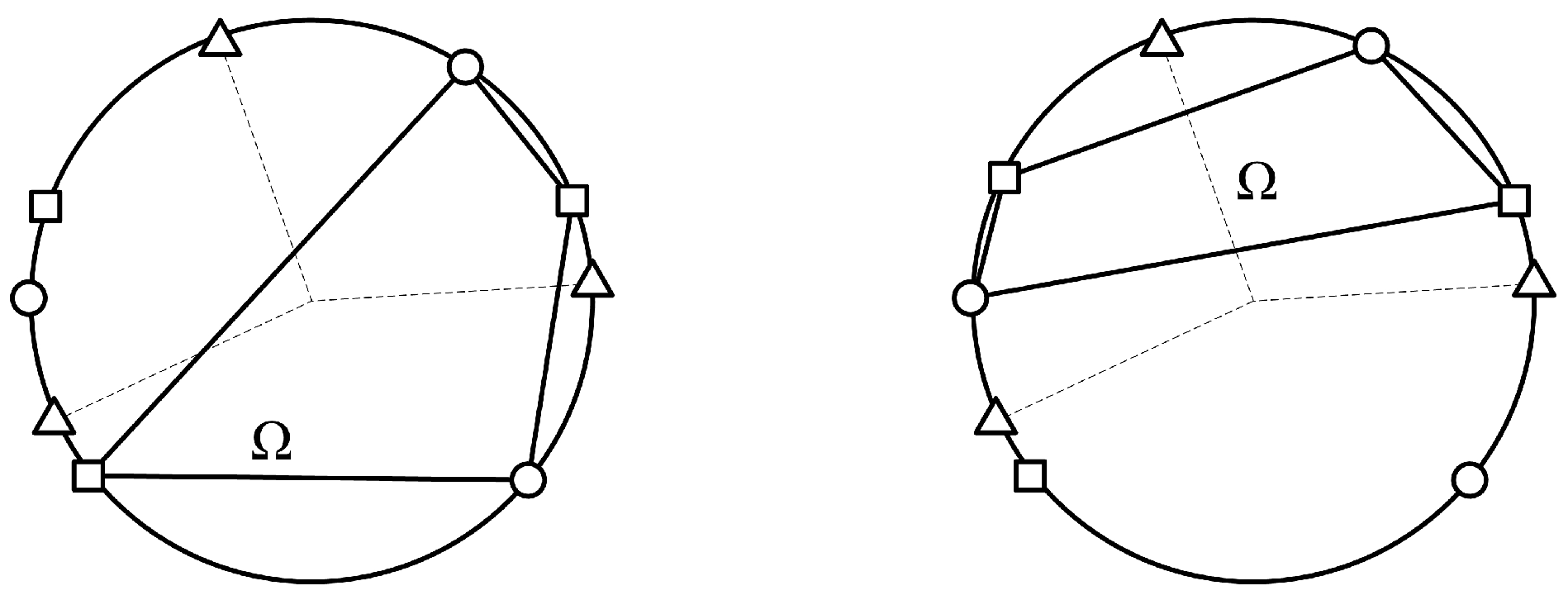
Figure 1 illustrates this in a two-dimensional case where
is at the centre of a circle that contains points of the three colours.
We carry the definitions of i-transversals and i-octahedra over to the hypergraph setting. Then any configuration hypergraph must satisfy:
Property 2. For any octahedron Ω of a hypergraph, the parity of the set of hyperedges using points from Ω and a fixed point for the ith coordinate is the same for all choices of .
Consider a colourful hypergraph whose vertices are
and whose hyperedges have exactly one element from each set. If the hypergraph satisfies Property 2 we call it an
octahedral system, if it additionally satisfies Property 1 we call it an
octahedral system without isolated vertex. A colourful configuration with
and
k colourful simplices containing
has a configuration hypergraph that is an octahedral system without isolated vertex with
k hyperedges. Let
be the minimum number of hyperedges in an octahedral system without isolated vertex with
colours. Then
. It is an interesting question whether there are any octahedral systems without isolated vertex not arising from any colourful configurations, and if not, whether
for some
d. This purely combinatorial approach was originally suggested by Bárány [
14].
Figure 1.
Two-dimensional cross-polytopes Ω containing and not containing .
Figure 1.
Two-dimensional cross-polytopes Ω containing and not containing .
Octahedral systems have the advantage of being combinatorial and finite. In principle, for any particular d and k we can check if there exists an octahedral system without isolated vertex on with up to k hyperedges by generating all the—finitely many—hypergraphs with up to k hyperedges, each containing one element from each and then testing if they satisfy Properties 1 and 2. The difficulty lies in the sheer number of such hypergraphs, and in verifying Property 2 efficiently.
We obtain lower bounds for by trying to build an octahedral system without isolated vertex by adding one hyperedge at a time. We can reduce the search space by exploiting the many combinatorial symmetries in such hypergraphs and considering only configurations that satisfy certain normalizations. However, this alone is not sufficient to improve the known lower bounds even for . We thus turn our attention to how to use Property 2 effectively.
We use two strategies. The first is to look at a particular subset of parity conditions that are relatively independent. The second is to use the following lemma, proved in [
15]. Call a hyperedge
e of a colourful hypergraph
isolated if there is no other hyperedge that differs from
e only in a single coordinate. Then:
Lemma 1. An octahedral system with or fewer hyperedges must not contain any isolated hyperedges.
Enumeration Details
We begin by fixing an arbitrary colour as colour 0 and an arbitrary 0-transversal. We can label the points in each set from 0 to d and, without loss of generality, take the transversal to contain the 0 point of each set. For convenience we write hyperedges as a string of numbers and transversals as string of d numbers with * corresponding to the omitted colour. Thus the 0-transversal considered is .
Consider the d octahedra generated by transversals , for . Note that the initial numberings are arbitrary, and we may fix them as part of our search algorithm. Given a colourful hypergraph, we can form a binary table by writing down for each the parity of the number of edges using vertices from the octahedron formed by and with initial coordinate s. We call this the parity table. If a colourful hypergraph satisfies Property 2, its parity table has constant rows.
The advantage of focusing on this table is that the entries are relatively independent. Only hyperedges of the form can change more than one entry of this table. After accounting for such hyperedges, each entry can only be affected by the hyperedges that are on the relevant octahedron with the given initial coordinate.
We now use the results of [
5] to break the problem into several cases based on
ℓ, the number of hyperedges containing
,
b, the number of the parity table octahedra that have odd parity, and
j, the minimum number of transversals covering any point of colour 0.
It is clear that for any octahedral system without isolated vertex and with
or fewer hyperedges we must have
and that the number of hyperedges is at least
. Further, [
5] shows that we must have
, and that the number of hyperedges must be at least
, as well as at least
assuming that the colour 0 is chosen to minimize
ℓ and that
. This last fact allows us to assume that
.
To rule out possible octahedral systems without isolated vertex of size 13, it is sufficient to consider cases where or , which in turn means or . In the case , we have at least simplices, so or , and in the case , we have so . In summary, we need to rule out systems where the triple is one of .
By reordering the points of colour 0, we can take the hyperedges
to be in the system for
, and not in the system for
. Consider the parity table after including these hyperedges with
, illustrated in
Table 1.
Table 1.
The parity table with .
Table 1.
The parity table with .
| | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Now if , then we are requiring that the parity table be comprised entirely of 1’s. So in this case the entries in the first three columns are correct, while the entries in the last two columns are incorrect.
For
we proceed to enumerate configurations as follows. Since
, we include initial hyperedges
. We then add hyperedges to correct each of the eight entries of
Table 1, which must be fixed to get the correct parity table for
. As previously remarked, adding any hyperedge not of the form
will change only a single entry in the parity table. For instance, the entry in the first row and fourth column can be changed only by a hyperedge of the form
where
. Given that that 30000 cannot be added to the configuration without changing
ℓ, there remain only 15 possible hyperedges that change the entry, and one must be in our configuration. In fact, by reordering the colours we can take it to be one of 31000, 31100, 31110 and 31111.
We could continue to exploit symmetries in this way—for instance depending on which of the previous 4 hyperedges is chosen, the next hyperedge could be one of 4 to 7 hyperedges fixing the next table entry. However, we did not do this so as to avoid extensive case analysis. Instead, we began branching on all 15 possible hyperedges that switch a given table entry until the table is correct and the partial configuration has 11 hyperedges.
As we branch we check two simple predictors that may indicate that the configuration requires several more hyperedges. First, we look for points that are not currently included in any hyperedge. If some colour still has k uncovered points, then we require k additional hyperedges. Second, since any vertex of colour 0 must be covered by at least j hyperedges, we examine which points of colour 0 are not contained in sufficiently many hyperedges, and get a score by summing up the undercounts. At the same time, we may find that all vertices of colour 0 are already covered by more than j hyperedges (especially when ), in which case the partial configuration no longer belongs to this subcase and can be excluded. Again, we require additional hyperedges. If either k or is sufficiently large (in this case 3), then the current partial configuration cannot extend to an octahedral system without isolated vertex with less than 14 hyperedges and is abandoned.
Otherwise, we examine the configuration to see if it has an isolated hyperedge. If it contains an isolated hyperedge e, then by Lemma 1, if the configuration is to extend to an octahedral system without isolated vertex with less than 17 hyperedges, it must include a hyperedge adjacent to e. That is, it must contain differing from e only in a single coordinate. There are only 20 such hyperedges so we can branch on them. We then repeat the process of applying predictors and looking for an isolated hyperedge until we either find an octahedral system without isolated vertex with less than 14 hyperedges, or all partial configurations with fewer hyperedges are exhausted.
If we do arrive at a partial configuration with no isolated hyperedges, then as a last resort we may have to branch on all possible hyperedges. However, this happens infrequently enough that the enumeration ends in a reasonable time.
The remaining cases, where is or are similar. Having exhausted all these cases, we conclude that , and hence .