Abstract
This paper describes 4-valent tiling-like structures, called pseudotilings, composed of barrel tiles and apeirogonal pseudotiles in Euclidean 3-space. These (frequently face-to-face) pseudotilings naturally rise in columns above 3-valent plane tilings by convex polygons, such that each column is occupied by stacked congruent barrel tiles or congruent apeirogonal pseudotiles. No physical space is occupied by the apeirogonal pseudotiles. Many interesting pseudotilings arise from plane tilings with high symmetry. As combinatorial structures, these are abstract polytopes of rank 4 with both finite and infinite 2-faces and facets.
1. Introduction
An n-gonal barrel is a simple polyhedron whose outer shell is easily constructed. Take two n-gons, surround each by a ring of n pentagons, then glue the two halves together at their respective boundaries. For example, a hexagonal barrel is shown in Figure 1a, and a pentagonal barrel is a (not necessarily regular) pentagonal dodecahedron.
This article defines and investigates structures in Euclidean 3-space which are closely related to both normal simple tilings by barrels and normal simple tilings in the plane. The deviation from classical tiling theory occurs when we introduce apeirobarrels, barrels over relatively tame apeirogons (infinite simple polygons in 3-space), which are not tiles in the typical sense as they contain no physical volume. For this reason, we call our constructed objects barrel pseudotilings.
Allowing infinite regular polygons as faces, Grünbaum [1] discovered many new regular polyhedra in Euclidean 3-space besides the already well-known Platonic solids, planar tessellations, Kepler–Poinsot polyhedra, and Petrie–Coxeter polyhedra (see also [2]). The list of 47 regular polyhedra presented in [1] was just one polyhedron short of being complete, which was remedied by Dress ([3,4]) a few years later, who also proved the completeness of the list. Later, Leytem [5] found an alternative way to obtain the elusive 48th Grünbaum–Dress polyhedron.
Over the last few decades, the development of the theory of abstract polytopes and their realizations provided a common framework for the investigation of regular and other polytopes. This generalization of polyhedra and polytopes to combinatorial objects seemed only natural after a long evolution of the terms polygon and polyhedron. While the Grünbaum–Dress polyhedra are regular (abstract) 3-polytopes, realized in 3-space, McMullen and Schulte [6] investigated faithful and discrete realizations of regular 4-polytopes in 3-space, in addition to providing a new proof of Dress’ completeness result. Their complete list encompasses 8 regular 4-apeirotopes (infinite polytopes) in 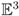 . The subject of abstract polytopes and their realizations has developed greatly since and is still evolving (see, e.g., [7,8]).
. The subject of abstract polytopes and their realizations has developed greatly since and is still evolving (see, e.g., [7,8]).
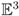 . The subject of abstract polytopes and their realizations has developed greatly since and is still evolving (see, e.g., [7,8]).
. The subject of abstract polytopes and their realizations has developed greatly since and is still evolving (see, e.g., [7,8]).After giving a first example of a barrel pseudotiling in Section 2, we review the terminology in Section 3, and then proceed to Section 4 for the proper definitions. We create each barrel pseudotiling from a normal, simple, plane tiling by convex polygons, by a process outlined in Section 5. After analyzing the properties of barrel pseudotilings in Section 6, we arrive at an equivalent definition for certain classes in the form of decorated plane triangulations (Section 7). More examples and some remarks follow in Section 8 and Section 9.
What makes the pseudotilings interesting, among other things, is that they are faithful realizations of certain abstract rank 4 polytopes (see Section 3.4 and Section 4). For faces of rank 0, 1, and 2, we have vertices, edges, and planar finite faces, as well as non-planar apeirogons. The tiles (barrels) and apeirogonal pseudotiles (apeirogonal barrels) form the set of 3-faces (facets). These polytopes are simple, as well as both infinite in all inner ranks and with (infinitely many) infinite rank 2 faces, but they can be realized faithfully in low-dimensional Euclidean 3-space with a translational symmetry in one direction. While realizations of regular and chiral abstract 4-polytopes in 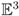 have received the most attention (e.g. [6,7], Section 7F of [8]), it still seems worthwhile to investigate other, less symmetrical, classes as well. The construction process connects the barrel pseudotilings to (partially) directed infinite graphs stemming from triangulations, many of which are visually appealing. It may be worth exploring these connections in the future.
have received the most attention (e.g. [6,7], Section 7F of [8]), it still seems worthwhile to investigate other, less symmetrical, classes as well. The construction process connects the barrel pseudotilings to (partially) directed infinite graphs stemming from triangulations, many of which are visually appealing. It may be worth exploring these connections in the future.
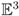 have received the most attention (e.g. [6,7], Section 7F of [8]), it still seems worthwhile to investigate other, less symmetrical, classes as well. The construction process connects the barrel pseudotilings to (partially) directed infinite graphs stemming from triangulations, many of which are visually appealing. It may be worth exploring these connections in the future.
have received the most attention (e.g. [6,7], Section 7F of [8]), it still seems worthwhile to investigate other, less symmetrical, classes as well. The construction process connects the barrel pseudotilings to (partially) directed infinite graphs stemming from triangulations, many of which are visually appealing. It may be worth exploring these connections in the future.As a note of caution to the reader, in deviating from the original usage in [1], the term apeirogon denotes in this paper any infinite, simple polygon. The prefix apeir- is used to emphasize the presence of infinite faces or infinitely many faces of some kind (similar to the usage in [6,8]), however it is not used to denote regularity or even a particular symmetry.
2. A First Example
Start with the regular hexagonal tiling (63) of the plane. Color the tiles in the tiling properly (i.e., such that no two adjacent tiles have the same color) with three colors, see Figure 2a. For reasons that will soon become clear, the color labels have been chosen from the set {0, 0.5, ∞}. Consider a hexagonal barrel stemming from a hexagonal right prism of height 1, such as in Figure 1b, with the prism’s mantle altered as shown “unwrapped” in Figure 1c. We can construct an infinite stack of pairwise congruent hexagonal barrels of this kind whose common faces are hexagons. Call this object in space a hex-stack. Now, consider our planar hexagonal tiling as situated on a horizontal plane in Euclidean 3-space. Each hexagon gives rise to a hexagonal column which extends indefinitely in either direction perpendicular to the plane. The columns associated to colors 0 and 0.5 of our base tiling can be filled up with directly congruent hex-stacks. It is possible to do that in such a way that all the inclined (i.e., neither horizontal nor vertical) edges in the barrels’ sides face a column associated to color ∞. Then, in order to obtain a partial face-to-face tiling (see Section 3 for terminology) of 3-space from all these hexagonal barrels, we have to match up the pentagons which, as points sets, appear as rectangles. For this we shift the columns over hexagonal tiles with color 0.5 vertically by half a step relative to those over hexagonal tiles with color 0 (see Figure 2b), which explains the choice of labels. Note that the planar tiling (63) functions merely as a guide in the construction of the columns. The plane in which (63) is situated serves as a reference plane for applying shifts when positioning adjacent barrel-filled columns relative to each other in order to match the pentagons.
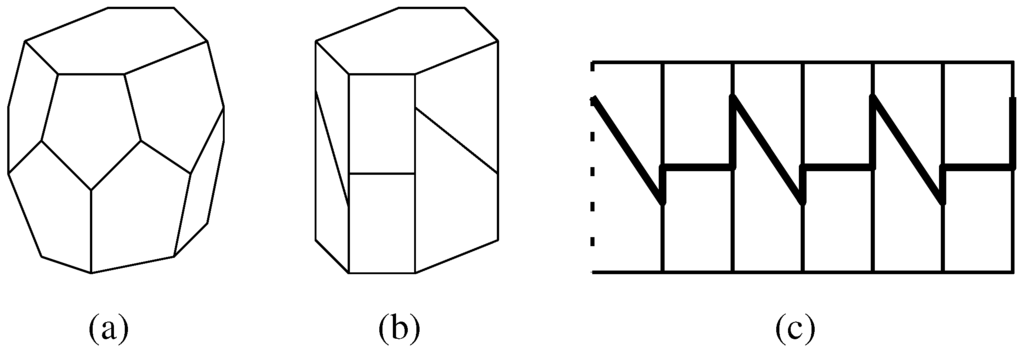
Figure 1.
(a) A hexagonal barrel; (b) A hexagonal barrel stemming from an hexagonal right prism; (c) The mantle of a hexagonal barrel stemming from an hexagonal right prism.
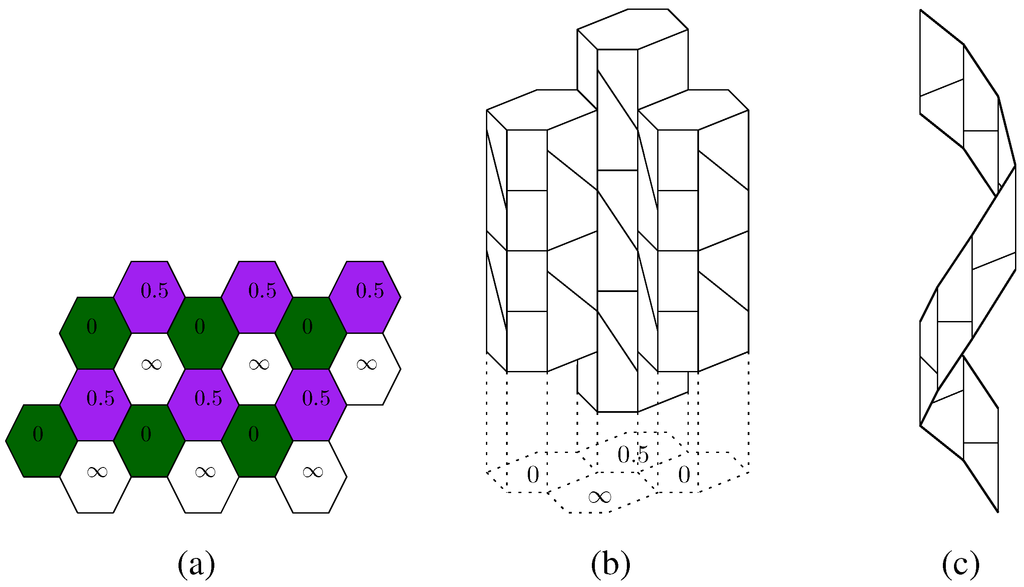
Figure 2.
(a) A proper 3-coloring of (63); (b) Part of the constructed barrel pseudotiling. Note the emerging face structure of the column associated to color ∞, particularly the apeirogons (spirals); (c) Part of a single apeirobarrel.
The remaining part of 3-space separates into infinite columns associated to tiles of color ∞. Let these columns inherit the boundary structure from the hexagonal barrels in adjacent columns. As a result, the boundary of each column colored ∞ falls apart into three “intertwined” or “stacked” apeirobarrels (see Figure 2b,c), where an apeirobarrel is defined as two parallel apeirogons joined by two infinite “rings” of pentagons. Even though no physical volume is occupied by these pseudotiles, the last set of columns can now also be regarded as “tiled”, preserving the face-to-face property and simplicity. Another way to say this is that apeirobarrels can be stacked so that the union of their mantles covers the mantle of an infinite prismatic column completely without overlaps, which is consistent with the way finite barrels stack. This can be done in a left-handed and a right-handed version in the obvious way.
Moreover, a similar construction is possible for several other plane tilings, including the uniform tilings (4.6.12) and (4.82), in which the regular convex polygons surrounding each vertex have four, six, and twelve, respectively four, eight, and eight vertices. Naturally, the question comes up which kinds of barrel pseudotilings arise this way. This is explored in this article.
Related kinds of tiling-like structures with apeirogons, but in the Euclidean plane instead of 3-space, have been investigated by Grünbaum, Miller, and Shephard in [9]. The similarity with the structures considered in this article is perhaps greatest in some of the planar structures (called strip tilings) depicted in Figure 6 of [9].
3. Basic Notions
In order to keep the exposition as self-contained as possible, we will now review basic notions from several areas of relevance.
3.1. Tilings and Barrel Polyhedra
A tiling of Euclidean d-space 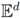 is a locally finite, countable collection of closed topological cells (tiles), which satisfy the following three conditions. First, each tile is a topological d-polytope, a homeomorphic image of a convex d-polytope. Second, the union of all tiles is
is a locally finite, countable collection of closed topological cells (tiles), which satisfy the following three conditions. First, each tile is a topological d-polytope, a homeomorphic image of a convex d-polytope. Second, the union of all tiles is 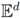 . Third, the intersection of any two distinct tiles is either empty or a proper face of each; in particular, if this intersection is a k-face of each tile, then it is a k-face of the tiling. In other places in the literature, such a tiling may be called face-to-face (compare [10,11]). A normal tiling is a tiling in which the tiles are uniformly bounded in size (i.e., each tile contains a d-ball of some small radius, and is contained in a d-ball of some larger radius). A tiling of
. Third, the intersection of any two distinct tiles is either empty or a proper face of each; in particular, if this intersection is a k-face of each tile, then it is a k-face of the tiling. In other places in the literature, such a tiling may be called face-to-face (compare [10,11]). A normal tiling is a tiling in which the tiles are uniformly bounded in size (i.e., each tile contains a d-ball of some small radius, and is contained in a d-ball of some larger radius). A tiling of 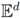 is simple if all vertices are (d + 1)-valent. However, this latter notion is only applicable when “vertices” and “edges” are well-defined, such as in the context of plane tilings or face-to-face tilings (for any d). The face poset of a (face-to-face) tiling, when amended by a unique largest and a unique smallest (empty) face, can be interpreted as an abstract polytope, see Section 3.4.
is simple if all vertices are (d + 1)-valent. However, this latter notion is only applicable when “vertices” and “edges” are well-defined, such as in the context of plane tilings or face-to-face tilings (for any d). The face poset of a (face-to-face) tiling, when amended by a unique largest and a unique smallest (empty) face, can be interpreted as an abstract polytope, see Section 3.4.
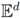 is a locally finite, countable collection of closed topological cells (tiles), which satisfy the following three conditions. First, each tile is a topological d-polytope, a homeomorphic image of a convex d-polytope. Second, the union of all tiles is
is a locally finite, countable collection of closed topological cells (tiles), which satisfy the following three conditions. First, each tile is a topological d-polytope, a homeomorphic image of a convex d-polytope. Second, the union of all tiles is 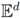 . Third, the intersection of any two distinct tiles is either empty or a proper face of each; in particular, if this intersection is a k-face of each tile, then it is a k-face of the tiling. In other places in the literature, such a tiling may be called face-to-face (compare [10,11]). A normal tiling is a tiling in which the tiles are uniformly bounded in size (i.e., each tile contains a d-ball of some small radius, and is contained in a d-ball of some larger radius). A tiling of
. Third, the intersection of any two distinct tiles is either empty or a proper face of each; in particular, if this intersection is a k-face of each tile, then it is a k-face of the tiling. In other places in the literature, such a tiling may be called face-to-face (compare [10,11]). A normal tiling is a tiling in which the tiles are uniformly bounded in size (i.e., each tile contains a d-ball of some small radius, and is contained in a d-ball of some larger radius). A tiling of 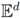 is simple if all vertices are (d + 1)-valent. However, this latter notion is only applicable when “vertices” and “edges” are well-defined, such as in the context of plane tilings or face-to-face tilings (for any d). The face poset of a (face-to-face) tiling, when amended by a unique largest and a unique smallest (empty) face, can be interpreted as an abstract polytope, see Section 3.4.
is simple if all vertices are (d + 1)-valent. However, this latter notion is only applicable when “vertices” and “edges” are well-defined, such as in the context of plane tilings or face-to-face tilings (for any d). The face poset of a (face-to-face) tiling, when amended by a unique largest and a unique smallest (empty) face, can be interpreted as an abstract polytope, see Section 3.4.A barrel over a topological n-gon is a simple topological 3-polytope with two disjoint distinguished n-gonal 2-faces, such that all other 2-faces are pentagonal and adjacent to exactly one of the distinguished faces. Thus, the distinguished faces—also called top and bottom (base) of the barrel—have n pentagonal adjacents each, giving a total of 2n pentagonal faces (if n = 5, all 12 = 2n + 2 faces are pentagons). In short, the sides of the barrel are formed by two rings of pentagons. In an extreme case, such a barrel can be obtained (but not as a convex polytope in the strict sense!) from an n-gonal right prism by partitioning the rectangles in the prism’s mantle accordingly (as indicated in Figure 1b). In this article, we will explicitly allow faces in polytopes to be coplanar, even when they are adjacent.
3.2. Plane Graphs
All graphs considered in this paper will be simple, which means that no multiple edges or loops occur, but they will not necessarily be finite. In fact, most graphs we encounter will be infinite.
Let G = (V, E) be such a (simple) graph. A dominating set (compare [12]) is a subset of vertices V′⊆ V, such that each vertex v ∈ V is either in V′ itself, or adjacent (via an edge) to a vertex in V′, or both. By contrast, a subset V′ ⊆ V is independent if no two distinct vertices v, w of V′are adjacent in G. A maximal independent set is an independent set V′ of vertices with the property that there is no independent superset (V′ cannot be enlarged without becoming dependent, i.e., without introducing a pair of distinct adjacent vertices). As such, maximal independent sets are equivalent to dominating independent sets ([12], p. 117, the result for finite graphs can be extended to infinite graphs).
3.3. Simplicial Complexes
A (geometric) simplicial complex Δ, in the classical sense, is a collection of geometric simplices (the convex hull of (d + 1) affinely independent points, where d denotes the dimension of the simplex) in some Euclidean space, with the following two properties. Faces of simplices in Δ are again in Δ, and the intersection of any two simplices from Δ is a face of each (and therefore in Δ). If Δ is not an empty collection, then these properties imply that it contains at least the empty face (as a (−1)-dimensional simplex). As usual, and compatible with the notions from graph theory or tiling theory, the zero-dimensional (one-dimensional, two-dimensional) simplices are called vertices (edges, triangles).
The (open) star of a vertex v, StΔ(v), is the collection of all simplices incident to v. By contrast, the simplicial neighborhood, or closed star, denoted NbΔ(v), is defined as the collection consisting of all simplices incident to v (i.e., containing v as a face), and all their (simplicial) faces. Therefore, the simplicial neighborhood is a simplicial complex. The link of a vertex v in Δ, denoted LkΔ(v), is defined as LkΔ(v) := NbΔ(v) \ StΔ(v). (For further reference, see also [13], pp. 31–42.)
For the purpose of this article, we will use the term geometric simplicial complex even when the simplices are only homeomorphic images of the standard simplex in the appropriate dimension, as long as all other properties are retained. For example, a (topological) triangulation of the plane is a two-dimensional geometric simplicial complex.
The k-skeleton of a simplicial complex ignores all faces of dimension greater than k, and is, in fact, a simplicial complex. We will use the notation G(Δ) to refer to the 1-skeleton, or induced edge graph, of a simplicial complex Δ.
3.4. Abstract Polytopes
We will only need some very basic ideas about abstract polytopes, which are combinatorial objects generalizing the previously existing notions of (convex or non-convex) polyhedra and polytopes. For a thorough discussion of abstract polytopes it is recommended to consult the standard reference by McMullen and Schulte [8]. Briefly, an abstract n-polytope  is a certain kind of graded poset of faces (including a unique smallest face of rank −1, and a unique largest face of rank n), with the partial order being incidence. The rank of a face corresponds to the notion of dimension for traditional polytopes (such as the convex polytopes), and so the traditional terms vertex and edge are used for the rank 0 and rank 1 faces, respectively. The poset
is a certain kind of graded poset of faces (including a unique smallest face of rank −1, and a unique largest face of rank n), with the partial order being incidence. The rank of a face corresponds to the notion of dimension for traditional polytopes (such as the convex polytopes), and so the traditional terms vertex and edge are used for the rank 0 and rank 1 faces, respectively. The poset  needs to satisfy the following two additional combinatorial properties taken from standard polytopes. First,
needs to satisfy the following two additional combinatorial properties taken from standard polytopes. First,  is strongly flag-connected, and second, if two incident faces F < G are exactly two ranks apart, then there exist precisely two faces H such that F < H < G (compare the definitions in [8], pp. 22–25).
is strongly flag-connected, and second, if two incident faces F < G are exactly two ranks apart, then there exist precisely two faces H such that F < H < G (compare the definitions in [8], pp. 22–25).
 is a certain kind of graded poset of faces (including a unique smallest face of rank −1, and a unique largest face of rank n), with the partial order being incidence. The rank of a face corresponds to the notion of dimension for traditional polytopes (such as the convex polytopes), and so the traditional terms vertex and edge are used for the rank 0 and rank 1 faces, respectively. The poset
is a certain kind of graded poset of faces (including a unique smallest face of rank −1, and a unique largest face of rank n), with the partial order being incidence. The rank of a face corresponds to the notion of dimension for traditional polytopes (such as the convex polytopes), and so the traditional terms vertex and edge are used for the rank 0 and rank 1 faces, respectively. The poset  needs to satisfy the following two additional combinatorial properties taken from standard polytopes. First,
needs to satisfy the following two additional combinatorial properties taken from standard polytopes. First,  is strongly flag-connected, and second, if two incident faces F < G are exactly two ranks apart, then there exist precisely two faces H such that F < H < G (compare the definitions in [8], pp. 22–25).
is strongly flag-connected, and second, if two incident faces F < G are exactly two ranks apart, then there exist precisely two faces H such that F < H < G (compare the definitions in [8], pp. 22–25).In order to understand the first condition, we need to know that a section of  is a graded poset defined for any two incident faces F ≤ G as {H ∈ P|F ≤ H ≤ G}, again with incidence as partial order. A flag is a maximal chain in a poset, and for graded posets of finite rank all flags have the same length (for example, all flags in
is a graded poset defined for any two incident faces F ≤ G as {H ∈ P|F ≤ H ≤ G}, again with incidence as partial order. A flag is a maximal chain in a poset, and for graded posets of finite rank all flags have the same length (for example, all flags in  have length n + 2).
have length n + 2).  is said to be strongly flag-connected if each section of
is said to be strongly flag-connected if each section of  (including
(including  itself) is flag-connected, that is, if each flag can be joined to any other flag (within the same section) via a sequence of flags, changing only one element (face) in the flag at a time.
itself) is flag-connected, that is, if each flag can be joined to any other flag (within the same section) via a sequence of flags, changing only one element (face) in the flag at a time.
 is a graded poset defined for any two incident faces F ≤ G as {H ∈ P|F ≤ H ≤ G}, again with incidence as partial order. A flag is a maximal chain in a poset, and for graded posets of finite rank all flags have the same length (for example, all flags in
is a graded poset defined for any two incident faces F ≤ G as {H ∈ P|F ≤ H ≤ G}, again with incidence as partial order. A flag is a maximal chain in a poset, and for graded posets of finite rank all flags have the same length (for example, all flags in  have length n + 2).
have length n + 2).  is said to be strongly flag-connected if each section of
is said to be strongly flag-connected if each section of  (including
(including  itself) is flag-connected, that is, if each flag can be joined to any other flag (within the same section) via a sequence of flags, changing only one element (face) in the flag at a time.
itself) is flag-connected, that is, if each flag can be joined to any other flag (within the same section) via a sequence of flags, changing only one element (face) in the flag at a time.The second condition is commonly called the diamond condition, as F, G, and the two faces H in between form the shape of a diamond in the Hasse diagram  . For example, in an abstract 4-polytope (which is the kind of polytope that we will encounter in this article), the diamond condition stipulates the following:
. For example, in an abstract 4-polytope (which is the kind of polytope that we will encounter in this article), the diamond condition stipulates the following:
 . For example, in an abstract 4-polytope (which is the kind of polytope that we will encounter in this article), the diamond condition stipulates the following:
. For example, in an abstract 4-polytope (which is the kind of polytope that we will encounter in this article), the diamond condition stipulates the following:- (1) Each edge is incident to precisely two vertices;
- (2) For each 2-face and each of its incident vertices, there are precisely two edges which are incident with both the 2-face and the vertex;
- (3) For each 3-face (facet) and each of its incident edges, there are precisely two 2-faces incident with both;
- (4) There are precisely two facets incident with each 2-face.
A faithful realization of an abstract polytope  is an injective mapping of its vertices into a suitable Euclidean space, along with a suitable interpretation of its combinatorial structure in the geometric setting. When considering realizations of abstract regular polytopes (see [6,7,8], Section 7F), one usually requires that the symmetry is retained, i.e., that the flag-transitive automorphism group of the abstract polytope carries over to a group of isometries which acts transitively on the flags of the realization. In this paper, however, we drop this requirement in order to obtain more realizations. To give an example of a realization of a 4-polytope that is not necessarily regular, any face-to-face, normal tiling of
is an injective mapping of its vertices into a suitable Euclidean space, along with a suitable interpretation of its combinatorial structure in the geometric setting. When considering realizations of abstract regular polytopes (see [6,7,8], Section 7F), one usually requires that the symmetry is retained, i.e., that the flag-transitive automorphism group of the abstract polytope carries over to a group of isometries which acts transitively on the flags of the realization. In this paper, however, we drop this requirement in order to obtain more realizations. To give an example of a realization of a 4-polytope that is not necessarily regular, any face-to-face, normal tiling of 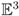 is a realization of a so-called abstract 4-apeirotope (polytope containing either infinitely many finite faces, or infinite faces, or both).
is a realization of a so-called abstract 4-apeirotope (polytope containing either infinitely many finite faces, or infinite faces, or both).
 is an injective mapping of its vertices into a suitable Euclidean space, along with a suitable interpretation of its combinatorial structure in the geometric setting. When considering realizations of abstract regular polytopes (see [6,7,8], Section 7F), one usually requires that the symmetry is retained, i.e., that the flag-transitive automorphism group of the abstract polytope carries over to a group of isometries which acts transitively on the flags of the realization. In this paper, however, we drop this requirement in order to obtain more realizations. To give an example of a realization of a 4-polytope that is not necessarily regular, any face-to-face, normal tiling of
is an injective mapping of its vertices into a suitable Euclidean space, along with a suitable interpretation of its combinatorial structure in the geometric setting. When considering realizations of abstract regular polytopes (see [6,7,8], Section 7F), one usually requires that the symmetry is retained, i.e., that the flag-transitive automorphism group of the abstract polytope carries over to a group of isometries which acts transitively on the flags of the realization. In this paper, however, we drop this requirement in order to obtain more realizations. To give an example of a realization of a 4-polytope that is not necessarily regular, any face-to-face, normal tiling of 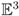 is a realization of a so-called abstract 4-apeirotope (polytope containing either infinitely many finite faces, or infinite faces, or both).
is a realization of a so-called abstract 4-apeirotope (polytope containing either infinitely many finite faces, or infinite faces, or both).4. Definition of Barrel Pseudotilings
This section is devoted to the proper, but rather technical, definition of a barrel pseudotiling. All the barrels in the considered pseudotilings stem from (right) prisms in one form or another, so we begin by explaining the concept of a stack of apeiroprisms.
Definition 4.1. Let D be a plane polygonal disc in a horizontal plane of 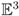 with unit normal vector u = (0, 0, 1). A STACK OF APEIROPRISMS, or an ∞-PRISM STACK, Φ associated with D, is a doubly infinite right prism, or cylinder, Z = D +
with unit normal vector u = (0, 0, 1). A STACK OF APEIROPRISMS, or an ∞-PRISM STACK, Φ associated with D, is a doubly infinite right prism, or cylinder, Z = D + 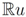 together with a family
together with a family 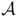 = {A0,...,Ak−1} of k > 1 mutually non-intersecting apeirogons in ∂Z = ∂D +
= {A0,...,Ak−1} of k > 1 mutually non-intersecting apeirogons in ∂Z = ∂D + 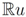 (the mantle of the cylinder) with the following properties:
(the mantle of the cylinder) with the following properties:
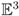 with unit normal vector u = (0, 0, 1). A STACK OF APEIROPRISMS, or an ∞-PRISM STACK, Φ associated with D, is a doubly infinite right prism, or cylinder, Z = D +
with unit normal vector u = (0, 0, 1). A STACK OF APEIROPRISMS, or an ∞-PRISM STACK, Φ associated with D, is a doubly infinite right prism, or cylinder, Z = D + 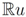 together with a family
together with a family 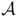 = {A0,...,Ak−1} of k > 1 mutually non-intersecting apeirogons in ∂Z = ∂D +
= {A0,...,Ak−1} of k > 1 mutually non-intersecting apeirogons in ∂Z = ∂D + 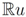 (the mantle of the cylinder) with the following properties:
(the mantle of the cylinder) with the following properties: - (1)
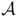 is strictly monotone in the direction of u, meaning that every section of Z by a plane parallel to aff(D) meets every apeirogon in
is strictly monotone in the direction of u, meaning that every section of Z by a plane parallel to aff(D) meets every apeirogon in 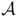 in exactly one point;
in exactly one point; - (2) Any two adjacent edges of an apeirogon in
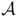 lie in adjacent bounding walls of Z. Thus, each apeirogon A in
lie in adjacent bounding walls of Z. Thus, each apeirogon A in 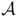 spirals around Z, in both directions, such that its vertices lie above the vertices of D;
spirals around Z, in both directions, such that its vertices lie above the vertices of D; - (3) For each i = 0,...,k − 1 and each x in Ai, we have x + ru ∈ Al for some l if and only if r ∈
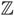 ; and in particular, x + ju ∈ Ai+j for each j ∈
; and in particular, x + ju ∈ Ai+j for each j ∈ 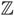 , with subscripts taken modulo k. (Thus, more informally, the points directly above x on apeirogons occur at integer distances from x, with the apeirogons repeating periodically modulo ku.)
, with subscripts taken modulo k. (Thus, more informally, the points directly above x on apeirogons occur at integer distances from x, with the apeirogons repeating periodically modulo ku.)
Any Ai + [0, 1]u (for i = 0, 1,...,k − 1) is the mantle of a single apeiroprism in a faithful realization (the apeiroprism itself, however, is an abstract polytope whose face poset contains all faces of the mantle, i.e., the parallelograms and their faces, as well as the apeirogons Ai and Ai+1, and a unique three-dimensional largest face). Subsequently, each apeiroprism gives rise to an apeirobarrel via a subdivision of the mantle parallelograms into pentagons.
Definition 4.2. A STACK OF APEIROBARRELS, or an ∞-STACK, Ω, is a stack of apeiroprisms as in Definition 4.1, together with a partition of its mantle into (topological) pentagon faces obtained in the following way. All edges of the apeirogons in  are retained as edges of pentagons; each vertical edge (parallel to u) of the mantle is split into three edges by two new vertices, called PARTITION VERTICES, in its relative interior; and each parallelogram on the mantle Ai + [0, 1]u of an apeiroprism (for i = 0, 1,...,k − 1) is subdivided into two coplanar pentagon faces by a new edge that connects a pair of new vertices on opposite vertical edges of the parallelogram. These new edges are called PARTITION EDGES.
are retained as edges of pentagons; each vertical edge (parallel to u) of the mantle is split into three edges by two new vertices, called PARTITION VERTICES, in its relative interior; and each parallelogram on the mantle Ai + [0, 1]u of an apeiroprism (for i = 0, 1,...,k − 1) is subdivided into two coplanar pentagon faces by a new edge that connects a pair of new vertices on opposite vertical edges of the parallelogram. These new edges are called PARTITION EDGES.
 are retained as edges of pentagons; each vertical edge (parallel to u) of the mantle is split into three edges by two new vertices, called PARTITION VERTICES, in its relative interior; and each parallelogram on the mantle Ai + [0, 1]u of an apeiroprism (for i = 0, 1,...,k − 1) is subdivided into two coplanar pentagon faces by a new edge that connects a pair of new vertices on opposite vertical edges of the parallelogram. These new edges are called PARTITION EDGES.
are retained as edges of pentagons; each vertical edge (parallel to u) of the mantle is split into three edges by two new vertices, called PARTITION VERTICES, in its relative interior; and each parallelogram on the mantle Ai + [0, 1]u of an apeiroprism (for i = 0, 1,...,k − 1) is subdivided into two coplanar pentagon faces by a new edge that connects a pair of new vertices on opposite vertical edges of the parallelogram. These new edges are called PARTITION EDGES.A staircase is any infinite polygon in the mantle of Ω whose successive edges consist alternately of partition edges and vertical edges, such that all traversed vertices are partition vertices (see Figure 3a for an example). Intuitively, the partition edges and vertical edges in these mathematical staircases correspond to the treads and risers of ordinary staircases. Note that staircases do not cross the apeirogonal bases of apeiroprisms (which, in extending the analogy, would take the role of stringers). The winding orientation of an ∞-stack is the orientation (clockwise or counterclockwise) in which the apeirogonal bases wind upwards (i.e., in the direction of u = (0, 0, 1)) and is already prescribed by the apeirogons in Φ.
Definition 4.3. Let B be a finite barrel stemming from an n-gonal right prism of height 1 whose polygonal disc base D is in a horizontal plane with unit normal vector u = (0, 0, 1). Call the added vertices in the vertical edges of the prism PARTITION VERTICES, and the added non-vertical edges separating a rectangle into pentagons PARTITION EDGES. Then, in this finite case, a STAIRCASE is a simple closed polygon consisting of edges of the barrel and passing only through partition vertices. A STACK OF n-GONAL BARRELS or n-STACK, Ω, is the set of barrels {B + lu | l ∈ 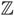 }, whose union fills the doubly infinite right prism (cylinder) Z = D +
}, whose union fills the doubly infinite right prism (cylinder) Z = D + 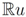 . A FINITE STACK is an n-stack for some finite n.
. A FINITE STACK is an n-stack for some finite n.
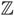 }, whose union fills the doubly infinite right prism (cylinder) Z = D +
}, whose union fills the doubly infinite right prism (cylinder) Z = D + 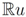 . A FINITE STACK is an n-stack for some finite n.
. A FINITE STACK is an n-stack for some finite n. Thus, every barrel in a finite stack has an “impossible staircase” (familiar, e.g., from Dutch artist
M.C. Escher’s print Ascending and Descending from 1960, see [14], p. 146): Partition edges (treads) and vertical edges linking partition edges (risers) close up to give a finite, non-planar polygon.
Definition 4.4. A BARREL PSEUDOTILING 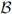 is a countable collection of vertical ∞-stacks and vertical finite stacks with the following two properties. First, the underlying family of doubly infinite prisms (cyclinders) gives a locally finite tiling of
is a countable collection of vertical ∞-stacks and vertical finite stacks with the following two properties. First, the underlying family of doubly infinite prisms (cyclinders) gives a locally finite tiling of 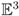 which, when cut by a horizontal plane, determines a locally finite, simple, face-to-face tiling in this plane. Second, any two barrels associated to distinct stacks in
which, when cut by a horizontal plane, determines a locally finite, simple, face-to-face tiling in this plane. Second, any two barrels associated to distinct stacks in  intersect, if at all, in a common finite face (vertex, edge, or pentagon). Note that the construction of the stacks implies that distinct barrels in the same finite stack also intersect either in a common face (finite polygon), or not at all.
intersect, if at all, in a common finite face (vertex, edge, or pentagon). Note that the construction of the stacks implies that distinct barrels in the same finite stack also intersect either in a common face (finite polygon), or not at all.
 is a countable collection of vertical ∞-stacks and vertical finite stacks with the following two properties. First, the underlying family of doubly infinite prisms (cyclinders) gives a locally finite tiling of
is a countable collection of vertical ∞-stacks and vertical finite stacks with the following two properties. First, the underlying family of doubly infinite prisms (cyclinders) gives a locally finite tiling of  which, when cut by a horizontal plane, determines a locally finite, simple, face-to-face tiling in this plane. Second, any two barrels associated to distinct stacks in
which, when cut by a horizontal plane, determines a locally finite, simple, face-to-face tiling in this plane. Second, any two barrels associated to distinct stacks in  intersect, if at all, in a common finite face (vertex, edge, or pentagon). Note that the construction of the stacks implies that distinct barrels in the same finite stack also intersect either in a common face (finite polygon), or not at all.
intersect, if at all, in a common finite face (vertex, edge, or pentagon). Note that the construction of the stacks implies that distinct barrels in the same finite stack also intersect either in a common face (finite polygon), or not at all.Observe that translation by u is a built-in symmetry of the pseudotiling  . The finite barrels by themselves form a tessellation of a noncompact 3-manifold with infinitely many boundary components. In a way, the boundary components get sewn together by the stacks of apeirobarrels.
. The finite barrels by themselves form a tessellation of a noncompact 3-manifold with infinitely many boundary components. In a way, the boundary components get sewn together by the stacks of apeirobarrels.
 . The finite barrels by themselves form a tessellation of a noncompact 3-manifold with infinitely many boundary components. In a way, the boundary components get sewn together by the stacks of apeirobarrels.
. The finite barrels by themselves form a tessellation of a noncompact 3-manifold with infinitely many boundary components. In a way, the boundary components get sewn together by the stacks of apeirobarrels.Combinatorially, the faces of the constructed object, together with a unique largest face of rank 4 and a unique smallest (empty) face of rank −1, form a graded poset as required for an abstract 4-polytope. The faces of rank 0 are the vertices, the faces of rank 1 are the edges of the pseudotiling, the faces of rank 2 are the planar polygons and non-planar apeirogons, and the faces of rank 3 are the tiles (barrels) and pseudotiles (apeirobarrels). There are infinitely many faces of each of these kinds. Additionally, we have infinite 2-faces, the bases of the apeirobarrels (i.e., the apeirogons). Strong flag-connectedness is easily verified. The diamond condition holds because the criteria for a 4-polytope as listed inSection 3.4 are fulfilled. In particular, each 2-face is incident to precisely two 3-faces; it is here where the condition of k > 1 apeirogons (and thus k > 1 apeirobarrels) per ∞-stack is required. Thus, the abstract polytope underlying  is a (non-regular) 4-apeirotope.
is a (non-regular) 4-apeirotope.
 is a (non-regular) 4-apeirotope.
is a (non-regular) 4-apeirotope.This 4-apeirotope is realized faithfully in Euclidean 3-space, such that all finite faces lie in an affine subspace of the appropriate dimension and coincide with the convex hull of their vertices (straight edges, plane polygons, finite barrels stemming from right prisms). The size of the finite barrels is uniformly bounded, so a property very close to normality is retained. All vertices are 4-valent, so, in many ways, barrel pseudotilings are similar to simple normal tilings of 3-space.
We conclude this section with a note on the face-to-face property.
Remark 4.1.  is FACE-TO-FACE, in the sense that any two distinct barrels (finite or infinite) intersect, if at all, in a common face, precisely when each ∞-stack consists of at least three apeirobarrels.
is FACE-TO-FACE, in the sense that any two distinct barrels (finite or infinite) intersect, if at all, in a common face, precisely when each ∞-stack consists of at least three apeirobarrels.
 is FACE-TO-FACE, in the sense that any two distinct barrels (finite or infinite) intersect, if at all, in a common face, precisely when each ∞-stack consists of at least three apeirobarrels.
is FACE-TO-FACE, in the sense that any two distinct barrels (finite or infinite) intersect, if at all, in a common face, precisely when each ∞-stack consists of at least three apeirobarrels.5. Outline of the Construction
A rough outline of constructing a pseudotiling by polygonal barrels and ∞-barrels is provided by the following five steps.
First of all, select a plane, simple, normal tiling  by (convex, simple) polygons, situated in the horizontal plane through the origin of
by (convex, simple) polygons, situated in the horizontal plane through the origin of 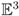 , where the unit normal vector u = (0, 0, 1) denotes the direction “up”. All plane tilings mentioned in this paper are assumed to be of this type (recall that our definition of tiling includes the face-to-face property). We call
, where the unit normal vector u = (0, 0, 1) denotes the direction “up”. All plane tilings mentioned in this paper are assumed to be of this type (recall that our definition of tiling includes the face-to-face property). We call  a base tiling. The faces of
a base tiling. The faces of  will not (or not necessarily) be used in the completed barrel pseudotiling; rather, its tiles serve as guides for the infinite columns in
will not (or not necessarily) be used in the completed barrel pseudotiling; rather, its tiles serve as guides for the infinite columns in 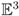 which will extend in the directions ±u. Second, for each n-gonal tile (n ≥ 3) of
which will extend in the directions ±u. Second, for each n-gonal tile (n ≥ 3) of  assign either a color in [0, 1), or ∞, according as the associated column is to be used for a stack of finite barrels, or apeirobarrels. We obtain a coloring or shift function f : T (
assign either a color in [0, 1), or ∞, according as the associated column is to be used for a stack of finite barrels, or apeirobarrels. We obtain a coloring or shift function f : T (  ) → [0, 1) ∪ {∞}, where T (
) → [0, 1) ∪ {∞}, where T (  ) denotes the set of tiles of
) denotes the set of tiles of  . Third, for each finite-colored polygon P, let P +
. Third, for each finite-colored polygon P, let P + 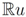 be the underlying cylinder for a stack of right prisms, with the (disjoint) union of prism bases being P +
be the underlying cylinder for a stack of right prisms, with the (disjoint) union of prism bases being P +  .
.
 by (convex, simple) polygons, situated in the horizontal plane through the origin of
by (convex, simple) polygons, situated in the horizontal plane through the origin of 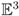 , where the unit normal vector u = (0, 0, 1) denotes the direction “up”. All plane tilings mentioned in this paper are assumed to be of this type (recall that our definition of tiling includes the face-to-face property). We call
, where the unit normal vector u = (0, 0, 1) denotes the direction “up”. All plane tilings mentioned in this paper are assumed to be of this type (recall that our definition of tiling includes the face-to-face property). We call  a base tiling. The faces of
a base tiling. The faces of  will not (or not necessarily) be used in the completed barrel pseudotiling; rather, its tiles serve as guides for the infinite columns in
will not (or not necessarily) be used in the completed barrel pseudotiling; rather, its tiles serve as guides for the infinite columns in 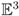 which will extend in the directions ±u. Second, for each n-gonal tile (n ≥ 3) of
which will extend in the directions ±u. Second, for each n-gonal tile (n ≥ 3) of  assign either a color in [0, 1), or ∞, according as the associated column is to be used for a stack of finite barrels, or apeirobarrels. We obtain a coloring or shift function f : T (
assign either a color in [0, 1), or ∞, according as the associated column is to be used for a stack of finite barrels, or apeirobarrels. We obtain a coloring or shift function f : T (  ) → [0, 1) ∪ {∞}, where T (
) → [0, 1) ∪ {∞}, where T (  ) denotes the set of tiles of
) denotes the set of tiles of  . Third, for each finite-colored polygon P, let P +
. Third, for each finite-colored polygon P, let P + 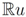 be the underlying cylinder for a stack of right prisms, with the (disjoint) union of prism bases being P +
be the underlying cylinder for a stack of right prisms, with the (disjoint) union of prism bases being P +  .
. The fourth step deserves a more detailed explanation and will be carefully analyzed in the next section: Shift each stack of n-prisms associated to a finite-colored tile P of  by the amount α = f(P) in [0, 1) in the direction of u, as prescribed by the function f (i.e., shifting by (0,0,α)). The disjoint union of prism bases is now at P + (
by the amount α = f(P) in [0, 1) in the direction of u, as prescribed by the function f (i.e., shifting by (0,0,α)). The disjoint union of prism bases is now at P + ( 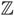 + α)u. The aim of our construction is to obtain a new face structure on each prism, turning each n-prism into an n-barrel. This is done by respecting topological adjacencies, in fact, by taking the final facial structure of the constructed object (up to rank 2) to be completely determined by the topology.
+ α)u. The aim of our construction is to obtain a new face structure on each prism, turning each n-prism into an n-barrel. This is done by respecting topological adjacencies, in fact, by taking the final facial structure of the constructed object (up to rank 2) to be completely determined by the topology.
 by the amount α = f(P) in [0, 1) in the direction of u, as prescribed by the function f (i.e., shifting by (0,0,α)). The disjoint union of prism bases is now at P + (
by the amount α = f(P) in [0, 1) in the direction of u, as prescribed by the function f (i.e., shifting by (0,0,α)). The disjoint union of prism bases is now at P + ( 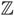 + α)u. The aim of our construction is to obtain a new face structure on each prism, turning each n-prism into an n-barrel. This is done by respecting topological adjacencies, in fact, by taking the final facial structure of the constructed object (up to rank 2) to be completely determined by the topology.
+ α)u. The aim of our construction is to obtain a new face structure on each prism, turning each n-prism into an n-barrel. This is done by respecting topological adjacencies, in fact, by taking the final facial structure of the constructed object (up to rank 2) to be completely determined by the topology.In order to assure that each rectangle in a prism’s mantle splits into precisely two 2-faces, it is necessary and sufficient to shift adjacent stacks (i.e., stacks over adjacent tiles in the underlying plane tiling  ) by different amounts. Since
) by different amounts. Since  is locally finite and consists of countably many tiles, it is clearly possible to find a shift function with this property. However, we need to be more restrictive in order to assure that the partition edges and vertices produce only pentagons. Therefore, consider any tile in
is locally finite and consists of countably many tiles, it is clearly possible to find a shift function with this property. However, we need to be more restrictive in order to assure that the partition edges and vertices produce only pentagons. Therefore, consider any tile in  . When cyclically traversing the adjacent tiles in counterclockwise order, and listing the corresponding function values of f (which will be the shift lengths applied to the stacks of finite prisms), using asterisks ∗ as placeholders for tiles colored ∞, we will obtain a symbol like (∗,α0,α1,..., ∗,...). Let us call such a symbol a neighborhood symbol for the respective tile. A neighborhood symbol for a tile is not unique, since the neighbors can be traversed from different starting points, although we do adopt the convention to list the values of f in counterclockwise order around the tile. All neighborhood symbols for the same tile (using the same coloring function f) differ only by a cyclic permutation, so we need to keep in mind that the neighborhood symbol is a cyclic symbol.
. When cyclically traversing the adjacent tiles in counterclockwise order, and listing the corresponding function values of f (which will be the shift lengths applied to the stacks of finite prisms), using asterisks ∗ as placeholders for tiles colored ∞, we will obtain a symbol like (∗,α0,α1,..., ∗,...). Let us call such a symbol a neighborhood symbol for the respective tile. A neighborhood symbol for a tile is not unique, since the neighbors can be traversed from different starting points, although we do adopt the convention to list the values of f in counterclockwise order around the tile. All neighborhood symbols for the same tile (using the same coloring function f) differ only by a cyclic permutation, so we need to keep in mind that the neighborhood symbol is a cyclic symbol.
 ) by different amounts. Since
) by different amounts. Since  is locally finite and consists of countably many tiles, it is clearly possible to find a shift function with this property. However, we need to be more restrictive in order to assure that the partition edges and vertices produce only pentagons. Therefore, consider any tile in
is locally finite and consists of countably many tiles, it is clearly possible to find a shift function with this property. However, we need to be more restrictive in order to assure that the partition edges and vertices produce only pentagons. Therefore, consider any tile in  . When cyclically traversing the adjacent tiles in counterclockwise order, and listing the corresponding function values of f (which will be the shift lengths applied to the stacks of finite prisms), using asterisks ∗ as placeholders for tiles colored ∞, we will obtain a symbol like (∗,α0,α1,..., ∗,...). Let us call such a symbol a neighborhood symbol for the respective tile. A neighborhood symbol for a tile is not unique, since the neighbors can be traversed from different starting points, although we do adopt the convention to list the values of f in counterclockwise order around the tile. All neighborhood symbols for the same tile (using the same coloring function f) differ only by a cyclic permutation, so we need to keep in mind that the neighborhood symbol is a cyclic symbol.
. When cyclically traversing the adjacent tiles in counterclockwise order, and listing the corresponding function values of f (which will be the shift lengths applied to the stacks of finite prisms), using asterisks ∗ as placeholders for tiles colored ∞, we will obtain a symbol like (∗,α0,α1,..., ∗,...). Let us call such a symbol a neighborhood symbol for the respective tile. A neighborhood symbol for a tile is not unique, since the neighbors can be traversed from different starting points, although we do adopt the convention to list the values of f in counterclockwise order around the tile. All neighborhood symbols for the same tile (using the same coloring function f) differ only by a cyclic permutation, so we need to keep in mind that the neighborhood symbol is a cyclic symbol.The requirement of splitting the rectangles in the mantle of an n-prism into pentagons necessitates a condition on the neighborhood symbols, which is explained subsequently. Let α be the amount of shift applied to the stack associated to the finite-colored n-gonal tile P with neighborhood symbol (∗,α0,α1,..., ∗,...). Let (∗, (α0 − α) mod 1, (α1 − α) mod 1,..., ∗,...) be the augmented neighborhood symbol for P, with the convention that “x mod 1” for x ∈ (−1, 0) equals x + 1 ∈ (0, 1). Then we require that, for finite-colored tiles, the (contiguous) subsequences of (cyclically) consecutive numbers in the augmented neighborhood symbol—as delimited by asterisks—are either all increasing or all decreasing. Violating this condition results in the introduction of hexagons and quadrilaterals on the mantle. An obvious consequence is that each tile which has not been colored by ∞ itself must be adjacent to an ∞-colored tile (so the neighborhood symbol for finite-colored tiles may be written down starting with ∗), otherwise we would have no delimiter, and the cyclic symbol would have to consist of ever increasing entries.
It may not be possible to carry out step four consistently, depending on earlier decisions, i.e., selection and coloring of the plane tiling. However, if step four can be carried out successfully, then step five is to fit a stack of apeirogonal barrels (∞-stack) on each infinite column P + 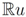 perpendicular to an ∞-colored tile P of the plane tiling. Again, depending on earlier decisions, this may or may not be possible (recall that the condition in step four was only a necessary one). The next section investigates the conditions on f which must be satisfied so that the last two steps of the outline can be carried out.
perpendicular to an ∞-colored tile P of the plane tiling. Again, depending on earlier decisions, this may or may not be possible (recall that the condition in step four was only a necessary one). The next section investigates the conditions on f which must be satisfied so that the last two steps of the outline can be carried out.
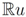 perpendicular to an ∞-colored tile P of the plane tiling. Again, depending on earlier decisions, this may or may not be possible (recall that the condition in step four was only a necessary one). The next section investigates the conditions on f which must be satisfied so that the last two steps of the outline can be carried out.
perpendicular to an ∞-colored tile P of the plane tiling. Again, depending on earlier decisions, this may or may not be possible (recall that the condition in step four was only a necessary one). The next section investigates the conditions on f which must be satisfied so that the last two steps of the outline can be carried out.6. Barrel Pseudotilings with Isolated Apeirostacks
Recall that for the remainder of this article, we consider our plane base tiling  as situated in the horizontal plane π through the origin of
as situated in the horizontal plane π through the origin of 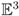 , always looking at the plane tiling from “above”, where u = (0, 0, 1) denotes the direction “up”. Recall further that
, always looking at the plane tiling from “above”, where u = (0, 0, 1) denotes the direction “up”. Recall further that  functions as an aid in the construction of a barrel pseudotiling
functions as an aid in the construction of a barrel pseudotiling 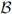 , and that its faces (vertices, edges, tiles) need not be present in
, and that its faces (vertices, edges, tiles) need not be present in 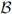 .
.
 as situated in the horizontal plane π through the origin of
as situated in the horizontal plane π through the origin of 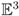 , always looking at the plane tiling from “above”, where u = (0, 0, 1) denotes the direction “up”. Recall further that
, always looking at the plane tiling from “above”, where u = (0, 0, 1) denotes the direction “up”. Recall further that  functions as an aid in the construction of a barrel pseudotiling
functions as an aid in the construction of a barrel pseudotiling  , and that its faces (vertices, edges, tiles) need not be present in
, and that its faces (vertices, edges, tiles) need not be present in  .
.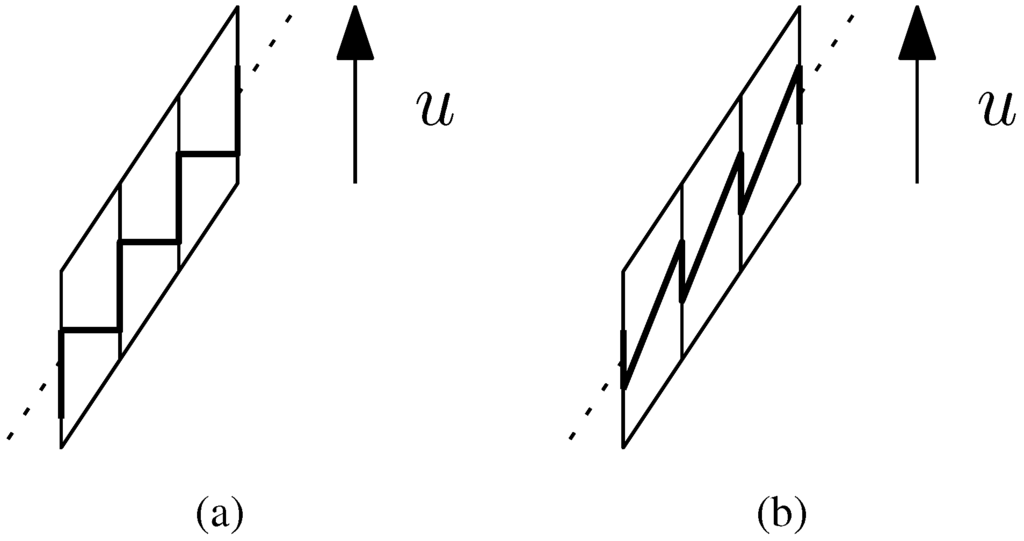
Figure 3.
Unwrapped: An apeirobarrel winding up upstairs (a); and an apeirobarrel winding up downstairs (b). The staircases are highlighted.
To each barrel and apeirobarrel in a barrel pseudotiling  based on
based on  there is an associated upstairs orientation (clockwise or counterclockwise): This is the orientation in which the staircase in the mantle leads “upstairs”, if one were to step on the partition edges (treads), so this is either counterclockwise (up) or clockwise (up). For example, in Figure 1c we go upstairs from left to right, so if what is depicted corresponds to the unwrapped view of the mantle when walking around the outside of the barrel, then the upstairs orientation is counterclockwise. By contrast, remember that the winding orientation of an ∞-stack is the orientation (clockwise or counterclockwise) in which the apeirogonal bases wind upwards. Note here that, for apeirobarrels, the upstairs orientation does not generally correspond to the winding orientation, compare the examples of unwrapped apeirobarrels in Figure 3. However, in pseudotilings with only isolated ∞-stacks there is indeed such a correspondence, see Lemma 6.3. Before concentrating on pseudotilings with only isolated ∞-stacks, let us establish two general facts.
there is an associated upstairs orientation (clockwise or counterclockwise): This is the orientation in which the staircase in the mantle leads “upstairs”, if one were to step on the partition edges (treads), so this is either counterclockwise (up) or clockwise (up). For example, in Figure 1c we go upstairs from left to right, so if what is depicted corresponds to the unwrapped view of the mantle when walking around the outside of the barrel, then the upstairs orientation is counterclockwise. By contrast, remember that the winding orientation of an ∞-stack is the orientation (clockwise or counterclockwise) in which the apeirogonal bases wind upwards. Note here that, for apeirobarrels, the upstairs orientation does not generally correspond to the winding orientation, compare the examples of unwrapped apeirobarrels in Figure 3. However, in pseudotilings with only isolated ∞-stacks there is indeed such a correspondence, see Lemma 6.3. Before concentrating on pseudotilings with only isolated ∞-stacks, let us establish two general facts.
 based on
based on  there is an associated upstairs orientation (clockwise or counterclockwise): This is the orientation in which the staircase in the mantle leads “upstairs”, if one were to step on the partition edges (treads), so this is either counterclockwise (up) or clockwise (up). For example, in Figure 1c we go upstairs from left to right, so if what is depicted corresponds to the unwrapped view of the mantle when walking around the outside of the barrel, then the upstairs orientation is counterclockwise. By contrast, remember that the winding orientation of an ∞-stack is the orientation (clockwise or counterclockwise) in which the apeirogonal bases wind upwards. Note here that, for apeirobarrels, the upstairs orientation does not generally correspond to the winding orientation, compare the examples of unwrapped apeirobarrels in Figure 3. However, in pseudotilings with only isolated ∞-stacks there is indeed such a correspondence, see Lemma 6.3. Before concentrating on pseudotilings with only isolated ∞-stacks, let us establish two general facts.
there is an associated upstairs orientation (clockwise or counterclockwise): This is the orientation in which the staircase in the mantle leads “upstairs”, if one were to step on the partition edges (treads), so this is either counterclockwise (up) or clockwise (up). For example, in Figure 1c we go upstairs from left to right, so if what is depicted corresponds to the unwrapped view of the mantle when walking around the outside of the barrel, then the upstairs orientation is counterclockwise. By contrast, remember that the winding orientation of an ∞-stack is the orientation (clockwise or counterclockwise) in which the apeirogonal bases wind upwards. Note here that, for apeirobarrels, the upstairs orientation does not generally correspond to the winding orientation, compare the examples of unwrapped apeirobarrels in Figure 3. However, in pseudotilings with only isolated ∞-stacks there is indeed such a correspondence, see Lemma 6.3. Before concentrating on pseudotilings with only isolated ∞-stacks, let us establish two general facts.Lemma 6.1. All barrels (both finite and infinite) in a barrel pseudotiling  have the same upstairs orientation. This is the GLOBAL UPSTAIRS ORIENTATION of
have the same upstairs orientation. This is the GLOBAL UPSTAIRS ORIENTATION of  .
.
 have the same upstairs orientation. This is the GLOBAL UPSTAIRS ORIENTATION of
have the same upstairs orientation. This is the GLOBAL UPSTAIRS ORIENTATION of  .
.Proof. Consider any vertex v of the plane base tiling  in the plane π, and assume that tiles P1, P2, and P3 meet there as pictured in Figure 4 (in particular, (P1,P2,P3) is the listing of tiles in counterclockwise order around v). In the pseudotiling, v corresponds to a line v +
in the plane π, and assume that tiles P1, P2, and P3 meet there as pictured in Figure 4 (in particular, (P1,P2,P3) is the listing of tiles in counterclockwise order around v). In the pseudotiling, v corresponds to a line v +  perpendicular to the plane. We move upwards on this line (in direction u = (0, 0, 1)) starting at v, and we mark all vertices of the pseudotiling (note that v may not be one of them). In addition, we label a vertex on this line 1, 2, or 3, depending on whether the vertex in question is incident to a base of a (finite or infinite) barrel of the stack associated to P1, P2, or P3. We obtain a repeating pattern since translation by the vertical unit vector u is a built-in symmetry of the pseudotiling. If the repeating pattern is (1, 2, 3) (i.e., coherent with the right-hand rule), then the upstairs orientation of each barrel meeting a point on this line is counterclockwise, as can easily be seen. Otherwise, if the repeating pattern is (1, 3, 2), then the upstairs orientation of each barrel meeting a point of the line is clockwise. Moreover, if the upstairs orientation for barrels in one stack is set (e.g., in a construction process), then this determines the orientations for all barrels in adjacent stacks. These stacks, in turn, determine the orientations for all stacks adjacent to them, and so forth. Thus, the upstairs orientations of barrels must be globally compatible, i.e., the same.
perpendicular to the plane. We move upwards on this line (in direction u = (0, 0, 1)) starting at v, and we mark all vertices of the pseudotiling (note that v may not be one of them). In addition, we label a vertex on this line 1, 2, or 3, depending on whether the vertex in question is incident to a base of a (finite or infinite) barrel of the stack associated to P1, P2, or P3. We obtain a repeating pattern since translation by the vertical unit vector u is a built-in symmetry of the pseudotiling. If the repeating pattern is (1, 2, 3) (i.e., coherent with the right-hand rule), then the upstairs orientation of each barrel meeting a point on this line is counterclockwise, as can easily be seen. Otherwise, if the repeating pattern is (1, 3, 2), then the upstairs orientation of each barrel meeting a point of the line is clockwise. Moreover, if the upstairs orientation for barrels in one stack is set (e.g., in a construction process), then this determines the orientations for all barrels in adjacent stacks. These stacks, in turn, determine the orientations for all stacks adjacent to them, and so forth. Thus, the upstairs orientations of barrels must be globally compatible, i.e., the same.
 in the plane π, and assume that tiles P1, P2, and P3 meet there as pictured in Figure 4 (in particular, (P1,P2,P3) is the listing of tiles in counterclockwise order around v). In the pseudotiling, v corresponds to a line v +
in the plane π, and assume that tiles P1, P2, and P3 meet there as pictured in Figure 4 (in particular, (P1,P2,P3) is the listing of tiles in counterclockwise order around v). In the pseudotiling, v corresponds to a line v +  perpendicular to the plane. We move upwards on this line (in direction u = (0, 0, 1)) starting at v, and we mark all vertices of the pseudotiling (note that v may not be one of them). In addition, we label a vertex on this line 1, 2, or 3, depending on whether the vertex in question is incident to a base of a (finite or infinite) barrel of the stack associated to P1, P2, or P3. We obtain a repeating pattern since translation by the vertical unit vector u is a built-in symmetry of the pseudotiling. If the repeating pattern is (1, 2, 3) (i.e., coherent with the right-hand rule), then the upstairs orientation of each barrel meeting a point on this line is counterclockwise, as can easily be seen. Otherwise, if the repeating pattern is (1, 3, 2), then the upstairs orientation of each barrel meeting a point of the line is clockwise. Moreover, if the upstairs orientation for barrels in one stack is set (e.g., in a construction process), then this determines the orientations for all barrels in adjacent stacks. These stacks, in turn, determine the orientations for all stacks adjacent to them, and so forth. Thus, the upstairs orientations of barrels must be globally compatible, i.e., the same.
perpendicular to the plane. We move upwards on this line (in direction u = (0, 0, 1)) starting at v, and we mark all vertices of the pseudotiling (note that v may not be one of them). In addition, we label a vertex on this line 1, 2, or 3, depending on whether the vertex in question is incident to a base of a (finite or infinite) barrel of the stack associated to P1, P2, or P3. We obtain a repeating pattern since translation by the vertical unit vector u is a built-in symmetry of the pseudotiling. If the repeating pattern is (1, 2, 3) (i.e., coherent with the right-hand rule), then the upstairs orientation of each barrel meeting a point on this line is counterclockwise, as can easily be seen. Otherwise, if the repeating pattern is (1, 3, 2), then the upstairs orientation of each barrel meeting a point of the line is clockwise. Moreover, if the upstairs orientation for barrels in one stack is set (e.g., in a construction process), then this determines the orientations for all barrels in adjacent stacks. These stacks, in turn, determine the orientations for all stacks adjacent to them, and so forth. Thus, the upstairs orientations of barrels must be globally compatible, i.e., the same.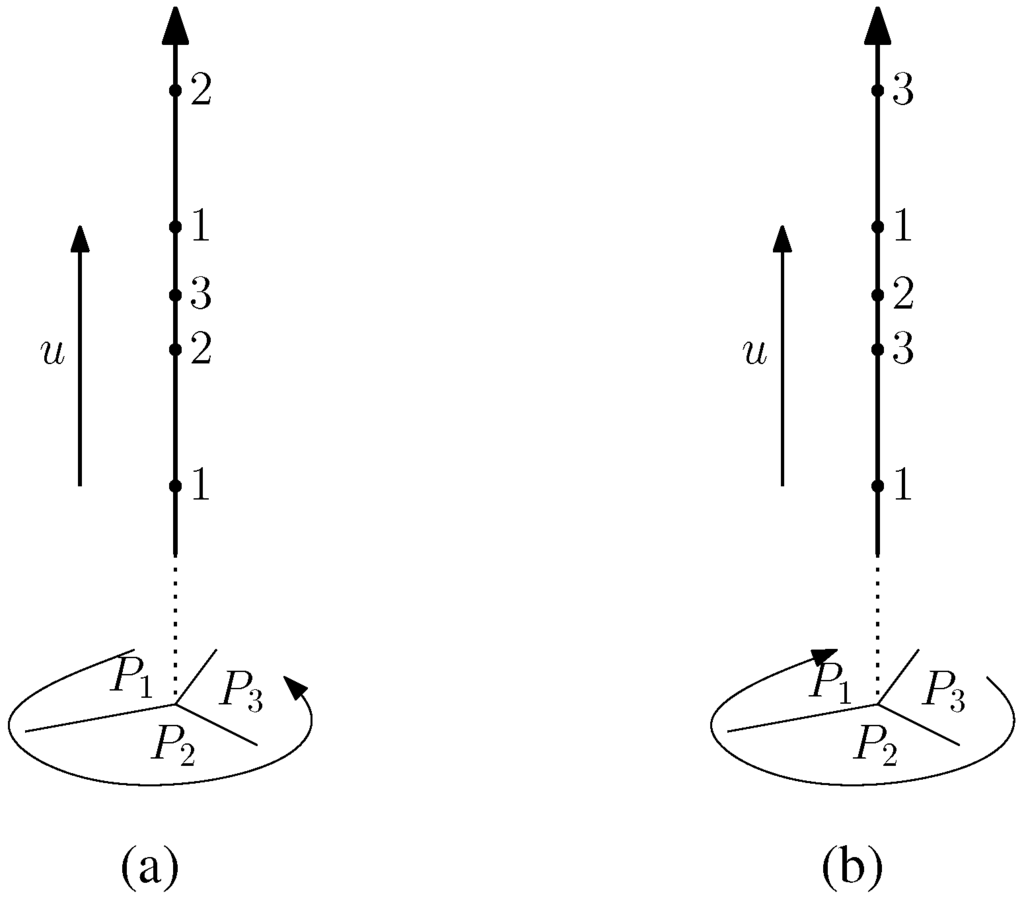
Figure 4.
Determining upstairs orientations: (a) Counterclockwise; (b) clockwise.
Remark 6.1. From the proof of Lemma 6.1 follows that if P1, P2, P3 are assigned FINITE colors α1, α2, α3, respectively, of which w.l.o.g. α1 is the smallest, then the global upstairs orientation is counterclockwise if α1 < α2 < α3, and clockwise if α1 < α3 < α2. Incidentally, any shift function f which assigns its finite values around such vertices of  coherently with a particular global upstairs orientation automatically satisfies the necessary condition on the augmented neighborhood symbols for finite-colored tiles (see step four in Section 5). Thus, we have a new and more practical necessary condition on f.
coherently with a particular global upstairs orientation automatically satisfies the necessary condition on the augmented neighborhood symbols for finite-colored tiles (see step four in Section 5). Thus, we have a new and more practical necessary condition on f.
 coherently with a particular global upstairs orientation automatically satisfies the necessary condition on the augmented neighborhood symbols for finite-colored tiles (see step four in Section 5). Thus, we have a new and more practical necessary condition on f.
coherently with a particular global upstairs orientation automatically satisfies the necessary condition on the augmented neighborhood symbols for finite-colored tiles (see step four in Section 5). Thus, we have a new and more practical necessary condition on f.Lemma 6.2. If a colored plane tiling (  , f) gives rise to a barrel pseudotiling in one upstairs orientation, then the same base tiling—with altered coloring—also gives rise to a barrel pseudotiling in the reverse upstairs orientation.
, f) gives rise to a barrel pseudotiling in one upstairs orientation, then the same base tiling—with altered coloring—also gives rise to a barrel pseudotiling in the reverse upstairs orientation.
 , f) gives rise to a barrel pseudotiling in one upstairs orientation, then the same base tiling—with altered coloring—also gives rise to a barrel pseudotiling in the reverse upstairs orientation.
, f) gives rise to a barrel pseudotiling in one upstairs orientation, then the same base tiling—with altered coloring—also gives rise to a barrel pseudotiling in the reverse upstairs orientation.Proof. One way to construct a compatible barrel pseudotiling is to reflect the existing barrel pseudotiling in the plane π, which clearly yields a barrel pseudotiling of opposite upstairs orientation. Note that, in this case, the winding orientation in each apeirostack changes as well, whereas the altered coloring f′ ' of the base tiling  is given by:
is given by:
 is given by:
is given by: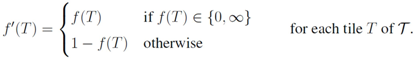
This fact allows us to adopt the convention that, unless otherwise stated, all subsequent barrel pseudotilings are assumed to have a counterclockwise upstairs orientation. We now focus on the properties of barrel pseudotilings with only isolated ∞-stacks, i.e., barrel pseudotilings where apeirostacks are not directly adjacent.
Lemma 6.3. In a barrel pseudotiling with only isolated ∞-stacks the winding orientation of any ∞-stack is coherent with (i.e., the same as) the global upstairs orientation.
Proof. Select any ∞-stack Ω. Because Ω has no faces in common with other ∞-stacks, the infinite staircases in the mantle of Ω have horizontal steps. Consequently, when unwinding the mantle as pictured in Figure 5, all staircases will be monotonically increasing when following the global upstairs orientation.
Let A be any apeirogonal face (base apeirogon of an apeirobarrel) in the ∞-stack. Suppose the winding orientation of A is opposed to the global upstairs orientation. Then A must intersect a staircase, which is impossible. Therefore, the winding orientation of A, and thus of any apeirogonal face, is coherent with the global upstairs orientation.
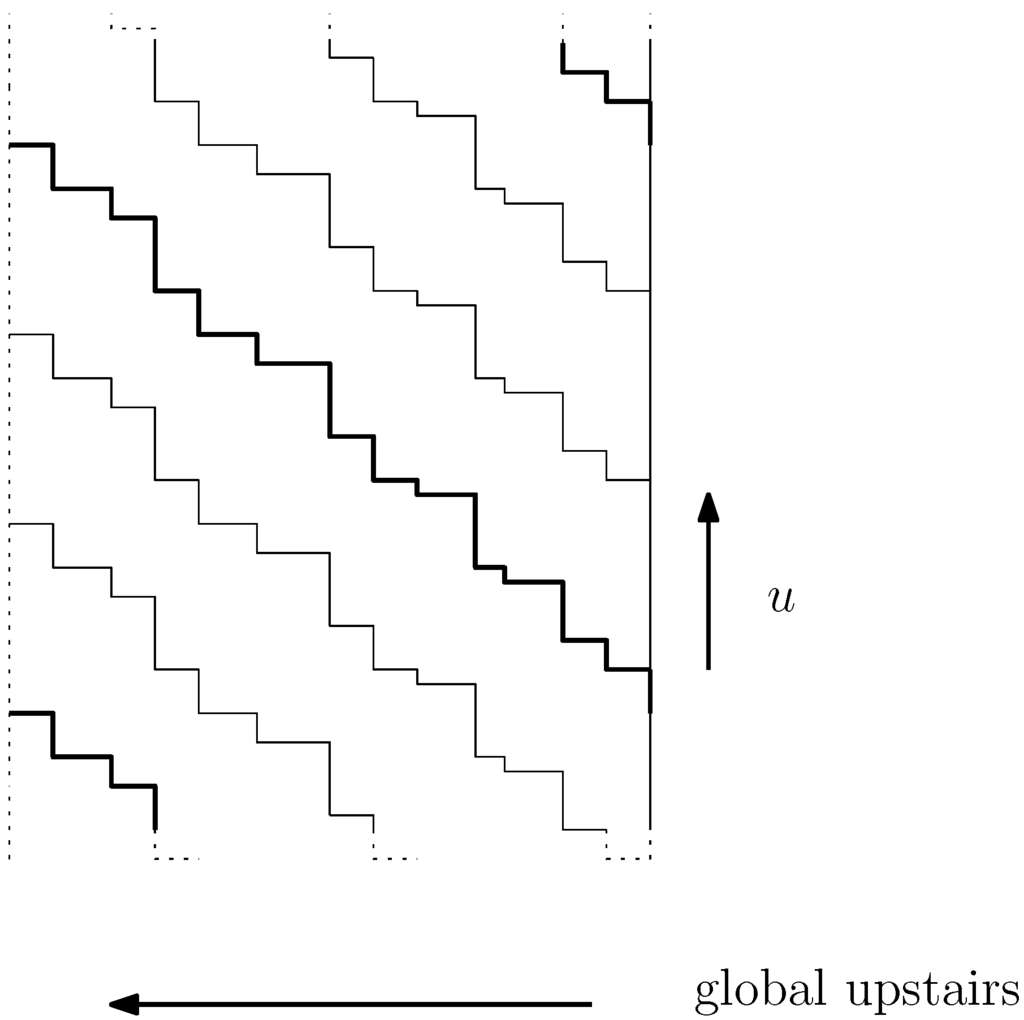
Figure 5.
Staircase lines on unwrapped mantle of ∞-stack (schematic). Other edges have been omitted for clarity.
It is not known if there is any such correspondence for pseudotilings with adjacent ∞-stacks, which makes it harder to explore them. Therefore, for the remainder of this article, all considered barrel pseudotilings have only isolated apeirostacks.
The following Lemma characterizes when isolated ∞-stacks are compatible with a given shift function f and a counterclockwise global upstairs orientation. Recall that the neighborhood symbol is taken in counterclockwise orientation, so it corresponds to our default choice of upstairs orientation.
Lemma 6.4. Let T be an n-gonal tile in the base tiling  with f(T) = ∞ and a neighborhood symbol (α0,α1,...,αn−1) with finite entries. Assume the global upstairs orientation is counterclockwise. An isolated ∞-stack Ω with k ≥ 2 distinct apeirogonal faces (spirals), which consequently consists of k distinct apeirogonal barrels, can be constructed over T if and only if we have αi > αi+1 for precisely k mutually distinct indices i (indices modulo n).
with f(T) = ∞ and a neighborhood symbol (α0,α1,...,αn−1) with finite entries. Assume the global upstairs orientation is counterclockwise. An isolated ∞-stack Ω with k ≥ 2 distinct apeirogonal faces (spirals), which consequently consists of k distinct apeirogonal barrels, can be constructed over T if and only if we have αi > αi+1 for precisely k mutually distinct indices i (indices modulo n).
 with f(T) = ∞ and a neighborhood symbol (α0,α1,...,αn−1) with finite entries. Assume the global upstairs orientation is counterclockwise. An isolated ∞-stack Ω with k ≥ 2 distinct apeirogonal faces (spirals), which consequently consists of k distinct apeirogonal barrels, can be constructed over T if and only if we have αi > αi+1 for precisely k mutually distinct indices i (indices modulo n).
with f(T) = ∞ and a neighborhood symbol (α0,α1,...,αn−1) with finite entries. Assume the global upstairs orientation is counterclockwise. An isolated ∞-stack Ω with k ≥ 2 distinct apeirogonal faces (spirals), which consequently consists of k distinct apeirogonal barrels, can be constructed over T if and only if we have αi > αi+1 for precisely k mutually distinct indices i (indices modulo n).Remark 6.2. The case k = 1 would lead to a degenerate ∞-stack and cannot happen in a pseudotiling (compare Definitions 4.1 and 4.2).
Proof. Let us first show that a constructed ∞-stack Ω with k distinct apeirobarrels implies the condition on the neighborhood symbol. In Ω, any of the k apeirogonal bases climbs k units before making a complete turn around the stack, and consequently, so do the k staircases. By definition, in an isolated ∞-stack all entries in the neighborhood symbol are finite. Consequently, any staircase consists of vertical and horizontal segments only, is monotone in the direction of u, and the height of two partition vertices stemming from any base in the i-th adjacent stack determines the corresponding shift entry αi in the neighborhood symbol (by taking the remainder of the height modulo 1, i.e., disregarding full units of distance and reducing to an entry in [0, 1)). Fixing an arbitrary staircase in Ω and starting at a step (tread) on height r which reduces to the smallest αi, w.l.o.g. α1, the corresponding contiguous entries in the neighborhood symbol increase as long as the staircase is trapped between r and  + 1. Only when the staircase reaches a step at a height of
+ 1. Only when the staircase reaches a step at a height of  + 1 or greater will there be a jump from a larger to a smaller entry in the neighborhood symbol. Subsequently, the next jump will occur when a height of
+ 1 or greater will there be a jump from a larger to a smaller entry in the neighborhood symbol. Subsequently, the next jump will occur when a height of  + 2 or greater is reached and so forth. Thus, if the staircase climbs k units when following the global upstairs orientation once around the stack, we obtain k jumps from an αi to a strictly smaller αi+1 in the neighborhood symbol.
+ 2 or greater is reached and so forth. Thus, if the staircase climbs k units when following the global upstairs orientation once around the stack, we obtain k jumps from an αi to a strictly smaller αi+1 in the neighborhood symbol.
 + 1. Only when the staircase reaches a step at a height of
+ 1. Only when the staircase reaches a step at a height of  + 1 or greater will there be a jump from a larger to a smaller entry in the neighborhood symbol. Subsequently, the next jump will occur when a height of
+ 1 or greater will there be a jump from a larger to a smaller entry in the neighborhood symbol. Subsequently, the next jump will occur when a height of  + 2 or greater is reached and so forth. Thus, if the staircase climbs k units when following the global upstairs orientation once around the stack, we obtain k jumps from an αi to a strictly smaller αi+1 in the neighborhood symbol.
+ 2 or greater is reached and so forth. Thus, if the staircase climbs k units when following the global upstairs orientation once around the stack, we obtain k jumps from an αi to a strictly smaller αi+1 in the neighborhood symbol.Conversely, in constructing an ∞-stack Ω, any apeirogonal faces are constructed as polygonal lines not intersecting the staircases. Any time there is a jump in the entries of the neighborhood symbol from an αi to a strictly smaller αi+1, the staircase has climbed another unit. Consequently, if there are k such jumps, the staircase climbs k units before making a complete turn around the stack. An apeirogonal base must therefore also climb k units. Translations in the direction of u by integer multiples are prescribed symmetries of the pseudotiling. A translation by ku is a symmetry that transforms the staircase under consideration into itself, but this is not true for translation by less than k units in the direction of u. Thus, we must have k staircases in total in Ω, and therefore k apeirogonal faces and barrels.
Observe that the condition formulated in Remark 6.1 assures that step four of the construction outline can be carried out, whereas the condition in Lemma 6.4 assures that ∞-stacks can be fitted in step five (as long as f isolates all ∞-stacks). This, however, constructs not only the apeirostacks, but also the missing vertices and edges on the finite stacks, so we are done. We are now in the position to summarize the necessary and sufficient conditions for when a pair (  , f) of a base tiling and coloring (shift) function gives rise to a barrel pseudotiling with only isolated ∞-stacks.
, f) of a base tiling and coloring (shift) function gives rise to a barrel pseudotiling with only isolated ∞-stacks.
 , f) of a base tiling and coloring (shift) function gives rise to a barrel pseudotiling with only isolated ∞-stacks.
, f) of a base tiling and coloring (shift) function gives rise to a barrel pseudotiling with only isolated ∞-stacks.Theorem 6.1. A pair (  , f) of a normal, simple, plane base tiling
, f) of a normal, simple, plane base tiling  and a coloring (shift) function
and a coloring (shift) function
 , f) of a normal, simple, plane base tiling
, f) of a normal, simple, plane base tiling  and a coloring (shift) function
and a coloring (shift) function f : T (  ) → [0, 1) ∪ {∞} gives rise to a barrel pseudotiling with only isolated ∞-stacks and counterclockwise global upstairs orientation if and only if the following two conditions hold.
) → [0, 1) ∪ {∞} gives rise to a barrel pseudotiling with only isolated ∞-stacks and counterclockwise global upstairs orientation if and only if the following two conditions hold.
 ) → [0, 1) ∪ {∞} gives rise to a barrel pseudotiling with only isolated ∞-stacks and counterclockwise global upstairs orientation if and only if the following two conditions hold.
) → [0, 1) ∪ {∞} gives rise to a barrel pseudotiling with only isolated ∞-stacks and counterclockwise global upstairs orientation if and only if the following two conditions hold. - (1) For each vertex v of
 where tiles P1, P2, P3 meet in counterclockwise order around v, such that their colors α1 = f(P1), α2 = f(P2), α3 = f(P3) are finite, and of which w.l.o.g. α1 is the smallest, the inequality α1 < α2 < α3 holds;
where tiles P1, P2, P3 meet in counterclockwise order around v, such that their colors α1 = f(P1), α2 = f(P2), α3 = f(P3) are finite, and of which w.l.o.g. α1 is the smallest, the inequality α1 < α2 < α3 holds; - (2) For each n-gonal tile P of
 with f(P ) = ∞, all entries in a neighborhood symbol (α0,α1,...,αn−1) are finite, and there are at least two distinct indices i such that αi > αi+1 (indices taken modulo n).
with f(P ) = ∞, all entries in a neighborhood symbol (α0,α1,...,αn−1) are finite, and there are at least two distinct indices i such that αi > αi+1 (indices taken modulo n).
7. Barrel Pseudotilings and Decorated Plane Triangulations
Any normal simple tiling of the plane has a normal simple dual, which is a (topological) triangulation of the plane (cf. [10], Chapter 4.2). We can thus formulate properties of any simple, normal, plane base tiling  with associated coloring of tiles, which gives rise to a barrel pseudotiling with isolated ∞-stacks, in terms of a (normal) dual triangulation
with associated coloring of tiles, which gives rise to a barrel pseudotiling with isolated ∞-stacks, in terms of a (normal) dual triangulation  . We do this not only for the sake of having dual statements, but also to draw connections to plane graphs (specifically, edge graphs of triangulations of the plane). Note that we do not make the assumption of convexity in the dual, since it is not generally known whether any tiling by convex polygons has a dual which also consists of convex polygons (cf. [10], p. 174).
. We do this not only for the sake of having dual statements, but also to draw connections to plane graphs (specifically, edge graphs of triangulations of the plane). Note that we do not make the assumption of convexity in the dual, since it is not generally known whether any tiling by convex polygons has a dual which also consists of convex polygons (cf. [10], p. 174).
 with associated coloring of tiles, which gives rise to a barrel pseudotiling with isolated ∞-stacks, in terms of a (normal) dual triangulation
with associated coloring of tiles, which gives rise to a barrel pseudotiling with isolated ∞-stacks, in terms of a (normal) dual triangulation  . We do this not only for the sake of having dual statements, but also to draw connections to plane graphs (specifically, edge graphs of triangulations of the plane). Note that we do not make the assumption of convexity in the dual, since it is not generally known whether any tiling by convex polygons has a dual which also consists of convex polygons (cf. [10], p. 174).
. We do this not only for the sake of having dual statements, but also to draw connections to plane graphs (specifically, edge graphs of triangulations of the plane). Note that we do not make the assumption of convexity in the dual, since it is not generally known whether any tiling by convex polygons has a dual which also consists of convex polygons (cf. [10], p. 174).Assume that  is a normal, simple, plane tiling by convex polygons with an appropriate coloring f on the tiles, which gives rise to a barrel pseudotiling with only isolated ∞-stacks in counterclockwise global upstairs orientation (as usual). Then let
is a normal, simple, plane tiling by convex polygons with an appropriate coloring f on the tiles, which gives rise to a barrel pseudotiling with only isolated ∞-stacks in counterclockwise global upstairs orientation (as usual). Then let  be a dual to
be a dual to  , which is a (normal, topological) triangulation of the plane with vertex set V (
, which is a (normal, topological) triangulation of the plane with vertex set V (  ). By slight abuse of notation we also denote the associated infinite geometric simplicial complex with
). By slight abuse of notation we also denote the associated infinite geometric simplicial complex with  . The vertices of
. The vertices of  inherit the coloring or shift function
inherit the coloring or shift function 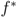 : V = V (
: V = V (  ) → [0, 1) ∪ {∞} from the function f on the tiles of
) → [0, 1) ∪ {∞} from the function f on the tiles of  . This adds decoration to the triangulation, but we will also add further decoration by directing some of the edges. Let V0 = (
. This adds decoration to the triangulation, but we will also add further decoration by directing some of the edges. Let V0 = (  )−1 ([0, 1)) denote the set of vertices of
)−1 ([0, 1)) denote the set of vertices of  with finite value under
with finite value under 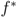 , and let
, and let  0 denote the simplicial subcomplex of
0 denote the simplicial subcomplex of  induced by V0 (it contains all simplices which have only vertices in V0, and the empty simplex).
induced by V0 (it contains all simplices which have only vertices in V0, and the empty simplex).
 is a normal, simple, plane tiling by convex polygons with an appropriate coloring f on the tiles, which gives rise to a barrel pseudotiling with only isolated ∞-stacks in counterclockwise global upstairs orientation (as usual). Then let
is a normal, simple, plane tiling by convex polygons with an appropriate coloring f on the tiles, which gives rise to a barrel pseudotiling with only isolated ∞-stacks in counterclockwise global upstairs orientation (as usual). Then let  be a dual to
be a dual to  , which is a (normal, topological) triangulation of the plane with vertex set V (
, which is a (normal, topological) triangulation of the plane with vertex set V (  ). By slight abuse of notation we also denote the associated infinite geometric simplicial complex with
). By slight abuse of notation we also denote the associated infinite geometric simplicial complex with  . The vertices of
. The vertices of  inherit the coloring or shift function
inherit the coloring or shift function 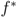 : V = V (
: V = V (  ) → [0, 1) ∪ {∞} from the function f on the tiles of
) → [0, 1) ∪ {∞} from the function f on the tiles of  . This adds decoration to the triangulation, but we will also add further decoration by directing some of the edges. Let V0 = (
. This adds decoration to the triangulation, but we will also add further decoration by directing some of the edges. Let V0 = ( 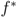 )−1 ([0, 1)) denote the set of vertices of
)−1 ([0, 1)) denote the set of vertices of  with finite value under
with finite value under 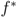 , and let
, and let  0 denote the simplicial subcomplex of
0 denote the simplicial subcomplex of  induced by V0 (it contains all simplices which have only vertices in V0, and the empty simplex).
induced by V0 (it contains all simplices which have only vertices in V0, and the empty simplex).Note 7.1. The set V∞ := V \ V0 is a dominating independent set in the edge graph of  (see [12] or Section 3 of this article for terminology).
(see [12] or Section 3 of this article for terminology).
 (see [12] or Section 3 of this article for terminology).
(see [12] or Section 3 of this article for terminology). This is simply the dual version of the statement that all tiles are either colored ∞, or adjacent to an ∞-colored tile, but not both. As a consequence,  0 contains no complete simplicial neighborhood of a vertex in
0 contains no complete simplicial neighborhood of a vertex in  , i.e., there are no vertices of
, i.e., there are no vertices of  0 which lie in its interior (we do not use the term relative interior here because
0 which lie in its interior (we do not use the term relative interior here because  0 may be a one-dimensional subcomplex of
0 may be a one-dimensional subcomplex of  ). We have:
). We have:
 0 contains no complete simplicial neighborhood of a vertex in
0 contains no complete simplicial neighborhood of a vertex in  , i.e., there are no vertices of
, i.e., there are no vertices of  0 which lie in its interior (we do not use the term relative interior here because
0 which lie in its interior (we do not use the term relative interior here because  0 may be a one-dimensional subcomplex of
0 may be a one-dimensional subcomplex of  ). We have:
). We have:Note 7.2. The underlying topological space |  0| of
0| of  0 is (path-)connected. In fact, |
0 is (path-)connected. In fact, |  0| is obtained from
0| is obtained from  by deleting the mutually disjoint open discs given by the open stars of the vertices in V∞ .
by deleting the mutually disjoint open discs given by the open stars of the vertices in V∞ .
 0| of
0| of  0 is (path-)connected. In fact, |
0 is (path-)connected. In fact, |  0| is obtained from
0| is obtained from  by deleting the mutually disjoint open discs given by the open stars of the vertices in V∞ .
by deleting the mutually disjoint open discs given by the open stars of the vertices in V∞ .Furthermore, the function 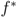 naturally induces directions on the edges in
naturally induces directions on the edges in  0, where {x, y} turns into the directed edge, or arc, (x, y) with tail x and head y if
0, where {x, y} turns into the directed edge, or arc, (x, y) with tail x and head y if 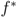 (x) <
(x) < 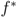 (y) (these values are finite, by definition of
(y) (these values are finite, by definition of  0). Furthermore, every arc is oriented in mathematically positive or negative direction with respect to an incident triangle, depending on whether it runs counterclockwise or clockwise around a point in the triangle’s interior. Since the global upstairs orientation is assumed as mathematically positive (for the pseudotiling based on
0). Furthermore, every arc is oriented in mathematically positive or negative direction with respect to an incident triangle, depending on whether it runs counterclockwise or clockwise around a point in the triangle’s interior. Since the global upstairs orientation is assumed as mathematically positive (for the pseudotiling based on  ), Remark 6.1 implies that every triangle in
), Remark 6.1 implies that every triangle in  0 has two mathematically positive and one mathematically negative oriented arcs. Note that the resulting directed edge graph of
0 has two mathematically positive and one mathematically negative oriented arcs. Note that the resulting directed edge graph of  0, which we denote by
0, which we denote by  , must not have directed cycles, as the value of
, must not have directed cycles, as the value of 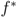 increases for successive vertices along directed paths.
increases for successive vertices along directed paths.
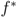 naturally induces directions on the edges in
naturally induces directions on the edges in  0, where {x, y} turns into the directed edge, or arc, (x, y) with tail x and head y if
0, where {x, y} turns into the directed edge, or arc, (x, y) with tail x and head y if 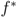 (x) <
(x) < 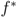 (y) (these values are finite, by definition of
(y) (these values are finite, by definition of  0). Furthermore, every arc is oriented in mathematically positive or negative direction with respect to an incident triangle, depending on whether it runs counterclockwise or clockwise around a point in the triangle’s interior. Since the global upstairs orientation is assumed as mathematically positive (for the pseudotiling based on
0). Furthermore, every arc is oriented in mathematically positive or negative direction with respect to an incident triangle, depending on whether it runs counterclockwise or clockwise around a point in the triangle’s interior. Since the global upstairs orientation is assumed as mathematically positive (for the pseudotiling based on  ), Remark 6.1 implies that every triangle in
), Remark 6.1 implies that every triangle in  0 has two mathematically positive and one mathematically negative oriented arcs. Note that the resulting directed edge graph of
0 has two mathematically positive and one mathematically negative oriented arcs. Note that the resulting directed edge graph of  0, which we denote by
0, which we denote by  , must not have directed cycles, as the value of
, must not have directed cycles, as the value of 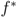 increases for successive vertices along directed paths.
increases for successive vertices along directed paths.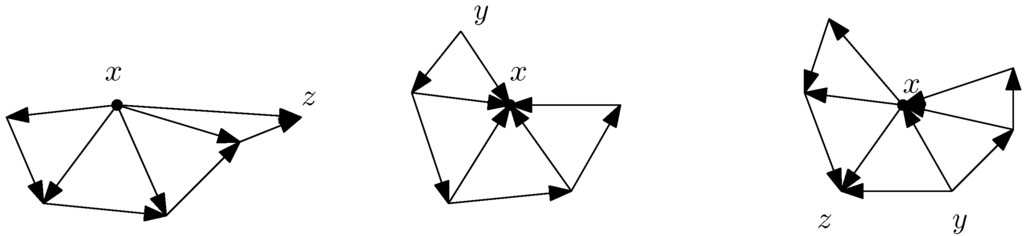
Figure 6.
The neighborhood of a regular vertex v in  0.
0.
 0.
0.
A cut-vertex—for the purpose of this paper—is a vertex x of  0 such that the underlying topological space
0 such that the underlying topological space  of its link in
of its link in  0 is disconnected. A vertex of
0 is disconnected. A vertex of  0 which is not a cut-vertex is called a regular vertex. Note that the simplicial neighborhood
0 which is not a cut-vertex is called a regular vertex. Note that the simplicial neighborhood 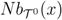 of any regular vertex x in
of any regular vertex x in  0 has as underlying topological space a closed disc whose boundary is a simple cycle containing x (as x cannot be an interior vertex). With directed arcs, there are three types of neighborhoods for regular vertices x, see Figure 6, as classified by the digraph of edges in that neighborhood (closed star), denoted
0 has as underlying topological space a closed disc whose boundary is a simple cycle containing x (as x cannot be an interior vertex). With directed arcs, there are three types of neighborhoods for regular vertices x, see Figure 6, as classified by the digraph of edges in that neighborhood (closed star), denoted  :
:
 0 such that the underlying topological space
0 such that the underlying topological space  of its link in
of its link in  0 is disconnected. A vertex of
0 is disconnected. A vertex of  0 which is not a cut-vertex is called a regular vertex. Note that the simplicial neighborhood
0 which is not a cut-vertex is called a regular vertex. Note that the simplicial neighborhood 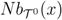 of any regular vertex x in
of any regular vertex x in  0 has as underlying topological space a closed disc whose boundary is a simple cycle containing x (as x cannot be an interior vertex). With directed arcs, there are three types of neighborhoods for regular vertices x, see Figure 6, as classified by the digraph of edges in that neighborhood (closed star), denoted
0 has as underlying topological space a closed disc whose boundary is a simple cycle containing x (as x cannot be an interior vertex). With directed arcs, there are three types of neighborhoods for regular vertices x, see Figure 6, as classified by the digraph of edges in that neighborhood (closed star), denoted  :
: - • x is the tail of all incident arcs, i.e., a source in
 . In this case, x is the only source in
. In this case, x is the only source in  . The boundary cycle has a single edge, (x, z), which is oriented negatively (with respect to (wrt) an interior point of the neighborhood), and z is the only sink in
. The boundary cycle has a single edge, (x, z), which is oriented negatively (with respect to (wrt) an interior point of the neighborhood), and z is the only sink in  ;
; - • x is the head of all incident arcs, i.e., a sink in
 . In this case, x is the only sink in
. In this case, x is the only sink in  , the boundary cycle of
, the boundary cycle of  has a single edge, (y, x), which is oriented negatively, and y is the only source in
has a single edge, (y, x), which is oriented negatively, and y is the only source in  ;
; - • x is neither a source nor a sink in
 . In this case, x is incident to a unique triangle yxz (labelled counterclockwise) for which it is a transition vertex, that is x is the head of (y, x) and the tail of (x, z) . The only source and sink in
. In this case, x is incident to a unique triangle yxz (labelled counterclockwise) for which it is a transition vertex, that is x is the head of (y, x) and the tail of (x, z) . The only source and sink in  are y and z, respectively. The boundary cycle of
are y and z, respectively. The boundary cycle of 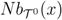 has a single negatively oriented edge, (y, z).
has a single negatively oriented edge, (y, z).
For cut-vertices x, the neighborhood splits into components for which x is a regular vertex, or which are single arcs containing x.
We call two triangles s, t of  0 triangle-connected if there is a finite sequence s = t0,t1,...,tn = t of triangles in
0 triangle-connected if there is a finite sequence s = t0,t1,...,tn = t of triangles in  0, such that for i =1,...,n the triangles ti−1 and ti are adjacent (i.e., they share an edge). We call a simplicial subcomplex of
0, such that for i =1,...,n the triangles ti−1 and ti are adjacent (i.e., they share an edge). We call a simplicial subcomplex of  0 induced by a set of mutually triangle-connected triangles of
0 induced by a set of mutually triangle-connected triangles of  0 a triangle component. By definition, the underlying topological space of any triangle component is connected. However, we can also prove the following:
0 a triangle component. By definition, the underlying topological space of any triangle component is connected. However, we can also prove the following:
 0 triangle-connected if there is a finite sequence s = t0,t1,...,tn = t of triangles in
0 triangle-connected if there is a finite sequence s = t0,t1,...,tn = t of triangles in  0, such that for i =1,...,n the triangles ti−1 and ti are adjacent (i.e., they share an edge). We call a simplicial subcomplex of
0, such that for i =1,...,n the triangles ti−1 and ti are adjacent (i.e., they share an edge). We call a simplicial subcomplex of  0 induced by a set of mutually triangle-connected triangles of
0 induced by a set of mutually triangle-connected triangles of  0 a triangle component. By definition, the underlying topological space of any triangle component is connected. However, we can also prove the following:
0 a triangle component. By definition, the underlying topological space of any triangle component is connected. However, we can also prove the following:Lemma 7.1. If S is a (maximal) triangle component of  0, then its underlying topological space |S| is simply connected. In particular, for finite triangle components S, the space |S| is a closed disc.
0, then its underlying topological space |S| is simply connected. In particular, for finite triangle components S, the space |S| is a closed disc.
 0, then its underlying topological space |S| is simply connected. In particular, for finite triangle components S, the space |S| is a closed disc.
0, then its underlying topological space |S| is simply connected. In particular, for finite triangle components S, the space |S| is a closed disc.Proof. Assume the contrary, i.e., that there exists a noncontractible (topological) cycle C in |S|. Then there exists a finite triangle-connected subcomponent S′ of S whose underlying space still contains C. We prove inductively that |S′| is a closed topological disc (the second statement), and thus contains no nontrivial cycle, which implies that |S| is simply connected.
First of all, observe that, by definition, any (finite) triangle component S′ of S can be built up by successively attaching triangles along at least one edge (arc) to smaller triangle components. We now make use of the directed edges and their orientation with respect to incident triangles, in particular on the boundary of the component. Since S′ is finite, |S′| is bounded and has finitely many boundary arcs (after assigning directions). We show that, topologically, the boundary is a simple closed curve, and thus encloses a disc.
A single triangle, as the base case, has two positively and exactly one negatively oriented arc (wrt an interior point). Suppose now that after k steps we have built up a component Sk which has exactly one negatively oriented arc on its boundary (wrt an interior point of the incident boundary triangle). We know that directed cycles cannot occur in the directed graph of our constructed component. When adding a triangle to the component in order to obtain Sk+1 the following cases need to be considered:
- • The new triangle is glued on at a single positive boundary arc only. In this case this positive boundary arc (which now is no longer on the boundary) is replaced by two positive boundary arcs in Sk+1, and Sk+1 retains exactly one negative arc on its boundary;
- • The new triangle is glued on at a single negative boundary arc only. In this case this negative boundary arc is replaced by a positive and a negative boundary arc in Sk+1, and Sk+1 still has exactly one negative arc on its boundary;
- • The new triangle is glued to two boundary arcs. Since by the induction hypothesis there is only one negative arc in the boundary of Sk, and the new triangle cannot be glued to two previously positive arcs (because they would have to match up with two negative arcs in the triangle), exactly one of those arcs must be positive, and one must be negative. These boundary arcs are replaced by a single positive boundary arc, leading to Sk+1 having only positive arcs in its boundary. This is impossible because it would lead to an oriented cycle in the boundary, i.e., to cyclically ever increasing values of
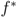 on the traversed vertices;
on the traversed vertices; - • The new triangle is glued to three boundary arcs. This is also impossible, because as in the previous case, two positive and one negative arc would be removed from the boundary, leading to an oriented cycle in the boundary;
- • The new triangle is glued on at a single positive (negative) boundary arc, and its third vertex is also glued. However, then the new boundary would (topologically) not be a simple closed curve, as four boundary arcs meet at that (glued) vertex, creating more than one cycle (regardless of edge direction) in the boundary. As there is still only one negatively oriented arc, this would lead to an oriented cycle in the boundary, which is forbidden.
Thus, in passing from Sk to Sk+1, the new triangle can only be attached along a single edge on the boundary of Sk, as described in the first two cases. The boundary must form a simple closed curve (dangling edges etc. do not occur by definition). In particular, |Sk+1| is a closed topological disc because it is also a bounded region. The component Sk+1 then has one more arc on the boundary, which is positively oriented, and retains one negatively oriented arc. This satisfies the induction hypothesis, so we have established that |S′| is a closed topological disc.
Note that if a finite triangle component S consists of n triangles, then the boundary contains (n + 1) positive arcs and one negative arc.
We can now give a dual version of Theorem 6.1, which is not formulated in terms of a precise coloring 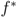 , but in terms of directed and undirected edges. This seems easier to handle in any kind of construction attempt, as the images in the next section show.
, but in terms of directed and undirected edges. This seems easier to handle in any kind of construction attempt, as the images in the next section show.
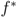 , but in terms of directed and undirected edges. This seems easier to handle in any kind of construction attempt, as the images in the next section show.
, but in terms of directed and undirected edges. This seems easier to handle in any kind of construction attempt, as the images in the next section show.Theorem 7.1. A normal simple tiling  of
of  by convex polygons gives rise to a barrel pseudotiling with isolated ∞-stacks and counterclockwise upstairs orientation if and only if some edges of the (any) dual triangulation
by convex polygons gives rise to a barrel pseudotiling with isolated ∞-stacks and counterclockwise upstairs orientation if and only if some edges of the (any) dual triangulation  can be directed such that the following conditions are all satisfied:
can be directed such that the following conditions are all satisfied:
 of
of  by convex polygons gives rise to a barrel pseudotiling with isolated ∞-stacks and counterclockwise upstairs orientation if and only if some edges of the (any) dual triangulation
by convex polygons gives rise to a barrel pseudotiling with isolated ∞-stacks and counterclockwise upstairs orientation if and only if some edges of the (any) dual triangulation  can be directed such that the following conditions are all satisfied:
can be directed such that the following conditions are all satisfied:- (1) The set of vertices which are only incident to UNDIRECTED edges, denoted V∞, is a dominating independent set in the edge graph G(
 );
); - (2) For each x in V∞, the boundary of
 has at least two directed arcs going in CLOCKWISE ORIENTATION around an interior point;
has at least two directed arcs going in CLOCKWISE ORIENTATION around an interior point; - (3) Each triangle in
 which has all its boundary edges oriented contains precisely one clockwise arc and two counterclockwise arcs.
which has all its boundary edges oriented contains precisely one clockwise arc and two counterclockwise arcs.
Remark 7.1. We note without proof that condition (3) can be rephrased as follows. Each maximal triangle component of  0 has, when edges are directed, exactly one arc on its boundary which is negatively oriented with respect to an interior point. It is not entirely obvious, and therefore remarkable, that conditions (1), (2), (3) prevent directed cycles in the partially directed edge graph of
0 has, when edges are directed, exactly one arc on its boundary which is negatively oriented with respect to an interior point. It is not entirely obvious, and therefore remarkable, that conditions (1), (2), (3) prevent directed cycles in the partially directed edge graph of  (note that a directed cycle should not contain undirected edges).
(note that a directed cycle should not contain undirected edges).
 0 has, when edges are directed, exactly one arc on its boundary which is negatively oriented with respect to an interior point. It is not entirely obvious, and therefore remarkable, that conditions (1), (2), (3) prevent directed cycles in the partially directed edge graph of
0 has, when edges are directed, exactly one arc on its boundary which is negatively oriented with respect to an interior point. It is not entirely obvious, and therefore remarkable, that conditions (1), (2), (3) prevent directed cycles in the partially directed edge graph of  (note that a directed cycle should not contain undirected edges).
(note that a directed cycle should not contain undirected edges). 8. A Small Zoo of Examples
For all examples shown in this section, we still implicitly assume that the global upstairs direction is mathematically positive (i.e., counterclockwise).
A class of base tilings which reproduce the examples mentioned in Section 2 are the simple normal plane tilings which are properly 3-colorable. In this case, we can assume the colors (shifts) to be 0, 0.5, and ∞. Figure 7a,b show (in the dual base tiling) how barrel pseudotilings can arise from the uniform tilings (63) and (4.82). Recall that the uniform tilings of the plane are precisely the vertex-transitive tilings by regular convex polygons. Recall further that (n1,n2,...,nk) is the standard notation for a uniform tiling of the plane where each vertex is cyclically surrounded by an n1-gon, n2-gon, and so forth, in that order (compare [10], chapter 2.1). Further 3-colorable tilings are also shown in parts Figure 7c–h. The ease of finding barrel pseudotilings for these lies in the consequences of 3-colorability for the conditions in Theorem 6.1. The first condition is automatically fulfilled with an ∞-colored tile at each vertex; and ∞-colored tiles have at least four adjacents, so their neighborhood symbols fall apart into at least two cyclically increasing subsequences, thus satisfying the second condition.
Figure 7.
Decorated duals of the uniform base tilings (63) and (4.82) (a,b). The small boxes  indicate ∞-colored vertices, and arrows indicate an increase in the function
indicate ∞-colored vertices, and arrows indicate an increase in the function 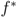 . Patches of properly 3-colorable normal simple plane tilings, (c)–(e) periodic, (f)–(h) non-periodic.
. Patches of properly 3-colorable normal simple plane tilings, (c)–(e) periodic, (f)–(h) non-periodic.
 indicate ∞-colored vertices, and arrows indicate an increase in the function
indicate ∞-colored vertices, and arrows indicate an increase in the function 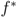 . Patches of properly 3-colorable normal simple plane tilings, (c)–(e) periodic, (f)–(h) non-periodic.
. Patches of properly 3-colorable normal simple plane tilings, (c)–(e) periodic, (f)–(h) non-periodic.
More interesting things happen when the base tiling is not 3-colorable, or if one deliberately uses more than three colors or shift lengths (possibly infinitely many). In this case, the conditions on the neighborhood symbol have significant implications, unlike in the previous case. In the decorated dual base tiling we can now see longer paths and possibly nonempty triangle components forming. Figure 8 shows some examples, all of which yield periodic pseudotilings, i.e., barrel pseudotilings with translational symmetry in three linearly independent directions, almost all of which are face-to-face. Observe that the absolute magnitude of the (finite) shift lengths is of little relevance, but rather is the shift difference among neighboring tiles (or vertices, in the dual). Finitely many colors (shift lengths) are sufficient if and only if all oriented paths in the decorated dual base tiling are of finite length, and the minimal number of colors needed is the same as the number of vertices on the longest directed path.
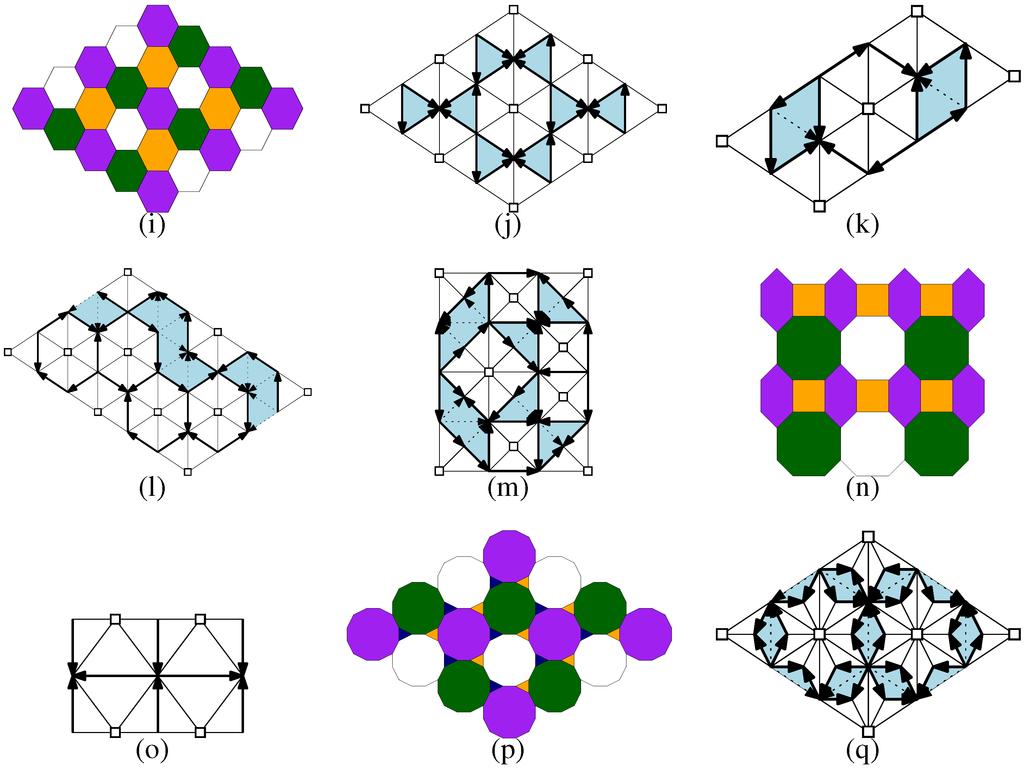
Figure 8.
Barrel pseudotilings arise from the information encoded in a coloring of (63) with four (a) and (b), five (c), and nine (d) colors. More examples stem from (4.82) with eleven colors (e), from a 4-colored tiling (f) and (g), and a 5-colored version of (3.122) (h) and (i). All except (e) give face-to-face barrel pseudotilings.
9. Remarks
We conclude the paper with some remarks about barrel pseudotilings and suggestions for further investigation in more general settings. In Section 8, many periodic examples of barrel pseudotilings were shown. It would be nice to have an algorithm to construct periodic barrel pseudotilings from periodic base tilings. As we have seen, not all suitable base tilings are periodic, but periodic base tilings seem to be a more interesting case because of their additional symmetry. Furthermore, the terrain is wide open when it comes to allowing adjacent ∞-stacks; it is unclear if there is a connection between winding orientation and upstairs orientation along the lines of Lemma 6.3, as well as how a decorated planar triangulation could capture all of the essential information in this case.
We have made many assumptions and chosen the definitions in this article in a certain way. First, we require that (finite) barrels stem from a right prism and that planar base tilings consist of convex polygons. However, it is conceivable that this is only a technical assumption to simplify the description of statements and procedures. It may be possible—but it has not been investigated—to deform the pseudotilings so that no coplanar adjacent 2-faces occur. For some pseudotilings, it may even be possible to have strictly convex polytopes emerge as the finite cells.
Second, we selected the definitions so as to produce structures which are realizations of abstract rank 4 polytopes. Several very similarly arising structures have been discarded on the grounds of not being associated with an abstract rank 4 polytope. Nevertheless, it may be of interest to chemists or crystallographers to identify the corresponding 4-valent atomic networks. Figure 9 shows an example patch of a structure, which has translational symmetry in three directions (and additional symmetries) yet fails to be classified as a barrel pseudotiling because only one apeirogon appears per stack (the degenerate case mentioned in Remark 6.2).
Figure 9.
This patch with base (63) is not part of a barrel pseudotiling, as the face structure of the object does not correspond to an abstract 4-polytope.
In order to further explore the connection with abstract polytopes, one could use a similar construction not only on tilings of the plane, but also on polyhedral maps. This would not fit as nicely into  , but perhaps it would still produce interesting results. Finally, it should be possible to quotient by a multiple of u in order to produce and study finite objects.
, but perhaps it would still produce interesting results. Finally, it should be possible to quotient by a multiple of u in order to produce and study finite objects.
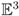 , but perhaps it would still produce interesting results. Finally, it should be possible to quotient by a multiple of u in order to produce and study finite objects.
, but perhaps it would still produce interesting results. Finally, it should be possible to quotient by a multiple of u in order to produce and study finite objects.Acknowledgments
The author would like to thank Egon Schulte for his careful reading and many helpful suggestions. Also, the author would like to thank the two anonymous referees for their insightful comments which led to the improvement of this paper.
References and Notes
- Grünbaum, B. Regular polyhedra—old and new. Aequ. Math. 1977, 16, 1–20. [Google Scholar] [CrossRef]
- Schulte, E. Symmetry of polytopes and polyhedra. In Handbook of Discrete and Computational Geometry, 2nd; Goodman, J.E., O’Rourke, J., Eds.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; pp. 431–454. [Google Scholar]
- Dress, A.W.M. A combinatorial theory of Grünbaum’s new regular polyhedra, Part I: Günbaums’s new regular polyhedra and their automorphism group. Aequ. Math. 1981, 23, 252–265. [Google Scholar] [CrossRef]
- Dress, A.W.M. A combinatorial theory of Grünbaums’s new regular polyhedra, Part II: Complete enumeration. Aequ. Math. 1985, 29, 222–243. [Google Scholar] [CrossRef]
- Leytem, C. Pseudo-Petrie operators on Grünbaumpolyhedra. Math. Slovaca 1997, 47, 175–188. [Google Scholar]
- McMullen, P.; Schulte, E. Regular polytopes in ordinary space. Discrete Comput. Geom. 1997, 17, 449–478. [Google Scholar] [CrossRef]
- McMullen, P.; Schulte, E. Regular and chiralpolytopes in low dimensions. In The Coxeter Legacy: Reflections and Projections; Davis, C., Ellers, E.W., Eds.; AMS: Providence, RI, USA, 2005; pp. 87–106. [Google Scholar]
- McMullen, P.; Schulte, E. Abstract Regular Polytopes (Encyclopedia of Mathematics and its Applications); Cambridge University Press: Cambridge, UK, 2002; Volume 92. [Google Scholar]
- Grünbaum, B.; Shephard, G.C.; Miller, J.C.P. Uniform tilings with hollow tiles. In The Geometric Vein: The Coxeter Festschrift; Davis, C., Grünbaum, B., Sherk, F.A., Eds.; Springer: New York, NY, USA, 1981; pp. 17–64. [Google Scholar]
- Grünbaum, B.; Shephard, G.C. Tilingsand Patterns; W.H. Freeman and Company: New York, NY, USA, 1987. [Google Scholar]
- Schattschneider, D.; Senechal, D. Tilings. In Handbook of Discrete and Computational Geometry, 2nd; Goodman, J.E., O’Rourke, J., Eds.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; pp. 53–72. [Google Scholar]
- West, D.B. Introduction to Graph Theory; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Maunder, C.R.F. Algebraic Topology; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Locher, J.L. The Magic of M.C. Escher; Harry N. Abrams: New York, NY, USA, 2000. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).