1. Introduction
In the context of his work on thought experiments, Brown [
2,
3,
4] discusses a remarkable argument meant to refute the Continuum Hypothesis (CH). The argument takes the form of a probabilistic
reductio: there exists a scenario (I will call it
Double Dart Throw) in which CH, together with a set of reasonable assumptions, entails the inevitable occurrence of events of zero probability, characterized as such
in advance of their occurrence. This would be absurd. So we should reject CH. This argument, originally formulated by Freiling [
1], initially seems quite attractive. It has interest apart from its importance for Brown’s account of thought experiments. The argument is intriguing because it rests on a combination of precise mathematical assumptions and powerful intuitions about symmetry.
The main purpose of this paper is to assess this argument. A number of people have criticized Brown’s argument, notably Norton [
5,
6] and Hauser [
7]. My criticisms have something in common with theirs, but the former paper concentrates on thought experiments and the latter on the implications of adopting Freiling’s “symmetry axiom” in set theory. I am interested in the significance of the argument for the philosophy of probability. It is a symmetry argument that fails on technical grounds: there is no way to incorporate all of the assumptions and intuitions into a single probability model.
Yet the argument is significant for two reasons. First: it exemplifies a distinctive type of failure. In the famous probability paradoxes, intuitions about symmetry practically by themselves generate inconsistent probabilistic conclusions. In Double Dart Throw, by contrast, the symmetry intuitions are coherent but come into conflict with other plausible probabilistic assumptions. Second: assessment of the Brown-Freiling argument suggests that philosophers and statisticians should extend the notion of non-conglomerability beyond finitely additive measures on a countable partition.
Section 2 and
Section 3 present and criticize the argument offered by Brown and Freiling.
Section 4 discusses an analogous argument based on a simpler scenario without involving fancy set theory (I will call it
Double Lottery). The analyses in these sections show that both arguments fail; furthermore, the fact that the two arguments have the same structure suggests that CH is not the obvious culprit even if an alternative version of the Brown-Freiling argument does imply an absurdity.
The remainder of the paper explores one possible alternative, using the symmetries of the scenario to define a finitely additive probability measure. On this new approach, however, we encounter a problem of non-conglomerability and the reductio argument still fails. I conclude by arguing that non-conglomerability (or an extended notion thereof) also plagues the original version of the argument. The example thus provides subtle but valuable lessons about the limitations of reasoning from symmetry to probabilistic conclusions.
2. Brown on the Continuum Hypothesis
2.1. Brown’s Version
This section presents Brown’s argument (with a brief discussion of Freiling’s earlier formulation). The argument rests on probabilistic assumptions and some set theory.
1 On the probabilistic side, Brown makes use of the one-dimensional Lebesgue measure,
m, which assigns a non-negative real number to measurable subsets of [0, 1]. In particular,
m(
A) = 0 if
A consists of a single point. The Lebesgue measure is
finitely additive: the measure of a finite union of disjoint sets is the finite sum of the individual measures. This extends to
countable additivity:
- (CA)
m( An) = m(An) , provided the sets An are disjoint and measurable.
Not every subset of [0, 1] has a well-defined Lebesgue measure, but most reasonable sets do. The measurable sets constitute a σ-field, closed under countable unions and complementation in [0, 1]. It is of particular importance to Brown’s argument that if A is a countable set of points, then A is measurable and m(A) = 0.
In addition to this general background, Brown makes some probabilistic assumptions about a particular scenario, Double Dart Throw. He asks us to imagine throwing two darts at the closed interval [0, 1]. The tip of each dart has no extension: the darts land on two mathematical points, p and q. Brown asks us to grant three assumptions:
- (i)
Randomness. Each throw selects a point randomly: Any two sub-intervals of equal length are equally likely to receive the dart. More generally: If we specify any measurable subset E of [0, 1], the probability Pr(x ∈ E) that the dart will hit a point x in E is given by the Lebesgue measure m(E).
- (ii)
Independence. The two throws are independent: neither has any influence on the other. Formally, if E and F are any two (measurable) subsets of [0, 1], then Pr(x ∈ E/y ∈ F) = Pr(x ∈ E) and Pr(y ∈ F / x ∈ E) = Pr(y ∈ F).
- (iii)
Symmetry. Brown writes [
2]: “The independence and randomness of the darts guarantees the symmetry of the throws. Consequently, either dart may be considered the first throw.” Brown means: In determining the probability of any outcome for the darts taken singly or as a pair, we may freely suppose that either dart is the first throw.
Notice that distinct intuitions about symmetry play a role in motivating two of these assumptions.
Randomness (assumption (i)) may be interpreted as symmetry under translation: the Lebesgue measure gives the correct probability distribution for
each throw taken separately.
2 Symmetry under permutation gives us assumption (iii): The order should not matter for the
pair of throws.
As noted, Brown also makes use of elementary set theory. He takes for granted ZFC: the Zermelo-Frankel axioms of set theory, together with the Axiom of Choice. A well-known consequence is the
Well-Ordering Principle: any set X can be totally ordered by a relation < in such a way that any nonempty subset of X has a first element. We can apply this principle to obtain a well-ordering < of the interval [0, 1]. This ordering is
total: for any
p and
q, we must have either
p <
q or
q <
p. Obviously, the ordering will be different from the usual ordering relation ≤ on the real numbers. Let
Sq = {
x ∈ [0, 1]/
x <
q}, the
initial segment of [0, 1] that precedes
q in the well-ordering. An important fact about well-ordered sets is that no well-ordered set is order-isomorphic to any of its initial segments.
3At this point, Brown brings in the Continuum Hypothesis:
- (CH)
The cardinality of the real numbers, and hence of [0, 1], is ℵ1: the least uncountable cardinal number.
Brown assumes, for
reductio, that CH is true. He needs only one consequence of CH: for any
q ∈ [0, 1], the initial segment
Sq is a countable set.
4Now to Brown’s argument. Suppose that the two dart points are p and q. We must have either p < q or q < p. Suppose p < q, so that p ∈ Sq. By Symmetry, we may regard the throw that lands on q as having occurred first, giving us the value of q and fixing the countable set Sq. By Independence and Randomness, the probability that the other dart lands in Sq is Pr(p < q) = m(Sq) = 0, since Sq is a countable set. In effect, the first dart fixes a set of measure zero (namely, Sq), and the second dart throw is thus a near-miraculous event: the selection of a point in that measure-zero set. There is a parallel result if q < p, since m(Sp) = 0 as well. Thus, every time a pair of darts is thrown, an event of zero probability will occur. While logically possible, this is absurd. The upshot is that we should abandon CH.
Notice: the use of the well-ordering < is absolutely crucial to this argument, since this (in conjunction with CH) is what gives us m(Sq) = 0 for each q. If we employ the usual ordering relation ≤ instead, then the initial segment {x/0 ≤ x ≤ q} would have measure q, for each q, and there is no paradoxical conclusion.
As Brown recognizes, the crux of this argument is his
Symmetry assumption, the claim that we may regard the greater value
q, and hence the set
Sq, as fixed prior to the second throw, so that we may identify
Pr(
p <
q) with
m(
Sq). He clarifies [
2]: “A prediction based on either throw cannot be dismissed in the way we might dismiss someone who said of a license number on a passing car: ‘Wow, there was only a one in a million chance of that happening.’ We are rightly impressed only if the number is fixed independently of the outcome (
i.e., predicted before the result is known).”
2.2. Freiling’s Version
Freiling’s earlier version [
1] of the argument is very close to Brown’s formulation. His argument against CH hinges on the
Freiling Symmetry Axiom:
- (FSA)
(∀f: ℝ → ℝℵ0)∃x ∃y(y ∉ f(x) & x ∉ f(y))
Here, ℝℵ0 is the set of all countable subsets of ℝ. FSA says: If f assigns a countable set of real numbers to each real number, then we can find two real numbers x and y such that x is not in f(y) and y is not in f(x). Freiling’s refutation of CH now breaks into two steps: a short preliminary proof that FSA is equivalent to ~CH, and a probabilistic argument for FSA. Since there is no question about the validity of the first step, let us look at his probabilistic argument.
Suppose
f: ℝ → ℝ
ℵ0. For any real number
x,
f(
x) is a countable set and thus
m(
f(
x)) = 0. Select two points
p and
q in [0, 1] randomly and independently–as in Brown’s version, we may assume this is done by tossing darts. If FSA is false, then either
p ∈
f(
q) or
q ∈
f(
p). Without loss of generality, suppose
p ∈
f(
q). The assumption of independence implies that we may consider the choice of
q as prior and that we can identify
Pr(
p ∈
f(
q)) with
m(
f(
q)).
5 In defense of this crucial presumption that one may regard
q as selected first, Freiling takes the same stance as Brown: “the real number line does not really know which dart was thrown first or second.” Since
Pr(
p ∈
f(
q)) =
m(
f(
q)) = 0, every time we select points
p and
q at random, an event of zero probability occurs. That is absurd, so we should accept FSA. The parallel with Brown’s argument is obvious: Brown works with the instance of FSA where
f(
x) = {
y/
y <
x}. Notice, however, that Freiling’s argument does not depend upon the choice of
f. Thus, if we can refute Brown’s argument, we also refute Freiling’s version of the argument.
3. Critique of the Argument
The basic difficulty with Brown’s argument is simple: why should we identify Pr(p < q) with m(Sq)? As we saw, Brown justifies this step by appealing to his principle of Symmetry for the dart tosses: “either dart could be considered the first throw.” Neither dart toss has any causal influence on the other, so why should the order of the tosses matter? We may proceed as if the throw that hits the <-larger number, q, comes first, so that Sq may be regarded as fixed.
To see that something is wrong with this argument, note that, by parity of reasoning, it is equally legitimate to fix the <-smaller number,
p, as the first throw. In that case, we may identify
Pr(
p <
q) with the probability that
q belongs to
= {
x ∈ [0, 1]/
p <
x and
p ≠
x}, the
complement of
Sp, and this probability is appropriately given by the Lebesgue measure of
(see
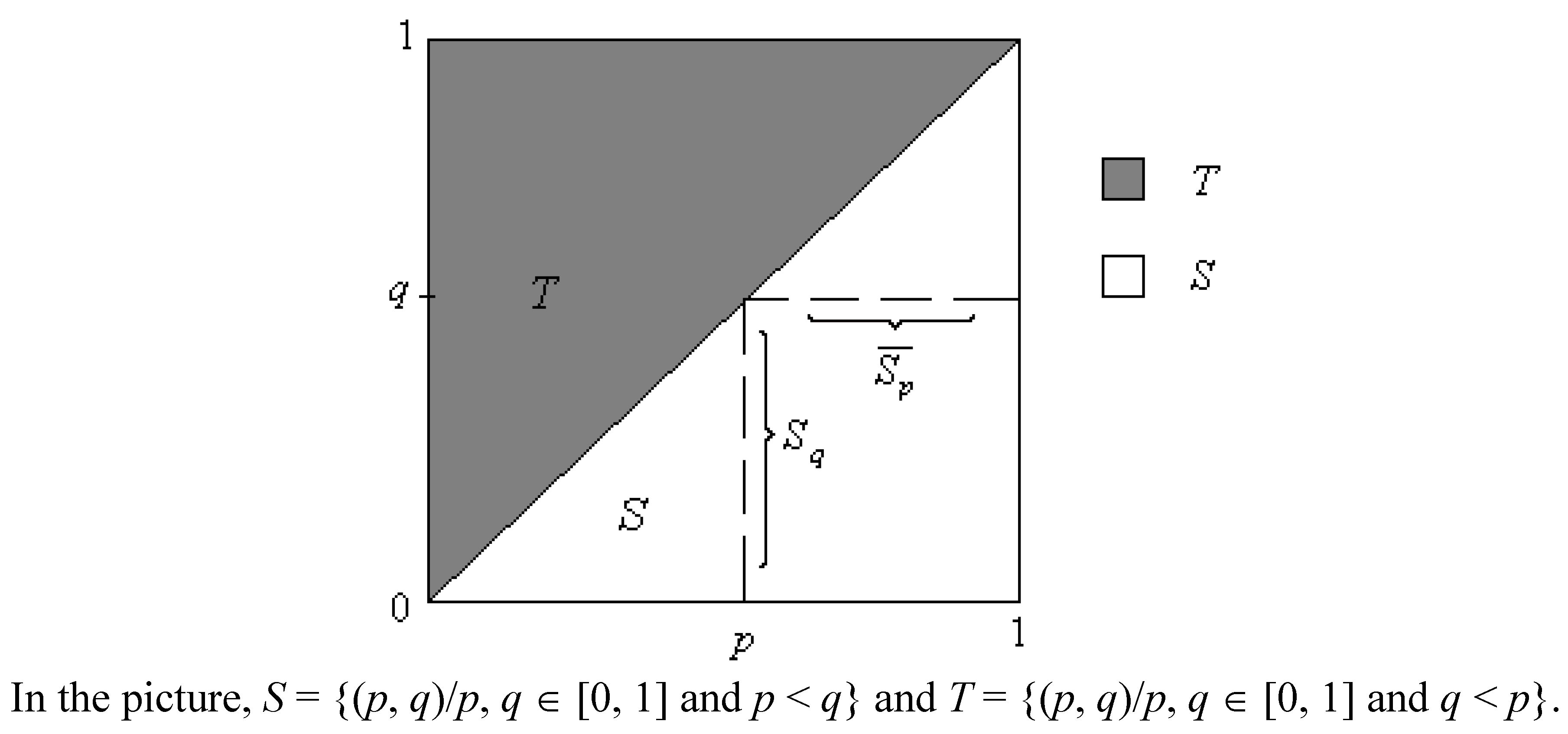
Figure 1). But
m(
) = 1, so we now have
Pr(
p <
q) = 1, rather than 0! Clearly, there is something wrong with both Brown’s argument, and this one.
A slight clarification is in order. We could simply specify that the larger value will always be designated the ‘first toss’, q. But if this is the case, then the Lebesgue measure m(Sq) is irrelevant: we must have Pr(p < q) = 1. Similarly, we could specify that the lesser value is always designated the ‘first toss’, p, in which case we once again have Pr(p < q) = 1. And so on. Let us rule out these possibilities as incompatible with Brown’s description of the problem.
Brown’s Symmetry principle thus leads to two distinct probability assignments for Pr(p < q): m(Sq) (=0), and m() (=1). The correct Symmetry principle, however, is not that we may consider either dart to have been tossed first, but rather that the probability Pr(p < q) (and of course all probabilities of outcomes for the pair of darts) should be invariant under permutation of the order of tosses.
To appreciate this point, consider how we might handle a simpler but analogous case. Let us use the two dart throws on [0, 1], but substitute the ordering < on the real numbers in place of <. Once again, let p and q be the points where the darts land, and suppose that we happen to have p < q. How do we compute the probability Pr(p < q) that this happened, in the absence of any protocol about which dart counts as first? If we follow Brown, we should reason that, by symmetry, we may consider q to be the first throw. The probability Pr(p < q) is thus the measure of [0, q), i.e., q. But this is a mistake. If the dart throws are independent, we compute Pr(p < q) as a weighted average (determined by integration) of probabilities for p < q over all possible values of q, rather than treating the actual value of q as fixed. Equivalently, we can specify that the outcome space here is [0, 1] × [0, 1] = {(p, q)/0 ≤ p, q ≤ 1}, and use the product measure to compute Pr(p < q). Either way, we get the answer ½, invariant under the order of throws. The way to interpret the probability of an event involving two independent variables is with the product measure–in this case, the two-dimensional Lebesgue measure.
Let us return to Brown’s scenario. Since
p and
q are independent variables, the correct way to compute
Pr(
p <
q) is to compute the product measure of
S = {(
p,
q)/
p,
q ∈ [0, 1] and
p <
q}. We can go a little further. Let
T = {(
p,
q)/
p,
q ∈ [0, 1] and
q <
p}, as shown in
Figure 1. The legitimate
Symmetry assumption here is that the order of tosses should not affect any of the probabilities; hence, the measures of
S and
T should be the same
if they are well-defined. More precisely: either both
S and
T are non-measurable sets, or both are measurable with equal measure. Indeed,
T = ρ(
S), where ρ is reflection over the line
q =
p, and Lebesgue measure is invariant under isometries. Further,
S ∪
T is equal to the unit square minus the line
q =
p, which has measure 0. It follows that either both sets are measurable, with measure ½, or both are non-measurable. Either way, Brown’s argument fails.
6 When we use the product measure, the contradiction disappears and with it the
reductio for the Continuum Hypothesis.
It is easy to be misled by the fact that each vertical cross-section Sq has one-dimensional measure 0. Indeed, that suggests that the two-dimensional measure of S must be 0, by appeal to Fubini’s Theorem, which tells us how to compute iterated integrals ‘by slices’. However, it is not obvious that the requirements for the application of Fubini’s Theorem are met in our example.
Indeed, we can say something stronger: the set
S is not a measurable set, and consequently
Pr(
p <
q) is
not defined. If it were, then the conditions for applying Fubini’s Theorem would be satisfied. We could compute the measure of
S by iterated integrals and it would not matter whether we used horizontal or vertical cross-sections. These two ways of computing the integral would give the same result. We know that they do not: The measure of each vertical cross-section is 0, while the measure of each horizontal cross-section is 1. Hence,
S is not measurable.
7The hard mathematical reality here is that the following cannot all be true of our probability measure on [0, 1] × [0, 1]:
- (i)
Each of the cross-sections Sq and Sp has a well-defined one-dimensional measure of 0.
- (ii)
The probability distribution for the pair of throws is given by the product measure.
- (iii)
S has a well-defined two-dimensional measure (e.g., m(S) = Pr(p < q) = ½).
These statements correspond to Brown’s three original assumptions: randomness, independence, symmetry. One or more of them has to go. If we use the Lebesgue measure in (i) and (ii), then we have to give up (iii). Given randomness and independence, the probability Pr(p < q) is undefined. (For future reference, we still have a weak form of symmetry: both S and T are non-measurable.)
Yet two puzzles remain. First: why do we not have
Pr(
p <
q) = ½, given the symmetry of the set-up? Despite the mathematical argument above, the intuition that
p <
q and
q <
p are equiprobable remains strong. What should we say about this intuition? Freiling appears to think we should give such intuitions priority. He writes (in a slightly different context) that his argument [
1] depends upon a principle
...not meant to be a mathematical statement of the Lebesgue measurability of a certain type of set. Rather, it is an expression of an obvious, almost physical intuition concerning the inherently nonmathematical notions of prediction, accuracy, and time independence.
Yet an appeal to symmetry, where we cannot produce a coherent mathematical model, is unreliable, as we know from the many paradoxes associated with the Principle of Insufficient Reason.
The second puzzle has to do with the sequential version of the dart throw. On this version, you throw one dart (first), observe the result q, and then throw a second dart (second) with result p. The value of first is settled prior to the second throw. So we have Pr(second < first/first = q) = m(Sq) = 0. The conditional probability of seeing a lower value is indeed zero. If you update your probability for second < first by Bayesian conditionalization, then you must expect (with probability 1) to see a higher value for the second dart. This is puzzling because it is reasoning to a foregone conclusion. Conditional upon any observed value, you believe with probability 1 that the value selected by the next dart will be larger. This is very strange, given the symmetry of the situation. Indeed, you half expect that you will be wrong (well, not precisely half, since Pr(p < q) is undefined). To my mind, this anomaly is the core of Brown’s reductio argument.
I will return to the first of these two puzzles in
Section 5, and the second in
Section 6. As a preliminary step, let us first examine an argument that is strongly analogous to Brown’s, but formulated in a much simpler setting.
4. The Double Lottery
Can we define a uniform probability distribution over a countable partition?
8 Picturesquely: can there be a lottery with one ticket for each positive integer, in which each ticket has an equal (subjective) probability of winning? The answer is clearly negative if one accepts countable additivity (CA): If each ticket has equal probability
k of winning, then both
k = 0 and
k > 0 are impossible. De Finetti [
11], who held that such a lottery is conceivable, dropped countable additivity. If
Pr is a merely finitely additive measure, then one can have a uniform distribution that assigns each ticket probability
k = 0 of winning.
9 Something similar can be done with non-standard probabilities.
10There is an illuminating analogy between
Double Lottery (the above lottery with two tickets) and
Double Dart Throw. Indeed, Brown [
2] considers (and rejects) this analogy in the following passage:
The refutation of CH made use of a principle to the effect that when picking out an initial segment, we end up with a set of lower cardinality. We can use this fact to get apparently paradoxical results from smaller well-ordered sets. For instance, pick a pair of natural numbers at random. Let them be m and n. Suppose m is chosen at random. What is the probability that m is less than n? It is zero. Similarly, the probability that n is less than m is also zero. Does this refute the view that the cardinality of the natural numbers is ℵ0? The answer is No, but we should reject the claim that this argument is parallel to Freiling’s. The conclusion this argument actually justifies is that we cannot talk about the probability of picking natural numbers at random… We cannot throw darts at the natural numbers in the same way we can throw them at the reals between [0, 1].
The analogy merits further attention. The two scenarios–
Double Dart Throw and
Double Lottery– have a great deal in common. In both cases, we allegedly have
Randomness,
Independence (of the two draws/throws) and
Symmetry (order is unimportant). In both cases, we have a total ordering with the peculiar property that every initial segment
Sq = {
p/
p <
q} for the dart throw [
Sq = {
p/
p <
q} for the lottery] has lower cardinality than that of the full outcome space, and each such initial segment is a set of measure 0.
11 The only difference is that CH is needed for the latter result in the Brown-Freiling case, while CA must be dropped if we are to accept
Randomness in the de Finetti lottery.
The analogy suggests that anyone who endorses the Brown-Freiling argument against CH has a parallel argument
for retaining CA (
i.e., for rejecting a merely finitely additive measure as one’s subjective probability function) in the case of a countable partition.
12 I think that this is an interesting way of re-interpreting Brown’s conclusion in the cited passage: if we drop CA, then we have a uniform finitely additive probability distribution over the natural numbers, and that leads to an absurd conclusion. Suppose that μ is a merely finitely additive probability measure, defined on an algebra 𝒜 of subsets of ℕ, such that μ(
E) = 0 for every finite set
E. (We do not specify 𝒜, but it must at minimum include all finite and co-finite sets.) The
reductio argument against adopting μ corresponds to Brown’s
reductio against CH. Let
p and
q be two randomly selected ticket numbers, with
p <
q. Suppose that there is no basis for assigning priority to either ticket. By analogy with Brown’s argument, we may consider the larger number,
q, to be the first one drawn. Under a uniform finitely additive distribution, the measure of any finite set of ticket numbers, and hence of
Sq = {
p/
p <
q}, is 0. So
Pr(
p <
q) = 0. So, each time we draw a pair of tickets, a near-miraculous (probability 0) event occurs—one that is foreseeable. This, it is alleged, is absurd.
13This argument, however, faces obstacles directly analogous to those just raised against the Brown-Freiling argument. Why not consider the smaller number to be the first one drawn, in which case
Pr(
p <
q) = 1? The correct way of proceeding, once again, is to work with the (finitely additive) product measure on ℕ × ℕ. But if we use the product measure, then
Pr(
p <
q) is undefined:
S = {(
p,
q)/
p <
q} is not a measurable set.
14 So the argument fails.
In short, the following cannot all be true of a probability measure μ on ℕ × ℕ:
- (i)
Each of the cross-sections Sq = {p ∈ ℕ/p < q} has one-dimensional measure 0. (Any two tickets are equally good; each ticket must have zero probability of winning.)
- (ii)
The probability distribution for the pair of tickets is given by the product measure.
- (iii)
S has a well-defined two-dimensional measure: μ(S) = Pr(p < q) = ½. (There is no reason why either ticket number should have a higher chance of being larger.)
One or more of these properties has to go. If we use a uniform finitely additive measure in (i) and (ii), then we have to give up (iii). (Once again, though, we still have a weak form of symmetry: both S = {(p, q)/p < q} and T = {(p, q)/q < p} are non-measurable.)
To complete the analogy: Double Lottery exhibits the same two puzzling features as the Brown-Freiling example. First, it is surprising that we cannot have Pr(p < q) = ½. Second, in the sequential version, where a first ticket is drawn and examined before the second, we once again have reasoning to a foregone conclusion: no matter what value q is observed on the first ticket, your conditional probability Pr(second < first/first = q) = 0. You are bound to conclude that the second ticket has a higher value than the first.
Summarizing, Double Lottery has the very same structural features as Double Dart Board, without the Continuum Hypothesis or the Axiom of Choice. The reductio argument against finite additivity has the same structure as the Brown-Freiling argument against CH. The defect in the reductio argument is also the same: without any clear protocol as to which ticket draw counts as first, the probability Pr(p < q) is undefined, rather than 0. There are as yet unresolved puzzles about symmetry, and about the sequential versions of both arguments. But even if these puzzles remain unresolved, we cannot put the blame entirely on either CH or finite additivity; rather, the problem derives from a common probabilistic structure to which CH and finite additivity contribute.
5. Symmetry and Finitely Additive Measures
5.1. Paradoxical Sets and Finitely Additive Measures
So far, we have been unable to accommodate the intuition that Pr(p < q) = ½ in Double Dart Throw (and Pr(p < q) = ½ in Double Lottery). Of course, there are well known cases, such as the Bertrand Paradox, where strongly held intuitions about symmetry lead to incoherence. But it does not seem right to locate the Brown-Freiling example in this group. The symmetries here seem “almost physical” (in Freiling’s words). Furthermore, they are defined independently of each other: Translation invariance applies to each dart throw separately, and invariance under permutation applies to the pair of throws. This is very different from the famous cases where incoherent probability assignments arise from alternative ways of partitioning the space of outcomes into equiprobable alternatives.
In fact, there is a consistent mathematical representation of all relevant symmetries, in both Double Dart Throw and Double Lottery. Indeed, it is pretty much the same representation for both examples. The key idea is to identify a class of symmetry mappings (on a slightly larger outcome space) and to show that these mappings define consistent relationships of equiprobability. I will show this in this section. We will see, however, that this does not help Brown’s argument.
To illustrate the approach, let us start with a simple case: The de Finetti lottery with a single draw. The outcome space is X = ℕ, the set of all possible ticket numbers. We want to represent relationships of equiprobability between sets of tickets. Specifically, we want to find a consistent way to represent a situation where {i} and {j} are equiprobable for any positive integers i and j. We know that we can do this with a finitely additive measure that assigns 0 to every finite set. But there is an alternative approach, based on the idea that we can define relationships of equiprobability by stipulating relationships of invariance. We specify these invariances in terms of a group G of symmetry transformations, or bijections on X. Our intention is that if A and B are subsets of ℕ, and θ(A) = B for some θ ∈ G, then A and B are equiprobable.
In the de Finetti example, one good choice for
G is the set of finite permutations τ on ℕ: permutations that fix all but finitely many elements. It is easy to see that
G is a group. Furthermore, if τ permutes
i and
j, then τ({
i}) = {
j}, so any two singleton sets count as equiprobable. Another possible choice is to take
G as the group of mappings σ
k(x) = x +
k (where
k is a fixed integer), but in order to make
G a group (with inverses), we must enlarge the outcome space to X = ℤ (and later restrict our attention to subsets of ℕ). For any pair
i,
j we can find σ
k such that σ
k(
i) =
j, so once again we have the equiprobability of any two singleton sets. For this choice for
G, we get additional interesting relationships:
Even = {2, 4, 6, ...} and
Odd = {1, 3, 5, ...} are equiprobable.
15In general: let X be any
outcome space, and let
G be any group of bijections on X, which we refer to as
symmetries. A group
G is said to
act on a set X if there is a mapping
such that (σ, (τ,
x)) = (στ,
x) and (1,
x) =
x, for all σ, τ ∈
G and all
x ∈ X. Here,
G is a group of bijections on X and the mapping that defines the group action is just (τ,
x) = τ(
x). Since this is the only type of group action that we consider in this paper, we write σ(
x) in place of (σ,
x) and σ(
E) for {σ(
x)/
x ∈
E}, for any subset
E of
X.
We shall consider various outcome spaces X, with their candidate group
G of symmetries, intending that if
A,
B are subsets of X and θ(
A) =
B for some θ in
G, then
A and
B are equiprobable. But some choices of X and
G lead to paradox. Suppose there is a subset
E =
A ∪
B where
A and
B are disjoint, θ
1(
A) =
E and θ
2(
B) =
E for θ
1, θ
2 in
G. Then
E is “equiprobable” with each of
A,
B and thus ‘twice as probable’ as itself! This problem arises most notoriously in the Banach-Tarski paradox. Happily, it does not arise in the de Finetti lottery, an easy consequence of the simple test for paradoxicality that I state next. This test, developed by Tarski and others, is sufficient for all of the examples considered in this paper. My (abbreviated) presentation is based on Wagon [
9].
In general, a subset
E of X is
G-paradoxical if for positive integers
m,
n there are pairwise disjoint subsets A
1, ..., A
n, B
1, ..., B
m of
E and θ
1, ..., θ
n, σ
1, ..., σ
m ∈
G such that
E = ∪θ
i(A
i) and
E = ∪σ
j(B
j). That is:
E has two disjoint subsets ∪A
i and ∪B
j, each of which may be taken apart and rearranged via symmetry mappings in
G to cover all of
E (Wagon [
9]). This definition is a generalization of the worrisome case just raised in connection with the de Finetti example. The existence of a
G-paradoxical subset implies that
G cannot consistently represent a set of equiprobability relationships among subsets of X. An important theorem of Tarski asserts that the existence or nonexistence of such subsets is equivalent to the nonexistence or existence of a finitely additive measure.
Theorem 5.1 (Tarski; Wagon [9]). The nonexistence of a G-paradoxical decomposition of E is equivalent to the existence of a finitely additive, G-invariant measure μ on (X) (the set of all subsets of X) with μ(E) = 1. A significant and much-studied special case is when X = ℝ
n and
G is any sub-group of
isometries,
i.e., distance-preserving bijections. We have already seen an example of such a group in the de Finetti single-ticket lottery: the set of translations by a fixed integer. This is a group of isometries on the real line ℝ
1: if θ
d(
x) =
x +
d, then the distance between θ
d(
x) and θ
d(
y) is the same as the distance between
x and
y. Two elegant results tell us exactly when a group
G of isometries on ℝ
n generates a
G-paradoxical subset.
16Theorem 5.2 (Wagon [9]). Suppose G is a group of isometries on ℝ
n.
Then the following are equivalent: - (1)
For any E ⊆ ℝn, E ≠ >, there is a finitely additive, G-invariant measure μ on (ℝn) such that μ(E) = 1.
- (2)
No nonempty subset E of ℝn is G-paradoxical.
- (3)
No nonempty subset E of ℝn contains two disjoint subsets A, B such that A = σ(E) and B = τ(E) for σ, τ ∈ G.
Theorem 5.3 (Wagon [9]). Suppose G is a group of bijections (symmetries) on X, and σ, τ ∈ G. Then the following are equivalent: - (1)
Some nonempty subset E of X is such that A = σ(E) and B = τ(E) are disjoint subsets of E.
- (2)
There is some x ∈ X such that whenever w1 and w2 are ‘words’ in σ, τ beginning with σ and τ, respectively, then w1(x) ≠ w2(x).
A ‘word’ in σ,
τ is just a finite string of symbols from {σ, σ
−1, τ, τ
−1} with no trivial pairings (occurrences of σσ
−1, σ
−1σ, τ τ
−1 or ττ
−1). Two examples: τστσ
−1, στ
−1σ. A word thus corresponds to a finite sequence of successive applications of the mappings σ, σ
−1, τ, τ
−1 (with no trivial pairings along the way).
If G is a group of isometries on ℝn, Theorems 5.2 and 5.3 combine for a simple test for the existence of G-paradoxical subsets of ℝn (equivalently: a test of whether G defines a coherent set of equiprobability relationships).
Test for G-paradoxical subsets.
There is a G-paradoxical subset if and only if there are σ, τ ∈ G and some x ∈ ℝn such that w1(x) ≠ w2(x) where w1 and w2 are finitely many successive (non-trivial) applications of σ, σ-1, τ, τ-1 beginning with σ for w1, and τ for w2.
Consider the de Finetti lottery (single ticket) once again. Let
G = {θ
d: θ
d(x) = x +
d,
d ∈ Z}. If we let X = ℝ
1, we can apply the test. Since
G is commutative, it is immediately clear from the test that there is no G-paradoxical subset. Tarski’s Theorem then tells us that there is a finitely additive measure on X with μ(ℕ) = 1.
17 5.2. Application to Examples
We can apply these results to Double Dart Throw and Double Lottery. In both cases, it follows easily that there are no paradoxical sets, and hence that there is a finitely additive probability with most of the features identified in Brown’s argument. We deal with both examples at once by noticing that both of the relevant outcome spaces can be embedded in X = ℝ2.
For both examples, there are two kinds of probabilistic invariance that we want to represent, corresponding to Brown’s two assumptions of Randomness and Symmetry. The relevant group G of symmetries must contain:
Translations: θ(x, y) = (x + a, y + b), where a, b ∈ ℝ.
Reflection over the line x=y: ρ(x, y) = (y, x).
Any finite composition of these two types can always be reduced to a translation or a translation followed by ρ.
18 The same holds true for the inverse mappings. Thus, we may take:
G is a group of isometries on ℝ
2, and we may apply the test for
G-paradoxical subsets of ℝ
2. The application is straightforward: the test shows that there are no
G-paradoxical subsets.
19For
Double Dart Throw, we restrict our attention to subsets of
E = [0, 1] × [0, 1]. The preceding result tells us that, without paradox, we can consider any two subsets of
E related by translation to be equiprobable, and also the two sets of
Figure 1,
S = {(
p,
q)/
p,
q ∈ [0, 1] and
p <
q} and
T = {(
p,
q)/
p,
q ∈ [0, 1] and
p >
q}, as equiprobable. Tarski’s Theorem now ensures that there is a finitely additive
G-invariant measure μ on ℝ
2 with μ(
E) = 1. Clearly, μ(
S) = μ(
T) = ½, and the restriction of μ to
E is the probability measure that we seek. So we have a coherent representation of all symmetries in the example–though with a finitely additive measure, instead of the two-dimensional (countably additive) Lebesgue measure.
For Double Lottery, we again start with ℝ2 and the same group G of isometries, but this time we restrict our attention to subsets of F = ℕ × ℕ. Our result tells us that, without paradox, we can maintain that any two subsets of F related by translation are equiprobable, and also that S = {(p, q)/p, q ∈ ℕ and p < q} and T = {(p, q)/p, q ∈ ℕ and p > q} are equiprobable. Tarski’s Theorem now ensures that there is a finitely additive G-invariant measure η on ℝ2 with η(F) = 1, η(S) = η(T) = ½. The restriction of η to F is the probability measure that we seek. Again, we have a coherent representation of all of the symmetries in the problem – though once again, not with the usual product measure.
Let us summarize the facts about the two examples. Let
Pr* stand for the probability function based on μ [or η, for
Double Lottery], and
Pr for the probability function of
Section 3 [or 4].
| Double dart throw | | Double lottery |
| 1) Pr*(x ∈ E) = 0 for countable E | | 1) Pr*(x ∈ E) = 0 for finite E |
| 2) Pr*(p < q) = ½ | | 2) Pr*(p < q) = ½ |
| 3) Pr*(second < first / first = q) = 0.20 | | 3) Pr*(second < first/ first = q) = 0.21 |
Brown based his argument on three assumptions:
randomness,
independence and
symmetry. In
Section 3, we showed that the Lebesgue measure has the first two properties but that
Pr(
p <
q) is undefined rather than 0. The alternative measure put forward in this section has the first and third properties, gives up
Independence, and has the property that
Pr*(
p <
q) = ½, rather than 0. An analogous story can be told for
Double Lottery and its associated measure. Although the new measures demonstrate the compatibility of Brown’s two symmetry assumptions, they do not vindicate his argument.
A final point: if we abstract away from the finitely additive measure, we can focus on the symmetries and the family of equiprobability relationships as the primary object of interest. These relationships may be regarded as a constraint on any acceptable probability assignment for the scenarios. This point applies even to the measures discussed earlier. In the case of Double Dart Throw, for instance, the two-dimensional Lebesgue measure satisfies this symmetry constraint. S and T are both non-measurable sets, but may still be regarded as equiprobable.
6. Sequential Throws and Non-Conglomerability
The remaining problem is to deal with the sequential versions of Double Dart Throw and Double Lottery, where the value of one dart [ticket] is observed prior to the other value. Actually, there are four separate problems, given that we have two candidate probability measures and two examples. The problem is the same in each case: if we update via conditionalization in the usual way, then we are reasoning to a foregone conclusion. Regardless of which value is observed first, the conditional probability for a higher second value is 1. This seems absurd.
In exactly one of our four situations, there is a technical term for this phenomenon. In the case of Double Lottery where Pr*(p < q) = ½, we have a non-conglomerable measure. After explaining this concept, I argue that there is good reason to reject unrestricted conditionalization if our subjective probability function is a non-conglomerable finitely additive measure. I then argue that this conclusion extends to the other three cases.
The following notion of
weak conglomerability was formulated by de Finetti [
18] and is discussed in Kadane
et al. [
19] and Seidenfeld
et al. [
20]:
- (CNG)
Let < = {hn: n = 1, ...} be an exhaustive partition of a countable space X. Then a probability distribution P is conglomerable for events in an algebra 𝒜 if the following holds for all A ∈ 𝒜:
-
If c1 ≤ P(A/hn) ≤ c2 (n = 1, 2, ...), then c1 ≤ P(A) ≤ c2.
Conglomerability fails if there is an event whose unconditional probability does not fall between the lower and upper bounds of all of the conditional probabilities relative to elements of the partition. That is just what happens in Double Lottery with Pr*. We have Pr*(second < first/first = q) = 0 for q = 1, 2, ..., but Pr*(second < first) = ½.
Failures of conglomerability are problematic. As Kadane
et al. [
19] write, “the door to foregone conclusions is opened whenever
P is not conglomerable”. But non-conglomerability of a probability measure
P is not a decisive reason to reject it. For one thing,
every finitely additive measure on a countable space X is non-conglomerable for some partition (Schervish
et al. [
21]).
In a discussion of possible responses to non-conglomerability, Kadane
et al. consider a variety of options: abandoning Bayesian conditionalization altogether; refusing to collect evidence that will lead to a foregone conclusion; circumscribing the allowable partitions on which one can conditionalize; and finally “proscribing the use of merely finitely additive probabilities altogether” (
Kadane et al. [
19]). They reach no definite conclusion, noting only that each option carries a significant price and that the matter requires further debate.
The common thread in all four options is this: Do not update your probability for A via conditionalization on elements of a partition if that leads to a violation of (CNG). In support of this position, it is worth noting the following two points:
- (1)
The ordinary dynamic Dutch Book argument for conditionalization fails in this setting; and
- (2)
There is a dynamic Dutch Book argument against an update policy that yields a foregone conclusion.
For (1): in general, the Lewis-Teller Dutch Book argument for PE(A) = P(A/E), i.e., for adopting P(A/E) as your new probability for A on learning only E, requires a conditional bet on A given E, a bet on E, and a bet on A that is placed only if and when we learn that E is true. For a guaranteed loss in the case where E is false, the second of these bets must be non-trivial. If P(E) = 0, however, there will be no non-trivial bet on E. That is just what happens in Double Lottery, where E is the proposition first = q for some q = 1, 2, … . This argument can be salvaged, but only if we allow a betting system with countably many bets, one pair for each positive integer.
For (2): at t1, Prt1(second < first) = Pr*(second < first) = ½. But you (and the bookie) know that at t2, you will find out the value of first and update via conditionalization to Prt2(second < first) = Pr*(second < first/first = q) = 0, regardless of the value q. So, at t1, the following bets are acceptable (the second is better than fair):
Pay $1 for a bet that pays [$2 if second < first, $0 otherwise];
After inspecting the first ticket at t2: pay $1.99 for new bet [$2 if first < second, $0 otherwise].
This is equivalent to selling your first bet, which you now regard as worthless, for a penny at t2. The system of bets guarantees a loss of $0.99. All of this is foreseeable at t1.
In short: we have good reason to reject the claim that, in the sequential version of Double Lottery, after learning the value of first, your new probability for second < first must be 0–good reason, provided that we countenance Dutch Book arguments with a finite set of bets. Of course, this argument is unconvincing if you reject dynamic Dutch Book arguments, and it is also unconvincing if you have an expanded notion of Dutch Book arguments allowing for an infinite number of bets. But in these cases, we are left with (respectively) no justification for conditionalization, or conflicting justifications both for and against conditionalization. The argument thus casts serious doubt upon the use of conditionalization on elements of a partition that leads to violations of conglomerability. That is sufficient.
The next step is to extend this reasoning to the case of Double Dart Throw with probability distribution Pr*. We have an analogue to non-conglomerability: Pr*(p < q) = ½, but Pr*(second < first/first = q) = 0 for all q ∈ [0, 1]. The space is not countable, but the problem is exactly the same, and we have exactly the same reasons for rejecting updating via conditionalization. Indeed, the Dutch Book argument against updating to a foregone conclusion still works, while the Dutch Book argument for conditionalization would require an uncountable betting system.
Finally, we have two more cases:
Double Dart Throw and
Double Lottery with the original probability distributions outlined in
Section 2 and
Section 4. In these cases too, we have updating to a foregone conclusion, but the relevant prior probabilities
Pr(
p <
q) and
Pr(
p <
q) are undefined. Without well-defined priors, we cannot offer the same Dutch Book argument against updating to a foregone conclusion. Nevertheless, with a bit of thought, the analogy still works: conditionalization in these two original cases should be rejected, or at least stands in dire need of justification.
We can formulate a modified Dutch Book argument by exploiting a point made briefly at the end of
Section 5: we can accept relationships of equiprobability for both examples, even when we cannot assign a probability. I will focus on the more important case,
Double Dart Throw, with probability distribution
Pr identical to two-dimensional Lebesgue measure. Independently of the fact that
Pr(
p <
q) is undefined, we can express the relationship of equiprobability between
p <
q and
q <
p in terms of a
trade-off between a bet on one proposition and a bet on the other. Specifically, we regard as fair a betting system in which we win
$k if
p <
q and lose
$k if
q <
p; no money changes hands if
p =
q.
22 There are no betting quotients for either proposition, but the system as a whole reflects our judgment that they are equiprobable.
With this type of betting system at our disposal, we can construct a Dutch Book in sequential Double Dart Throw against anyone whose policy is to update probabilities via conditionalization on the value of the first dart. At t1, second < first and first < second are equiprobable. But you (and the bookie) know that at t2, you will learn the value of first and update to Prt2(second < first) = Pr(second < first/first = q) = 0, regardless of the value q. So, at t1, the following bets are acceptable (the second is better than fair):
Win $1 if second < first; lose $1 if first < second.
After inspecting the first ticket at t2: pay $1.99 for new bet [$2 if first < second, $0 otherwise].
As before, this system of bets guarantees a loss of $0.99, so we have a Dutch Book. A similar set-up works for the original version of Double Lottery.
Whether or not the above Dutch Book arguments are fully persuasive, I believe that they establish at least that conditionalization in these cases must not be taken for granted. It is hard to see what the justification could be.
7. Conclusion
The Brown-Freiling
reductio argument of
Section 2 depends crucially on a particular interpretation of symmetry under permutation in the order of the dart throws. In
Section 3, we saw that the argument fails if there is no set priority, because the probability that one dart precedes the other in the well-ordering is undefined. In
Section 6, we saw that the argument fails even if we toss the darts in sequence, because it takes for granted the validity of updating via conditionalization, and as we have seen, there are good reasons for calling conditionalization into question in that scenario.
The argument should nevertheless be of interest to anyone with a philosophical interest in probability, for at least two reasons. First, it signals the need to distinguish among three types of outcome for symmetry-based probabilistic reasoning:
Outright success: the symmetries are consistent (non-paradoxical) and can be incorporated into an adequate probability model (representing all features of the problem).
Intermediate case: the symmetries are consistent, but cannot be represented by an adequate probability model.
Outright paradox: the symmetries themselves lead to inconsistency.
It is important to acknowledge the existence of the intermediate category where symmetries still convey coherent probabilistic information, but cannot be combined with other probabilistic assumptions into a single model. For example, the models of
Section 5 capture the relevant symmetries but fail to incorporate independence.
The second interesting point is that the Brown-Freiling argument motivates the extension of the concept of non-conglomerability to non-countable outcome spaces, and provides a reminder that the principle of updating via conditionalization cannot be taken for granted.