1. Introduction
Symmetry invited itself on several occasions while I was performing psychophysical work on a number of topics, including unpublished work on geometrical illusions, and work on visual short term memory. In the latter, I measured the time to detect the difference between two nearly symmetric patterns. By design, the experiments were probing our sensitivity to asymmetries. They indicated that symmetry violations were detected faster than repetition violations [
1], as already known from the work of Bruce and Morgan [
2]. I also spent a fair amount of time producing symmetric patterns from random textures, trying to generate suggestive shapes that would extend as far as possible from the symmetry axis. [
3]. In assembling strips of texture, I noticed a color effect: color differences between strips were attenuated when strips slightly differing in color were symmetrically juxtaposed [
4], as though the existence of a symmetry axis was forcing the resemblance between the halves on the two sides of the axis. The results on symmetry violations (in the case of shapes) and on the attenuation of color differences in symmetric strips seemed to be pulling in opposite directions. A case study on a patient with brain damage, who became unable to read or write normal text, but could easily read or write text in mirror-inverted form [
5] boosted my interest in possible neuro-anatomical explanations for symmetry perception, and encouraged me to present here a “transparent sheet” model, together with some original data and observations that, up until now, had only been briefly summarized in congress abstracts [
1,
4].
Published theoretical ideas on symmetry perception have also been pulling in divergent directions. There are contributions inspired by gestalt ideas, e.g., [
6,
7], there are filtering models inspired by neurophysiology, e.g., [
8,
9,
10,
11], and proposals on neuro-anatomical implementations, e.g., [
12]. Commenting on the observation that symmetrical patterns are best detected when eye fixation is on the axis of symmetry [
13], Braitenberg [
14] wrote that “the two symmetrical halves of the picture are projected onto symmetrical positions of the right and left brain. (...). Apparently, there are fiber systems in the brain which are able to compare and establish the identity or non-identity of symmetrical points of the visual field. Such fiber systems are of course well known; the 200 million fibers of the corpus callosum and several other commissural bundles may well serve this purpose”.
The detection of bilateral symmetry being of paramount importance in animal life [
15,
16], there may in fact be a multiplicity of systems that operate in parallel towards the same goal, possibly at different resolutions and time scales. It is also often the case that both bottom-up and top-down processes intervene in visual interpretation, and that some consensus may be reached through back and forth negotiations between low level and high level processing units [
17,
18,
19]. While most psychophysical studies on symmetry perception involve stimuli presentations in the 100 ms time scale, my own data or observations were made in situations of free inspection without time limitation.
2. Time to Detect Symmetry Violations
In order to measure the amount of information that is normally extracted from an image, Nicolas Brunel and I developed an experimental approach which is derived from the well-known “spot-the-error” game. In this game, two slightly different images are presented side by side. The player has to find out the differences. He/she moves the eyes freely from one image to the other. During a saccade from one image to the other, the trace in memory of the first image may not be detailed enough to allow the player to spot a difference with the second image although it may stand just in front of his eyes. Thus, finding the differences may be tedious, and the time taken to find them is an indirect measure of the level of detail at which visual memory is maintained over a saccade. The game could be rather more difficult when the left and right images are presented in a mirror symmetric way. Thus, in a visual games book by Agostini [
20] there are two realistic drawings of a complex natural scene and each image expands over a whole page of the book. A conscious effort seems to be required to match the remote symmetric parts of the two images. Whether the problem has to do with symmetry
per se, or with distance is unclear.
Brunel and I asked subjects to compare abstract random patterns formed by square lattices of black or white quadrangles (see
Figure 1). The most interesting results were obtained with an experimental protocol in which the two images to be compared were nearly identical in half the cases, and differed at a single position in the other cases. When the images have low complexity, a left image may be entirely memorized and transferred without loss during a saccade to the right, so the judgment of identity, or the detection of a difference can be made in one shot. In this case the decision times are expected to be nearly equal for the two conditions. When the two images are rather complex, they must be scanned. When a difference is detected, the answer is clear, and visual scanning terminates. If not, scanning must be completed to allow an identity judgment to be made with some confidence.
Clear-cut results were found [
21]. With low complexity images, composed of 1 to 9 elementary quadrangles, both the error-rates and the reaction times were nearly equal in the two conditions. However, at higher complexities (4 × 4 or more complex images), the reaction times started to be larger in the identity condition (top left panel in
Figure 2). The errors, mostly false negative ones (making a “no difference” response when there was one) also started to rise when 4 × 4 images were compared. The insensitivity to a difference, it was said [
22], can be taken as an example of the striking phenomenon of “change blindness” (e.g., [
23]).
Brunel and I proposed that there was some limiting visual capacity for black and white shapes, somewhere in between the 3 × 3 and the 4 × 4 images. We proposed 12 ± 3 bits as the amount of visual information captured on an image that survives a saccade. The result was extended to images with colored quadrangles. There were four colors in the stimuli (red, yellow, blue, and green), and the same 12 bits boundary was found [
24]. While a black or white quadrangle corresponds to one bit, a quadrangle having one among four colors corresponds to two bits of information. Then, our result indicated that comparing side by side matrix patterns formed of eight elementary colored elements takes about the same time as comparing matrix patterns composed of 16 black or white elements. It should be said however that there was a large inter subject variability in the reactions to colored patterns. Once we chose to plot the subject-averaged reaction times as a function of the number of bits rather than the number of elements in the pattern, the experimental data took place on exactly the same curves (top right panel in
Figure 2). When blocks of capital letters were compared, the split between same and different responses occurred above 12 bits, it was closer to 20 bits (five letters, under our conditions, bottom panel in
Figure 2). Presumably, the letters are encoded in a robust way and survive better than shapes to a saccade.
It was tempting to extend these experiments to symmetry perception. Data were collected on 3 × 3, 4 × 4 and 5 × 5 pairs of images, symmetrically presented with or without separation (right side of
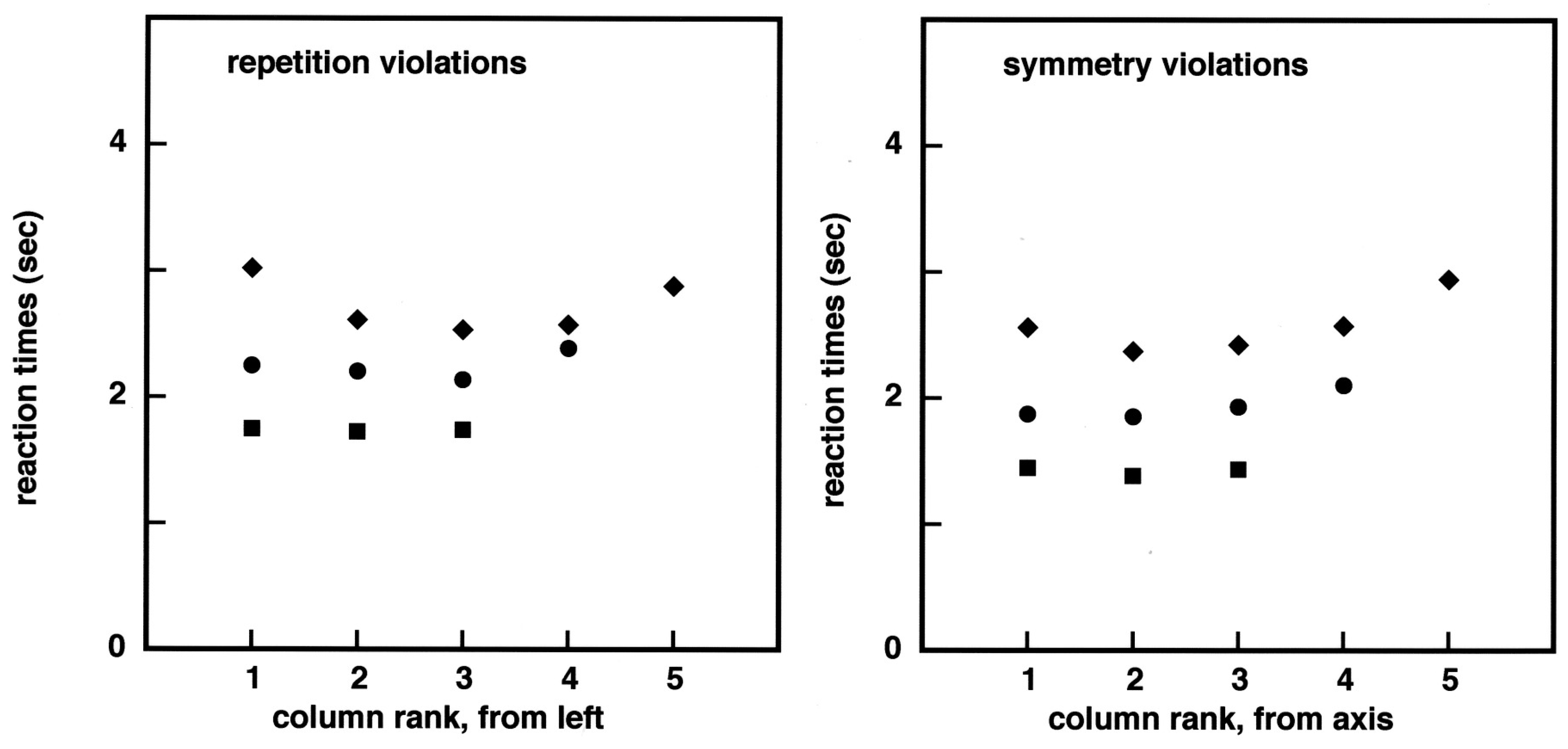
Figure 1). The divergence between the ‘same’ and the ‘different’ reaction times as a function of image complexity is similar to that observed in the case of repetition, except that it might start at 9 bits or earlier in the case of symmetry, but this feature may not be statistically significant. Since there is much interest in how symmetry detection succeeds as a function of the distance to the symmetry axis [
25], I plotted in
Figure 3 the reaction times as a function of column position for both the previous repetition experiments, and the new symmetry experiments. Error rate determinations are less precise, due to the paucity of errors, but in rough agreement with the reaction time data. Reaction times are smaller in the case of the symmetry experiments, but this will become much more explicit in the experiments reported next (in
Figure 4).
The dominant feature in
Figure 3 is a stratification of the reaction times as a function of image complexity. There is also a distance to the symmetry axis effect, but mainly for 5 × 5 images. This pattern of results may be surprising in the field of symmetry perception, but it is in line with our previous work, showing a 50 to 60 ms increase in RTs per binary element in the images. Furthermore, the fact that reaction times are smaller, for columns 2–4 than they are for both column 1 and column 5, in the case of 5 × 5 images is in agreement with a mechanism of visual capture of information by areas of about 9–1 2 elements.
In order to go further into the analysis of the data, I looked into reaction time
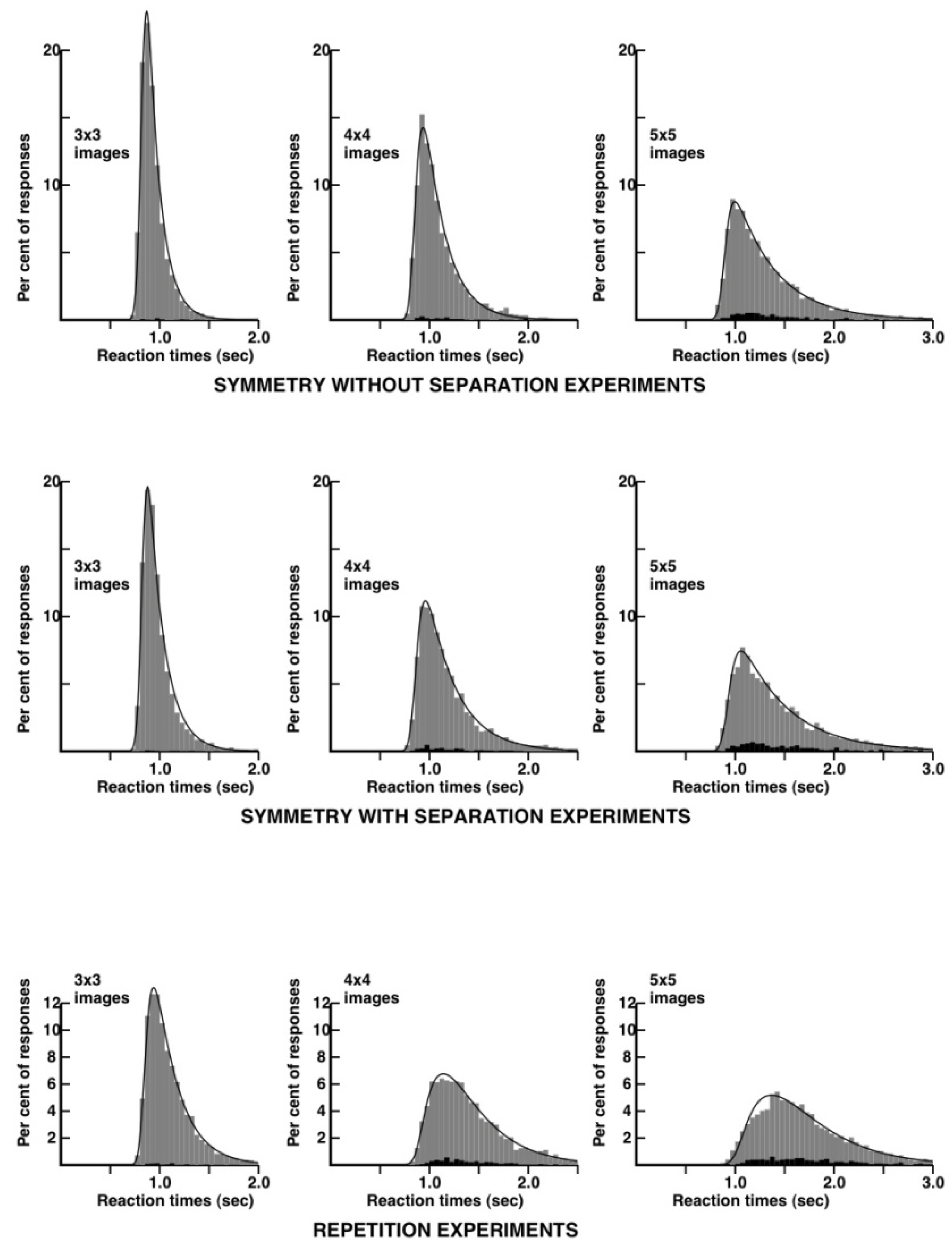
distributions. I performed, as a subject, extensive experiments on repetition violations and symmetry violations and in this case, both with separated and non-separated images. I alternated several times between 20 to 30 mn experimental runs on each of the three conditions. All the reaction time distributions are shown in
Figure 4.
Here, we see a remarkable difference between the repetition and the symmetry without separation conditions. The reaction time distributions are much narrower in the case of the symmetry condition. The distribution for 3 × 3 patterns can be modeled, in the case of symmetry, by a very simple kinetic scheme, involving a lag and an exponential decay widened by a gaussian (an “ex-gaussian” in RT distribution terminology). The corresponding distribution for the repetition condition requires one more kinetic step, following the principles proposed in [
26] and explained in more detail in the
Appendix. In the case of 5 × 5 patterns, the reaction time distribution is, in the symmetry condition, quite close to what it is for 3 × 3 patterns in the repetition condition. The reaction time distribution for 5 × 5 patterns is quite wide in the repetition condition. I would have expected some widening of the RT distributions in the symmetry condition, reflecting occasional mental rotations to match the external borders of the 5 × 5 patterns, but there is no evidence for such a step. In contradistinction, mental flipping requiring about 3/10th of a second can be detected in memory experiments with images of opposite polarity of contrast [
27].
As a provisional conclusion, both repetition and symmetry violations seem to be detected through the comparisons of patches of about 9–12 bits of information. Reaction times and error-rates would be at their lowest close to the symmetry axis, but at the centre of the patches, thus on the second column in the case of symmetric patterns with five columns on each side. The most striking difference between the repetition and the symmetry experiments is in the reaction times distributions, which are much narrower in the case of symmetry, a feature which I will try to explain in the Discussion.
3. A Color Equalization Effect
There are too often conspicuous differences in hue between two reproductions in color of a same picture (e.g., photographs derived from a same negative but processed in different baths, or copies of a same numerical document on two different printers). Recently, in assembling in a mirror-symmetric way strips from different photographs of a same colored texture, I inadvertently mixed strips differing in hues. I became aware of the incongruity much later, when I made a count of the strips taken from different photographs. I then explored the insensitivity to hue inequality by preparing computer generated colored textures in which the color components were varied in a controlled way. Three pictures were selected and presented in a poster at the 31st ECVP congress [
4].
These pictures used the strips shown in
Figure 5, except the bottom right strips. There were three pairs of strips representing exactly the same patterns, but with different colors. Within a pair, the color components were pulled apart by a small amount in opposite directions, thus they were pulled apart along a red-green axis for the top left panels, along a cyan-magenta axis for the top right panels, and along a red-blue axis for the bottom left panels. The two panels of each pair were then assembled as triptychs, with the mirror-image of one panel in the centre, and a copy of the other panel on each side. There were therefore two local bilateral symmetry axes in each panel (
Figure 6). The differences in hues along the two symmetry axes are less salient than in the case of the side-by-side presentation of
Figure 5. About 25 out of the 30 congress participants who examined the poster and wished to discuss it with the author were definitely sensitive to the equalization effect, at least with one of the three pictures (displayed at a 19 cm × 25 cm size). The equalization effect was rather less salient in grey-level variants that were also displayed in the poster. Among the few resistant people who did not see any effect there were high level specialists with sharp vision. In my case, having examined with attention many such images, and being sensitive to the equalization effect, I feel that, as with some other illusory phenomena, the effect might build up with repeated viewing.
My interpretation of the phenomenon, as presented in [
4], was in terms of a “transparent sheet” model (see the next section). However, one of the scientists who attended the poster, Frederic Boy—of the School of Psychology, University of Cardiff—made a counterproposal: He suggested that colors were apparently equalized on the two sides of the symmetry axis because the two sides would fall into the receptive fields of the same neurons, and a single color may thus be bound to a receptive field that crossed the symmetry axis. This was reasonable enough, and it made a link with filtering models of symmetry perception. In order to test Boy’s proposal, I designed a colored texture panel such that the colors on the left and right borders were exactly matched (bottom right panels in
Figure 5). When panels differing in hues are laid down side by side the color equalization effect occurs, it seems, with the same magnitude, as it does in the symmetrical case (
Figure 7). Therefore, symmetry would be an easy way to produce the effect, but it is not essential. Nevertheless, there is an important message in this study—that repetition controls in symmetry experiments should take into account the potentially disruptive effects of unmatched borders.
4. A Conjecture on Symmetry Judgments
It has been known for a long time that a main difficulty encountered by children in the acquisition of the written alphabet was in making the distinction between pairs of letters that are related by mirror symmetry, such as a “b” and a “d”. Adults too encounter difficulty segregating an area containing, for instance, the capital letter R at all orientations from a nested area containing their mirror symmetric pseudo letters. This type of observation was a key argument in Julesz promotion of his texton theory of texture perception [
28]. Human’s general difficulty in distinguishing a shape from its mirror image led to the proposal (see e.g., [
29]) that when the brain represents a shape, it constructs automatically the mirror-image representation of that shape. This is what I call a “folded sheet” model because it is a reminder of Rorschach method for producing symmetrical shapes from inkblots squeezed between the two halves of a folded sheet. The two brain hemispheres could be recruited for a similar purpose, as Braitenberg reminds us [
14]. However, if we start thinking in these terms, we would also wish to use the two brain hemispheres for image comparison in stereo vision, but with the images in the same orientation. Note also that symmetry perception does not require binocularity.
In a remarkable case study, Pflugshaupt
et al. [
5] described a patient who, after cerebral damage produced by hypoxia could not read normal text or write in the standard way, but could read text reflected in a mirror, and write in a mirror-inverted way. The authors interpreted their data in terms of a folded sheet model: the brain, under normal conditions would construct both the normal representation of a visual stimulus, and its mirror-inverted form. Following brain damage in some specific site, the standard representation would be unavailable, and the brain would use the mirror-image representation.
Being influenced by the observations on the attenuation of color differences in symmetric patterns, I thought of an alternative possibility. I conjectured that somewhere in the brain, patterns would be represented like images printed on a transparent sheet: depending on the side of the sheet you are looking at, you see this pattern in its standard form, or in its mirror-inverted form. Such a model, I thought incorrectly, could account for the color equalization effect: imagine that each eye captures one side of a symmetric pattern, and paints it on its corresponding side of the transparent sheet, then the color on one side should be perceived as somewhat blended with the color painted on the other side.
Furthermore, the model could nicely explain the observations on mirror-inverted writing in some brain damaged patients. Consider again the difficulty encountered by young children when they have to learn that a “b” and a “d” are not the same letter. Assume there is, at some stage of visual processing, a common representation of the two letters, and assume that two bundles of neurons have access to this representation from two sides, one bundle connecting the representation, say, to the left hemisphere, and the other connecting it to the right hemisphere. Then, through learning, a child would acquire a mechanism that inhibits the functioning of one of the two bundles, at least during reading and writing. If, due to brain damage, the other bundle cannot operate, then inhibition can be removed, and the person would become able to read and write in a mirror-inverted way.
However, a model involving simultaneous dual representations, would do as well in explaining mirror-inverted writing in the brain damage patients, it might simply require additional neuronal circuitry (or not). So, what did we gain other than elegance, in presenting a new metaphorical explanation? In agreement with Jan Koenderink [
30], I feel that there is virtue in pursuing theoretical ideas for their own sake, not trying to look for an immediate quantitative fit with the data. However, it also turns out, as I will attempt to show in the Discussion, that quite unexpectedly, both the transparent sheet model and the color equalization effect may throw some light on my first data set—that on reaction times in short term memory experiments.
5. Discussion
The work presented here was, at the beginning, an extension of work on short term visual memory experiments, so it used patterns, tools and concepts that were developed in the memory experiments, and are unusual in the field of symmetry perception. I measured the time to detect a single symmetry violation in patterns of moderate complexities (using at most 25 quadrangles in each image). In the symmetry perception field, random-dot patterns are often used, with sometimes as many as 300,000 dots [
25]. Furthermore, the focus is more on the symmetry
versus random noise ratio, than on single symmetry violations [
31,
32,
33]. What happens when the two images forming a pair match each other, but one image is a distorted version of the other? The topic is actively discussed in the field of symmetry perception [
34,
35]. Reaction times remain constant, in repetition experiments, when moderate uncorrelated distortions are introduced in the images to be compared [
21], but I have no comparable data on symmetric pairs.
Ideally, we always wish to set up experiments in which there are different conditions, and comparisons can be made between situations in which all parameters, except one, are identical. Unfortunately, it is in most cases impossible to change voluntarily one feature, without changing at the same time, unknowingly, some other feature. For instance, in the case of black and white
versus colored patterns (
Figure 2, top right panel), when the black or white elements are replaced with colored ones taking four different color values, many subjects expect to perform better, due to color saliency. Actually, their results expressed in seconds/quadrangle worsen (for a link with work on symmetry, compare with [
36]). The color and the black and white data agree only when they are expressed in seconds/bit. Actually, when colors are added to a pattern, there is a side effect: previously connected black or white areas that are important for shape perception become disrupted into smaller colored pieces. As shown earlier, pixellization does not facilitate repetition judgments [
21].
In the repetition comparisons, there is a potential artifact that I noticed in my work on memory: A shape is, so to speak, contaminated by the neighboring shapes. The perception of the left column in the right image is influenced by the patterns (and especially the black/white balance) of the neighboring right column of the left image. Using another terminology, I would say that the perceptual groupings in one image are influenced by the features that are present on the closest border of the other image. When two identical images are presented in the repetition mode, several groupings may be tried. They would compete, as in a Stroop effect, thus lengthening the reaction times. Furthermore, when repeated images are presented without spacing, artificial unrepeated patterns are created at the junction between the two images. This generates an experimental bias against repetition, and may again cause an exaggerated evaluation of the advantage of mirror symmetry in reaction time studies. In contradistinction, the equivalence between the two sides of the symmetry axis, in the symmetric presentations could force the spread of the same perceptual groupings in the two images of a symmetric pair. Therefore, a low level filtering mechanism that would impose a common fate on the two sides of the axis (and presumably contribute to the color equalization effect) would also play a role at a higher level, by canalizing the perceptual groupings on the two sides of the symmetry axis.
The finding to which I attach the greatest significance in this article is the narrowing of the reaction times distributions in the case of the symmetry comparisons. An intuitive way to analyze RT distributions is to use the kind of models commonly used in chemical and enzyme kinetics. There, a “decision” (make a product, after an enzyme-substrate interaction, or abort) is made after following a number of more or less reversible steps on a reaction pathway. Each elementary step follows a law of exponential decay, see e.g., [
37] and the
Appendix. This type of model is quite easy to handle, but is very unusual in psychopyhsics. In order to transpose such models to my memory experiments, I needed to add two ingredients: a lag, and a widening (through a convolution by a gaussian). This approach gives me satisfaction as it provides intuitive, rather coherent interpretations of the data. The experimental curves of
Figure 4 can be analyzed with the help of a quantitative model involving four adjustable parameters (see
Table 1).
The first parameter, the lag, includes the time to perform the motor response after the brain has determined whether or not there is a repetition or a symmetry violation in the stimulus. Note that this part of the RT distribution mostly reflects the latest events in the sequence of steps that lead to the motor response (a left or right key press on the computer mouse). The lag is expected to grow somewhat with image complexity, but here the effect is small in the case of repetition, and absent in the case of symmetry. I put this, on account of my extensive training, as a subject.
The gaussian widening factor has a tendency to grow with stimulus complexity in the case of repetition comparisons, but shows little variation in the symmetry comparisons. Its variations here in the case of the repetition experiments are taken as reflecting sources of heterogeneity that are absent in the symmetry experiments. It turns out (perhaps due to over training) that I had rather small differences in average RTs between the “same” and the ‘different’ responses at all image complexities in the symmetry, but not the repetition experiments.
We can focus now on the two really important parameters, the k1’s and k2’s that hopefully, reflect the kinetics of the mental process. Two parameters are sufficient to account for the RT distributions (with the lag and the gaussian factor playing a cosmetic role). There are two consecutive irreversible steps, with a slow component, k1, and a faster component, k2. The theoretical RT distributions are unchanged if k1 and k2 are permuted, so one cannot say whether the slow component precedes or follows the fast one. I conjecture that k1 mostly reflects the construction of the representation of the stimuli, and k2 mostly reflects the ’identity’ or the ’violation’ decision that is taken, once the representation is available.
The variations in k1 can now be interpreted in the following way: at low image complexities (3 × 3 and 4 × 4 images) the stimuli are represented in the brain more rapidly in the case of symmetry than in the case of repetition. This is no longer true at higher image complexities. The variations in k2 can now be interpreted as follows: There is a standard kinetic constant of 20/s to make a “same” or a “different” judgment. The average decision time would be the reciprocal of k1, that is 50 ms. This would account for all six symmetry experiments, and for the 3 × 3 repetition experiments. The k1 values would be abnormally low in the 4 × 4 and 5 × 5 repetition experiments, perhaps due to the disrupting border effect discussed above.
If this analysis is correct, perceptual decisions about repetition or symmetry violations take about the same basic time: 50 ms. Decisions concerning repetition violations with 4 × 4 or 5 × 5 stimuli would be slowed down due to confusing influences at the borders of the images. The major advantage of symmetry appears to be where it was not expected: in the construction of a representation of the stimuli. This advantage is reflected in the ratio of the k1’s for repetition versus symmetry. The ratio is close to 1.75 with 3 × 3 and 4 × 4 images. The advantage might turn into a disadvantage with more complex images, as the k1’s ratio equals 0.9 with 5 × 5 images.
A most striking aspect of the kinetic analysis in
Table 1 is the
absence of a feature that might have been present: There is absolutely no room for an additional ‘mental rotation’ step in the symmetry data. If such a step existed, it could have been reflected in an increased lag, an increased gaussian widening, or an additional kinetic constant k3. Quite to the contrary, none of the four parameters gives an advantage to repetition comparisons. This raises the possibility that the representations of a pair of mirror-images are constructed faster than the representation of a single image. This is not an absurd idea, in the field of memory: two different views of the same object allow one to recognize the object better than a single view. The two views are pointing towards the same engram of the object, allowing it to be retrieved with greater facility. In my opinion, the kinetic data in
Table 1 could indicate that, at least with 3 × 3 and 4 × 4 patterns, there is no mental rotation involved in the symmetry judgments, so, at least metaphorically, there would be no room for a folded sheet model, and we would be closer to a transparent sheet situation in which two mirror images would be two views of basically the same pattern. Thus, if my interpretation is correct, the reaction times distributions are narrower in the case of symmetric patterns, not because decisions occur faster, but because
the construction of the representation would go faster, in the case of symmetry. This conjecture might be tested in the future by exploring situations in which complementary information are sent simultaneously [
38] or asynchronously [
39,
40] to the two eyes, and studying the reaction time distributions as a function of the presentation delays.