Reduction of Image Complexity Explains Aesthetic Preference for Symmetry
Abstract
:1. Introduction
2. Method
2.1. Stimuli
2.2. Procedure
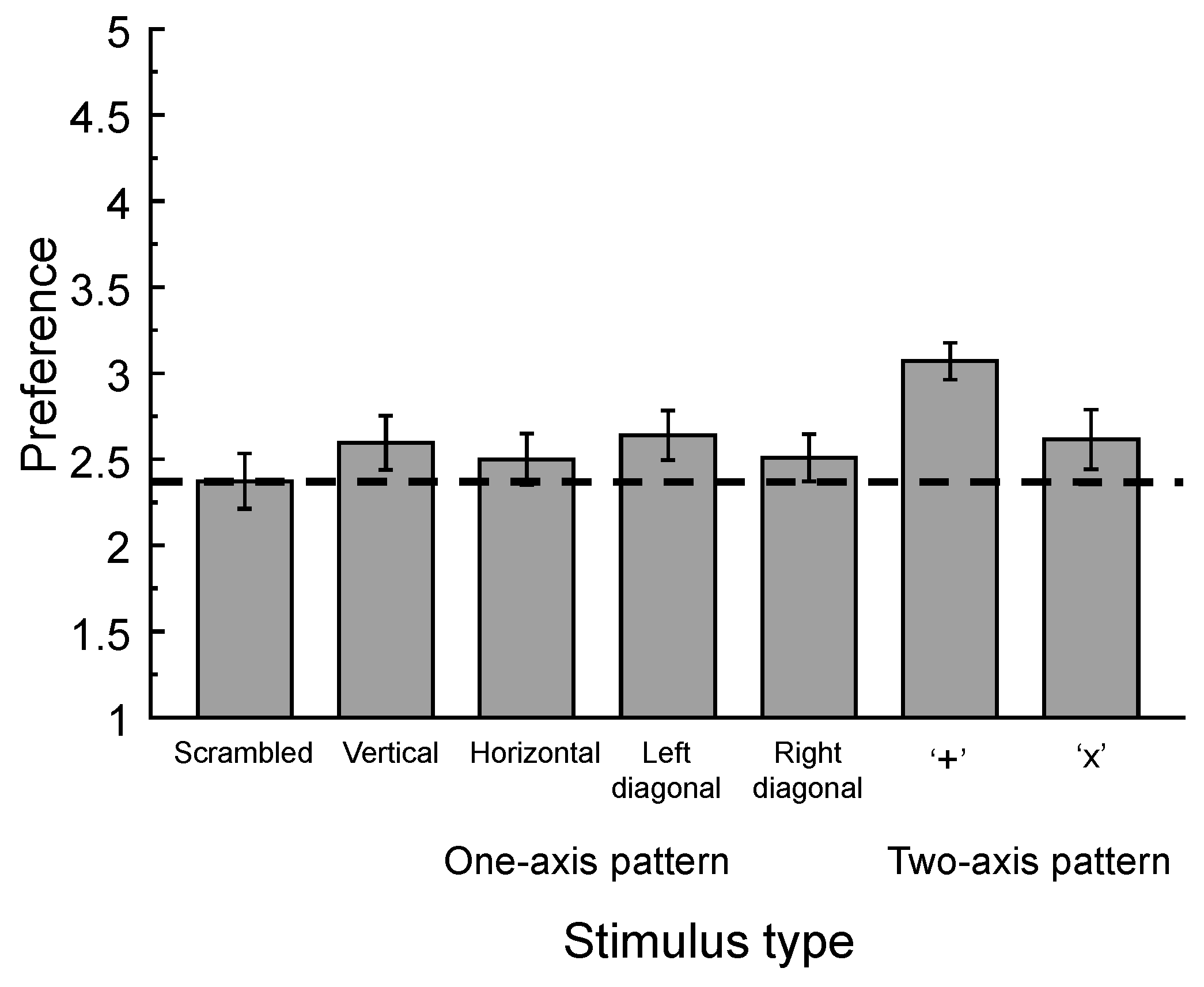
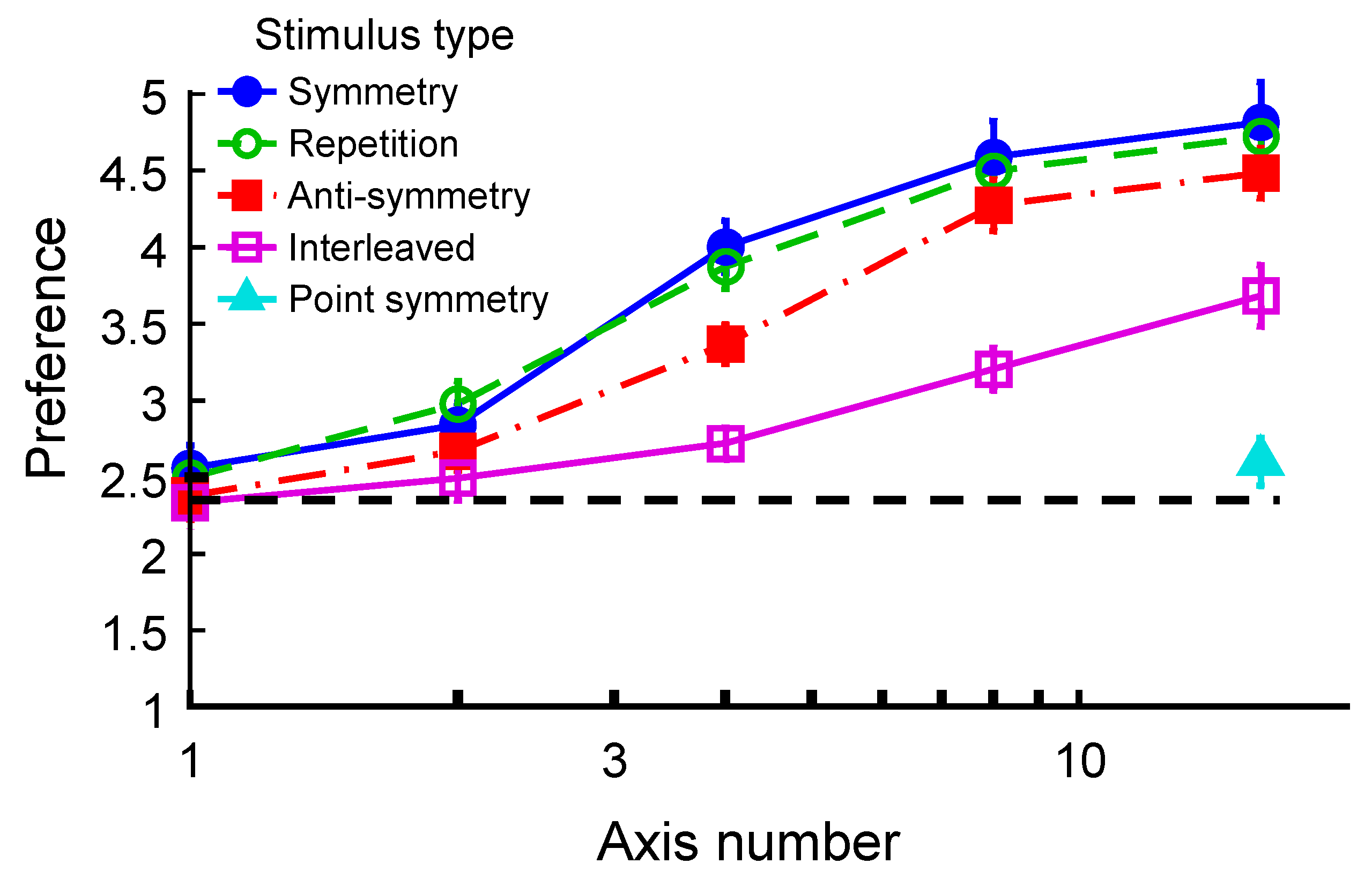
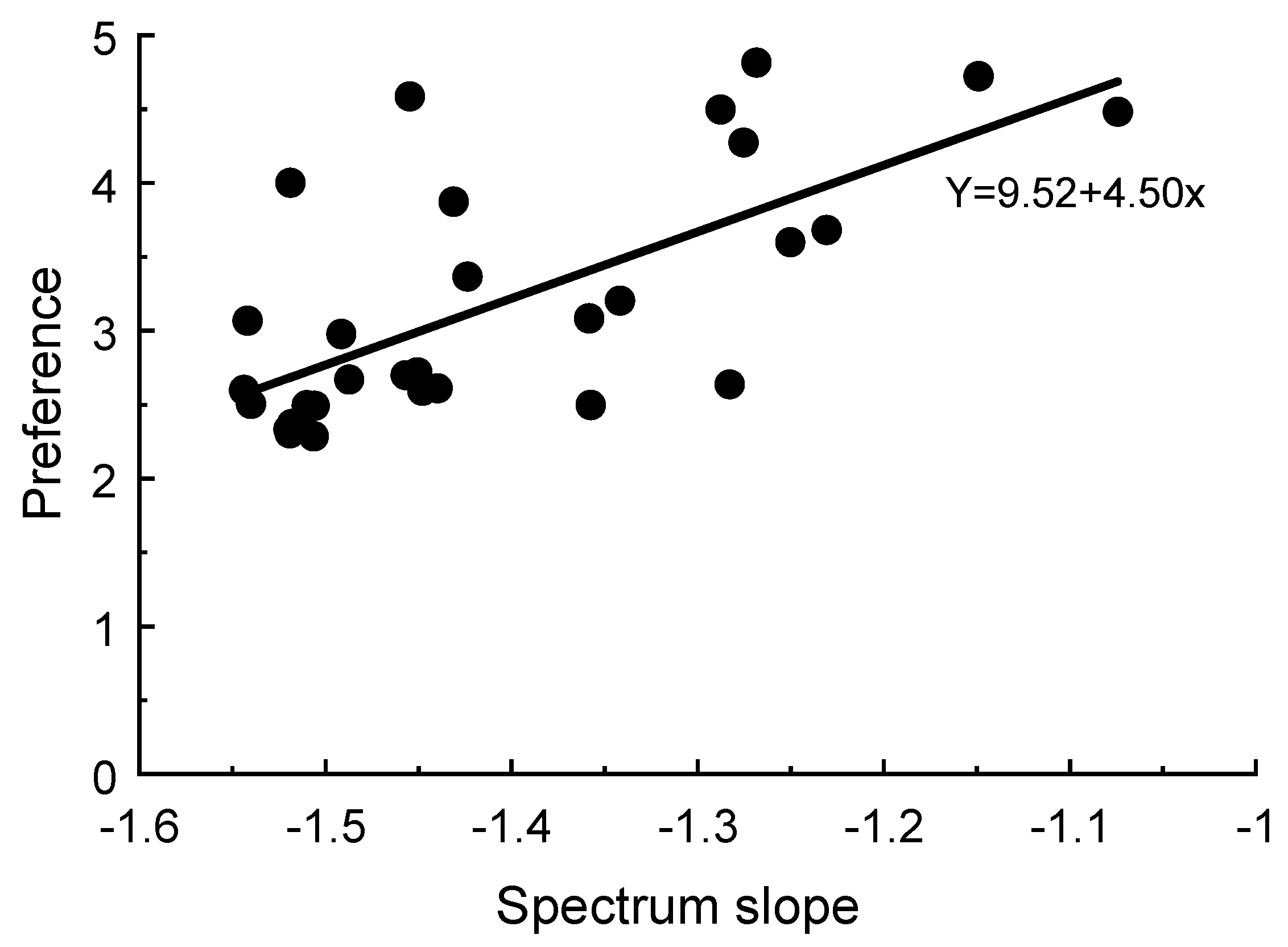
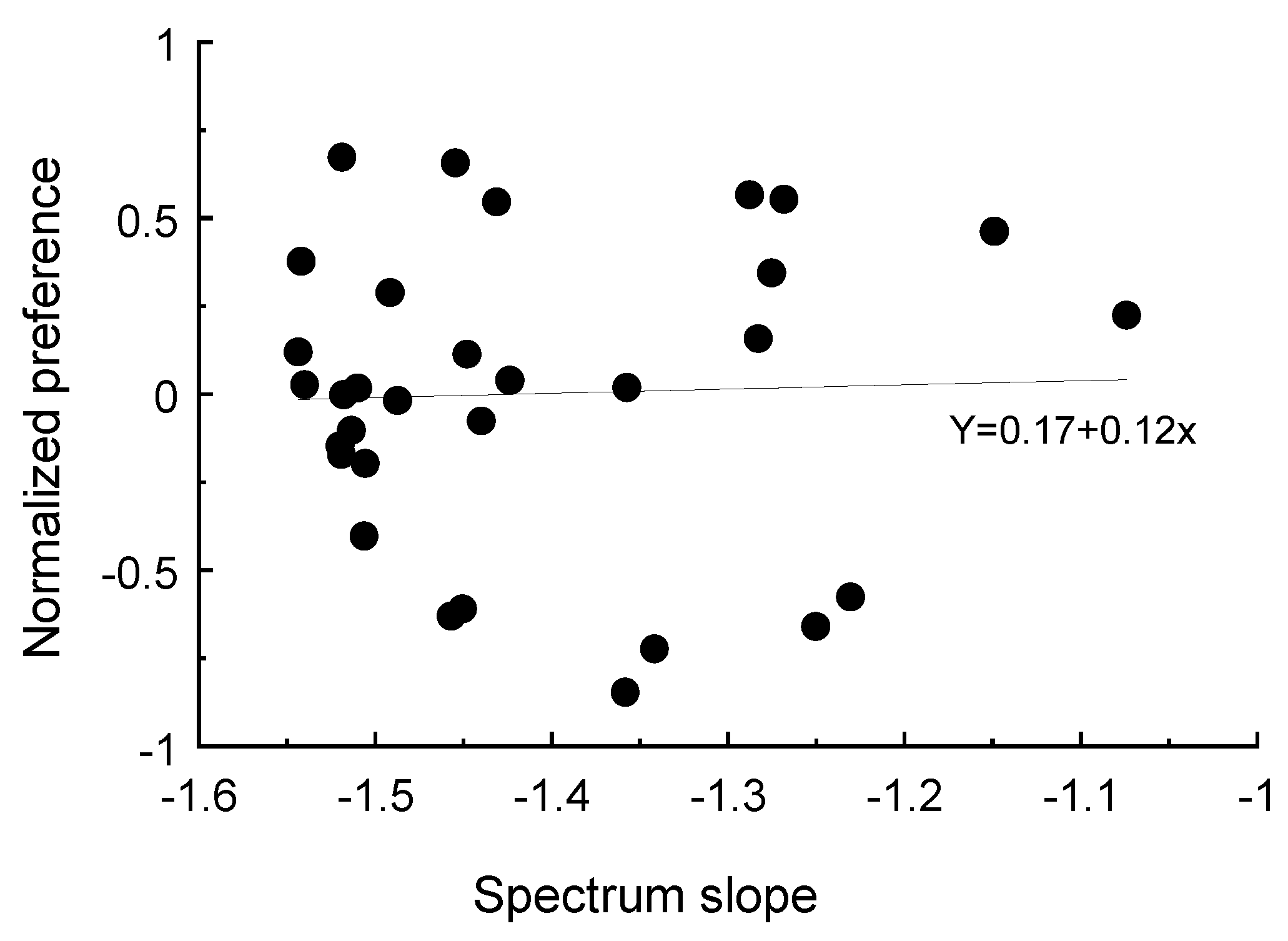
3. Result
4. Discussion
4.1. Comparison between Preference and Detection Performance
4.2. Theoretic Implications
5. Conclusion
Acknowledgement
References
- Morgan, M.H. Vitruvius: The Ten Books on Architecture, Translated by Morris Hicky Morgan; Harvard University Press: Cambridge, MA, USA, 1914. [Google Scholar]
- Ching, F.D.K. Architecture: Form, Space, and Order, 3rd ed.; Wiley: New York, NY, USA, 2007. [Google Scholar]
- van Tonder, G.J.; Lyons, M.J.; Ejima, Y. Perception psychology: Visual structure of a Japanese Zen Garden. Nature 2002, 419, 359–360. [Google Scholar] [CrossRef] [PubMed]
- Rhodes, G. The evolutionary psychology of facial beauty. Annu. Rev. Psychol. 2006, 57, 199–226. [Google Scholar] [CrossRef] [PubMed]
- Naini, F.B.; Gill, D.S. Facial aesthetics: 1. Concepts and canons. Dent. Update 2008, 35, 102–107. [Google Scholar] [CrossRef] [PubMed]
- Tovee, M.J.; Tasker, K.; Benson, P.J. Is symmetry a visual cue to attractiveness in the human female body? Evol. Hum. Behav. 2000, 21, 191–200. [Google Scholar] [CrossRef]
- Dissanayake, E. What Is Art for? University of Washington Press: Seattle, WA, USA, 1988. [Google Scholar]
- Pinker, S. How the Mind Works; W. W. Norton: New York, NY, USA, 1997. [Google Scholar]
- Tooby, J.; Cosmides, L. Does beauty build adapted minds? Toward an evolutionary theory of aesthetics, fiction and the arts. Substance 2001, 94/95, 6–27. [Google Scholar]
- Tyler, C.W. Theoretical issues in symmetry perception. Spat. Vis. 1994, 8, 383–391. [Google Scholar] [CrossRef] [PubMed]
- Moller, A.P. Female swallow preference for symmetrical male sexual ornaments. Nature 1992, 357, 238–240. [Google Scholar] [CrossRef] [PubMed]
- Brookes, M.; Pomiankowski, A. Symmetry is in the eye of the beholder. Trends Ecol. Evol. 1994, 9, 201–202. [Google Scholar] [CrossRef]
- Watson, P.J.; Thornhill, R. Fluctuating asymmetry and sexual selection. Trends Ecol. Evol. 1994, 9, 21–25. [Google Scholar] [CrossRef]
- Moller, A.P.; Thornhill, R. Bilateral symmetry and sexual selection: A meta-analysis. Am. Nat. 1998, 15, 174–192. [Google Scholar]
- Swaddle, J.P.; Cuthill, I.C. Preference for symmetric males by female zebra finches. Nature 1994, 367, 165–166. [Google Scholar] [CrossRef]
- Perrett, D.I.; Burt, D.M.; Penton-Voak, I.S.; Lee, K.J.; Rowland, D.A.; Edwards, R. Symmetry and human facial attractiveness. Evol. Hum. Behav. 1999, 20, 295–307. [Google Scholar] [CrossRef]
- Enquist, M.; Arak, A. Symmetry, beauty and evolution. Nature 1994, 372, 169–172. [Google Scholar] [CrossRef] [PubMed]
- Johnston, R.A. Female preference for symmetrical males as a by-product of selection for mate recognition. Nature 1994, 372, 172–175. [Google Scholar] [CrossRef] [PubMed]
- Day, H.I. Evaluations of subjective. Psychophys complexity, pleasingness and interestingness for a series of random polygons varying in complexity. Atten. Percept. Psychophys. 1967, 2, 281–286. [Google Scholar] [CrossRef]
- Vitz, P.C. Preference for different amounts of visual complexity. Behav. Sci. 1966, 11, 105–114. [Google Scholar] [CrossRef]
- Kaplan, R.; Kaplan, S. The Experience of Nature: A Psychological Perspective; Cambridge University Press: Cambridge, MA, USA, 1989. [Google Scholar]
- Reber, R.; Schwarz, N.; Winkielman, P. Processing fluency and aesthetic pleasure: Is beauty in the perceiver’s processing experience? Pers. Soc. Psychol. Rev. 2004, 8, 364–382. [Google Scholar] [CrossRef]
- Tolhurst, D.J.; Tadmor, Y.; Chao, T. The amplitude spectra of natural images. Ophthalmic Physiol. Opt. 1992, 12, 229–232. [Google Scholar] [CrossRef]
- Billock, V.A. Neural acclimation to 1/f spatial frequency spectra in natural images transduced by the human visual system. Phys. D 2001, 137, 379–391. [Google Scholar] [CrossRef]
- Field, D.J. Scale-Invariance and Self-Similar “Wavelet” Transforms: An Analysis of Natural Scenes and Mammalian Visual Systems. In Wavelets, Fractals and Fourier Transforms; Farge, M., Hunt, J., Vassilicos, J.C., Eds.; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Graham, D.J.; Field, D.J. Statistical regularities of art images and natural scenes: Spectra, sparseness and nonlinearities. Spat. Vis. 2007, 21, 149–164. [Google Scholar] [CrossRef]
- Graham, D.J.; Field, D.J. Variations in intensity statistics for representational and abstract art, and for art from the Eastern and Western hemispheres. Perception 2008, 37, 1341–1352. [Google Scholar] [CrossRef] [PubMed]
- Wenderoth, P. The salience of vertical symmetry. Perception 1994, 23, 221–236. [Google Scholar] [CrossRef] [PubMed]
- Barlow, H.B.; Reeves, B.C. The versatility and absolute efficiency of detecting mirror symmetry in random dot displays. Vis. Res. 1979, 19, 783–793. [Google Scholar] [CrossRef]
- Chen, C.C.; Tyler, C.W. Symmetry: Modeling the effects of masking noise, axial cueing and salience. PLoS ONE 2010, 5. [Google Scholar] [CrossRef]
- Wagemans, J. Detection of visual symmetries. Spat. Vis. 1995, 9, 9–32. [Google Scholar] [CrossRef]
- Palmer, S.E.; Hemenway, K. Orientation and symmetry: Effects of multiple, rotational, and near symmetries. J. Exp. Psychol. Hum. Percept. Perform. 1978, 4, 691–702. [Google Scholar] [CrossRef] [PubMed]
- Wagemans, J.; van Gool, L.; Swinnen, V.; van Horebeek, J. Higher-order structure in regularity detection. Vis. Res. 1993, 33, 1067–1088. [Google Scholar] [CrossRef]
- Treder, M.S.; van der Vloed, G.; van der Helm, P.A. Interactions between constituent single symmetries in multiple symmetry. Atten. Percept. Psychophys. 2011, 73, 1487–1502. [Google Scholar] [CrossRef]
- Corballis, M.C.; Roldan, C.E. On the perception of symmetrical and repeated patterns. Percept. Psychophys. 1974, 16, 136–142. [Google Scholar] [CrossRef]
- Tyler, C.W.; Hardage, L. Mirror Symmetry Detection: Predominance of Second Order Pattern Processing Throughout the Visual Field. In Human Symmetry Perception and its Computational Analysis; Tyler, C.W., Ed.; VSP: Utrecht, The Netherlands, 1996; pp. 157–171. [Google Scholar]
- Saarinen, J.; Levi, D.M. Perception of mirror symmetry reveals long-range interactions between orientation-selective cortical filters. Neuroreport 2000, 11, 2133–2138. [Google Scholar] [CrossRef]
- Van der Zwan, R.; Badcock, D.R.; Parkin, B. Global form perception: Interactions between luminance and texture information. Aust. N. Z. J. Ophthalmol. 1999, 27, 268–270. [Google Scholar] [CrossRef] [PubMed]
- Mancini, S.; Sally, S.L.; Gurnsey, R. Detection of symmetry and anti-symmetry. Vis. Res. 2005, 45, 2145–2160. [Google Scholar] [CrossRef] [PubMed]
- Berlyne, D.E. Novelty, complexity, and hedonic value. Percept. Psychophys. 1970, 8, 279–286. [Google Scholar] [CrossRef]
- Park, J.; Shimojo, E.; Shimojo, S. Roles of familiarity and novelty in visual preference judgments are segregated across object categories. Proc. Natl. Acad. Sci. USA 2010, 107, 14552–14555. [Google Scholar] [CrossRef] [PubMed]
- Berlyne, D.E. Conflict, Arousal and Curiosity; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Krupinski, E.; Locher, P. Skin conductance and aesthetic evaluative responses to nonrepresentational works of art varying in symmetry. Bull. Psychon. Soc. 1988, 26, 355–358. [Google Scholar] [CrossRef]
- Locher, P.; Nodine, C. The perceptual value of symmetry. Comput. Math. Appl. 1989, 17, 475–484. [Google Scholar] [CrossRef]
- Palmer, S.E. On Goodness, Gestalt, Groups, and Garner: Local Symmetry Subgroups as a Theory of Figural Goodness. In The Perception of Structure: Essays in Honor of Wendell R. Garner; Lockhead, G., Pomerantz, J., Eds.; American Psychological Association: Washington, DC, USA, 1991. [Google Scholar]
- van der Helm, P.A. The Influence of Perception on the Distribution of Multiple Symmetries in Nature and Art. Symmetry 2011, 3, 54–71. [Google Scholar] [CrossRef]
- Boselie, F.; Leeuwenberg, E.L.J. Birkhoff revisited: Beauty as a function of effect and means. Am. J. Psychol. 1985, 98, 1–39. [Google Scholar] [CrossRef] [PubMed]

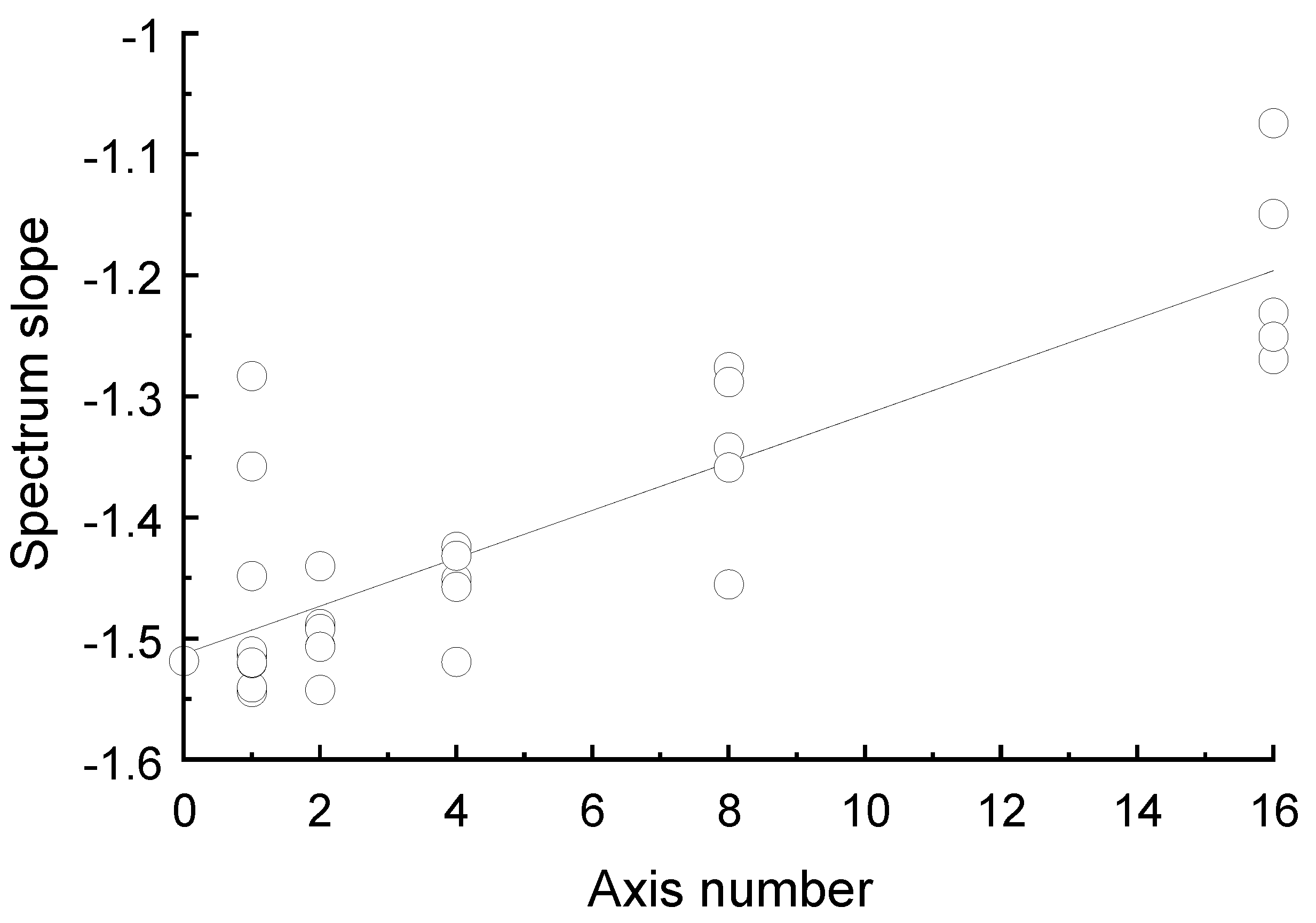
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chen, C.-C.; Wu, J.-H.; Wu, C.-C. Reduction of Image Complexity Explains Aesthetic Preference for Symmetry. Symmetry 2011, 3, 443-456. https://doi.org/10.3390/sym3030443
Chen C-C, Wu J-H, Wu C-C. Reduction of Image Complexity Explains Aesthetic Preference for Symmetry. Symmetry. 2011; 3(3):443-456. https://doi.org/10.3390/sym3030443
Chicago/Turabian StyleChen, Chien-Chung, Jo-Hsuan Wu, and Chia-Ching Wu. 2011. "Reduction of Image Complexity Explains Aesthetic Preference for Symmetry" Symmetry 3, no. 3: 443-456. https://doi.org/10.3390/sym3030443



