Lorentz Harmonics, Squeeze Harmonics and Their Physical Applications

Abstract

Among the symmetries in physics, the rotation symmetry is most familiar to us. It is known that the spherical harmonics serve useful purposes when the world is rotated. Squeeze transformations are also becoming more prominent in physics, particularly in optical sciences and in high-energy physics. As can be seen from Dirac’s light-cone coordinate system, Lorentz boosts are squeeze transformations. Thus the squeeze transformation is one of the fundamental transformations in Einstein’s Lorentz-covariant world. It is possible to define a complete set of orthonormal functions defined for one Lorentz frame. It is shown that the same set can be used for other Lorentz frames. Transformation properties are discussed. Physical applications are discussed in both optics and high-energy physics. It is shown that the Lorentz harmonics provide the mathematical basis for squeezed states of light. It is shown also that the same set of harmonics can be used for understanding Lorentz-boosted hadrons in high-energy physics. It is thus possible to transmit physics from one branch of physics to the other branch using the mathematical basis common to them.

1. Introduction

In this paper, we are concerned with symmetry transformations in two dimensions, and we are accustomed to the coordinate system specified by x and y variables. On the $xy$ plane, we know how to make rotations and translations. The rotation in the $xy$ plane is performed by the matrix algebra

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$$

(1)

but we are not yet familiar with

$$\left(\begin{array}{c}{z}^{\prime }\\ t^{\prime }\end{array}\right)=\left(\begin{array}{cc}cosh\eta & sinh\eta \\ sinh\eta & cosh\eta \end{array}\right)\left(\begin{array}{c}z\\ t\end{array}\right)$$

(2)

We see this form when we learn Lorentz transformations, but there is a tendency in the literature to avoid this form, especially in high-energy physics. Since this transformation can also be written as

$$\left(\begin{array}{c}{u}^{\prime }\\ v^{\prime }\end{array}\right)=\left(\begin{array}{cc}exp\left(\eta \right)& 0\\ 0& exp(-\eta )\end{array}\right)\left(\begin{array}{c}u\\ v\end{array}\right)$$

(3)

with

$$u=\frac{z+t}{\sqrt{2}},v=\frac{z-t}{\sqrt{2}}$$

(4)

where the variables u and v are expanded and contracted respectively, we call Equation (2) or Equation (3) squeeze transformations [1].

From the mathematical point of view, the symplectic group $Sp\left(2\right)$ contains both the rotation and squeeze transformations of Equations (1) and (2), and its mathematical properties have been extensively discussed in the literature [1,2]. This group has been shown to be one of the essential tools in quantum optics. From the mathematical point of view, the squeezed state in quantum optics is a harmonic oscillator representation of this $Sp\left(2\right)$ group [1].

We are interested in this paper in “squeeze transformations” of localized functions. We are quite familiar with the role of spherical harmonics in three dimensional rotations. We use there the same set of harmonics, but the rotated function has different linear combinations of those harmonics. Likewise, we are interested in a complete set of functions which will serve the same purpose for squeeze transformations. It will be shown that harmonic oscillator wave functions can serve the desired purpose. From the physical point of view, squeezed states define the squeeze or Lorentz harmonics.

In 2003, Giedke et al. used the Gaussian function to discuss the entanglement problems in information theory [3]. This paper allows us to use the oscillator wave functions to address many interesting current issues in quantum optics and information theory. In 2005, the present authors noted that the formalism of Lorentz-covariant harmonic oscillators leads to a space-time entanglement [4]. We developed the oscillator formalism to deal with hadronic phenomena observed in high-energy laboratories [5]. It is remarkable that the mathematical formalism of Giedke et al. is identical with that of our oscillator formalism.

While quantum optics or information theory is a relatively new branch of physics, the squeeze transformation has been the backbone of Einstein’s special relativity. While Lorentz, Poincaré, and Einstein used the transformation of Equation (2) for Lorentz boosts, Dirac observed that the same equation can be written in the form of Equation (3) [6]. Unfortunately, this squeeze aspect of Lorentz boosts has not been fully addressed in high-energy physics dealing with particles moving with relativistic speeds.

Thus, we can call the same set of functions “squeeze harmonics” and “Lorentz harmonics” in quantum optics and high-energy physics respectively. This allows us to translate the physics of quantum optics or information theory into that of high-energy physics.

The physics of high-energy hadrons requires a Lorentz-covariant localized quantum system. This description requires one variable which is hidden in the present form of quantum mechanics. It is the time-separation variable between two constituent particles in a quantum bound system like the hydrogen atom, where the Bohr radius measures the separation between the proton and the electron. What happens to this quantity when the hydrogen atom is boosted and the time-separation variable starts playing its role? The Lorentz harmonics will allow us to address this question.

In Section 2, it is noted that the Lorentz boost of localized wave functions can be described in terms of one-dimensional harmonic oscillators. Thus, those wave functions constitute the Lorentz harmonics. It is also noted that the Lorentz boost is a squeeze transformation.

In Section 3, we examine Dirac’s life-long efforts to make quantum mechanics consistent with special relativity, and present a Lorentz-covariant form of bound-state quantum mechanics. In Section 4, we construct a set of Lorentz-covariant harmonic oscillator wave functions, and show that they can be given a Lorentz-covariant probability interpretation.

In Section 5, the formalism is shown to constitute a mathematical basis for squeezed states of light, and for quantum entangled states. In Section 6, this formalism can serve as the language for Feynman’s rest of the universe [7]. Finally, in Section 7, we show that the harmonic oscillator formalism can be applied to high-energy hadronic physics, and what we observe there can be interpreted in terms of what we learn from quantum optics.

2. Lorentz or Squeeze Harmonics

Let us start with the two-dimensional plane. We are quite familiar with rigid transformations such as rotations and translations in two-dimensional space. Things are different for non-rigid transformations such as a circle becoming an ellipse.

We start with the well-known one-dimensional harmonic oscillator eigenvalue equation

$$\frac{1}{2}\left[-{\left(\frac{\partial }{\partial x}\right)}^2+x^2\right]{\chi }_n\left(x\right)=\left(n+\frac{1}{2}\right){\chi }_n\left(x\right)$$

(5)

For a given value of integer $n,$ the solution takes the form

$${\chi }_n\left(x\right)={\left[\frac{1}{\sqrt{\pi }{2}^{n}n!}\right]}^{1/2}{H}_n\left(x\right)exp\left(\frac{-x^2}{2}\right)$$

(6)

where $H_n\left(x\right)$ is the Hermite polynomial of the n-th degree. We can then consider a set of functions with all integer values of n. They satisfy the orthogonality relation

$$\int {\chi }_n\left(x\right){\chi }_{n^{\prime }}\left(x\right)={\delta }_{n{n}^{\prime }}$$

(7)

This relation allows us to define $f\left(x\right)$ as

$$f\left(x\right)=\sum _n{A}_n{\chi }_n\left(x\right)$$

(8)

with

$$A_n=\int f\left(x\right){\chi }_n\left(x\right)dx$$

(9)

Let us next consider another variable added to Equation (5), and the differential equation

$$\frac{1}{2}\left\{\left[-{\left(\frac{\partial }{\partial x}\right)}^2+x^2\right]+\left[-{\left(\frac{\partial }{\partial y}\right)}^2+y^2\right]\right\}\varphi (x,y)=\lambda \varphi (x,y)$$

(10)

This equation can be re-arranged to

$$\frac{1}{2}\left\{-{\left(\frac{\partial }{\partial x}\right)}^2-{\left(\frac{\partial }{\partial y}\right)}^2+x^2+y^2\right\}\varphi (x,y)=\lambda \varphi (x,y)$$

(11)

This differential equation is invariant under the rotation defined in Equation (1). In terms of the polar coordinate system with

$$r=\sqrt{x^2+y^2},tan\theta =\left(\frac{y}{x}\right)$$

(12)

this equation can be written:

$$\frac{1}{2}\left\{-\frac{{\partial }^2}{\partial r^2}-\frac{1}{r}\frac{\partial }{\partial r}-\frac{1}{r^2}\frac{{\partial }^2}{\partial {\theta }^2}+r^2\right\}\varphi (r,\theta )=\lambda \varphi (r,\theta )$$

(13)

and the solution takes the form

$$\varphi (r,\theta )=e^{-r^2/2}{R}_{n,m}\left(r\right)\left\{A_{m}cos\left(m\theta \right)+B_{n}sin\left(m\theta \right)\right\}$$

(14)

The radial equation should satisfy

$$\frac{1}{2}\left\{-\frac{{\partial }^2}{\partial r^2}-\frac{1}{r}\frac{\partial }{\partial r}+\frac{m^2}{r^2}+r^2\right\}{R}_{n,m}\left(r\right)=(n+m+1)R_{n,m}\left(r\right)$$

(15)

In the polar form of Equation (14), we can achieve the rotation of this function by changing the angle variable $\theta$.

On the other hand, the differential equation of Equation (10) is separable in the x and y variables. The eigen solution takes the form

$${\varphi }_{n_x,n_y}(x,y)={\chi }_{n_x}\left(x\right){\chi }_{n_y}\left(y\right)$$

(16)

with

$$\lambda =n_x+n_y+1$$

(17)

If a function $f(x,y)$ is sufficiently localized around the origin, it can be expanded as

$$f(x,y)=\sum _{n_x,n_y}{A}_{n_x,n_y}{\chi }_{n_x}\left(x\right){\chi }_{n_y}\left(y\right)$$

(18)

with

$$A_{n_x,n_y}=\int f(x,y){\chi }_{n_x}\left(x\right){\chi }_{n_y}\left(y\right)dxdy$$

(19)

If we rotate $f(x,y)$ according to Equation (1), it becomes $f(x^{*},y^{*})$, with

$$x^{*}=(cos\theta )x-(sin\theta )y,y^{*}=(sin\theta )x+(cos\theta )y$$

(20)

This rotated function can also be expanded in terms of ${\chi }_{n_x}\left(x\right)$ and ${\chi }_{n_y}\left(y\right)$:

$$f(x^{*},y^{*})=\sum _{n_x,n_y}{A}_{n_x,n_y}^{*}{\chi }_{n_x}\left(x\right){\chi }_{n_y}\left(y\right)$$

(21)

with

$$A_{n_x,n_y}^{*}=\int f(x^{*},y^{*}){\chi }_{n_x}\left(x\right){\chi }_{n_y}\left(y\right)dxdy$$

(22)

Next, let us consider the differential equation

$$\frac{1}{2}\left\{-{\left(\frac{\partial }{\partial z}\right)}^2+{\left(\frac{\partial }{\partial t}\right)}^2+z^2-t^2\right\}\psi (z,t)=\lambda \psi (z,t)$$

(23)

Here we use the variables z and t, instead of x and y. Clearly, this equation can be also separated in the z and t coordinates, and the eigen solution can be written as

$${\psi }_{n_z,n_t}(z,t)={\chi }_{n_z}\left(z\right){\chi }_{n_t}(z,t)$$

(24)

with

$$\lambda =n_z-n_t.$$

(25)

The oscillator equation is not invariant under coordinate rotations of the type given in Equation (1). It is however invariant under the squeeze transformation given in Equation (2).

The differential equation of Equation (23) becomes

$$\frac{1}{4}\left\{-\frac{\partial }{\partial u}\frac{\partial }{\partial v}+uv\right\}\psi (u,v)=\lambda \psi (u,v)$$

(26)

Both Equation (11) and Equation (23) are two-dimensional differential equations. They are invariant under rotations and squeeze transformations respectively. They take convenient forms in the polar and squeeze coordinate systems respectively as shown in Equation (13) and Equation (26).

The solutions of the rotation-invariant equation are well known, but the solutions of the squeeze-invariant equation are still strange to the physics community. Fortunately, both equations are separable in the Cartesian coordinate system. This allows us to study the latter in terms of the familiar rotation-invariant equation. This means that if the solution is sufficiently localized in the z and t plane, it can be written as

$$\psi (z,t)=\sum _{n_z,n_t}{A}_{n_z,n_t}{\chi }_{n_z}\left(z\right){\chi }_{n_t}\left(t\right)$$

(27)

with

$$A_{n_z,n_t}=\int \psi (z,t){\chi }_{n_z}\left(z\right){\chi }_{n_t}\left(t\right)dzdt$$

(28)

If we squeeze the coordinate according to Equation (2),

$$\psi (z^{*},t^{*})=\sum _{n_z,n_t}{A}_{n_z,n_t}^{*}{\chi }_{n_z}\left(z\right){\chi }_{n_t}\left(t\right)$$

(29)

with

$$A_{n_z,n_t}^{*}=\int \psi (z^{*},t^{*}){\chi }_{n_z}\left(z\right){\chi }_{n_t}\left(t\right)dzdt$$

(30)

Here again both the original and transformed wave functions are linear combinations of the wave functions for the one-dimensional harmonic oscillator given in Equation (6).

The wave functions for the one-dimensional oscillator are well known, and they play important roles in many branches of physics. It is gratifying to note that they could play an essential role in squeeze transformations and Lorentz boosts, see

Table 1. Cylindrical and hyperbolic equations. The cylindrical equation is invariant under rotation while the hyperbolic equation is invariant under squeeze transformation

	Equation	Invariant under	Eigenvalue
	Cylindrical	Rotation	$\lambda =n_x+n_y+1$
	Hyperbolic	Squeeze	$\lambda =n_x-n_y$

. We choose to call them Lorentz harmonics or squeeze harmonics.

3. The Physical Origin of Squeeze Transformations

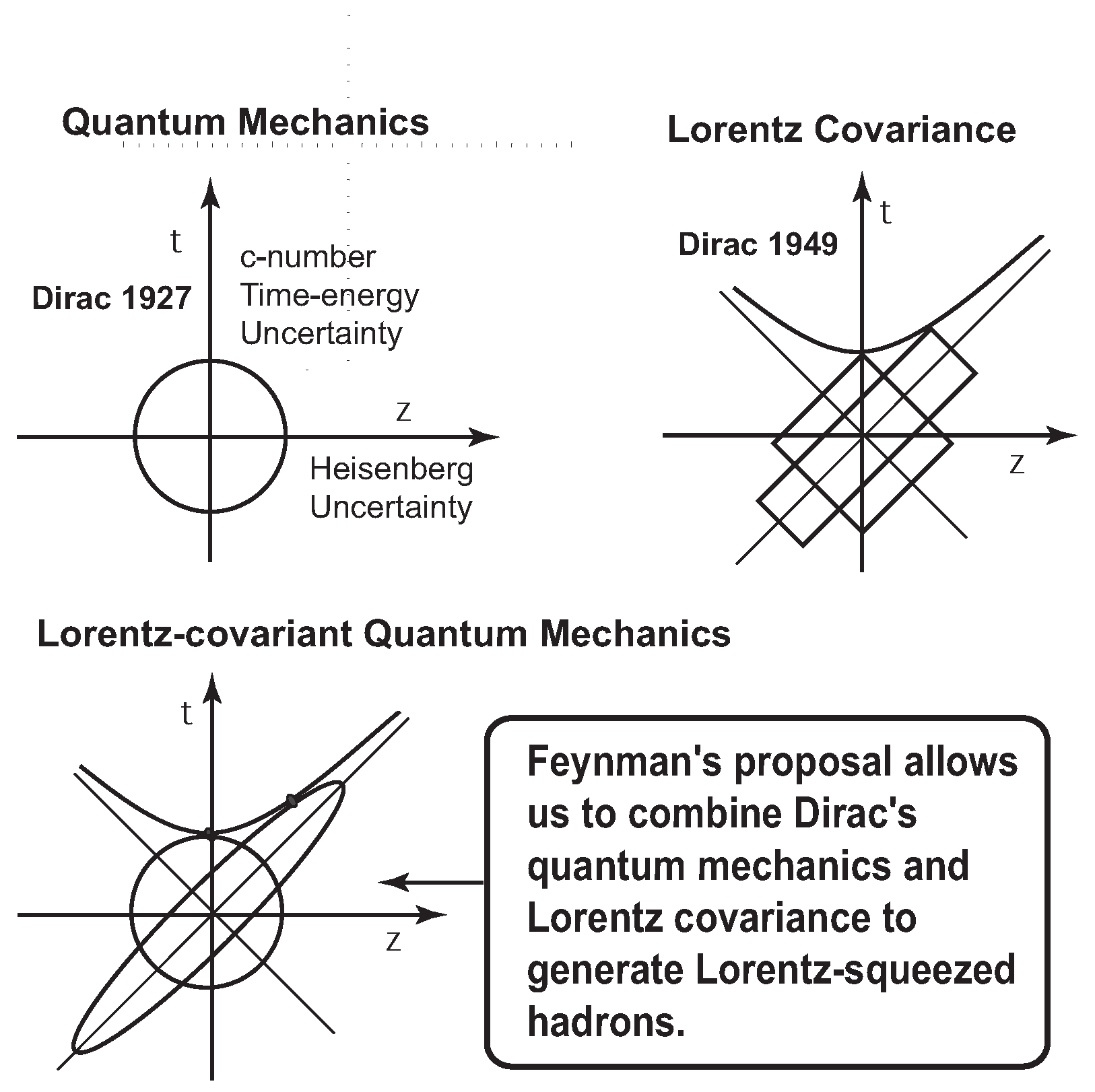
Paul A. M. Dirac made it his life-long effort to combine quantum mechanics with special relativity. We examine the following four of his papers.

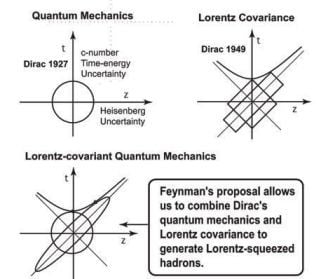
• In 1927 [8], Dirac pointed out the time-energy uncertainty should be taken into consideration for efforts to combine quantum mechanics and special relativity.
• In 1945 [9], Dirac considered four-dimensional harmonic oscillator wave functions with

  $$exp\left\{-\frac{1}{2}\left(x^2+y^2+z^2+t^2\right)\right\}$$

  (31)

  and noted that this form is not Lorentz-covariant.
• In 1949 [6], Dirac introduced the light-cone variables of Equation (4). He also noted that the construction of a Lorentz-covariant quantum mechanics is equivalent to the construction of a representation of the Poncaré group.
• In 1963 [10], Dirac constructed a representation of the (3 + 2) deSitter group using two harmonic oscillators. This deSitter group contains three (3 + 1) Lorentz groups as its subgroups.

In each of these papers, Dirac presented the original ingredients which can serve as building blocks for making quantum mechanics relativistic. We combine those elements using Wigner’s little groups [11] and and Feynman’s observation of high-energy physics [12,13,14].

First of all, let us combine Dirac’s 1945 paper and his light-cone coordinate system given in his 1949 paper. Since x and y variables are not affected by Lorentz boosts along the z direction in Equation (31), it is sufficient to study the Gaussian form

$$exp\left\{-\frac{1}{2}\left(z^2+t^2\right)\right\}$$

(32)

This form is certainly not invariant under Lorentz boost as Dirac noted. On the other hand, it can be written as

$$exp\left\{-\frac{1}{2}\left(u^2+v^2\right)\right\}$$

(33)

where u and v are the light-cone variables defined in Equation (4). If we make the Lorentz-boost or Lorentz squeeze according to Equation (3), this Gaussian form becomes

$$exp\left\{-\frac{1}{2}\left(e^{-2\eta }{u}^2+e^{2\eta }{v}^2\right)\right\}$$

(34)

If we write the Lorentz boost as

$$z^{\prime }=\frac{z+\beta t}{\sqrt{1-{\beta }^2}}{t}^{\prime }=\frac{t+\beta z}{\sqrt{1-{\beta }^2}}$$

(35)

where $\beta$ is the the velocity parameter $v/c$, then $\beta$ is related to $\eta$ by

$$\beta =tanh\left(\eta \right)$$

(36)

Let us go back to the Gaussian form of Equation (32), this expression is consistent with Dirac’s earlier paper on the time-energy uncertainty relation [8]. According to Dirac, this is a c-number uncertainty relation without excitations. The existence of the time-energy uncertainty is illustrated in the first part of Figure 1.

In his 1927 paper, Dirac noted the space-time asymmetry in uncertainty relations. While there are no time-like excitations, quantum mechanics allows excitations along the z direction. How can we take care of problem?

If we suppress the excitations along the t coordinate, the normalized solution of this differential equation, Equation (24), is

$$\psi (z,t)={\left(\frac{1}{\pi 2^{n}n!}\right)}^{1/2}{H}_n\left(z\right)exp\left\{-\left(\frac{z^2+t^2}{2}\right)\right\}$$

(37)

If we boost the coordinate system, the Lorentz-boosted wave functions should take the form

$$\begin{array}{c}{\psi }_{\eta }^n(z,t)={\left(\frac{1}{\pi 2^{n}n!}\right)}^{1/2}{H}_n\left(zcosh\eta -tsinh\eta \right)\hfill \\ \times exp\left\{-\left[\frac{(cosh2\eta )(z^2+t^2)-4(sinh2\eta )zt}{2}\right]\right\}\hfill \end{array}$$

(38)

These are the solutions of the phenomenological equation of Feynman et al. [12] for internal motion of the quarks inside a hadron. In 1971, Feynman et al. wrote down a Lorentz-invariant differential equation of the form

$$\frac{1}{2}\left\{-{\left(\frac{\partial }{\partial x_{\mu }}\right)}^2+x_{\mu }^2\right\}\psi \left(x_{\mu }\right)=(\lambda +1)\psi \left(x_{\mu }\right)$$

(39)

where $x_{\mu }$ is for the Lorentz-covariant space-time four vector. This oscillator equation is separable in the Cartesian coordinate system, and the transverse components can be seprated out. Thus, the differential of Equation (23) contains the essential element of the Lorentz-invariant Equation (39).

However, the solutions contained in Reference [12] are not normalizable and therefore cannot carry physical interpretations. It was shown later that there are normalizable solutions which constitute a representation of Wigner’s $O\left(3\right)$-like little group [5,11,15]. The $O\left(3\right)$ group is the three-dimensional rotation group without a time-like direction or time-like excitations. This addresses Dirac’s concern about the space-time asymmetry in uncertainty relations [8]. Indeed, the expression of Equation (37) is considered to be the representation of Wigner’s little group for quantum bound states [11,15]. We shall return to more physical questions in Section 7.

4. Further Properties of the Lorentz Harmonics

Let us continue our discussion of quantum bound states using harmonic oscillators. We are interested in this section to see how the oscillator solution of Equation (37) would appear to a moving observer.

The variable z and t are the longitudinal and time-like separations between the two constituent particles. In terms of the light-cone variables defined in Equation (4), the solution of Equation (37) takes the form

$${\psi }_0^n(z,t)={\left[\frac{1}{\pi n!2^n}\right]}^{1/2}{H}_n\left(\frac{u+v}{\sqrt{2}}\right)exp\left\{-\left(\frac{u^2+v^2}{2}\right)\right\}$$

(40)

and

$${\psi }_{\eta }^n(z,t)={\left[\frac{1}{\pi n!2^n}\right]}^{1/2}{H}_n\left(\frac{e^{-\eta }u+e^{\eta }v}{\sqrt{2}}\right)exp\left\{-\left(\frac{e^{-2\eta }{u}^2+e^{2\eta }{v}^2}{2}\right)\right\}$$

(41)

for the rest and moving hadrons respectively.

It is mathematically possible to expand this as [5,16]

$${\psi }_{\eta }^n(z,t)={\left(\frac{1}{cosh\eta }\right)}^{(n+1)}\sum _k{\left[\frac{(n+k)!}{n!k!}\right]}^{1/2}{(tanh\eta )}^k{\chi }_{n+k}\left(z\right){\chi }_n\left(t\right)$$

(42)

where ${\chi }_n\left(z\right)$ is the n-th excited state oscillator wave function which takes the familiar form

$${\chi }_n\left(z\right)={\left[\frac{1}{\sqrt{\pi }{2}^{n}n!}\right]}^{1/2}{H}_n\left(z\right)exp\left(\frac{-z^2}{2}\right)$$

(43)

as given in Equation (6). This is an expansion of the Lorentz-boosted wave function in terms of the Lorentz harmonics.

If the hadron is at rest, there are no time-like oscillations. There are time-like oscillations for a moving hadron. This is the way in which the space and time variable mix covariantly. This also provides a resolution of the space-time asymmetry pointed out by Dirac in his 1927 paper [8]. We shall return to this question in Section 6. Our next question is whether those oscillator equations can be given a probability interpretation.

Even though we suppressed the excitations along the t direction in the hadronic rest frame, it is an interesting mathematical problem to start with the oscillator wave function with an excited state in the time variable. This problem was adressed by Rotbart in 1981 [17].

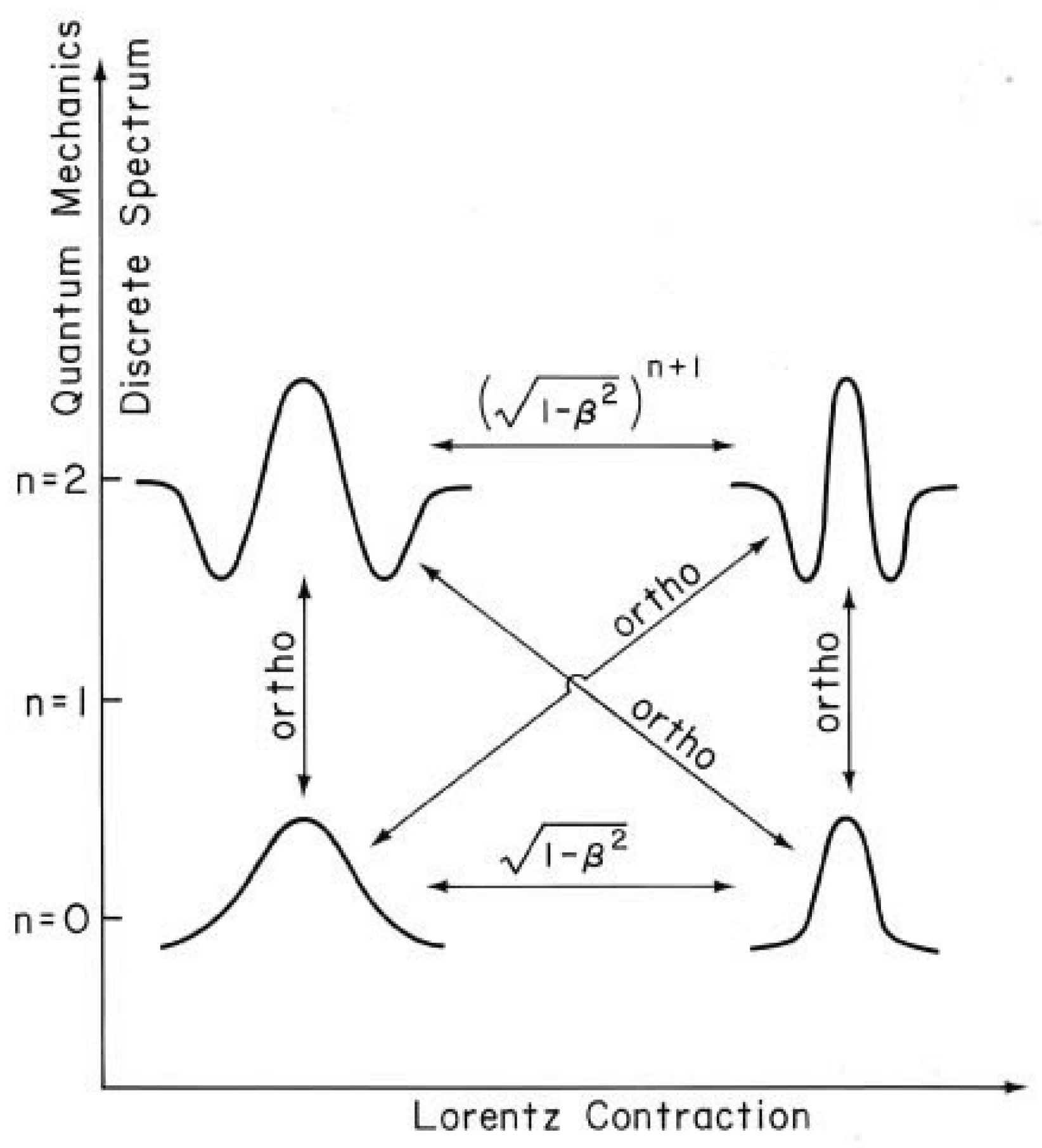
4.1. Lorentz-Invariant Orthogonality Relations

Let us consider two wave functions ${\psi }_{\eta }^n(z,t).$ If two covariant wave functions are in the same Lorentz frame and have thus the same value of $\eta$, the orthogonality relation

$$\left({\psi }_{\eta }^{n^{\prime }},{\psi }_{\eta }^n\right)={\delta }_{n{n}^{\prime }}$$

(44)

is satisfied.

If those two wave functions have different values of $\eta$, we have to start with

$$\left({\psi }_{{\eta }^{\prime }}^{n^{\prime }},{\psi }_{\eta }^n\right)=\int {\left({\psi }_{{\eta }^{\prime }}^{n^{\prime }}(z,t)\right)}^{*}{\psi }_{\eta }^n(z,t)dzdt$$

(45)

Without loss of generality, we can assume ${\eta }^{\prime }$ = 0 in the system where $\eta =0$, and evaluate the integration. The result is [18]

$$\left({\psi }_0^{n^{\prime }},{\psi }_{\eta }^n\right)=\int {\left({\psi }_0^{n^{\prime }}(z,t)\right)}^2{\psi }_{\eta }^n(z,t)dxdt={\left(\sqrt{1-{\beta }^2}\right)}^{(n+1)}{\delta }_{n,n^{\prime }}$$

(46)

where $\beta =tanh\left(\eta \right),$ as given in Equation (36). This is like the Lorentz-contraction property of a rigid rod. The ground state is like a single rod. Since we obtain the first excited state by applying a step-up operator, this state should behave like a multiplication of two rods, and a similar argument can be give to n rigid rods. This is illustrated in Figure 2.

With these orthogonality properties, it is possible to give quantum probability interpretation in the Lorentz-covariant world, and it was so stated in our 1977 paper [19].

4.2. Probability Interpretations

Let us study the probability issue in terms of the one-dimensional oscillator solution of Equation (6) whose probability interpretation is indisputable. Let us also go back to the rotationally invariant differential equation of Equation (11). Then the product

$${\chi }_{n_x}\left(x\right){\chi }_{n_y}\left(y\right)$$

(47)

also has a probability interpretation with the eigen value $\left(n_x+n_y+1\right).$ Thus the series of the form [1,5]

$${\varphi }_{\eta }^n(x,y)={\left(\frac{1}{cosh\eta }\right)}^{(n+1)}\sum _k{\left[\frac{(n+k)!}{n!k!}\right]}^{1/2}{(tanh\eta )}^k{\chi }_{n+k}\left(x\right){\chi }_n\left(y\right)$$

(48)

also has its probability interpretation, but it is not in an eigen state. Each term in this series has an eigenvalue $(2n+k+1)$. The expectation value of Equation (11) is

$${\left(\frac{1}{cosh\eta }\right)}^{2(n+1)}\sum _k\frac{(2n+k+1)(n+k)!}{n!k!}{(tanh\eta )}^{2k}$$

(49)

If we replace the variables x and y by z and t respectively in the above expression of Equation (48), it becomes the Lorentz-covariant wave function of Equation (42). Each term ${\chi }_{n+k}\left(z\right){\chi }_k\left(t\right)$ in the series has the eigenvalue n. Thus the series is in the eigen state with the eigenvalue n.

This difference does not prevent us from importing the probability interpretation from that of Equation (48).

In the present covariant oscillator formalism, the time-separation variable can be separated from the rest of the wave function, and does not requite further interpretation. For a moving hadron, time-like excitations are mixed with longitudinal excitations. Is it possible to give a physical interpretation to those time-like excitations? To address this issue, we shall study in Section 5 two-mode squeezed states also based on the mathematics of Equation (48). There, both variables have their physical interpretations.

5. Two-Mode Squeezed States

Harmonic oscillators play the central role also in quantum optics. There the $n^{th}$ excited oscillator state corresponds to the n-photon state $|n>$. The ground state means the zero-photon or vacuum state $|0>$. The single-photon coherent state can be written as

$$|\alpha >=e^{-\alpha {\alpha }^{*}/2}\sum _n\frac{{\alpha }^n}{\sqrt{n!}}|n>$$

(50)

which can be written as [1]

$$|\alpha >=e^{-\alpha {\alpha }^{*}/2}\sum _n\frac{{\alpha }^n}{n!}{\left({\widehat{a}}^{†}\right)}^n|0>=\left\{e^{-\alpha {\alpha }^{*}/2}\right\}exp\left\{\alpha {\widehat{a}}^{†}\right\}|0>$$

(51)

This aspect of the single-photon coherent state is well known. Here we are dealing with one kind of photon, namely with a given momentum and polarization. The state $|n>$ means there are n photons of this kind.

Let us next consider a state of two kinds of photons, and write $|n_1,n_2>$ as the state of $n_1$ photons of the first kind, and $n_2$ photons of the second kind [20]. We can then consider the form

$$\frac{1}{cosh\eta }exp\left\{(tanh\eta ){\widehat{a}}_1^{†}{\widehat{a}}_2^{†}\right\}|0,0>$$

(52)

The operator ${\widehat{a}}_1^{†}{\widehat{a}}_2^{†}$ was studied by Dirac in connection with his representation of the deSitter group, as we mentioned in Section 3. After making a Taylor expansion of Equation (52), we arrive at

$$\frac{1}{cosh\eta }\sum _k{(tanh\eta )}^k|k,k>$$

(53)

which is the squeezed vacuum state or two-photon coherent state [1,20]. This expression is the wave function of Equation (48) in a different notation. This form is also called the entangled Gaussian state of two photons [3] or the entangled oscillator state of space and time [4].

If we start with the n-particle state of the first photon, we obtain

$$\begin{array}{c}{\left[\frac{1}{cosh\eta }\right]}^{(n+1)}exp\left\{(tanh\eta ){\widehat{a}}_1^{†}{\widehat{a}}_2^{†}\right\}|n,0>\hfill \\ ={\left[\frac{1}{cosh\eta }\right]}^{(n+1)}\sum _k{\left[\frac{(n+k)!}{n!k!}\right]}^{1/2}{(tanh\eta )}^k|k+n,k>\hfill \end{array}$$

(54)

which is the wave function of Equation (42) in a different notation. This is the n-photon squeezed state [1].

Since the two-mode squeezed state and the covariant harmonic oscillators share the same set of mathematical formulas, it is possible to transmit physical interpretations from one to the other. For two-mode squeezed state, both photons carry physical interpretations, while the interpretation is yet to be given to the time-separation variable in the covariant oscillator formalism. It is clear from Equation (42) and Equation (54) that the time-like excitations are like the second-photon states.

What would happen if the second photon is not observed? This interesting problem was addressed by Yurke and Potasek [21] and by Ekert and Knight [22]. They used the density matrix formalism and integrated out the second-photon states. This increases the entropy and temperature of the system. We choose not to reproduce their mathematics, because we will be presenting the same mathematics in Section 6.

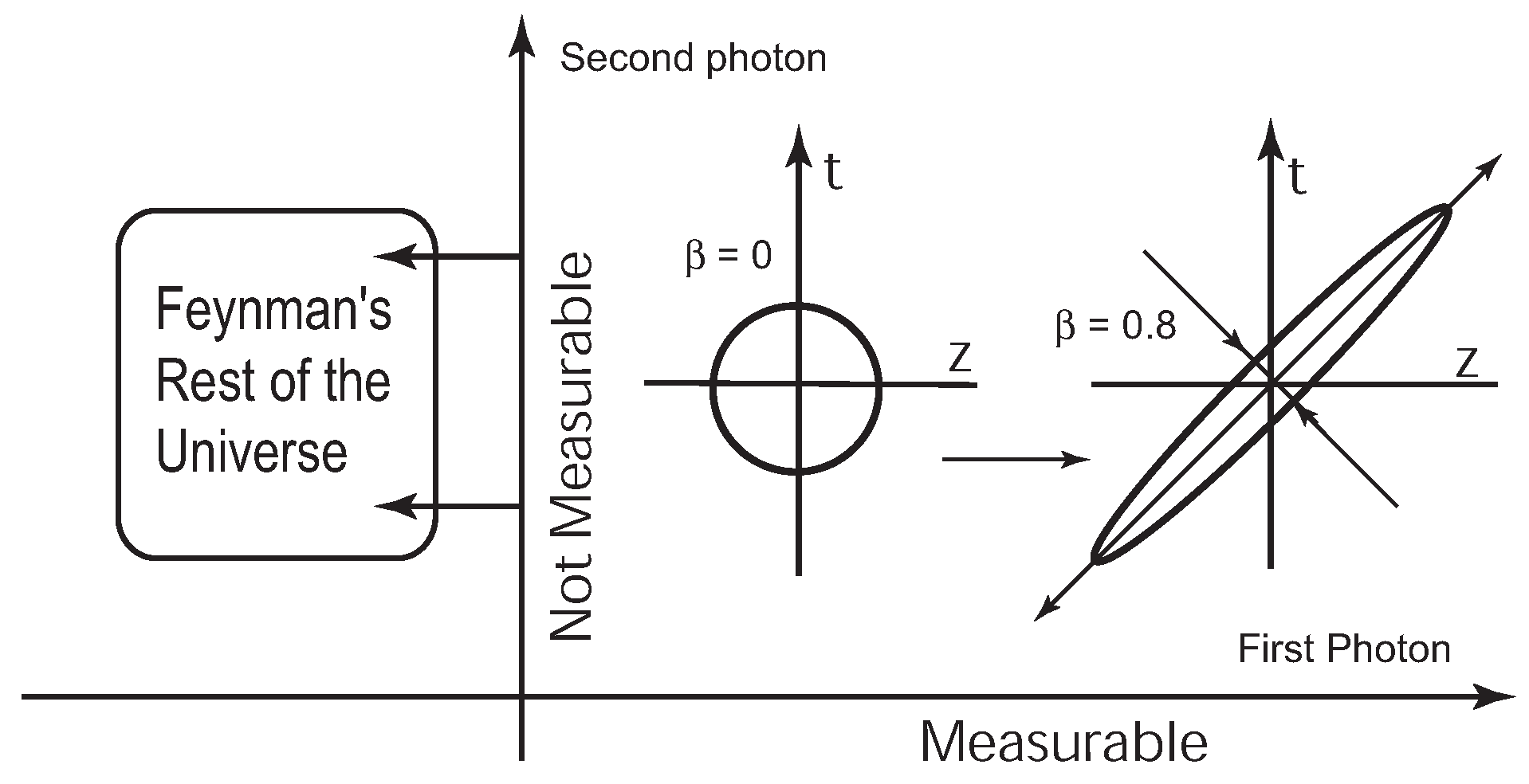
6. Time-Separation Variable in Feynman’s Rest of the Universe

As was noted in the previous section, the time-separation variable has an important role in the covariant formulation of the harmonic oscillator wave functions. It should exist wherever the space separation exists. The Bohr radius is the measure of the separation between the proton and electron in the hydrogen atom. If this atom moves, the radius picks up the time separation, according to Einstein [23].

On the other hand, the present form of quantum mechanics does not include this time-separation variable. The best way we can interpret it at the present time is to treat this time-separation as a variable in Feynman’s rest of the universe [24]. In his book on statistical mechanics [7], Feynman states

When we solve a quantum-mechanical problem, what we really do is divide the universe into two parts - the system in which we are interested and the rest of the universe. We then usually act as if the system in which we are interested comprised the entire universe. To motivate the use of density matrices, let us see what happens when we include the part of the universe outside the system.

The failure to include what happens outside the system results in an increase of entropy. The entropy is a measure of our ignorance and is computed from the density matrix [25]. The density matrix is needed when the experimental procedure does not analyze all relevant variables to the maximum extent consistent with quantum mechanics [26]. If we do not take into account the time-separation variable, the result is an increase in entropy [27,28].

For the covariant oscillator wave functions defined in Equation (42), the pure-state density matrix is

$${\rho }_{\eta }^n(z,t;z^{\prime },t^{\prime })={\psi }_{\eta }^n(z,t){\psi }_{\eta }^n(z^{\prime },t^{\prime })$$

(55)

which satisfies the condition ${\rho }^2=\rho :$

$${\rho }_{\eta }^n(z,t;x^{\prime },t^{\prime })=\int {\rho }_{\eta }^n(z,t;x^{″},t^{″}){\rho }_{\eta }^n(z^{″},t^{″};z^{\prime },t^{\prime })d{z}^{″}d{t}^{″}$$

(56)

However, in the present form of quantum mechanics, it is not possible to take into account the time separation variables. Thus, we have to take the trace of the matrix with respect to the t variable. Then the resulting density matrix is

$$\begin{array}{c}{\rho }_{\eta }^n(z,z^{\prime })=\int {\psi }_{\eta }^n(z,t){\psi }_{\eta }^n(z^{\prime },t)dt\hfill \\ ={\left(\frac{1}{cosh\eta }\right)}^{2(n+1)}\sum _k\frac{(n+k)!}{n!k!}{(tanh\eta )}^{2k}{\psi }_{n+k}\left(z\right){\psi }_{n+k}^{*}\left(z^{\prime }\right)\hfill \end{array}$$

(57)

The trace of this density matrix is one, but the trace of ${\rho }^2$ is less than one, as

$$\begin{array}{cc}& Tr\left({\rho }^2\right)=\int {\rho }_{\eta }^n(z,z^{\prime }){\rho }_{\eta }^n(z^{\prime },z)dzd{z}^{\prime }\hfill \\ & ={\left(\frac{1}{cosh\eta }\right)}^{4(n+1)}\sum _k{\left[\frac{(n+k)!}{n!k!}\right]}^2{(tanh\eta )}^{4k}\hfill \end{array}$$

(58)

which is less than one. This is due to the fact that we do not know how to deal with the time-like separation in the present formulation of quantum mechanics. Our knowledge is less than complete.

The standard way to measure this ignorance is to calculate the entropy defined as

$$S=-Tr\left(\rho ln\left(\rho \right)\right)$$

(59)

If we pretend to know the distribution along the time-like direction and use the pure-state density matrix given in Equation (55), then the entropy is zero. However, if we do not know how to deal with the distribution along t, then we should use the density matrix of Equation (57) to calculate the entropy, and the result is

$$\begin{array}{cc}& S=2(n+1)\left\{{(cosh\eta )}^{2}ln(cosh\eta )-(sinh\eta )ln(sinh\eta )\right\}\hfill \\ & -{\left(\frac{1}{cosh\eta }\right)}^{2(n+1)}\sum _k\frac{(n+k)!}{n!k!}ln\left[\frac{(n+k)!}{n!k!}\right]{(tanh\eta )}^{2k}\hfill \end{array}$$

(60)

In terms of the velocity v of the hadron,

$$\begin{array}{cc}& S=-(n+1)\left\{ln\left[1-{\left(\frac{v}{c}\right)}^2\right]+\frac{{(v/c)}^{2}ln{(v/c)}^2}{1-{(v/c)}^2}\right\}\hfill \\ & -\left[1-{\left(\frac{1}{v}\right)}^2\right]\sum _k\frac{(n+k)!}{n!k!}ln\left[\frac{(n+k)!}{n!k!}\right]{\left(\frac{v}{c}\right)}^{2k}\hfill \end{array}$$

(61)

Let us go back to the wave function given in Equation (41). As is illustrated in Figure 3, its localization property is dictated by the Gaussian factor which corresponds to the ground-state wave function. For this reason, we expect that much of the behavior of the density matrix or the entropy for the $n^{th}$ excited state will be the same as that for the ground state with $n=0.$ For this state, the density matrix and the entropy are

$$\rho (z,z^{\prime })={\left(\frac{1}{\pi cosh\left(2\eta \right)}\right)}^{1/2}exp\left\{-\frac{1}{4}\left[\frac{{(z+z^{\prime })}^2}{cosh\left(2\eta \right)}+{(z-z^{\prime })}^{2}cosh\left(2\eta \right)\right]\right\}$$

(62)

and

$$S=2\left\{{(cosh\eta )}^{2}ln(cosh\eta )-{(sinh\eta )}^{2}ln(sinh\eta )\right\}$$

(63)

respectively. The quark distribution $\rho (z,z)$ becomes

$$\rho (z,z)={\left(\frac{1}{\pi cosh\left(2\eta \right)}\right)}^{1/2}exp\left(\frac{-z^2}{cosh\left(2\eta \right)}\right)$$

(64)

The width of the distribution becomes $\sqrt{cosh\eta }$, and becomes wide-spread as the hadronic speed increases. Likewise, the momentum distribution becomes wide-spread [5,29]. This simultaneous increase in the momentum and position distribution widths is called the parton phenomenon in high-energy physics [13,14]. The position-momentum uncertainty becomes $cosh\eta$. This increase in uncertainty is due to our ignorance about the physical but unmeasurable time-separation variable.

Let us next examine how this ignorance will lead to the concept of temperature. For the Lorentz-boosted ground state with $n=0$, the density matrix of Equation (62) becomes that of the harmonic oscillator in a thermal equilibrium state if ${(tanh\eta )}^2$ is identified as the Boltzmann factor [29]. For other states, it is very difficult, if not impossible, to describe them as thermal equilibrium states. Unlike the case of temperature, the entropy is clearly defined for all values of n. Indeed, the entropy in this case is derivable directly from the hadronic speed.

The time-separation variable exists in the Lorentz-covariant world, but we pretend not to know about it. It thus is in Feynman’s rest of the universe. If we do not measure this time-separation, it becomes translated into the entropy.

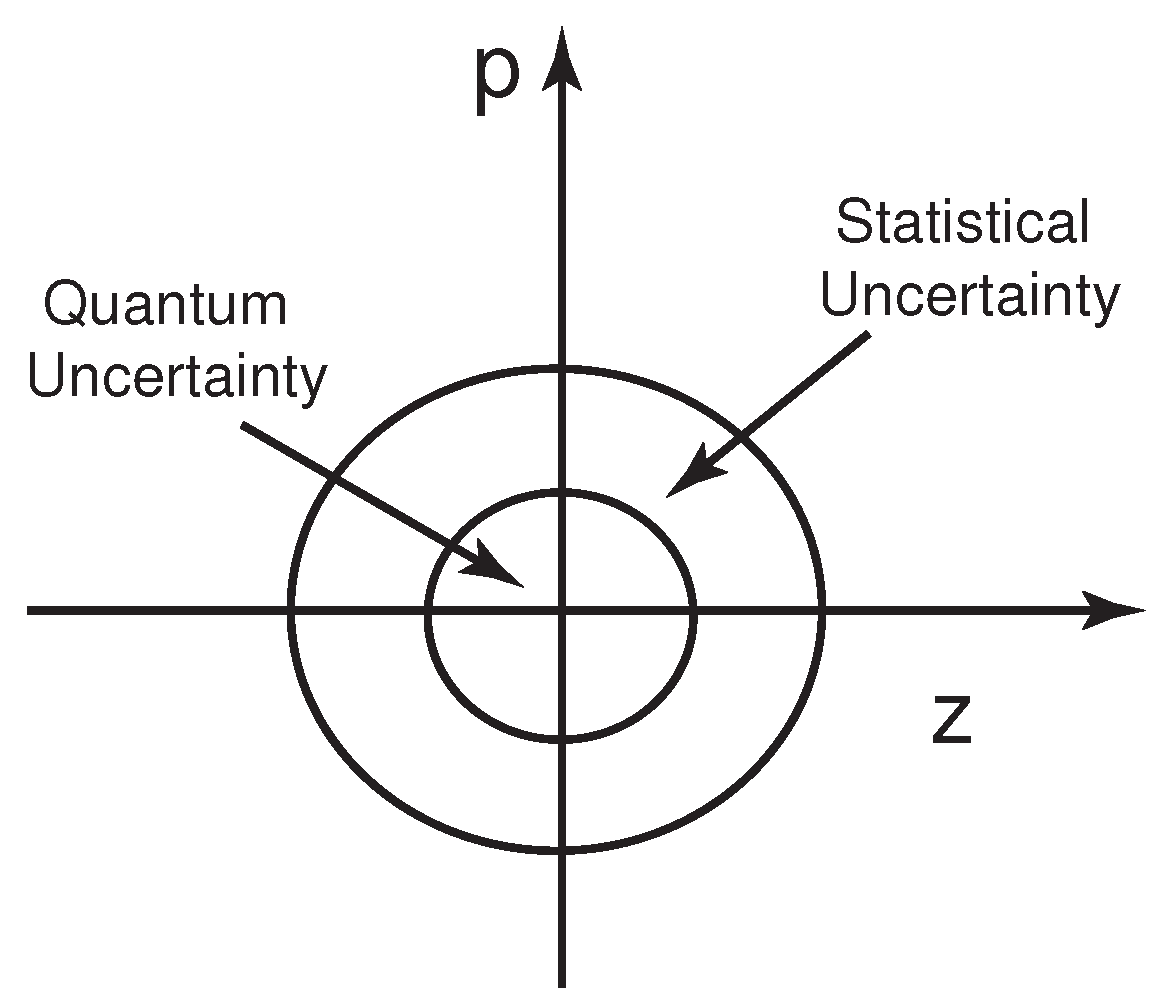
We can see the uncertainty in our measurement process from the Wigner function defined as

$$W(z,p)=\frac{1}{\pi }\int \rho (z+y,z-y)e^{2ipy}dy$$

(65)

After integration, this Wigner function becomes

$$W(z,p)=\frac{1}{\pi cosh\left(2\eta \right)}exp\left\{-\left(\frac{z^2+p^2}{cosh\left(2\eta \right)}\right)\right\}$$

(66)

This Wigner phase distribution is illustrated in Figure 4. The smaller inner circle corresponds to the minimal uncertainty of the single oscillator. The larger circle is for the total uncertainty including the statistical uncertainty from our failure to observe the time-separation variable. The two-mode squeezed state tells us how this happens. In the two-mode case, both the first and second photons are observable, but we can choose not to observe the second photon.

7. Lorentz-Covariant Quark Model

The hydrogen atom played the pivotal role while the present form of quantum mechanics was developed. At that time, the proton was in the absolute Galilean frame of reference, and it was thinkable that the proton could move with a speed close to that of light.

Also, at that time, both the proton and electron were point particles. However, the discovery of Hofstadter et al. changed the picture of the proton in 1955 [30]. The proton charge has its internal distribution. Within the framework of quantum electrodynamics, it is possible to calculate the Rutherford formula for the electron-proton scattering when both electron and proton are point particles. Because the proton is not a point particle, there is a deviation from the Rutherford formula. We describe this deviation using the formula called the “proton form factor” which depends on the momentum transfer during the electron-proton scattering.

Indeed, the study of the proton form factor has been and still is one of the central issues in high-energy physics. The form factor decreases as the momentum transfer increases. Its behavior is called the “dipole cut-off” meaning an inverse-square decrease, and it has been a challenging problem in quantum field theory and other theoretical models [31]. Since the emergence of the quark model in 1964 [32], the hadrons are regarded as quantum bound states of quarks with space-time wave functions. Thus, the quark model is responsible for explaining this form factor. There are indeed many papers written on this subject. We shall return to this problem in Subsection 7.2.

Another problem in high-energy physics is Feynman’s parton picture [13,14]. If the hadron is at rest, we can approach this problem within the framework of bound-state quantum mechanics. If it moves with a speed close to that of light, it appears as a collection of an infinite number of partons, which interact with external signals incoherently. This phenomenon raises the question of whether the Lorentz boost destroys quantum coherence [33]. This leads to the concept of Feynman’s decoherence [34]. We shall discuss this problem first.

7.1. Feynman’s Parton Picture and Feynman’s Decoherence

In 1969, Feynman observed that a fast-moving hadron can be regarded as a collection of many “partons” whose properties appear to be quite different from those of the quarks [5,14]. For example, the number of quarks inside a static proton is three, while the number of partons in a rapidly moving proton appears to be infinite. The question then is how the proton looking like a bound state of quarks to one observer can appear different to an observer in a different Lorentz frame? Feynman made the following systematic observations.

• The picture is valid only for hadrons moving with velocity close to that of light.
• The interaction time between the quarks becomes dilated, and partons behave as free independent particles.
• The momentum distribution of partons becomes widespread as the hadron moves fast.
• The number of partons seems to be infinite or much larger than that of quarks.

Because the hadron is believed to be a bound state of two or three quarks, each of the above phenomena appears as a paradox, particularly (b) and (c) together. How can a free particle have a wide-spread momentum distribution?

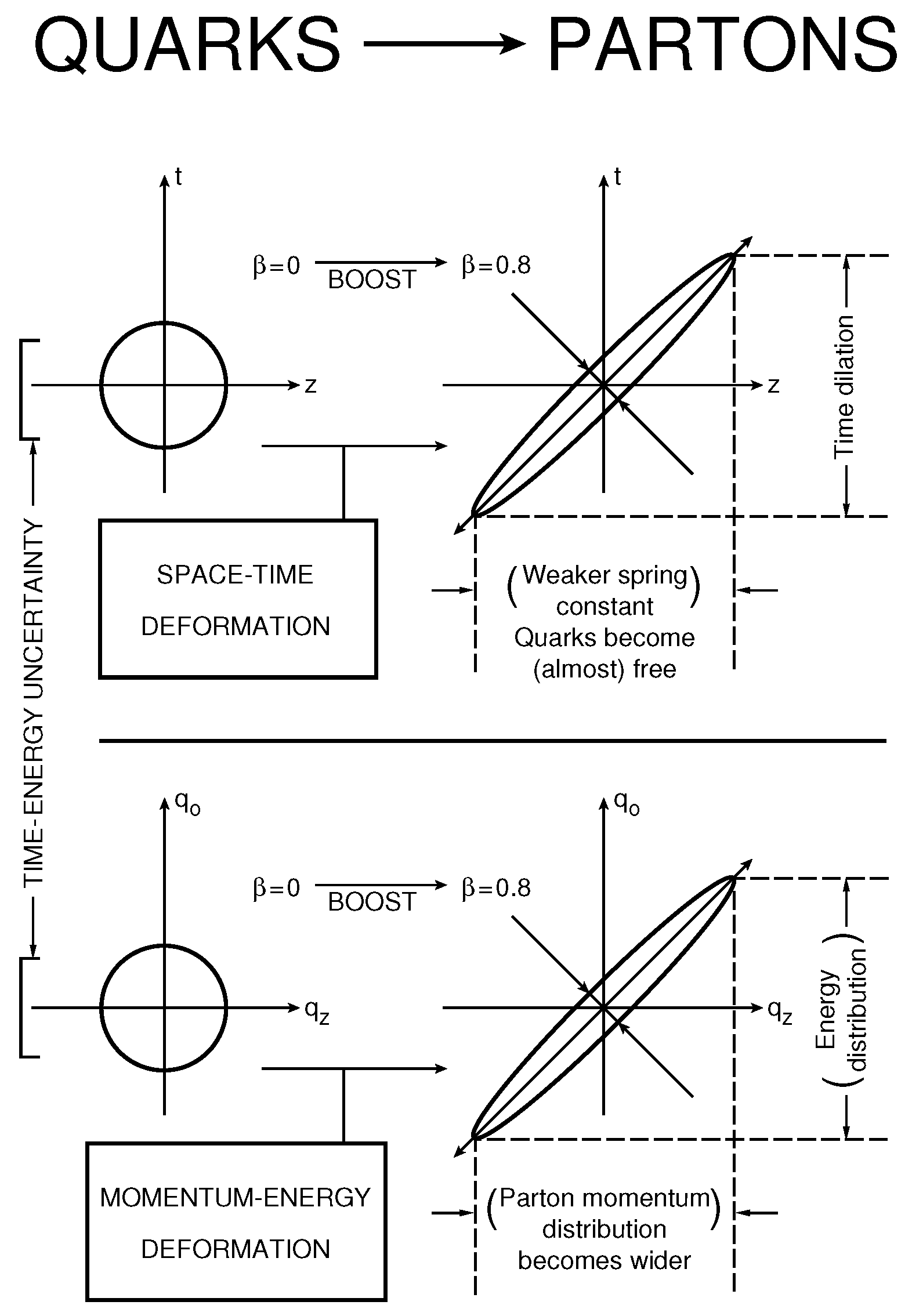
In order to address this question, let us go to Figure 5, which illustrates the Lorentz-squeeze property of the hadron as the hadron gains its speed. If we use the harmonic oscillator wave function, its momentum-energy wave function takes the same form as the space-time wave function. As the hadron gains its speed, both wave functions become squeezed.

As the wave function becomes squeezed, the distribution becomes wide-spread, the spring constant appear to become weaker. Consequently, the constituent quarks appear to become free particles.

If the constituent particles are confined in the narrow elliptic region, they become like massless particles. If those massless particles have a wide-spread momentum distribution, it is like a black-body radiation with infinite number of photon distributions.

We have addressed this question extensively in the literature, and concluded Gell-Mann’s quark model and Feynman’s parton model are two different manifestations of the same Lorentz-covariant quantity [19,35,36]. Thus coherent quarks and incoherent partons are perfectly consistent within the framework of quantum mechanics and special relativity [33]. Indeed, this defines Feynman’s decoherence [34].

More recently, we were able to explain this decoherence problem in terms of the interaction time among the constituent quarks and the time required for each quark to interact with external signals [4].

7.2. Proton Form Factors and Lorentz Coherence

As early as in 1970, Fujimura et al. calculated the electromagnetic form factor of the proton using the wave functions given in this paper and obtained the so-called “dipole” cut-off of the form factor [37]. At that time, these authors did not have a benefit of the differential equation of Feynman and his co-authors [12]. Since their wave functions can now be given a bona-fide covariant probability interpretation, their calculation could be placed between the two limiting cases of quarks and partons.

Even before the calculation of Fujimura et al. in 1965, the covariant wave functions were discussed by various authors [38,39,40]. In 1970, Licht and Pagnamenta also discussed this problem with Lorentz-contracted wave functions [41].

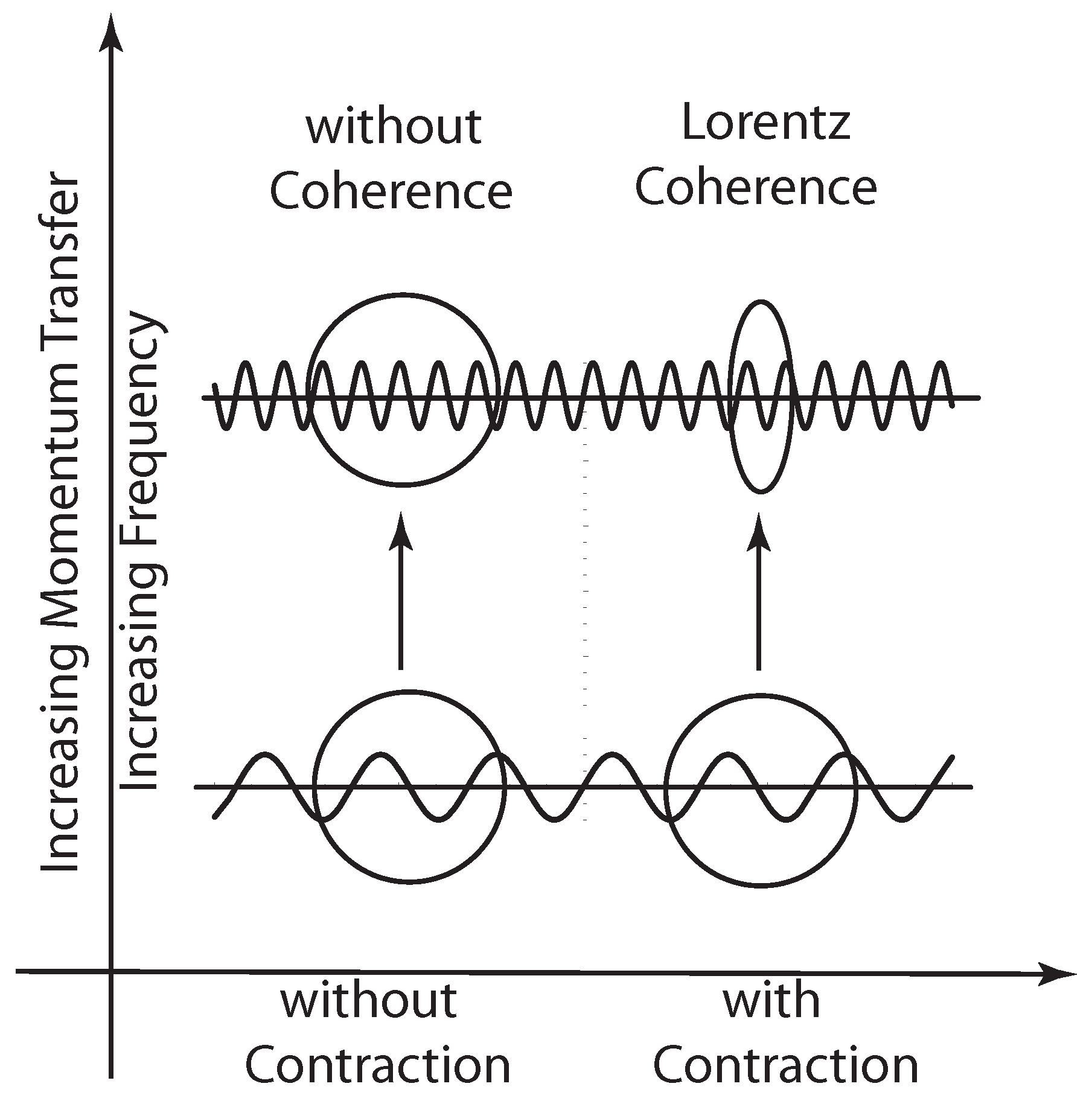
In our 1973 paper [42], we attempted to explain the covariant oscillator wave function in terms of the coherence between the incoming signal and the width of the contracted wave function. This aspect was explained in terms of the overlap of the energy-momentum wave function in our book [5].

In this paper, we would like to go back to the coherence problem we raised in 1973, and follow-up on it. In the Lorentz frame where the momentum of the proton has the opposite signs before and after the collision, the four-momentum transfer is

$$(p,E)-(-p,E)=(2p,0)$$

(67)

where the proton comes along the z direction with its momentum p, and its energy $\sqrt{p^2+m^2}$.

Then the form factor becomes

$$F\left(p\right)=\int e^{2ipz}{\left({\psi }_{\eta }(z,t)\right)}^{*}{\psi }_{-\eta }(z,t)dzdt$$

(68)

If we use the ground-state oscillator wave function, this integral becomes

$$\frac{1}{\pi }\int e^{2ipz}exp\left\{-cosh\left(2\eta \right)\left(z^2+t^2\right)\right\}dzdt$$

(69)

After the t integration, this integral becomes

$$\frac{1}{\sqrt{\pi cosh\left(2\eta \right)}}\int e^{2ipz}exp\left\{-z^{2}cosh\left(2\eta \right)\right\}dz$$

(70)

The integrand is a product of a Gaussian factor and a sinusoidal oscillation. The width of the Gaussian factor shrinks by $1/\sqrt{cosh\left(2\eta \right)}$, which becomes $exp(-\eta )$ as $\eta$ becomes large. The wave length of the sinusoidal factor is inversely proportional to the momentum p. The wave length decreases also at the rate of $exp(-\eta ).$ Thus, the rate of the shrinkage is the same for both the Gaussian and sinusoidal factors. For this reason, the cutoff rate of the form factor of Equation (68) should be less than that for

$$\int e^{2ipz}{\left({\psi }_0(z,t)\right)}^{*}{\psi }_0(z,t)dzdt=\frac{1}{\sqrt{\pi }}\int e^{2ipz}exp\left(-z^2\right)dz$$

(71)

which corresponds to the form factor without the squeeze effect on the wave function. The integration of this expression lead to $exp\left(-p^2\right),$ which corresponds to an exponential cut-off as $p^2$ becomes large.

Let us go back to the form factor of Equation (68). If we complete the integral, it becomes

$$F\left(p\right)=\frac{1}{cosh\left(2\eta \right)}exp\left\{\frac{-p^2}{cosh\left(2\eta \right)}\right\}$$

(72)

As $p^2$ becomes large, the Gaussian factor becomes a constant. However, the factor $1/cosh\left(2\eta \right)$ leads the form factor decrease of $1/p^2$, which is a much slower decrease than the exponential cut-off without squeeze effect.

There still is a gap between this mathematical formula and the observed experimental data. Before looking at the experimental curve, we have to realize that there are three quarks inside the hadron with two oscillator mode. This will lead to a ${\left(1/p^2\right)}^2$ cut-off, which is commonly called the dipole cut-off in the literature.

There is still more work to be done. For instance, the effect of the quark spin should be addressed [43,44]. Also there are reports of deviations from the exact dipole cut-off [45]. There have been attempts to study the form factors based on the four-dimensional rotation group [46], and also on the lattice QCD [47],

Yet, it is gratifying to note that the effect of Lorentz squeeze lead to the polynomial decrease in the momentum transfer, thanks to the Lorentz coherence illustrated in Figure 6. We started our logic from the fundamental principles of quantum mechanics and relativity.

8. Conclusions

In this paper, we presented one mathematical formalism applicable both to the entanglement problems in quantum optics [3] and to high-energy hadronic physics [4]. The formalism is based on harmonic oscillators familiar to us. We have presented a complete orthonormal set with a Lorentz-covariant probability interpretation.

Since both branches of physics share the same mathematical base, it is possible to translate physics from one branch to the other. In this paper, we have given a physical interpretation to the time-separation variable as a hidden variable in Feynman’s rest of the universe, in terms of the two-mode squeezed state where both photons are observable.

This paper is largely a review paper with an organization to suit the current interest in physics. For instance, the concepts of entanglement and decoherecne did not exist when those original papers were written. Furthermore, the probability interpretation given in Subsection 4.2 has not been published before.

The rotation symmetry plays its role in all branches of physics. We noted that the squeeze symmetry plays active roles in two different subjects of physics. It is possible that the squeeze transformation can serve useful purposes in many other fields, although we are not able to specify them at this time.