Spontaneous Symmetry Breaking and Nambu–Goldstone Bosons in Quantum Many-Body Systems
Abstract
:1. Introduction
2. Basic Properties of Spontaneously Broken Symmetries
2.1. Ground state and finite symmetry transformations
2.2. Explicit symmetry breaking and the choice of the ground state
3. Example: Free Nonrelativistic Particle
3.1. Hilbert space and inequivalent ground states
3.2. Spontaneous symmetry breaking and the Nambu–Goldstone boson
4. Achieving Spontaneous Symmetry Breaking: Minimization of Higgs Potentials
4.1. Group action on the order parameter space
4.2. Minimization of Higgs potentials
4.3. Example: spin-one color superconductor
5. Goldstone Theorem and The Counting of Nambu–Goldstone Bosons
5.1. Goldstone theorem
5.2. Goldstone boson counting: Dispersion relations
5.3. Goldstone boson counting: Charge densities
5.4. Linear sigma model
6. Further Examples
6.1. Nonrelativistic Boulware–Gilbert model
6.2. Heisenberg ferromagnet
6.3. Linear sigma model
7. Low-Energy Effective Field Theory for NG Bosons
7.1. Coset construction of effective Lagrangians
7.2. Geometric interpretation
7.3. Nonrelativistic effective Lagrangians
7.4. Applications of effective field theory
8. Conclusions
Acknowledgments
References
- Weinberg, S. The Quantum Theory of Fields; Cambridge University Press: Cambridge, UK, 1995; Volume I. [Google Scholar]
- Guralnik, G.S.; Hagen, C.R.; Kibble, T.W.B. Broken symmetries and the Goldstone theorem. In Advances in Particle Physics, Cool, R.L., Marshak, R.E., Eds.; Wiley: New York, NY, USA, 1968; Volume II, pp. 567–708. [Google Scholar]
- Nielsen, H.B.; Chadha, S. On how to Count Goldstone Bosons. Nucl. Phys. 1976, B105, 445–453. [Google Scholar] [CrossRef]
- Leutwyler, H. Nonrelativistic effective Lagrangians. Phys. Rev. 1994, D49, 3033–3043. [Google Scholar] [CrossRef]
- Georgi, H. Effective Field Theory. Annu. Rev. Nucl. Part. Sci. 1993, 43, 209–252. [Google Scholar] [CrossRef]
- Kaplan, D.B. Effective Field Theories. Lectures given at 7th Summer School in Nuclear Physics: “Symmetries”, Seattle, WA, USA, 19-30 June, 1995. arXiv:nucl-t/9506035.
- Manohar, A.V. Effective Field Theories. In Perturbative and Nonperturbative Aspects of Quantum Field Theory: Proceedings of the 35. Internationale Universitätswochen für Kern- und Teilchenphysik, Schladming, Austria, 2–9 March, 1996; Latal, H., Schweiger, W., Eds.; Springer: Berlin, Germany, 1997; Volume 479, pp. 311–362. [Google Scholar]
- Pich, A. Effective Field Theory. In Probing the Standard Model of Particle Interactions; Gupta, R., Morel, A., de Rafael, E., David, F., Eds.; North Holland: Amsterdam, The Netherlands, 1999; pp. 949–1049. [Google Scholar]
- Burgess, C.P. Goldstone and pseudo-Goldstone bosons in nuclear, particle and condensed-matter physics. Phys. Rep. 2000, 330, 193–261. [Google Scholar] [CrossRef]
- Scherer, S. Introduction to chiral perturbation theory. Adv. Nucl. Phys. 2003, 27, 277–538. [Google Scholar]
- Bijnens, J. Chiral perturbation theory beyond one loop. Prog. Part. Nucl. Phys. 2007, 58, 521–586. [Google Scholar] [CrossRef]
- Scherer, S. Chiral perturbation theory: Introduction and recent results in the one-nucleon sector. Prog. Part. Nucl. Phys. 2010, 64, 1–60. [Google Scholar] [CrossRef]
- Fabri, E.; Picasso, L.E. Quantum Field Theory and Approximate Symmetries. Phys. Rev. Lett. 1966, 16, 408–410. [Google Scholar] [CrossRef]
- Lange, R.V. Nonrelativistic Theorem Analogous to the Goldstone Theorem. Phys. Rev. 1966, 146, 301–303. [Google Scholar] [CrossRef]
- Weinberg, S. The Quantum Theory of Fields; Cambridge University Press: Cambridge, UK, 1996; Volume II. [Google Scholar]
- Yang, C.N. Concept of Off-Diagonal Long-Range Order and the Quantum Phases of Liquid He and of Superconductors. Rev. Mod. Phys. 1962, 34, 694–704. [Google Scholar] [CrossRef]
- Miransky, V.A. Dynamical Symmetry Breaking in Quantum Field Theories; World Scientific: Singapore, 1993. [Google Scholar]
- Barut, A.O.; Raczka, R. Theory of Group Representations and Applications; Polish Scientific Publishers: Warszawa, Poland, 1977. [Google Scholar]
- Araki, H.; Woods, E.J. Representations of the Canonical Commutation Relations Describing a Nonrelativistic Infinite Free Bose Gas. J. Math. Phys. 1963, 4, 637–662. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Michel, L.; Radicati, L.A. Properties of the Breaking of Hadronic Internal Symmetry. Ann. Phys. 1971, 66, 758–783. [Google Scholar] [CrossRef]
- Michel, L. Symmetry defects and broken symmetry. Configurations Hidden Symmetry. Rev. Mod. Phys. 1980, 52, 617–651. [Google Scholar] [CrossRef]
- Kim, J.S. General Method for Analyzing Higgs Potentials. Nucl. Phys. 1982, B196, 285–300. [Google Scholar] [CrossRef]
- Vollhardt, D.; Wölfle, P. The Superfluid Phases of Helium 3; Taylor and Francis: London, UK, 1990. [Google Scholar]
- Slansky, R. Group Theory for Unified Model Building. Phys. Rep. 1981, 79, 1–128. [Google Scholar] [CrossRef]
- Meljanac, S. Origin of Counter-Examples to Michel’s Conjecture. Phys. Lett. 1986, B168, 371–375. [Google Scholar] [CrossRef]
- Abud, M.; Sartori, G. The Geometry of Spontaneous Symmetry Breaking. Ann. Phys. 1983, 150, 307–372. [Google Scholar] [CrossRef]
- Iida, K.; Baym, G. The superfluid phases of quark matter: Ginzburg–Landau theory and color neutrality. Phys. Rev. 2001, D63, 074018:1–074018:19. [Google Scholar] [CrossRef]
- Brauner, T. Helical ordering in the ground state of spin-one color superconductors as a consequence of parity violation. Phys. Rev. 2008, D78, 125027:1–125027:19. [Google Scholar] [CrossRef]
- Bailin, D.; Love, A. Superfluidity and Superconductivity in Relativistic Fermion Systems. Phys. Rep. 1984, 107, 325–385. [Google Scholar] [CrossRef]
- Schmitt, A. Ground state in a spin-one color superconductor. Phys. Rev. 2005, D71, 054016:1–054016:28. [Google Scholar] [CrossRef]
- Mermin, N.D. d-wave pairing near the transition temperature. Phys. Rev. 1974, A9, 868–872. [Google Scholar] [CrossRef]
- Alford, M.G.; Schmitt, A.; Rajagopal, K.; Schäfer, T. Color superconductivity in dense quark matter. Rev. Mod. Phys. 2008, 80, 1455–1515. [Google Scholar] [CrossRef]
- Goldstone, J. Field Theories with Superconductor Solutions. Nuovo Cim. 1961, 19, 154–164. [Google Scholar] [CrossRef]
- Goldstone, J.; Salam, A.; Weinberg, S. Broken Symmetries. Phys. Rev. 1962, 127, 965–970. [Google Scholar] [CrossRef]
- Low, I.; Manohar, A.V. Spontaneously Broken Spacetime Symmetries and Goldstone’s Theorem. Phys. Rev. Lett. 2002, 88, 101602:1–101602:4. [Google Scholar] [CrossRef] [PubMed]
- Boulware, D.G.; Gilbert, W. Connection between Gauge Invariance and Mass. Phys. Rev. 1962, 126, 1563–1567. [Google Scholar] [CrossRef]
- Englert, F.; Brout, R. Broken Symmetry and the Mass of Gauge Vector Mesons. Phys. Rev. Lett. 1964, 13, 321–322. [Google Scholar] [CrossRef]
- Guralnik, G.S.; Hagen, C.R.; Kibble, T.W.B. Global Conservation Laws and Massless Particles. Phys. Rev. Lett. 1964, 13, 585–587. [Google Scholar] [CrossRef]
- Elitzur, S. Impossibility of Spontaneously Breaking Local Symmetries. Phys. Rev. 1975, D12, 3978–3982. [Google Scholar] [CrossRef]
- Frishman, Y.; Katz, A. Corollaries of the Goldstone Theorem. Phys. Rev. Lett. 1966, 16, 370–371. [Google Scholar] [CrossRef]
- Sachdev, S.; Senthil, T. Zero Temperature Phase Transitions in Quantum Heisenberg Ferromagnets. Ann. Phys. 1996, 251, 76–122. [Google Scholar] [CrossRef]
- Ho, T.L. Spinor Bose Condensates in Optical Traps. Phys. Rev. Lett. 1998, 81, 742–745. [Google Scholar] [CrossRef]
- Ohmi, T.; Machida, K. Bose–Einstein Condensation with Internal Degrees of Freedom in Alkali Atom Gases. J. Phys. Soc. Jpn. 1998, 67, 1822–1825. [Google Scholar] [CrossRef]
- Uchino, S.; Kobayashi, M.; Ueda, M. Bogoliubov Theory and Lee–Huang–Yang Correction in Spin-1 and Spin-2 Bose–Einstein Condensates in the Presence of the Quadratic Zeeman Effect. 2009; arXiv:0912.0355 [cond-mat.quant-gas]. [Google Scholar]
- Honerkamp, C.; Hofstetter, W. Ultracold Fermions and the SU(N) Hubbard Model. Phys. Rev. Lett. 2004, 92, 170403:1–170403:4. [Google Scholar] [CrossRef] [PubMed]
- Honerkamp, C.; Hofstetter, W. BCS pairing in Fermi systems with N different hyperfine states. Phys. Rev. 2004, B70, 094521:1–094521:10. [Google Scholar]
- He, L.; Jin, M.; Zhuang, P. Superfluidity in a three-flavor Fermi gas with SU(3) gauge symmetry. Phys. Rev. 2006, A74, 033604:1–033604:8. [Google Scholar]
- Schäfer, T.; Son, D.T.; Stephanov, M.A.; Toublan, D.; Verbaarschot, J.J.M. Kaon condensation and Goldstone’s theorem. Phys. Lett. 2001, B522, 67–75. [Google Scholar] [CrossRef]
- Miransky, V.A.; Shovkovy, I.A. Spontaneous Symmetry Breaking with Abnormal Number of Nambu–Goldstone Bosons and Kaon Condensate. Phys. Rev. Lett. 2002, 88, 111601:1–111601:4. [Google Scholar] [CrossRef] [PubMed]
- Andersen, J.O. Pion and kaon condensation at finite temperature and density. Phys. Rev. 2007, D75, 065011:1–065011:11. [Google Scholar] [CrossRef]
- Beraudo, A.; De Pace, A.; Martini, M.; Molinari, A. Spontaneous symmetry breaking and response functions. Ann. Phys. 2005, 317, 444–473. [Google Scholar] [CrossRef]
- Blaschke, D.; Ebert, D.; Klimenko, K.G.; Volkov, M.K.; Yudichev, V.L. Abnormal number of Nambu–Goldstone bosons in the color-asymmetric dense color superconducting phase of a Nambu–Jona-Lasinio-type model. Phys. Rev. 2004, D70, 014006:1–014006:11. [Google Scholar] [CrossRef]
- Buballa, M.; Hošek, J.; Oertel, M. Anisotropic admixture in color-superconducting quark matter. Phys. Rev. Lett. 2003, 90, 182002:1–182002:4. [Google Scholar] [CrossRef] [PubMed]
- Brauner, T. Goldstone boson counting in linear sigma models with chemical potential. Phys. Rev. 2005, D72, 076002:1–076002:10. [Google Scholar] [CrossRef]
- Brauner, T. Goldstone bosons in presence of charge density. Phys. Rev. 2007, D75, 105014:1–105014:13. [Google Scholar] [CrossRef]
- Kapusta, J.I.; Gale, C. Finite-Temperature Field Theory: Principles and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Georgi, H. Lie Algebras in Particle Physics. In Frontiers in Physics; Perseus Books: Reading, MA, USA, 1999. [Google Scholar]
- Brauner, T. Spontaneous symmetry breaking in the linear sigma model at finite chemical potential: One-loop corrections. Phys. Rev. 2006, D74, 085010:1–085010:13. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological Lagrangians. Physica 1979, A96, 327–340. [Google Scholar] [CrossRef]
- Coleman, S.R.; Wess, J.; Zumino, B. Structure of Phenomenological Lagrangians. I. Phys. Rev. 1969, 177, 2239–2247. [Google Scholar] [CrossRef]
- Callan, C.G.; Coleman, S.R.; Wess, J.; Zumino, B. Structure of Phenomenological Lagrangians. II. Phys. Rev. 1969, 177, 2247–2250. [Google Scholar] [CrossRef]
- Leutwyler, H. On the Foundations of Chiral Perturbation Theory. Ann. Phys. 1994, 235, 165–203. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory to One Loop. Ann. Phys. 1984, 158, 142–210. [Google Scholar] [CrossRef]
- Gasser, J.; Leutwyler, H. Chiral Perturbation Theory: Expansions in the Mass of the Strange Quark. Nucl. Phys. 1985, B250, 465–516. [Google Scholar] [CrossRef]
- Roman, J.M.; Soto, J. Effective Field Theory Approach to Ferromagnets and Antiferromagnets in Crystalline Solids. Int. J. Mod. Phys. 1999, B13, 755–789. [Google Scholar] [CrossRef]
- Hofmann, C.P. Spin-wave scattering in the effective Lagrangian perspective. Phys. Rev. 1999, B60, 388–405. [Google Scholar] [CrossRef]
- Hofmann, C.P. Spontaneous magnetization of the O(3) ferromagnet at low temperatures. Phys. Rev. 2002, B65, 094430:1–094430:12. [Google Scholar] [CrossRef]
- Hofmann, C.P. Effective analysis of the O(N) antiferromagnet: Low-temperature expansion of the order parameter. Phys. Rev. 1999, B60, 406–413. [Google Scholar] [CrossRef]
- Kämpfer, F.; Moser, M.; Wiese, U.J. Systematic low-energy effective theory for magnons and charge carriers in an antiferromagnet. Nucl. Phys. 2005, B729, 317–360. [Google Scholar] [CrossRef]
- Brügger, C.; Kämpfer, F.; Moser, M.; Pepe, M.; Wiese, U.J. Two-hole bound states from a systematic low-energy effective field theory for magnons and holes in an antiferromagnet. Phys. Rev. 2006, B74, 224432. [Google Scholar] [CrossRef]
- Hofmann, C.P. Thermodynamics of O(N) antiferromagnets in 2 + 1 dimensions. Phys. Rev. 2010, B81, 014416:1–014416:17. [Google Scholar]
- Andersen, J.O. Theory of the weakly interacting Bose gas. Rev. Mod. Phys. 2004, 76, 599–639. [Google Scholar] [CrossRef]
- Andersen, J.O. Effective Field Theory for Goldstone Bosons in Nonrelativistic Superfluids. 2002; arXiv:cond-mat/0209243. [Google Scholar]
- Yukalov, V.I. Representative statistical ensembles for Bose systems with broken gauge symmetry. Ann. Phys. 2008, 323, 461–499. [Google Scholar] [CrossRef]
- Son, D.T.; Wingate, M. General coordinate invariance and conformal invariance in nonrelativistic physics: Unitary Fermi gas. Ann. Phys. 2006, 321, 197–224. [Google Scholar] [CrossRef]
- Son, D.T. Low-Energy Quantum Effective Action for Relativistic Superfluids. 2002; arXiv:hep-ph/0204199. [Google Scholar]
- Manuel, C.; Dobado, A.; Llanes-Estrada, F.J. Shear viscosity in a CFL quark star. J. High Energy Phys. 2005, 09, 076:1–076:22. [Google Scholar] [CrossRef]
- Weinberg, S. Approximate Symmetries and Pseudo-Goldstone Bosons. Phys. Rev. Lett. 1972, 29, 1698–1701. [Google Scholar] [CrossRef]
- Coleman, S.R.; Weinberg, E.J. Radiative Corrections as the Origin of Spontaneous Symmetry Breaking. Phys. Rev. 1973, D7, 1888–1910. [Google Scholar] [CrossRef]
- Volovik, G.E.; Khazan, M.V. Dynamics of the A-phase of 3He at low pressures. Sov. Phys. -JETP 1982, 55, 867–871. [Google Scholar]
- Volovik, G.E.; Khazan, M.V. A classification of the collective modes of the order parameter in superfluid 3He. Sov. Phys. -JETP 1983, 58, 551–555. [Google Scholar]
- Müther, H.; Sedrakian, A. Breaking rotational symmetry in two-flavor color superconductors. Phys. Rev. 2003, D67, 085024:1–085024:6. [Google Scholar] [CrossRef]
- Sannino, F.; Schäfer, W. Relativistic massive vector condensation. Phys. Lett. 2002, B527, 142–148. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Miransky, V.A.; Shovkovy, I.A. Spontaneous rotational symmetry breaking and roton like excitations in gauged σ-model at finite density. Phys. Lett. 2004, B581, 82–92. [Google Scholar] [CrossRef]
- Leutwyler, H. Phonons as Goldstone bosons. Helv. Phys. Acta 1997, 70, 275–286. [Google Scholar]
- Casalbuoni, R.; Nardulli, G. Inhomogeneous superconductivity in condensed matter and QCD. Rev. Mod. Phys. 2004, 76, 263–320. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
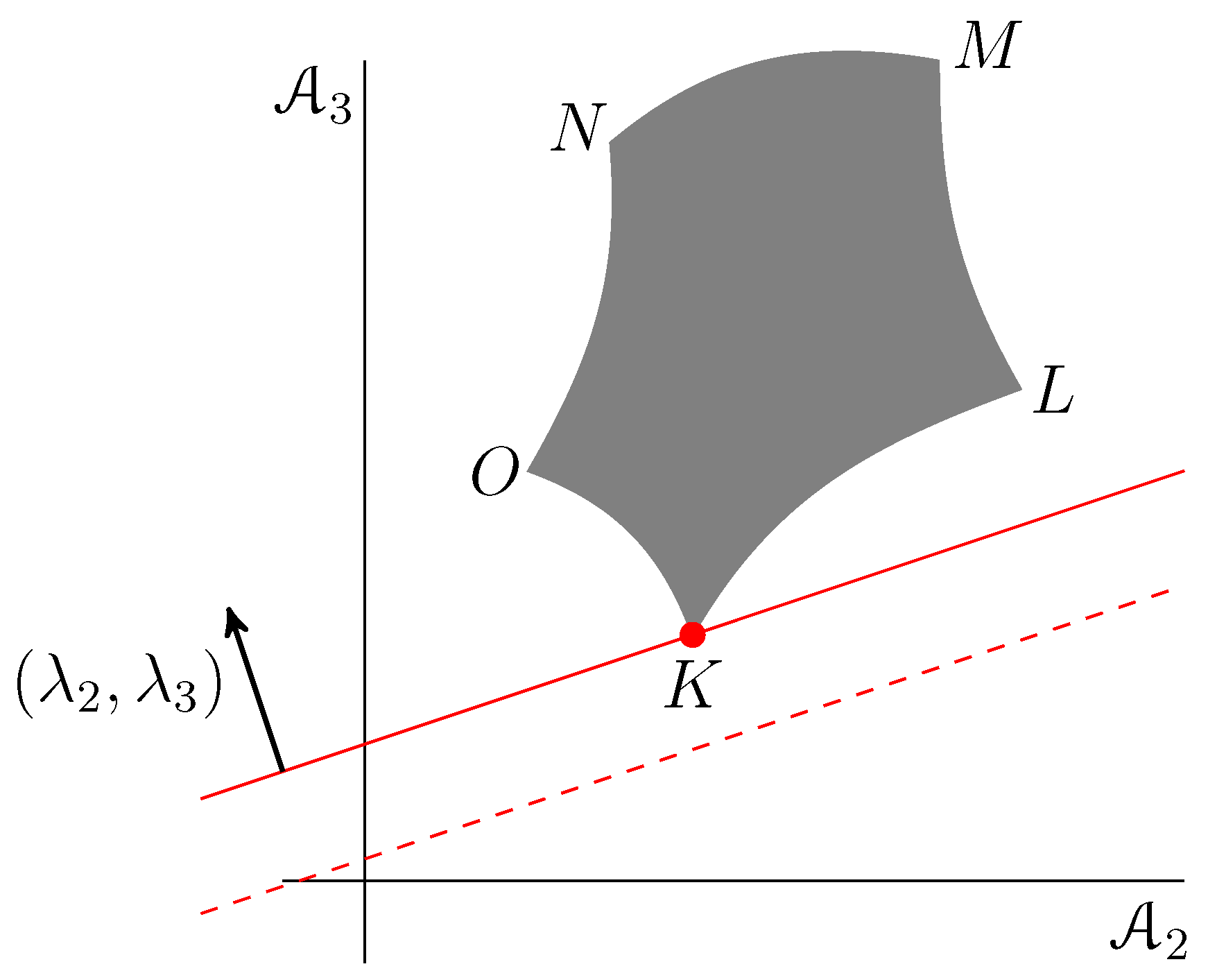
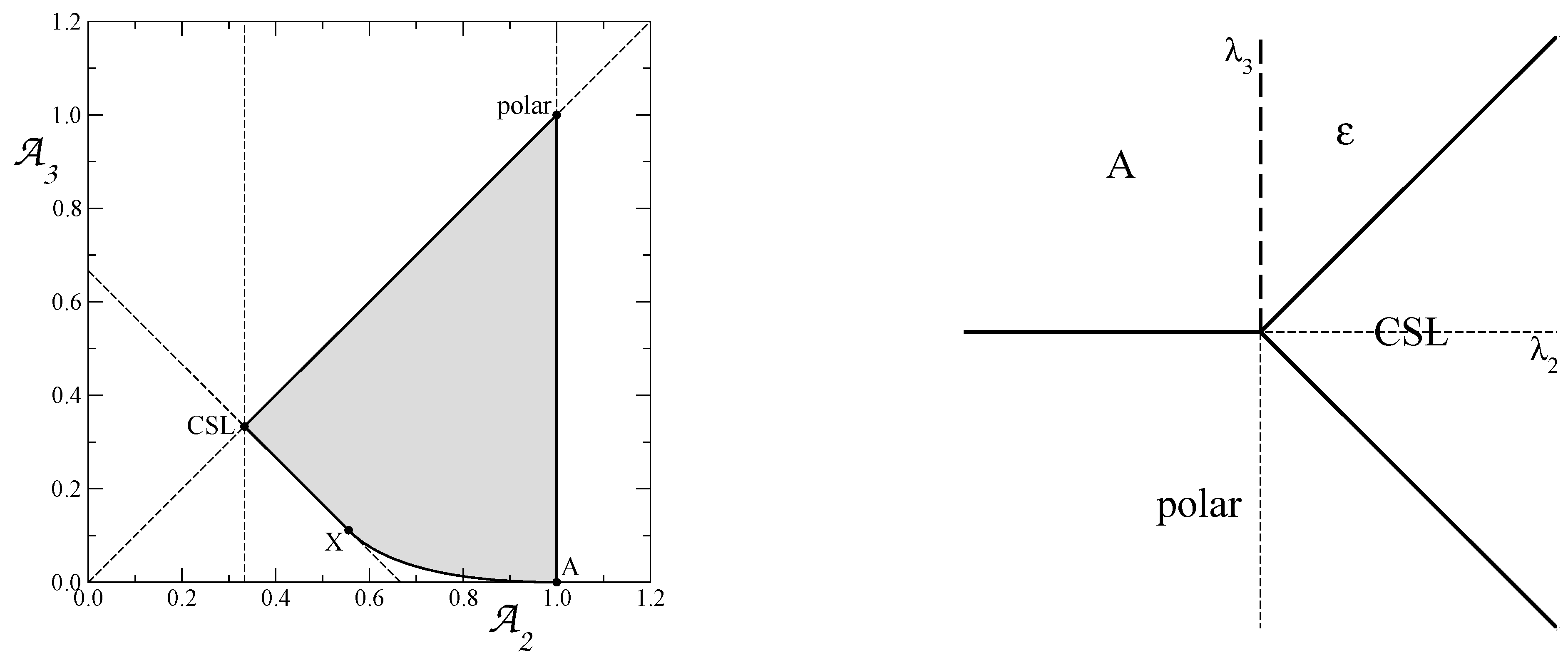
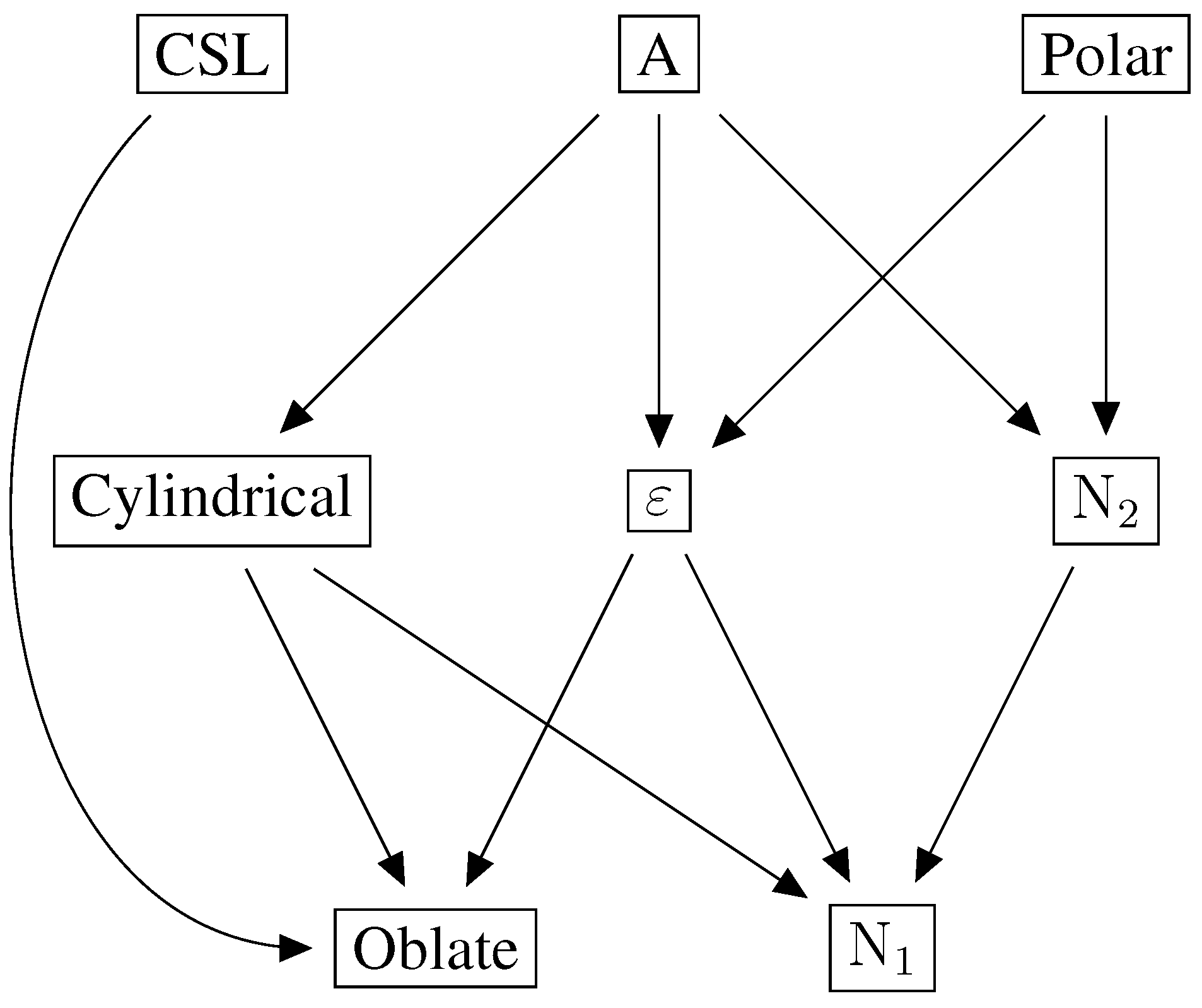
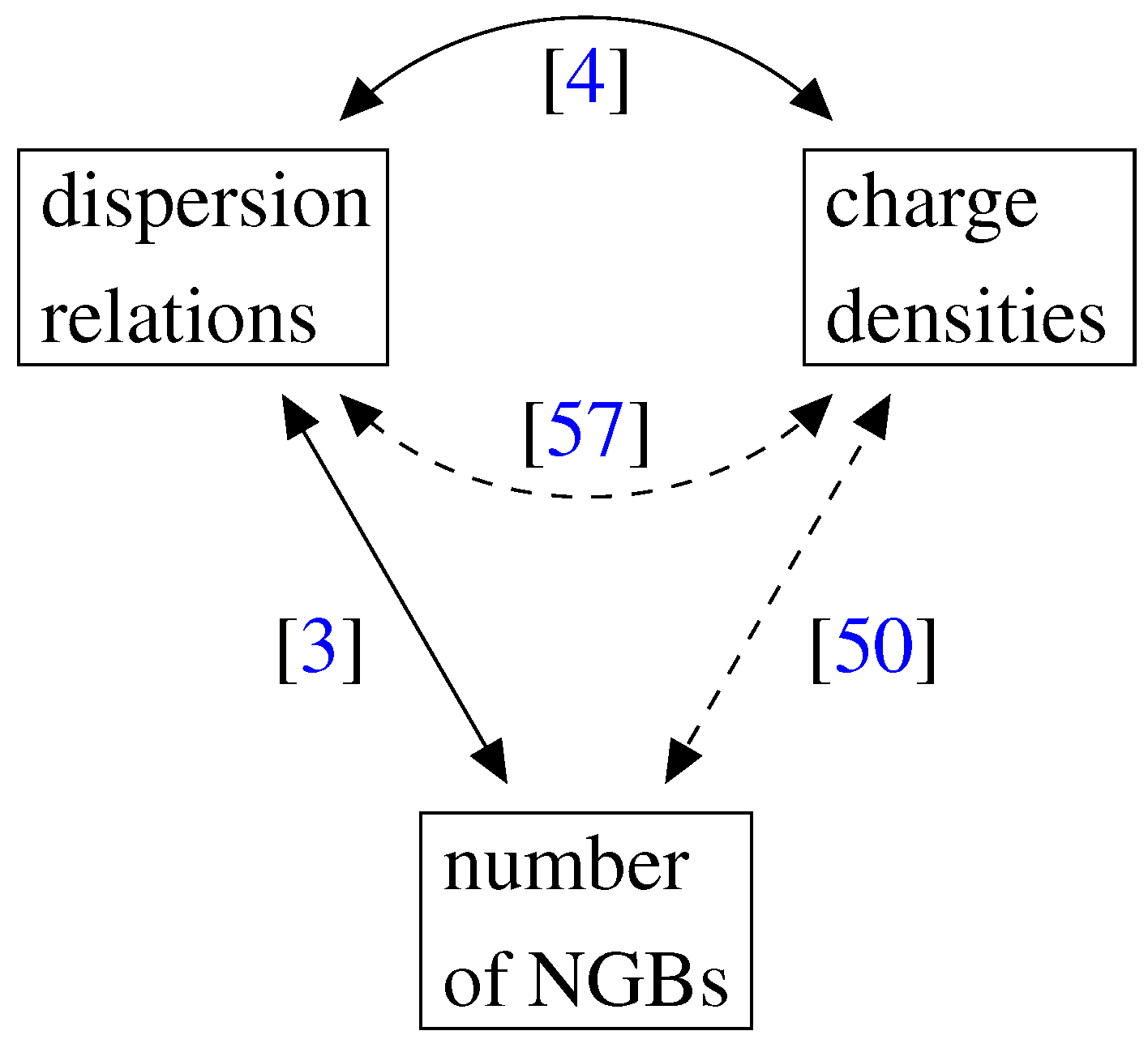
| Oblate | Cylindrical | A | |
| CSL | Polar | ||
© 2010 by the author; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Brauner, T. Spontaneous Symmetry Breaking and Nambu–Goldstone Bosons in Quantum Many-Body Systems. Symmetry 2010, 2, 609-657. https://doi.org/10.3390/sym2020609
Brauner T. Spontaneous Symmetry Breaking and Nambu–Goldstone Bosons in Quantum Many-Body Systems. Symmetry. 2010; 2(2):609-657. https://doi.org/10.3390/sym2020609
Chicago/Turabian StyleBrauner, Tomáš. 2010. "Spontaneous Symmetry Breaking and Nambu–Goldstone Bosons in Quantum Many-Body Systems" Symmetry 2, no. 2: 609-657. https://doi.org/10.3390/sym2020609
APA StyleBrauner, T. (2010). Spontaneous Symmetry Breaking and Nambu–Goldstone Bosons in Quantum Many-Body Systems. Symmetry, 2(2), 609-657. https://doi.org/10.3390/sym2020609




