The Number of Symmetric Colorings of the Quaternion Group

Abstract

We compute the number of symmetric r-colorings and the number of equivalence classes of symmetric r-colorings of the quaternion group.

The symmetry of a group G with respect to an element $g\in G$ is the mapping

$${\sigma }_g:G\ni x\mapsto g{x}^{-1}g\in G.$$

This is an old notion, which can be found in the book [1]. And it is a very natural one, since

$${\sigma }_g={\lambda }_g\circ \iota \circ {\lambda }_g^{-1}={\rho }_g\circ \iota \circ {\rho }_g^{-1},$$

where

$${\lambda }_g:G\ni x\mapsto gx\in G,{\rho }_g:G\ni x\mapsto xg\in G,\mathrm{and}\iota :G\ni x\mapsto x^{-1}\in G$$

are the left translation, the right translation, and the inversion, respectively. Indeed, it follows from ${\lambda }_g\left(x\right)=gx$ that ${\lambda }_g^{-1}\left(gx\right)=x$, so ${\lambda }_g^{-1}\left(x\right)=g^{-1}x$. Consequently, ${\lambda }_g^{-1}={\lambda }_{g^{-1}}$. Similarly, ${\rho }_g^{-1}={\rho }_{g^{-1}}$. Then

$$\begin{array}{cc}\hfill {\lambda }_g\circ \iota \circ {\lambda }_g^{-1}\left(x\right)& ={\lambda }_g\circ \iota \circ {\lambda }_{g^{-1}}\left(x\right)=g{\left(g^{-1}x\right)}^{-1}=g{x}^{-1}g\mathrm{and}\hfill \\ \hfill {\rho }_g\circ \iota \circ {\rho }_g^{-1}\left(x\right)& ={\rho }_g\circ \iota \circ {\rho }_{g^{-1}}\left(x\right)={\left(x{g}^{-1}\right)}^{-1}=g{x}^{-1}g.\hfill \end{array}$$

Various aspects of symmetries on groups had been studied in [2].

Now let G be a finite group and let $r\in \mathbb{N}$. An r-coloring of G is any mapping $\chi :G\to \{1,\dots ,r\}$. A coloring $\chi$ of G is symmetric if there is $g\in G$ such that $\chi \left(g{x}^{-1}g\right)=\chi \left(x\right)$ for all $x\in G$. That is, a coloring is symmetric if it is invariant under some symmetry. Define the equivalence relation ∼ on the set of all r-colorings of G by

$$\chi \sim \phi \mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\mathrm{there}\mathrm{is}g\in G\mathrm{such}\mathrm{that}\chi \left(x{g}^{-1}\right)=\phi \left(x\right)\mathrm{for}\mathrm{all}x\in G.$$

That is, colorings are equivalent if one of them can be obtain from the other by a right translation.

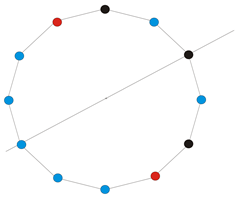
Note that in the case of a finite cyclic group ${\mathbb{Z}}_n$ these notions have a very simple geometric illustration. Identifying ${\mathbb{Z}}_n$ with the vertices of a regular n-gon we obtain that a coloring is symmetric if it is invariant with respect to some mirror symmetry with an axis crossing the center of the polygon and one of its vertices.

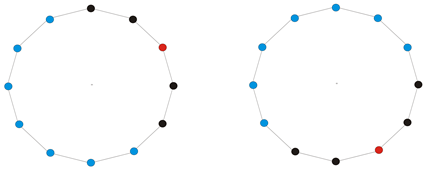
Colorings are equivalent if one of them can be obtained from the other by rotating about the center of the polygon.

Obviously, the number of all r-colorings of G is $r^{\left|G\right|}$. Applying Burnside’s Lemma [3, I, §3] shows that the number of equivalence classes of r-colorings of G is equal to

$$\frac{1}{\left|G\right|}\sum _{g\in G}{r}^{|G:\langle g\rangle |},$$

where $\langle g\rangle$ is the subgroup generated by g. However, counting symmetric r-colorings and equivalence classes of symmetric r-colorings of G turned out to be quite a difficult question.

Let $S_r\left(G\right)$ denote the set of symmetric r-colorings of G. In [4] it was shown that if G is Abelian, then

$$\begin{array}{cc}\hfill |S_r\left(G\right)|& =\sum _{X\le G}\sum _{Y\le X}\frac{\mu (Y,X)|G/Y|}{\left|B\right(G/Y\left)\right|}{r}^{\frac{|G/X|+\left|B\right(G/X\left)\right|}{2}}\mathrm{and}\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill |S_r\left(G\right)/\sim |& =\sum _{X\le G}\sum _{Y\le X}\frac{\mu (Y,X)}{\left|B\right(G/Y\left)\right|}{r}^{\frac{|G/X|+\left|B\right(G/X\left)\right|}{2}}.\hfill \end{array}$$

(2)

Here, X runs over subgroups of G, Y over subgroups of X, $\mu (Y,X)$ is the Möbius function of the lattice of subgroups of G, and $B\left(G\right)=\{x\in G:x^2=e\}$.

Given a finite partially ordered set, the Möbius function is defined as follows:

$$\mu (a,b)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}a=b\hfill \\ -\sum _{a<z\le b}\mu (z,b)\hfill & \mathrm{if}a<b\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

See [3, IV] for more information about the Möbius function.

In the case of ${\mathbb{Z}}_n$ formulas 1, 2 were reduced to the following elementary ones [4]:

If n is odd then

$$\begin{array}{cc}\hfill |S_r\left({\mathbb{Z}}_n\right)/\sim |& =r^{\frac{n+1}{2}}\mathrm{and}\hfill \\ \hfill |S_r\left({\mathbb{Z}}_n\right)|& =\sum _{d|n}d\prod _{p|\frac{n}{d}}(1-p)r^{\frac{d+1}{2}}.\hfill \end{array}$$

If $n=2^{l}m$, where $l\ge 1$ and m is odd, then

$$\begin{array}{cc}\hfill |S_r\left({\mathbb{Z}}_n\right)/\sim |& =\frac{r^{\frac{n}{2}+1}+r^{\frac{m+1}{2}}}{2}\mathrm{and}\hfill \\ \hfill |S_r\left({\mathbb{Z}}_n\right)|& =\sum _{d|\frac{n}{2}}d\prod _{p|\frac{n}{2d}}(1-p)r^{d+1}.\hfill \end{array}$$

As usual, p denotes a prime number.

Recently, an approach for computing $|S_r\left(G\right)|$ and $|S_r\left(G\right)/\sim |$ in the case of an arbitrary finite group G has been found [5]. The approach is based on constructing the partially ordered set of so called optimal partitions of G.

Given a partition $\pi$ of G, the stabilizer and the center of $\pi$ are defined by

$$\begin{array}{cc}\hfill St\left(\pi \right)& =\{g\in G:\mathrm{for}\mathrm{every}x\in G,x\mathrm{and}x{g}^{-1}\mathrm{belong}\mathrm{to}\mathrm{the}\mathrm{same}\mathrm{cell}\mathrm{of}\pi \}\mathrm{and}\hfill \\ \hfill Z\left(\pi \right)& =\{g\in G:\mathrm{for}\mathrm{every}x\in G,x\mathrm{and}g{x}^{-1}g\mathrm{belong}\mathrm{to}\mathrm{the}\mathrm{same}\mathrm{cell}\mathrm{of}\pi \}.\hfill \end{array}$$

$St\left(\pi \right)$ is a subgroup of G and $Z\left(\pi \right)$ is a union of left cosets of G modulo $St\left(\pi \right)$. Furthermore, if $e\in Z\left(\pi \right)$, then $Z\left(\pi \right)$ is also a union of right cosets of G modulo $St\left(\pi \right)$ and for every $a\in Z\left(\pi \right)$, $\langle a\rangle \subseteq Z\left(\pi \right)$. We say that a partition $\pi$ of G is optimal if $e\in Z\left(\pi \right)$ and for every partition ${\pi }^{\prime }$ of G with $St\left({\pi }^{\prime }\right)=St\left(\pi \right)$ and $Z\left({\pi }^{\prime }\right)=Z\left(\pi \right)$, one has $\pi \le {\pi }^{\prime }$. The latter means that every cell of $\pi$ is contained in some cell of ${\pi }^{\prime }$, or equivalently, the equivalence corresponding to $\pi$ is contained in that of ${\pi }^{\prime }$. The partially ordered set of optimal partitions of G can be naturally identified with the partially ordered set of pairs $(A,B)$ of subsets of G such that $A=St\left(\pi \right)$ and $B=Z\left(\pi \right)$ for some partition $\pi$ of G with $e\in Z\left(\pi \right)$. For every partition $\pi$, we write $\left|\pi \right|$ to denote the number of cells of $\pi$.

In [5] it was shown that for every finite group G and $r\in \mathbb{N}$,

$$\begin{array}{cc}\hfill |S_r\left(G\right)|& =\left|G\right|\sum _{x\in P}\sum _{y\le x}\frac{\mu (y,x)}{\left|Z\right(y\left)\right|}{r}^{\left|x\right|}\mathrm{and}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill |S_r\left(G\right)/\sim |& =\sum _{x\in P}\sum _{y\le x}\frac{\mu (y,x)\left|St\right(y\left)\right|}{\left|Z\right(y\left)\right|}{r}^{\left|x\right|}\hfill \end{array}$$

(4)

where P is the partially ordered set of optimal partitions of G.

The partially ordered set of optimal partitions $\pi$ of G together with parameters $\left|St\right(\pi \left)\right|$, $\left|Z\right(\pi \left)\right|$ and $\left|\pi \right|$ can be constructed by starting with the finest optimal partition $\{\{x,x^{-1}\}:x\in G\}$ and using the following fact:

Let $\pi$ be an optimal partition of G and let $A\subseteq G$. Let ${\pi }_1$ be the finest partition of G such that $\pi \le {\pi }_1$ and $A\subseteq St\left({\pi }_1\right)$, and let ${\pi }_2$ be the finest partition of G such that $\pi \le {\pi }_2$ and $A\subseteq Z\left({\pi }_2\right)$. Then the partitions ${\pi }_1$ and ${\pi }_2$ are also optimal.

In this note we compute explicitly the numbers $|S_r\left(Q\right)|$ and $|S_r\left(Q\right)/\sim |$ where $Q=\{\pm 1,\pm i,\pm j,\pm k\}$ is the quaternion group.

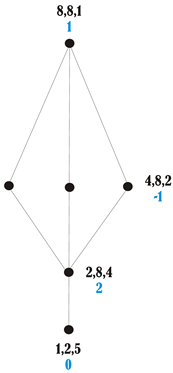
First, we list all optimal partitions $\pi$ of Q together with parameters $\left|St\right(\pi \left)\right|$, $\left|Z\right(\pi \left)\right|$ and $\left|\pi \right|$.

The finest partition

• $\pi$: $\left\{1\right\}$, $\{-1\}$, $\{\pm i\}$, $\{\pm j\}$, $\{\pm k\}$.
• $St\left(\pi \right)=\left\{1\right\}$, $Z\left(\pi \right)=\{\pm 1\}$.
• $\left|St\right(\pi \left)\right|=1$, $\left|Z\right(\pi \left)\right|=2$, $\left|\pi \right|=5$.

Then one partition

• $\pi$: $\{\pm 1\}$, $\{\pm i\}$, $\{\pm j\}$, $\{\pm k\}$.
• $St\left(\pi \right)=\{\pm 1\}$, $Z\left(\pi \right)=Q$.
• $\left|St\right(\pi \left)\right|=2$, $\left|Z\right(\pi \left)\right|=8$, $\left|\pi \right|=4$.

Three partitions of the form

• $\pi$: $\{\pm 1,\pm i\}$, $\{\pm j,\pm k\}$.
• $St\left(\pi \right)=\{\pm 1,\pm i\}$, $Z\left(\pi \right)=Q$.
• $\left|St\right(\pi \left)\right|=4$, $\left|Z\right(\pi \left)\right|=8$, $\left|\pi \right|=2$.

And the coarsest partition

• $\pi$: $\left\{Q\right\}$.
• $\left|St\right(\pi \left)\right|=8$, $\left|Z\right(\pi \left)\right|=8$, $\left|\pi \right|=1$.

Next, we draw the partially ordered set P of optimal partitions together with parameters $\left|St\right(\pi \left)\right|$, $\left|Z\right(\pi \left)\right|$, $\left|\pi \right|$. The picture below shows also the values of the Möbius function of the form $\mu (a,1)$. Finally, by formulas 3, 4, we obtain that

$$\begin{array}{cc}\hfill |S_r\left(Q\right)|& =\left|Q\right|\sum _{x\in P}\sum _{y\le x}\frac{\mu (y,x)}{\left|Z\right(y)|}{r}^{\left|x\right|}\hfill \\ & =8(r^5\frac{1}{2}+r^4(\frac{1}{8}-\frac{1}{2})+3r^2(\frac{1}{8}-\frac{1}{8})+r(\frac{1}{8}-\frac{3}{8}+\frac{2}{8}))\hfill \\ & =4r^5-3r^4,\hfill \end{array}$$

$$\begin{array}{cc}\hfill |S_r\left(Q\right)/\sim |& =\sum _{x\in P}\sum _{y\le x}\frac{\mu (y,x)|St(y)|}{\left|Z\right(y\left)\right|}{r}^{\left|x\right|}\hfill \\ & =r^5\frac{1}{2}+r^4(\frac{1}{4}-\frac{1}{2})+3r^2(\frac{1}{2}-\frac{1}{4})+r(1-\frac{3}{2}+\frac{1}{2})\hfill \\ & =\frac{1}{2}{r}^5-\frac{1}{4}{r}^4+\frac{3}{4}{r}^2.\hfill \end{array}$$

Thus, we have showed that

Proposition. 

For every $r\in \mathbb{N}$, $|S_r\left(Q\right)|=4r^5-3r^4$ and $|S_r\left(Q\right)/\sim |=\frac{1}{2}{r}^5-\frac{1}{4}{r}^4+\frac{3}{4}{r}^2$.

In particular, $|S_2\left(Q\right)|=80$ and $|S_2\left(Q\right)/\sim |=15$, while the number all 2-colorings of Q is $2^8=256$ and the number of equivalence classes of all 2-colorings of Q is

$$\frac{1}{\left|Q\right|}\sum _{g\in Q}{2}^{|Q/\langle g\rangle |}=\frac{1}{8}(2^8+2^4+{62}^2)=37.$$

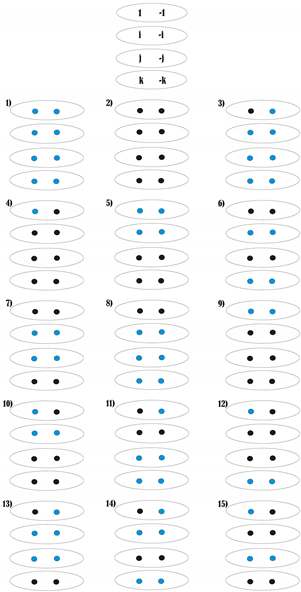
We conclude this note with the list of all symmetric 2-colorings of Q, up to equivalence.