Key Noise Evaluation of Analog Front-End in Microradian-Level Phasemeter for Space Gravitational Wave Detection

Abstract

For microradian-level phasemeters aimed at space-based gravitational wave detection, the analog front-end circuitry plays a critical role in determining the system’s phase noise. This paper focuses on the symmetric differential structure-based operational amplifier analog front-end between the Quadrant Photodiode output and the high-resolution ADC input. An equivalent additive noise model is established, and the mechanism of noise conversion into phase noise is derived. The noise performance within the target 5–25 MHz band is evaluated through LTspice simulations and experimental verification. Experimental results show that, after suppressing sampling timing jitter with a 37.5 MHz pilot tone, the noise contribution of the front-end analog circuit to the phasemeter system is significantly better than the phase measurement noise requirement of 2π $\mathsf{\mu }\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{H}\mathrm{z}}^{1/2}$ in the 0.1 mHz–1 Hz band for space-based gravitational wave detection. Compared with a transformer-based front-end, the differential amplifier solution exhibits significant advantages in low-frequency noise suppression and signal stability. Further analysis using the digital phase-locked loop closed-loop transfer function confirms that the noise amplitude is proportional to phase noise and inversely proportional to signal amplitude, providing a theoretical basis for analog front-end circuit optimization and system-level noise budgeting. The results offer a reliable reference for the design of high-precision phasemeters and the engineering implementation of space-based gravitational wave detection missions.

1. Introduction

In 1916, Einstein first predicted the existence of gravitational waves when he proposed general relativity. A century later, in 2015, the Laser Interferometer Gravitational-Wave Observatory (LIGO) achieved the first direct detection in human history [1,2], opening a new chapter in the rapid development of gravitational wave astronomy. Currently, several space-based gravitational wave detection missions have been proposed internationally. These missions generally adopt a triangular constellation formed by three spacecraft, with representative examples including the Laser Interferometer Space Antenna (LISA) led by the European Space Agency, as well as China’s “Taiji” and “Tianqin” programs [3,4,5].

These missions are based on the principle of laser heterodyne interferometry, where the relative displacement between spacecraft is obtained by observing the phase variations of the heterodyne signals. As the core payload of the interferometer, the phasemeter must achieve microradian-level phase extraction in a complex noise environment. According to system requirements, the ranging sensitivity of the phasemeter should reach 1 pm, corresponding to a phase measurement noise better than 2π $\mathsf{\mu }\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{H}\mathrm{z}}^{1/2}$ in the 0.1 mHz–1 Hz band [6,7,8], with a laser wavelength of 1064 nm.

In achieving the required precision, the analog front-end circuitry of the phasemeter plays a critical role. The Quadrant Photodiode (QPD) already integrates a transimpedance amplifier (TIA) [9,10] that converts photocurrent into voltage signals, so the TIA is not within the scope of this paper. The focus here is on the analog front-end link between the QPD output and the input of the high-resolution analog-to-digital converter (ADC). The primary function of this link is to process the heterodyne signal from the QPD and deliver it to the ADC for sampling. The digital phase-locked loop (DPLL) then performs phase extraction [11]. The noise and distortion characteristics of the analog front-end circuitry directly determine the signal-to-noise ratio of the system and the accuracy of phase measurement.

In the analog front-end circuitry of phasemeters, common structures include differential operational amplifiers and transformer inputs [12,13]. Transformer-based front-ends offer good impedance matching and common-mode rejection, but their noise suppression for pilot tone is limited at low frequencies [6]. In contrast, differential operational amplifiers with their inherent symmetric differential input/output architecture can effectively suppress common-mode disturbances and provide higher design flexibility and integration, thereby improving the system’s signal-to-noise ratio (SNR) and immunity to interference.

The noise sources coupled into the DPLL mainly include additive noise, direct phase noise, truncation dither noise, and numerically controlled oscillator (NCO) noise [14]. Among these sources, this paper primarily focuses on the impact of additive noise in the development of the analog front-end circuit. Specifically, the thermal noise of resistors, the voltage noise of operational amplifiers, and bias drifts are all categorized as additive noise, which ultimately manifests as phase noise in phase measurement [15]. The fundamental relationship can be summarized as follows. Phase noise is proportional to the noise amplitude, but inversely proportional to the root mean square (RMS) amplitude of the signal. This implies that when the input signal amplitude is relatively low, the same level of electronic noise from the phasemeter will have a more significant impact on phase measurement [16]. In other words, thermal noise, current noise, and bias drift in the analog front-end contribute to noise in the heterodyne signal during amplification and subsequently appear as phase measurement noise after ADC sampling and DPLL processing. Without a thorough understanding of these mechanisms, their contribution may be underestimated in phasemeter design, leading to a discrepancy between the expected and actual system performance.

Therefore, it is necessary to establish a systematic modeling and analysis approach to quantitatively describe the noise transfer paths of the analog front-end circuitry differential amplifier and to evaluate their impact on phase measurement noise. This not only provides a theoretical basis for component selection and parameter optimization in the circuitry, but also supports system-level performance prediction.

Based on this, the present work establishes a noise model for the phasemeter analog front-end differential amplifier, derives the mechanism by which additive noise is converted into phase noise, and validates its contribution within the target frequency band through experiments. Furthermore, a comparative analysis of differential amplifiers and transformer-based front-ends is conducted, revealing the potential of differential amplifiers to meet the design requirements of high-precision phasemeters for space-based gravitational wave detection. The results provide not only a quantitative reference for future phasemeter circuit optimization but also a foundation for the engineering implementation of space-based gravitational wave detection missions.

2. System Modeling and Noise Propagation Mechanism

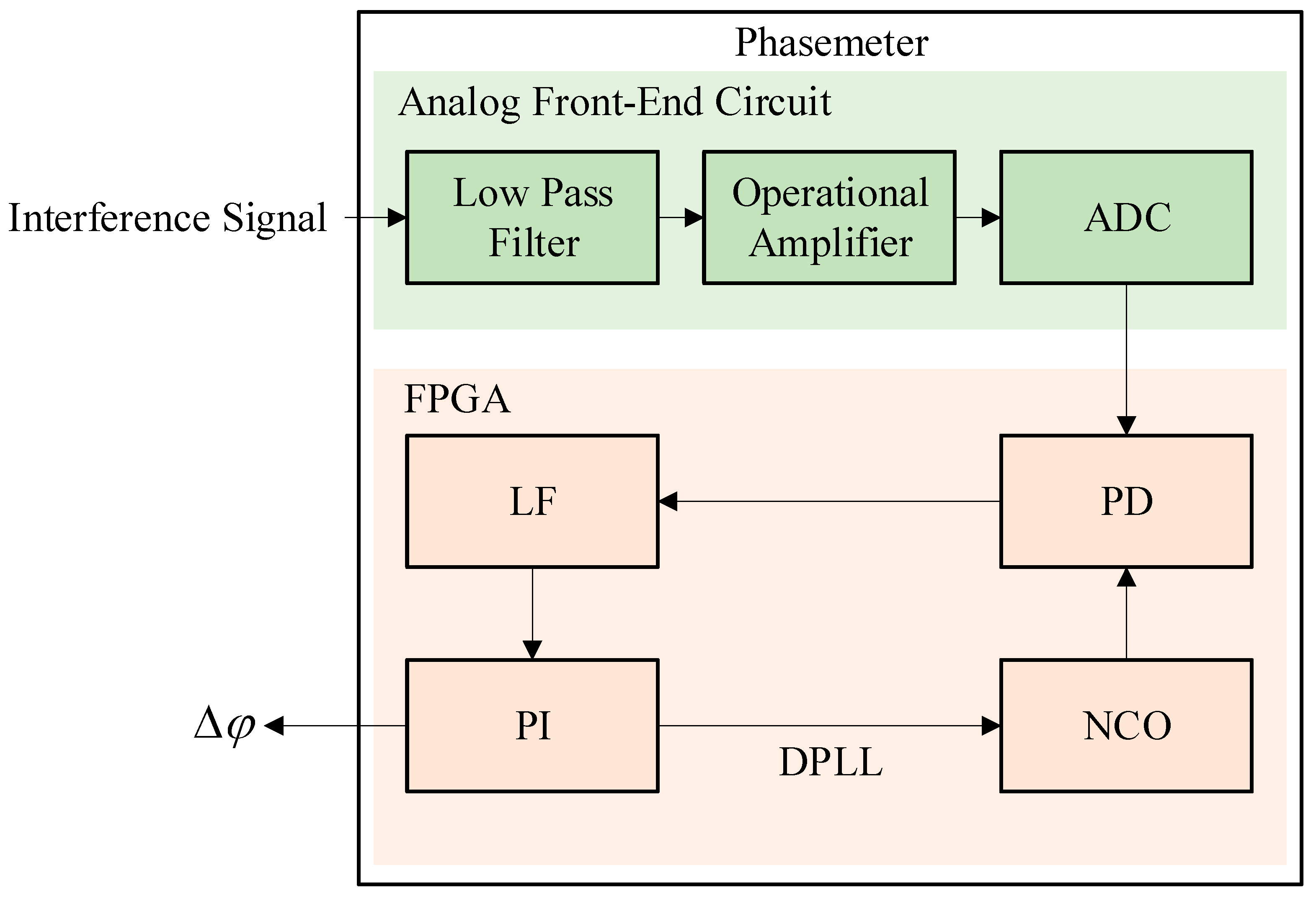
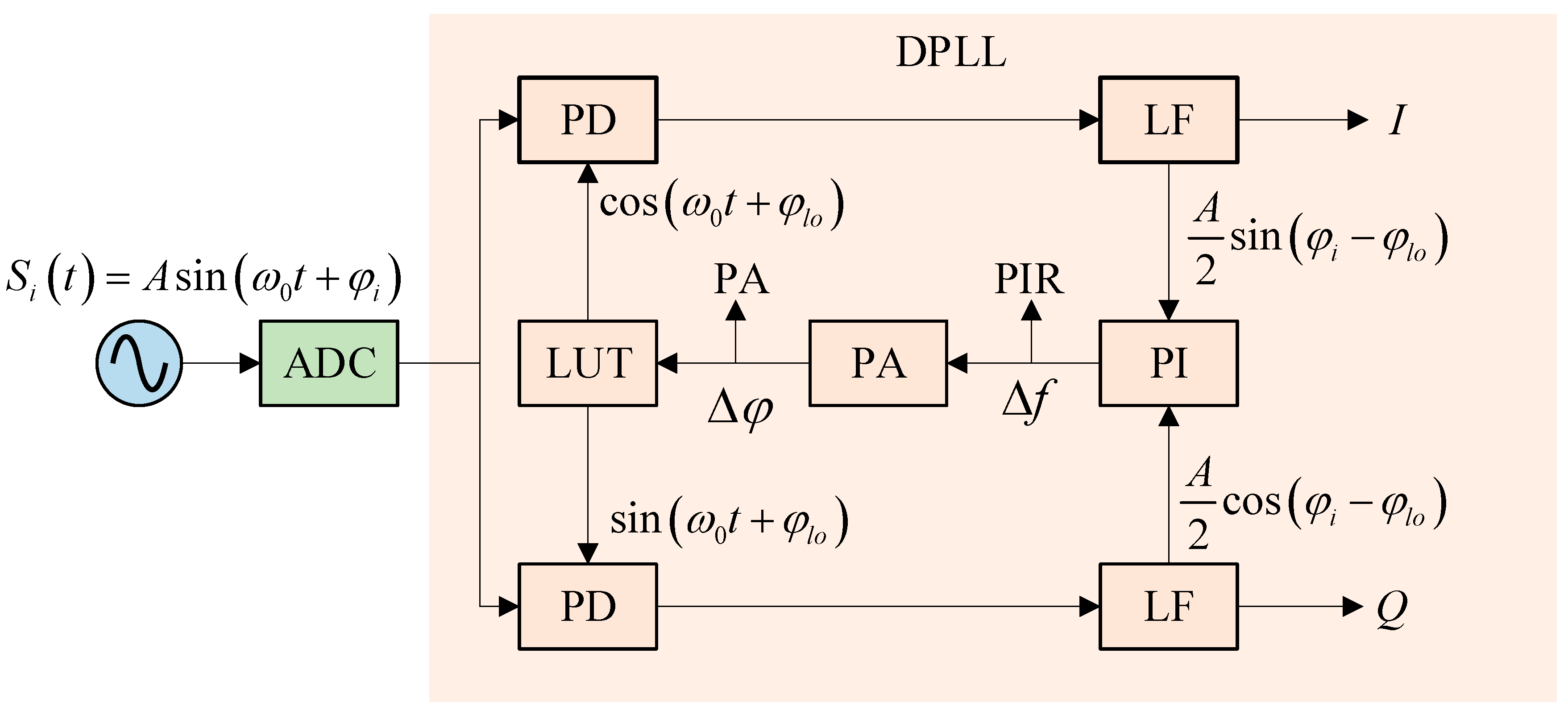
2.1. System Architecture and Signal Flow

The core role of the phasemeter is to perform high-precision phase extraction from the heterodyne signals of the QPD. Its signal processing chain primarily consists of the analog front-end circuitry and the DPLL. As shown in Figure 1, the heterodyne signal is first passed through a low-pass filter to suppress high-frequency noise components, and then converted and amplified by a differential operational amplifier to improve the signal-to-noise ratio (SNR) and match the requirements of subsequent sampling. The signal processed by the front-end is sampled by a high-resolution ADC and transmitted to the DPLL within the FPGA for digital processing.

The DPLL consists of a phase detector (PD), a loop filter (LF), and an NCO [17]. Its fundamental function is to achieve real-time tracking and extraction of the input signal phase in the digital domain. Specifically, the PD calculates the phase difference between the input signal and the NCO output to obtain the phase error. The LF then adjusts the bandwidth of the error signal and suppresses high-frequency noise. Finally, the NCO continuously updates the local reference phase based on the filtered result, thereby achieving locking and precise phase extraction of the input signal.

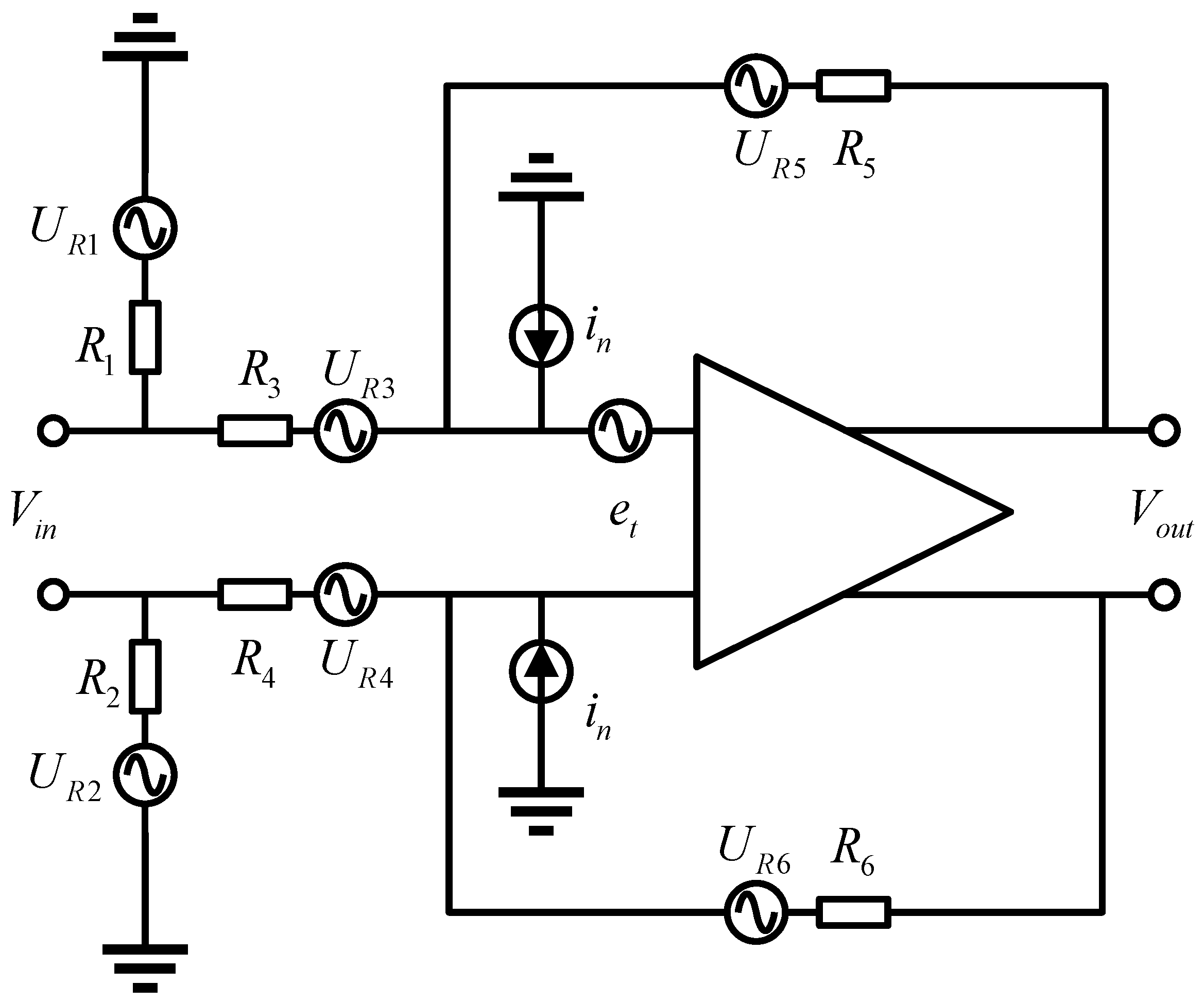
2.2. Input Signal and Noise Model

In the phasemeter system, the heterodyne signal with additive noise can be expressed as:

$$S\left(t\right)=A\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_{0}t+\phi \right)+\tilde{A}.$$

(1)

Here, $A$ denotes the signal amplitude, ${\omega }_0$ is the angular frequency of the heterodyne, $\phi$ represents the phase information to be measured, and $\tilde{A}$ denotes the RMS value of the additive noise.

During processing by the analog front-end circuitry, the differential operational amplifier introduces additional intrinsic noise [18]. These noises are typically characterized using an equivalent input noise model and mainly include three types: input voltage noise $e_t\left(t\right)$, input current noise $i_n\left(t\right)$, and resistor thermal noise $e_r\left(t\right)$, as illustrated in the equivalent circuit shown in Figure 2.

Input voltage noise $e_t\left(t\right)$: Mainly originates from the thermal noise and shot noise of the operational amplifier’s input stage devices. Its power spectral density is typically specified in the datasheet in $\mathrm{n}\mathrm{V}/{\mathrm{H}\mathrm{z}}^{1/2}$.

Input current noise $i_n\left(t\right)$: Primarily introduced by the reverse-biased currents of the input transistors and their associated noise, which act on the source impedance to form an equivalent voltage noise. Its power spectral density is usually expressed in $\mathrm{p}\mathrm{A}/{\mathrm{H}\mathrm{z}}^{1/2}$.

Resistor thermal noise $e_r\left(t\right)$: Resistors in the input and feedback networks generate Johnson-Nyquist thermal noise, with an RMS value given by:

$$e_r\left(t\right)=\sqrt{4kTBR}.$$

(2)

Here, $k$ is the Boltzmann constant, $T$ is the thermodynamic temperature, $B$ is the noise bandwidth of the system, and $R$ is the resistance value.

According to Figure 2, the equivalent input noise of the differential operational amplifier can be decomposed into three components, where $U_{Ri},i=1\dots 6$ represents the equivalent thermal noise of the resistors:

• Input voltage noise:

$$U_{N1}^O=\left(1+{\displaystyle \frac{R_5}{R_1+R_3}}\right)e_t\left(t\right).$$

(3)

2.

Input current noise:

$$U_{II}^O=R_5{i}_n\left(t\right).$$

(4)

$$U_{I2}^O=R_6{i}_n\left(t\right).$$

(5)

3.

Resistor thermal noise:

$$U_{R1}^O=\left({\displaystyle \frac{R_5}{R_1+R_3}}\right)U_{R1}.$$

(6)

$$U_{R2}^O=\left({\displaystyle \frac{R_6}{R_2+R_4}}\right)U_{R2}.$$

(7)

$$U_{R3}^O=\left(1+{\displaystyle \frac{R_5}{R_1+R_3}}\right)U_{R3}.$$

(8)

$$U_{R4}^O=\left(1+{\displaystyle \frac{R_6}{R_2+R_4}}\right)U_{R4}.$$

(9)

$$U_{R5}^O=U_{R5}.$$

(10)

$$U_{R6}^O=U_{R6}.$$

(11)

Therefore, the input signal of the analog front-end circuitry differential amplifier can be uniformly modeled as:

$$U_{NO}=\sqrt{{\left(U_{NI}^O\right)}^2+{\left(U_{II}^O\right)}^2+{\left(U_{I2}^O\right)}^2+{\left(U_{R1}^O\right)}^2+{\left(U_{R2}^O\right)}^2+{\left(U_{R3}^O\right)}^2+{\left(U_{R4}^O\right)}^2+{\left(U_{R5}^O\right)}^2+{\left(U_{R6}^O\right)}^2}.$$

(12)

In the phasemeter, the DPLL is the core unit for phase extraction of the heterodyne signal [19], and its basic structure is shown in Figure 3. The heterodyne signal is first sampled by an ADC and then transmitted to the DPLL. Inside the DPLL, a lookup table (LUT) generates local quadrature reference signals $\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_{0}t+{\phi }_{lo}\right)$ and $\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{0}t+{\phi }_{lo}\right)$, where ${\phi }_{lo}$ is the phase of the reference signal. These are correlated with the input signal in the phase detector (PD) to obtain the in-phase (I) and quadrature (Q) components:

$$I={\displaystyle \frac{A}{2}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\phi }_i-{\phi }_{lo}\right).$$

(13)

$$Q={\displaystyle \frac{A}{2}}\mathrm{c}\mathrm{o}\mathrm{s}\left({\phi }_i-{\phi }_{lo}\right).$$

(14)

After the $I/Q$ components are filtered by the LF to remove high-frequency components, they are sent to the phase assessment (PA) to compute the phase error $∆\phi ={\phi }_i-{\phi }_{lo}$. This error signal is further dynamically adjusted and accumulated in the proportional-integral (PI) controller and PA, and corrects the frequency deviation in the phase increment register (PIR). Finally, the NCO generates an updated local reference signal based on the LUT, achieving real-time tracking of the input signal phase.

For the DPLL loop described above, its open-loop transfer function can be expressed as:

$$G\left(z\right)=2^{M+N-3}{\displaystyle \frac{V_{in}}{V_F}}\left(K_p+{\displaystyle \frac{K_{I}T}{1-z^{-1}}}\right){\displaystyle \frac{f_s}{2^A}}\left({\displaystyle \frac{2\pi T}{1-z^{-1}}}\right).$$

(15)

Here, $N$ is the number of ADC conversion bits, $M$ is the number of NCO bits, $A$ is the number of PIR bits, $K_p$ and $K_I$ are the proportional and integral parameters of the PI module, $V_{in}$ denotes the actual voltage amplitude of the analog input signal, $V_F$ is the full-scale voltage of the ADC, $f_s$ and $T$ represent the ADC sampling frequency and period, respectively. Based on these, the DPLL closed-loop transfer function and noise transfer function can be obtained:

$$H\left(z\right)={\displaystyle \frac{G\left(z\right)}{1+G\left(z\right)}}$$

(16)

$$E\left(z\right)={\displaystyle \frac{1}{1+G\left(z\right)}}$$

(17)

According to Equation (1), when additive noise is mixed into the heterodyne signal, its equivalent phase noise can be expressed as $\tilde{\phi }.$ The variance of the phase noise [20] can be calculated by integrating the product of the phase noise and the loop error function $E\left(z\right)$:

$${\phi }_{phase}^2={\int }_{-\infty }^{\infty }{\tilde{\phi }}^2\left(z\right)E^2\left(z\right)dz$$

(18)

The equivalent phase noise resulting from the additive noise is first obtained through the phase detector. By multiplying this phase noise with the system closed-loop transfer function and integrating the result, the phase variance introduced by the additive noise can be computed.

$${\sigma }_{add}^2={\int }_{-\infty }^{\infty }{\tilde{\phi }}^2\left(z\right)H^2\left(z\right)dz={\int }_{-\infty }^{\infty }{{\left({\displaystyle \frac{\sqrt{2}\tilde{A}}{A}}\right)}^{2}H}^2\left(z\right)dz$$

(19)

From Equation (19), it can be seen that the equivalent contribution of additive noise to the phase measurement is proportional to the RMS value of the additive noise $\tilde{A}$ and inversely proportional to the amplitude of the heterodyne signal $A$. In the phasemeter system, phase noise and additive noise usually coexist. The former directly affects the DPLL locking and phase measurement results without conversion, and its effect is described by the noise transfer function $E\left(z\right)$. However, additive noise influences the signal phase indirectly by entering the DPLL loop through the nonlinear conversion in the phase detector and must be analyzed using the closed-loop transfer function $H\left(z\right)$.

3. Differential Operational Amplifier Analog Front-End Design and Simulation

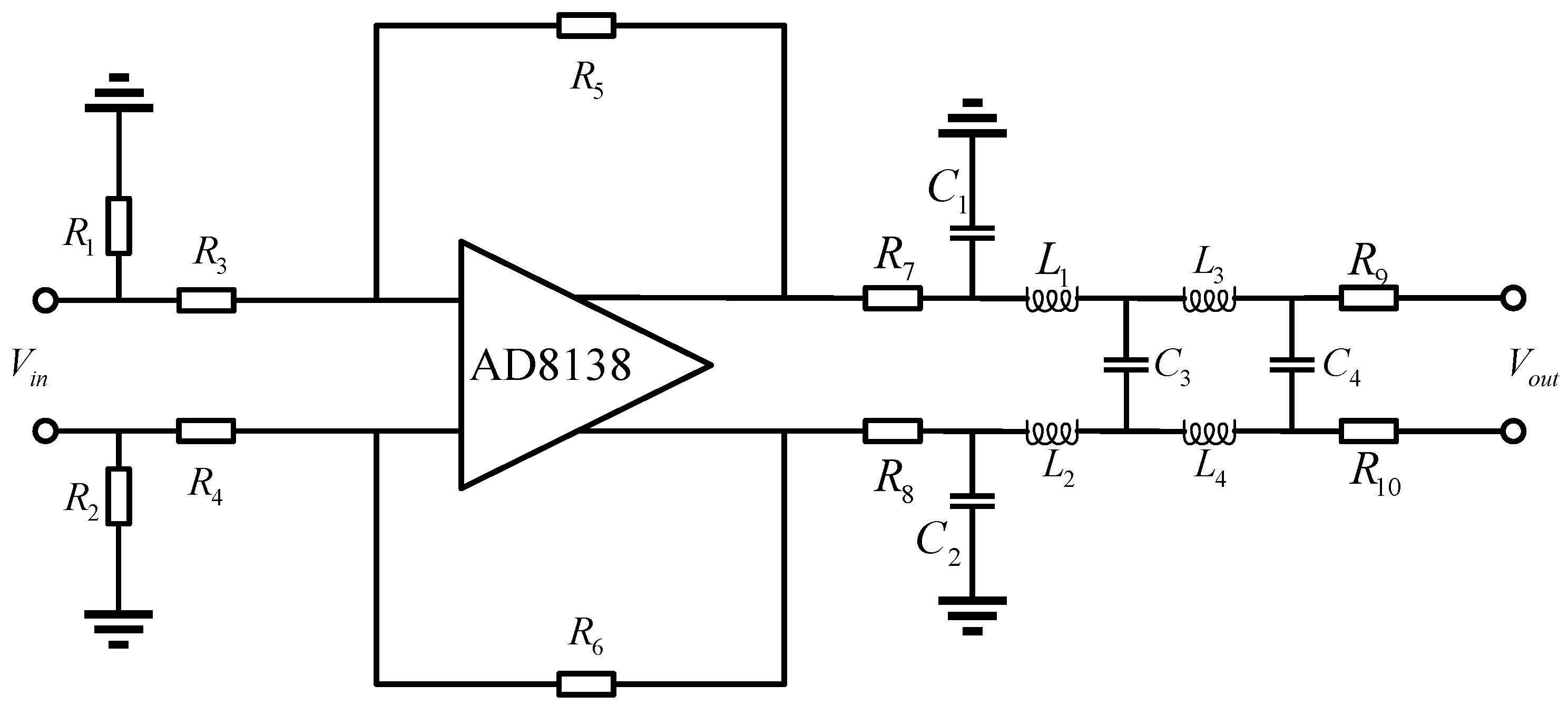
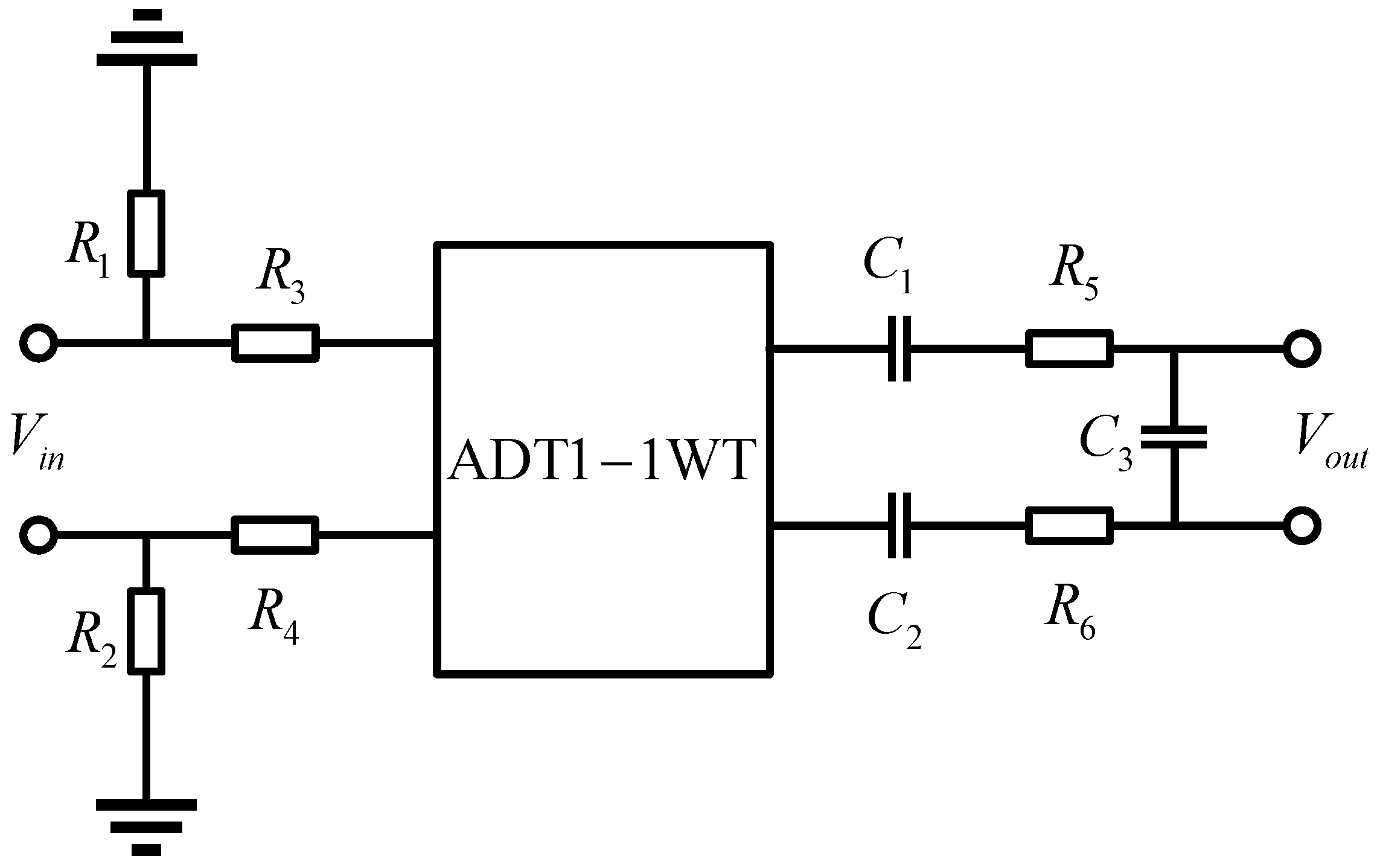
3.1. Differential Operational Amplifier Front-End Architecture

As discussed in the previous section, the equivalent contribution of additive noise to phase measurement in a phasemeter is proportional to its amplitude and inversely proportional to the amplitude of the heterodyne signal. Therefore, in the design of the analog front end, the additive noise level should be minimized as much as possible.

In this paper, a differential amplifier circuit was constructed based on the AD8138 [12], and its topological structure is shown in Figure 4. According to the official datasheet, the AD8138 is a low-noise, wide-bandwidth differential driver. Its internal feedback network provides balanced differential outputs, featuring a −3 dB bandwidth of 320 MHz and a slew rate of 1150 $\mathrm{V}/\mathsf{\mu }\mathrm{s}$, while maintaining extremely low harmonic distortion across the operating bandwidth. The input voltage noise density is 5 $\mathrm{n}\mathrm{V}/{\mathrm{H}\mathrm{z}}^{1/2}$ and the input current noise density is 2 $\mathrm{p}\mathrm{A}/{\mathrm{H}\mathrm{z}}^{1/2}$, enabling effective suppression of front-end noise in high-precision phase measurement applications. Following the AD8138 driver output, a low-pass filter and impedance-matching network are cascaded to further optimize noise performance and preserve signal integrity.

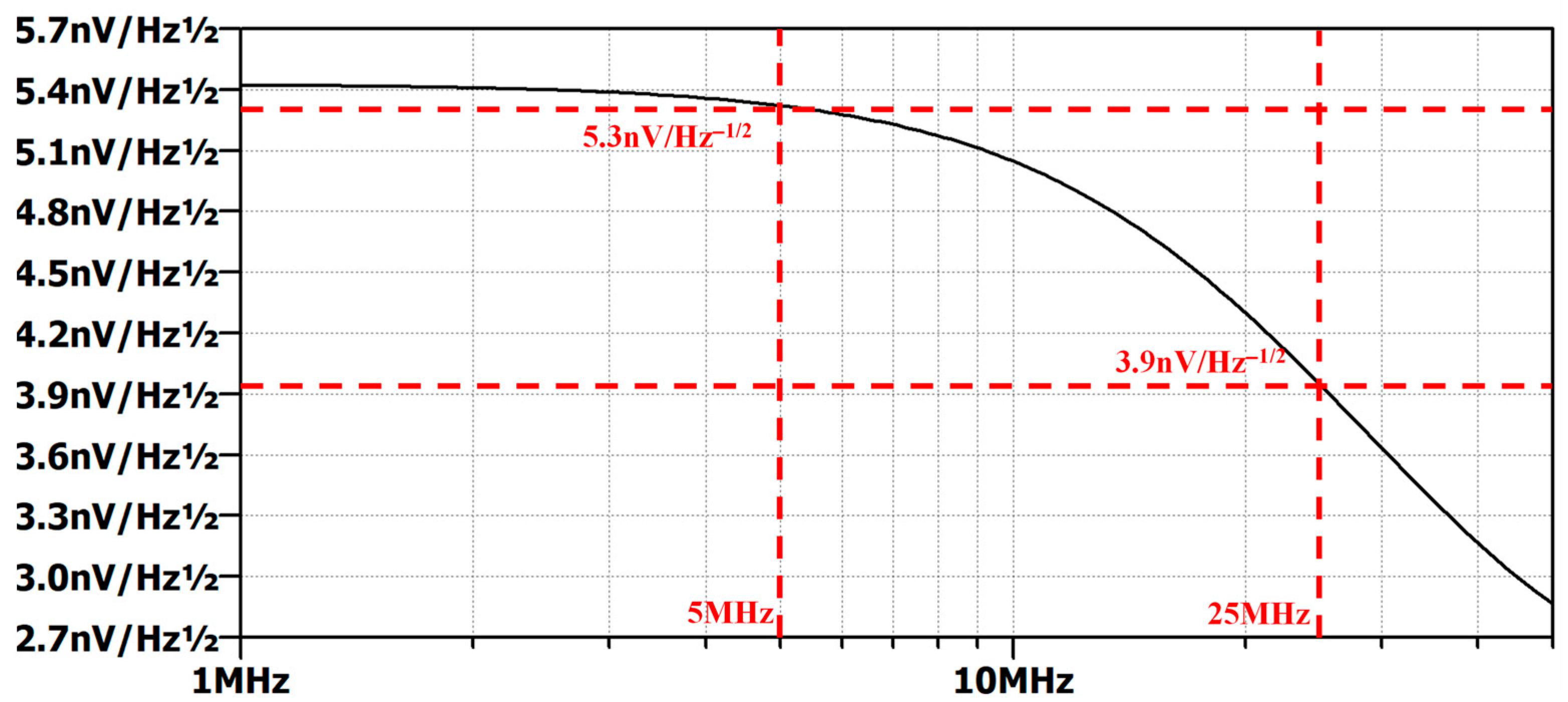
3.2. Noise Simulation of the Front-End Circuit

To evaluate the noise characteristics of the proposed circuit, a simulation model was built in LTspice. The model includes the operational amplifier’s equivalent input voltage noise, input current noise, as well as the thermal noise of the resistor network. The input noise parameters were taken from the AD8138 datasheet, specified as 5 $\mathrm{n}\mathrm{V}/{\mathrm{H}\mathrm{z}}^{1/2}$ and 2 $\mathrm{p}\mathrm{A}/{\mathrm{H}\mathrm{z}}^{1/2}$, respectively. By performing noise analysis, the noise spectral density at the differential output was obtained, as shown in Figure 5.

The simulation results show that within the target measurement bandwidth of 5–25 MHz, the output noise spectral density remains in the range of approximately 3.9–5.3 $\mathrm{n}\mathrm{V}/{\mathrm{H}\mathrm{z}}^{1/2}$, which is consistent with the typical values given in the AD8138 datasheet. Overall, the simulation validates that the designed differential amplification circuit exhibits stable low-noise performance within the target frequency range.

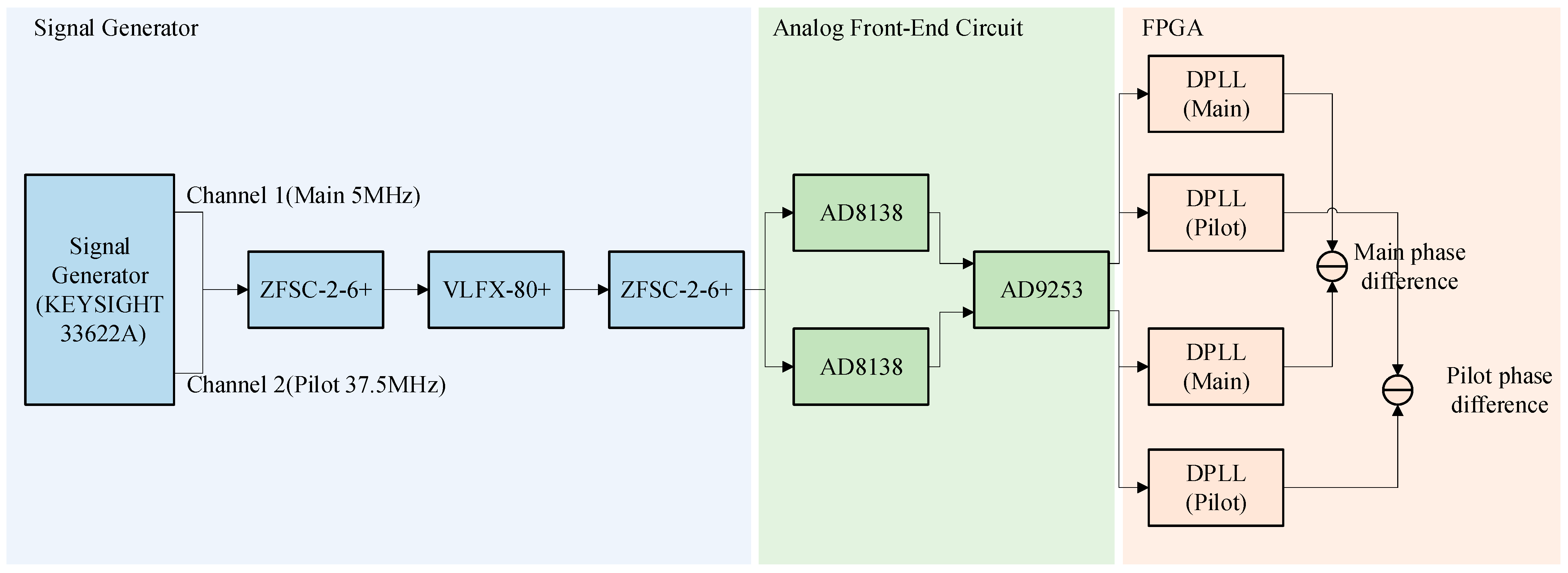
4. Experimental Verification

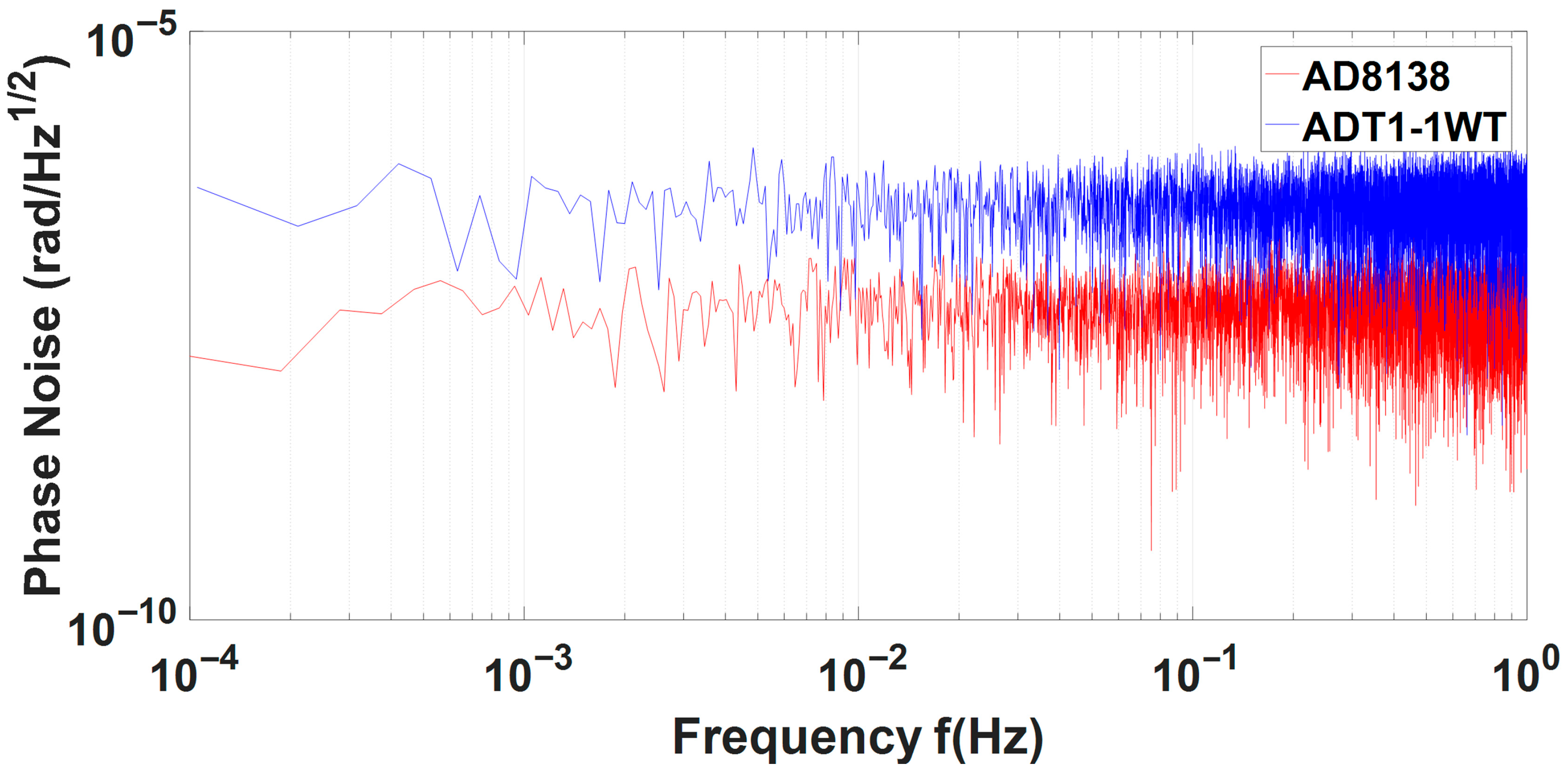
4.1. Comparison Between Differential Operational Amplifier and Transformer

This paper also investigates a transformer-based front-end circuit for comparison. As shown in Figure 6, the experiment adopts the ADT1-1WT transformer from Mini-Circuits, whose insertion loss is approximately 1 dB within a 400 MHz bandwidth. The measured signal is fed through a low-pass filter into the transformer-based front-end circuit, and after processing by the ADT1-1WT, it is delivered to the ADC for data conversion.

To further validate the accuracy of the noise model and the actual performance of the front-end circuit, an experimental platform was constructed (Figure 7) to compare the differential operational-amplifier-based design with the transformer-based design. The experiment employs the Zurich Instruments MFLI lock-in amplifier, which features low intrinsic noise, high sampling rate, and high resolution, and is widely used in precision measurement scenarios. The test conditions are as follows: input signal frequency of 5 MHz, amplitude of 1 V, differential input, and internal reference source. The signal passes through the front-end circuit and enters the MFLI lock-in amplifier, and the output data are then post-processed in MATLAB 2021b to obtain the phase-noise spectral density.

In Figure 8, the phase-noise spectra appear flat at low frequencies. This results from internal data handling in the MFLI before the data are sent to the computer. Therefore, Figure 8 serves to compare the two front-end architectures but does not indicate the circuits’ intrinsic noise floors.

The topologies of the two front-end structures are illustrated in Figure 4 and Figure 6. The AD8138 employs an internal feedback network to achieve broadband balanced output, offering short signal paths, effectively suppressing common-mode interference and maintaining low noise. However, it suffers from relatively high power consumption and a more complex biasing scheme. In contrast, the transformer-based front-end circuit is simple, passive, and capable of signal isolation, but its low-frequency response is limited, and parasitic parameters significantly affect performance; additionally, its gain is not adjustable.

The experimental results show that at a frequency of 5 MHz, the phase noise of the differential operational-amplifier-based analog front-end using the AD8138 is approximately one order of magnitude lower than that of the transformer-based approach. This is consistent with the simulation results and confirms that the differential-amplifier-based design offers superior performance for the target application. Due to the bandwidth limitation of the MFLI, the experiment was conducted only at the single frequency point of 5 MHz.

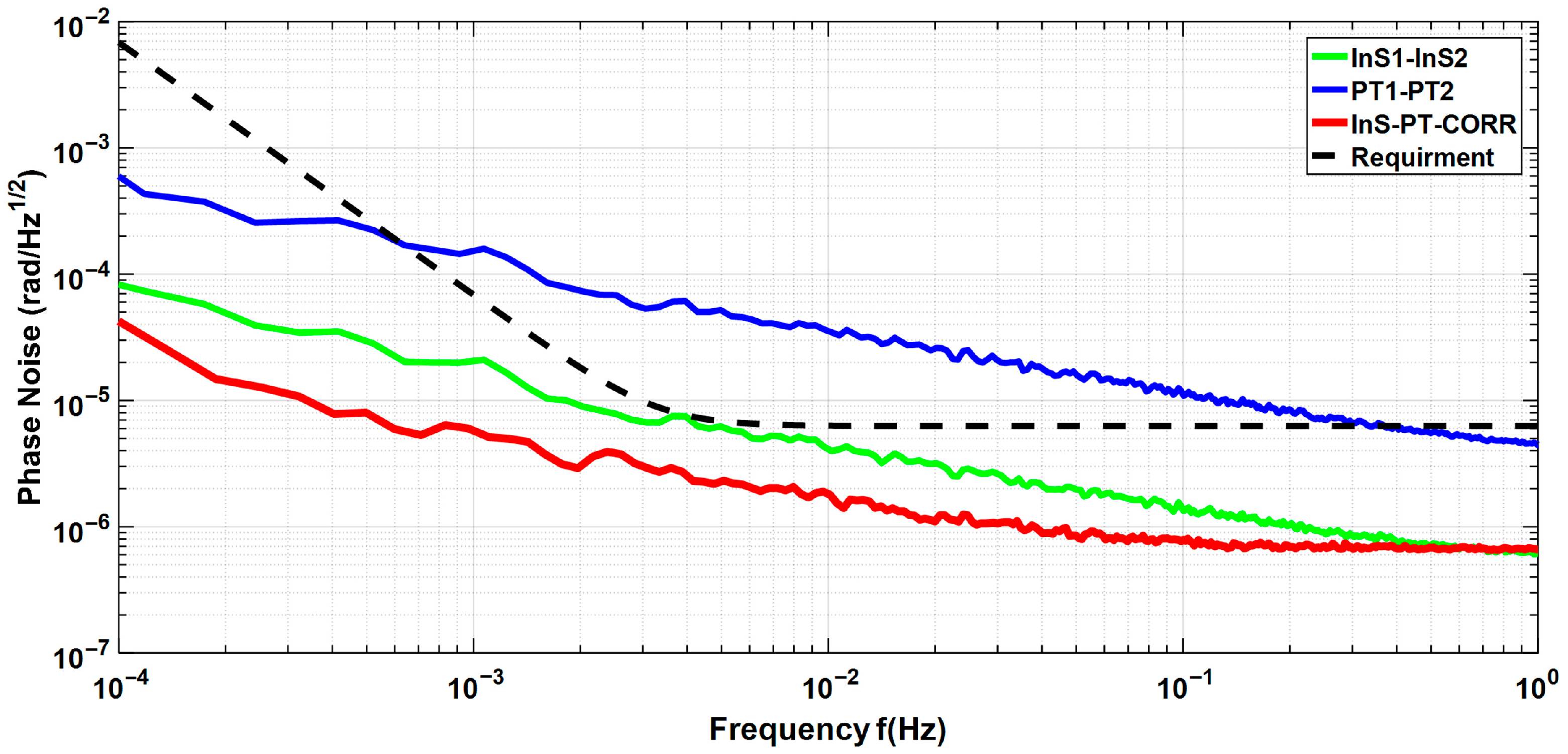
4.2. Differential Operational Amplifier Noise Evaluation Method

To evaluate the impact of additive noise in the analog front-end circuitry on phase measurement, this paper improves upon the original method [6] and conducts experiments directly on the PCB rather than using flying wires. In the measurement chain, the signal under test is split into two differential operational amplifiers and simultaneously sampled by different channels of the same ADC, with the inter-channel differences considered negligible. The noise introduced by the differential operational amplifiers appears as non-common-mode components in the two input channels and cannot be canceled by subtraction. Therefore, the system’s measurement results directly reflect the equivalent contribution of the analog front-end additive noise.

The experimental system is illustrated in Figure 9 and Figure 10. A Keysight 33622A signal generator produces the main beat-note (5 MHz) and the pilot tone (37.5 MHz); the former simulates the heterodyne signal, while the latter serves as the ADC jitter correction signal [21]. The signals pass through a power splitter (ZFSC-2-6+) and a low-pass filter (VLFX-80+) before entering the analog front-end. Two AD8138 differential amplifiers perform signal conditioning, followed by digitization through a 16-bit ADC (AD9253). The FPGA is configured with four parallel DPLL modules to track the phases of both the main beat-note and pilot tone.

The experiment is conducted in a normal-temperature laboratory environment without additional shielding or temperature control. The results are shown in Figure 11. The curves PT1-PT2 and InS1-InS2 represent the phase measurement noise of the pilot tone and main beat-note after common-mode noise suppression, respectively. The curve InS-PT-CORR corresponds to the phase noise obtained after suppressing the sampling timing jitter noise using the 37.5 MHz pilot tone, which reflects the contribution of the analog front-end circuit additive noise to the phase noise of the phasemeter system. Across the frequency range of 0.1 mHz to 1 Hz, it remains at the level of 2π $\mathsf{\mu }\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{H}\mathrm{z}}^{1/2}$.

5. Discussion and Conclusions

This paper evaluates the impact of additive noise from the analog front-end circuitry differential operational amplifier on phase measurement in a microradian-level phasemeter for space-based gravitational wave detection. By establishing an equivalent noise model, conducting simulations, and performing experimental validation, the results show that within the target frequency band of 5–25 MHz, the output noise of the AD8138-based differential amplifier analog front-end circuitry remains at a low level. After suppressing the sampling timing jitter using the 37.5 MHz pilot tone, the contribution of the analog front-end noise to the phasemeter system stays below 2π $\mathsf{\mu }\mathrm{r}\mathrm{a}\mathrm{d}/{\mathrm{H}\mathrm{z}}^{1/2}$ over the 0.1 mHz–1 Hz range, meeting the requirements for high-precision measurement. Comparison with the transformer-based front-end (ADT1-1WT) demonstrates that the differential amplifier approach offers significant advantages in low-frequency noise suppression and signal stability, particularly in controlling the low-frequency noise of the pilot tone.

This paper employs the DPLL closed-loop transfer function to analyze how additive noise is converted into phase noise. The results show that phase noise increases with noise amplitude and decreases with the RMS amplitude of the signal. This analysis clarifies the propagation of analog front-end noise in the digital domain and provides guidance for loop optimization. With appropriate circuit design, low-noise components, and optimized DPLL parameters, microradian-level phase measurement can be achieved, offering a reliable reference for space-based gravitational wave detection.