Modeling and Solving Two-Sided Disassembly Line Balancing Problem Under Partial Disassembly of Parts

Abstract

In two-sided disassembly lines, stations are symmetrically arranged on both sides of the conveyor, which is suitable for large-sized waste products. During the disassembly process, evenly assigning parts to workstations while satisfying various constraints and optimizing some disassembly objectives is a challenging task. Therefore, this study deals with a two-sided partial disassembly line balancing problem, and a multi-objective mathematical model for this problem is built. While satisfying various constraints, four objectives, namely, the hazard index, profit, smoothness index, and demand index, are optimized. Due to the NP-hard nature of the problem, an improved discrete whale optimization algorithm is proposed. According to the characteristics of the feasible solutions, an encoding method based on a one-dimensional integer array is designed, which can effectively decrease the memory space and simplify the design of neighbor structures. In the three stages of encircling prey, random wandering, and bubble-net attacking, based on the search features of each stage, different neighbor operators and search strategies are designed to enhance the local exploitation and global exploration capabilities. Finally, the performance of the proposed algorithm was tested against other algorithms for different types of instances and a disassembly case. The results show that the proposed algorithm can not only solve various types of disassembly line balancing problems but also shows superior performance.

1. Introduction

The rapid development of science and technology, as well as the growth in consumption per person, has led to an accelerated pace of product renewal and replacement. As a result, the quantity of end-of-life (EOL) products is growing at an astonishing rate, causing great harm to the environment and leading to the serious waste of resources. Therefore, the recycling and reusing of EOL products are receiving more and more attention. Disassembly plays a vital role in product recovery by allowing for the selective extraction of desired parts and raw materials. A disassembly line is the best choice for large-scale EOL products thanks to its higher productivity and suitability for automation. However, whether the tasks can be evenly distributed among the workstations of the disassembly lines directly affects disassembly indicators such as energy consumption, disassembly efficiency, profit, and environmental hazards [1]. Consequently, the disassembly line balancing problem (DLBP) has gained a great deal of attention from researchers in recent years.

The DLBP can be simply described as searching for an optimal disassembly scheme, which satisfies precedence constraints based on a given EOL product, evenly assigns tasks to each workstation, and satisfies cycle time constraints while optimizing the number of opened workstations and other disassembly objectives [2]. Since the DLBP was presented by Gungor and Gupta [3], it has garnered the interest of many researchers. Due to variations in the types and structures of EOL products, recycling quality, and disassembly requirements, the disassembly process exhibits significant differences. Consequently, DLBPs can be classified in multiple ways. According to the layout forms of disassembly lines, DLBPs can be divided into four categories, including linear, U-shaped, parallel, and two-sided DLBPs.

The linear disassembly line, which involves disassembly on one side of the line, characterized by its simple layout and convenient operation, was initially employed in industry. In the published literature, most studies are centered around the linear disassembly line balancing problem. It was first introduced by Gungor and Gupta [3] and was solved by a solution-oriented heuristic method. Subsequently, a lot of relevant studies based on that study have been conducted, and many heuristics, exact methods, and metaheuristics were designed for DLBPs. Kose et al. [4] presented a DLBP with multi-manned workstations considering worker satisfaction and proposed novel heuristics utilizing game-theory-oriented approaches to address the problem. Chu and Chen [5] investigated a DLBP with different work modes and developed a reinforcement learning-based Hyper-Heuristics algorithm to solve it. To obtain the exact solution, Edis et al. [6] designed mixed-integer programming approaches to deal with the partial DLBP. Considering sequence-dependent setup times, Kizilay [7] developed a constraint programming model for a sequence-dependent DLBP with AND/OR precedence relations. Due to the NP-hard nature of the DLBP, exact methods do not perform well when obtaining optimal solutions for large DLBPs. Therefore, metaheuristic algorithms, which can find satisfactory solutions within a reasonable time, are being applied more and more widely. Zhou and Bian [8] employed a Harris Hawks optimization to handle robotic DLBPs. Yin et al. [9] used a hybrid driving algorithm to address a DLBP with multi-robot workstations. Wang et al. [10] considered a sequence-dependent DLBP and proposed an improved bee colony algorithm for it.

A parallel disassembly line, which uses two or more linear lines in parallel, enables workers to rotate and perform disassembly tasks on different lines within stations, so it can be used to deal with multi-type EOL products. A parallel DLBP with two straight lines was first presented by Hezer and Kara [11] and solved through a method based on a network-based shortest route model. Zhang et al. [12] considered a multi-line parallel DLBP and developed two constraint programming models for the problem. Considering the stochastic disassembly time, Wang et al. [13] established a stochastic parallel DLBP model with multiple objectives and proposed a genetic simulated annealing algorithm.

The U-shaped disassembly line arranges workstations in the shape of a letter U, allowing workers to simultaneously handle disassembly tasks at the front and back areas of the line, which can improve the balance capacity while meeting lean disassembly requirements. Agrawal and Tiwari [14] first reported the balancing problem for a mixed-model U-shaped disassembly line and used a collaborative ant colony algorithm to deal with it. Later, Avikal and his coworkers [15,16] developed heuristic approaches to tackle U-shaped DLBPs. Regarding the interactions between two tasks on some occasions, Li et al. [17] proposed an iterated local search algorithm to solve the sequence-dependent U-shaped DLBP with multiple objectives. To achieve maximum disassembly profit, Li et al. [18] provided an attempt to study a profit-oriented U-shaped partial DLBP and solved it using a novel discrete cuckoo search algorithm.

According to the layout features, linear, U-shaped, and parallel disassembly lines are suitable for dealing with small-sized EOL products. For large-sized EOL products, such as waste agricultural machinery and scrapped vehicles, a two-sided disassembly line is the best choice, because workers are allowed to disassemble parts on both sides of the line, which can greatly reduce worker movement distances and significantly improve disassembly efficiency. In recent years, there has been an increase in research on the two-sided DLBP. Wang et al. [19] introduced a two-sided stochastic DLBP and modeled it mathematically for the first time, in which uncertainty of operating time was represented by stochastic variables obeying a normal distribution. Based on this study, some scholars have conducted further research on the two-sided DLBP in recent years. Liang et al. [20] applied triangular fuzzy numbers to represent uncertain disassembly time and solved a fuzzy multi-objective two-sided DLBP by employing a novel flatworm algorithm based on Pareto dominance. Kucukkoc [21] developed a powerful genetic algorithm to solve a two-sided DLBP with complex AND/OR precedence relations. Considering additional energy consumption caused by hazardous tasks, Liang et al. [22] proposed a dual-individual simulated annealing algorithm for the multi-objective two-sided DLBP with complex execution constraints. To obtain the maximum total profit from product disassembly, an integer linear programming model was developed to solve a profit-oriented two-sided DLBP [23].

From the above literature review, we conclude that many kinds of DLBPs have been studied in the past two decades, but there are only a few studies on two-sided DLBPs, and almost all of them consider complete disassembly for optimizing line efficiency. However, partial disassembly is not studied extensively, although it usually occurs in real-world practice, to gain the hazardous and valuable parts with the aims of minimizing the environmental hazards and maximizing the disassembly profit. To the authors’ best knowledge, there have been some studies on partial disassembly for the linear [6,9,24], U-shaped [18], and parallel [12,13] disassembly lines, but only one study considers partial disassembly in the two-sided DLBP [19], in which disassembly time is considered to be an uncertain variable, and the mathematical model is not suitable for deterministic disassembly scenarios. Moreover, in these studies on two-sided DLBPs, none of them used one integer vector as the encoding method to satisfy precedence constraints and operation direction constraints simultaneously, which leads to a complex decoding process and affects the search efficiency. In addition, the diversity of neighbor structure operators is insufficient, which limits sufficient exploitation and exploration of the solution space. There are also limited metaheuristics applied to deal with two-sided DLBPs for large-sized EOL products. Hence, this paper conducts further research on the two-sided partial DLBP (TPDLBP). Due to the NP-hard nature of the TPDLBP, an effective metaheuristic method (an improved discrete whale optimization algorithm, IDWOA) is proposed to solve it for the first time. The whale optimization algorithm (WOA) is a newly developed evolutionary algorithm [25]. Due to its simplicity and ease of implementation, WOA has recently aroused much interest and has been applied to many kinds of optimization problems [26,27,28,29,30]. As it still suffers from issues such as insufficient search accuracy and a tendency to get stuck in local optima, improvements are required for WOA to solve these problems effectively. Hence, according to the characteristics of the presented TPDLBP, some effective methods and strategies are developed in the search process for WOA, such as a simple discrete encoding method, different neighbor operators in each search phase, efficient search strategies, and a balance between local exploitation and global exploration.

The rest of the paper is organized as follows. The problem description and the mathematical model are given in Section 2. Section 3 presents the proposed method for the problem with a detailed search process. Computational experiments are provided in Section 4. Finally, Section 5 concludes our work and discusses directions for future research.

2. Problem Description and Modeling

2.1. Problem Description

The layout of a two-sided disassembly line is shown in Figure 1. The stations are symmetrically arranged on both sides of the conveyor, thereby forming two independent operation areas. A pair of facing stations constitutes a mated-station which also can be referred to as a workstation, and they refer to each other as a companion station. During the disassembly process, the parts are assigned to corresponding stations on the left or right side of the line based on their physical positions on the EOL product. Specifically, some parts can only be disassembled on the left side or the right side, while some parts can be disassembled on either side. These constraints, which specify that parts must be disassembled on the left side (L), right side (R), or both sides (E), are defined as disassembly direction constraints.

An example of a disassembly precedence graph for a 12-part product is given in Figure 2. The number inside a node denotes a task. The label (o_i, t_i) above a node indicates the disassembly direction and the operating time of task i. Nodes with a gray background indicate that the corresponding parts are hazardous, and arrows represent the precedence relationships between tasks. Taking node 8 as an example, it represents part 8 with hazardous attribute. Task 8 cannot be distributed until its immediate predecessor task 7 is disassembled, and it will be disassembled in seven time units on a left-side station. The TPDLBP studied in this paper can be briefly described as follows: ignoring workers’ walking time and uncertainties in operating time caused by worker skills and part conditions, the tasks are assigned to the workstations while satisfying precedence constraints, disassembly direction constraints, and cycle time constraints and achieving multiple objectives.

2.2. Notations

The following symbols are used to describe the mathematical formulations.

• Parameters:
• m: Number of mated stations (workstations);
• n: Number of tasks (parts);
• i, j, k: Task number, i, j, k = 1, 2, …, n;
• w: Workstation number, w = 1, 2, …, m;
• l: Side of workstation, l = 1, 2; 1 means the left side; 2 means the right side.
• ls: Set of tasks which can only assigned to the left side of the line;
• rs: Set of tasks which can only assigned to the right side of the line;
• d_i: Demand attribute of part i; if part i is in demand, d_i = 1, else d_i = 0;
• h_i: Hazard attribute of part i; if part i is hazardous, h_i = 1, else h_i = 0;
• t_i: Operating time of disassembly task i;
• t_i^s: Start time of disassembly task i;
• t_i^e: End time of disassembly task i;
• t_i^d: Waiting time of task i before disassembly;
• ct: Cycle time;
• st_wl: Total disassembly time on the l side of workstation w;
• PS_lk: kth task assigned on the l side of the line (e.g., tasks 3, 4, 7, 6, and 2 assigned on left side of the line, PS₁₃ = 7);
• PN_i: Set of preceding tasks for task i;
• r_i: Benefit of disassembly part i;
• c: Disassembly cost of unit time when disassembling tasks;
• c_s: Running cost of unit time for each station;
• c_m: Startup cost of each workstation;
• c_h: Additional cost of station for handling hazardous components.
• Decision variables:

$$z_w=\left\{\begin{array}{l}1 \mathrm{if} \mathrm{workstation} w \mathrm{is} \mathrm{opened}\\ 0 \mathrm{otherwise}\end{array}\right.$$

$$s_{wl}=\left\{\begin{array}{l}1 \mathrm{if} \mathrm{the} l \mathrm{side} \mathrm{of} \mathrm{workstation} w \mathrm{is} \mathrm{actived}\\ 0 \mathrm{otherwise}\end{array}\right.$$

$$x_{iwl}=\left\{\begin{array}{l}1 \mathrm{if} \mathrm{task} i \mathrm{is} \mathrm{assigned} \mathrm{on} \mathrm{the} l \mathrm{side} \mathrm{of} \mathrm{workstation} w\\ 0 \mathrm{otherwise}\end{array}\right.$$

2.3. Mathematical Model

Disassembly efficiency, profit, and environmental protection are the main disassembly evaluation indicators in process of handling EOL products. Therefore, this study constructs a mathematical model for the TPDLBP with the objectives of minimizing the environmental hazards, maximizing the disassembly profit, balancing the assignment of tasks among workstations, and minimizing the demand index. The mathematical model is presented as follows:

• Objective function:

$$\min f_1={\displaystyle \sum _{l=1}^2{\displaystyle \sum _{k=1}^{n}k\cdot h_{P{S}_{lk}}}}$$

(1)

$$\max f_2={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{w=1}^m{\displaystyle \sum _{l=1}^2{x}_{iwl}\cdot p_i}}}-c\cdot {\displaystyle \sum _{i=1}^n{\displaystyle \sum _{w=1}^m{\displaystyle \sum _{l=1}^2{x}_{iwl}\cdot t_i}}}-c_m\cdot {\displaystyle \sum _{w=1}^m{z}_w}-c_s\cdot ct\cdot {\displaystyle \sum _{w=1}^m{\displaystyle \sum _{l=1}^2{s}_{wl}}}-c_h\cdot {\displaystyle \sum _{w=1}^m{\displaystyle \sum _{l=1}^2\underset{1\le i\le n}{\max }}}\left\{x_{iwl}\cdot h_i\right\}$$

(2)

$$\min f_3=\sqrt{{\displaystyle \sum _{w=1}^m{\displaystyle \sum _{l=1}^2{s}_{wl}\cdot {(ct-S{T}_{wl})}^2}}}$$

(3)

$$\min f_4={\displaystyle \sum _{l=1}^2{\displaystyle \sum _{k=1}^{n}k\cdot d_{P{S}_{lk}}}}$$

(4)

• Constraints:

$${\displaystyle \sum _{i=1}^n{x}_{iwl}\cdot (t_i+t_i^d)}\le ct\hspace{1em}\forall w=1,2,\cdots ,m,l=1,2$$

(5)

$${\displaystyle \sum _{w=1}^m{\displaystyle \sum _{l=1}^{2}w\cdot x_{jwl}}}\le {\displaystyle \sum _{v=1}^m{\displaystyle \sum _{l=1}^{2}v\cdot x_{ivl}}}\hspace{1em}\forall i=1,2 , \dots ,n, j\in P{N}_i$$

(6)

$$x_{ivl}\cdot t_i^s\ge x_{jwl}\cdot t_i^e\hspace{1em}\forall i=1,2, \dots ,n, \forall l=1,2, \forall v=w,j \in P{N}_i$$

(7)

$${\displaystyle \sum _{w=1}^m{\displaystyle \sum _{l=1}^2{x}_{iwl}}}=1\hspace{1em}\forall i\in \{i|h_i+d_i\ge 1\}$$

(8)

$${\displaystyle \sum _{w=1}^m{\displaystyle \sum _{l=1}^2{x}_{iwl}}}\le 1\hspace{1em}\forall i\in \{i|h_i+d_i=0\}$$

(9)

$${\displaystyle \sum _{i=1}^n{x}_{iwl}\cdot s_{wl}}\ge 1\hspace{1em}\forall w=1,2,\cdots ,m, \forall l=1,2$$

(10)

$${\displaystyle \sum _{l=1}^2{s}_{wl}}\le 2\cdot z_w\hspace{1em}\forall w=1,2,\cdots ,m$$

(11)

$${\displaystyle \sum _{w=1}^m{x}_{iw2}}=0\hspace{1em}\forall i\in ls$$

(12)

$${\displaystyle \sum _{w=1}^m{x}_{iw1}}=0\hspace{1em}\forall i\in rs$$

(13)

$$x_{iwl},s_{wl},z_w\in \{0,1\}, \forall w=1,2,\cdots ,m, l=1,2,i=1,2,\cdots ,n$$

(14)

Objective function: Equation (1) aims to minimize environmental hazards, which prioritizes the removal of hazardous components to reduce hazards to the environment and subsequent operational risks during the disassembly process. Equation (2) aims to maximize the disassembly profit, which can ensure that the valuable parts are removed from the EOL products. Equation (3) aims to evenly assign tasks among opened stations to guarantee a relatively balanced workload for workers. Equation (4) aims to disassemble the parts with demand as early as possible to avoid being damaged in the disassembly process.

Constraints: Equation (5) represents the cycle time constraint, which stipulates that the sum of the processing time and waiting time of tasks assigned to each station cannot exceed the cycle time. Equations (6) and (7) are precedence constraints: Equation (6) indicates that if the tasks are not assigned to the same workstation, the workstation assigned for a task must be located after the workstations assigned for its predecessor tasks; Equation (7) specifies that if the tasks are assigned to the same workstation, the start time of a task must not be earlier than the end time of its predecessor tasks. Equation (8) denotes that parts with hazard or demand attributes must be disassembled. Equation (9) means that parts without hazard or demand attributes can be disassembled optionally. Equation (10) states that there must be tasks on the running stations. Equation (11) ensures that at least one side station is running in an open workstation. Equations (12) and (13) represent disassembly direction constraints, which ensure that the tasks cannot be assigned to the opposite side of the line in accordance with their specified disassembly directions. Equation (14) defines the decision variables.

3. The Proposed Method

The whale optimization algorithm is a swarm intelligence optimization algorithm, which is inspired by the foraging behavior of humpback whales in nature [25,27,29]. It simulates the unique searching methods and encircling mechanisms of humpback whales, mainly including three phases: random wandering, encircling prey, and bubble-net attacking [25]. In WOA, the position of each humpback whale represents a feasible solution to the problem. By continuously updating the positions of the whales in the solution space, an optimal solution is finally obtained. WOA is originally designed for continuous function optimization. As the presented TPDLBP is a complex combinatorial optimization problem, some improvements and strategies should be developed for WOA to solve this problem effectively: (1) a combination generation method is used to initialize the population; (2) a new solution representation method based on a one-dimensional positive and negative integer array is designed; (3) different neighbor operators are constructed in the search process to obtain high-quality neighbor solutions; and (4) a nonlinear convergence factor is employed to achieve a proper balance between exploitation and exploration. The details of the improved WOA are described as follows.

3.1. Encoding and Decoding

A feasible solution of the TPDLBP refers to an effective disassembly sequence for EOL products on the two-sided disassembly line, which needs to satisfy precedence constraints and disassembly direction constraints. In addition, the TPDLBP is a partial disassembly problem, which means that not all the parts need to be disassembled from EOL products. Therefore, the disassembly depth (i.e., the total number of disassembled tasks) needs to be reflected in the feasible solution. Based on the above characteristics of the feasible solutions to the TPDLBP, a coding method based on a one-dimensional positive and negative integer array is designed, in which the last element represents the disassembly depth and the other elements with positive or negative signs denote the tasks and their disassembly direction. The order of the elements indicates the disassembly sequence of tasks. 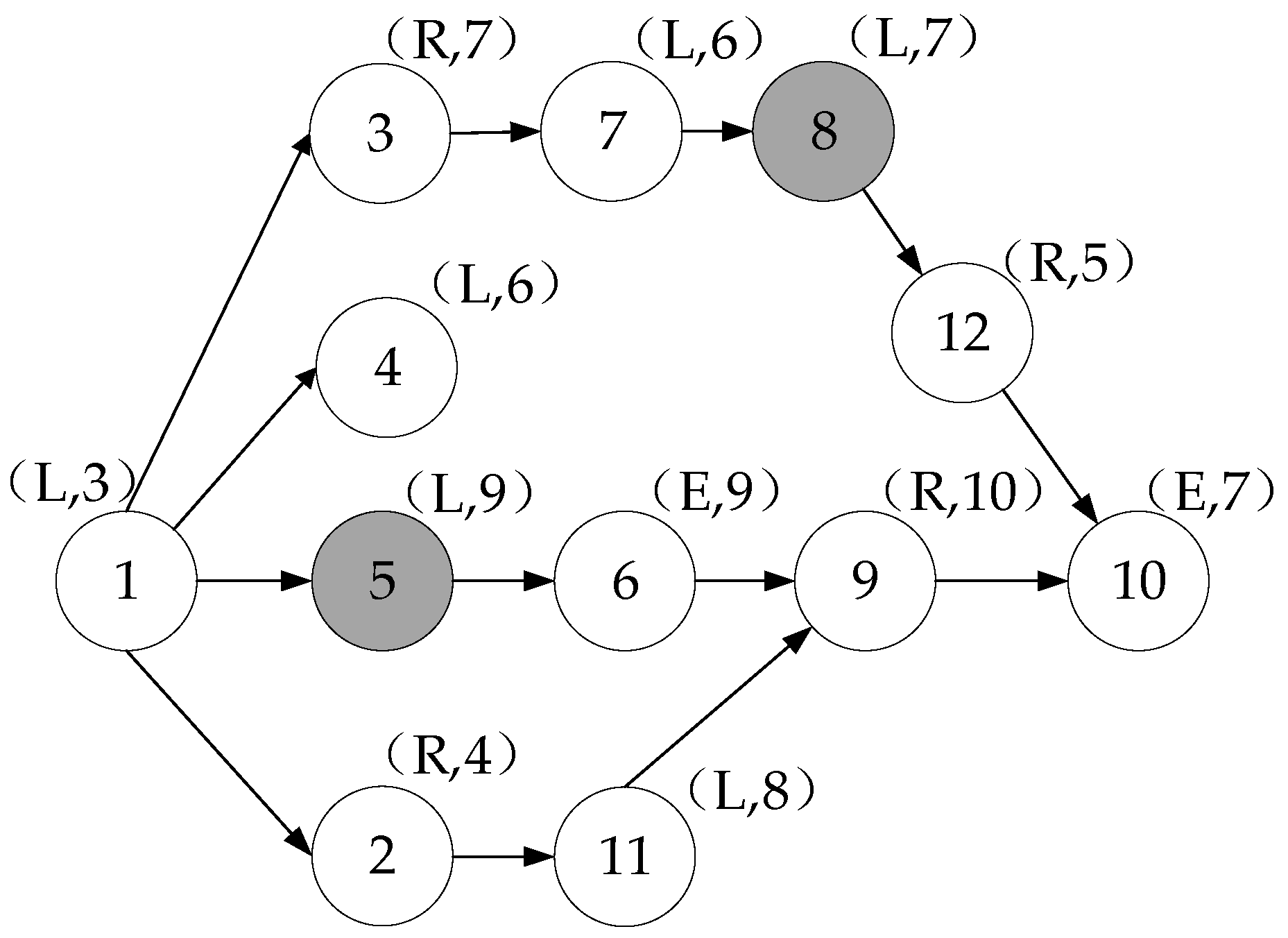Taking the disassembly process of the EOL product P12 (Figure 1) as an example, the integer array [−1, +2, −4, −5, +6, −11, +9, +3, −8, +12, +7, −10, 7], which satisfies precedence constraints and disassembly direction constraints and contains the information of the disassembly depth, can represent a feasible solution.

As the coding method can represent all the disassembly information, the decoding procedure is very simple, which is to allocate the tasks in the disassembly sequence to each workstation while satisfying the cycle time constraint. The details of the decoding procedure are described as follows.

Step 1: Input the integer array of the task disassembly sequence.

Step 2: Select the first element in the array, open the first workstation, and determine the disassembly depth.

Step 3: Determine whether the number of total disassembled tasks reaches the disassembly depth; if not, then go to step 4; otherwise, go to step 7.

Step 4: Assign the current task to the corresponding side of the workstation according to its disassembly direction.

Step 5: Calculate the start operating time and the end operating time of the current task and determine whether the end operating time is greater than the cycle time; if so, then open the next workstation and go to Step 4; otherwise, record the operating end time of the workstation.

Step 6: Select the next element in the array and go to step 3.

Step 7: Output the results.

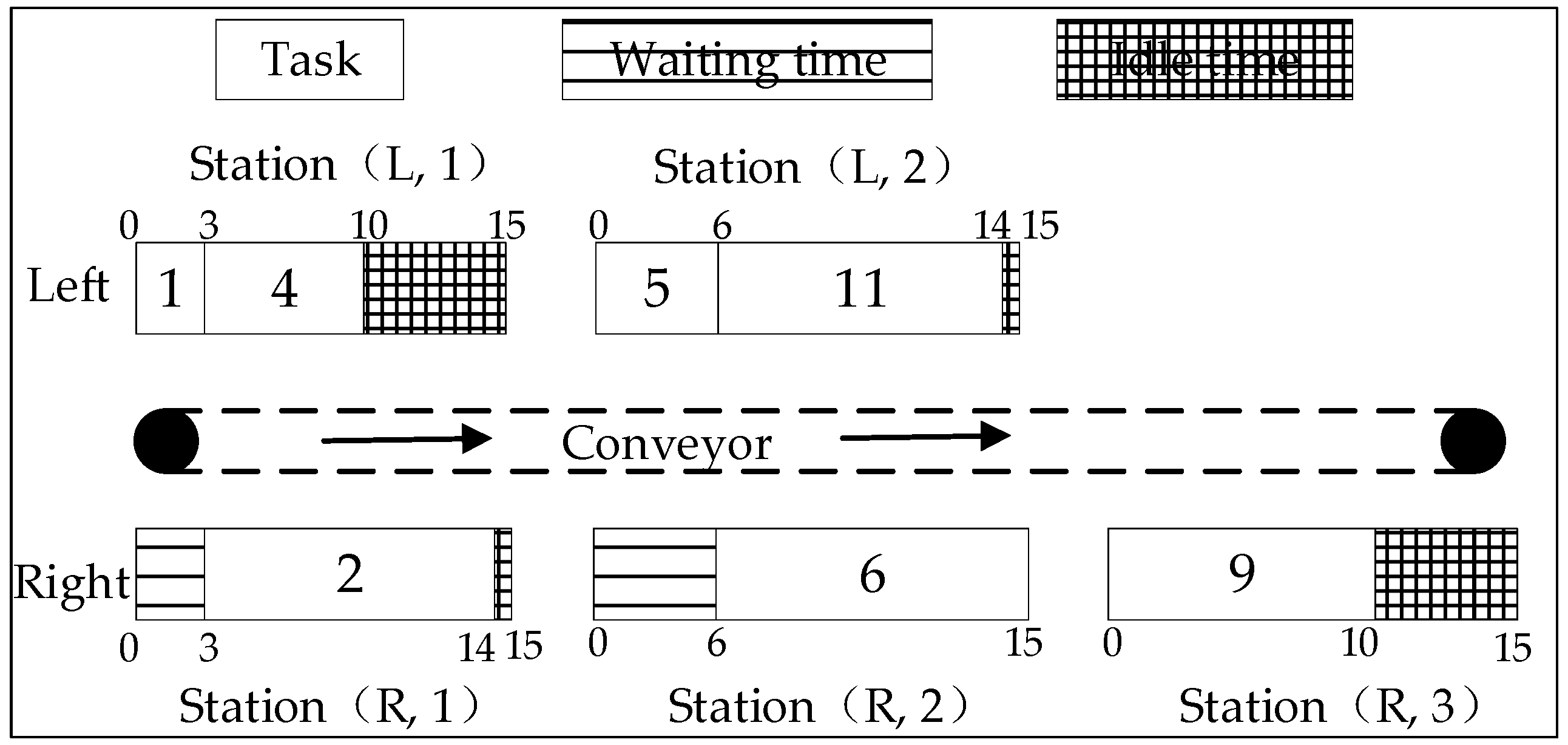
Taking the decoding process of the encoding scheme [−1, +2, −4, −5, +6, −11, +9, +3, −8, +12, +7, −10, 7] as an example, the cycle time is set to 15. Firstly, the first workstation is opened and the first element is assigned −1. The sign of this number is ‘−’, so the task will be assigned to the left side of workstation 1. The start operating time (ST) and the end operating time (ET) of task 1 are calculated. The ET of task 1 is 3, which is not greater than the cycle time, so it is assigned to the current station. Then, task 2 is assigned, the disassembly direction of which is the right side, but it cannot be assigned until its predecessor task 1 has been dismantled. So, the waiting time of task 2 is 3, and the ST and ET of task 2 are 3 and 14, respectively. Next, task 4 is assigned to the left side of workstation 1. This continues until the total number of disassembly tasks reaches 7. The decoding results are given in Figure 3. The proposed encoding method for the feasible solutions has advantages of a simple structure, low storage space occupancy, and ease of implementation. Moreover, it simplifies the decoding procedure and the design of neighbor operators.

3.2. Initialization Population

The diversity and quality of individuals in a population largely determine the search efficiency and convergence speed of swarm intelligence optimization algorithms. To balance the diversity and quality of the population, a combination generation method is proposed, in which some individuals are generated using a heuristic approach while others are generated randomly. The random generation method involves randomly selecting tasks for assignment during individual construction. The heuristic approach prioritizes the selection of hazardous parts. After all hazardous parts have been assigned, tasks are chosen based on their disassembly profit. Then, tasks with a short disassembly time are chosen. Finally, the demand parts are selected. The generation process is detailed as follows:

Step 1: Construct an N × N precedence relationship matrix A and a 1 × N disassembly direction matrix P. In the matrix A, the element a_ij = 1 indicates that task i is the direct predecessor of task j, while a_ij = 0 indicates that there is no direct relationship between tasks i and j; in the matrix P, the element p_i = 1 or 2 indicates that the disassembly direction of task i is the left or right side, and p_i = 0 indicates that both the left and right sides are acceptable.

Step 2: Filter the assignable tasks. The columns for which all elements are not equal to 1 in matrix A form the set of assignable tasks.

Step 3: Determine the assigned task. If the random method is used, a task from the set of assignable tasks is randomly selected. If the heuristic method is used, the tasks are selected according to the specific heuristic rules. After determining the assigned task, the disassembly direction of the task is specified by the matrix P. If the direction is the left or right side, the task number is marked with the sign of ‘−’ or ‘+’. If the task can be assigned to either side, it is marked with ‘+’ or ‘−’ randomly.

Step 4: Modify matrices A and P. In matrix A, the elements in the row and column corresponding to the task selected in step 3 are set to −1, and in matrix P, the corresponding element is marked as −1 which indicates that the task has been assigned.

Step 5: Repeat steps 2–4 until all tasks are selected.

3.3. Encircling Prey Phase

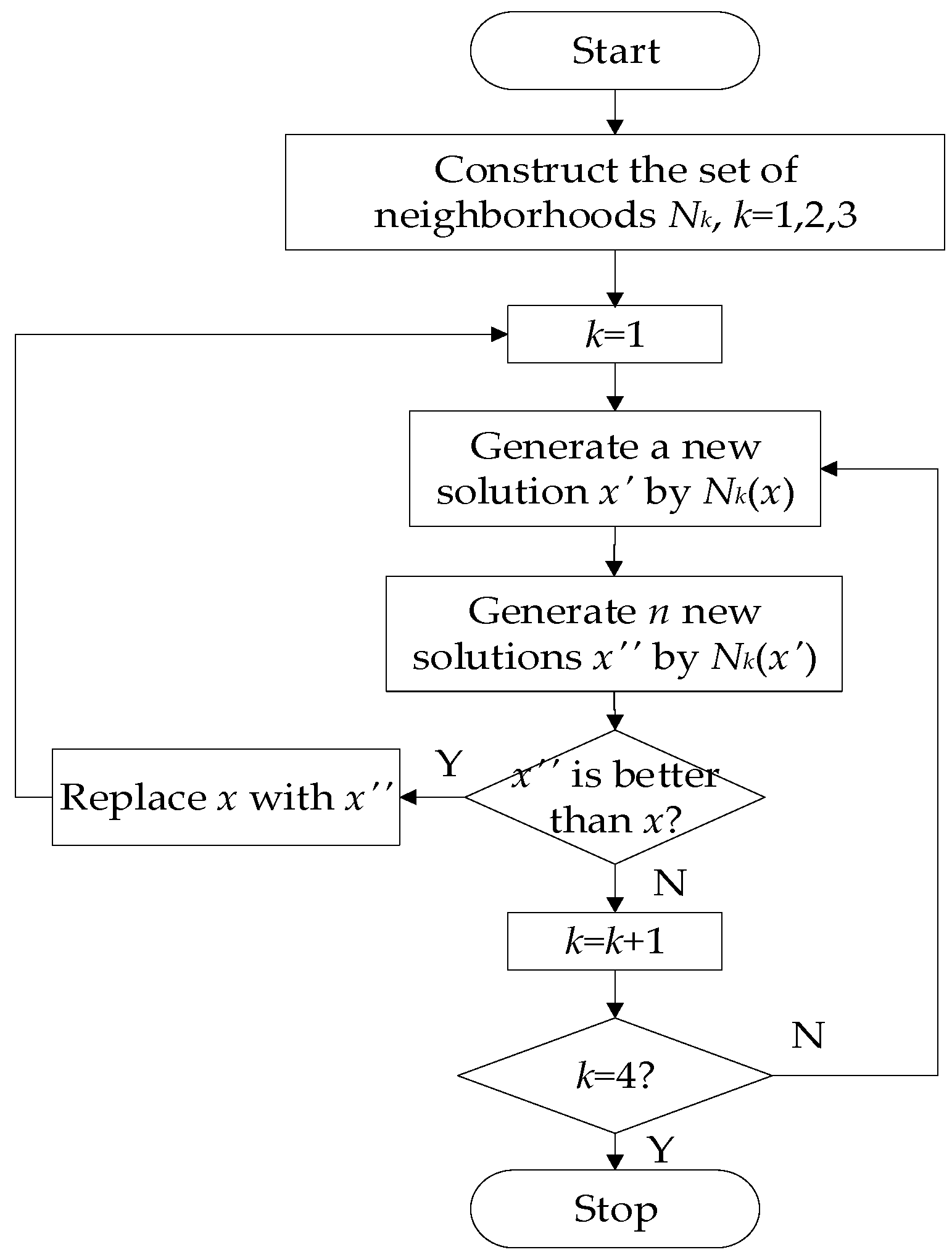
In the stage of encircling the prey, humpback whales can identify the location of their prey and form a circle around it. In WOA, since the optimal position in the search space is unknown, the position of the current optimal whale (solution) is regarded as the target prey. The whales then adjust their positions based on the target prey. To achieve an effective search of the area between whales and the prey, three different crossover operators are designed, as shown in Figure 4. The newly generated sequences consist of two parts: one part is a subsequence of one parent, and the other part is rearranged according to the other parent, which conforms to the order of tasks in the parent sequences, so they are feasible solutions. Then, the last element of the new solution sequence is randomly reset to change the disassembly depth while ensuring that all the demand and hazardous tasks can be dismantled. In order to further enhance the search efficiency, the variable neighborhood search (VNS) method is employed in the search process. It systematically changes the neighbor structures to realize the search of the region between the whale and the target prey for better solutions which may be difficult to find by a simple neighbor. The flowchart of the VNS is given in Figure 5.

3.4. Bubble-Net Attacking Phase

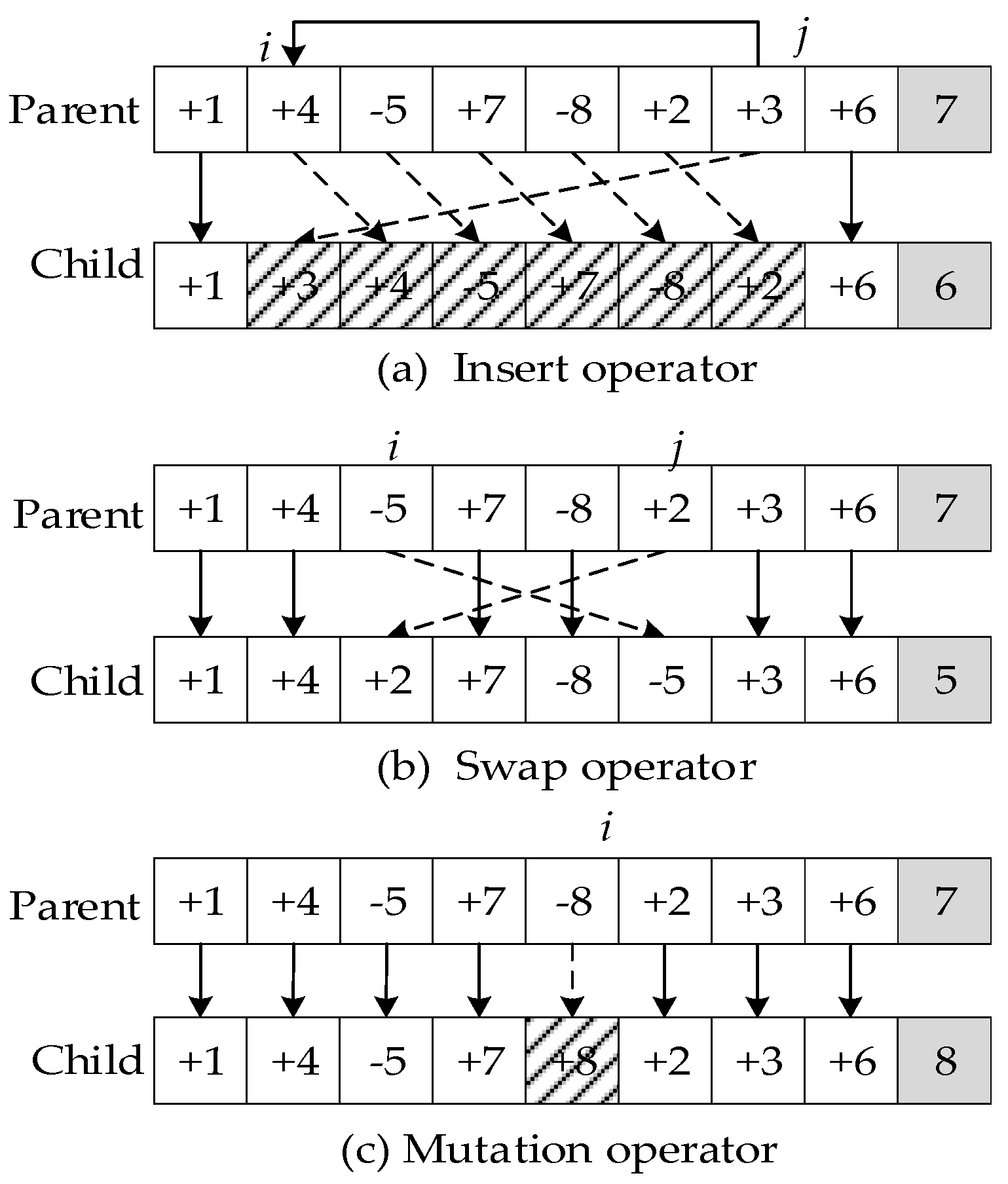
When humpback whales are sufficiently close to the prey, they employ a bubble-net to attack it. WOA mimics this behavior of humpback whales by generating a virtual bubble-net to gradually narrow down the search scope. So, in this phase, the whales mainly focus on the surrounding area of the prey, which could be the most promising region for better solutions. To achieve an effective search, three neighbor structures are constructed, as shown in Figure 5: an insertion operator, a swap operator, and a mutation operator. The insertion and swap operators are used to change the order of tasks in the sequence. If a new sequence generated by these two operators does not satisfy the precedence constraints, it will be abandoned. The mutation operator is used to change the assigned side of tasks which can be disassembled on either side of the line. The new solution sequence is generated based on the optimal whale by the neighbor operators, and then the last element of this sequence is adjusted to change the total number of disassembled parts. During the bubble-net attacking phase, the whales continuously exploit the neighbor area of the optimal solution using the VNS method to change the insertion, swap, and mutation neighbor structures.

3.5. Random Wandering Phase

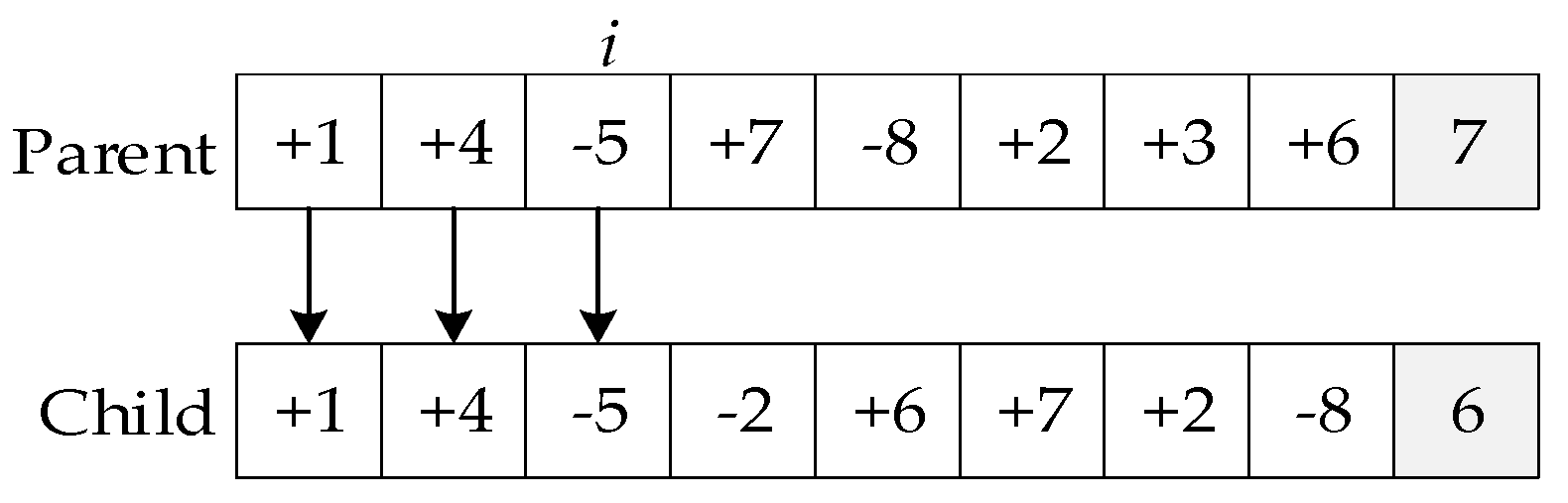
In this phase, WOA mimics the random search behavior of humpback whales for new prey. In contrast to the encircling prey phase, the position of a whale in this phase is updated according to a randomly chosen whale instead of the best whale found so far. In order to further enhance the efficiency of global search, we propose two new random search modes, namely, whales randomly searching for prey in their surrounding areas and in places far away from their current locations. Given the characteristics of the three random search modes in the random wandering phase, the crossover operator (Figure 4a), the insertion operator (Figure 6a) as well as the mutation operator (Figure 6c), and the truncation operator (Figure 7) are employed to realize each search mode, respectively. The crossover, insertion, and mutation operations are also used in other phases, but their parent individuals are different, resulting in distinct search regions within the solution space. The truncation operator randomly selects a point in the sequence, and the left subsegment of the point remains unchanged while the right subsegment is regenerated by using the random construction method for the feasible solution mentioned in Section 3.2. Notably, the value of the selected point directly determines the distance that the whales swim far away from their initial position. In order to reflect the randomness in the random wandering phase, a random neighborhood search (RNS) strategy is employed, the idea of which is random change in neighbor structures to explore the search space for better solutions.

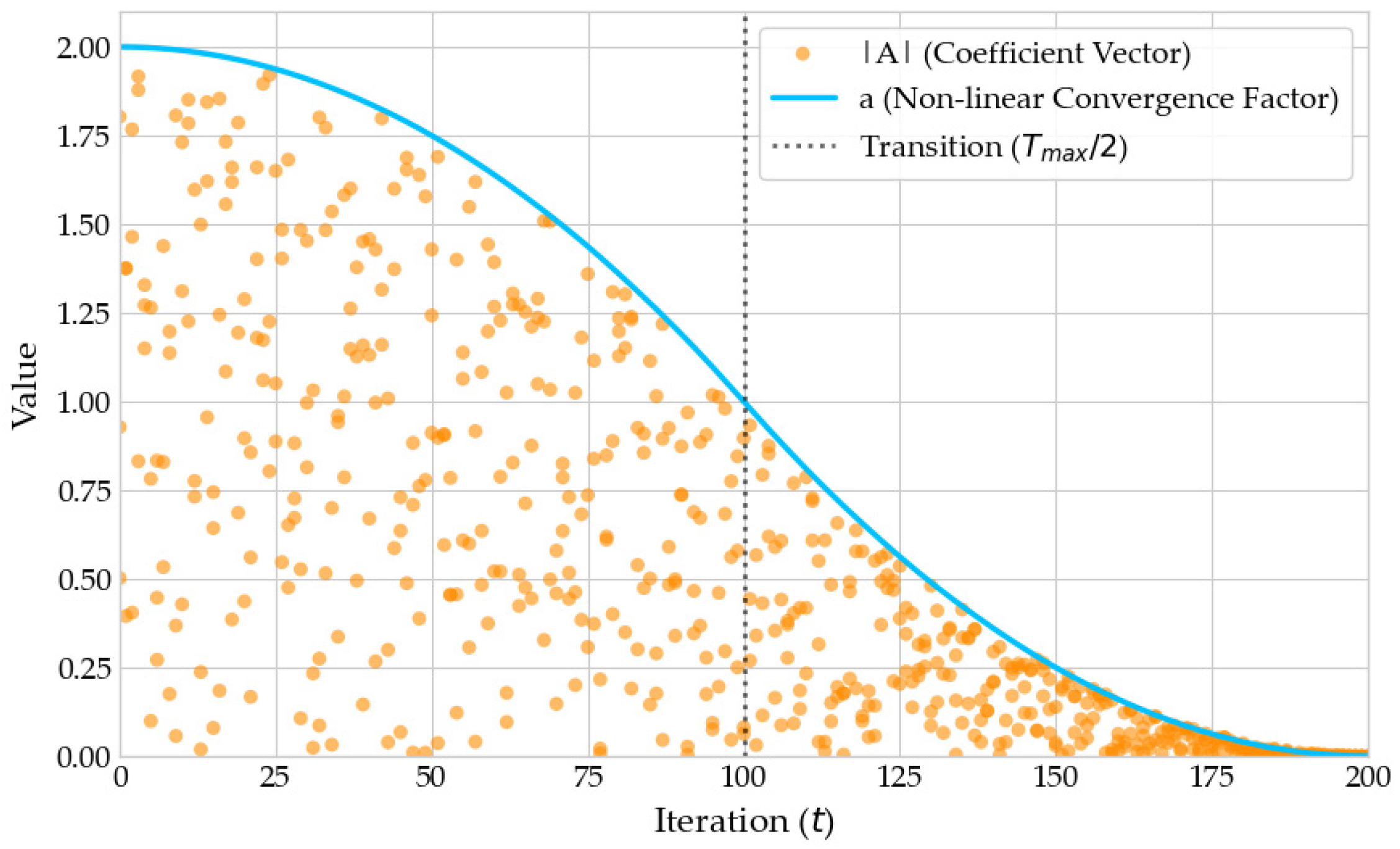
3.6. Nonlinear Convergence Factor

In the search process, the balance between global and local search is controlled by parameter A = 2 · a · rand − a, where rand is a random value in [0, 1] and a = 2 · (1 − t/T_max) is linearly decreased from 2 to 0. If |A| < 1, the whale enters the encircling prey phase; otherwise, it enters the random wandering phase. Obviously, the value of parameter A is significantly affected by the convergence factor a. The factor a is linearly decreased, and this may lead to insufficient exploration of the solution space in the early stages and slow convergence in the later stages, thereby affecting the overall optimization efficiency. Therefore, we propose a piecewise nonlinear convergence factor, as shown in Equation (15), where T_max is the maximum iteration number (or the maximum iteration time) and t is the current iteration number (or the current iteration time). Figure 8 illustrates the distribution of the nonlinear convergence factor a and |A|. It can be seen that in the early stages of the optimization process, using a smaller decay rate can ensure that the algorithm conducts extensive exploration in a larger search space, avoiding premature falling into local optima. This enhanced global search capability enables the algorithm to discover potential better solutions. In the later stages of the optimization process, a smaller convergence factor allows the algorithm to perform local searches with fine-grained fluctuations, further improving the accuracy of the solution. The nonlinear change in the convergence factor can better regulate the relationship between exploration and exploitation while preserving the original equilibrium points.

$$a=\left\{\begin{array}{ll}2-{\left({\displaystyle \frac{t}{T_{\max }/2}}\right)}^2& t\le T_{\max }/2 \\ 1-{\left({\displaystyle \frac{t-T_{\max }/2}{T_{\max }/2}}\right)}^2& t>T_{\max }/2\end{array}\right.$$

(15)

3.7. Evaluation Mechanism

The recycling and reuse of EOL products aims to protect the environment, reduce pollution, and achieve circular utilization of resources. Hence, during the disassembly process, hazardous components/parts such as mercury-containing lamps and cathode ray tubes must be removed first to minimize environmental hazards and reduce subsequent operational risks and health threats to workers. On this basis, enterprises further pursue profit from dismantling. Subsequently, the tasks will be evenly distributed among workstations to guarantee a relatively balanced workload for workers, and the components/parts in demand will be removed as early as possible to prevent damage during later operations that could diminish their value. Obviously, these objectives have a clear priority order in the disassembly process. Therefore, in this study, a lexicographic method is used for evaluating the solutions. Objectives are considered according to the priority orders. Hence, the algorithm tries to optimize the first objective in the model, then optimize the second objective, followed by the third one, and so on.

3.8. Algorithm Flow of IDWOA

In IDWOA, the feasible solutions are represented by a one-dimensional array of positive and negative integers. In the random wandering, encircling prey, and bubble-net attacking phases, different neighbor operators are constructed according to the characteristics of each search phase, and different search strategies are designed to enhance the efficiency of local exploitation and global exploration. The optimization procedure is given as follows:

Step 1: Parameter initialization. Set the number of whales and the maximum iteration number.

Step 2: Population initialization. Generate the initial whale population with the combination method and record the current optimal whale.

Step 3: Generate a random number r between 0 and 1. If r > 0.5, continue to judge the value of the parameter A. If |A| > 1, go to Step 4; otherwise, go to Step 5. If r < 0.5, go to Step 6.

Step 4: Encircling prey phase. Use the VNS method, which systematically changes left crossover, right crossover, and two-point crossover operators, to carry out local search in the area between the whales and the optimal solution.

Step 5: Random wandering phase. Apply the RNS method, which randomly selects crossover, insertion, mutation, and truncation operators, to realize exploration of the solution space.

Step 6: Bubble-net attacking phase. Employ the VNS method, which systematically changes insertion, swap, and mutation operators, to perform a precise search in the surrounding region of the current optimal solution.

Step 7: Check the termination condition. If the termination condition is met, stop the search and output the optimal solution; otherwise, return to Step 3.

4. Computational Study and Results

There are few relevant test instances for the TPDLBP. However, the DLBP with complete disassembly, the DLBP with partial disassembly, and the two-sided DLBP with complete disassembly can be regarded as three special forms of the TPDLBP: complete disassembly with only one side of workstations open, partial disassembly with only one side of workstations open, and complete disassembly with two-sided workstations open. Thus, the mathematical model for the TPDLBP is also applicable to the aforementioned three types of DLBPs. Hence, the performance of the proposed IDWOA can be tested through these three different types of instances. Meanwhile, the effectiveness of the proposed model and algorithm is further validated through a real case, and the task assignment of the obtained disassembly solution on the two-sided disassembly line is analyzed.

According to the structure of the proposed algorithm, there are three main parameters that directly affect the optimization result: the initial population size PS, convergence factor a, and coefficient A. Among these parameters, the factor a is decreased from 2 to 0, as shown in Figure 8, and A = 2 · a · rand − a is a random value in the interval [−a, a], the fluctuation range of which is also decreased by a. Hence, only the parameter PS needs to be calibrated. A set of experiments was conducted to find the best PS parameter value. The best value was found to be 50 (PS = 50). The proposed IDWOA was programmed in C++ and run on a VMware workstation allocated with 3 GB RAM and four processor cores from a computer with an Intel Core i5 CPU and 16 GB RAM.

4.1. Instance Test

The performance of the proposed IDWOA is tested in this section by three instances, including a complete disassembly of DLBP instance CP25 [19] (a 25-part mobile phone instance), a partial disassembly of DLBP instance PP47 [31] (a 47-part laptop instance), and a complete disassembly of two-sided DLBP instance CT52 [32] (a 52-part refrigerator instance). The detailed data of these instances can be referred to in the corresponding literature. To conduct effective testing, IDWOA is compared with other algorithms that have been used for the above three DLBPs.

4.1.1. Complete Disassembly of the DLBP Instance

For the CP25 instance of the DLBP under complete disassembly, the cycle time of the disassembly line is set to 40 s. In the existing literature, the disassembly solutions are evaluated by four aspects using a lexicographical ordering method: (1) minimizing the number of workstations (f₁), (2) minimizing the smoothing index (f₂), (3) minimizing the disassembly hazard index (f₃), and (4) prioritizing the removal of demanded components (f₄). As the average values and the optimal solutions for CP25 obtained by several algorithms have been compared in the literature [33], the proposed IDWOA is compared with these algorithms, and the results are shown in

Table 1. Solution results of the CP25 instance.

Method	Optimal Solution				Average Value
	f1	f2	f3	f4	f1	f2	f3	f4
ACO	-	-	-	-	9	10.2	87.2	924.4
MOACO	9	11	-	838	9	11	-	874.3
ABC	9	9	81	853	9	9	83.9	887.4
RL	9	9	97	862	-	-	-	-
SA	9	9	81	853	9	9	85.5	918.5
PSO	9	9	80	857	9	9	83.5	889.04
HGA	9	9	76	825	9	9	76	825
HDABC	9	9	76	825	9	9	76	825
IDWOA	9	9	76	825	9	9	76	825

. It can be found that the optimal solution (f₁ = 9, f₂ = 9, and f₃ = 76, f₄ = 825) found by IDWOA, HDABC, and HGA is significantly better than those of the other six algorithms. In addition, in terms of the average value, these three algorithms also had better performance than the other algorithms. Obviously, IDWOA, HDABC, and HGA exhibit excellent performance in solving the complete disassembly CP25 instance. Since the comparison results of different algorithms for the CP25 instance in the existing literature are limited to the average and optimal values, the performance among IDWOA, HDABC, and HGA cannot be further compared. However, based on the above analysis, we can conclude that IDWOA is an effective solution method for the complete disassembly of the DLBP.

4.1.2. Partial Disassembly of the DLBP Instance

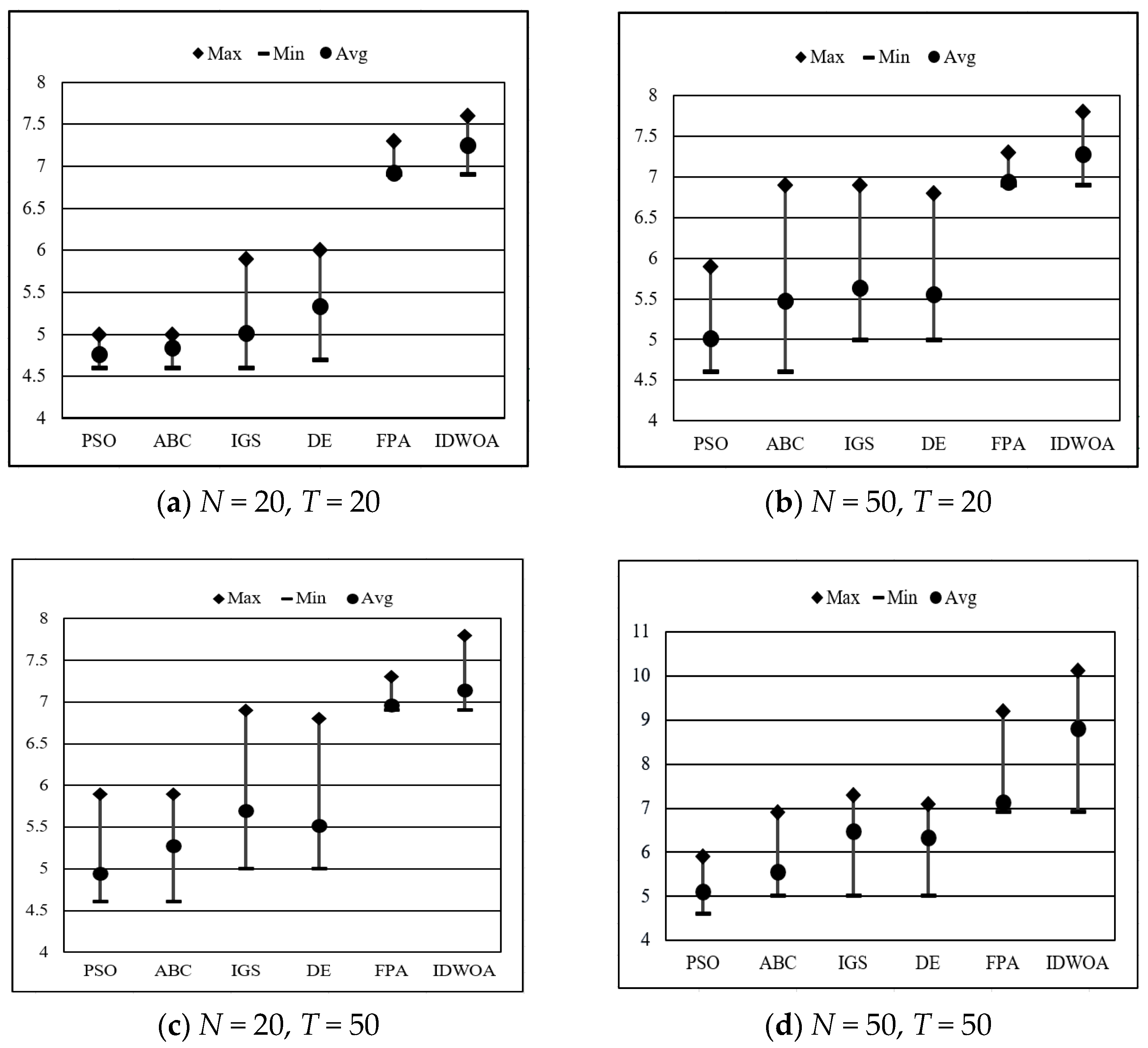
For the PP47 instance of partial disassembly with the objective of maximizing the disassembly profit, the proposed IDWOA is compared with five other different algorithms (PSP, ABC, FPA, IGS, and DE) that have been used to solve the PP47 instance reported in the literature [34]. The comparison results are shown in Figure 9. Here, N and T denote the population size and the number of iterations, respectively, while MIN, MAX, and AVG represent the minimum, maximum, and average values of the solutions, respectively. As can be seen from Figure 9, as the population size and iteration number increase, the quality of the solutions obtained by each algorithm continuously improves. Moreover, the figure reveals that no matter how the value of the population size N and iteration T changes, the results of IDWOA and FPA in terms of MAX, AVG, and MIN are significantly superior to those of PSP, ABC, IGS, and DE. A further comparison between FPA and IDWOA shows that although both algorithms can achieve the minimum value of 6.90 under different combinations of population size and iteration number, IDWOA is superior to FPA in terms of the maximum value and the average value. Apparently, IDWOA shows the best performance for the PP47 instance.

4.1.3. Complete Disassembly of the Two-Sided DLBP Instance

For the CT52 instance of the two-sided DLBP with complete disassembly, there are four disassembly indicators: the workstation index (f₁), idle index (f₂), demand index (f₃), and hazard index (f₄). The bat algorithm (BA) and the improved salp swarm algorithm (ISSA) employ Pareto dominance theory and an external archive method based on crowding distance to obtain a non-dominated solution set, in which the number of Pareto solutions is set to 8 [32]. In order to effectively validate the proposed IDWOA, it employs the same strategies as BA and ISSA to evaluate and screen the solutions, and the results are compared with those of the two algorithms, as shown in

Table 2. Solution results of the CT52 instance.

Algorithm	No.	f1	f2	f3	f4	Algorithm	No.	f1	f2	f3	f4	Algorithm	No.	f1	f2	f3	f4
BA	1	6	5907	461	42	ISSA	1	5	755	493	29	IDWOA	1	5	979	443	27
	2	6	6359	445	36		2	5	849	474	30		2	5	1039	447	24
	3	6	8757	517	25		3	5	977	467	32		3	6	6663	445	25
	4	7	16,859	454	34		4	5	849	473	31		4	6	8327	429	28
	5	7	19,657	481	26		5	6	6700	461	31		5	7	19,031	419	31
	6	8	28,533	485	24		6	6	7263	471	27		6	7	19,785	430	27
	7	9	48,711	433	34		7	7	15,827	444	32		7	8	35,987	431	25
	8	9	51,679	435	30		8	8	28,093	462	22		8	9	48,561	462	21

. We can observe from the table that the interval range in each objective obtained by the three algorithms varies greatly. In the first objective f₁, the values obtained by BA, ISSA, and IDWOA range from 6 to 9, 5 to 8, and 5 to 9, respectively. In objective f₂, the values obtained by these three algorithms range from 5907 to 51,679, 755 to 28,093, and 979 to 48,561, respectively. In objective f₃, the values range from 433 to 517, 444 to 493, 419 to 462, respectively. In objective f₄, the values range from 24 to 42, 22 to 32, and 21 to 31, respectively. From the above comparison, we can see ISSA has smaller interval ranges in objectives f₁ and f₂. Particularly in objective f₂, the lower limit value is better than those of BA and IDWOA. However, in objectives f₃ and f₄, the interval ranges of IDWOA are significantly superior to those of BA and ISSA, and their lower and upper values also outperform those of the other two algorithms. Next, the eight solutions obtained by each algorithm are further compared. The eighth solution in ISSA dominates the sixth solution in BA. The third solution in IDWOA dominates the fifth and sixth solutions in ISSA, as well as the second, third, fourth, and fifth solutions in BA, and the fourth solution in IDWOA dominates the seventh solution in ISSA. Thus, based on the above comparisons, we can conclude that the solutions in the Pareto optimal solution set of IDWOA are of higher quality, and IDWOA performs well in solving the two-sided DLBP with complete disassembly.

4.2. Case Study

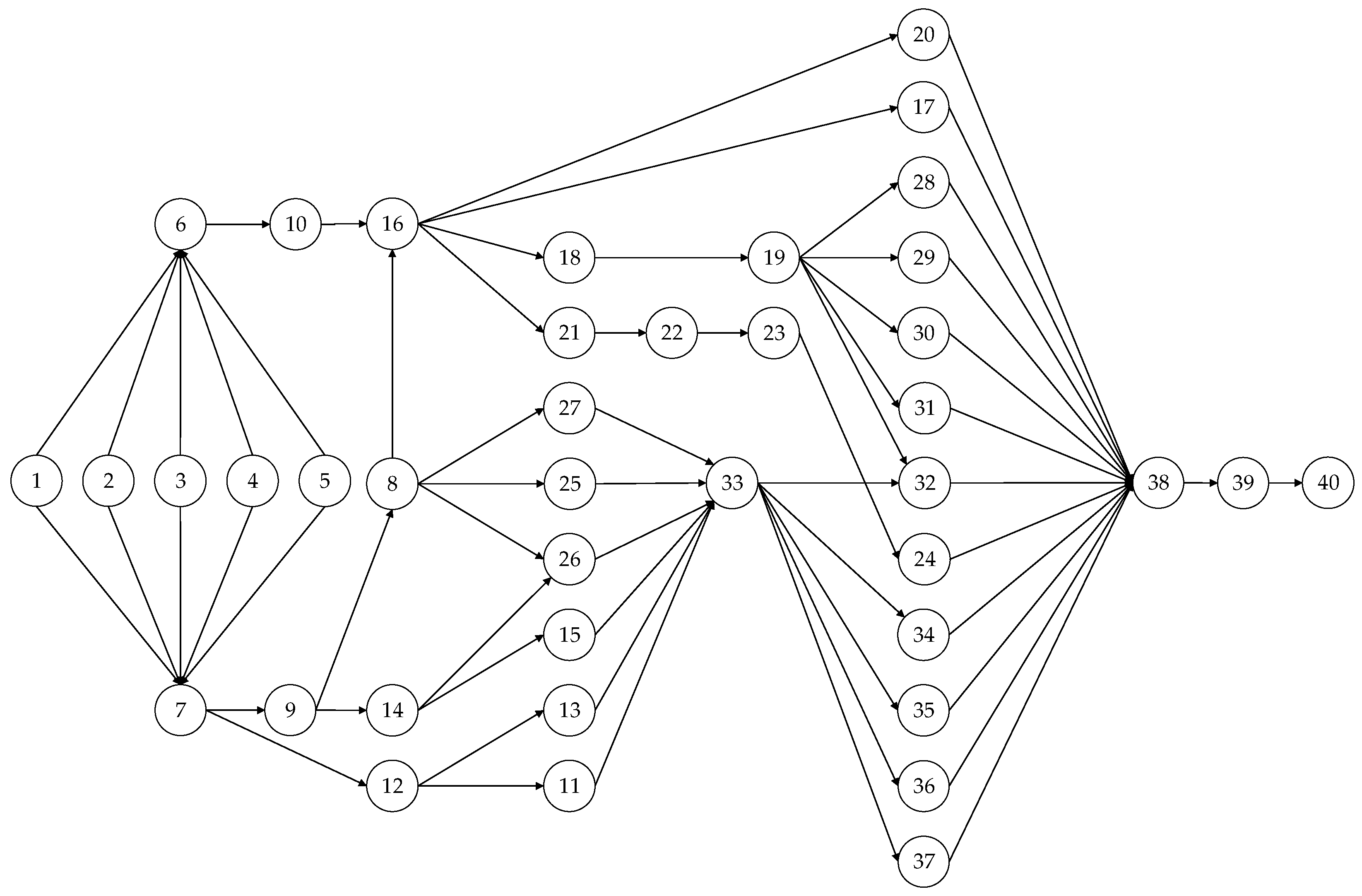
To further verify the effectiveness and practicality of the proposed model and algorithm, a case of partial dismantling of scrapped vehicles by a dismantling company in Qingdao, China, is studied in this section. The precedence relationships of parts in the scrapped vehicle are illustrated in Figure 10, and the disassembly information of each task such as the operating time t_i and the disassembly direction o_i is listed in

Table 3. Disassembly information of the EOL vehicle.

No.	Part	ti	hi	di	oi	ri	No.	Part	ti	hi	di	oi	ri
1	airbag	62	1	0	0	40	21	underbody shield	60	0	0	0	0
2	battery	62	1	1	1	102	22	exhaust pipe	74	1	1	2	240
3	waste oil and fluid	305	1	0	2	10	23	fuel tank	88	1	0	0	91
4	refrigerant	120	1	0	1	14	24	charcoal canister	28	0	0	1	0
5	wheel	130	0	1	0	400	25	radiator	112	0	0	2	114
6	door assembly	153	0	0	0	225	26	fluid reservoir	244	1	0	0	0
7	hood outer panel	50	0	0	1	148	27	air filter	50	0	0	0	0
8	bumper	120	0	0	0	41	28	brake component	70	0	1	1	37
9	lighting system	115	0	0	0	401	29	clutch pedal	52	0	0	1	0
10	trunk lid	82	0	0	0	85	30	accelerator pedal	58	0	0	1	0
11	front glass	60	1	0	0	312	31	HVAC system	132	0	0	0	0
12	wiper arm	53	0	0	0	5	32	steering system	240	0	1	0	23
13	wiper motor	58	0	0	0	17	33	engine bay pipes	172	0	0	0	0
14	fender	60	0	0	0	57	34	front suspension	231	0	1	0	421
15	mudguard	55	0	0	0	0	35	rear suspension	234	0	1	0	436
16	seat	138	0	0	0	0	36	transmission	210	0	1	1	850
17	safety belt system	115	0	0	0	25	37	engine	270	0	1	0	1500
18	steering wheel	105	0	0	1	30	38	interior components	240	1	0	0	0
19	dashboard	302	0	0	1	140	39	body accessories	98	0	0	0	0
20	gear lever	116	0	0	0	10	40	body harness	115	0	0	0	0

. In addition, the values for other disassembly parameters are set as follows: c_m = 25, c_s = 0.10, c = 0.12, and c_h = 20. First of all, the convergence of IDWOA is observed. Subsequently, IDWOA is compared with the discrete flower pollination algorithm (DFPA) [19] and discrete hummingbird algorithm (DHA) [35] on solving this case. DFPA and DHA have been applied to deal with the stochastic two-sided DLBP and the sequence-dependent DLBP with good performance, respectively. Finally, the disassembly process of the obtained optimal solution is analyzed.

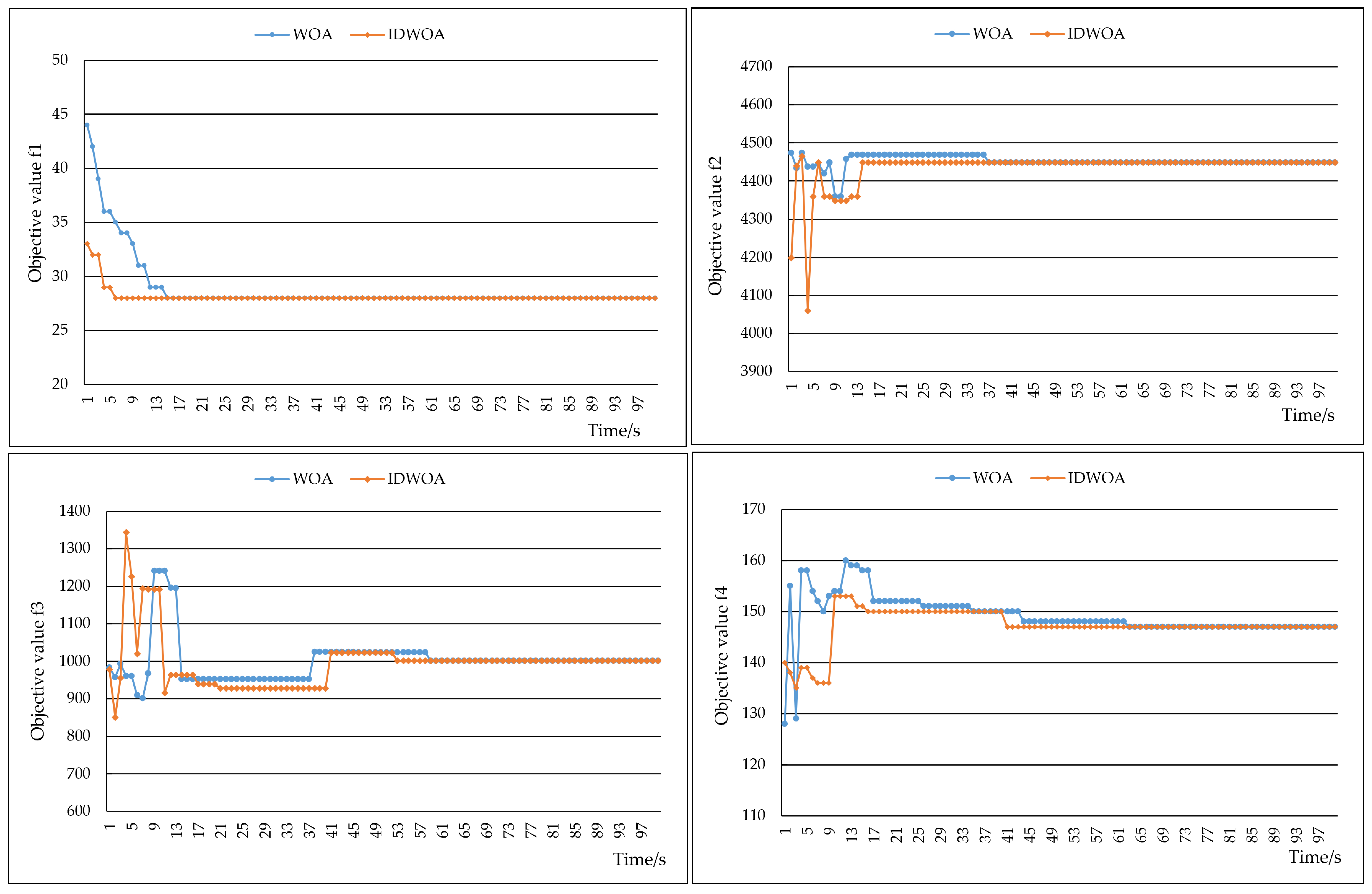
Figure 11 shows the convergence of IDWOA and the standard WOA. It can be observed that IDWOA converges significantly faster than the standard WOA and quickly tends towards stability with the increase in search time. Obviously, compared with the standard WOA, IDWOA can achieve rapid convergence. The reasons lie in the fact that its encoding method is simple and feasible, which can effectively save storage space, reduce decoding time, and simplify the construction of optimization operators. In addition, the neighbor structures and the neighbor change strategies designed according to the search characteristics of whales at each stage can effectively enhance local exploitation and global exploration.

Table 4. Results of three methods for the EOL vehicle.

Method	f1				f2				f3				f4
	MIN	MAX	AVG	SD	MIN	MAX	AVG	SD	MIN	MAX	AVG	SD	MIN	MAX	AVG	SD
DHA	28	28	28	0.00	4449	4449	4449	0.00	1001	1002	1001.35	0.85	150	154	151.95	2.61
DFPA	28	28	28	0.00	4449	4449	4449	0.00	1001	1001	1001.00	0.00	150	150	150.00	0.00
IDWOA	28	28	28	0.00	4449	4449	4449	0.00	1001	1001	1001.00	0.00	147	147	147.00	0.00

shows the maximum value (MAX), the minimum value (MIN), the average value (AVG), and the standard deviation value (SD) of 20 runs by IDWOA, DFPA, and DHA under an iteration time set to 60 s. We can see from the table that all the algorithms can obtain the same value in minimizing the hazard index (f₁ = 28) and maximizing the profit (f₂ = 4449) in every experiment. In terms of minimizing the smoothness index f₃, these three algorithms are the same in the minimum value, but in the maximum value, the average value, and the standard deviation value, DFPA and IDWOA are significantly superior to DHA. Due to the same value in objective f₃ obtained by DFPA and IDWOA, the performance of objective f₄ should be checked for further comparison. We can see that the values obtained by IDWOA and DFPA are 147 and 150, respectively, in each run. Obviously, IDWOA outperforms DFPA. Up to now, the performance of these three algorithms can be clearly distinguished, and they are ranked from best to worst as follows: IDWOA > DFPA > DHA. Additionally, it should be emphasized that IDWOA can find the optimal solution every time: f₁ = 28, f₂ = 4449, f₃ = 1001, and f₄ = 147, as shown in

Table 5. Disassembly sequence of the optimal solution.

Plan	Workstation	Disassembly Task	f1	f2	f3	f4
S1	Left side	[2-1-4-5-7-12-9-8-14], [6-10-16-21-13-15-27-33], [37-35-20-24-18], [36-19-32], [34-28-29-31-17-30]	28	4449	1001	147
	Right side	[3-11], [26-22-23-25], [38]

, demonstrating outstanding search stability. Based on the above comparisons, it can be concluded that IDWOA demonstrates excellent performance in solving the TPDLBP.

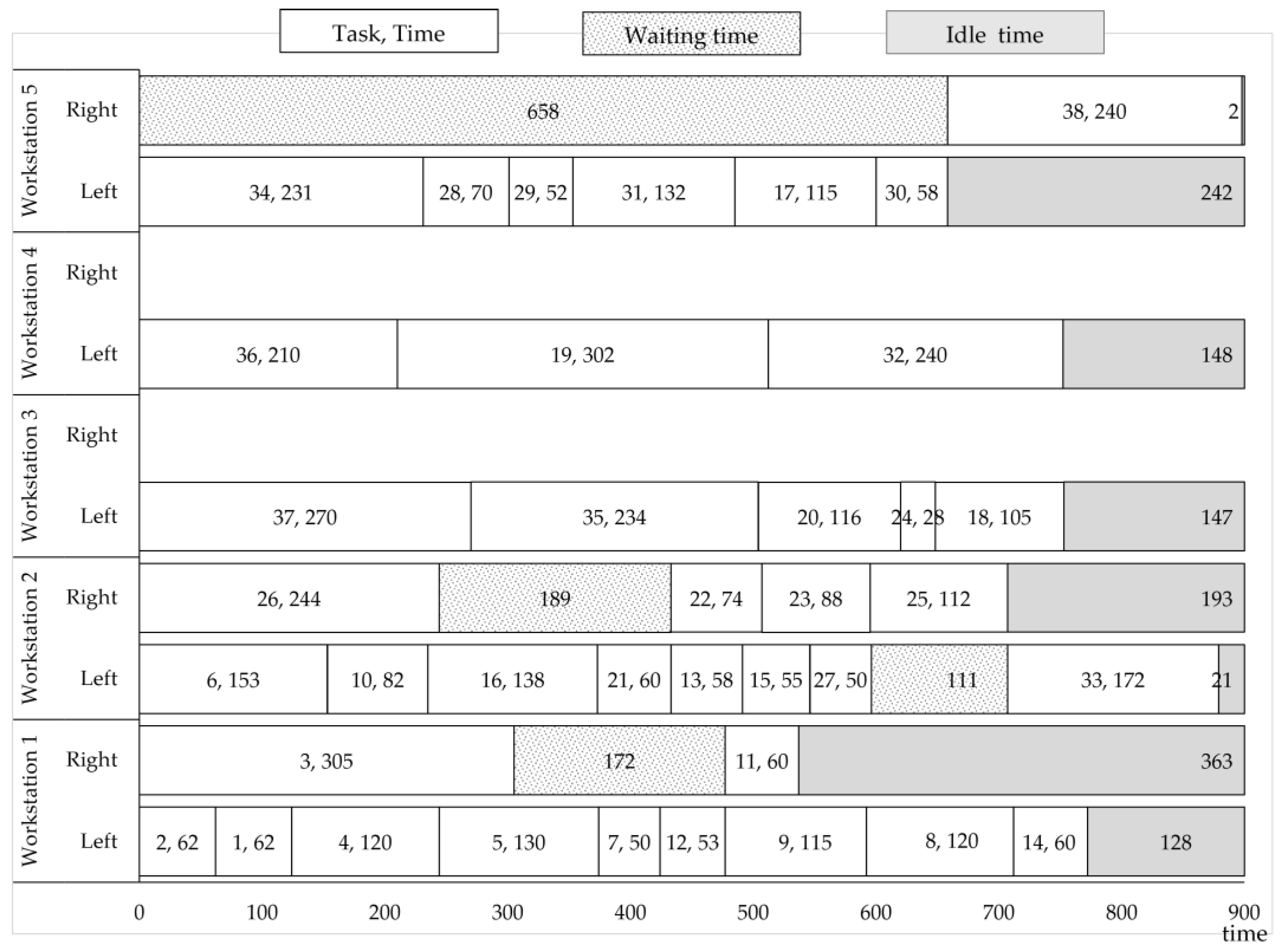
Figure 12 shows the task assignment of the optimal solution S1 listed in Table 5. It can be seen that a total of 38 parts from the EOL vehicle are disassembled. To disassemble these parts, five mated stations are opened, among which the right-side stations of mated-stations 3 and 4 are not activated, resulting in a total of ten activated stations. Using this disassembly scheme, the parts with a hazard attribute (i.e., parts 1, 2, 3, 4, 11, 22, 23, 26, and 38) can be disassembled first from the EOL vehicle. From the figure, we also can see that the parts with demand are disassembled as early as possible to avoid being damaged in the disassembly process. Due to the precedence relationships between tasks, disassembly waiting phenomena occur in the disassembly process. The waiting times are 172 s, 111 s, 189 s, and 658 s, respectively, before disassembling tasks 11, 33, 22, and 38. In the disassembly process, the tasks are distributed among the activated stations as evenly as possible, but some activated stations, especially right-side station 1 and left-side station 5, have more idle time, resulting in a lower utilization rate. One reason for this situation is that the balanced disassembly order of tasks is disrupted by the hazardous parts with disassembly priority. Taking part 38 for example, it is hazardous and it can be distributed either side of the line. In order to minimize the hazard index, it is assigned to right-side station 5, resulting in 658 s of waiting time in right-side station 5 and 242 s of idle time in left-side station 5. If part 38 can be distributed on left-side station 5, the waiting time will not be generated, and the idle time in left-side station 5 will decrease from 242 s to 2 s. Furthermore, right-side station 5 does not need to be opened. As a result, the disassembly efficiency is further improved, and the disassembly costs are also reduced. So, on the premise of ensuring environmental protection and worker health, if the sequences of some hazardous parts are appropriately adjusted, the disassembly line will be more balanced. From the above analysis, it can be concluded that optimizing the sequence and assignment of tasks is crucial in the process of disassembling EOL products. This not only affects the efficiency of the disassembly line but also influences other disassembly indicators such as the degree of environmental hazard and disassembly profit.

5. Conclusions

For the partial disassembly of large-sized EOL products on two-sided disassembly lines, a mathematical model for the two-sided disassembly line balancing problem under partial disassembly of parts is constructed, considering environmental, economic, and efficiency perspectives. An improved discrete whale optimization algorithm is proposed to solve this problem. In order to improve search efficiency, some effective methods and strategies are designed in the search phases of the proposed algorithm, such as a simple and effective representation method for feasible solutions and efficient neighbor structures. The performance of the proposed IDWOA is validated by a real case and three different types of instances. The results indicate that the proposed algorithm can not only be applied to various types of DLBPs but also exhibits excellent performance in solving these problems. Furthermore, through analyzing the task assignment of the optimal disassembly scheme, it can be found that reasonable sequencing and assignment of tasks can help to reduce harm to the environment, improve disassembly efficiency, and increase profit.

Since some parts may interfere with each other in the disassembly process, the most efficient disassembly operations cannot be used by workers to disassemble these parts. The disassembly time will increase due to additional operations. Therefore, considering the interactions among tasks in the disassembly process will be a direction for future research. In addition, for existing disassembly lines, the disassembly machinery and equipment are fixed. To improve disassembly efficiency, it is necessary to minimize the cycle time to increase the number of disassembled EOL products per unit time. Thus, the DLBP with a fixed number of workstations is another promising direction for future work.