Existence of Mild Solutions for the Generalized Anti-Periodic Boundary Value Problem to the Fractional Hybird Differential Equations with p(t)-Laplacian Operator
Abstract
1. Introduction
- •
- When , the -Laplacian operator under study becomes the classical p-Laplacian operator with constant coefficients. Similarly, when , the generalized Caputo fractional derivative becomes the classical Caputo derivative. Therefore, the existence results obtained in this paper extend the conclusions corresponding to those in reference [24].
- •
- Since the -Laplacian operator is an operator with non-standard growth, when we apply the Schaefer fixed point theorem to prove the existence of mild solutions, we need to construct a bounded convex closed set, which is somewhat difficult.
- •
- As far as we know, in the study of the BVP of fractional mixed differential equations with -Laplacian operators, the fractional derivatives usually adopted are Caputo derivatives (see [15]) or Riemann–Liouville derivatives (see [16]), while the application of generalized Caputo derivatives is still rare. Therefore, in a certain sense, this article enriches the research results of this type of issue.
2. Materials and Methods
3. Results
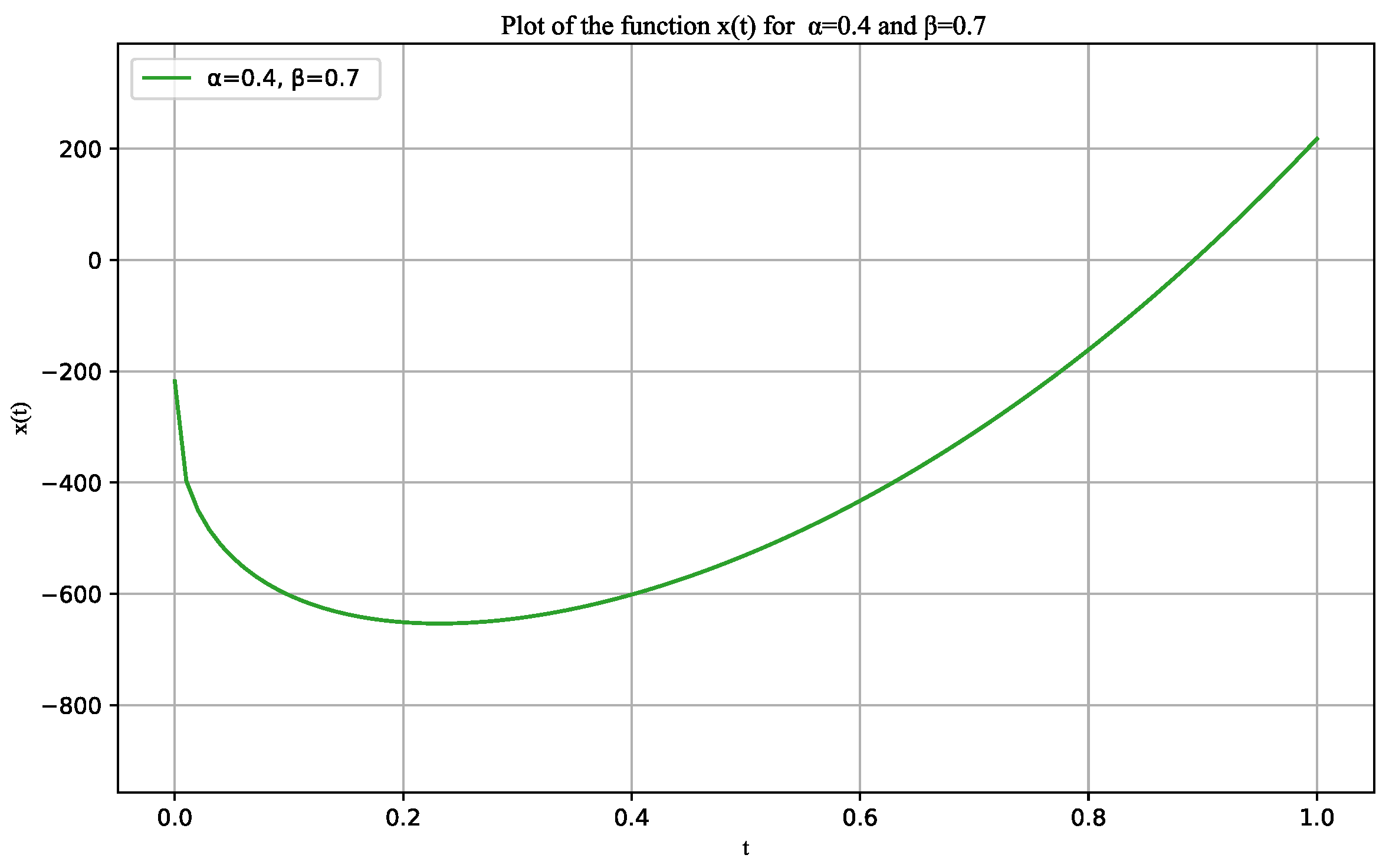
4. An Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, Z.; Nia, S.N.; Rabiei, F.; Shah, K.; Tan, M.K. A Semianalytical approach to the solution of time-fractional Navier-Stokes equation. Adv. Math. Phys. 2021, 2021, 5547804. [Google Scholar] [CrossRef]
- Ali, Z.; Rabiei, F.; Rashidi, M.M.; Khodadadi, T. A fractional-order mathematical model for COVID-19 outbreak with the effect of symptomatic and asymptomatic transmissions. Eur. Phys. J. Plus 2022, 137, 395. [Google Scholar] [CrossRef]
- Xu, K.; Chen, L.; Lopes, A.M.; Wang, M.; Wu, R.; Zhu, M. Fractional-order Zener model with temperature-order equivalence for viscoelastic dampers. Fractal Fract. 2023, 7, 714. [Google Scholar] [CrossRef]
- Abdel-Aty, A.H.; Khater, M.M.; Baleanu, M.M.; Abo-Dahab, S.M.; Bouslimi, J.; Omri, M. Oblique explicit wave solutions of the fractional biological population (BP) and equal width (EW) models. Adv. Differ. Equ. 2020, 2020, 552. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Zhou, Y. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2023. [Google Scholar]
- Ahmad, B.; Ntouyas, S.K.; Tariboon, J. A nonlocal hybrid boundary value problem of Caputo fractional integro-differential equations. Acta Math. Sci. 2016, 36, 1631–1640. [Google Scholar] [CrossRef]
- Fazli, H.; Nieto, J.J. Fractional Langevin equation with anti-periodic boundary conditions. Chaos Solitons Fractals 2018, 114, 332–337. [Google Scholar] [CrossRef]
- Baleanu, D.; Etemad, S.; Rezapour, S. On a fractional hybrid integro-differential equation with mixed hybrid integral boundary value conditions by using three operators. Alex. Eng. J. 2020, 59, 3019–3027. [Google Scholar] [CrossRef]
- Song, S.; Cui, Y. Existence of solutions for integral boundary value problems of mixed fractional differential equations under resonance. Bound. Value Probl. 2020, 2020, 23. [Google Scholar] [CrossRef]
- Abbas, M.I.; Alessandra Ragusa, M. Solvability of Langevin equations with two Hadamard fractional derivatives via Mittag-Leffler functions. Appl. Anal. 2022, 101, 3231–3245. [Google Scholar] [CrossRef]
- Fan, X.L.; Fan, X. A Knobloch-type result for p(t)-Laplacian systems. J. Math. Anal. Appl. 2003, 282, 453–464. [Google Scholar] [CrossRef]
- Xue, T.; Liu, W.; Shen, T. Existence of solutions for fractional Sturm-Liouville boundary value problems with p(t)-Laplacian operator. Bound. Value Probl. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Tang, X.; Wang, X.; Wang, Z.; Ouyang, P. The existence of solutions for mixed fractional resonant boundary value problem with p(t)-Laplacian operator. J. Appl. Math. Comput. 2019, 61, 559–572. [Google Scholar] [CrossRef]
- Lakoud, A.G.; Ashyralyev, A. Existence of Solutions for Weighted p(t)-Laplacian Mixed Caputo Fractional Dierential Equations at Resonance. Filomat 2022, 36, 231–241. [Google Scholar]
- Xue, T.; Fan, X.; Cao, H.; Fu, L. A periodic boundary value problem of fractional differential equation involving p(t)-Laplacian operator. Math. Biosci. Eng 2023, 20, 4421–4436. [Google Scholar] [CrossRef] [PubMed]
- Sun, B. Existence of solutions for nonlinear problems involving mixed fractional derivatives with p(x)-Laplacian operator. Demonstr. Math. 2024, 57, 20240045. [Google Scholar] [CrossRef]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef]
- Almeida, R. Functional differential equations involving the ψ-Caputo fractional derivative. Fractal Fract. 2020, 4, 29. [Google Scholar] [CrossRef]
- Ali, G.; Khan, R.U.; Kamran; Aloqaily, A.; Mlaiki, N. On qualitative analysis of a fractional hybrid Langevin differential equation with novel boundary conditions. Bound. Value Probl. 2024, 2024, 62. [Google Scholar] [CrossRef]
- Awad, Y. On the Existence and Stability of Positive Solutions of Eigenvalue Problems for a Class of p-Laplacian ψ-Caputo Fractional Integro-Differential Equations. J. Math. 2023, 2023, 3458858. [Google Scholar] [CrossRef]
- Al-Mazmumy, M.; Alyami, M.A.; Alsulami, M.; Alsulami, A.S. Reliable computational method for systems of fractional differential equations endowed with ψ-Caputo fractional derivative. Contemp. Math. 2024, 5, 4991–5011. [Google Scholar] [CrossRef]
- Poovarasan, R.; Govindaraj, V. Existence of Solutions for a Coupled System of ψ-Caputo Fractional Differential Equations with Integral Boundary Conditions. Math. Methods Appl. Sci. 2025, 48, 9456–9468. [Google Scholar] [CrossRef]
- Chen, T.; Liu, W. An anti-periodic boundary value problem for the fractional differential equation with a p-Laplacian operator. Appl. Math. Lett. 2012, 25, 1671–1675. [Google Scholar] [CrossRef]
- Zhang, Q. Existence of solutions for weighted p(r)-Laplacian system boundary value problems. J. Math. Anal. Appl. 2007, 327, 127–141. [Google Scholar] [CrossRef]
- Schaefer, H.H. Über die Methode der a priori-Schranken. Math. Ann. 1955, 129, 415–416. [Google Scholar] [CrossRef]
- Schaefer, H.H.; Wolff, M.P. Topological Vector Spaces, 2nd ed.; Springer: New York, NY, USA, 1999. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Jiang, G.; Shen, T. Existence of Mild Solutions for the Generalized Anti-Periodic Boundary Value Problem to the Fractional Hybird Differential Equations with p(t)-Laplacian Operator. Symmetry 2025, 17, 1569. https://doi.org/10.3390/sym17091569
Liu J, Jiang G, Shen T. Existence of Mild Solutions for the Generalized Anti-Periodic Boundary Value Problem to the Fractional Hybird Differential Equations with p(t)-Laplacian Operator. Symmetry. 2025; 17(9):1569. https://doi.org/10.3390/sym17091569
Chicago/Turabian StyleLiu, Jinxiu, Guanghao Jiang, and Tengfei Shen. 2025. "Existence of Mild Solutions for the Generalized Anti-Periodic Boundary Value Problem to the Fractional Hybird Differential Equations with p(t)-Laplacian Operator" Symmetry 17, no. 9: 1569. https://doi.org/10.3390/sym17091569
APA StyleLiu, J., Jiang, G., & Shen, T. (2025). Existence of Mild Solutions for the Generalized Anti-Periodic Boundary Value Problem to the Fractional Hybird Differential Equations with p(t)-Laplacian Operator. Symmetry, 17(9), 1569. https://doi.org/10.3390/sym17091569





