Formation of Periodic Mosaic Structures Using Operations in Galois Fields
Abstract
1. Introduction
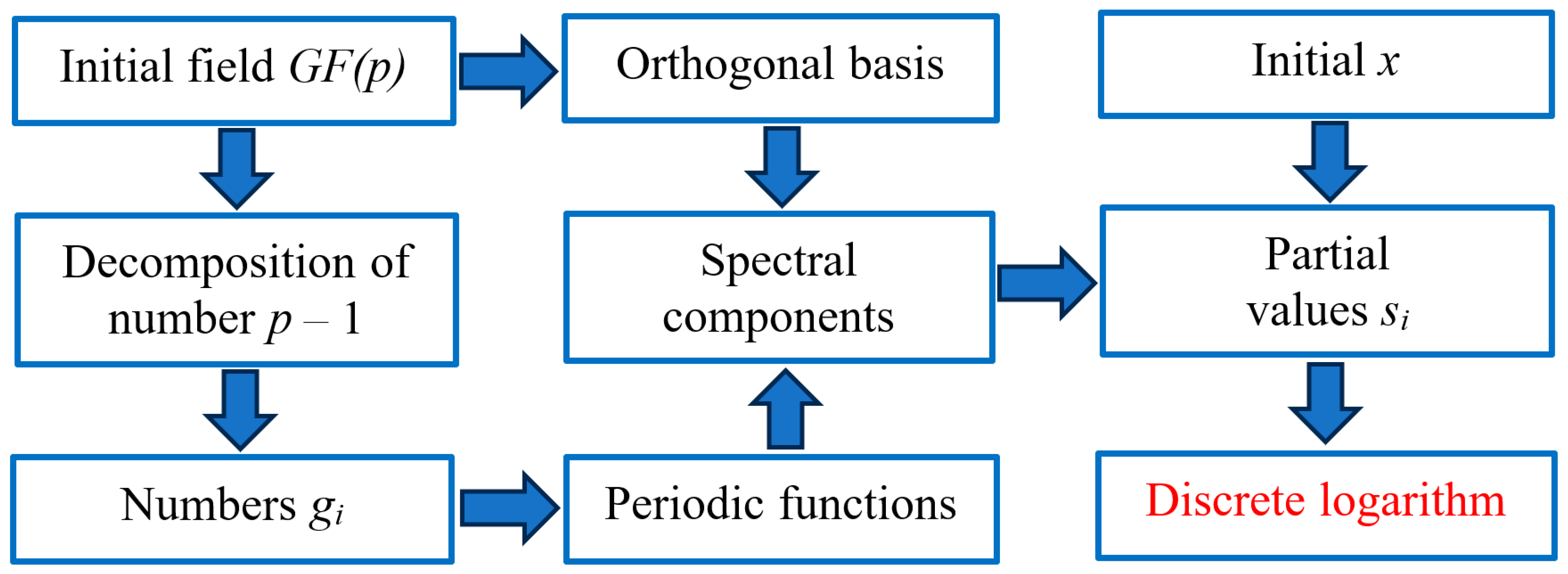
2. Methods
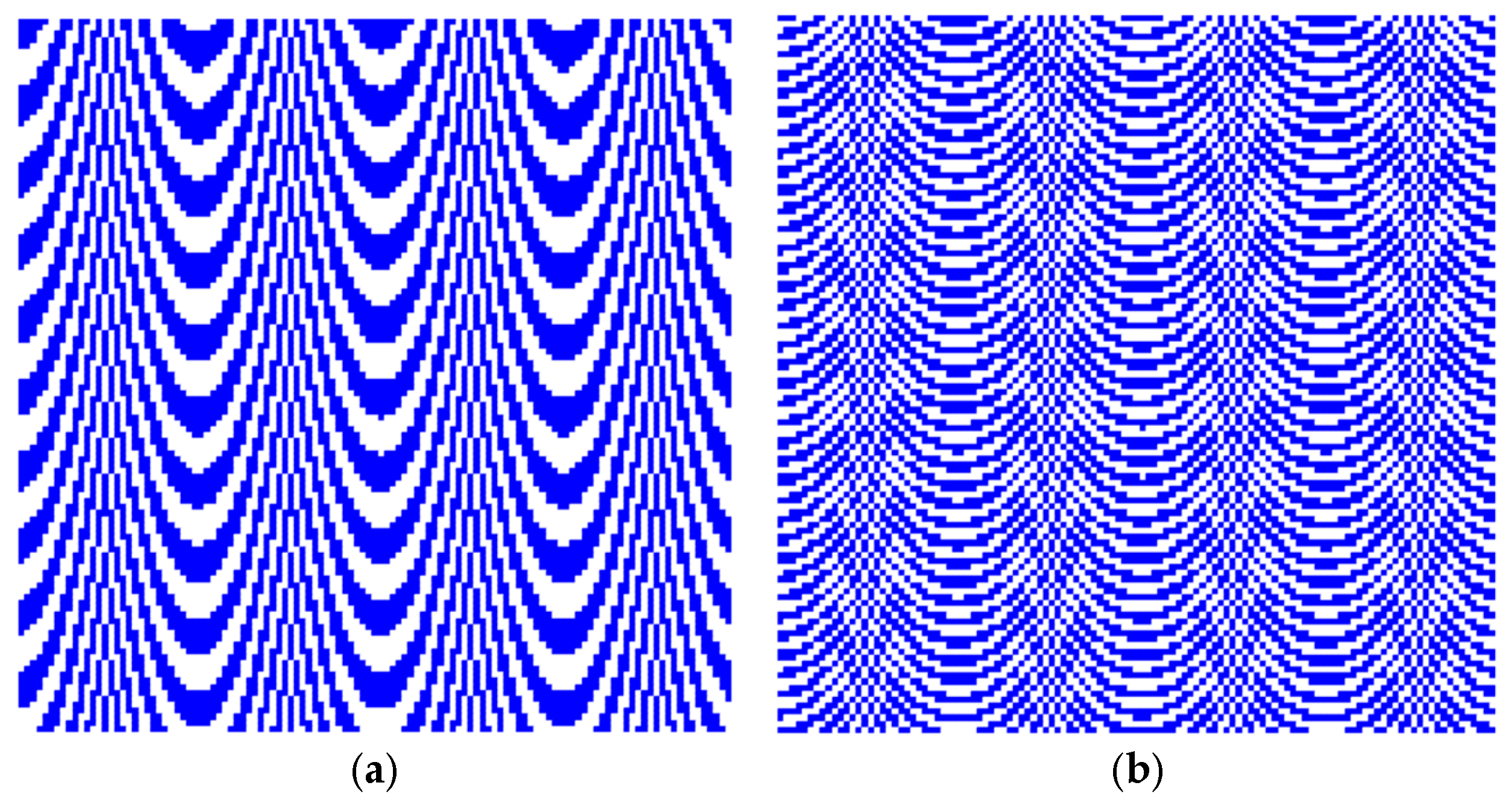
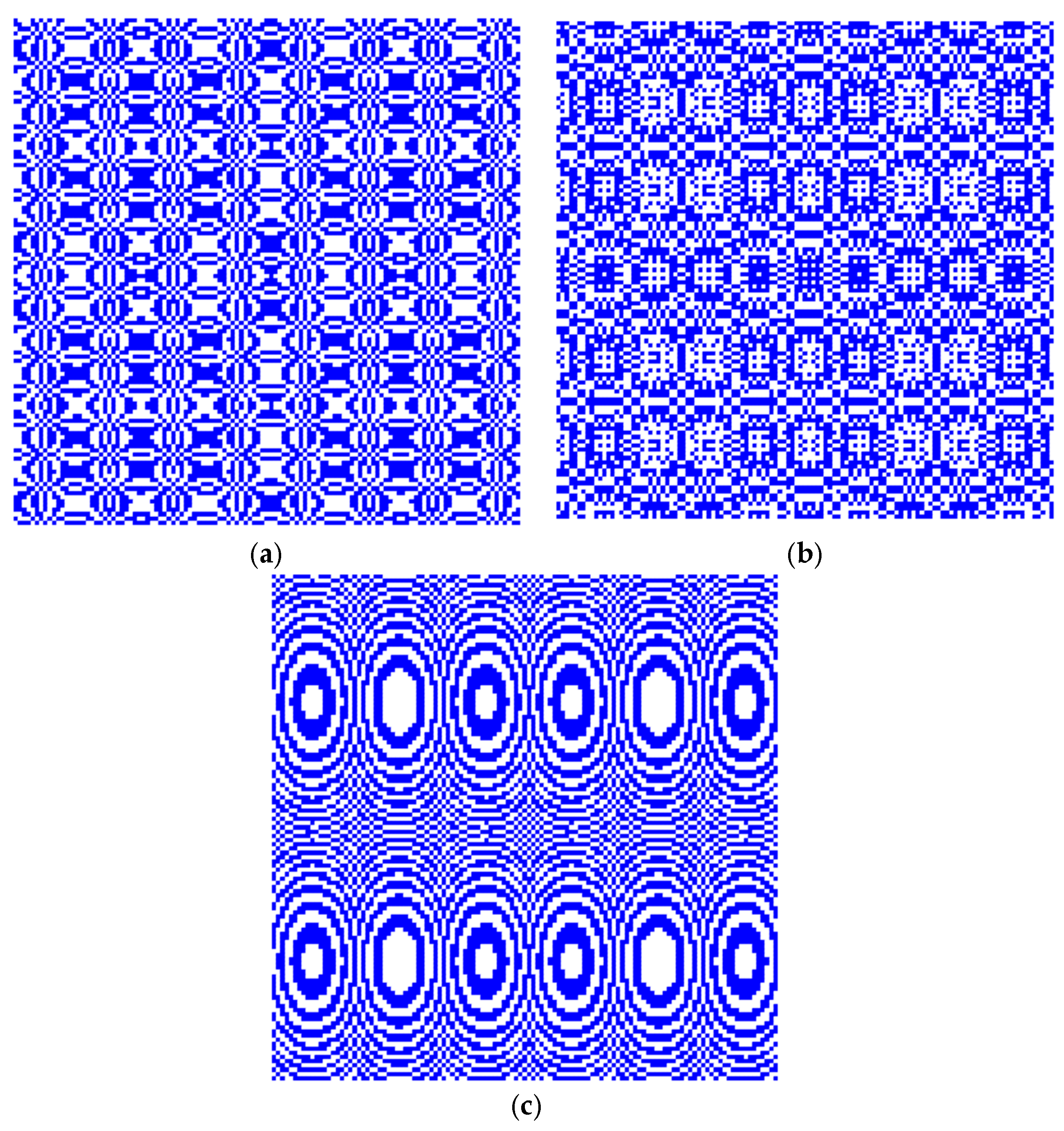
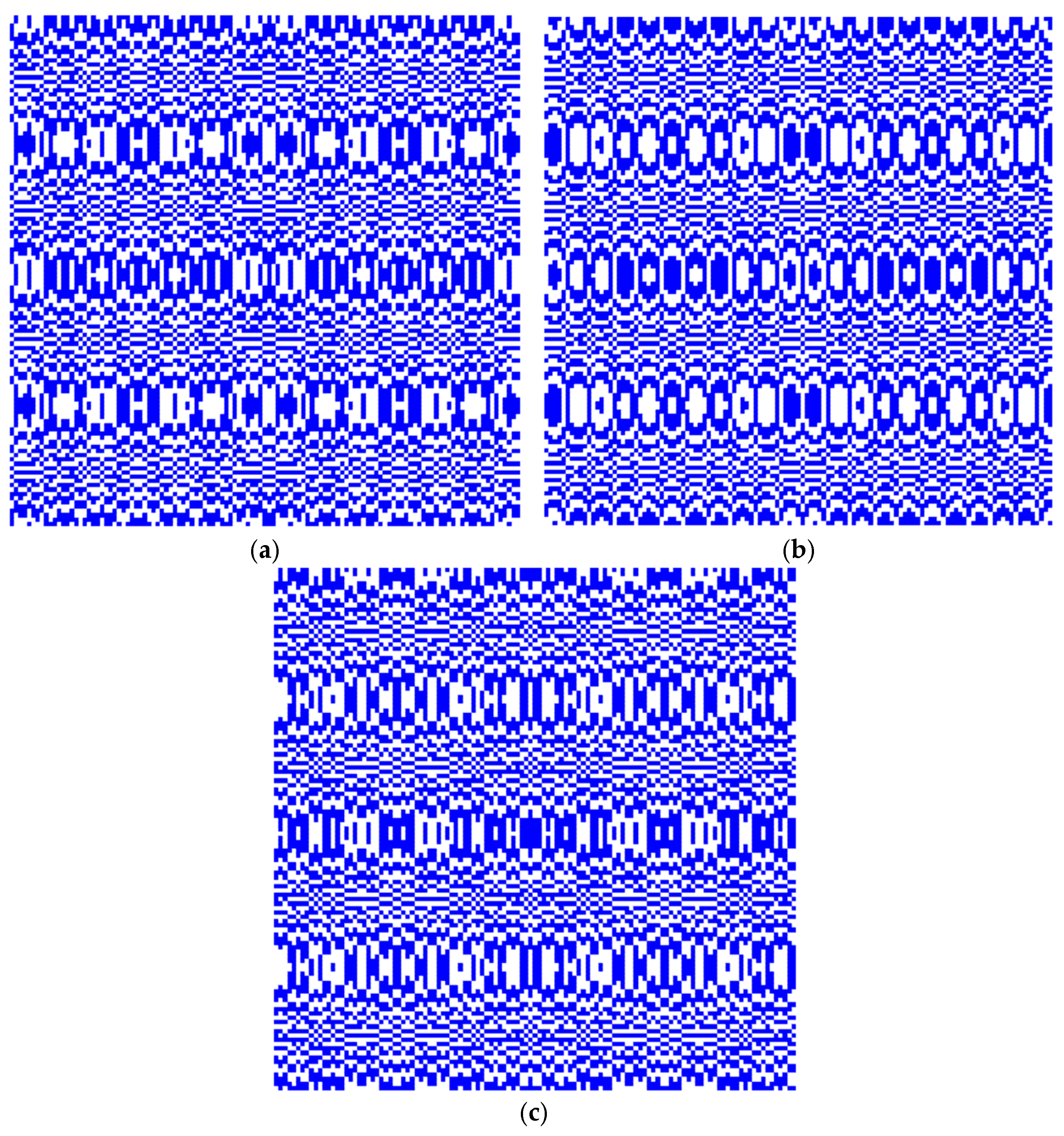
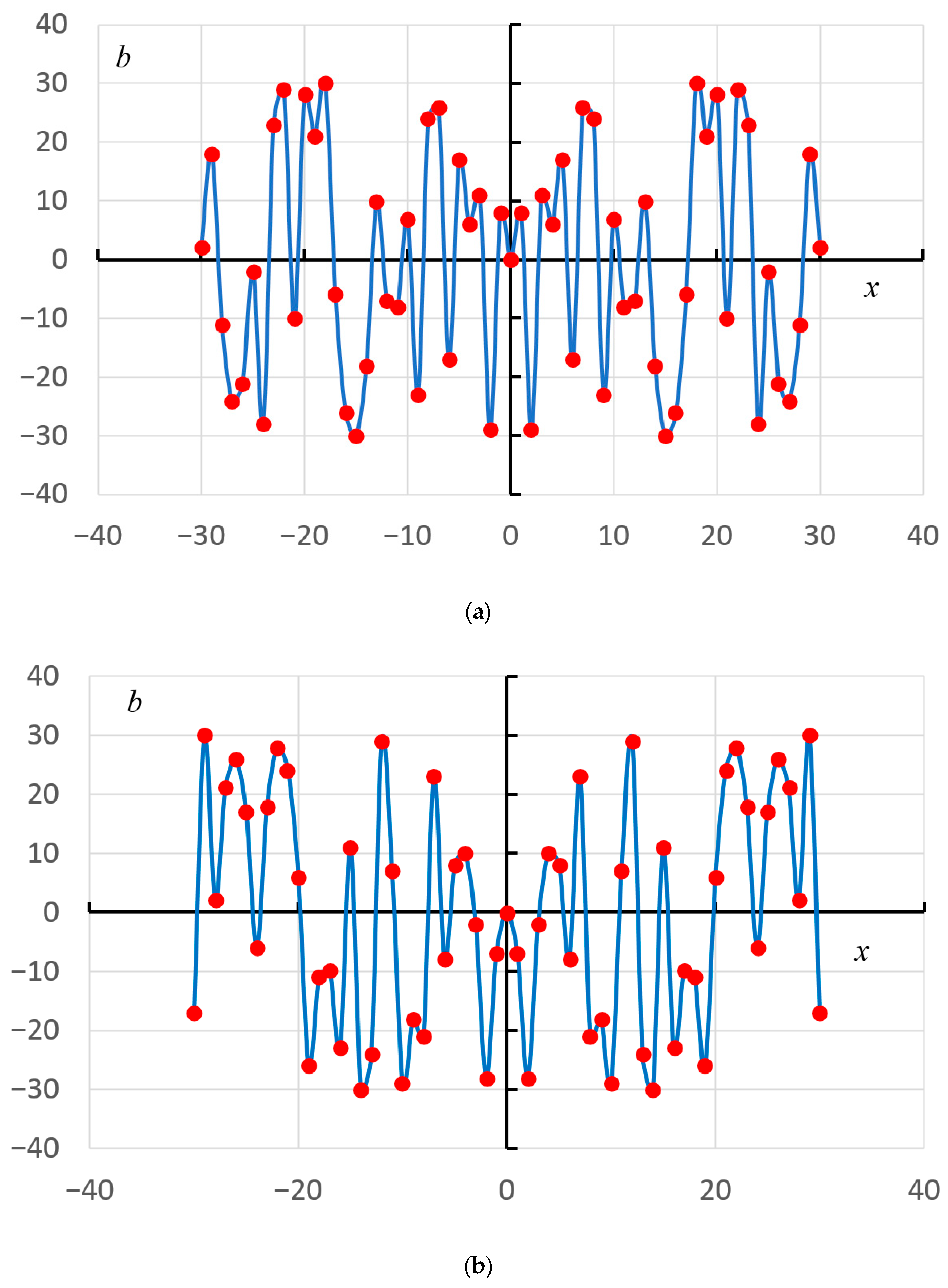
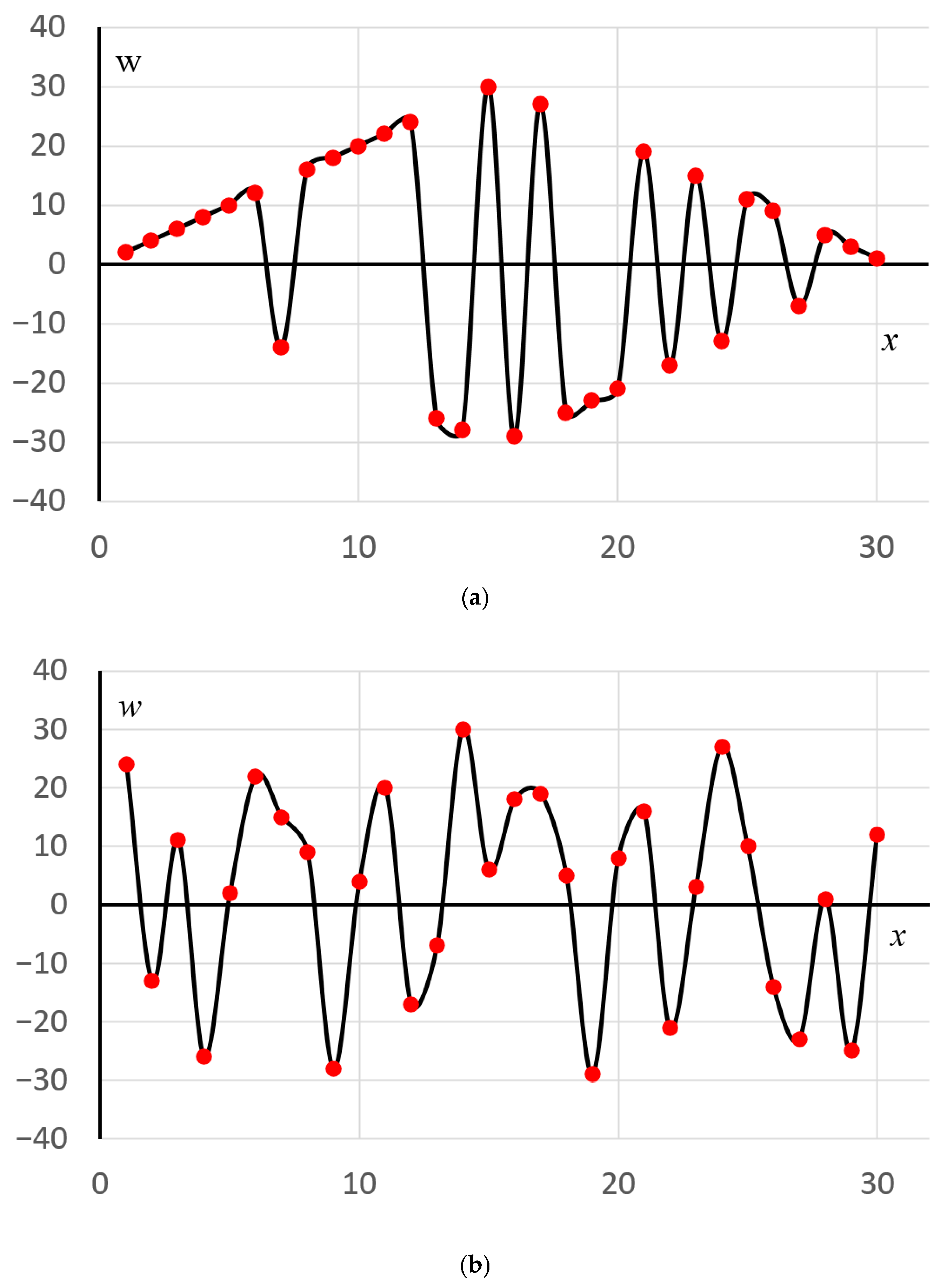
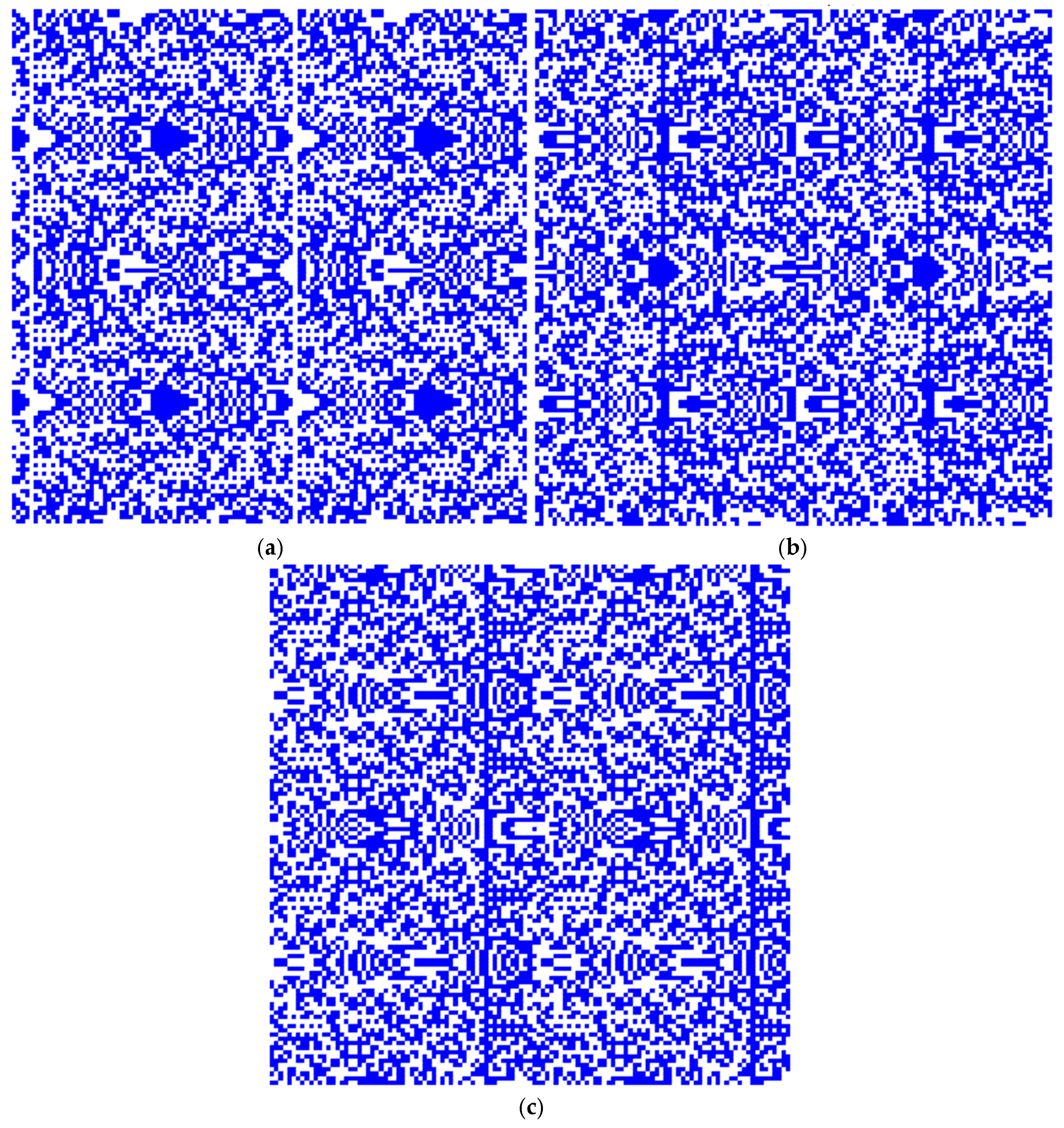
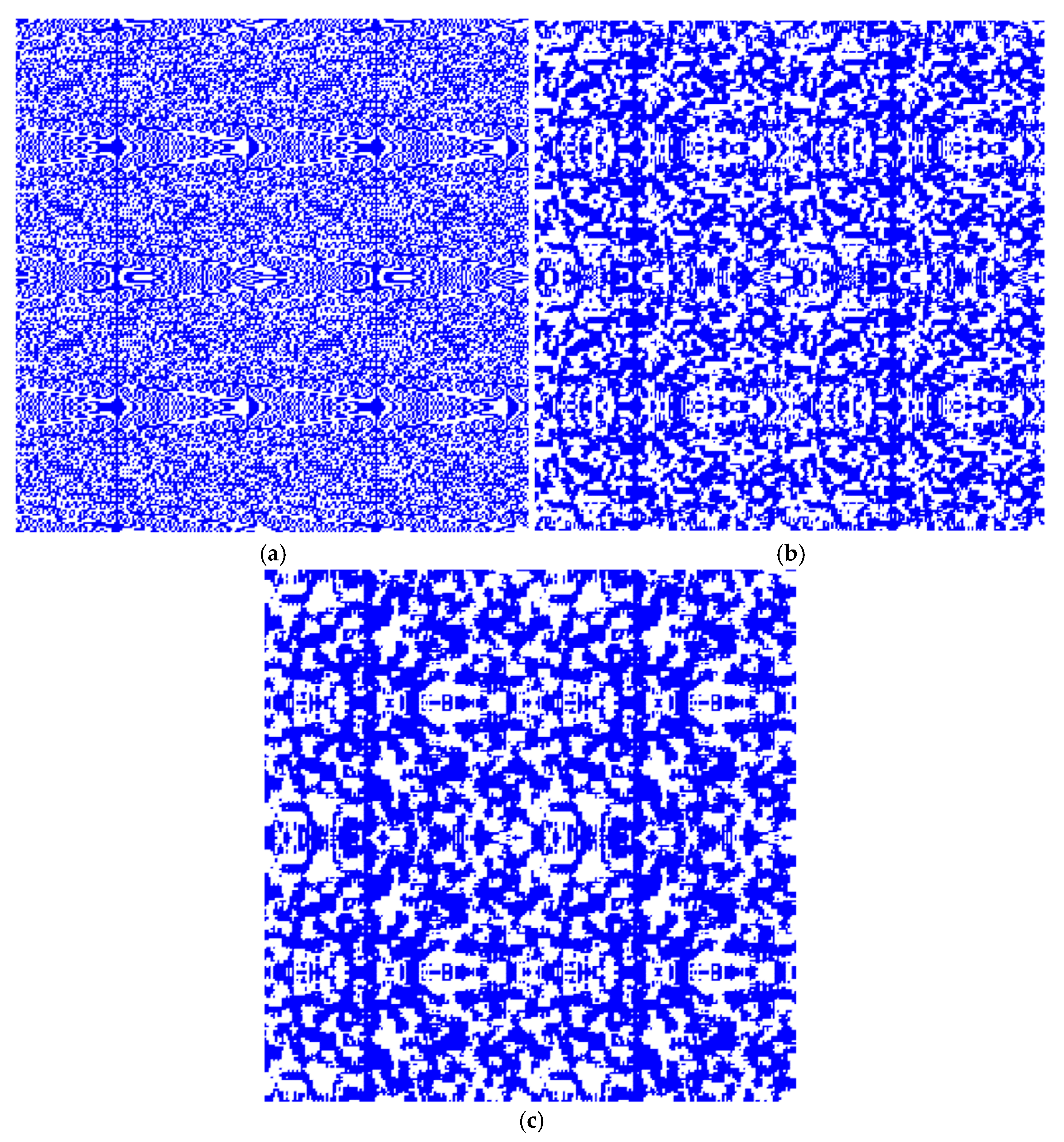
3. Results
4. Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pintus, R.; Pal, K.; Yang, Y.; Weyrich, T.; Gobbetti, E.; Rushmeier, H. A survey of geometric analysis in cultural heritage. Comput. Graph. Forum 2016, 35, 4–31. [Google Scholar] [CrossRef]
- Sobh, H.; Samy, H.A. Islamic geometric patterns as timeless architecture. J. Al-Azhar Univ. Eng. Sect. 2018, 13, 1074–1088. [Google Scholar] [CrossRef]
- Jebur, A.K. The techniques of cultural heritage: Literature review. Saudi J. Civ. Eng. 2022, 6, 108–114. [Google Scholar] [CrossRef]
- Jabi, W.; Potamianos, I. Geometry, light, and cosmology in the church of Hagia Sophia. Int. J. Archit. Comput. 2007, 5, 303–319. [Google Scholar] [CrossRef]
- Thalal, A.; Aboufadil, Y.; Elidrissi Raghni, M.A.; Jali, A.; Oueriagli, A.; Ait Rai, K. Symmetry in art and architecture of the Western Islamic world. Crystallogr. Rev. 2018, 24, 102–130. [Google Scholar] [CrossRef]
- Xu, P. The Mandala as a cosmic model used to systematically structure the Tibetan Buddhist Landscape. J. Archit. Plan. Res. 2010, 27, 181–203. [Google Scholar]
- Xiao, Y.-Q.; Kan, C.-W. Review on Development and Application of 3D-Printing Technology in Textile and Fashion Design. Coatings 2022, 12, 267. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, S. Textile-Based 3D Printing and Traditional Chinese Geometric Patterns for Fashion Textile Development. J. Text. Inst. 2024, 116, 2087–2099. [Google Scholar] [CrossRef]
- Arikan, C.O.; Doğan, S.; Muck, D. Geometric structures in textile design made with 3D printing. Tekstilec 2022, 65, 307–321. [Google Scholar] [CrossRef]
- Nilsson, L.; Vallgårda, A.; Worbin, L. Designing with Smart Textiles: A New Research Program. In Proceedings of the Nordes Making Design Matter, Helsinki, Finland, 29–31 May 2011. [Google Scholar]
- Matté, L.L.; Broega, A.C. The Evaluation of (Social-) Psychological Comfort in Clothing: A Possible Approach. IOP Conf. Ser. Mater. Sci. Eng. 2017, 254, 182008. [Google Scholar] [CrossRef]
- Stylios, G.K.; Chen, M. The concept of psychotextiles; interactions between changing patterns and the human visual brain, by a novel composite SMART fabric. Materials 2020, 13, 725. [Google Scholar] [CrossRef]
- Zeng, F.; Wang, G.; Qiao, J.; Wang, Q.; Wu, M.; Zeng, X.; Hong, X. Modeling the Relationship between Fabric Textures and the Evoked Emotions through Different Sensory Perceptions. J. Eng. Fibers Fabr. 2024, 19, 15589250241248761. [Google Scholar] [CrossRef]
- de Melo, M.J. Mosaic as an Experimental System: Materials, Practices and Knowledges in Art and Science; University of Amsterdam: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Zhang, J.; Zhang, K.; Peng, R.; Yu, J. Parametric modeling and generation of mandala thangka patterns. J. Comput. Lang. 2020, 58, 100968. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Gabrielyan, O.A.; Bakirov, A.S. Neural network approach to the interpretation of ancient Chinese geomancy feng shui practices. Eur. J. Sci. Theol. 2023, 19, 39–51. [Google Scholar]
- Teixeira, T.G.B.; de Medeiros, J.F.; Kolling, C.; Duarte Ribeiro, J.L.; Morea, D. Redesign in the Textile Industry: Proposal of a Methodology for the Insertion of Circular Thinking in Product Development Processes. J. Clean. Prod. 2023, 397, 136588. [Google Scholar] [CrossRef]
- An, M.H.; Jang, A.R. Development of textile pattern design by MC Escher’s tessellation technique using chaekgeori icons. Fash Text 2023, 10, 15. [Google Scholar] [CrossRef]
- Liu, S. A Method for Image Mosaic of Textile Printing Fabric Based on SIFT Feature Matching. In Proceedings of the 6th International Conference on Management, Education, Information and Control (MEICI 2016), Shenyang, China, 23–25 September 2016; Atlantis Press: Dordrecht, The Netherlands, 2016; pp. 953–957. [Google Scholar]
- Kunkhet, A.; Chudasri, D. Design Approaches for Tile Pattern Designs Inspired by Traditional Textiles. Processes 2022, 10, 1460. [Google Scholar] [CrossRef]
- Massarwe, K.; Verner, I.; Bshouty, D.; Verner, I. An ethnomathematics exercise in analyzing and constructing ornaments in a geometry class. J. Math. Cult. 2010, 5, 1–20. [Google Scholar]
- Wang, W.; Zhang, G.; Yang, L.; Wang, W. Research on garment pattern design based on fractal graphics. J. Image Video Proc. 2019, 2029, 29. [Google Scholar] [CrossRef]
- Furrer, W. Psychiatric test methods, especially the Lüscher color test. Ther. Present 1967, 106, 1290–1300. [Google Scholar]
- Borstelmann, L.J.; Klopfer, W.G. The Szondi Test: A review and critical evaluation. Psychol. Bull. 1953, 50, 12. [Google Scholar] [CrossRef]
- Mayall, K.; Dellinger, S. Your Personal Communication Style (Parenting Shape eBook) (Kindle Edition); Jade Ink: Oakland, CA, USA, 1953. [Google Scholar]
- Paluchowski, W.J.; Stemplewska-Żakowicz, K. The reliability of projective techniques as tools of psychological assessment. Part 1: Why it is unjustified to describe some of them as projective. Probl. Forensic Sci. 2013, 93, 421–430. [Google Scholar]
- Suleimenov, I.; Kostsova, M.; Grishina, A.; Matrassulova, D.; Vitulyova, Y. Empirical validation of the use of projective techniques in psychological testing using Galois fields. Front. Appl. Math. Stat. 2024, 10, 1455500. [Google Scholar] [CrossRef]
- Pianowski, G.; Villemor-Amaral, A.E.D.; Meyer, G.J. Comparing the validity of the Rorschach Performance Assessment System and Exner’s Comprehensive System to differentiate patients and nonpatients. Assessment 2023, 30, 2417–2432. [Google Scholar] [CrossRef]
- Khadivi, A. Review of a Special Issue of Rorschachiana: The Rorschach Test Today: An Update on the Research. J. Personal. Assess. 2023, 105, 578–579. [Google Scholar] [CrossRef]
- Bhaskar, R.; Dubey, P.K.; Kumar, V.; Rudra, A. Efficient Galois field arithmetic on SIMD architectures. In Proceedings of the 15th Annual ACM Symposium on Parallel Algorithms and Architectures (SPAA’03), San Diego, CA, USA, 7–9 June 2003; pp. 256–257. [Google Scholar] [CrossRef]
- Vitulyova, Y.S.; Bakirov, A.S.; Suleimenov, I.E. Galois fields for digital image and signal processing: Evidence for the importance of field specificity. In Proceedings of the 5th International Conference on Pattern Recognition and Artificial Intelligence (PRAI), Chengdu, China, 19–21 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 637–642. [Google Scholar]
- Kuang, R.; Perepechaenko, M.; Barbeau, M. A new quantum-safe multivariate polynomial public key digital signature algorithm. Sci. Rep. 2022, 12, 13168. [Google Scholar] [CrossRef]
- Thi, H.P.; Lee, H. Basic-Set Trellis Min–Max Decoder Architecture for Nonbinary LDPC Codes with High-Order Galois Fields. In IEEE Transactions on Very Large Scale Integration (VLSI) Systems; IEEE: Piscataway, NJ, USA, 2018; Volume 26, pp. 496–507. [Google Scholar] [CrossRef]
- Alinejad, M.; Hassan Zadeh, S.; Biranvand, N. Digital Signature with Elliptic Curves over the Finite Fields. J. Discret. Math. Sci. Cryptogr. 2022, 25, 1289–1301. [Google Scholar] [CrossRef]
- Larasati, H.T.; Kim, H. Quantum cryptanalysis landscape of shor’s algorithm for elliptic curve discrete logarithm problem. In International Conference on Information Security Applications; Springer: Cham, Switzerland, 2021; pp. 91–104. [Google Scholar]
- O’Keeffe, M.; Treacy, M.M.J. The Symmetry and Topology of Finite and Periodic Graphs and Their Embeddings in Three-Dimensional Euclidean Space. Symmetry 2022, 14, 822. [Google Scholar] [CrossRef]
- Evans, M.E.; Robins, V.; Hyde, S.T. Ideal geometry of periodic entanglements. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150254. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Vitulyova, Y.S.; Kabdushev, S.B.; Bakirov, A.S. Improving the efficiency of using multivalued logic tools. Sci. Rep. 2023, 13, 1108. [Google Scholar] [CrossRef]
- Odlyzko, A. Discrete Logarithms: The Past and the Future. Des. Codes Cryptogr. 2000, 19, 129–145. [Google Scholar] [CrossRef]
- Sarkar, A.; Guha Roy, D.; Datta, P. An Overview of the Discrete Logarithm Problem in Cryptography. In Proceedings of Third International Conference on Advanced Computing and Applications; ICACA 2024; Lecture Notes in Networks and Systems; Giri, D., Das, S., Corchado Rodríguez, J.M., De, D., Eds.; Springer: Singapore, 2024; Volume 1045. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Merembayev, T.; Kuchin, Y.; Malakhov, D.; Zaitseva, E.; Levashenko, V.; Popova, Y.; Symagulov, A.; Sagatdinova, G.; Amirgaliyev, Y. Soil Salinity Estimation for South Kazakhstan Based on SAR Sentinel-1 and Landsat-8,9 OLI Data with Machine Learning Models. Remote Sens. 2023, 15, 4269. [Google Scholar] [CrossRef]
- Atzberger, C. Advances in Remote Sensing of Agriculture: Context Description, Existing Operational Monitoring Systems and Major Information Needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Terekhov, A.; Amirgaliyev, Y.; Popova, Y.; Malakhov, D.; Kuchin, Y.; Sagatdinova, G.; Symagulov, A.; Muhamedijeva, E.; Gricenko, P. Using Pseudo-Color Maps and Machine Learning Methods to Estimate Long-Term Salinity of Soils. Agronomy 2024, 14, 2103. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Bakirov, A.S.; Matrassulova, D.K. A technique for analyzing neural networks in terms of ternary logic. J. Theor. Appl. Inf. Technol. 2021, 99, 2537–2553. [Google Scholar]
- van der Waerden, B.L. Algebra; Springer-Verlag New York, Inc.: New York, NY, USA, 1991; Volume 1, 265p. [Google Scholar]
- Tudunkaya, S.M.; Kiri, A.I. Galois groups of polynomials and the construction of finite fields. Pure Appl. Math. J. 2012, 1, 10–16. [Google Scholar] [CrossRef][Green Version]
- Kim, K.-S.; König, J. On Galois extensions with prescribed decomposition groups. J. Number Theory 2021, 220, 266–294. [Google Scholar] [CrossRef]
- Vitulyova, E.S.; Matrassulova, D.K.; Suleimenov, I.E. Construction of generalized Rademacher functions in terms of ternary logic: Solving the problem of visibility of using Galois fields for digital signal processing. Int. J. Electron. Telecommun. 2022, 68, 237–244. [Google Scholar] [CrossRef]
- Adj, G.; Menezes, A.; Oliveira, T.; Rodriguez-Henriquez, F. Computing discrete logarithms using Joux’s algorithm. ACM Commun. Comput. Algebra 2015, 49, 60. [Google Scholar] [CrossRef]
- Galbraith, S.D.; Wang, P.; Zhang, F. Computing Elliptic Curve Discrete Logarithms with Improved Baby-Step Giant-Step Algorithm; Cryptology ePrint Archive; American Institute of Mathematical Sciences: Springfield, MI, USA, 2015. [Google Scholar]
- Rubinstein-Salzedo, S. The Diffie–Hellman key exchange and the discrete logarithm problem. In Cryptography; Springer International Publishing: Cham, Switzerland, 2018; pp. 99–112. [Google Scholar]
- Pohlig, S.C.; Hellman, M.E. An improved algorithm for computing logarithms over GF (p) and its cryptographic significance. In Democratizing Cryptography: The Work of Whitfield Diffie and Martin Hellman; Association for Computing Machinery: New York, NY, USA, 2022; pp. 415–430. [Google Scholar]
- Lin, K.; Wang, W.; Wang, L.; Zhao, C.A. An alternative approach for computing discrete logarithms in compressed SIDH. arXiv 2021, arXiv:2111.10226. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for Quantum Computation: Discrete Logarithms and Factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science (FOCS’94), Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Ekerå, M. Revisiting Shor’s quantum algorithm for computing general discrete logarithms. arXiv 2019, arXiv:1905.09084. [Google Scholar]
- Kadyrzhan, K.; Kaldybekov, D.; Baipakbaeva, S.; Vitulyova, Y.; Matrassulova, D.; Suleimenov, I. Electronic Fourier–Galois Spectrum Analyzer for the Field GF(31). Appl. Sci. 2024, 14, 7770. [Google Scholar] [CrossRef]
- Suleimenov, I.; Kadyrzhan, A.; Matrassulova, D.; Vitulyova, Y. Peculiarities of Applying Partial Convolutions to the Computation of Reduced Numerical Convolutions. Appl. Sci. 2024, 14, 2076–3417. [Google Scholar] [CrossRef]
- Areh, I.; Verkampt, F.; Allan, A. Critical review of the use of the Rorschach in European courts. Psychiatry Psychol. Law. 2022, 29, 183–205. [Google Scholar] [CrossRef]
- Bakirov, A.; Matrassulova, D.; Vitulyova, Y.; Shaltykova, D.; Suleimenov, I. The specifics of the Galois field GF (257) and its use for digital signal processing. Sci. Rep. 2024, 14, 15376. [Google Scholar] [CrossRef]
- Suleimenov, I.E.; Vitulyova, Y.S.; Kabdushev, S.B.; Bakirov, A.S. Improving the Efficiency of Using Multivalued Logic Tools: Application of Algebraic Rings. Sci. Rep. 2023, 13, 22021. [Google Scholar] [CrossRef]
- Vitulyova, Y.; Kadyrzhan, K.; Kadyrzhan, A.; Shaltykova, D.; Suleimenov, I. Reducing the description of arbitrary wave field converters to tensor form. Int. J. Inf. Technol. 2024, 17, 1–10. [Google Scholar] [CrossRef]
- Ivashov, S.I.; Capineri, L.; Bechtel, T.D.; Razevig, V.V.; Inagaki, M.; Gueorguiev, N.L.; Kizilay, A. Design and Applications of Multi-Frequency Holographic Subsurface Radar: Review and Case Histories. Remote Sens. 2021, 13, 3487. [Google Scholar] [CrossRef]
- SIvashov, I.; Razevig, V.V.; Vasiliev, I.A.; Zhuravlev, A.V.; Bechtel, T.D.; Capineri, L. Holographic Subsurface Radar of RASCAN Type: Development and Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 763–778. [Google Scholar] [CrossRef]
- Lombardi, F.; Lualdi, M. Step-Frequency Ground Penetrating Radar for Agricultural Soil Morphology Characterisation. Remote Sens. 2019, 11, 1075. [Google Scholar] [CrossRef]






| −11 | 13 | -3 | 2 | 1 |
| −1 | −14 | 9 | 4 | 2 |
| 11 | 1 | −27 | 8 | 3 |
| 1 | 13 | 20 | 16 | 4 |
| −11 | −14 | 1 | −29 | 5 |
| −1 | 1 | −3 | 3 | 6 |
| 11 | 13 | 9 | 6 | 7 |
| 1 | −14 | −27 | 12 | 8 |
| −11 | 1 | 20 | 24 | 9 |
| −1 | 13 | 1 | −13 | 10 |
| 11 | −14 | −3 | −26 | 11 |
| 1 | 1 | 9 | 9 | 12 |
| −11 | 13 | −27 | 18 | 13 |
| −1 | −14 | 20 | −25 | 14 |
| 11 | 1 | 1 | 11 | 15 |
| 1 | 13 | −3 | 22 | 16 |
| −11 | −14 | 9 | −17 | 17 |
| −1 | 1 | −27 | 27 | 18 |
| 11 | 13 | 20 | −7 | 19 |
| 1 | −14 | 1 | −14 | 20 |
| −11 | 1 | −3 | −28 | 21 |
| −1 | 13 | 9 | 5 | 22 |
| 11 | −14 | −27 | 10 | 23 |
| 1 | 1 | 20 | 20 | 24 |
| −11 | 13 | 1 | −21 | 25 |
| −1 | −14 | −3 | 19 | 26 |
| 11 | 1 | 9 | −23 | 27 |
| 1 | 13 | −27 | 15 | 28 |
| −11 | −14 | 20 | 30 | 29 |
| −1 | 1 | 1 | −1 | 30 |
| 11 | 13 | −3 | −2 | 31 |
| 1 | −14 | 9 | −4 | 32 |
| −11 | 1 | −27 | −8 | 33 |
| −1 | 13 | 20 | −16 | 34 |
| 11 | −14 | 1 | 29 | 35 |
| 1 | 1 | −3 | −3 | 36 |
| −11 | 13 | 9 | −6 | 37 |
| −1 | −14 | −27 | −12 | 38 |
| 11 | 1 | 20 | −24 | 39 |
| 1 | 13 | 1 | 13 | 40 |
| −11 | −14 | −3 | 26 | 41 |
| −1 | 1 | 9 | −9 | 42 |
| 11 | 13 | −27 | −18 | 43 |
| 1 | −14 | 20 | 25 | 44 |
| −11 | 1 | 1 | −11 | 45 |
| −1 | 13 | −3 | −22 | 46 |
| 11 | −14 | 9 | 17 | 47 |
| 1 | 1 | −27 | −27 | 48 |
| −11 | 13 | 20 | 7 | 49 |
| −1 | −14 | 1 | 14 | 50 |
| 11 | 1 | −3 | 28 | 51 |
| 1 | 13 | 9 | −5 | 52 |
| −11 | −14 | −27 | −10 | 53 |
| −1 | 1 | 20 | −20 | 54 |
| 11 | 13 | 1 | 21 | 55 |
| 1 | −14 | −3 | −19 | 56 |
| −11 | 1 | 9 | 23 | 57 |
| −1 | 13 | −27 | −15 | 58 |
| 11 | −14 | 20 | −30 | 59 |
| 1 | 1 | 1 | 1 | 60 |
| 1 | 1 | 1 | 2 | 1 | 0 | |
| 2 | 2 | 2 | 4 | 2 | 1 | |
| 3 | 0 | 3 | 8 | 3 | 1 | |
| 0 | 1 | 4 | 16 | 4 | 2 | |
| 1 | 2 | 0 | −29 | 5 | 2 | |
| 2 | 0 | 1 | 3 | 6 | 3 | |
| 3 | 1 | 2 | 6 | 7 | 3 | |
| 0 | 2 | 3 | 12 | 8 | 4 | |
| 1 | 0 | 4 | 24 | 9 | 4 | |
| 2 | 1 | 0 | −13 | 10 | 5 | |
| 3 | 2 | 1 | −26 | 11 | 5 | |
| 0 | 0 | 2 | 9 | 12 | 6 | |
| 1 | 1 | 3 | 18 | 13 | 6 | |
| 2 | 2 | 4 | −25 | 14 | 7 | |
| 3 | 0 | 0 | 11 | 15 | 7 | |
| 0 | 1 | 1 | 22 | 16 | 8 | |
| 1 | 2 | 2 | −17 | 17 | 8 | |
| 2 | 0 | 3 | 27 | 18 | 9 | |
| 3 | 1 | 4 | −7 | 19 | 9 | |
| 0 | 2 | 0 | −14 | 20 | 10 | |
| 1 | 0 | 1 | −28 | 21 | 10 | |
| 2 | 1 | 2 | 5 | 22 | 11 | |
| 3 | 2 | 3 | 10 | 23 | 11 | |
| 0 | 0 | 4 | 20 | 24 | 12 | |
| 1 | 1 | 0 | −21 | 25 | 12 | |
| 2 | 2 | 1 | 19 | 26 | 13 | |
| 3 | 0 | 2 | −23 | 27 | 13 | |
| 0 | 1 | 3 | 15 | 28 | 14 | |
| 1 | 2 | 4 | 30 | 29 | 14 | |
| 2 | 0 | 0 | −1 | 30 | 15 | |
| 3 | 1 | 1 | −2 | 31 | 15 | |
| 0 | 2 | 2 | −4 | 32 | 16 | |
| 1 | 0 | 3 | −8 | 33 | 16 | |
| 2 | 1 | 4 | −16 | 34 | 17 | |
| 3 | 2 | 0 | 29 | 35 | 17 | |
| 0 | 0 | 1 | −3 | 36 | 18 | |
| 1 | 1 | 2 | −6 | 37 | 18 | |
| 2 | 2 | 3 | −12 | 38 | 19 | |
| 3 | 0 | 4 | −24 | 39 | 19 | |
| 0 | 1 | 0 | 13 | 40 | 20 | |
| 1 | 2 | 1 | 26 | 41 | 20 | |
| 2 | 0 | 2 | −9 | 42 | 21 | |
| 3 | 1 | 3 | −18 | 43 | 21 | |
| 0 | 2 | 4 | 25 | 44 | 22 | |
| 1 | 0 | 0 | −11 | 45 | 22 | |
| 2 | 1 | 1 | −22 | 46 | 23 | |
| 3 | 2 | 2 | 17 | 47 | 23 | |
| 0 | 0 | 3 | −27 | 48 | 24 | |
| 1 | 1 | 4 | 7 | 49 | 24 | |
| 2 | 2 | 0 | 14 | 50 | 25 | |
| 3 | 0 | 1 | 28 | 51 | 25 | |
| 0 | 1 | 2 | −5 | 52 | 26 | |
| 1 | 2 | 3 | −10 | 53 | 26 | |
| 2 | 0 | 4 | −20 | 54 | 27 | |
| 3 | 1 | 0 | 21 | 55 | 27 | |
| 0 | 2 | 1 | −19 | 56 | 28 | |
| 1 | 0 | 2 | 23 | 57 | 28 | |
| 2 | 1 | 3 | −15 | 58 | 29 | |
| 3 | 2 | 4 | −30 | 59 | 29 | |
| 0 | 0 | 0 | 1 | 60 | 30 |
| Criterion | Proposed Approach | Previously Known Approaches |
|---|---|---|
| Mosaic periodicity | Periodicity arises automatically due to the properties of Galois fields, even for simple algebraic expressions | Periodicity must be imposed artificially, typically requiring a special algorithm [15,18,20] |
| Need for an initial pattern | Not required | An initial pattern is necessary [15,18,20] |
| Mosaic modification and control | Stepwise transitions between different types of mosaics are possible | Mechanisms for transitioning between patterns of different types are either not provided [15,20] or require direct operator intervention [18,19,22] |
| Implementation complexity | The code is extremely simple (example—SI-1); computations use only integers | Algorithm implementation involves computational complexities [19,21,22] or requires searching for the initial pattern [15,18,20] |
| Scalability/detail level | Details can be enhanced straightforwardly by increasing the field characteristic | Detail enhancement is possible, but operations required for it are comparable in complexity to generating a new mosaic [15,18,19,20,21] |
| Post-processing/complexity management | Simple smoothing (analogous to 3 × 3 or 5 × 5 moving window) helps reveal periodicity and reduce excessive complexity | The use of smoothing filters is not provided [15,18,20,21] |
| Limitations | Requires a simple modulus pp; special cases for pp of the form 2 m −1 (quasi-Mersenne primes), and the possibility to relax the requirement via finite rings | Limitations depend on the method (tiling rules, geometric/numerical constraints, etc.) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaltykova, D.; Vitulyova, Y.; Bakirov, A.S.; Suleimenov, I. Formation of Periodic Mosaic Structures Using Operations in Galois Fields. Symmetry 2025, 17, 1415. https://doi.org/10.3390/sym17091415
Shaltykova D, Vitulyova Y, Bakirov AS, Suleimenov I. Formation of Periodic Mosaic Structures Using Operations in Galois Fields. Symmetry. 2025; 17(9):1415. https://doi.org/10.3390/sym17091415
Chicago/Turabian StyleShaltykova, Dina, Yelizaveta Vitulyova, Akhat S. Bakirov, and Ibragim Suleimenov. 2025. "Formation of Periodic Mosaic Structures Using Operations in Galois Fields" Symmetry 17, no. 9: 1415. https://doi.org/10.3390/sym17091415
APA StyleShaltykova, D., Vitulyova, Y., Bakirov, A. S., & Suleimenov, I. (2025). Formation of Periodic Mosaic Structures Using Operations in Galois Fields. Symmetry, 17(9), 1415. https://doi.org/10.3390/sym17091415






